Constrained backorders inventory system with varying order cost: Lead time demand uniformly distributed

1 Introduction

Many authors including Feldman (1978), Richards (1975) and Sahin (1979) have studied continuous review inventory models with constant units of cost and stationary distributions of inventory level. The inventory models under continuous review with stationary distribution of inventory level, or inventory position in the case of positive lead-time, have been derived using renewal theory as in Arrow et al. (1958). In addition, Ben-Daya and Abdul (1994) examined unconstrained inventory model with constant units of cost, demand follows a normal distribution and the lead-time is one of the decision variables.

Taha (1997) treated unconstrained probabilistic inventory problems with constant units of cost. Hadley and Whitin (1963) discussed probabilistic continuous review inventory models with constant units of cost and the lead-time demand is a random variable. Their work gives heuristic approximate treatment for each of the backorders and the lost sales cases. Fabrycky and Banks (1967) studied the probabilistic single-item, single source (SISS) inventory system with zero lead-time, using the classical optimization. Abou-El-Ata et al. (2003) introduced a probabilistic multi-item inventory model with varying order cost; zero lead-time demand under two restrictions and no shortage are to be allowed. Fergany and El-Wakeel (2006a,b), applied several continuous distributions for constrained probabilistic lost sales inventory models with varying order cost using Lagrangian method. Recently, Kotb and Fergany (2011) deduced multi-item EOQ model with varying holding cost using geometric programming approach.

This paper considering the backorders inventory model with varying order cost, a restriction on the expected annual holding cost and the lead-time demand follows Uniform distribution. The policy variables of this model are the order quantity and the reorder point, which minimize the annual total cost. Finally, two special cases are deduced, which have been previously published and a numerical illustrative example is added with its graphs.

2 Assumptions and notations

The following assumptions are usually made in the simple treatments for developing the mathematical model:

1. The reorder point r is positive.

2. The demand is a random variable with known probability.

3. An order quantity of size Q per cycle is placed every time the stock level reaches a certain reorder point r.

4. Assume that the system repeats itself in the sense that the inventory position varies between r and r + Q during each cycle.

The following notations are adopted for developing our model:

3 The mathematical model

Using the expression of the expected value of a random variable, it is possible to develop the expected annual total cost as follows:

The optimal values Q^∗ and r^∗ can be found by setting each of the corresponding first partial derivatives of Eq. (9) equal to zero at Q = Q^∗ and r = r^∗ respectively, we obtain:

• Step 1: Assume that $\bar{B}=0$ and r = E(x), then from Eq. (10) we have:

  (12)
  $$Q_1={\left(\frac{2(1-\beta )c_o\bar{D}}{(1+\lambda )c_h}\right)}^{\frac{1}{2-\beta }}$$

• Step 2: Substituting from Eq. (12) into Eq. (11) we get:

  (13)
  $$P(r_1)=\frac{(1+\lambda )c_h}{c_b\bar{D}}{\left(\frac{2(1-\beta )c_o\bar{D}}{(1+\lambda )c_h}\right)}^{\frac{1}{2-\beta }}$$

• Step 3: Substituting by r₁ from Eq. (13) into Eq. (10) to find Q₂ as:

  (14)
  $$Q_2^2+\frac{2(\beta -1)c_o\bar{D}}{(1+\lambda )c_h}{Q}_2^{\beta }-\frac{2c_b\bar{D}}{(1+\lambda )c_h}\bar{B}(r_1)=0$$ The procedure is to varyλ in Eqs. (13) and (14) until the smallest value of λ. > 0 is found such that the constraint holds for the different values of β.

• Step 4: Repeating the steps 2 and 3 until obtaining successive values of Q and r, such that they are sufficiently close, which are the optimal values Q^∗ and r^∗.

4 The uniform model

To get an exact solution, assume that the lead-time demand follows the Uniform distribution, as follows:

Let $$f(x)=\frac{1}{b}\text{;}0⩽x⩽b\text{,}\text{with}E(x)=\frac{b}{2}\text{and}P(r)=1-\frac{r}{b}$$ and

5 Special cases

We deduce two special cases of our model as follows:

• Case 1:

  Let β = 0 and K →  ∞ ⇒ C_o(Q) = c_o and λ = 0. Thus Eqs. (10) and (11) become: $$Q^{\ast }=\sqrt{\frac{2\bar{D}(c_o+c_b\bar{B}(r))}{c_h}}\text{and}P(r^{\ast })=\frac{c_h}{c_b\bar{D}}{Q}^{\ast }$$ This is unconstrained probabilistic inventory model with backorders case and constant units of cost, which are the same results as in Hadley and Whitin (1963).

• Case 2:

  Let β = 0 and K →  ∞ ⇒ C_o(Q) = c_o and λ = 0, when the lead-time demand has the Uniform distribution. In this case, we obtain an exact solution of the optimal inventory policy. So Eqs. (21) and (22) will be in the form: $$Q^{\ast }=\sqrt{\frac{2c_o{c}_b{\bar{D}}^2}{c_h(c_b\bar{D}-{\mathit{bc}}_h)}}\text{and}{r}^{\ast }=b\left(1-\frac{c_h}{c_b\bar{D}}{Q}^{\ast }\right)$$

This is unconstrained probabilistic inventory model under backorders case with uniformly lead-time demand and constant units of cost. Which are the same results as in Fabrycky and Banks (1967) when we consider that the unit cost c_P of the item is a constant independent of Q.

6 An illustrative example

Consider an item for the demand treated as a constant, the average demand being 100 units per year. The cost of placing an order is a function of Q and equal to $40.00.The item’s holding cost is $4.00 per year. The procurement lead-time is not a constant and the lead-time demand is distributed uniformly in the interval 0–20 units. All demands occurring when the system is out of stock are backordered, and the cost is $7.00 per backorder. The inventory is controlled using a 〈Q, r〉 system under the constraint that the average holding cost is either less than or equal $120 per year. Determine Q^∗ and r^∗ for this model.

Using Eqs. (21) and (22), we can obtain the optimal values Q^∗ and r^∗ for different values of β at varying values of λ that yield the holding constraint as shown in Table 1.

From the above table, we can draw each of E(OC) and min E(TC) against β as shown in Fig. 1.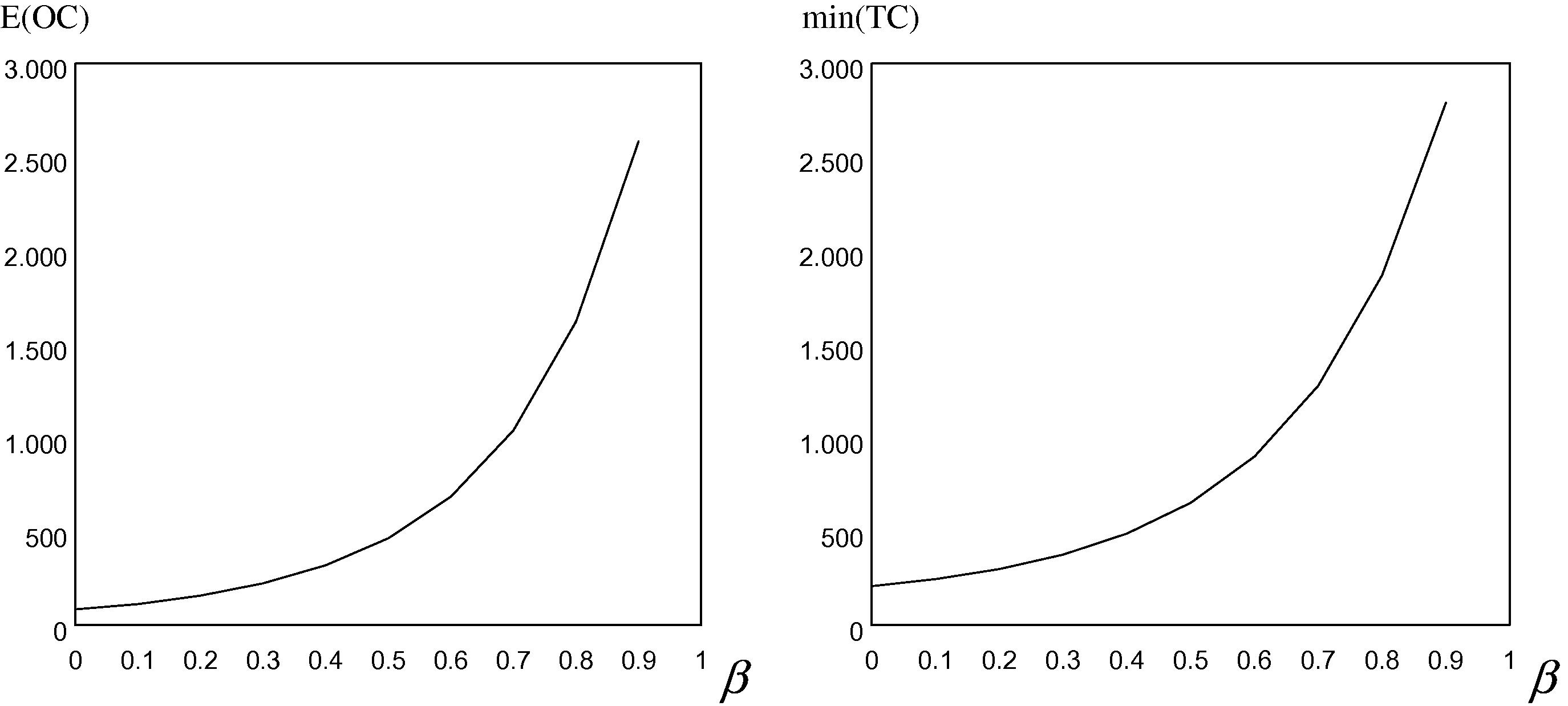

Close

Figure 1

The expected order cost and the expected total cost via the values of β.

Export to PPT

7 Conclusion

This paper investigating probabilistic backorder inventory system with varying order cost and continuous lead time demand under the holding cost restriction. We have calculated Q^∗ and r^∗ numerically and obtain the min (TC) for different values of β by using Lagranian multiplier technique. In the Uniform model, we can evaluate the exact solution for each Q^∗ and r^∗ at different values of β, which minimize the expected total cost, mathematically.