Conformal geometry of the turtle shell

1 Introduction

The turtle shell is made up of various bony components, usually called after related bones in new vertebrates, and a sequence of keratin sautes (a thickened bony plate on a turtle’s shell) which are furthermore exclusively entitled. Some of those bones that create the upper of the shell are changed from surface to another. Our study is based on the convex part of the shell structure of a turtle, which is called the carapace involving of the animal’s hardened ribs welded with the dermal bone. The progress (growth) of the turtle’s shell is unique because of how the carapace characterizes changed backs and ribs (Romer, 1956; Zangerl, 1969; Lyson et al., 2013; Cordero, 2017).

The geometry of the shell can be explained in two dimensions, the mechanism is essentially three dimensional: the center of gravity G is formulated not only by the central cross-section but by the whole body. Therefore, the structure must be involved in solid cylinder planar discs to imply convex, homogenous three-dimensional objects with just one stable and equilibrium may occur (Abelson and Andrea, 1986).

In this work, our contribution is to deliver a new geometric representation of the shell shape of a Southeast Asian turtle by utilizing CG method. This method accepted important differences in shell shape of turtles, like the symmetry, stability and equilibrium of shells. The method is based on formulating a symmetric differential operator using its roots to study the shell shape. 2D printing tool paths are recognized for these shells. We shall use Wolfram Mathematica 11.2 and the Javascript conformal map viewer to code our algorithm.

2 Related works

Domokos and Varkonyi (2007) introduced a geometric structure of the turtle shell in three steps: (i) transverse, this step is in a polar coordinate system; (ii) longitudinal, this step is describing side- and top-view contours of the shell; (iii) 3D- representing, this step is a surface model combining a series of horizontal and vertically scaled versions of the main transverse section, coinciding the longitudinal contours. They established the model parameters to separate measured turtle shapes, and then to control the equilibrium class of the 3D-model$$P(\alpha ,r,\kappa )=\frac{p_0}{\cos \left(\alpha \right)},\alpha \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right],$$where P is the polar system, $p_0$ is a scaling factor and $\kappa$ is the contour of the cross-section with radius r.More generalization of the above construction is given by Krauss et al. (2009). They added other factors such as length, viscosity and a geometric factor $\epsilon$ to recognize the zigzag structure.

Zhang et al. (2012) studied the dynamical representation of the shell by using optimization and numerical methods (2-DFinite element model). P2 is a two-dimensional problem (Dirichlet problem)$$\mathrm{P}(2-\mathrm{D}):\left\{\begin{array}{cc}{\mu }_{\mathit{xx}}(x,y)+{\mu }_{\mathit{yy}}(x,y)=\phi (x,y)\hfill & \mathrm{in}\mathrm{\Omega },\hfill \\ \mu =0\hfill & \mathrm{on}\partial \mathrm{\Omega },\hfill \end{array}\right.$$where $\mathrm{\Omega }$ is a connected open region in the $(x,y)$plane whose boundary $\partial \mathrm{\Omega }$ is a smooth domain (in our model, we shall suggest the open unit disk), and ${\mu }_{\mathit{xx}}$and ${\mu }_{\mathit{yy}}$ represent to the second derivatives with respect to x and y, respectively. Fig. 1 shows the structures of the turtle shell for Domokos and Varkonyi (2007) and Zhang et al. (2012) respectively.

Close

Fig. 1

Geometric methods which are given in Domokos and Varkonyi (2007) and Zhang et al. (2012) respectively.

Export to PPT

Djumas et al. (2016) established a new method by utilizing a geometric topological method (topological interlocking). The idea is based on the segmentation of solid materials into particularly aimed, discrete matching units which interlock in 3-D to form an assembly. In this method, each component is controlled by the geometry of its neighbouring components, given that the assembly a tool to have load-bearing mechanical integrity without the need for connectors or folders. A global control in the form of a frame, angle ties or tension supports is required to keep the general structure.

Recently, by using statistical methods in data science (such as segmentation, hypothesis, etc.), Hosseini et al. (2019) and Van Le et al. (2019) provided a 3-D geometrical structure of the shell. Ferreira and Werneburg (2019), based on 3D reforms method in geometry, they proposed a theoretical model for a turtle with a complete shell. The significant stage toward the accepting the growth of those muscles in turtles. Finally, Brejcha et al. (2019) studied the color of the skin based on the Fourier analysis of some spatial distributions. The Fourier analysis of such a function ($\phi$) is given by the formula$$\phi \left(x\right)={\displaystyle \sum _{n=-\infty }^{\infty }}{K}_n{e}^{2\pi i\left(\frac{n}{T}\right)x}={\displaystyle \sum _{n=-\infty }^{\infty }}\widehat{\phi }\left({\eta }_n\right)e^{2\pi i{\eta }_{n}x}\mathrm{\Delta }\eta \text{.}$$

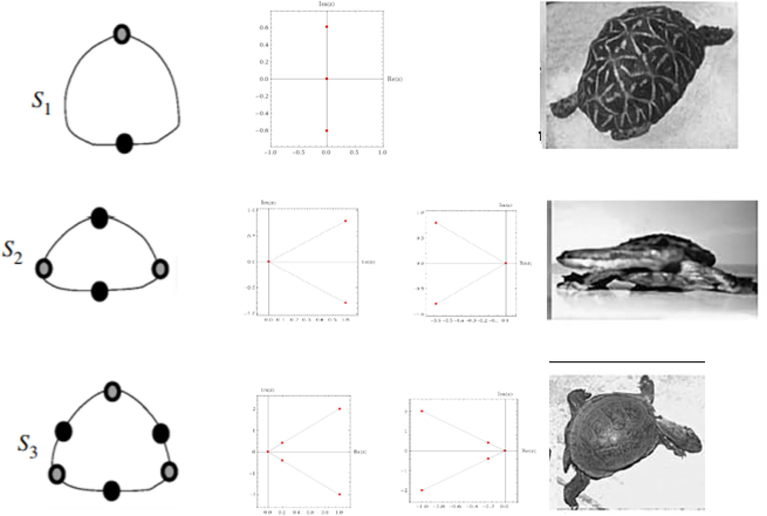
We note that there are three original shapes for the turtle shell, Diamond shell, Leaf shell and Flap shell (see Fig. 2), where other types are hybrids of these three types. Our study focuses on the leaf turtle shell.

Close

Fig. 2

Shapes of turtle shell.

Export to PPT

3 Methodology

In this section, we illustrate some important concepts that will be used in the sequel.

3.1

3.1 DDO

We deliver the new DDO in the open unit disk. Let $\mathrm{\Lambda }$ be the class of analytic function formulated by

(1)

$$\phi \left(z\right)=z+{\displaystyle \sum _{n=2}^{\infty }}{\phi }_n{z}^n,z\in U=\{z:|z|<1\}\text{.}$$

This class of analytic functions provides the geometric construction of any conformal mappings (Duren, 1983). This class involves the special class of analytic functions called the univalent functions, which implies stalikeness, convexity and concavity of conformal mappings in the open unit disk.

For a function $\phi \in \mathrm{\Lambda }$, we present a new differential operator in U

(2)

$$\begin{array}{cc}\hfill & {\mathrm{\Delta }}_{\beta }^0\phi \left(z\right)=\phi \left(z\right)\hfill \\ \hfill & {\mathrm{\Delta }}_{\beta }^1\phi \left(z\right)=\left(\frac{\beta }{\overline{\beta }}\right)z\phi \prime \left(z\right)-\left(1-\frac{\beta }{\overline{\beta }}\right)z\phi \prime (-z),\hfill \end{array}$$where for m iteration, the operator (2) becomes:$$\begin{array}{cc}{\mathrm{\Delta }}_{\beta }^m\phi \left(z\right)\hfill & ={\mathrm{\Delta }}_{\beta }\left({\mathrm{\Delta }}_{\beta }^{m-1}\phi \right(z\left)\right)\hfill \\ \hfill & =z+{\displaystyle \sum _{n=2}^{\infty }}{\left(n\left(\frac{\beta }{\overline{\beta }}-(1-\frac{\beta }{\overline{\beta }}){(-1)}^n\right)\right)}^m{\phi }_n{z}^n,\hfill \end{array}$$where $\beta$ is a complex number. Table 1 shows some examples which are useful in our study.

Table 1 Examples of ${\mathrm{\Delta }}_{\alpha }^m\left(z\right),z\in \mathbb{U}$. The roots are illustrated in symmetric structures.

$\phi \left(z\right)$	${\mathrm{\Delta }}_{\nu }^m\left(z\right),\nu =\frac{\beta }{\overline{\beta }}$	Roots in the complex plane
$\frac{z}{1-z}$	${\mathrm{\Delta }}_{0.2}^1=\frac{0.2z}{{(1-z)}^2}+\frac{0.8z}{{(1+z)}^2}$	$0,0.6\pm 0.8i$
–	${\mathrm{\Delta }}_{0.8}^1=\frac{0.8z}{{(1-z)}^2}+\frac{0.2z}{{(1+z)}^2}$	$0,-0.6\pm 0.8i$
$\frac{z}{{(1-z)}^2}$	${\mathrm{\Delta }}_{0.2}^1=-\frac{0.2z(1+z)}{{(z-1)}^3}+\frac{0.8z(1-z)}{{(1+z)}^3}$	$0,0.2\pm 0.4i,1\pm 2i$
–	${\mathrm{\Delta }}_{0.8}^1=-\frac{0.8z(1+z)}{{(z-1)}^3}+\frac{0.2z(1-z)}{{(1+z)}^3}$	$0,-0.2\pm 0.4i,-1\pm 2i$
$\frac{z}{{(1-z)}^3}$	${\mathrm{\Delta }}_{0.2}^1=\frac{0.2z(1+2z)}{{(1-z)}^4}-\frac{0.8z(2z-1)}{{(1+z)}^4}$	$0,0.1\pm 0.2i,0.3\pm 1i$
–	${\mathrm{\Delta }}_{0.8}^1=\frac{0.8z(1+2z)}{{(1-z)}^4}-\frac{0.2z(2z-1)}{{(1+z)}^4}$	$0,-0.1\pm 0.2i,-0.3\pm 1i$

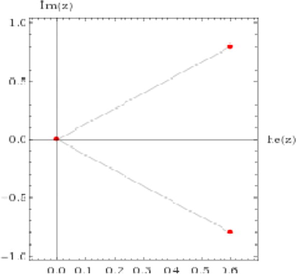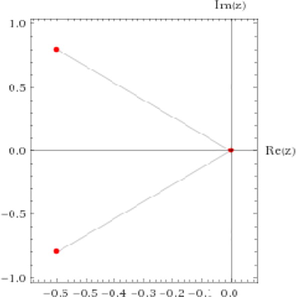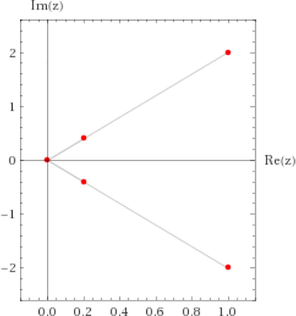
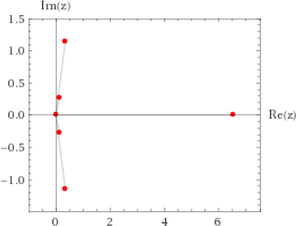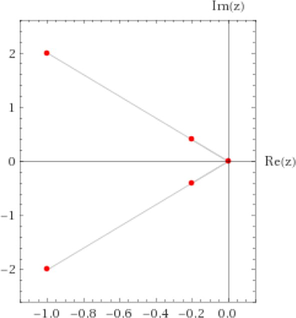
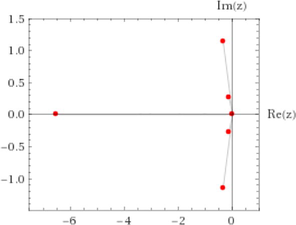Domokos and Varkonyi (2007) have classified turtle shells into three classes depending on the equilibrium points in the two planes of reflection symmetry such that the y-coordinate is to be calculated (Fig. 3).

Close

Fig. 3

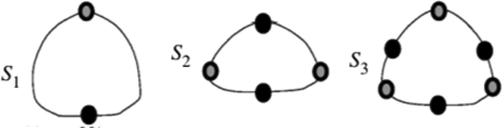
Classes of turtle shall in (Domokos and Varkonyi, 2007). Class ${\mathrm{S}}_1$ is signified by a rather small domain, tall turtles are unusually close to ${\mathrm{S}}_1$, i.e. they tend to be monochromatic and ${\mathrm{S}}_2$ for mote symmetrical shells including the flap shape, the popularity of standard turtle’s shell drops into ${\mathrm{S}}_3$.

Export to PPT

3.2

3.2 Energy

In this work, the algorithm is based on conformal mappings in the open unit disk. Therefore, the energy should take its value as a complex number. Follow the technique of complex fractional entropy (IIbrahim and Darus, 2018), we have construct the value of energy. Moreover, since the study is in the open unit disk, therefore, at best value of the energy does not exceed one.

Let $\mathbf{Z}$ be the set of N- roots of DDO (2) in U,$$\mathbf{Z}=\{{\eta }_1,\dots ,{\eta }_N\}\subset U\text{.}$$

Hence, the total information is a complex vector determining from the complex fractional entropy

(3)

$$I_{\rho }\left(\eta \right)={\displaystyle \sum _{k=1}^N}\frac{{\eta }_k}{\rho -1},\rho \ne 1,\eta \in \mathbf{Z},$$

Moreover, large amount of information occurs from both theoretical investigations and numerical calculations from (3). The stability of (3) is realized by the energy equation

(4)

$${\mathrm{\Xi }}_{\rho }=\frac{I_{\rho }\left(\eta \right){\bar{I}}_{\rho }\left(\eta \right)}{N},$$where ${\bar{I}}_{\rho }\left(\eta \right)$ is the conjugate of $I_{\rho }\left(\eta \right)$. The energy gives a tool for studying the dynamics of DDO. Table 2 shows the distribution of our results for some useful conformal mappings. These conformal mappings are utilized to describe the shell shape under the operator (2). The first function $\phi \left(z\right)=z+0.9z^3$ represents to ${\mathrm{S}}_1$ model, the second mapping ($\phi \left(z\right)=z/(1-z)$) acts as the ${\mathrm{S}}_2$-type and the third mapping ($\phi \left(z\right)=z/{(1-z)}^2$) performs the ${\mathrm{S}}_3$-design (see Fig. 4). Experimentally, the value $\rho =3$ implies a higher energy for the system $({\mathrm{\Xi }}_{\rho }\approx 1$ for ${\mathrm{S}}_2$). This method implies guarantee the energy is less or equal to 1, because of the value of $\rho$.

Table 2 The energy of DDO (2) for $\rho =3$. In our discussion, $S_1$ distributes the energy equally, $S_2$ the energy is high on the boundary of the unit disk, and $S_3$ shows the distribution for different roots are not equal on the shell shape.

$\phi \left(z\right)$	${\mathrm{\Xi }}_{\rho }\left(\eta \right),\rho =3$	2-D energy distribution
$S_1:z+0.9z^3$	${\mathrm{\Xi }}_3=\frac{{0.608}^2}{2}=0.184$ (two roots)
$S_s:\frac{z}{1-z}$	${\mathrm{\Xi }}_3\approx 1$ (two roots)
$S_3:\frac{z}{{(1-z)}^2}$	${\mathrm{\Xi }}_3=\frac{1.44}{4}=0.36$ (4 roots)

Close

Fig. 4

Comparison between Domokos and Varkonyi (2007) geometry and our algorithm.

Export to PPT

4 Discussion

Fig. 4 shows the comparison with the suggested geometry in (Domokos and Varkonyi, 2007) and the symmetric distribution of roots in the open unit disk for the operating (2). Obviously, we can see the congruence of roots in left and right distributions for ${\mathrm{S}}_2$ and ${\mathrm{S}}_3$. For ${\mathrm{S}}_1$, we suggested the function $\phi \left(z\right)=z+0.9z^3$, where this function gives two imaginary roots $r_{1,2}=\pm 0.608i$ in the open unit disk differ from the origin (zero root). By experimental rotation, to get symmetric shape, we have considered $\nu =\frac{\beta }{\overline{\beta }}=0.2$ and $m=1$ for all ${\mathrm{S}}_j,j=1,2,3$.

The advantageous of this algorithm are recognized as follows:

• The conformal segments involve a set of center, radii and roots;

• DDO (2) is normalized in the open unit disk; therefore, no need to use a weighted space;

• The energy is determined by the roots of DDO in the open unit disk; therefore, there is no wasting of energy (high accuracy of evaluation);

• This technique is iterative, hence the DDO collects the connected data regarding the shape of a shell.

5 Conclusion

Shell shape is an essential component of analysis and classification in turtles. We introduced a new study based on the conformal mappings theory by formulating a new symmetric differential operator in the open unit disk. We considered the roots of operator (2), that is: ${\mathrm{\Delta }}_{\nu }^m{\phi }_i\left(z\right)=0,i=1,2,3$, where $\nu =\beta /\overline{\beta }$ and ${\phi }_1\left(z\right)=z+0.9z^3$ represents to ${\mathrm{S}}_1$ model, the second mapping ${\phi }_2\left(z\right)=z/(1-z)$ symbolizes the ${\mathrm{S}}_2$-type and the third mapping ${\phi }_3\left(z\right)=z/{(1-z)}^2$ introduces the ${\mathrm{S}}_3$-type. We conclude that the roots of the ${\mathrm{\Delta }}_{\nu }^m{\phi }_i\left(z\right)$ coincided with the shapes that recognized in (Domokos and Varkonyi, 2007). Moreover, we examined the stability and the energy by using entropy with complex values.