Translate this page into:
Computable generalization of fractional kinetic equation with special functions
⁎Corresponding author. ilyaskhan@tdtu.edu.vn (Ilyas Khan)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The primarily object of this article is to derive the solutions of modified fractional kinetic equations (MFKEs) containing the incomplete Aleph functions by using the application of Elzaki and inverse Elzaki transforms and hereto we also established some novel results such as the Elzaki transform of well-known the Riemann–Liouville operator and the incomplete Aleph functions (IAFs). The solutions of modified FKEs discusses in this article can be utilized to figures out the variation of the chemical composition in our solar system. In this article, we also see that the character of thermonuclear function is presented in terms of the incomplete functions and many more special functions through some interesting corollaries. Finally, we established here a compact and easily figure out solutions in form of incomplete special functions and display the graphs of the obtained results in the end of this article to show the behavior of integral operator of fractional order on reaction rate of the particle. Furthermore, results holds here are also associated to the recent investigation of feasible astrophysical solutions of solar system problems. The derived results notify the known results more precisely.
Keywords
Fractional kinetic equation
Riemann-Liouville fractional integral operator
Incomplete Aleph function
Elzaki transform
1 Introduction
Stars have attracted scientists and astronomers equally. Some amazing things whether it is our sun-like stars or solar system akin to our other galaxies. A star is creating when a bit of gas is destroyed onto its own gravity. When mass and length of interstellar cloud extend to certain limits, then the clouds diverge from entity in hydrostatic equilibrium (HE) and are destroyed. If its gravitational force is equal is equal to its internal pressure then in this situation the system is said to be hydrostatic equilibrium. Therefore the system is neither burst nor collapse. Nevertheless in the formation of a star the gravitational force inside the cloud should be more than its internal pressure. As the interstellar cloud collapse inward due to the variation of force inside, the temperature jump up when the cloud temperature reaches k, then nuclear fusion will begin. Because of nuclear fusion the cloud radiate the light and protostar come in existence. In this phase stellar is known as pre-main sequence.
In thermal and HE, a star can be considered as a uniform gas sphere with insignificant spinning and magnetic field. The internal structure of star is entirely gases and it is characterized by three parameters; temperature, pressure & mass. Mathematical models (MMs) and structures of stars are examined and it is depend upon the above parameters as well as its based on equation of state, translucence and rate of nuclear energy produce. The hypothesis of thermal and HE show that there is no dependency on time in the MMs as well as in the equations expressing the inside formation of the star (Kourganoff, 1973; Perdang, 1976; Clayton, 1983). The assessment of the star is conducted by a system of differential equation. A system of differential equation is used in assessment of the star like sun, kinetic equation (KE) is an equation that is appear in non-equilibrium statistical physics (Lebowitz and Montroll, 1984). The result obtained from kinetic-equation estimate the distribution function of the movable position of a solitary particle, which is normally based on time & velocity. Thus, we can say that KEs characterize the rate of change of chemical composition of star for every kind in the form of reaction rate for production & destruction of that kind (Kourganoff, 1973; Perdang, 1976; Clayton, 1983).
Let us assume a random reaction identify by a time dependent quantity
=
. Then we estimate the
by the following equation
where refer the function presented as
Haubold and Mathai (2000) considered a particular case of (2), when the quantity
are ignored, then the Eq. (2) become
if we drop index
due to sake of brevity in Eq. (3), then Haubold and Mathai (2000), after integration demonstrate the SKE (3) as
here
denote the standard R-L operator. After this the operator mention in Eq. (5), is generalized into arbitrary order operator and it is defined as
finally, the solution of SKE (6) obtained in series form Haubold and Mathai (2000) as
So far, a lot of research has been done in last three decades to improve the reaction rate of particle via FKE. A number of methods are used for solving the generalized FKE (GFKE) and it is solved earlier by several authors such as Saichev and Zaslavsky (1997), investigated the potential generalization of the normal diffusion equation by using FKE as well as they established the relation between FKE and Montroll-Weiss equation and generalized the Kolmogorov-Feller equation. In a series of research papers so far, many authors have investigated FKE and derived the solution in easy and compact form to figure out the particle reaction rate such as Haubold and Mathai (2000), developed the solution of KE to calculate the variation of chemical composition of stars and discuss the contribution of thermonuclear function in terms of G & H functions. After this Saxena et al. (2002), investigated the FKE and derived the generalized FKE in-terms of the Mittag-Leffler (M-L) function, which was an increment of what had been done by Haubold and Mathai (2000), in other article, Saxena et al. (2004a), established the solutions of three GFKE in form of generalized M-L functions. Further, Saxena et al. (2004b), explored the solution of integrated form of FKE and presented the solution in the form of the Wright function. In 2008, Saxena and Kalla (2008), introduced a new way to solve the FKEs which was in addition to the Laplace transform technique. At the same time Chaurasia and Pandey (2008), developed a compact and effortless computable solution of GFKE and presented it in the form of the Lorenzo-Hartely function which is very helpful to compute the reaction rate. In continuation of solution of GFKE, Chaurasia and Kumar (2010), established the solution of GFKE in associated with M-series and derived some particular cases in form of well-known GMLF. Recently Chaurasia and Singh (2015), further derived the solution of GFKE involving GMLF and the Rathie I-function. Very recently, Bansal et al. (2020b), introduced a new concept of the incomplete I- function and derived the solution of FKE involving the incomplete I-function (IIF). For the last few decades, we are seeing that a lot of researcher has solved GFKE and has contributed greatly to modify the particle reaction rate for more detail sees (Chaurasia and Singh, 2011; Nisar et al., 2016; Nisar and Qi, 2017). The potential uses of FKEs in several problems come to the light in some astrophysical problems, Science and engineering can be referring these monographs (Podlubny, 1999; Hilfer, 2000; Kilbas et al., 2006). In the present article the results are achieved in a compact form in terms of the incomplete functions (Bansal et al., 2020c), by using the application of Elzaki and inverse Elzaki transform (Elzaki, 2011; Singh et al., 2019a, 2019b). The article is unified as follows, Section 2 hold the definition of IGFs, incomplete Aleph-functions, Elzaki transform and R-L operator. In Section 3, we investigate the Elzaki transform of R-L operator and the incomplete Aleph-functions. After that in Section 4, we established the solution of MFKE while some special cases, are also discussed in Section 5 through corollaries in terms of the incomplete –I functions (IIFs), function, H-function. The results established in this article come up with an addition of consequences that are given in recent paper Bansal et al. (2020b). Finally, we plot the graph of the obtained results and found that the reaction rate decreases with enhancement of time and continuously depends on the value of fractional parameter.
In view of great significance and widely used of KE in diverse physical problems, especially in astrophysics. So that we further, derived the solution of MFKE associated with the incomplete functions.
In the history of mathematics, the incomplete gamma functions (IGFs) are kinds of special-functions that appear as solutions of diverse problems of mathematical for instance some specific integrals are extensively used in several area of mathematics in addition to other areas such as probability theory, Kinematics (specially come to know time, displacement & velocity), thermodynamics (to look into the change in free energy b/w two states). The IGFs has a very old history of research (see e.g. Prym, 1877; Abramowitz and Stegun, 1984; Arfken, 1985; Chaudhry and Zubair, 1995). After that researcher has been done a lots of work and take a step to proceed the research and development of well-known IGFs and defined in (8) & (9).The IGFs are very crucial part of special function in view of their widely used and great importance in statistics, Physics, engineering and many more area of mathematics as mention above.
Recentaly, Srivastava et al. (2012), explore a well-known the incomplete pochhammer symbols and discuss their utility and fundamental properties to the incomplete Gauss hypergeometric (IGH) function and other associated functions which are probably very helpful in definite and semi-definite integrals of several special functions and can be implement these function in communication theory, probability theory and ground water pumping modeling (GWPM). The important aspect of the gamma function is that it decompose into IGFs and seems to be a closed form solution to a significant number of problems arise in plasma wave, science, engineering, astrophysics, mathematics and statistics as well as in configuration of particle acceleration can be demonstrate in terms of the IGFs given by (8) & (9). Taking inspiring from his current research work Srivastava et al. (2012), explore a well-established incomplete H-function and (z) along with develop some special cases like Incomplete Fox-Wright generalized hypergeometric functions and established many fascinating basic properties such as decomposition, several Integral transforms, derivative formulas and many more (Srivastava et al., 2018). Recently, Srivastava et al. (2012, 2018), investigated the incomplete Pochhammer symbols, incomplete H-functions and incomplete – functions. Enthusiastic by the novel research work of incomplete special functions which is done by some author’s mention earlier, Bansal and Kumar (2020); Bansal et al. (2020c), investigated the IIFs and the IAFs. Therefore keeping in mind the greatness and utility of KE in classical astrophysical problems, we further, investigate the compact and computable solution of MFKE involving the incomplete functions.
2 Definitions and preliminaries
In this section, we develop a few important fundamental definition associated to fractional calculus, Elzaki transform and special function to understand the further results and lemmas.
2.1 Incomplete gamma functions and
The well-known incomplete gamma functions
and
(also known as Prym, 1877) functions are expressed in the following manner Abramowitz and Stegun, 1984; Arfken, 1985; Chaudhry and Zubair, 1995):
and
respectively, hold the following decomposition formula:
Each of these functions play a vital role in the analysis of an analytic solutions of a numbers of problems in various field of GWP modeling, theory of Probability, quantum physics, Communication theory, Mathematical Physics, Science and engineering (see, for instance, Kilbas et al., 2006; Prym, 1877; Andrews, 1984; Andrews et al., 1999; Srivastava and Karlsson, 1985; Temme, 1996; Kumar et al., 2019, 2020; Singh et al., 2019a, 2019b; Gill et al., 2019; Baleanu et al., 2020; Bansal et al., 2020a; Modi et al., 2020).
2.2 Incomplete Aleph functions
The Incomplete Aleph functions
consisting the incomplete gamma functions
and
recently, introduced by Bansal et al. (2020c), and defined as:
where
and
and
where
and
for details of existence conditions see Bansal et al. (2020c).
2.3 Elzaki transform
Let the function belongs to a class ,
Where = such that if ,
Elzaki transform of function
introduced by Tarig M. Elzaki is defined as (Elzaki, 2011):
2.4 Convolution property
The Elzaki convolution property of
is given by
2.5 R-L integral operator
A well-known integral operator introduced by Riemann-Liouville and presented as (Oldham and Spanier, 1974; Miller and Ross, 1993).
3 Elazki transform of Riemann-Liouville integral operator & incomplete Aleph functions
In this portion, we introduce a formula of the Elzaki transform of R-L integral operator and the incomplete function.
Lemma 3.1. The Elzaki transform of R-L integral operator is given by
Proof. Elzaki transform of the function defined in (18) is given by
applying the convolution property of the Elzaki transform on above equation, we have
finally, yield the desired result.
Lemma 3.2. The Elzaki transform of the incomplete Aleph functions
is given by
and
provided that each member exit in (20) and (21).
Proof. We begin the proof of (20), by taking the Elzaki transform of left hand side in (20), then
where is given by (13).
Changing the order of integration that is acceptable under the prescribed condition of the incomplete function, then we have
By using result of the Elzaki transform, then
At last, after the little simplification and with the help of Eqs. (12) and (13), we arrive at desired result.
4 Fractional – order kinetic equations
Here, we derive the solution of modified FKEs involving the Incomplete Aleph functions (12) and (14) and established some parallel corollaries.
Theorem 1.
the modified FKE:
Proof. On applying the Elzaki transform (Elzaki, 2011; Singh et al., 2019a, 2019b) on both sides of (22), we have
using the result defined in (19), we arrive at
where is given by (13).
After little simplification the above equation can be express as
Now, implementing the inverse Elzaki transform on both sides of (25), then
Finally, after rearrangement of terms, we obtained our desired solution (23).
Theorem 2.
then the modified FKE:
has the solution as follows:
Proof. We can get the proof of Theorem 2, in the same way as we did in Theorem 1.
5 Special cases
In this segment, we set up some significant corollaries of our leading results
Corollary 1.
then the modified FKE:
has holds the solution will be as follows:
Proof. If we set , in (22), we arrive at the required result in terms of the Aleph-function (Chaurasia and Singh, 2012, 2014; Südland et al., 1998, 2001) and which is known result recently obtained by Dutta et al. (2011; p. 44, Eq. (17)).
Corollary 2.
then the modified FKE:
has the solution obtained in terms of the incomplete –I function as follows:
Proof. If we set , in (22), we arrive at the required result and which is recently attained by Bansal et al. (2020b; p. 5, Eq. (26)).
Corollary 3.
then the modified FKE:
has holds the solution will be as follows:
Proof. Again, if we set , in (26), we get the desired result and which is recently attained by Bansal et al. (2020b; p. 6, Eq. (28)).
Corollary 4.
(
, then the modified FKE:
has holds the solution will be as follows:
Proof. If we assign suitable value to the parameters in (12), then we have the following relation given in the monograph by Mathai et al. (2010; p.25, Eq. (1.139)), where is the generalized Bessel-Maitland function, and if we use this relation in (22), then after little simplification, we obtained the desired result given by (35).
6 Numerical simulation
In this part, we compute the results numerically for the MFKE (22) by assigning separate values to the distinct variables and parameters demonstrated through the Figs. 1–3. The effect of time and order of R-L integral operator of arbitrary order on the reaction rate is demonstrated in Figs. 1–3. It is observed from the Figs. 1–3 that the reaction rate decreases with enhancement of time and continuously depends on the value of fractional parameter.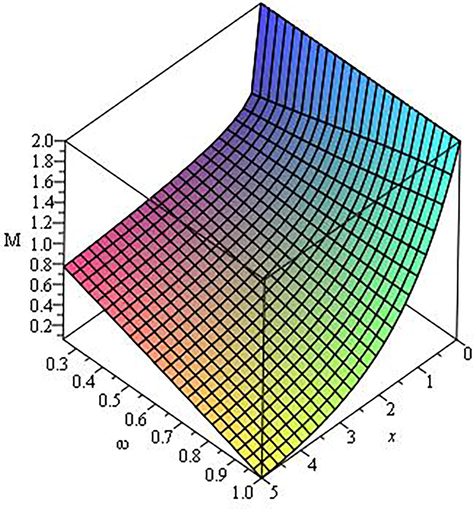
Surface of solution when
and
.
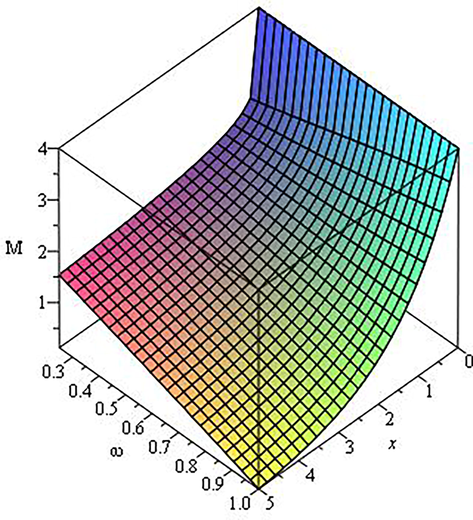
Surface of solution when
and
.
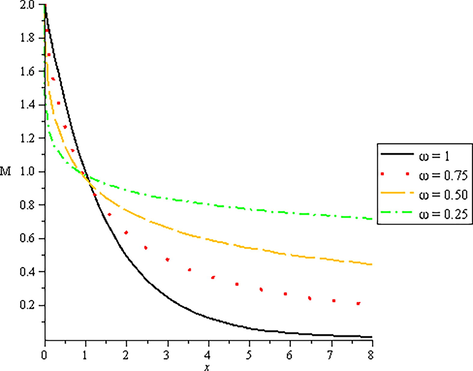
Plots of solution when
and
for different values of fractional parameter.
7 Conclusions
We summarize this investigation by keeping in mind the potential uses and greatness of the KE in astrophysical problems. The objective of this paper is to figure out the reaction rate of particle by making use of MFKE for stars. A lot of authors have contributed to calculate the reaction rate of particle such as Saxena et al. (2002); (2004a; 2004b; 2008;), have a huge contribution to systematically studied the standard KE and generalized to FKE and expressed their results in the form of special functions which are used to figure out the variation of chemical composition in our solar system.
In the present work, we have investigated the modified FKE and derived the solution and this solution can play a vital role to figures out the reaction rate of the particle and with this, we have also established the Elazki transform of R-L integral operator and IAF. The MFKE investigated in this article involving the incomplete Aleph functions and established the results in terms of special functions. From this work we can easily find out known and novel FKEs and their results respectively. It should be noted that the MFKE discussed here consist new and known results which are obtained very recently by Bansal et al. (2020c), Dutta et al. (2011), and these results hold here are also associated with the recent investigation of feasible astrophysical solution of solar system problems. In the solution of MFKE (6) given in Eqs. (23) and (27), the standard exponential decay is obtained for .
To validate the results discussed here, we plot the graphs and compute the results numerically for MFKE at distinct values of variables and parameters to show the behavior of reaction rate decreases with enhancement of time and continuously depends on the value of fractional parameter. All the novel results derived in this article have been come out by the use of incomplete special function for fractional calculus, notably the incomplete Aleph functions and by the application of the Elzaki transform.
Finally, the current investigation highlights the effectiveness and greatness of the MFKE involving the IAF by using the Elzaki transform and on the basis of this study we can say that it would be potentially useful in astrophysics. Such a potential connection needs further investigation.
CRediT authorship contribution statement
Yudhveer Singh: Investigation, Writing - original draft, Writing - review & editing. Vinod Gill: Formal analysis, Writing - original draft. Jagdev Singh: Conceptualization, Investigation, Writing - review & editing. Devendra Kumar: Conceptualization, Formal analysis, Methodology, Writing - original draft. Ilyas Khan: Formal analysis, Writing - original draft, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abramowitz, M., Stegun, I.A., 1984. Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables, Applied Mathematics Series 55, National Bureau of Standards, Washington DC, USA, 9th edition.
- Special Functions for Engineers and Applied Mathematicians. New York: Macmillan Company; 1984.
- Special Functions, Encyclopedia of Mathematics and its Applications 71. Cambridge: Cambridge University Press; 1999.
- The incomplete gamma functions and related functions. In: Orlando F.L., ed. Mathematical Methods for Physicists (3rd ed.). Academic Press; 1985. p. :565-572.
- [Google Scholar]
- A fractional derivative with two singular kernels and application to a heat conduction problem. Adv. Difference Equ.. 2020;2020:252.
- [CrossRef] [Google Scholar]
- Fractional differential equation pertaining to an integral operator involving incomplete H−function in the Kernel. Math Meth Appl. Sci. 2020
- [CrossRef] [Google Scholar]
- On the integral operators pertaining to a family of incomplete I-functions. AIMS Math.. 2020;5:1247-1259.
- [CrossRef] [Google Scholar]
- Fractional Kinetic equations associated with incomplete I-function. Fractal Fract.. 2020;4(2):1-12.
- [CrossRef] [Google Scholar]
- Certain fractional calculus and integral transform results of incomplete ℵ-functions with applications. Math. Meth. Appl. Sci.. 2020;2020:1-13.
- [CrossRef] [Google Scholar]
- On the decomposition of generalized incomplete Gamma functions with applications to Fourier transforms. J. Comput. Appl. Math.. 1995;59(101):253-284.
- [Google Scholar]
- On the new computable solution of the generalized fractional kinetic equations involving the generalized function for the fractional calculus and related functions. Astrophys. Space Sci.. 2008;317:213-219.
- [Google Scholar]
- On the solutions of generalized fractional kinetic equations. Adv. Stud. Theor. Phys.. 2010;4:773-780.
- [Google Scholar]
- Application of Sumudu transform in fractional Kinetic equations. Gen. Math. Notes.. 2011;2(1):86-95.
- [Google Scholar]
- New generalization of integral equations of Fredholm type using Aleph-function. Int. J. Modern Math. Sci.. 2014;9(3):208-220.
- [Google Scholar]
- A novel computable extension of fractional kinetic equations arising in astrophysics. Int. J. Adv. Appl. Math. Mech.. 2015;3(1):1-9.
- [Google Scholar]
- Principles of Stellar Evolution and Nucleo synthesis (Second ed.). Chicago and London: The University of Chicago Press; 1983.
- On the solution of fractional Kinetic equation. Gen. Math. Notes.. 2011;6(1):40-48.
- [Google Scholar]
- The new integral transform “Elzaki Transform” fundamental properties investigations and applications. Global J. Pure Appl. Mathem.. 2011;7(1):57-64.
- [Google Scholar]
- Analytical solution of generalized space-time fractional advection-dispersion equation via coupling of Sumudu and Fourier transforms. Front. Phys.. 2019;6(151):1-6.
- [CrossRef] [Google Scholar]
- The fractional kinetic equation and thermonuclear functions. Astrophys. Space Sci.. 2000;273(1):53-63.
- [Google Scholar]
- Applications of Fractional Calculus in Physics. New York: World Scientific Publishing Co.; 2000.
- Theory and Applications of Fractional Differential Equations; North-Holland Mathematical Studies. Amsterdam, The Netherlands; London, UK; New York, USA: Elsevier (North-Holland) Science Publishers; 2006. p. :204.
- Introduction to the Physics of Stellar Interiors. Dordrecht: D. Reidel Publishing Company; 1973.
- A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler Laws. Int. J. Heat Mass Transf.. 2019;138:1222-1227.
- [Google Scholar]
- A model for describing the velocity of a particle in Brownian motion by Robotnov function based fractional operator. Alex. Eng. J.. 2020;59(3):1435-1449.
- [CrossRef] [Google Scholar]
- Nonequilibrium Phenomena II: From Stochastic to Hydrodynamic. Amsterdam: Elsevier Science Pub. Co; 1984.
- The H-Function: Theory and Applications. New York: Springer; 2010.
- An Introduction to the Fractional Calculus and Fractional Differential Equations. New York, USA: John Wiley & Sons INC.; 1993.
- A new family of distribution with applications on two real datasets on survival problem. Sci. Technol. Asia. 2020;25(1):1-10.
- [CrossRef] [Google Scholar]
- Generalized fractional kinetic equations involving generalized Struve function of the first kind. J. King Saud Univ. Sci.. 2016;28(2):167-171.
- [Google Scholar]
- On solutions of fractional kinetic equations involving the generalized k-Bessel function. Note di Matematica. 2017;37(2):11-20.
- [Google Scholar]
- Fractional Calculus: Theory and Applications of Differentiation and Integration of Arbitrary Order. New York, NY, USA: Academic Press; 1974.
- Lecture Notes in Stellar Stability, Part I and II. Padova: Instituto di Astronomia; 1976.
- Fractional Differential Equations. San Diego, CA, USA: Academic Press; 1999.
- Unified fractional kinetic equations and a fractional diffusion equation. Astrophys. Space Sci.. 2004;290:299-310.
- [Google Scholar]
- On the solutions of certain fractional kinetic equations. Appl. Math. Comput.. 2008;199:504-511.
- [Google Scholar]
- On the Elzaki transform and its application in fractional free electron laser equation. Acta Univ. Sapientiae Mathem.. 2019;11(2):419-429.
- [Google Scholar]
- A new approach to solve Cattaneo-Hristov diffusion model and fractional diffusion equations with Hilfer-Prabhakar derivative. AIMS Math.. 2019;5(2):843-855.
- [CrossRef] [Google Scholar]
- The incomplete Pochhammer symbols and their applications to hypergeometric and related functions. Integr Transf Spec F.. 2012;23(9):659-683.
- [Google Scholar]
- Some families of the incomplete H-functions and the incomplete ¯H-functions and associated integral transforms and operators of fractional calculus with applications. Russ. J. Math. Phys.. 2018;25:116-138.
- [Google Scholar]
- Multiple Gaussian Hypergeometric Series, Halsted Press (Ellis Horwood Limited, Chichester). NewYork: John Wiley and Sons; 1985.
- Who know about the Aleph (ℵ)- function? Fract. Clac. Appl. Anal.. 1998;1(4):401-402.
- [Google Scholar]
- Fractional driftless Fokker-Planck equation with power law diffusion coefficients. In: Gangha V.G., Mayr E.W., Vorozhtsov W.G., eds. Computer Algebra in Scientific Computing (ASC Konstanz 2001). Berlin: Springer; 2001. p. :513-525.
- [Google Scholar]
- Special Functions: An Introduction to Classical Functions of Mathematical Physics. New York: John Wiley and Sons; 1996.







