Bright and singular soliton solutions to the Atangana-Baleanu fractional system of equations for the ISALWs

Hadi Rezazadeh; Waleed Adel; Eric Tala-Tebue; Shao-Wen Yao; Mustafa Inc

doi:10.1016/j.jksus.2021.101420

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

06 2021

:33;

101420

doi:

10.1016/j.jksus.2021.101420

Bright and singular soliton solutions to the Atangana-Baleanu fractional system of equations for the ISALWs

Hadi Rezazadeh^{^a}, Waleed Adel^{^b}, Eric Tala-Tebue^{^c}, Shao-Wen Yao^{^d,⁎}, Mustafa Inc^{^e,^f,^g,⁎}

a Faculty of Engineering Technology, Amol University of Special Modern Technologies, Amol, Iran

b Department of Mathematics and Engineering Physics, Faculty of Engineering, Mansoura University, Mansoura, Egypt

c Laboratoire d'Automatiqueetd'InformatiqueAppliquee (LAIA), IUT-FV of Bandjoun, The University Of Dschang, BP 134, Bandjoun, Cameroon

d School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo 454000, China

e Department of Computer Engineering, Biruni University, Istanbul, Turkey

f Department of Mathematics, Science Faculty, Firat University, 23119 Elazig, Turkey

g Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan

⁎Corresponding authors. yaoshaowen@hpu.edu.cn (Shao-Wen Yao), minc@firat.edu.tr (Mustafa Inc)

Received: 2020-11-15, Accepted: 2021-3-23,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

This work searches for new soliton solutions to the Atangana-Baleanu (AB) fractional system of equations for the ion sound and Langmuir waves (ISALWs). A new auxiliary equation scheme (NAES) is implemented to solve this model with the aid of a symbolic software. The hyperbolic and trigonometric function forms of this equation have been obtained. Due to the good performance of the NAEM, it is believed that this method is a promising technique to handle a wide variety of AB fractional evolution systems.

Keywords

Newauxiliary equation scheme

Equations for the ISALWs

Atangana-Baleanu fractional derivative

Show Related Articles from PubMed

1 Introduction

Over the past few years, the search for new results of fractional differential equations and especially nonlinear evolution types (NLFEEs) have captured the interest of many scientists in different areas of science and engineering. Seeking the solution of these types of equations in the form of travelling wave play an important role in understanding some ofthe real-life physical phenomena with a particular interest in nonlinear models. These nonlinear models may appear in different areas of science including plasma physics, optical fibers, fluid dynamics, biology, and solid-state physics. Hence, it is an important topic to find wave solutions for these types of equations to better understand their nature. Numerous methods have been utilized to reveal these solutions such as the $G' / G$ -expansion method (Abazariet al., 2016; Abazari, 2013), first integral method (Aminikhah et al., 2015; Çenesiz et al., 2017), Jacobi elliptic function expansion scheme (Kurt, 2019; Tasbozan et al., 2016), Exp-function method (Hosseini et al., 2020a, 2020b), expanded sinh-Gordon system expansion scheme (Sulaiman et al. 2020; Bulut et al. 2018a, 2018b), modified Kudryashov method (Rezazadeh et al., 2019a; Biswas et al., 2018), fractional Sine-Gordon Equation method (Rezazadeh et al., 2019b; Korkmaz et al., 2020), modified auxiliary equation method (Khater et al., 2019a, 2019b) and much more relative methods (Akinyemiet al. (2021a, 2021b); Şenol et al. (2019); Akinyemi 2020; Hashemi and Akgül, 2018; Hashemi, 2018; Najafiet al., 2017; Ghanbariet al., 2020, 2019; Rahmanet al., 2020; Munusamyet al., 2020; Hosseini et al., 2020c; Rizvi et al., 2021, 2020a, 2020b, 2020c, 2020d; Younis et al., 2021 ; Younis et al. 2020a; Younis et al. 2020b; Wanget al. 2014).

This manuscript aims at findingsome new form of soliton solutions for the system with AB fractional-order derivative of the ISALWs defined for $α = 1$ from (Yajima and Oikawa, 1976) as

(1)

\begin{matrix} _{t}^{ABR} D_{0^{+}}^{α} E + \frac{1}{2} \frac{\partial^{2} E}{\partial x^{2}} - n E = 0, t > 0, 0 < α ⩽ 1 . \\ _{t}^{ABR} D_{0^{+}}^{α} n - \frac{\partial^{2} n}{\partial x^{2}} - 2 \frac{\partial^{2} ({|E|}^{2})}{\partial x^{2}} = 0, \end{matrix}

where

n

can be defined as the perturbation with normalized density and

E e^{- i w_{p} t}

is the normalized electric field associated with the Langmuir oscillations (Yajima and Oikawa, 1976). Both

x

and

t

variables are normalized and

_{t}^{ABR} D_{0^{+}}^{α}

are the AB fractional operator with order

α \in (0, 1)

in the t- direction defined as (Atangana and Koca, 2016; Atangana and Gómez-Aguilar, 2018).

(2)

_{t}^{ABR} D_{a^{+}}^{α} f (t) = \frac{ϖ (α)}{1 - α} \frac{d}{dt} \int_{a}^{t} f (x) Ξ_{α} (\frac{- α {(t - α)}^{α}}{1 - α}) d x,

Where

Ξ_{α} (.)

is the one parameter Mittag-Leffler function, provided in the form

Ξ_{α} (\frac{- α {(t - α)}^{α}}{1 - α}) = \sum_{n = 0}^{\infty} \frac{{(\frac{- α}{1 - α})}^{r} {(t - x)}^{α r}}{Γ (α r + 1)},

and $ϖ (α)$ can be defined as the normalization function. Thus, the AB fractional operator for $f (t)$ becomes $_{t}^{ABR} D_{a^{+}}^{α} f (t) = \frac{ϖ (α)}{1 - α} \sum_{r = 0}^{\infty} {(\frac{- α}{1 - α})}^{r}^{RL} I_{a}^{α r} f (t) .$

The organization of the paper is as follows: the section 2 shows the introduction of the major ideas and steps of the NAEM. Section 3 describes thefour new soliton solutions to system (1) involving different parameters. In section 4 two-dimensional and three-dimensional graphs are presented to illustrate some physical features of the obtained results. Finally, section 5 gives detailed conclusions.

₂

₂ _Methods

The new auxiliary equation scheme was first presented by Sirendaoreji (Sirendaoreji, 2006) to help in finding new wave results for some nonlinear partial differential equations. The method depends on some basic steps beginning with considering the following NLFNEE with $u$ which is a dependent variable as

(3)

K (_{t}^{ABR} D_{0^{+}}^{α} u, \frac{\partial u}{\partial x},_{t}^{ABR} D_{0^{+}}^{2 α} u, \frac{\partial^{2} u}{\partial x^{2}}, \dots) = 0, t > 0, 0 < α ⩽ 1,

where $K$ is a polynomial in $u .$ We shall use the wave transformation as (Yue et al., 2020; Khater et al., 2020; Park et al., 2020 ) in the form

(4)

u (x, t) = u (η), η = x + \frac{κ (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)}, κ \neq 0,

which can be used to convert Eq. (3) into a nonlinear ODE in the form

(5)

J (u, u^{'}, u^{″}, u^{‴}, \dots) = 0,

where

u

is a function in

η

and the prime denotes the differentiation for

η

. For the solution of Eq. (5), we assume that the solution takes the following form

(6)

u (η) = \sum_{j = 0}^{M} B_{j} Φ^{j} (η),

where

B_{j} (0 ⩽ j ⩽ M)

are parameters to be determinate later. We reach

M

by plugging Eq. (14) into Eq. (5) and equating the highest derivative and nonlinear terms together. The function

Φ (η)

simplifies the first-order nonlinear ODEs as

(7)

{(\frac{d Φ}{d η})}^{2} = m_{1} Φ^{2} (η) + m_{2} Φ^{4} (η) + m_{3} Φ^{6} (η),

where

m_{1}, m_{2}

and

m_{3}

are constants. Then, by plugging Eq. (6) into Eq. (5) and utilizing Eq. (7) when required, we reach a class of algebraic equations for

B_{j} (0 ⩽ j ⩽ M), m_{1}, m_{2}, m_{3}

and

κ .

With some manipulations, we evaluate the class of equations, and find the values

B_{j} (0 ⩽ j ⩽ M), m_{1}, m_{2}, m_{3}

and

κ .

. The general solutions of Eq. (15) are given as

(8)

Φ_{1} (η) = {(\frac{- m_{1} m_{2} {sech}^{2} (\sqrt{m_{1}} η)}{m_{2}^{2} - m_{1} m_{3} {(1 + ε tanh (\sqrt{m_{1}} η))}^{2}})}^{\frac{1}{2}}, m_{1} > 0 .

(9)

Φ_{2} (η) = {(\frac{m_{1} m_{2} {csch}^{2} (\sqrt{m_{1}} η)}{m_{2}^{2} - m_{1} m_{3} {(1 + ε coth (\sqrt{m_{1}} η))}^{2}})}^{\frac{1}{2}}, m_{1} > 0 .

(10)

Φ_{3} (η) = {(\frac{2 m_{1}}{ε \sqrt{Δ} cosh (2 \sqrt{m_{1}} η) - m_{2}})}^{\frac{1}{2}}, m_{1} > 0, Δ > 0 .

(11)

Φ_{4} (η) = {(\frac{2 m_{1}}{ε \sqrt{Δ} cos (2 \sqrt{- m_{1}} η) - m_{2}})}^{\frac{1}{2}}, m_{1} < 0, Δ > 0 .

(12)

Φ_{5} (η) = {(\frac{2 m_{1}}{ε \sqrt{- Δ} sinh (2 \sqrt{m_{1}} η) - m_{2}})}^{\frac{1}{2}}, m_{1} > 0, Δ < 0 .

(13)

Φ_{6} (η) = {(\frac{2 m_{1}}{ε \sqrt{Δ} sin (2 \sqrt{- m_{1}} η) - m_{2}})}^{\frac{1}{2}}, m_{1} < 0, Δ > 0 .

(14)

Φ_{7} (η) = {(\frac{- m_{1} {sech}^{2} (\sqrt{m_{1}} η)}{m_{2}^{2} - 2 ε \sqrt{m_{1} m_{3}} tanh (\sqrt{m_{1}} η)})}^{\frac{1}{2}}, m_{1}, m_{3} > 0 .

(15)

Φ_{8} (η) = {(\frac{- m_{1} {sec}^{2} (\sqrt{- m_{1}} η)}{m_{2}^{2} + 2 ε \sqrt{- m_{1} m_{3}} tan (\sqrt{- m_{1}} η)})}^{\frac{1}{2}}, m_{1} < 0, m_{3} > 0 .

(16)

Φ_{9} (η) = {(\frac{m_{1} {csch}^{2} (\sqrt{m_{1}} η)}{m_{2}^{2} + 2 ε \sqrt{m_{1} m_{3}} coth (\sqrt{m_{1}} η)})}^{\frac{1}{2}}, m_{1} > 0, m_{3} > 0 .

(17)

Φ_{10} (η) = {(\frac{- m_{1} csc (\sqrt{- m_{1}} η)}{m_{2}^{2} + 2 ε \sqrt{- m_{1} m_{3}} tanh (\sqrt{- m_{1}} η)})}^{\frac{1}{2}}, m_{1} < 0, m_{3} > 0 .

(18)

Φ_{11} (η) = {(- \frac{m_{1}}{m_{2}} (1 + ε tanh (\frac{\sqrt{m_{1}}}{2} η)))}^{\frac{1}{2}}, m_{1} > 0, Δ = 0 .

(19)

Φ_{12} (η) = {(- \frac{m_{1}}{m_{2}} (1 + ε coth (\frac{\sqrt{m_{1}}}{2} η)))}^{\frac{1}{2}}, m_{1} > 0, Δ = 0 .

(20)

Φ_{13} (η) = 4 {(\frac{m_{1} e^{2 ε \sqrt{m_{1}} η}}{{(e^{2 ε \sqrt{m_{1}} η} - 4 m_{2})}^{2} - 64 m_{1} m_{3}})}^{\frac{1}{2}} m_{1} > 0 .

(21)

Φ_{14} (η) = 4 {(\frac{\pm m_{1} e^{2 ε \sqrt{m_{1}} η}}{(1 - 64 m_{1} m_{3} e^{4 ε \sqrt{m_{1}} η}})}^{\frac{1}{2}}, m_{1} > 0, m_{2} = 0,

where

Δ = m_{2}^{2} - 4 m_{1} m_{3}

and

ε = \pm 1

.Hence, the multiple exact solutions to the NLFNEE of Eq. (5) can be reached by considering Eq. (6) along with Eqs. (8)-(21).

Next, we will investigate the application of the previous illustrated method for solving the system of Eq. (1).

3 Exact bright and singular solitons of system (1)

In this section, the effectiveness of the methodis being tested for solving equation Eq. (1). First, assume that

(22)

\begin{matrix} E (x, t) = u (η) e^{i μ}, n (x, t) = v (η), \\ μ = k x + \frac{ω (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)}, \\ η = γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)}, \end{matrix}

where

β

and

ω

are considered constants. Then, by plugging Eq. (22) into Eq. (1) yields the following

(23)

\frac{1}{2} γ^{2} u^{″} + i (β + k γ) u^{'} - 0.5 (k^{2} + 2 w) u - u v = 0,

(24)

(β^{2} - γ^{2}) v^{″} + 4 γ^{2} (u^{^{'} 2} - u u^{″}) = 0 .

By dividing the resulting equation into real and imaginary parts which provide

(25)

β = - k γ,

and then by double integrating Eq. (24) with respect to $η$ , we reach

(26)

v = \frac{2 γ^{2}}{β^{2} - γ^{2}} u^{2} = \frac{2}{k^{2} - 1} u^{2} .

Plugging Eq. (25) and Eq. (26) into Eq. (23), finally results in

(27)

u^{″} - \frac{4}{γ^{2} (k^{2} - 1)} u^{3} - \frac{(k^{2} + 2 w)}{γ^{2}} u = 0,

_or

(28)

u^{″} = \frac{(k^{2} + 2 w)}{γ^{2}} u + \frac{4}{γ^{2} (k^{2} - 1)} u^{3} .

Fo the last step, we balance the two terms of $u^{″}$ and $u^{3}$ with the aid of homogeneous principle which will provide $M = 1 .$ With $M = 1$ , Eq. (28) has the form

(29)

u (η) = B_{0} + B_{1} Φ (η),

with $B_{0}$ and $B_{1}$ being constant terms to be determined. Finally, replacing Eq. (29) into Eq. (28) by the fact that Eq. (7) is satisfied to adjust all coefficients of $Φ^{i} (η)$ for $(i = 0, 1, 2, \dots)$ to zero, we reach an algebraic class of systems, which can be simplified as

(30)

n_{0} = 0, n_{1} = \pm \frac{1}{2} \sqrt{2 γ^{2} m_{2} (k^{2} - 1)}, m_{3} = 0, ω = \frac{1}{2} (γ^{2} m_{1} - k^{2}) .

The following cases can be considered:

Case

I: When $m_{1} > 0,$ the solution takes the form

(31)

\begin{matrix} E_{1}^{\pm} (x, t) = \pm \frac{γ \sqrt{- 2 m_{1} (k^{2} - 1)}}{2} sech (\sqrt{m_{1}} (γ x - \frac{β (α - 1) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \\ n_{1} (x, t) = - γ^{2} m_{1} {sech}^{2} (\sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \end{matrix}

(32)

\begin{matrix} E_{2}^{\pm} (x, t) = \pm \frac{γ \sqrt{2 m_{1} (k^{2} - 1)}}{2} csch (\sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \\ n_{2} (x, t) = γ^{2} m_{1} {sech}^{2} (\sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \end{matrix}

(33)

\begin{matrix} E_{3}^{\pm} (x, t) = \pm \sqrt{\frac{m_{1} γ^{2} (k^{2} - 1)}{cosh (2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}} \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(\frac{α}{α - 1})}^{r} Γ (1 - α r)})), \\ n_{3} (x, t) = \frac{2 m_{1} γ^{2}}{cosh (2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}, \end{matrix}

(34)

\begin{matrix} E_{4}^{\pm} (x, t) = \pm \sqrt{\frac{m_{1} γ^{2} (k^{2} - 1)}{i sinh (2 \sqrt{m_{1}} (γ x - \frac{β (α - 1) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}} \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(\frac{α}{α - 1})}^{r} Γ (1 - α r)})), \\ n_{4} (x, t) = \frac{2 m_{1} γ^{2}}{i sinh (2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}, \end{matrix}

(35)

\begin{matrix} E_{5}^{\pm} (x, t) = \frac{\sqrt{8 γ^{2} m_{1} m_{2} (k^{2} - 1) e^{2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})}}}{e^{2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})} - 4 m_{2}} \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \\ n_{5} (x, t) = \frac{16 γ^{2} m_{1} m_{2} e^{2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})}}{{(e^{2 \sqrt{m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})} - 4 m_{2})}^{2}} . \end{matrix}

Case

II: When $m_{1} < 0,$ the solution can take the following form

(36)

\begin{matrix} E_{6}^{\pm} (x, t) = \pm \sqrt{\frac{m_{1} γ^{2} (k^{2} - 1)}{cos (2 \sqrt{- m_{1}} (γ x - \frac{β (α - 1) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}} \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \\ n_{6} (x, t) = \frac{2 m_{1} γ^{2}}{cos (2 \sqrt{- m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}, \end{matrix}

(37)

\begin{matrix} E_{7}^{\pm} (x, t) = \pm \sqrt{\frac{m_{1} γ^{2} (k^{2} - 1)}{sin (2 \sqrt{- m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1}} \\ \times exp (i (kx + \frac{(γ^{2} m_{1} - k^{2}) (1 - α) t^{- r}}{2 B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})), \\ n_{7} (x, t) = \frac{2 m_{1} γ^{2}}{sin (2 \sqrt{- m_{1}} (γ x + \frac{β (1 - α) t^{- r}}{B (α) \sum_{r = 0}^{\infty} {(- \frac{α}{1 - α})}^{r} Γ (1 - α r)})) - 1} . \end{matrix}

Considering $ε = 1$ the results given above. One may reach the remaining other results for $ε = - 1$ by utilizing Eqs. (8)-(21).

In the next section, the graphical representation for the solutions for different cases are provided.

4 Results

In this section, we present the plots based on two and three-dimensions to present some of the revealed outcomes. The acquired solutions are given by (Fig. 1 and 2).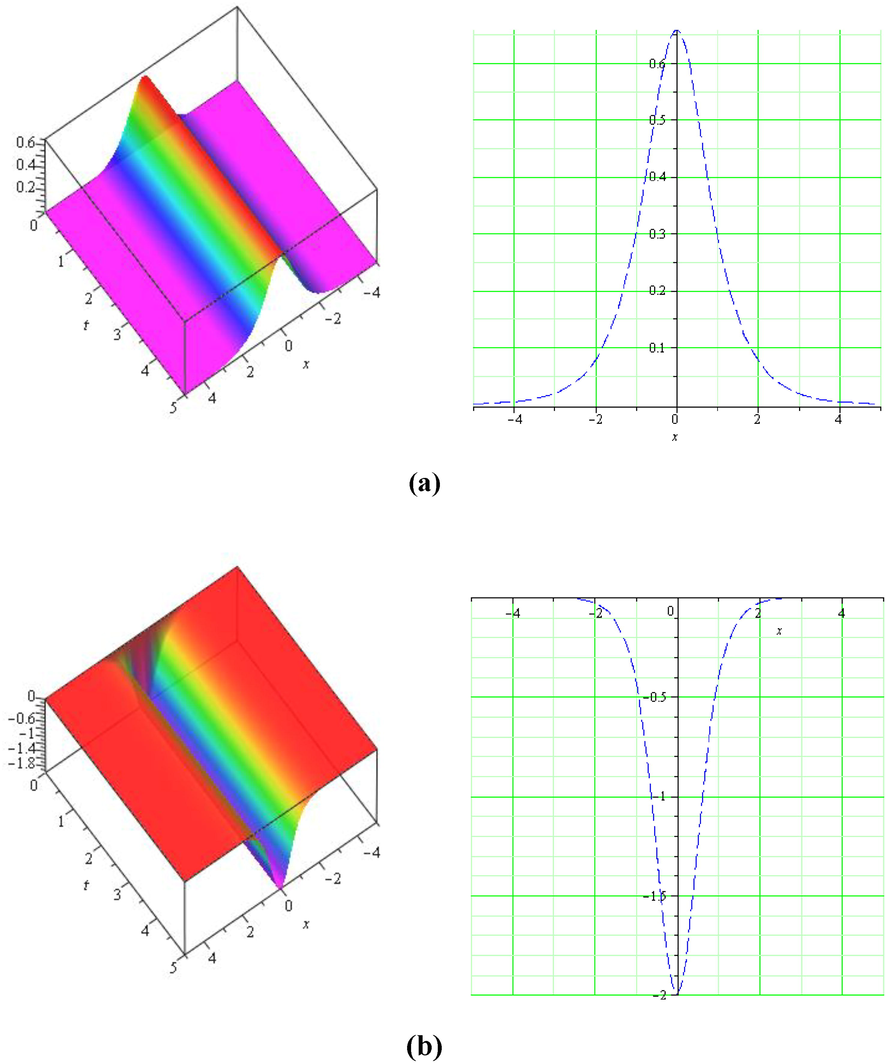

(a) The graphs of the modulus of the bright solitons of E 1 + (b) The two and three-dimensional graphs of the modulus of the bright solitons of n 1 at t = 1 respectively, when γ = 1 , β = 1.5 , m 1 = 2 , k = 0.5 , and α = 0.95 .

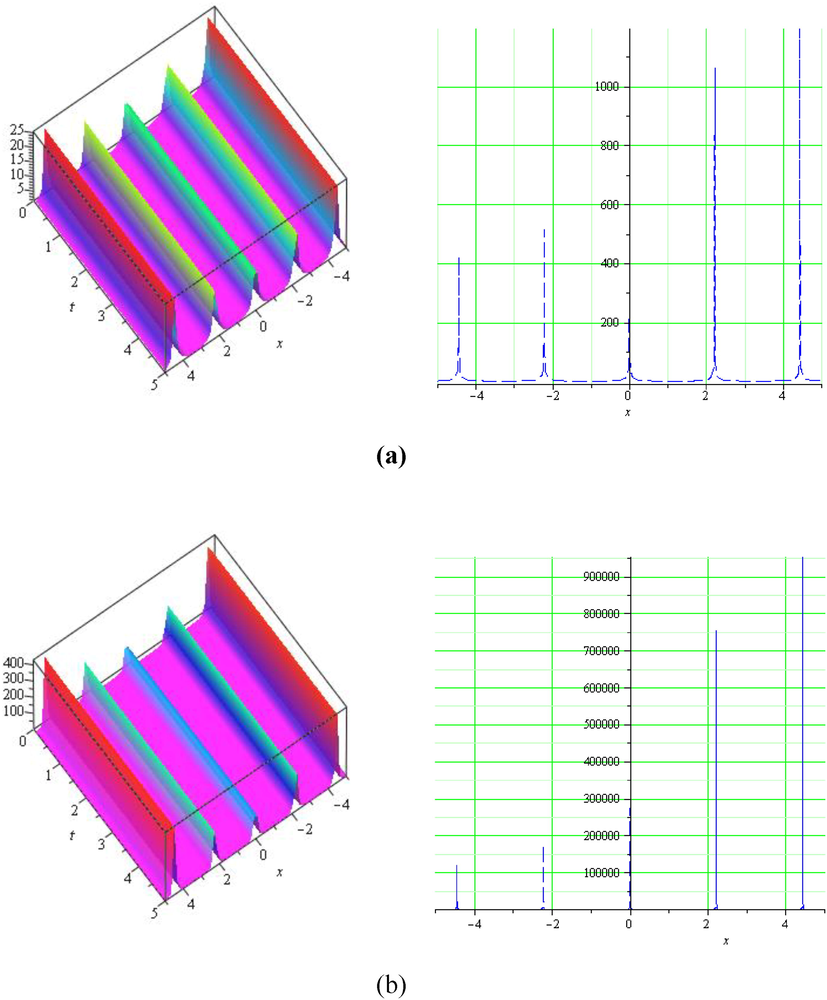
(a) The graphs of the modulus of the bright solitons of E 6 + (b) The two and three-dimensional graphs of the modulus of the bright solitons of n 6 at t = 1 respectively, when γ = 1 , β = 1 , m 1 = - 2 , k = 2 , and α = 0.9 .

5 Conclusion

In this work, we have derived hyperbolic and trigonometric exact wave solutions for the ISALWs system of AB fractional-order using the NAEM. From our solutions obtained in this letter, we conclude that the NAEM is a convenient, efficient, and powerful method for NLFNEEs. Moreover, the results of the proposed NLFNEE in this paper possess many potential usages in engineering and physics. To the best of our knowledge, the solutions revealed for the AB fractional system of equations for the ISALWs are new and have not been submitted to the literature.

Funding

National Natural Science Foundation of China (No. 71601072) and Key Scientific Research Project of Higher Education Institutions in Henan Province of China (No. 20B110006).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Abazari R., Jamshidzadeh S., Biswas A., . Solitary wave solutions of coupled boussinesq equation. Complexity. 2016;21(S2):151-155.
[Google Scholar]
Abazari R., . Solitary-wave solutions of the Klein-Gordon equation with quintic nonlinearity. J. Appl. Mech. Tech. Phys.. 2013;54(3):397-403.
[Google Scholar]
Akinyemi L., Şenol M., Iyiola O.S., . Exact solutions of the generalized multidimensional mathematical physics models via sub-equation method. Math. Comput. Simul. 2021;182:211-233.
[Google Scholar]
Akinyemi L., Şenol M., Huseen S.N., . Modified homotopy methods for generalized fractional perturbed Zakharov-Kuznetsov equation in dusty plasma. Adv. Difference Eq.. 2021;2021(1):1-27.
[Google Scholar]
Akinyemi L., . A fractional analysis of Noyes-Field model for the nonlinear Belousov-Zhabotinsky reaction. Comput. Appl. Math.. 2020;39:1-34.
[Google Scholar]
Aminikhah H., Sheikhani A.R., Rezazadeh H., . Exact solutions for the fractional differential equations by using the first integral method. Nonlinear Eng.. 2015;4(1):15-22.
[Google Scholar]
Atangana A., Koca I., . Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solitons Fractals. 2016;89:447-454.
[Google Scholar]
Atangana A., Gómez-Aguilar J.F., . Numerical approximation of Riemann-Liouville definition of fractional derivative: from Riemann-Liouville to Atangana-Baleanu. Numerical Methods Partial Differential Equations. 2018;34(5):1502-1523.
[Google Scholar]
Biswas A., Rezazadeh H., Mirzazadeh M., Eslami M., Ekici M., Zhou Q., Belic M., . Optical soliton perturbation with Fokas-Lenells equation using three exotic and efficient integration schemes. Optik. 2018;165:288-294.
[Google Scholar]
Bulut H., Sulaiman T.A., Baskonus H.M., Rezazadeh H., Eslami M., Mirzazadeh M., . Optical solitons and other solutions to the conformable space–time fractional Fokas-Lenells equation. Optik. 2018;172:20-27.
[Google Scholar]
Bulut H., Sulaiman T.A., Baskonus H.M., . Dark, bright optical and other solitons with conformable space-time fractional second-order spatiotemporal dispersion. Optik. 2018;163:1-7.
[Google Scholar]
Çenesiz Y., Baleanu D., Kurt A., Tasbozan O., . New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Medium. 2017;27(1):103-116.
[Google Scholar]
Ghanbari B., Nisar K.S., Aldhaifallah M., . Abundant solitary wave solutions to an extended nonlinear Schrödinger’s equation with conformable derivative using an efficient integration method. Adv. Difference Equations. 2020;2020(1):1-25.
[Google Scholar]
Ghanbari B., Yusuf A., Baleanu D., . The new exact solitary wave solutions and stability analysis for the (2+1)-dimensional Zakharov-Kuznetsov equation. Adv. Difference Equations. 2019;2019(1):1-15.
[Google Scholar]
Hashemi M.S., Akgül A., . Solitary wave solutions of time–space nonlinear fractional Schrödinger’s equation: two analytical approaches. J. Comput. Appl. Math.. 2018;339:147-160.
[Google Scholar]
Hashemi M.S., . Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals. 2018;107:161-169.
[Google Scholar]
Hosseini K., Mirzazadeh M., Rabiei F., Baskonus H.M., Yel G., . Dark optical solitons to the Biswas-Arshed equation with high order dispersions and absence of self-phase modulation. Optik. 2020;164576
[Google Scholar]
Hosseini K., Osman M.S., Mirzazadeh M., Rabiei F., . Investigation of different wave structures to the generalized third-order nonlinear Scrödinger equation. Optik. 2020;206:164259.
[CrossRef] [Google Scholar]
Hosseini K., Mirzazadeh M., Ilie M., Gómez-Aguilar J.F., . Biswas-Arshed equation with the beta time derivative: optical solitons and other solutions. Optik. 2020;217:164801.
[CrossRef] [Google Scholar]
Khater M., Attia R., Lu D., . Modified auxiliary equation method versus three nonlinear fractional biological models in present explicit wave solutions. Math. Comput. Appl.. 2019;24(1):1.
[Google Scholar]
Khater M.M.A., Lu D., Attia R.A.M., . Dispersive long wave of nonlinear fractional Wu-Zhang system via a modified auxiliary equation method. AIP Adv.. 2019;9(2):025003.
[CrossRef] [Google Scholar]
Khater M.M., Attia R.A., Abdel-Aty A.H., Alharbi W., Lu D., . Abundant analytical and numerical solutions of the fractional microbiological densities model in bacteria cell as a result of diffusion mechanisms. Chaos Solitonsand Fractals. 2020;136:109824
[Google Scholar]
Korkmaz A., Hepson O.E., Hosseini K., Rezazadeh H., Eslami M., . Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud Univ.-Sci.. 2020;32(1):567-574.
[Google Scholar]
Kurt A., . New periodic wave solutions of a time fractional integrable shallow water equation. Appl. Ocean Res.. 2019;85:128-135.
[Google Scholar]
Munusamy K., Ravichandran C., Nisar K.S., Ghanbari B., . Existence of solutions for some functional integrodifferential equations with nonlocal conditions. Math. Methods Appl. Sci.. 2020;43(17):10319-10331.
[Google Scholar]
Najafi R., Bahrami F., Hashemi M.S., . Classical and nonclassical Lie symmetry analysis to a class of nonlinear time-fractional differential equations. Nonlinear Dyn.. 2017;87(3):1785-1796.
[Google Scholar]
Park C., Khater M.M., Abdel-Aty A.H., Attia R.A., Rezazadeh H., Zidan A.M., Mohamed A.B., . Dynamical analysis of the nonlinear complex fractional emerging telecommunication model with higher-order dispersive cubic-quintic. Alexandria Eng. J.. 2020;59(3):1425-1433.
[Google Scholar]
Rahman G., Nisar K.S., Ghanbari B., Abdeljawad T., . On generalized fractional integral inequalities for the monotone weighted Chebyshev functionals. Adv. Difference Equations. 2020;2020(1):1-19.
[Google Scholar]
Rezazadeh H., Kumar D., Sulaiman T.A., Bulut H., . New complex hyperbolic and trigonometric solutions for the generalized conformable fractional Gardner equation. Mod. Phys. Lett. B. 2019;33(17):1950196.
[CrossRef] [Google Scholar]
Rezazadeh H., Mirhosseini-Alizamini S.M., Neirameh A., Souleymanou A., Korkmaz A., Bekir A., . Fractional sine-gordon equation approach to the coupled higgs system defined in time-fractional form. Iran. J. Sci. Technol. Trans. A: Sci.. 2019;43(6):2965-2973.
[Google Scholar]
Rizvi S.T.R., Khan S.-D., Hassan M., Fatima I., Khan S.-D., . Stable propagation of optical solitons for nonlinear Schrödinger equation with dispersion and self phase modulation. Math. Comput. Simul. 2021;179:126-136.
[Google Scholar]
Rizvi S.T.R., Ali K., Ahmad M., . Optical solitons for Biswas-Milovic equation by new extended auxiliary equation method. Optik. 2020;204:164181.
[CrossRef] [Google Scholar]
Rizvi S.T.R., Ali I., Ali K., Mustafa G., . Conserved densities and fluxes for nonlinear Schrödinger equations using scaling invariance approach. Mod. Phys. Lett. B. 2020;34(26):2050275.
[CrossRef] [Google Scholar]
Rizvi S.T.R., Afzal I., Ali K., . Dark and singular optical solitons for Kundu-Mukherjee-Naskar model. Mod. Phys. Lett. B. 2020;34(06):2050074.
[CrossRef] [Google Scholar]
Rizvi S.T.R., Safdar U., Bibi I., Ali K., Zhou Q., . Solitons of the complex nonlinear Schrödinger equation with parity-time-symmetric linear-nonlinear lattice potentials. Roman. Rep. Phys.. 2020;72:111.
[Google Scholar]
Şenol M., Iyiola O.S., Kasmaei H.D., Akinyemi L., . Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent-Miodek system with energy-dependent Schrödinger potential. Adv. Difference Equations. 2019;2019(1):462.
[Google Scholar]
Sirendaoreji. (2006). A new auxiliary equation and exact travelling wave solutions of nonlinear equations. Phys. Lett. A. 356: 124-130.
Sulaiman T.A., Bulut H., Baskonus H.M., . Optical solitons to the fractional perturbed NLSE in nano-fibers. Discr. Continuous Dyn. Syst.-S.. 2020;13(3):925.
[Google Scholar]
Tasbozan O., Çenesiz Y., Kurt A., . New solutions for conformable fractional Boussinesq and combined KdV-mKdV equations using Jacobi elliptic function expansion method. Eur. Phys. J. Plus. 2016;131(7):244.
[Google Scholar]
Wang G.-W., Xu T.-Z., Abazari R., Jovanoski Z., Biswas A., . Shock waves and other solutions to the Benjamin-Bona-Mahoney-Burgers equation with dual power-law nonlinearity. Acta Phys. Pol. A. 2014;126(6):1221-1225.
[Google Scholar]
Yajima N., Oikawa M., . Formation and interaction of sonic-Langmuir solitons: inverse scattering method. Progress Theoret. Phys.. 1976;56(6):1719-1739.
[Google Scholar]
Younas U., Seadawy Aly R., Younis M., Rizvi S.T.R., . Dispersive of propagation wave structures to the dullin-Gottwald-Holm dynamical equation in a shallow water waves. Chin. J. Phys.. 2020;68:348-364.
[Google Scholar]
Younis M., Yousaf U., Ahmed N., Rizvi S.T.R., Iqbal M.S., Baleanu D., . Investigation of electromagnetic wave structures for a coupled model in antiferromagnetic spin-ladder medium. Front. Phys.. 2020;8:215.
[Google Scholar]
Younis M., Ali S., Rizvi S.T.R., Tantawy M., Tariq K.U., Bekir A., . Investigation of solitons and mixed lump wave solutions with (3+ 1)-dimensional potential-YTSF equation. Commun. Nonlinear Sci. Numer. Simul.. 2021;94:105544
[Google Scholar]
Yue C., Khater M.M., Attia R.A., Lu D., . The plethora of explicit solutions of the fractional KS equation through liquid-gas bubbles mix under the thermodynamic conditions via Atangana-Baleanu derivative operator. Adv. Difference Equations. 2020;2020(1):1-12.
[Google Scholar]

Introduction

Methods

Exact bright and singular solitons of system (1)

Results

Conclusion

Funding

Fulltext Views
28

PDF downloads
10

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abazari R., Jamshidzadeh S., Biswas A., . Solitary wave solutions of coupled boussinesq equation. Complexity. 2016;21(S2):151-155.
[Google Scholar]

[2] Abazari R., . Solitary-wave solutions of the Klein-Gordon equation with quintic nonlinearity. J. Appl. Mech. Tech. Phys.. 2013;54(3):397-403.
[Google Scholar]

[3] Akinyemi L., Şenol M., Iyiola O.S., . Exact solutions of the generalized multidimensional mathematical physics models via sub-equation method. Math. Comput. Simul. 2021;182:211-233.
[Google Scholar]

[4] Akinyemi L., Şenol M., Huseen S.N., . Modified homotopy methods for generalized fractional perturbed Zakharov-Kuznetsov equation in dusty plasma. Adv. Difference Eq.. 2021;2021(1):1-27.
[Google Scholar]

[5] Akinyemi L., . A fractional analysis of Noyes-Field model for the nonlinear Belousov-Zhabotinsky reaction. Comput. Appl. Math.. 2020;39:1-34.
[Google Scholar]

[6] Aminikhah H., Sheikhani A.R., Rezazadeh H., . Exact solutions for the fractional differential equations by using the first integral method. Nonlinear Eng.. 2015;4(1):15-22.
[Google Scholar]

[7] Atangana A., Koca I., . Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solitons Fractals. 2016;89:447-454.
[Google Scholar]

[8] Atangana A., Gómez-Aguilar J.F., . Numerical approximation of Riemann-Liouville definition of fractional derivative: from Riemann-Liouville to Atangana-Baleanu. Numerical Methods Partial Differential Equations. 2018;34(5):1502-1523.
[Google Scholar]

[9] Biswas A., Rezazadeh H., Mirzazadeh M., Eslami M., Ekici M., Zhou Q., Belic M., . Optical soliton perturbation with Fokas-Lenells equation using three exotic and efficient integration schemes. Optik. 2018;165:288-294.
[Google Scholar]

[10] Bulut H., Sulaiman T.A., Baskonus H.M., Rezazadeh H., Eslami M., Mirzazadeh M., . Optical solitons and other solutions to the conformable space–time fractional Fokas-Lenells equation. Optik. 2018;172:20-27.
[Google Scholar]

[11] Bulut H., Sulaiman T.A., Baskonus H.M., . Dark, bright optical and other solitons with conformable space-time fractional second-order spatiotemporal dispersion. Optik. 2018;163:1-7.
[Google Scholar]

[12] Çenesiz Y., Baleanu D., Kurt A., Tasbozan O., . New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Medium. 2017;27(1):103-116.
[Google Scholar]

[13] Ghanbari B., Nisar K.S., Aldhaifallah M., . Abundant solitary wave solutions to an extended nonlinear Schrödinger’s equation with conformable derivative using an efficient integration method. Adv. Difference Equations. 2020;2020(1):1-25.
[Google Scholar]

[14] Ghanbari B., Yusuf A., Baleanu D., . The new exact solitary wave solutions and stability analysis for the (2+1)-dimensional Zakharov-Kuznetsov equation. Adv. Difference Equations. 2019;2019(1):1-15.
[Google Scholar]

[15] Hashemi M.S., Akgül A., . Solitary wave solutions of time–space nonlinear fractional Schrödinger’s equation: two analytical approaches. J. Comput. Appl. Math.. 2018;339:147-160.
[Google Scholar]

[16] Hashemi M.S., . Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals. 2018;107:161-169.
[Google Scholar]

[17] Hosseini K., Mirzazadeh M., Rabiei F., Baskonus H.M., Yel G., . Dark optical solitons to the Biswas-Arshed equation with high order dispersions and absence of self-phase modulation. Optik. 2020;164576
[Google Scholar]

[18] Hosseini K., Osman M.S., Mirzazadeh M., Rabiei F., . Investigation of different wave structures to the generalized third-order nonlinear Scrödinger equation. Optik. 2020;206:164259.
[CrossRef] [Google Scholar]

[19] Hosseini K., Mirzazadeh M., Ilie M., Gómez-Aguilar J.F., . Biswas-Arshed equation with the beta time derivative: optical solitons and other solutions. Optik. 2020;217:164801.
[CrossRef] [Google Scholar]

[20] Khater M., Attia R., Lu D., . Modified auxiliary equation method versus three nonlinear fractional biological models in present explicit wave solutions. Math. Comput. Appl.. 2019;24(1):1.
[Google Scholar]

[21] Khater M.M.A., Lu D., Attia R.A.M., . Dispersive long wave of nonlinear fractional Wu-Zhang system via a modified auxiliary equation method. AIP Adv.. 2019;9(2):025003.
[CrossRef] [Google Scholar]

[22] Khater M.M., Attia R.A., Abdel-Aty A.H., Alharbi W., Lu D., . Abundant analytical and numerical solutions of the fractional microbiological densities model in bacteria cell as a result of diffusion mechanisms. Chaos Solitonsand Fractals. 2020;136:109824
[Google Scholar]

[23] Korkmaz A., Hepson O.E., Hosseini K., Rezazadeh H., Eslami M., . Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud Univ.-Sci.. 2020;32(1):567-574.
[Google Scholar]

[24] Kurt A., . New periodic wave solutions of a time fractional integrable shallow water equation. Appl. Ocean Res.. 2019;85:128-135.
[Google Scholar]

[25] Munusamy K., Ravichandran C., Nisar K.S., Ghanbari B., . Existence of solutions for some functional integrodifferential equations with nonlocal conditions. Math. Methods Appl. Sci.. 2020;43(17):10319-10331.
[Google Scholar]

[26] Najafi R., Bahrami F., Hashemi M.S., . Classical and nonclassical Lie symmetry analysis to a class of nonlinear time-fractional differential equations. Nonlinear Dyn.. 2017;87(3):1785-1796.
[Google Scholar]

[27] Park C., Khater M.M., Abdel-Aty A.H., Attia R.A., Rezazadeh H., Zidan A.M., Mohamed A.B., . Dynamical analysis of the nonlinear complex fractional emerging telecommunication model with higher-order dispersive cubic-quintic. Alexandria Eng. J.. 2020;59(3):1425-1433.
[Google Scholar]

[28] Rahman G., Nisar K.S., Ghanbari B., Abdeljawad T., . On generalized fractional integral inequalities for the monotone weighted Chebyshev functionals. Adv. Difference Equations. 2020;2020(1):1-19.
[Google Scholar]

[29] Rezazadeh H., Kumar D., Sulaiman T.A., Bulut H., . New complex hyperbolic and trigonometric solutions for the generalized conformable fractional Gardner equation. Mod. Phys. Lett. B. 2019;33(17):1950196.
[CrossRef] [Google Scholar]

[30] Rezazadeh H., Mirhosseini-Alizamini S.M., Neirameh A., Souleymanou A., Korkmaz A., Bekir A., . Fractional sine-gordon equation approach to the coupled higgs system defined in time-fractional form. Iran. J. Sci. Technol. Trans. A: Sci.. 2019;43(6):2965-2973.
[Google Scholar]

[31] Rizvi S.T.R., Khan S.-D., Hassan M., Fatima I., Khan S.-D., . Stable propagation of optical solitons for nonlinear Schrödinger equation with dispersion and self phase modulation. Math. Comput. Simul. 2021;179:126-136.
[Google Scholar]

[32] Rizvi S.T.R., Ali K., Ahmad M., . Optical solitons for Biswas-Milovic equation by new extended auxiliary equation method. Optik. 2020;204:164181.
[CrossRef] [Google Scholar]

[33] Rizvi S.T.R., Ali I., Ali K., Mustafa G., . Conserved densities and fluxes for nonlinear Schrödinger equations using scaling invariance approach. Mod. Phys. Lett. B. 2020;34(26):2050275.
[CrossRef] [Google Scholar]

[34] Rizvi S.T.R., Afzal I., Ali K., . Dark and singular optical solitons for Kundu-Mukherjee-Naskar model. Mod. Phys. Lett. B. 2020;34(06):2050074.
[CrossRef] [Google Scholar]

[35] Rizvi S.T.R., Safdar U., Bibi I., Ali K., Zhou Q., . Solitons of the complex nonlinear Schrödinger equation with parity-time-symmetric linear-nonlinear lattice potentials. Roman. Rep. Phys.. 2020;72:111.
[Google Scholar]

[36] Şenol M., Iyiola O.S., Kasmaei H.D., Akinyemi L., . Efficient analytical techniques for solving time-fractional nonlinear coupled Jaulent-Miodek system with energy-dependent Schrödinger potential. Adv. Difference Equations. 2019;2019(1):462.
[Google Scholar]

[37] Sirendaoreji. (2006). A new auxiliary equation and exact travelling wave solutions of nonlinear equations. Phys. Lett. A. 356: 124-130.

[38] Sulaiman T.A., Bulut H., Baskonus H.M., . Optical solitons to the fractional perturbed NLSE in nano-fibers. Discr. Continuous Dyn. Syst.-S.. 2020;13(3):925.
[Google Scholar]

[39] Tasbozan O., Çenesiz Y., Kurt A., . New solutions for conformable fractional Boussinesq and combined KdV-mKdV equations using Jacobi elliptic function expansion method. Eur. Phys. J. Plus. 2016;131(7):244.
[Google Scholar]

[40] Wang G.-W., Xu T.-Z., Abazari R., Jovanoski Z., Biswas A., . Shock waves and other solutions to the Benjamin-Bona-Mahoney-Burgers equation with dual power-law nonlinearity. Acta Phys. Pol. A. 2014;126(6):1221-1225.
[Google Scholar]

[41] Yajima N., Oikawa M., . Formation and interaction of sonic-Langmuir solitons: inverse scattering method. Progress Theoret. Phys.. 1976;56(6):1719-1739.
[Google Scholar]

[42] Younas U., Seadawy Aly R., Younis M., Rizvi S.T.R., . Dispersive of propagation wave structures to the dullin-Gottwald-Holm dynamical equation in a shallow water waves. Chin. J. Phys.. 2020;68:348-364.
[Google Scholar]

[43] Younis M., Yousaf U., Ahmed N., Rizvi S.T.R., Iqbal M.S., Baleanu D., . Investigation of electromagnetic wave structures for a coupled model in antiferromagnetic spin-ladder medium. Front. Phys.. 2020;8:215.
[Google Scholar]

[44] Younis M., Ali S., Rizvi S.T.R., Tantawy M., Tariq K.U., Bekir A., . Investigation of solitons and mixed lump wave solutions with (3+ 1)-dimensional potential-YTSF equation. Commun. Nonlinear Sci. Numer. Simul.. 2021;94:105544
[Google Scholar]

[45] Yue C., Khater M.M., Attia R.A., Lu D., . The plethora of explicit solutions of the fractional KS equation through liquid-gas bubbles mix under the thermodynamic conditions via Atangana-Baleanu derivative operator. Adv. Difference Equations. 2020;2020(1):1-12.
[Google Scholar]

Bright and singular soliton solutions to the Atangana-Baleanu fractional system of equations for the ISALWs

Abstract

Keywords

Newauxiliary equation scheme

Equations for the ISALWs

Atangana-Baleanu fractional derivative

1 Introduction

2 Methods

3 Exact bright and singular solitons of system (1)

4 Results

5 Conclusion

Funding

Declaration of Competing Interest

References

Suggested read for related articles:

₂ _Methods