Bottle atom trapping configuration by optical dipole forces

1 Introduction

It is an established fact that optical dipole traps are based on the electric dipole interaction of a laser beam with a two-level atom in the regime of large detuning (Grimm et al., 2000). Typically the trap depths correspond to kinetic temperatures in the range of hundreds of microkelvins. Since the detuning can be quite large, the optical excitation is extremely low, so that in such a trap we avoid the light induced mechanisms which dominate in radiation pressure traps (Cohen-Tannoudji and Guéry-Odelin, 2011; Letokhov, 2007). In such a trapping scheme ultra cold atoms are confined in an almost conservative potential where the influence from spontaneous photon emission is negligible (Grimm et al., 2000). A crucial parameter for trapping is the detuning Δ = ω₀ − ω_L, i.e. the difference between the atomic transition frequency ω₀ and the frequency of the laser beam ω_L. When the interaction of atom with the light field is such that the detuning is negative, the so called “red” detuning regime (Δ < 0), the dipole potential is negative and attracts the atoms into regions of high field intensity. On the contrary, when the detuning is positive, the so called “blue” detuning regime (Δ > 0), the dipole interaction repels atoms away from high intensity regions towards regions of zero light field intensity (Grimm et al., 2000). The basic idea of a blue detuned trap is to create a spatial region which is enclosed by repulsive laser light. The blue detuned trap has been studied because it has two substantial advantages in experimental applications: (a) it provides very deep potentials which ensure tight confinement and (b) it provides box-like potential, with hard repulsive walls (Grimm et al., 2000).

In this work we study the construction of the basic bottle beam configuration consisting of two co-propagating L–G mode beams carrying zero angular momentum (l = 0), but with index p = 0 and p = 2, respectively. The paper is organised as follows: Section 2 summarises the theory of the dipole force, Section 3 develops analytically the theory of the bottle atom trap, and finally, the results, some conclusions and prospects for future work are summarised in Section 4.

2 The dipole force

We first review the average dipole force which is exerted on a two-level atom or ion and offers the advantage of confining atomic particles in all hyperfine levels, thus, the two-level approximation remains valid for large detuning (Grimm et al., 2000). We consider the light as a coherent beam of a complex amplitude a and with a Laguerre–Gaussian (L–G) distribution (Power et al., 1995), and of frequency ω_L. The beam is considered as linearly polarised. The atom is considered as a two-level system having a ground state |1〉 and an excited state |2〉 separated by an amount of energy ℏω₀.

The interaction Hamiltonian H_int describes (Loudon, 2000) the coupling of the atom with the electromagnetic field assuming electric dipole approximation and is given by

The electric field vector of a Laguerre–Gaussian mode which propagates along the z-axis is given by:

The vector $\widehat{\mathbf{e}}$ stands for the polarisation vector in the (x–y) plane. The photon destruction operator is denoted by a. The amplitude and phase terms appearing in Eq. (2) are given as follows

With $C_{\mathit{lp}}=\sqrt{p!/(|l|+p)!}$ the normalisation constant; w(z) is given by: $w^2(z)=2(z^2+z_{\text{R}}^2)/{\mathit{kz}}_R$ . Where z_R is the Rayleigh range (Andrews and Babiker, 2012). The integer indices l, p characterises the L–G mode. The quantity $L_p^{|l|}$ is the associated Laguerre polynomial. The quantity lℏ represents the orbital angular momentum of each photon of the beam (Andrews and Babiker, 2012). The mode index l is also associated with the ratio between the beam radius and the width of the intensity ring The higher the index l, the larger is this ratio and, thus, a harder repulsive radial potential and a weaker atom heating by photon scattering are ensured (Grimm et al., 2000). Finally the term E_k00 corresponds to the amplitude of a plane-wave with an axial wave vector k. The plane wave amplitude and phase emerge directly from Eqs. (3) and (4) by setting l = 0, p = 0, and z_R → ∞. In Eqs. (2)–(4) with R we define the position vector in cylindrical coordinates given by (r, φ, z). The interaction between the atom and the field is given by:

where ${\pi }^{†}$ is the atomic raising operator, $G(\mathbf{R})=({\mathbf{D}}_{\mathbf{12}}·\widehat{\mathbf{e}})E_{\mathit{klp}}(\mathbf{R})\hslash$ and H.c stands for the Hermitian conjugate. Using Heisenberg’s operators perturbation techniques (Power et al., 1995; Andrews and Babiker, 2012; Loudon, 2000) and starting from Eq. (5) we end up with the well-known expression for the optical dipole potential (Cohen-Tannoudji and Guéry-Odelin, 2011):

Where Γ is the excited state line width associated with the spontaneous emission from the excited to the ground state, Δ = ω₀ − ω_L is the detuning and the Rabi frequency is given by: $\mathrm{\Omega }(\mathbf{R})=\sqrt{n_{\text{k}}}G(\mathbf{R})$ , where n_k is the mean photon number in the coherent state of the field.

3 The bottle beam trapping configuration

Blue detuned traps created by interference of Laguerre–Gaussian beams have been experimentally demonstrated in the past (Kuga et al., 1997; Ozeri et al., 1999; Cacciapuoti et al., 2001). Kuga successfully constructed a dark trap with a Laguerre–Gaussian beam blue-detuned with respect to the atomic resonance, trapping 10⁸ atoms for as long as 150 ms. In this trap Kuga and his colleagues created a radial potential barrier of about 40 mK. Radial trapping was achieved by means of a p = 0, l = 3 Laguerre–Gaussian mode, with orbital angular momentum 3ℏ per photon. The axial trapping potential in the direction of propagation was achieved by collecting the beam, dividing it into two beams 2 mm apart and sending the two new beams at a right-angle through the basic beam. The region of trapping was thus defined by the 2 mm space and the near-zero on-axis intensity of the main beam.

Subsequently a trap for long spin relaxation times of ∼300 ms by ingeniously creating a dark region by the insertion of a small phase plate which gave a π difference of phase between two parts of the same beam had been created. Destructive interference between the two parts of the beam, when focussed, ensured a dark region otherwise surrounded by light in all directions (Ozeri et al., 1999). This kind of trap has been used for the demonstration of the trapping of a single Rb atom (Xu et al., 2010). Recently a blue-detuned crossed dipole trap has been used for achieving a fast compression of a large sample of Rb atoms with high densities (Bienaimé et al., 2012) while an optical-box trap has also been formed combining one hollow tube beam with two sheet beams in order to create the necessary repulsive potential for the atoms (Gaunt et al., 2013). The above traps were achieved by the interception of different light beams. Blue detuned traps have also been constructed by using only one beam either in combination with a conical lens (Cacciapuoti et al., 2001) or in combination with gravitational field (Ovchinnikov et al., 1998).

The present work investigates the atomic trapping capacity of the beam configuration (Arlt and Padgett, 2000), where a (0, 0)-mode with a co-lateral (0, 2)-mode was interfered to create what was called a bottle beam. Careful relative phasing of the component modes generated in a hologram, created a dark region of interference near the focus of a lens. Both beams must have an on-axis intensity for the interference to occur which is why l = 0 for each of the beams and consequently neither has any orbital angular momentum. We must also point out that the first of the two beams has p = 0 while for the second one p = 2. The beams, also, have a phase difference equal to π.

The total electric field which corresponds to this configuration is given by the superposition of the following electric fields

In bottle beam configuration the Rabi frequency (Allen et al., 1999) assumes the form

With the expression of the Rabi frequency above we can determine the most important feature of the trap, namely the trapping potential. There are also two other very important parameters for the quality of the trap; the photon scattering rate and the collision rate, which determines the trap lifetime.

The scattering rate can be estimated by the average potential energy seen by the atom. We assume that the z-axis is along the vertical and we also take into account the gravitational potential energy. The average potential energy seen by the atom is given by Bienaimé et al. (2012),

The average scattering rate is given from the relation,

The trap loss rate due to collisions can be estimated by the following relation (Bienaimé et al., 2012):

The beam waist size determines the size of the volume of the trap and is, thus, related to the scattering rate, the potential depth and the collision rate.

We proceed here in numerical estimations of the trapping potential of the bottle beam and other parameters which are going to show us the trapping capacity of our trap and allow comparison with other blue detuned traps mentioned earlier.

The bottle beam trap has been used by Xu et al. (2010) for the trapping of a single atom. The isolation of a single atom in a narrow trap is a result of a mechanism known as collisional blockade (Schlosser et al., 2001b). We need for such a purpose a low trap with a small beam waist and a relatively large detuning. Under such conditions the light-assisted collisions will eject atoms from the trap leaving on average one atom trapped in it.

We consider the trapping of ⁸⁷Rb atoms blue detuned with respect to the D2 line. In our simulation we use a laser power of 40 mW and we consider that the atoms are loaded in the trap having previously cooled in a MOT to a kinetic temperature equal to 100 μK. We also consider a background pressure equal to 10⁻¹⁰ torr. Using the above parameters we get the following plots for the maximum trapping potential and collision rates in the radial direction as presented in Figs. 1 and 2 respectively as functions of the beam waist and detuning.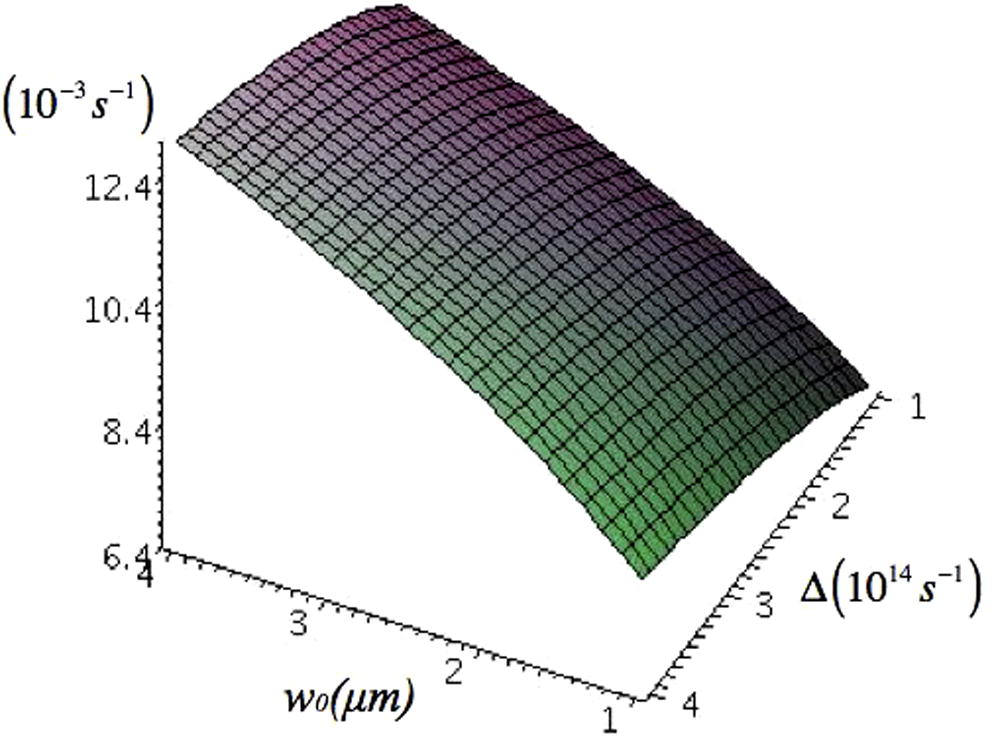

Close

Figure 1

The collision rate in the radial direction as a function of beam waist (in μm) and detuning (in 10¹⁴ s⁻¹). We have assumed a power equal to 40 mW, a background pressure P = 1.0 × 10⁻¹⁰ torr and that the atoms have previously been cooled in a MOT trap to a kinetic temperature of 100 μK.

Export to PPT

Close

Figure 2

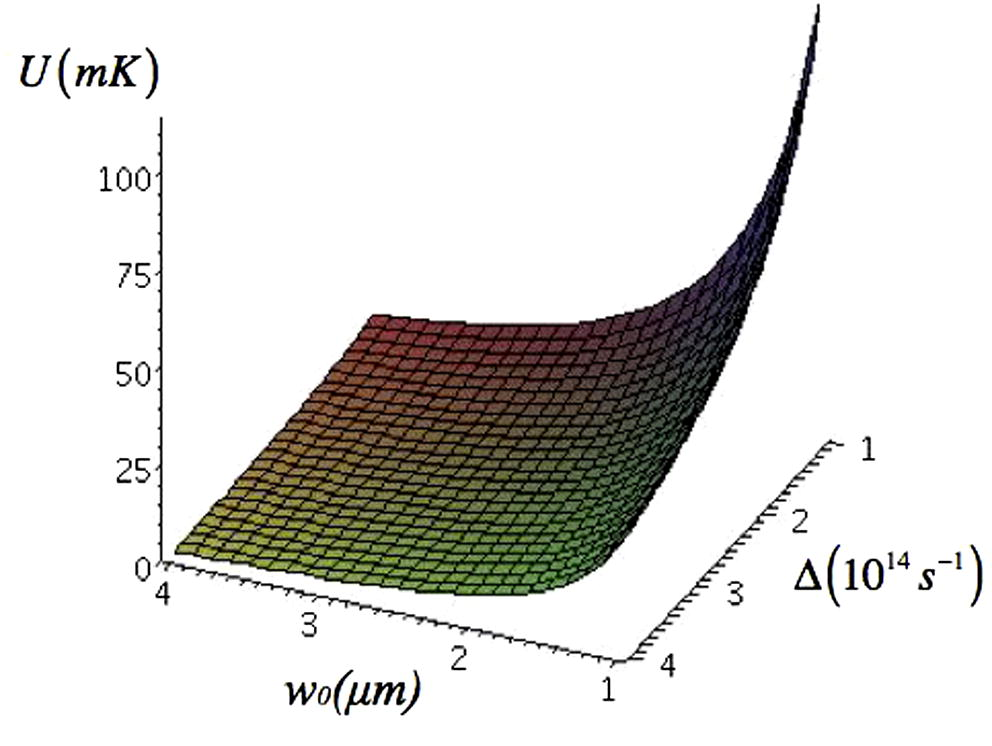
The maximum potential in the radial as a function of beam waist (in μm) and detuning (in 10¹⁴ s⁻¹). We have assumed a power equal to 40 mW, a background pressure P = 1.0 × 10⁻¹⁰ torr and that the atoms have previously been cooled in a MOT trap to a kinetic temperature of 100 μK.

Export to PPT

From Figs. 1 and 2 we see that a low potential is achieved for larger values of beam waists and detuning but for which we have larger collision rates. We choose a beam waist of w₀ = 3 × 10⁻⁶ m and a detuning equal to 2.0 × 10¹⁴ s⁻¹ and we give the trapping potential in Fig. 3.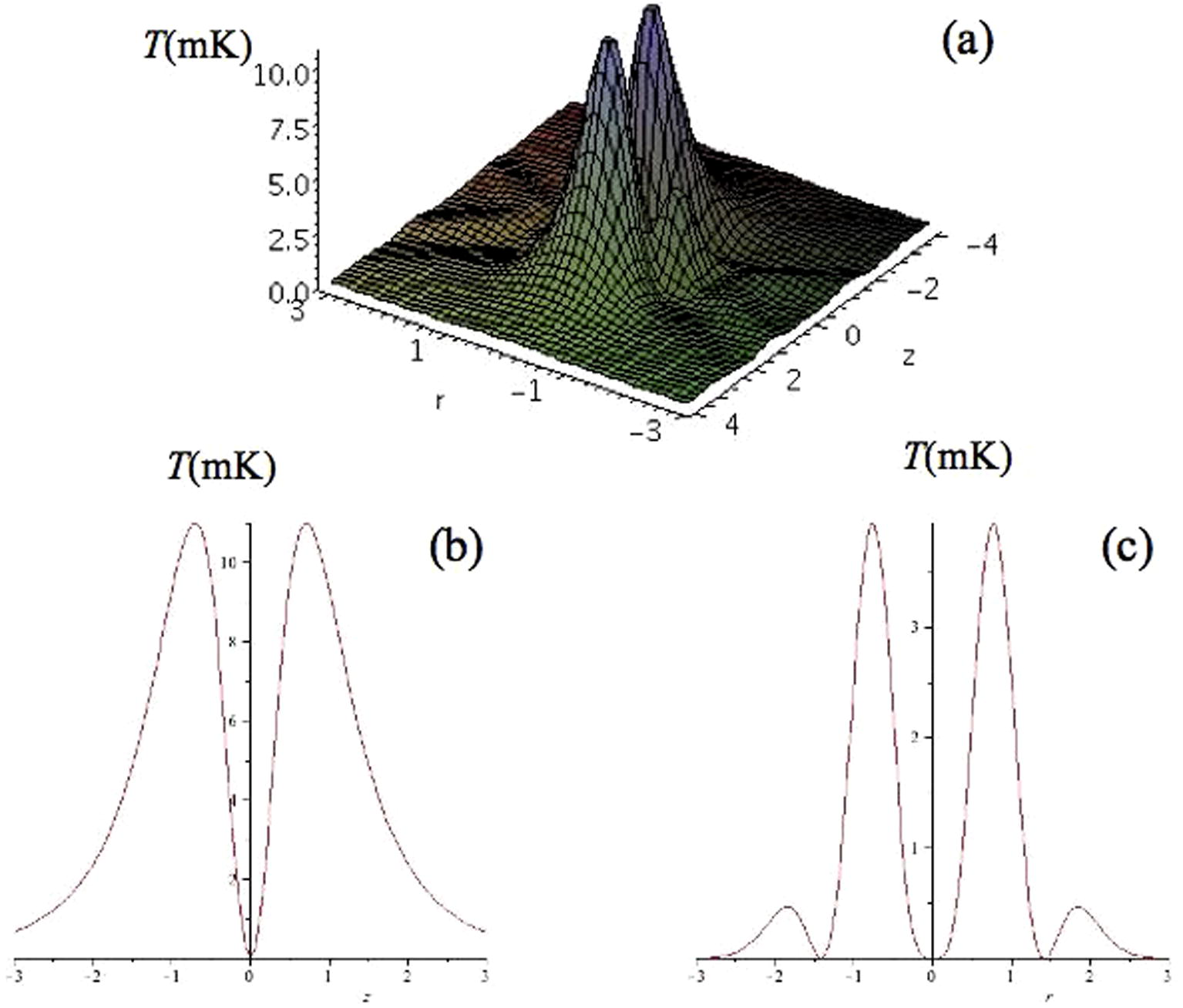

Close

Figure 3

(a) The dipole potential energy for the bottle beam configuration. (b) The dipole potential energy for the bottle beam configuration when r = 0. (c) The dipole potential energy for the bottle beam configuration when z = 0. In all the plots the potential energy is expressed in mK units, the direction along z-axis is scaled in z_R (z_R = 3.6 × 10⁻⁵ m) units while the radial direction is scaled in w₀ units (w₀ = 3 × 10⁻⁶ m).

Export to PPT

Fig. 3a depicts the potential against the radial and axial direction while Fig. 3b and c reflect the potential against the axial and radial direction respectively. In all the plots the potential energy is expressed in mK units, the direction along z-axis is scaled in z_R units while the radial direction is scaled in w₀ units.

It is clear from the graphs that this beam configuration provides a genuine non-assisted blue detuned dipole trap. Since $w_0^2=\lambda z_{\text{R}}/\pi$ , it is clear that for optical transitions, w₀ is much smaller than z_R so the trapping region is elongated along the axial direction fully justifying the term “bottle trap”. In our example z_R ≈ 36 μm, which is about 12 times larger than w₀. Along the radial direction there are potential maxima at r = 0.765w₀, 1.847w₀ and minima at r = 0, 1.414w₀, while along the axial direction we have maxima at z = ±0.836z_R and minimum at z = 0. We also note that the maximum potential along the radial direction is more about three times lower than that in the axial direction. In our trapping scheme the potential maximum in the axial (z) direction is given by

In the above expressions P is the power of the beam and I_s the saturation intensity. Eqs. (14) and (15) are very good approximations for cases where the detuning is much larger than the Rabi frequency.

The bottle trap has a cylindrical geometry. The volume of this trap is given by $\pi w_0^2·0.836z_{\text{R}}$ but since the Rayleigh range and the beam waist are related by $w_0^2=\lambda z_{\text{R}}/\pi$ we can see that the volume of the trap is given by $0.836{\pi }^2{w}_0^4/\lambda$ .

The average scattering rate has been estimated to a value 〈Γ_sc〉 ≈ 3.61 s⁻¹ while for the collision rates we arrive at a value γ_z = 0.0094 s⁻¹ for the trapping along the z-direction and γ_r = 0.011 s⁻¹ in the radial direction. These rates correspond to lifetimes of T_z = 105 s and T_r = 78 s respectively.

The scattering rate depends on all the relevant parameters of the trapping. In Fig. 4 we present a graph of the scattering rate against the beam waist for fixed values of power and detuning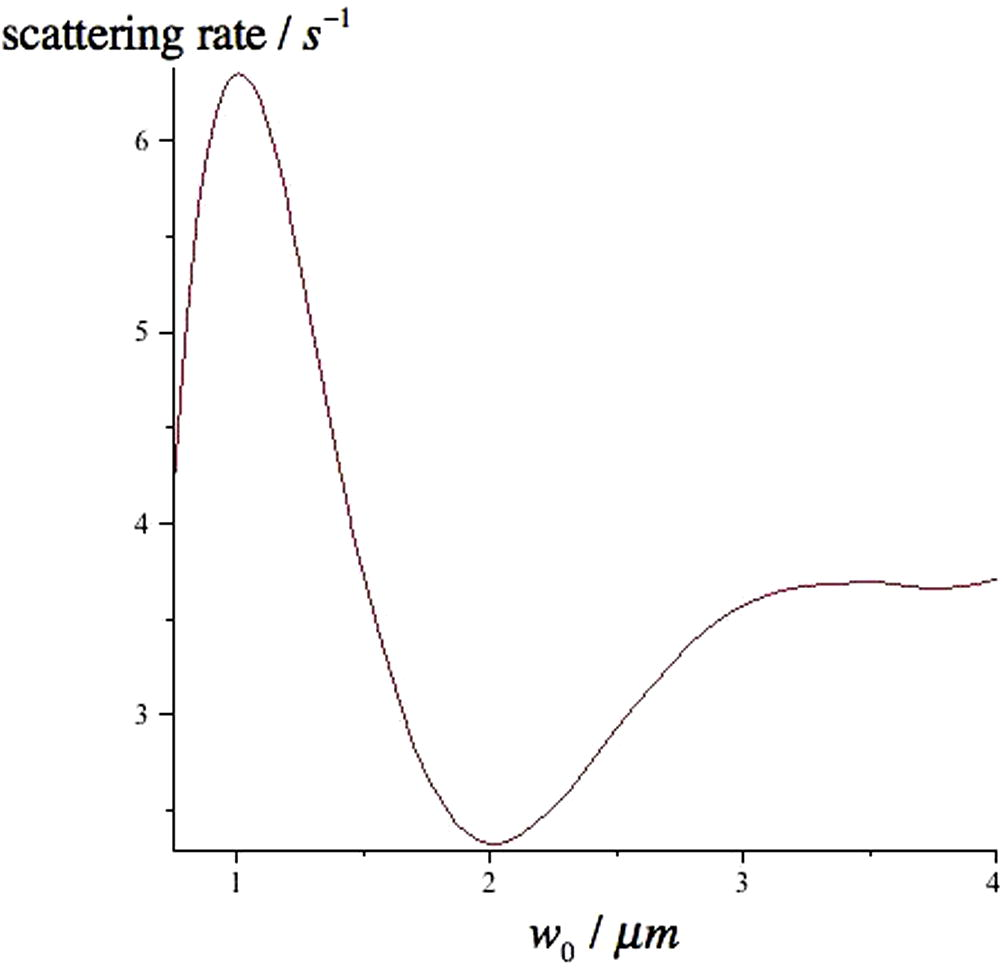

Close

Figure 4

The photon scattering rate as a function of beam waist. We have assumed a power equal to 40 mW and a detuning of 2.0 × 10¹⁴ s⁻¹.

Export to PPT

From Fig. 4 we see a clear dependence of the scattering rate on the beam waist, which presents a minimum around a value of 2 μm. The choice of the best parameters must combine low scattering and collision rates with a small beam waist and maximum trap depth. For example, if we have chosen a beam waist of 2 μm we would have of course a lower scattering rate but a deeper potential.

Finally, gravity is a factor that can push the atoms out of the trap. With the above parameters we found that it suffices a displacement of the atom by few nanometers along the vertical for the trap restoring force, along the z-axis, to balance the weight.

Our numerical work shows results very close to those taken by experimental groups which tried to trap a single atom in dipole traps. An experiment performed by Xu et al. (2010) showed the trapping of a single atom in a bottle-like blue detuned trap. Here with a relatively smaller power of 40 mW (they had 80 mW) but with larger detuning 2.0 × 10¹⁴ s⁻¹ (2.57 × 10¹³ s⁻¹) we arrived at a similar scattering rate of 3.61 s⁻¹ (3.0 s⁻¹) and a larger lifetime of 78 s (50 s). Of course our trap is deeper, around 3.5 mK (in the radial direction) compared to their 1 mK but this can be adjusted by reducing the power. The desired trap depth is also strongly related to the minimum kinetic energy with which the atoms are prepared in the MOT trap before they are loaded in the dipole trap.

The bottle beam seems to have one possible advantage over other proposed blue detuned trapping schemes; it would seem that the centre of gravity of the interference between the two parts of their beam can be affected by moving the focussing lens. This property thus can be used to shift in space a group of trapped atoms in an organised way (Schmid et al., 2006). A shift of the beam may cause the atoms to escape from the trap. To estimate the stability of the trap against the motion of the trap we proceed in the following simple argument (Leng, 2008). The maximum force exerted by the trap along the z-direction is around $F_z^{\max }\approx 1.0\times {10}^{-20}\text{N}$ . This force corresponds to an acceleration of $a_z^{\max }\approx 6.9\times {10}^4{\text{m/s}}^2$ . The maximum acceleration, which can be exerted by moving the trap, is given by $a_z\approx 2x/T^2$ where x is the displacement and T is the time needed for this displacement. If we consider that x = 200 mm and the time around 0.2 s, (Leng (2008)), this gives us an acceleration equal to $a_z\approx 10{\text{m/s}}^2$ . This is a far smaller acceleration than the one exerted by the trap so there is no escape of the atom from the trap for the chosen parameters. This means that we can shift the trap at larger distances in even smaller times while keeping the atom inside it.

So far we have studied the bottle beam configuration as a trapping mechanism for a single atom. We can check the case of trapping larger samples of atoms. A blue detuned trap for fast compression of a cold atomic cloud has been created by Bienaimé et al. (2012) where the authors, using beams with a beam waist equal to 65 μm, have achieved a trapping region with radius 500 μm. This is a large volume trap. To achieve such a volume with our trap we need a large beam waist of around 700 μm which corresponds to a Rayleigh range of about 2 m. Moreover, as our numerics have shown that the forces exerted on the atom by the trap would be weaker than the gravity thus the atoms could not remain in the trap. Our trapping scheme cannot compete traps like the one created by Bienaimé et al. (2012) for efficient trapping and compression of large atom samples. We can consider though a trap of smaller volume. We consider a bottle beam of a beam waist equal to 300 μm, power of 0.1 W, a detuning equal to 20 × 10⁻⁹ s⁻¹, a background pressure equal to 133 × 10⁻¹⁰ Pa and we assume that the atoms were cooled in a MOT trap to a kinetic temperature of 22 μK. The spatial distribution of the potential is similar to the one presented in Fig. 3 so we do not repeat it here. In brackets we give the corresponding quantities for the trap created by Bienaimé et al. (2012). The maximum trapping depth is about 40 mK in the z-direction and about 17 mK (1 mK) in the radial direction. The average scattering rate is 28 s⁻¹ (41 s⁻¹). If we load the trap with Rb atoms the trap loss rate due to collisions is equal to γ_z = 0.0076 s⁻¹ and γ_r = 0.0088 s⁻¹ (0.14 s⁻¹). Obviously we achieve far lower losses due to collisions and we ensure about ten times larger lifetimes.

As we have already said blue detuned traps have been used for the fast compression of atoms towards Bose–Einstein condensation. We are going to investigate some important parameters of such a procedure if we were going to use our trap. The first important step is the efficiency of the loading of the dipole trap with atoms captured and cooled in a MOT. As has been shown, (Bienaimé et al., 2012), the fraction of the number of atoms N/N₀ that are trapped during loading is given by

Inserting our parameters we get N/N₀ ≈ 0.18. Our numerical work has shown a considerable stability of this value as we change the power, the detuning and the size of the beam.

The compression of an atomic cloud in a trap is achieved by a dynamical reduction of the size of the trap. Very important parameters in this process are the maximum compression speed, the heating of the atoms and the potential height evolution, which is related to the escape of atoms from the trap.

The maximum compression speed can be estimated by the relation, (Bienaimé et al., 2012),

Inserting our parameters we find a value v_max ≈ 2.4 ms⁻¹. If the barrier moves by 300 μm the minimal time needed to compress the cloud is about 0.12 ms.

The heating of the atoms can be approximated as an adiabatic reversible process of an ideal monoatomic gas, with TV^γ−1 = const, where T is the temperature of the gas, V is the volume and γ is the adiabatic index. For a monoatomic gass, γ = 5/3. Since the volume of our trap is given by $V=0.836{\pi }^2{w}_0^4/\lambda$ a cloud of initial temperature T_i and of beam waist w_0i will reach a final temperature

When we compress the atom cloud its temperature increases and the atoms tend to escape from the trap by jumping above the potential barrier. However if we try to decrease the size of the trap the potential barrier increases. Form Eqs. (14) and (15) we can see that the initial and final potential barriers are related to the corresponding beam waists by U_f = U_i(w_0i/w_0f)². Using Eqs. (18) and (19) we can show that

Using our parameters we get w_0f = 0.0056 μm, which is a value far smaller than 0.75 μm, the minimum value allowed by diffraction in most experiments. We thus consider the 0.75 μm as our minimum achievable value for the beam waist. If, for example, we load an atom cloud of about N₀ = 5 × 10⁷ atoms in the trap we will end up with N = 9 × 10⁶ atoms and this will correspond to a final atom density of about 2.7 × 10¹² atoms per cubic centimetre. This is well above the densities, which allow strong-localisation phase transitions (Bienaimé et al., 2012). Of course this is a theoretical result. In a real experiment the number of atoms depends strongly on the method with which the trap is compressed, on the time needed for the compression as well as on the method with which we load the precooled atoms to the trap. The very long Rayleigh range (here about 36 cm) may complicate all the above processes. We must also mention that for our parameters the maximum value of the force along the vertical z-direction is more than 10 times larger than the weight of the atom and it suffices a displacement of the atom by 0.2 mm along the z-direction for the trap restoring force to balance the weight.

4 Discussion

We have studied the atom trapping capacity of the bottle beam trap. After calculating the general expression for the trapping potential we proceeded in specific numerical calculations for two different cases namely the case of using this trap for the trapping of a single atom and for fast compression of a large sample of atoms. We compared our numerical results with experimental findings. As our numerical work has shown our trapping scheme gives almost similar potentials and scattering rates but better collisional rates for single atom trapping as compared to other blue detuned traps, like the one by Xu et al. (2010), for the same values of power, detuning and beam waists. For trapping of larger atomic samples it cannot compete traps as the one presented by Bienaimé et al. (2012) for similar volumes since it gives very weak trapping forces and a very long spatial extension along the axis. If we reduce the trapping volumes it gives encouraging results for compression of an atomic cloud towards Bose–Einstein condensation.

From an experimental point of view, the maximal limit on the bottle beam is that the overall laser power needed to generate the desired trap depth is very high, so it is not suitable to expand to multi-traps. But its advantages are lower scattering rate and long coherence time for atoms. So if the experiment only needs one blue detuned trap and is critical for coherence time, our bottle beam trap is a choice. Finally it is worth noting that, as shown in Fig. 3c, there is a second minimum in the radial direction at a distance $w_0\sqrt{2}$ . This shows that there is a secondary bottle-trapping region, shallower than the principal one. It is an issue for a future work to investigate if and how this region can be exploited for atom trapping and also in combination with the main region to atom channelling.

A dark atom trap could be used to overcome two significant disadvantages of the MOT trap (Letokhov, 2007) which have their origin in the relatively high excitation in this kind of trap: (a) the fluorescent light by the atoms in the trap is responsible for a repulsive force between atoms thus limits the density of atoms in the trap, (b) the collision rate for excited atoms is higher than atoms in their ground state. Optical confinement of a BEC condensate was demonstrated for the first time in 1998 where a far-detuned optical trap was used, ensuring very high transfer efficiencies, and negligible photon scattering (Stamper-Kurn et al., 1998). Using the advantages of various specific features of dipole traps we can study various aspects of Bose–Einstein condensation, which cannot be investigated in magnetic traps (Miller et al., 1993).

The bottle trap possesses a three dimensional dark trapping region with cylindrical geometry, the radial and axial sizes of which can be altered by choosing the waist and the Rayleigh region of the incident beams. The bottle trap, thus, belongs to the family of the so-called “cigar-like” traps due to its elongated shape (Cohen-Tannoudji and Guéry-Odelin, 2011). These traps have played an important role in the trapping of Bose–Einstein condensates (Haroche and Raimond, 2006).

The present study has revealed that the atomic trapping capacity of the so-called bottle-beam configuration could serve as an effective optical dipole trap for atoms with a cylindrical symmetry and an elongated “cigar-like” shape. Combinations of Laguerre–Gauss modes possessing orbital angular momentum can provide atomic traps with a variety of symmetries and topologies. The quantum mechanical and/or the classical treatment of the atomic motion in such traps and the associated energy eigenvalue problem of the Hamiltonian operator would reveal interesting features and robustness estimations of the trapping. The blue detuned bottle trap could serve as an experimental mechanism to investigate problems like loading of single atoms in a trap, or achieving high phase space density for stored atoms (Frese et al., 2000; Schlosser et al., 2001a,b). It is also a nice candidate for serving as an optical tweezer mechanism for the spatial translation of BECs (Couvert et al., 2008). As an optical tweezer it could also be used for trapping micron-sized dielectric particles (Foot, 2005). A blue-detuned bottle trap may be useful for the trapping of bacteria like E. coli. Bottle beam tweezers may also be useful in the study of the elastic response of large molecular chains as those in DNA (Cohen-Tannoudji and Guéry-Odelin, 2011). Finally we must report that recently the mechanism of bottle beams has been used for the manipulation of airborne particles using the photophoretic force (Shvedov et al., 2011).