Translate this page into:
Approximate analytical solutions of fractional reaction-diffusion equations
*Corresponding author. Tel.: +92 2135040516 njbalam@yahoo.com (Najeeb Alam Khan),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 14 August 2010
Abstract
The homotopy analysis method (HAM) of S.J. Liao has proven useful in obtaining analytical/numerical solutions to various nonlinear differential equations. In this work, the HAM is employed to obtain the analytical/numerical solutions of the nonlinear reaction-diffusion equations with time-fractional derivatives. The fractional derivatives are described in the Caputo sense. This approach transforms the solution of nonlinear reaction-diffusion equations into the solution of a hierarchy of linear equations. The solution is simple yet highly accurate and compare favorably with the solutions obtained early in the literature.
Keywords
Reaction-diffusion (RD)
Homotopy analysis method (HAM)
Fractional partial differential equations (FPDE)
1 Introduction
Nonlinear reaction-diffusion (RD) equations have been widely studied throughout recent years. These equations arise naturally as description models of many evolution problems in the real world, as in chemistry (Slepchenko et al., 2000; Vidal and Pascault, 1986), biology (Murray, 1977), etc. As is well known, complex behavior is a peculiarity of systems modeled by reaction diffusion equations, and the Belousov–Zhabotinskii reaction (Muller et al., 1987; Winfree, 1972) provides a classic example.
The RD equations describe a population of diploid individuals (i.e., the ones that carry two genes) distributed in a at two-dimensional habitat. Assuming that a gene occurs in two forms a and A, called alleles, one can divide the population into three genotypes aa, aA, and AA. The RD equations are employed to describe the co-oxidation on Pt(1 1 0) (Bar et al., 1994), the study of temporal and spatial patterns of cytoplasmic Ca2+ dynamics under the effects of Ca2+-release activated Ca2+ (CRAC) channels in T cells (Cong-Xin et al., 2010), problems in finance (Gorenflo et al., 2001; Mainardi et al., 2000; Raberto et al., 2002), and hydrology (Benson et al., 2000). Burke (Burke et al., 1993) obtained solutions for an enzyme–suicide substrate reaction with an instantaneous point source of substrate. Grimson and Barker (1993) introduced a continuum model for the spatio-temporal growth of bacterial colonies on the surface of a solid substrate which utilizes a RD equation for growth. Many cellular and sub-cellular biological processes (Erban and Chapman, 2009) can be described in terms of diffusing and chemically reacting species (e.g. enzymes). A traditional approach to the mathematical modeling of such RD processes is to describe each biochemical species by its (spatially dependent) concentration.
The nature of diffusion is characterized by temporal scaling of the mean-square displacement which is proportional to power of order . This type of diffusion is characterized as sub-diffusion, normal diffusion, and super diffusion processes as the cases where , and , respectively.
In recent time, interest in fractional RD equations (Henry and Wearne, 2000; Grafiychuk et al., 2006, 2007; Saxena et al., 2006) has increased because the equation exhibits self-organization phenomena and introduces a new parameter, the fractional index, into the equation. Additionally, the analysis of fractional RD equations is of great interest from the analytical and numerical point of view. From a mathematical point of view, they also offer a rich and promising area of research. RD equations have been investigated for certain boundary and initial conditions and in most cases explicit solutions cannot been found. We present solutions of a more general model of time-fractional RD equations:
Let
be the concentration of the members of the population with the mutant gene and
the concentration of the members of the population whose off springs have the mutant gene (x is a position in the habitat). One can assume that
. Denote by
the intensity of selection in favor of the mutant gene, which we assume to be independent of
. The nonlinear RD equation (1) is given by
Fitzhugh (1961) suggested a model for the propagation of voltage impulse through a nerve axon which is substantially simpler than the Hodgkin–Huxley model and therefore, is often used in applications. Fitzhugh treated the nerve cell as a nonlinear electric oscillator (Fitzhugh, 1969; Nagumo et al., 1962). The nonlinear RD equation (1) is given by
The widely applied techniques (i.e., perturbation method) are of great interest to be used in engineering and science. To eliminate the limitation of “small parameter”, which is assumed in the perturbation method, a new technique based on the homotopy terminology has been proposed. Accordingly, a nonlinear problem is transformed into an infinite number of simple problems without using the perturbation technique. We used an elegant method which has proved effectiveness and efficiency in solving many type of nonlinear problems (Liao et al., 2002; Sanjay and Wiese, 2003). Homotopy analysis method (HAM) (Liao, 2004) properly overcomes restrictions of perturbation techniques because it does not need any small or large parameters to be contained in the problems. Khan et al. (2010b) studied the fourth-order parabolic partial differential equation via HAM. The validity of the HAM is varied through illustrative examples of Cauchy reaction-diffusion equation (Bataineh et al., 2008) linear and nonlinear fractional diffusion-wave equation (Jafri and Seifi, 2009) and multi-term diffusion-wave (Jafri et al., 2010) equations. Also, it is shown that homotopy perturbation method (HPM) (Khan et al., 2009, 2010c; Mohyud-Din et al., 2010; Yıldırım, 2010), variational iteration method (VIM) (Wang and He, 2008; Mohyud-Din and Yıldırım, 2010), differential transform method (DTM) (Rida et al., 2010), Adomian decomposition method (ADM) (Wazwaz and Gorguis, 2004; Khan et al., 2010a) are just special case of HAM.
2 Basic definitions of fractional calculus
We give some basic definitions and properties of the fractional calculus theory which are used in this paper.
Caputo’s definition of the fractional-order derivative is defined as
For m to be the smallest integer that exceeds α and n to be the smallest integer that exceeds
, the Caputo time-fractional derivative operator of order
is defined as
The Riemann–Liouville fractional integral operator of order, of a function f,
3 The HAM
In this paper, we apply the HAM to the nonlinear problems to be discussed. In order to show the basic idea of HAM consider the following nonlinear fractional differential equation:
The convergence of the solution (14) depends upon the auxiliary parameter
. If it is convergent at
, one has
This must be one of the solutions of the original nonlinear equations, as proved by Liao. Define the vectors
Differentiating the zeroth-order deformation equation (12) m-times with respect to q and then dividing them by m! and finally setting
we get the following mth-order deformation equation:
The solution of the mth-order deformation equation (18) is readily found to be
It should be emphasized that is governed by equation (19) with the initial conditions that come from the original problems, which can be easily solved by symbolic computation software such as MATHEMATICA.
4 Time-fractional reaction-diffusion equations
To incorporate our discussion above, we consider nonlinear reaction-diffusion equations with time-fractional derivative which are arising in diverse phenomenon.
4.1 Application 1
Consider the time-fractional RD problem (Wazwaz and Gorguis, 2004)
Subject to a constant initial condition
To solve the above problem by HAM, we choose the auxiliary operators as follows with the property
Using the above definition, we construct the zeroth-order deformation equations
Differentiating the zeroth-order deformation equation (22) m times with respect to p, and finally dividing by m!, we have the mth-order deformation equations
We use an 11-term approximate solution and set
The exact solution of the equation (20) as
is
4.2 Application 2
Let us consider the time-fractional Fisher equation (Wazwaz and Gorguis, 2004; Rida et al., 2010)
To solve the above problem by HAM, we chose the auxiliary operators as follows
With the properties
By mean of zeroth components
the remaining components
, can be completely determined such that each term is determined by using the previous terms, the components of solution for this case are
The approximate solution of equation (32) by the HAM is
Our approximation has one more interesting property, if we set and expand approximate solution using Taylor’s series about (0, 0) we obtain the same solution obtained by Rida et al. (Rida et al., 2010). If we set we obtain the same result obtained by Wazwaz and Gorguis (2004).
The exact solution of the equation (32) with condition (33) as
is
4.3 Application 3
Here, we consider time-fractional Fitzhugh–Nagumo equation (Wazwaz and Gorguis, 2004; Rida et al., 2010)
In genetics, the case is referred to as the heterozygote inferiority. The exact solution of equation (40) for obtained by Kawahara and Tanaka (1983), which describes the coalescence of two travelling fronts of the same sense into a front connecting two stable constant states is found.
To solve the above equation by HAM, we write
Subsequently solving the mth-order deformation equations one has
The approximate solution of equation (40) by the HAM is
If we set and expand approximate solution using Taylor’s series about (0,0) we obtain the same solution obtained by Rida et al. (Rida et al., 2010). If we set we obtain the same result obtained by Wazwaz and Gorguis (2004).
As
, the close form solution is given by
5 Closing remarks
Let us conclude this paper with a summary and discussion of the results presented here. We have studied three important applications of reaction-diffusion systems, namely the Fisher equations (with constant and variable initial conditions) and the time-fractional Fitzhugh–Nagumo equation. We are interested in the linearization of these equations, i.e. conversion of the nonlinear problem to linear problems.
We have derived solution for
, however figures are included here for some particular cases. Plotting the
curves, we have intervals [0, 1.6], [1.6, 2.2] and [−2, 2] as the valid region of
for first, second, and third applications. We test different values of
in the valid region and conclude that
is the one whose results did not give the minimum error. The solution surfaces for application 1 are displayed in Figs. 1 and 2. The solution surfaces for application 2 are depicted for different values of constants in Figs. 5 and 6. Finally, the approximate solution of Fitzhugh–Nagumo equation are depicted in Figs. 9 and 10. Figs. 3, 7 and 11 show the values of error function. The valid region of auxillary parameters are depicted in Figs. 4, 8 and 12 for first, second and third applications. The comparison of solution curves of application 2 and 3 is displayed in Figs. 13 and 14. The present solutions show the better performance than DTM solution. Recently Rida et al. (2010) have solved the problems we presented in application 2 and 3 using generalized differential transform method (GDTM), a method which provides approximate analytical solutions in the form of an infinite power series for nonlinear equations. The major lacks of GDTM are that it requires transformation and the given differential equation and related initial conditions are transformed into a recurrence equation that finally leads to the solution of a system of algebraic equations as coefficients of a power series solution.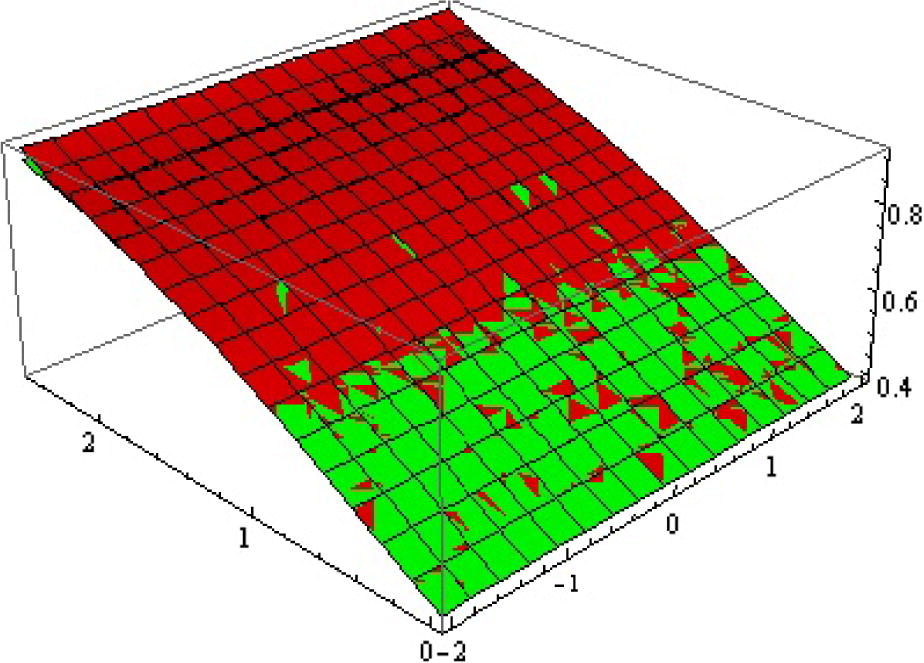
Exact, approx. (red, green) solution surfaces of
for
.
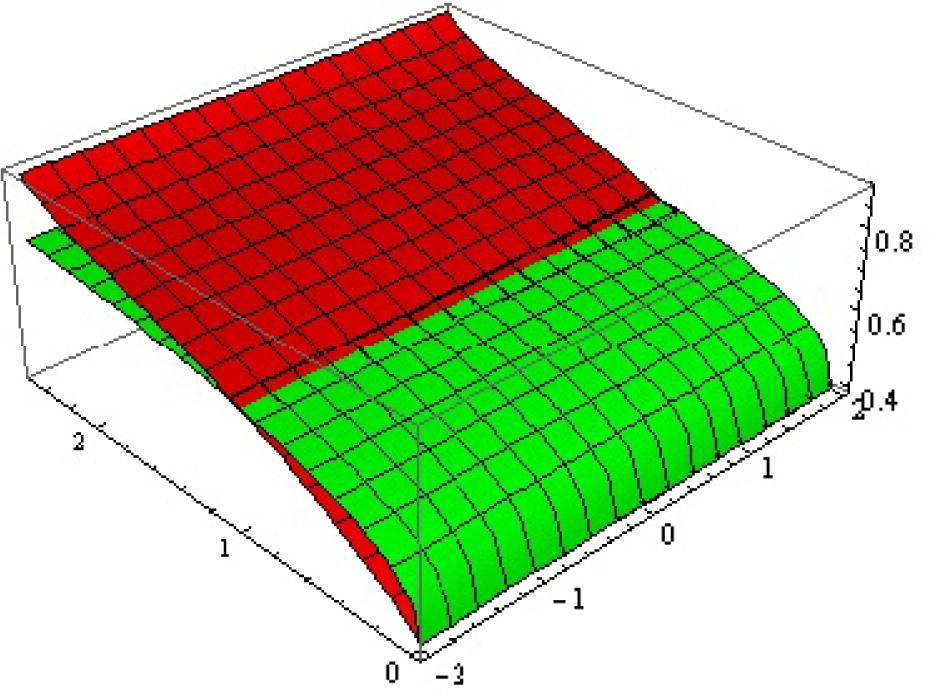
Approx. (red
, green
) solutions surfaces of
for
.
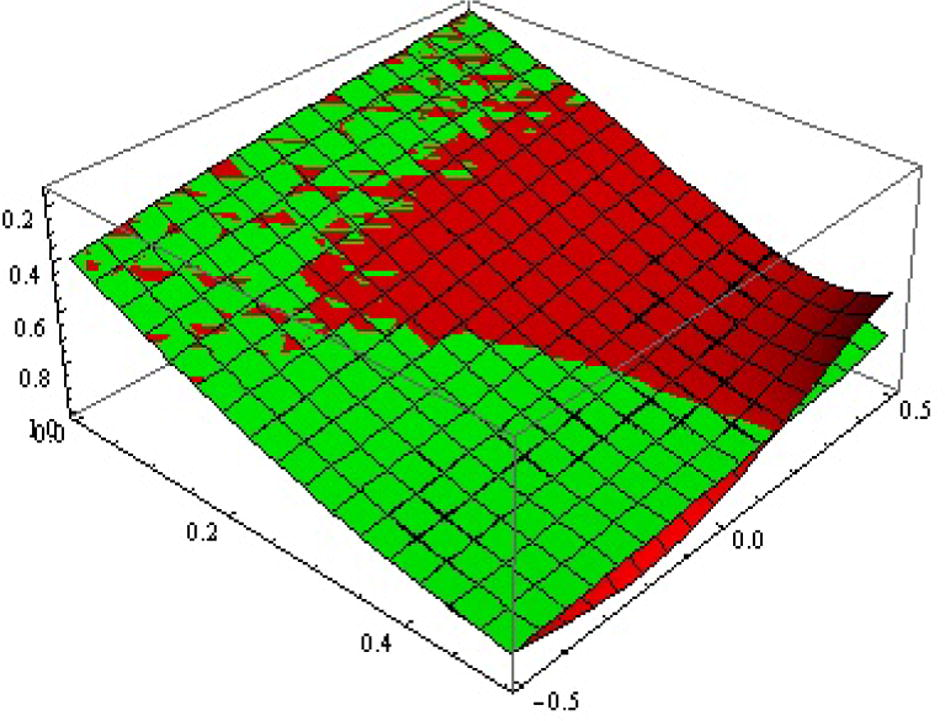
Exact, approx. (red, green) solution surfaces of
for
.
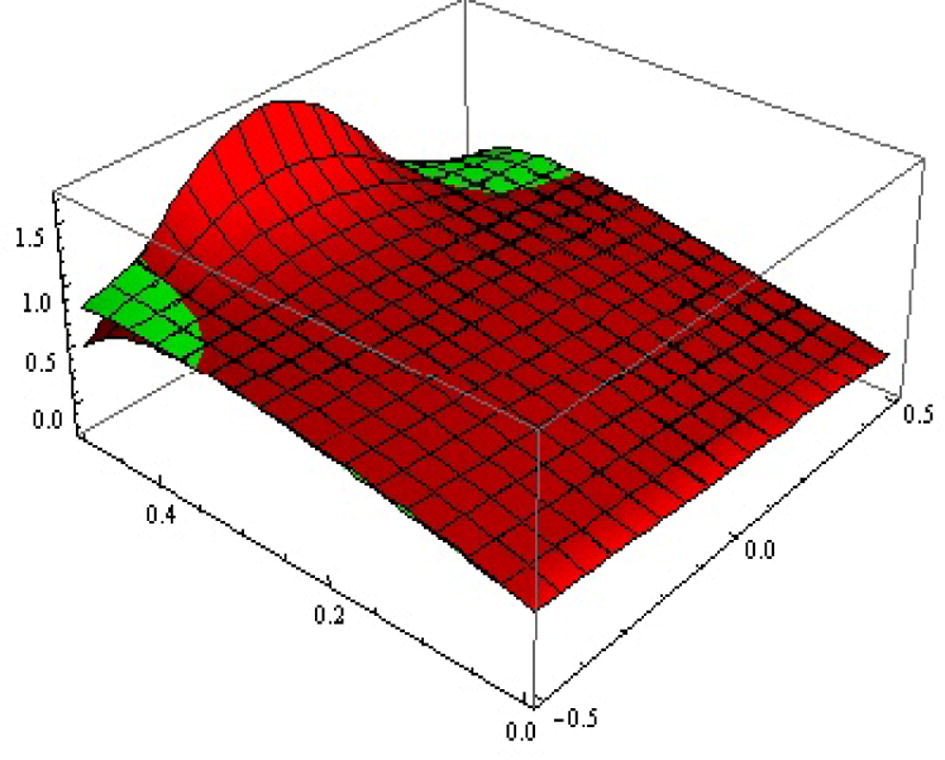
Approx. (red
, green
) solutions surfaces of
for
.
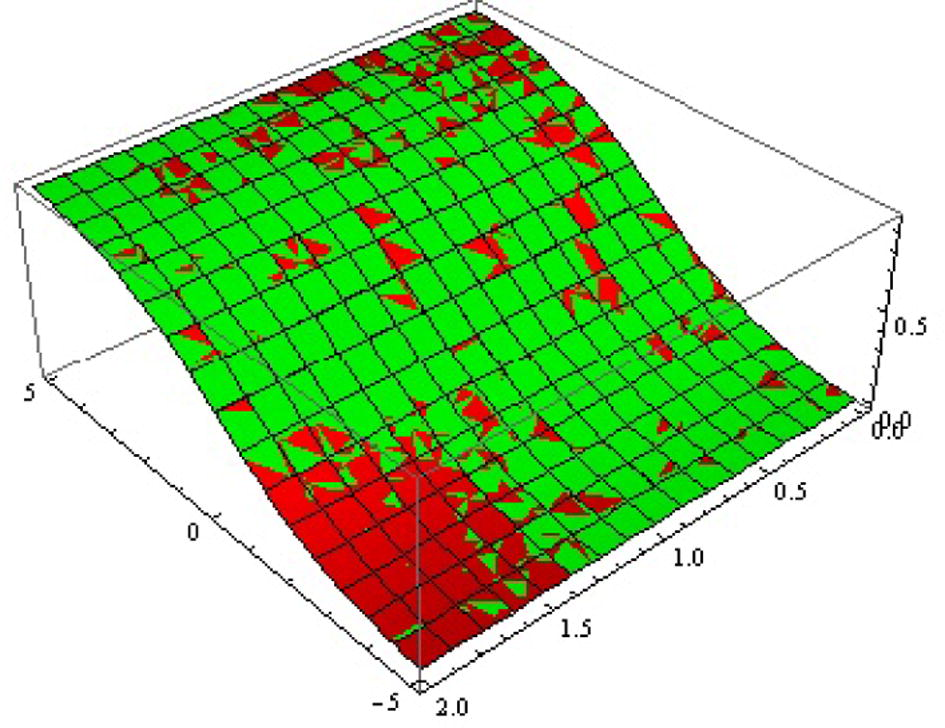
Exact, approx. (green, red) solution surfaces of
for
.
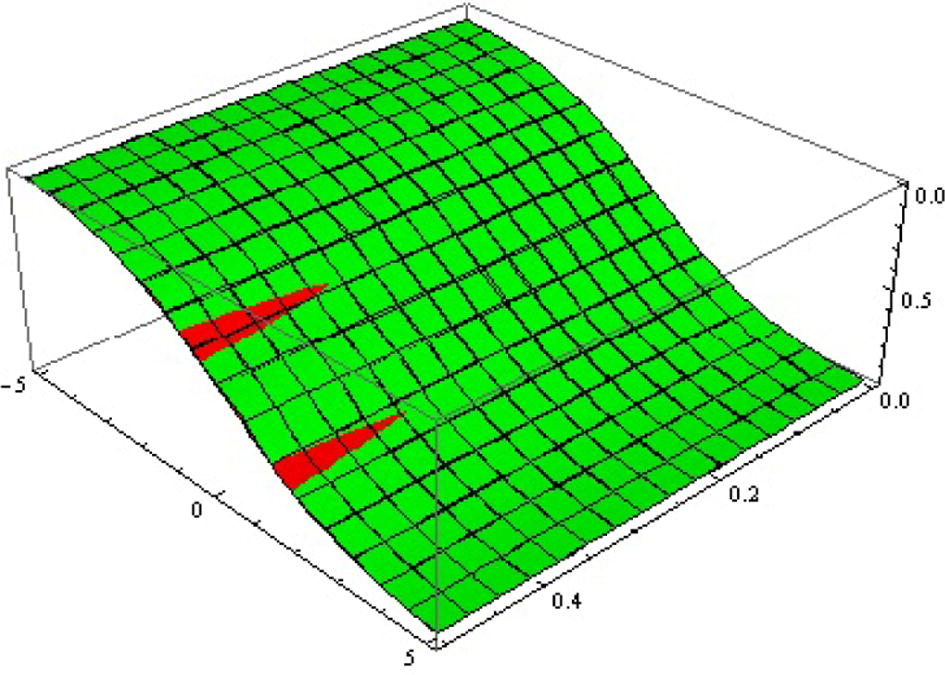
Approx. (red
, green
) solutions surfaces of
for
.
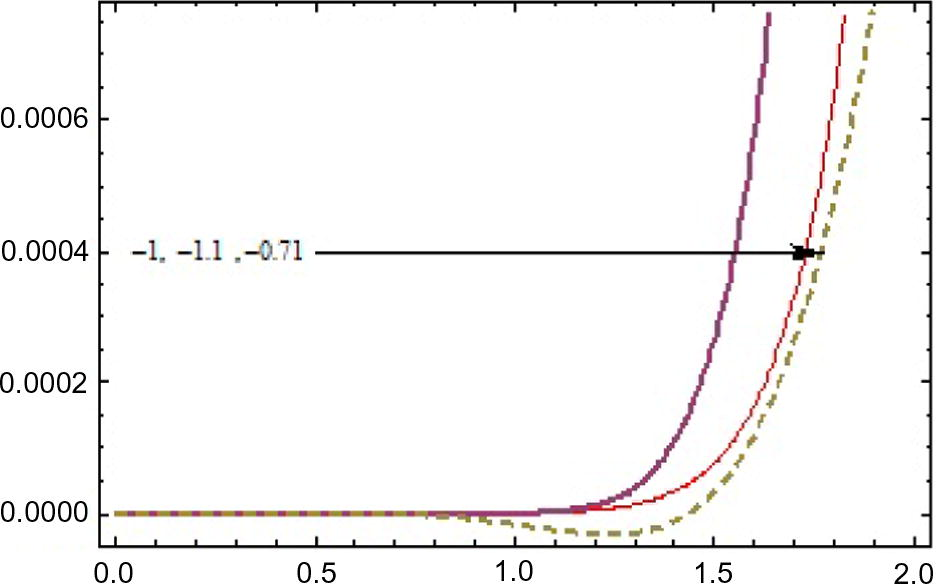
Error curves of
for
for different
.
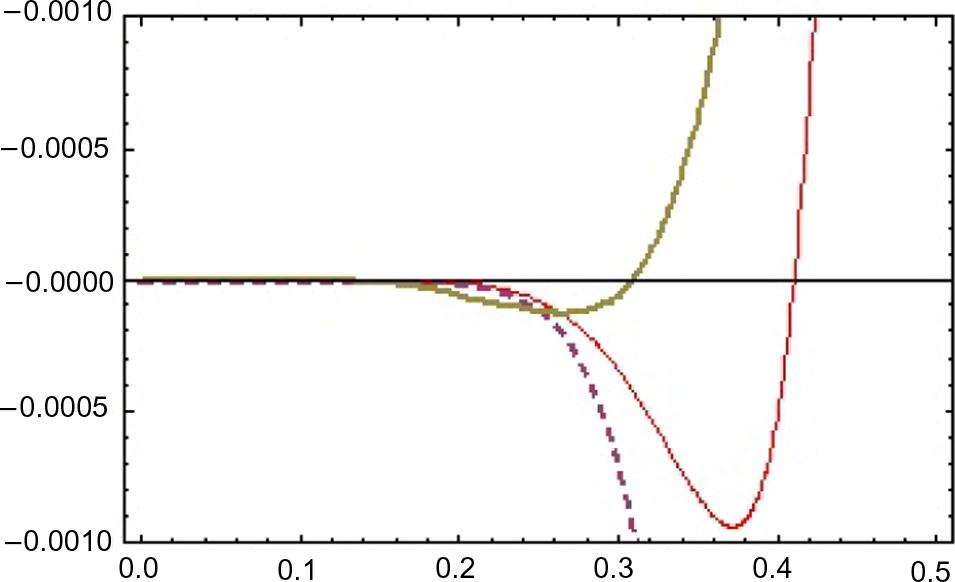
Error curves of
for
for different
(red, dashed and thick).
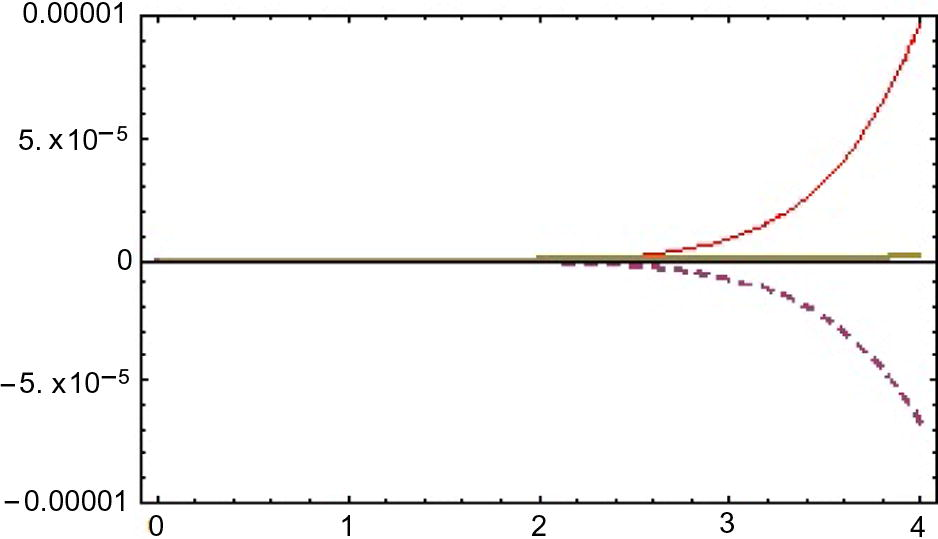
Error curves of
for
for different
(red, dashed, thick).
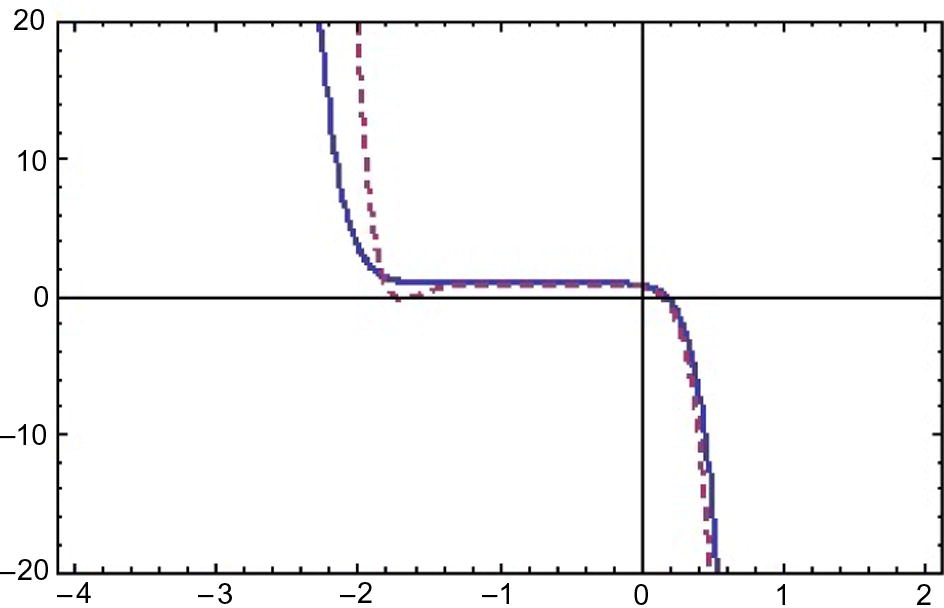
curves of
for
(thick),
(dashed).
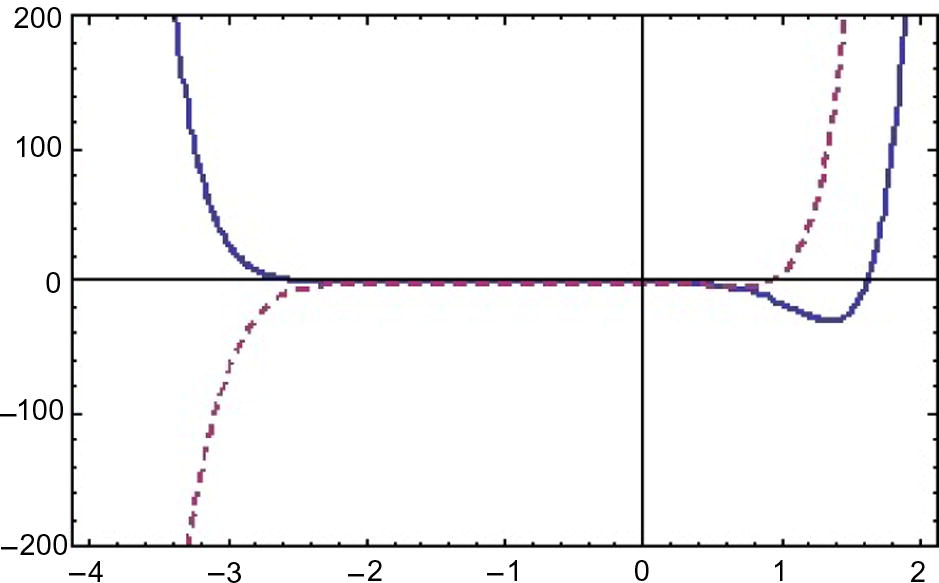
curves of
for
(thick),
(dashed).
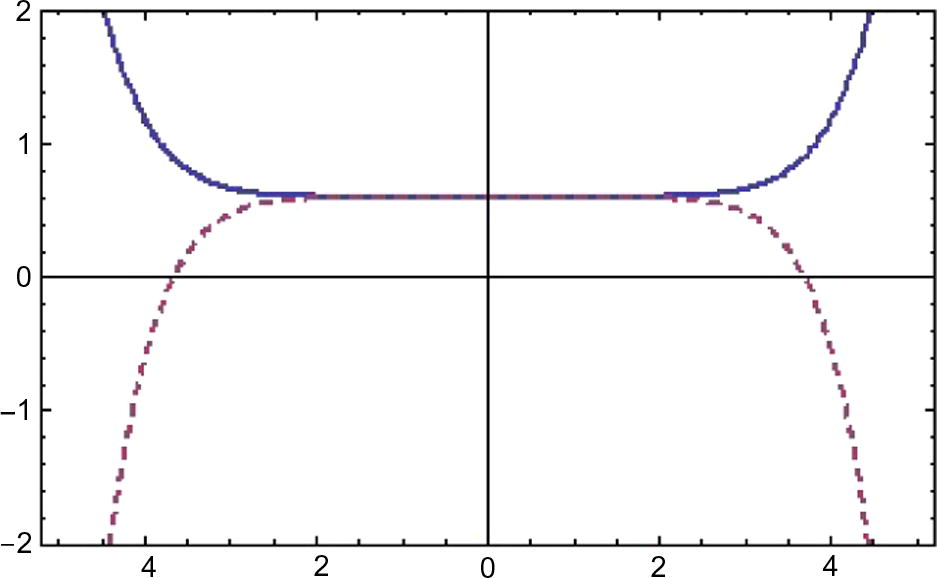
curves of
for
(thick),
(dashed).
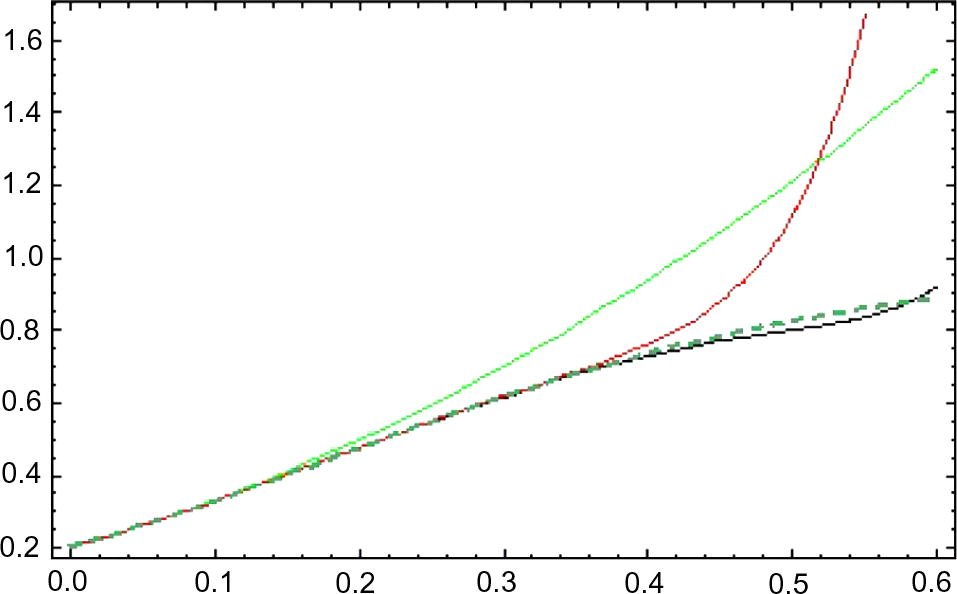
Approximation of
for
DTM, HAM (
), exact (green, black, red, dashed).
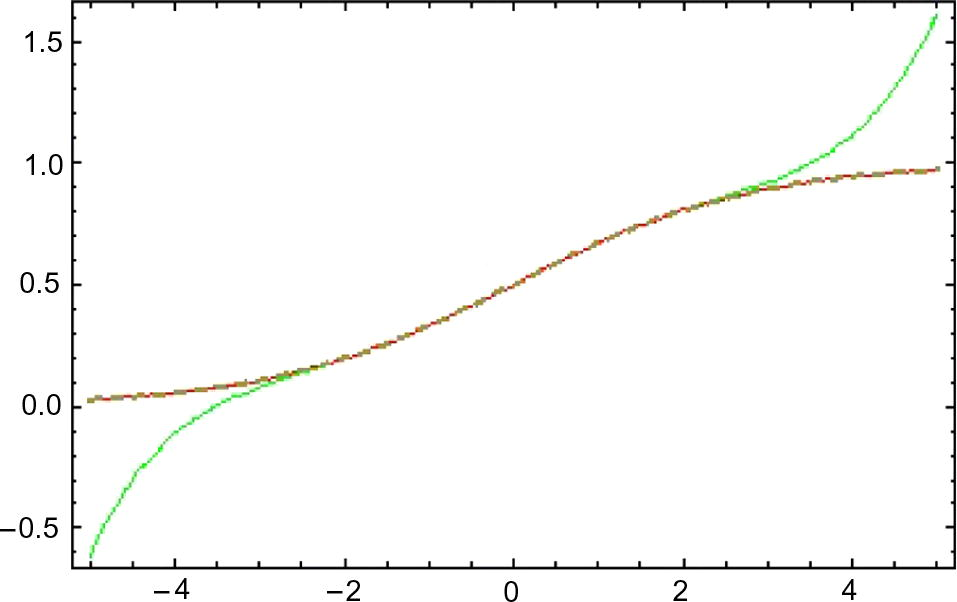
Approximation of
for
DTM, HAM (
), exact (green, red, dashed).
Acknowledgment
The authors would like to express their gratitude to the referees both for their careful assessment and for their fruitful comments regarding the first version of this paper. The author M. Jamil highly thankful and grateful to the Abdus Salam School of Mathematical Sciences, GC University, Lahore, Pakistan; Department of Mathematics & Basic Sciences, NED University of Engineering & Technology, Karachi-75270, Pakistan and also Higher Education Commission of Pakistan for supporting and facilitating this research work.
References
- Spiral waves in a surface reaction: model calculations. Journal of Chemical Physics. 1994;100:1202-1214.
- [Google Scholar]
- The homotopy analysis method for Cauchy reaction-diffusion problems. Physics Letters A. 2008;372(5):613-618.
- [Google Scholar]
- Application of a fractional advection dispersion equation. Water Resource Research. 2000;36:1403-1412.
- [Google Scholar]
- Suicide substrate reaction-diffusion equations varying the source. IMA Journal Mathematical Applications in Medicine and Biology. 1993;10:97-114.
- [Google Scholar]
- Effects of CRAC channel on spatiotemporal Ca2+ patterns in T cells. Chinese Physics Letters. 2010;27:028701.
- [Google Scholar]
- Stochastic modelling of reaction-diffusion processes: algorithms for bimolecular reactions. Physical Biology. 2009;6:046001.
- [Google Scholar]
- Impulse and physiological states in models of nerve membrane. Biophysics Journal. 1961;1:445-466.
- [Google Scholar]
- Biological Engineering. McGraw-Hill; 1969. pp. 1–85
- Fractional calculus and continuous time finance. III: The diffusion limit. Mathematical finance. Konstanz, 2000. Trends Math Birkhuser Basel 2001:171-180.
- [Google Scholar]
- Grafiychuk, V., Datsko, B., Meleshko, S.V., 2006. Mathematical modeling of pattern formation in sub- and superdiffusive reaction-diffusion systems. arxiv:nlin.AO/06110005 v3.
- Grafiychuk, V., Datsko, B., Meleshko, S.V., 2007. Nonlinear oscillations and stability domains in fractional reaction-diffusion systems. arXiv:nlin.PS/0702013 v1.
- A continuum model for the growth of bacterial colonies on a surface. Journal of Physics A: Mathematical General. 1993;26:5645-5654.
- [Google Scholar]
- Homotopy analysis method for solving linear and nonlinear diffusion-wave equations of fractional order. Communications in Nonlinear Science Numerical Simulation. 2009;14(5):2006-2012.
- [Google Scholar]
- Homotopy analysis method for solving multi-term linear and nonlinear diffusion-wave equations of fractional order. Computer and Mathematics with Applications. 2010;59(3):1337-1344.
- [Google Scholar]
- Interaction of travelling fronts: an exact solution of a nonlinear diffusion equation. Physics Letters A. 1983;97(8):311-314.
- [Google Scholar]
- Analytical study of Navier–Stokes equation with fractional orders using He’s homotopy perturbation and variation iteration method. International Journal of Non-Linear Science and Numerical Simulation. 2009;10:1127-1134.
- [Google Scholar]
- Khan, N.A., Khan, N.-U., Ayaz, M., Mahmood, A., Fatima, N., 2010a. Numerical study of time-fractional fourth-order differential equations with variable coefficients. Journal of King Saud University–Science. doi:10.1016/j.jksus.2010.06.012.
- Analytical aspect of fourth-order parabolic partial differential equations with variable coefficients. Mathematical and Computational Applications. 2010;15(3):481-489.
- [Google Scholar]
- Khan, N.A., Ara, A., Mahmood, A., 2010c. Approximate solution of time-fractional chemical engineering equations: a comparative study. International Journal of Chemical Reactor Engineering, 8, article A19.
- Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier; 2006.
- Beyond Perturbation: Introduction to Homotopy Analysis Method. Boca Raton: CRC Press/Chapman and Hall; 2004.
- An efficient high-order algorithm for solving systems of reaction-diffusion equations. Numerical Methods of Partial Differential Equation. 2002;18:340-354.
- [Google Scholar]
- Exact analytic solutions for the unsteady flow of a non-Newtonian fluid between two cylinders with fractional derivative model. Communications in Nonlinear Science Numerical Simulation. 2009;14:3309-3319.
- [Google Scholar]
- Mahmood, A., Fetecau, C., Khan, N.A., Jamil, M., 2010. Some exact solutions of the oscillatory motion of a generalized second grade fluid in an annular region of two cylinders. Acta Mechanica Sinica. doi:10.1007/s10409-010-0353-4.
- Fractional calculus and continuous-time finance. II: The waiting-time distribution. Physica A. 2000;287:468-481.
- [Google Scholar]
- Mohyud-Din, S.T., Yıldırım, A., 2010. A variational approach for soliton solutions of good Boussinesq equation, Journal of King Saud University–Science. doi:10.1016/j.jksus.2010.04.013.
- Traveling wave solutions of Whitham–Broer–Kaup equations by homotopy perturbation method. Journal of King Saud University-Science. 2010;22:173-176.
- [Google Scholar]
- Two-dimensional spectrophotometry of spiral wave propagation in the Belousov–Zhabotinskii reaction. I: Experiments and digital data representation. Physica D. 1987;24:71-78.
- [Google Scholar]
- Lectures on Non-Linear Differential Equation Models in Biology. Oxford: Clarenden; 1977.
- Nagumo, J.S., Arimoto, S., Yoshizawa, S., 1962. An active pulse transmission line simulating nerve axon. In: Proceeding of IRE, vol. 50, pp. 2061–2070.
- Waiting-times and returns in high frequency financial data: an empirical study. Physica A. 2002;314:749-755.
- [Google Scholar]
- Rida, S.Z., El-Sayed, A.M.A., Arafa, A.A.M., 2010. On the solutions of time-fractional reaction-diffusion equations. Communications in Nonlinear Science Numerical Simulation. doi:10.1016/j.cnsns.2010.02.007.
- Perturbative linearization of reaction-diffusion equations. Journal of Physics A: Mathematical General. 2003;36:2043-2054.
- [Google Scholar]
- Reaction-diffusion systems and nonlinear waves. Astrophysics and Space Science. 2006;305:297-303.
- [Google Scholar]
- Numerical approach to fast reactions in reaction-diffusion systems: application to buffered calcium waves in bistable models. Journal of Computational Physics. 2000;162:186-189.
- [Google Scholar]
- Non-equilibrium Dynamics in Chemical Systems. New York: Wiley; 1986.
- Variational iteration method for a reaction-diffusion process. International Journal of Chemical Reactor Engineering. 2008;6:1-8.
- [Google Scholar]
- An analytical study of Fisher’s equation by using Adomian decomposition method. Applied Mathematics and Computation. 2004;154:609-620.
- [Google Scholar]
- Yıldırım, A., 2010. Analytical approach to Fokker–Planck equation with space- and time-fractional derivatives by means of the homotopy perturbation method. Journal of King Saud University–Science. doi:10.1016/j.jksus.2010.05.008.







