Application of He's variational iteration method for solution of the family of Kuramoto–Sivashinsky equations

1 Introduction

In recent years, He's variational iteration method has been favorably applied to various kinds of problems; for example, this scheme is used for solving the fractional KdV–Burgers–Kuramoto equation (Safari et al., 2009). This technique computes the exact solution of equations using the initial condition only. It is also important to note that the present method does not require discretization of the equation. Therefore, it is not affected by computation round-off errors and one is not faced with the necessity of large computer memory and time. Furthermore, using this idea we do not need to solve any linear or non-linear system of equations. In Biazar and Ghazvini (2007) VIM is employed to solve fourth-order parabolic equations. Also, this method is employed in He (1997b) to solve delay differential equations. The interested reader is referred to Dehghan and Tatari (2006), Wazwaz (2007), Sweilam and Khader (2007) for some other applications of the method.

The Kuramoto–Sivashinsky equation is a non-linear evolution equation and has many applications in a variety of physical phenomena such as reaction diffusion systems (Kuramoto and Tsuzuki, 1976), long waves on the interface between two viscous fluids (Hooper and Grimshaw, 1985) and thin hydrodynamics films (Sivashinsky, 1983). The Kuramoto–Sivashinsky equation has been studied numerically by many authors (Akrivis and Smyrlis, 2004; Manickam et al., 1998; Uddin et al., 2009).

Consider the Kuramoto–Sivashinsky equation

Subject to the initial condition

And boundary conditions $$u(a\text{,}t)=g_1(t)\text{,}u(b\text{,}t)=g_2(t)\text{,}t>0\text{.}$$

In this paper we use VIM for solving this equation, which was first proposed by He (1997a), and the convergence of the method is systematically discussed by Tatari and Dehghan (2007).

2 Using VIM to solve Kuramoto–Sivashinsky equations

To clarify the basic ideas of VIM, we consider the following differential equation $$\mathit{Lu}(t)+\mathit{Nu}(t)=g(t)\text{,}$$ where L is a linear operator, N is a non-linear operator and g(t) an inhomogeneous term.

According to VIM, we can write down a correction functional as following $$u_{n+1}(t)=u_n(t)+{\int }_0^t\lambda (\xi )({\mathit{Lu}}_n(\xi )+N{\tilde{u}}_n(\xi )-g(\xi ))d\xi \text{.}$$ where λ is a Lagrange multiplier which could be identified optimally via variational theory, $u_n$ is the nth approximate solution, and ${\tilde{u}}_n$ denotes a restricted variation, i.e. $\delta {\tilde{u}}_n=0$ .

In this section the application of the VIM is discussed for solving Eq. (1). According to the correction functional in t – direction in the following form $$u_{n+1}(x\text{,}t)=u_n(x\text{,}t)+{\int }_0^t\lambda (\xi )\left\{\frac{\partial u_n(x\text{,}\xi )}{\partial \xi }+{\tilde{u}}_n(x\text{,}\xi )\frac{\partial {\tilde{u}}_n(x\text{,}\xi )}{\partial x}+\alpha \frac{{\partial }^2{\tilde{u}}_n(x\text{,}\xi )}{\partial x^2}+\gamma \frac{{\partial }^3{\tilde{u}}_n(x\text{,}\xi )}{\partial x^3}+\beta \frac{{\partial }^4{\tilde{u}}_n(x\text{,}\xi )}{\partial x^4}\right\}d\xi \text{.}$$

Taking the variation with respect to the independent variable $u_n$ and noticing that $\delta u_n(0)=0$ , we get $$\delta u_{n+1}=\delta u_n+\lambda \delta u_n{|}_{\xi =t}-{\int }_0^t{\lambda }^{\prime }\delta u_{n}d\xi =0\text{.}$$

Then we apply the following stationary conditions: $${\lambda }^{\prime }(\xi ){|}_{\xi =t}=0\text{,}1+\lambda (\xi ){|}_{\xi =t}=0\text{.}$$

The general Lagrange multiplier, therefore, could be readily identified: $$\lambda =-1\text{.}$$

And as result, we obtain the following iteration formula $$u_{n+1}(x\text{,}t)=u_n(x\text{,}t)-{\int }_0^t\left\{\frac{\partial u_n(x\text{,}\xi )}{\partial \xi }+u_n(x\text{,}\xi )\frac{\partial u_n(x\text{,}\xi )}{\partial x}+\alpha \frac{{\partial }^2{u}_n(x\text{,}\xi )}{\partial x^2}+\gamma \frac{{\partial }^3{u}_n(x\text{,}\xi )}{\partial x^3}+\beta \frac{{\partial }^4{u}_n(x\text{,}\xi )}{\partial x^4}\right\}d\xi \text{.}$$

We start with the initial approximation of $u(x\text{,}0)$ given by Eq. (2). Using the above iteration formula, we can obtain the other components as follows $$\begin{array}{c}{u}_0(x\text{,}t)=u(x\text{,}0)=f(x)\text{,}\hfill \\ u_1(x\text{,}t)=u_0(x\text{,}t)-{\int }_0^t\left\{\frac{\partial u_0(x\text{,}\xi )}{\partial \xi }+u_0(x\text{,}\xi )\frac{\partial u_0(x\text{,}\xi )}{\partial x}+\alpha \frac{{\partial }^2{u}_0(x\text{,}\xi )}{\partial x^2}\right.\hfill \\ \left.+\gamma \frac{{\partial }^3{u}_0(x\text{,}\xi )}{\partial x^3}+\beta \frac{{\partial }^4{u}_0(x\text{,}\xi )}{\partial x^4}\right\}d\xi \text{,}\hfill \\ u_2(x\text{,}t)=u_1(x\text{,}t)-{\int }_0^t\left\{\frac{\partial u_1(x\text{,}\xi )}{\partial \xi }+u_1(x\text{,}\xi )\frac{\partial u_1(x\text{,}\xi )}{\partial x}+\alpha \frac{{\partial }^2{u}_1(x\text{,}\xi )}{\partial x^2}\right.\hfill \\ \left.+\gamma \frac{{\partial }^3{u}_1(x\text{,}\xi )}{\partial x^3}+\beta \frac{{\partial }^4{u}_1(x\text{,}\xi )}{\partial x^4}\right\}d\xi \text{,}\hfill \\ ⋮\hfill \end{array}$$

3 Numerical results

In this section, we apply the technique discussed in the previous section to find numerical solution of the family of Kuramoto–Sivashinsky equations and compare our results with exact solutions. The results reveal that this method is very effective and simple.

Close

Figure 1

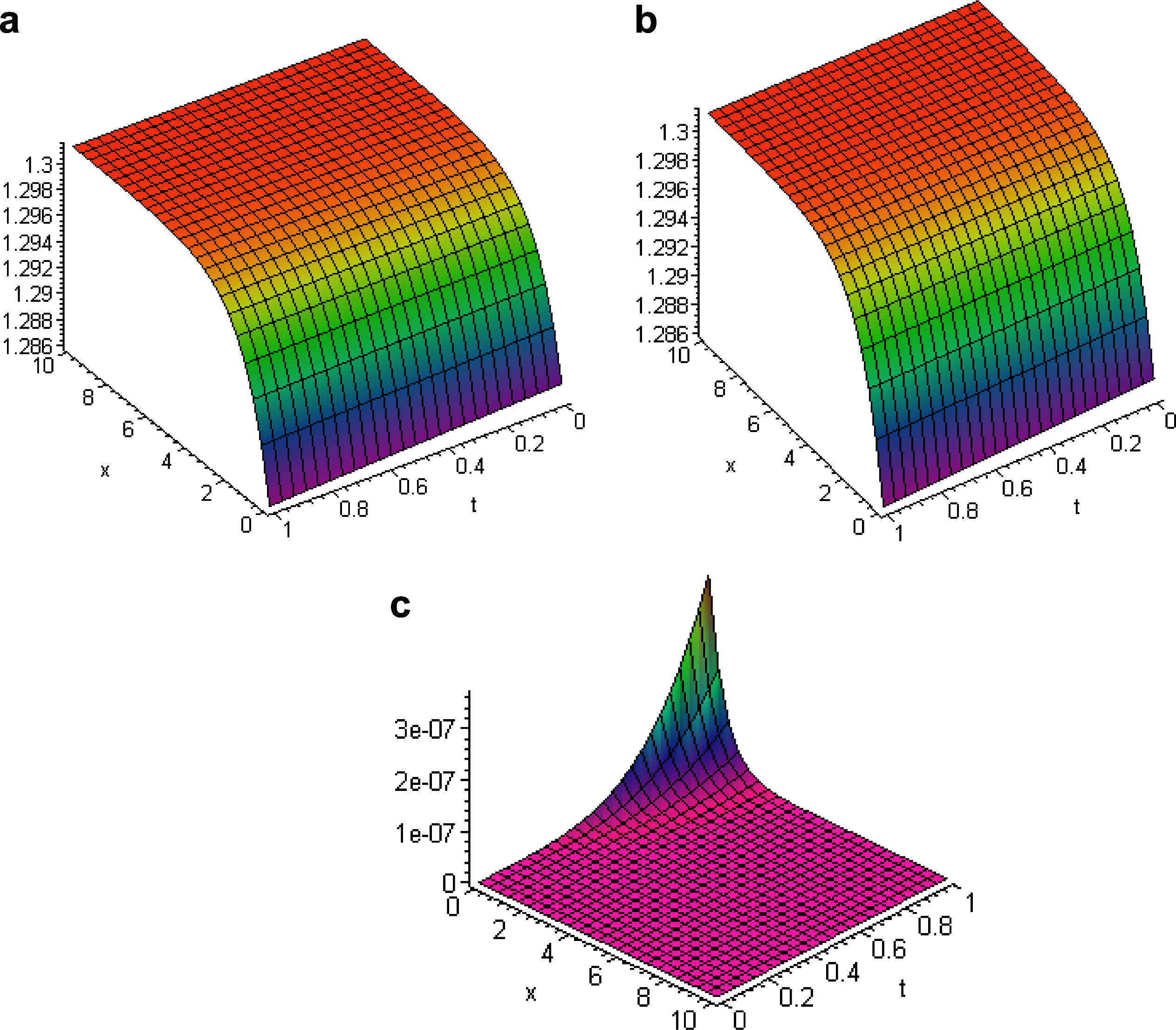
The surface shows the solution $u(x\text{,}t)$ for Example 1 when $c=0.1\text{,}k=\frac{1}{2}\sqrt{\frac{11}{19}}\text{,}{x}_0=-10$ : (a) exact solution (3), (b) 3th order of approximate solution (4) and (c) the absolute error between exact and numerical solutions.

Export to PPT

Close

Figure 2

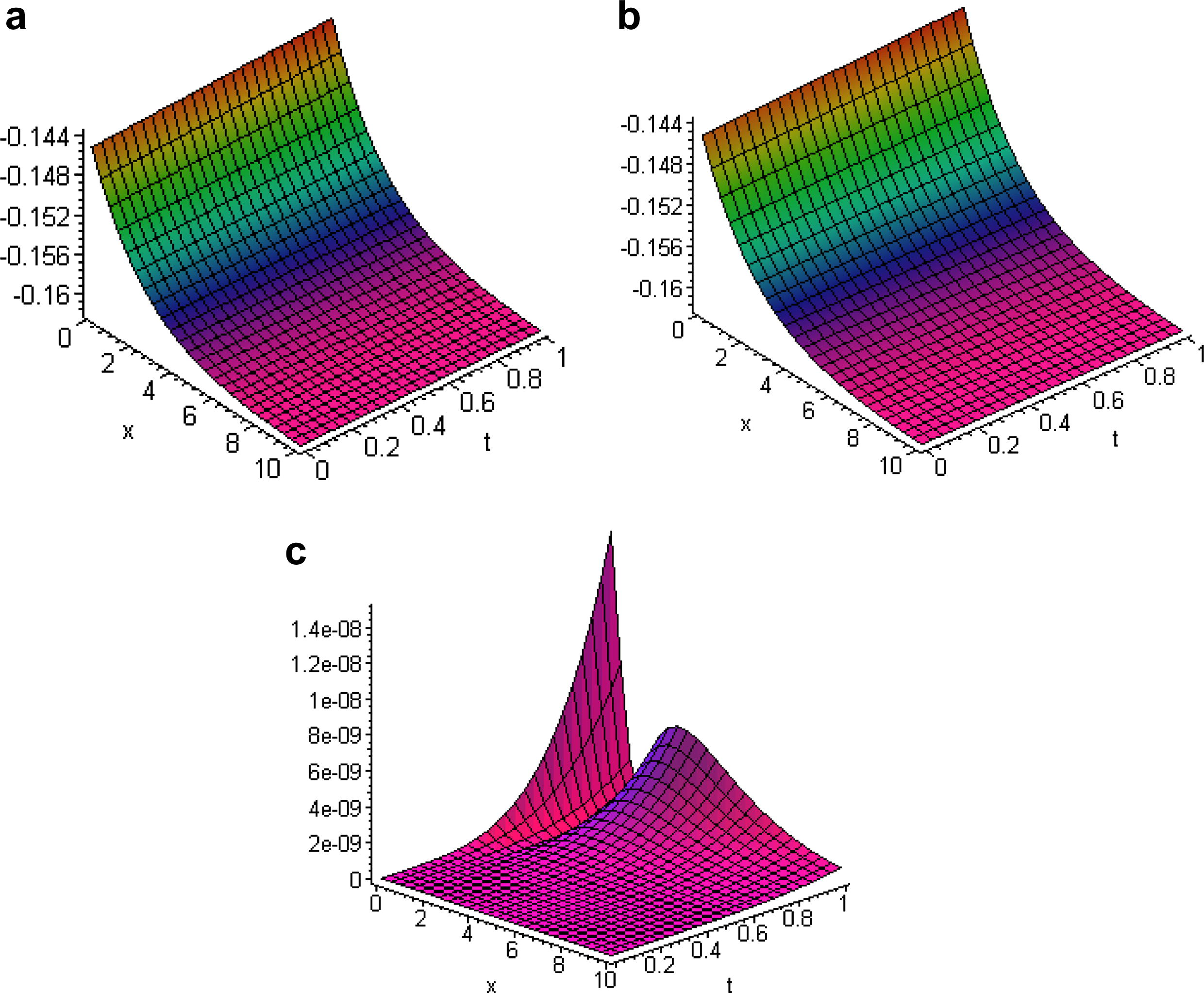
The surface shows the solution $u(x\text{,}t)$ for Example 2 when $c=0.2\text{,}k=\frac{1}{2\sqrt{19}}\text{,}{x}_0=-10$ : (a) exact solution (5), (b) 3th order of approximate solution (6) and (c) the absolute error between exact and numerical solutions.

Export to PPT

Close

Figure 3

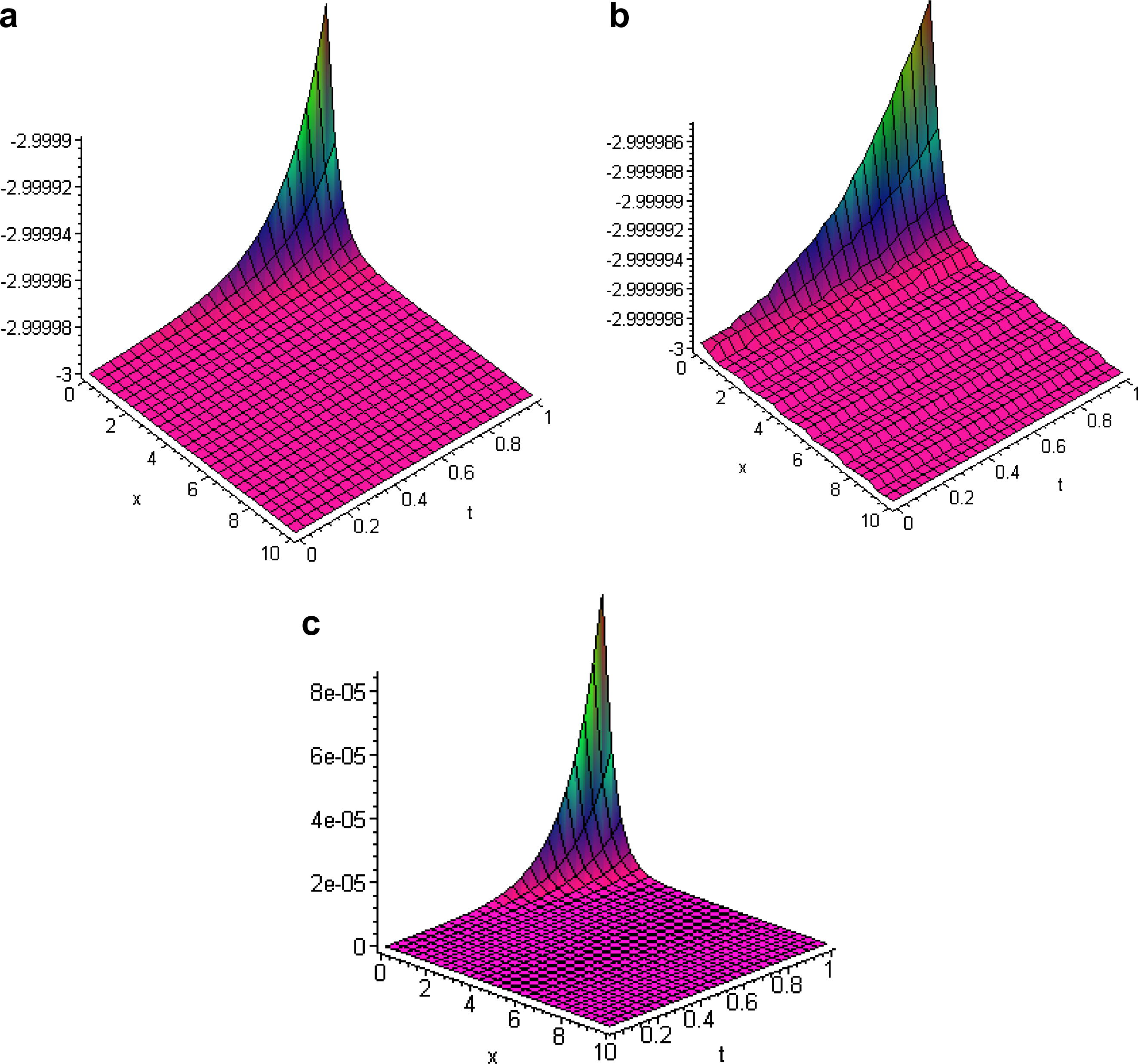
The surface shows the solution $u(x\text{,}t)$ for Example 3 when $c=3\text{,}k=\frac{1}{2}\text{,}{x}_0=-10$ : (a) exact solution (7), (b) 3th order of approximate solution (8) and (c) the absolute error between exact and numerical solutions.

Export to PPT

4 Conclusion

In this paper the He's variational iteration method is used to solve the Kuramoto–Sivashinsky equations. We described the method, used it on three test problems, and compared the results with their exact solutions in order to demonstrate the validity and applicability of the method. Moreover, only a small number of iterations are needed to obtain a satisfactory result. The given numerical examples support this claim.

We use the Maple Package to calculate the functions obtained from the variational iteration method