Application of a hybrid model to reduce bias and improve precision in population estimates for elk (Cervus elaphus) inhabiting a cold desert ecosystem

1 Introduction

Desert ecosystems cover 20–30% of the terrestrial surface of the earth (Hadley and Szarek, 1981) and another 25% is semi-desert (Pearson, 1965). These ecosystems support a myriad of wildlife and bird species, and are among the biomes with the highest number of threatened species globally (Baillie et al., 2004). Desert ecosystems contain high endemism and are at risk from the effects of global climate change (Baillie et al., 2004). Conservation of species in arid ecosystems is relevant to >50% of the global terrestrial landscape, so developing better tools to support the conservation and management of desert species is essential.

One of the most elementary needs for resource managers and conservationists is obtaining accurate population estimates. Understanding population size, growth rates and fluctuations in natural populations is crucial for management, and provides the ability to make predictions and provide a solid foundation for conservation actions. Population estimates are vulnerable to numerous sources of bias, usually resulting in undercounting (Samuel and Pollock, 1981; McCorquodale, 2001).This is particularly applicable to species found in groups, such as ungulates, in which detection of groups during surveys can vary grossly based on the size of the group and other factors that influence the likelihood of their detection (sighting variables). Applying group-specific correction factors to observed animal groups can compensate for effects of detection bias when estimating abundance and composition. There are several methods for estimating group-specific detection probabilities in aerial surveys, including sightability models (Steinhorst and Samuel, 1989), distance models (Burnham and Anderson, 1984; Buckland et al., 2004), mark-resight models (White, 1996; Skalski et al., 2005), double-observer models (Graham and Bell, 1989), and methods that combine two or more such techniques often referred to as “hybrid” models (Quang and Becker, 1997; Buckland et al., 2010; Burt et al., 2014). These techniques all have individual strengths and weaknesses (Griffin et al., 2013). By combining several techniques to form a hybrid model, the biases of each individual technique can be minimized, while strengthening their collective precision (Griffin et al., 2013).

We conducted population estimation research on elk (Cervus elaphus) inhabiting a high elevation desert ecosystem in the southern Rocky Mountains, USA. Elk are native ungulates of North America and central Asia with a polygonous mating strategy, in which females remain in groups year round and are joined by males during the breeding season or “rut”. Males form independent groups or remain solitary during the non-breeding season. The elk population we studied is free-roaming across a combination of state-, federal-, and privately-owned lands, each with very different management practices. To better manage the herd, an evaluation of the population on its entire range and across socio-political boundaries was needed to determine the whole-herd population size and support a strategy for cross-boundary management of elk.

We surveyed elk via helicopter and applied a hybrid population estimation model that combined 3 commonly used methods: (1) simultaneous double-observer (Cook and Jacobson, 1979; Seber, 1982; Pollock and Kendall, 1987; Bayliss and Yeomans, 1989; Graham and Bell, 1989; Rivest et al., 1995; Manley et al., 1996), (2) radiocollar mark-resight (Seber, 1982; Pollock et al., 1990; White and Burnham, 1999; McClintock et al., 2009), and (3) sightability correction models (Samuel et al., 1987; Steinhorst and Samuel, 1989). Estimating uncertainty for populations in which animals live in groups is problematic using available analytical formulae and software. Therefore we applied a numerical bootstrap algorithm following Wong (1996). The objective of our study was to estimate the elk population size and to analyze and present approaches for dealing with multiple sources of bias by evaluating the relative contribution of each bias correction to the final population estimate.

2 Study area

We conducted the present study in the San Luis Valley of Colorado, USA (37.7329°N, 105.5121W). The San Luis Valley is a high elevation arid ecosystem, often called a “cold desert.” The valley encompasses Great Sand Dunes National Park and Preserve, containing the tallest active sand dunes in North America (Fig. 1). Precipitation averages 28 cm/year and falls mostly during monsoonal rains in July–September. Summers are warm and average daytime temperatures range from 26.5 °C to 29.5 °C. Winters are cold and dry with average valley daytime temperatures ranging from −9.5 °C to 1.5 °C. Elevations on the valley floor range between 2285 m and 2440 m, and up to 3570 m at higher elevations where elk over-summer. The elk population range is approximately 2500 km² on the east side of the San Luis Valley, and includes federally owned and protected lands within Great Sand Dunes National Park and Preserve, the Baca National Wildlife Refuge, and adjacent privately-owned lands. The study area extended from Great Sand Dunes west to Highway CO-17, south to Blanca Peak, and north to Poncha Pass including the western slopes of the Sangre de Cristo Mountains (Fig. 1).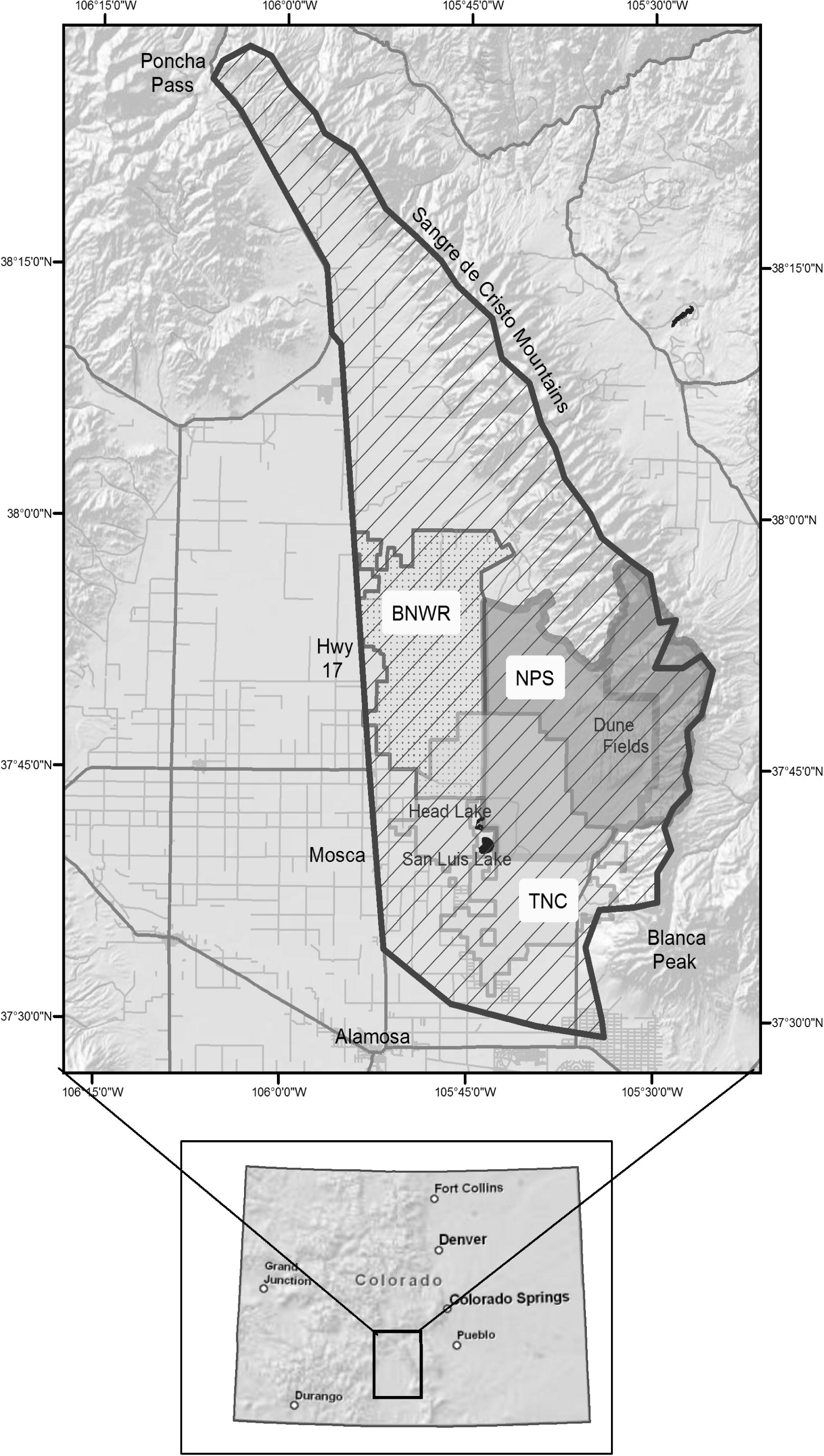

Close

Figure 1

Elk population survey area (hatched) on the east side of the San Luis Valley, a high elevation desert in southern Colorado, USA. The insert box shows location of the study area within Colorado. Federally-protected lands include the Baca National Wildlife Refuge (BNWR – dotted), and National Park Service (NPS; Great Sand Dunes National Park – dark gray). The Nature Conservancy’s (TNC) privately-owned lands are shown in light gray.

Export to PPT

Adjacent to the active dune field extend sandy plains of sand sheet and ‘sabkha’or salt flats, which are stabilized by herbaceous vegetation and shrubs. Vegetation is dominated by greasewood (Sarcobatus vermiculatus)/rabbitbrush (Chrysothamnus nauseosus) shrub lands, with riparian corridors containing willow (Salix spp.) and narrow leaf cottonwood (Populus angustifolia). Dominant graminoids include arctic rush (Juncus balticus), needle and thread grass (Hesperostipa comata), Indian rice grass (Achnatherum hymenoides), sand drop seed (Sporobolus cryptandrus), saltgrass (Distichlis spicata), slender wheatgrass (Elymus trachycaulus), and beardless wild rye (Leymus triticoides).

The Sangre de Cristo Mountains are characterized by lodge pole pine (Pinus contorta) and quaking aspen (Populus tremuloides) on mid-elevation slopes, Engelmann spruce (Picea engelmannii) and subalpine fir (Abies lasiocarpa) dominating upper slopes, and bristlecone pine (Pinus aristata) are found at the highest elevations (Barbour and Billings, 2000). Areas above timberline contain alpine tundra grasslands and wetlands, interspersed with patches of spruce-fir krummholz and alpine willow (primarily short fruit willow [Salix brachycarpa] and diamond leaf willow [S. planifolia]).

The history of elk in the San Luis Valley parallels their history in other areas of the western USA. They were once numerous throughout the valley, but were displaced when the land was inhabited by European settlers in the 1800s and the population was mostly eradicated by overhunting (Swift, 1945). The elk population on the west side of the San Luis Valley recovered from an estimated 25 individuals in 1905 to about 1500 in 1940 (Swift, 1945). On the east side of the valley, elk moved into the area from neighboring game units where their numbers increased (B. Weinmeister, Colorado Parks and Wildlife [CPW], pers. commun.) and some mixing between the east and west populations likely occurred.

3 Methods

4 Results

For the 2005 survey, 27 groups with radio collars were present in the study area, 44 elk groups (with or without radio collars) were detected by the helicopter crew, and an additional 4 elk groups with radio collars that were present in the survey area were not detected by the helicopter crew. Group size ranged from 1 to 667 elk. In 2007, there were 12 groups with radio collars in the valley portion of the survey area and 5 in the mountain portion. The helicopter crew detected 24 elk groups in the valley and 22 in the mountains and missed 3 radio collared groups in each of these sections of the survey area. Group size ranged from 1 to 865 elk in the valley and 1 to 525 elk in the mountains. In both years, there were a total of 44 radio collared groups available for detection by the helicopter crew, which represents the sample size available for estimating the residual heterogeneity parameter. The sample size for models M_D⁺ and M_H includes all 100 groups known to be present during any of the 3 surveys, including both those seen by the helicopter crew and those only known due to radio collars.

Over the course of the 3 surveys, back seat observers saw 3961 elk, whereas front seat observers (model M_F) saw 6052 (52.8% more), reflecting the fact that there was only a single back seat observer surveying on one side of the aircraft. The back seat observers saw 88 elk that the front seat observers did not, increasing the total seen by the helicopter crew (model M_C) to 6,140 elk, an increase of 1.5% over the front seat observer’s count. When photographs of the larger groups were scrutinized following the flights (model M_P), an additional 361 (5.9%) elk were detected that had not been counted by helicopter observers from the air.

Model weights for the 32 parameter variants of model M_D showed very strong support for a positive effect of group size and a negative effect of vegetation (Table 1). Support was moderate among these models for differences in sighting probability for the back seat observer and for differences among the 3 survey occasions. When the additional groups missed by the helicopter and known only due to radio collars were added and used to fit these same models (model M_D⁺), the strength of support for the 2007 valley and 2007 mountain effects increased substantially, whereas support for a back seat observer effect decreased, and support for group size and vegetation were reduced slightly (Table 1).

Model weights for the 64 parameter variants of model M_H were similar to those for model M_D⁺, but also revealed moderate support for a residual heterogeneity effect. After controlling for other effects (survey occasion, group size, and vegetation), groups with radio collars (i.e., those selected randomly, or unconditionally) were more difficult to detect on average than those without radio collars (i.e., those detected by helicopter observers). This difference indicates that elk groups in the visual observers data set were not representative of the total population of elk groups available to have been detected, but were biased toward more easily detected groups, even after accounting for the effects of the covariates we recorded.

In addition to the strength of support for each effect, the relative magnitude and direction of each is important. For a baseline example, consider the 2005 survey with a group size of 12 elk (the median value) and no vegetation present. In this instance the front observers had an estimated sighting probability of 85.5% for groups without radio collars and 68.9% for groups with radio collars (first row of Table 2). The back seat observer had higher sighting probabilities (Table 2). Bear in mind that sighting probability for groups on the opposite side of the aircraft from the back seat observer were fixed at zero, so estimated sighting probabilities for the back are conditional on the group being on the same side. Average sighting probabilities were lower for the 2007 valley survey and even lower for the 2007 mountain survey, relative to the baseline example for 2005. Estimated sighting probability rises gradually with group size and drops substantially when vegetation is present (Table 2). Of the groups detected, the lowest sighting probability estimated by model M_H was 11.7% for a group of 2 elk in the 2007 mountain survey that was not on the same side as the back seat observer and was found in a vegetated area. Across the 3 surveys, 21% of groups had sighting probability <30% and 35% had sighting probability ⩾ 80%.

In order to look closely at the relationship between the differing models and examine the contribution of each component of information, we pooled data from all 3 surveys as if they were one large survey. The sum of the population estimates across the 3 surveys based on the model-weighted average across the 32 fitted M_D models (Fig. 2) was 7076 (SE = 1196; CV = 16.9%). This is 575 (8.8%) more elk than the raw count obtained from the helicopter crew after using the photographs of large groups to account for undercount of these groups in the air (model M_P). Model M_D⁺, fitted to the dataset that included groups with radio collars missed by the helicopter crew, produced an estimate of 7365, which is 290 (4.1%) more elk than model M_D, and with better precision (SE = 929; CV = 12.6%). Model M_H, which accounted for the difference in sighting probability of conditionally detected groups (without radio collars) and unconditionally detected groups (with radio collars), increased the estimate by another 372 elk (5.1%) to a total of 7737, with better precision than model M_D⁺ (SE = 845; CV = 10.9%). When the same model was applied to estimate only groups without radio collars while those with radio collars were included as a known quantity (model M_H^∗), the final estimate was another 116 elk (1.5%) higher and more precise: the final estimate for the sum across surveys for model M_H^∗ was 7,853elk (SE = 697; CV = 8.9%). Using this best model, the elk population in the San Luis Valley was 3534 elk (SE = 71.5; CV = 2.0%) in 2005 and 4319 elk (SE = 698; CV = 16.2%) in 2007 (Fig. 2).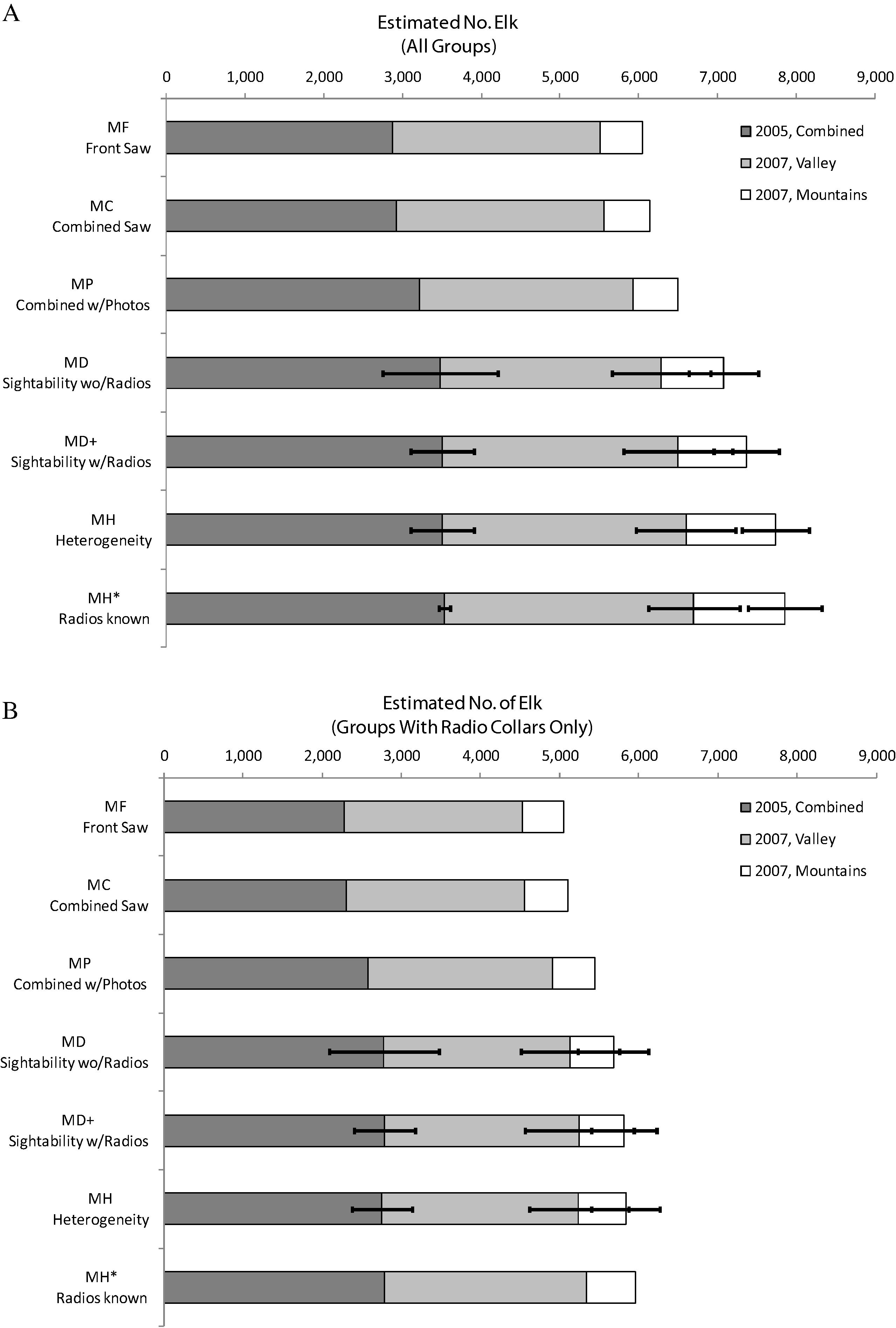

Close

Figure 2

Elk population estimates for 3 surveys in the east side of the San Luis Valley, based on 3 methods of obtaining a raw count uncorrected by statistical estimation of sighting probability, and estimates based on 4 statistical sighting probability modeling methods. See text for explanation of the 7 methods. Panel A shows estimates for all elk groups; panel B shows estimates only for radio collared elk groups. The final bar (Model M_H^∗) in panel B is the known, true population of radio collared elk. The true population in panel B can be compared to the other model estimates to observe the bias of each. The 2005 estimate covers both valley and mountain portions of the survey area, whereas the 2007 estimates for these portions of the study area were separated. The estimates from the 2 surveys were pool for this comparison, which focuses on the relative bias of each method. The error bars on the 4 statistical estimates are 1 standard error (SE) and apply to each of the 3 individual surveys, not to the cumulative total.

Export to PPT

During surveys, the back seat observer saw only 50.4% of the estimated total number of elk, and the front seat observers alone saw only 77.1% of the final estimate. The combined counts by both front and back seat observers, supplemented by more accurate counts from photographs raised the raw count to 82.8% of the final value. This adjusted raw count still missed 1352 elk that our best statistical estimates were able to reveal. Results for only those groups with radio collars, for which the true population was known, are similar: 91.6% of all elk in these groups were detected by the combined aerial observers after supplementing aerial observations with photographs (Fig. 2).

The best statistical model that could be estimated without radio collars (M_D) resulted in a population estimate that was 90.1% of the final value (M_H^∗) and 95.4% if considering only the radio collared portion of the population. When radio collar data were incorporated to increase the size of the data set and to estimate the residual heterogeneity parameter (difference between sightability of randomly selected and conditionally selected elk groups; M_H), the best estimate was 98.5% of the final value (M_H^∗) and 98.1% for the radio collared portion of the population.

5 Discussion

Each element of our method provided incremental gains in bias correction for population estimates. Adding a second, independent observer in the back seat to the aerial survey enabled us to reduce detection bias in 2 ways. First, the second observer saw elk groups not seen by the first. More importantly, using statistical models with data from multiple observers (model M_D) provided estimates of the different sighting probabilities for each unique observer specific to these surveys, which enabled us to estimate both the number of elk not observed by either observer and the precision of those estimates. However, sighting corrections based on just 2 observations are only unbiased if all groups have equal sighting probability or if the sighting covariates explain all of the variation in sighting probability among groups (Burt et al., 2014). This is only a plausible assumption where sighting probabilities are very high or sighting conditions are nearly uniform. However, a bias is likely when heterogeneity in sighting probability among groups is present and not adequately modeled. Therefore, we attempted to use covariates that we hypothesized would explain some of this variability in sighting probability among groups, to correct for several sources of bias that would have resulted in undercounting the true population.

Elk groups in this population during winter are often very large. Our largest group contained 865 elk. The combined motion of the elk and the helicopter makes accurate counting of groups this large unlikely without the use of high-resolution photographs. Consequently, using photography for all large groups improves accuracy. However, we acknowledge that even with the photographs, some negative bias (undercount) could still remain, but the magnitude of that bias is reduced substantially by using high-quality photography.

The sighting probability estimates calculated from double-observer data (models M_D and M_D⁺) enabled us to correct for elk not seen by either aerial observer. This bias can be corrected through the regular use of 2 (or, preferably 3 if both seats in the back are occupied to provide coverage on both sides of the aircraft) aerial observers so that sightability correction models can be calculated based on the observers and field conditions specific to each survey. Data from subsequent surveys conducted under similar conditions can usually be pooled to obtain a larger sample size of observations, enabling better estimates of sighting probability and the effects of individual covariates.

Unless all of the difference among groups is modeled with the selected covariates, however, a residual bias will persist. With the radio collars, we were able to estimate a residual heterogeneity parameter to account for the otherwise unmodeled (unaccounted for by our selected covariates) differences between randomly (unconditionally) selected groups (those with radio collars) and groups conditioned on being seen by the helicopter crew (those without radio collars). We concluded by comparing model M_D⁺ with M_H^∗ that a significant negative bias averaging 6.2% remained that was only correctable through this method, unless a better set of predictive covariates could be found and tested. This finding is consistent with similar results reported in Griffin et al. (2013).

Traditional sightability correction models attempt to correct for missed groups using individual covariates, however this correction is based on initial calibration of the sightability model when radio collars are present but is not updated or supplemented by accumulating data from subsequent surveys when radio collars are no longer available in the population. Thus, with traditional sightability models, future population estimates depend entirely on the assumption that the sightability corrections estimated from initial flights are universally applicable on later flights that have different observers and different environmental conditions. Our surveys used a small number of observers, all with extensive aerial survey experience, and the same aircraft. Despite this, we found strong evidence for different sighting probabilities for each of the 3 surveys. For this reason, we caution against applying the population estimation model fitted in this study to future surveys, even in the same location and with the same observers. Data from future surveys at this site could be pooled with surveys from 2005 and 2007 to obtain a larger sample size and greater precision, if statistical evidence supports such pooling. Sighting bias estimation as a function of observer and environmental covariates should always be included in future surveys, at least to confirm that the current corrections still work, and at best to continue to improve them over time as more elk group observation data accumulates.

Data collected on future elk surveys of this study area, when radio collars are no longer present, will add to the cumulative dataset available for fitting sightability models of the model M_H type. However, without radio collars, no additional information will be gathered about the residual heterogeneity parameter, only for the other parameters in the model. This means that, like a sightability model, it must be assumed that this residual heterogeneity effect remains constant in the future. However, this assumption is limited only to this single parameter, which explains only a small fraction of the bias – most of the bias is modeled by the parameters that can be updated after future surveys are conducted without radio collars. This leaves much less room for error due to unmeasured changes in this single parameter. To the extent that other parameters can be found to minimize the residual heterogeneity effect, errors caused by future changes in this residual heterogeneity parameter would be correspondingly reduced. There is some loss of accuracy in any survey without radio collars because model M_H^∗ cannot be applied, but the correction due to this additional information was small in our study (1.5%), although it also improved precision from CV = 10.9% to 8.9%. Repeating the radio collar study periodically to test for changes in and to update the estimate of the heterogeneity parameter would be desirable. This is especially true in this case, given that we were only able to apply a sample size of 44 groups to use in fitting the residual heterogeneity parameter.

As in most modeling, there are some uncertainties even in what we find to be our best modeling approach, and our estimates may rely on some extrapolation beyond observed conditions. We only placed collars on elk found in the survey area, which may not accurately represent all elk that occasionally use the area. Our estimates only apply to elk present in the survey area during the survey and do not account for other elk that may use the survey area intermittently. A far more extensive radio-collaring effort would be required to estimate the portion of the potentially larger population that occasionally uses the survey area that were actually present during a given survey.

A second limitation of our bias corrections is that all collars were placed on adult female elk. We cannot determine from our data (or any other available) whether these corrections apply equally to other age and sex classes. Calves are found in groups with females, so it is less likely that a different bias applies to this segment. Another work has documented a negative sighting bias for male elk in aerial surveys (McCorquodale, 2001), leading us to believe that our population estimate from model M_H^∗ may be low.

We acknowledge that several improvements could be made in our methods for future surveys. It is far better to have 2 observers in the back seat so that all elk groups are subject to sighting and resighting, not only those on one side of the aircraft with the single back seat observer. This would not only increase the raw count reducing the magnitude of the statistical correction, but also would provide a larger sample size for estimating sighting probabilities, which can only be done when ⩾2 observers are available to observe a particular group. We suspect that some of the residual heterogeneity that could only be estimated through the use of radio collars is due to variation in the distances from observers to elk groups. Collecting at least crude distance estimates could improve the ability to estimate sighting probability without depending as much on the residual heterogeneity parameter. Additional covariates that might also help explain visibility differences among groups could be considered, such as indicators for lighting condition (e.g., full sun, patchy sun, and overcast sky) and activity of elk (Griffin et al., 2013; Samuel et al., 1987; Anderson and Lindzey, 1996; Gilbert and Moeller, 2008; McIntosh et al., 2009). If different observers are used in the future, covariates to account for individual observer differences could improve precision and reduce bias. Separating the valley and mountain portions of the survey area (stratifying) in 2007 improved survey results, given the significant differences in sighting probabilities estimated for these distinctly different habitat types. To apply this method to other locations and species, experienced biologists and aerial observers who know what factors affect their ability to detect the target species in that area must carefully consider and select the list of covariates to be collected and tested. Statistical analysis requires that values for all of those candidate covariates must be recorded for each observed animal group.

We recognize the possibility that a larger dataset would likely support additional parameters to explain more of the differences in sighting probability among elk groups. In particular, interactions among main effects variables in our models are a possibility. For example, front and back seat observers may not respond identically to group size, vegetation, survey occasion, or the unknown heterogeneity effects captured by our heterogeneity parameter. The unknown heterogeneity might also not be constant, but might interact with group size, vegetation, or survey occasion. We were not able to model these potential interactions in our study without a larger sample size.

Surveys should be designed to hold as much constant as possible and repeated using consistent methods, pilots, aircraft, and observers over multiple years. By minimizing the variation that needs to be explained and increasing the sample size to facilitate estimation of more components of the remaining variation, even better estimates are possible. Nonetheless, using every available tool to correct for biases, as we did here, is an improvement over methods that rely on less information. No population estimation method will ever be perfect, but we’ve demonstrated that at least the following components of the survey design are important: (1) multiple observers, (2) counts for large groups based photographs, (3) statistical correction models incorporating measured covariates that influence sighting probability, and, when budgets permit, (4) additional statistical correction for unmodeled heterogeneity based on radio collar data.

Simple raw counts, often incorrectly referred to as a “census,” can produce severely biased estimates (undercounts) of ungulate populations, and provide no measure of precision with which to evaluate the usefulness of the estimate. In this study, 22.9% of the estimated population would have been missed by a simple raw count using a single aerial observer and pilot. The validity of a traditional sightability model, calibrated for different observers, locations, conditions, and populations is questionable. Simple double-observer methods (i.e., a Lincoln–Peterson estimator, as in Graham and Bell, 1989) without sighting covariates is likely to be substantially biased by heterogeneity (differences in sightability) among elk groups (Burt et al., 2014).

Using hybrid methods that combine double observer data with sighting covariates greatly improves the reliability of population estimates. Much accuracy and precision can be gained using the double-observer method (model M_D) alone, but the use of radio collars during an initial study period enables the use of model M_H, which can further improve results and increase confidence in their reliability.

The hybrid method we applied (model M_H or M_H^∗ when collars are present) is suitable for most aerial surveys of large terrestrial wildlife species. It may be particularly applicable in arid environments, where there tends to be relatively little vegetation that obstructs aerial observers’ view of wildlife. The field methods are only slightly more complex and generally no more costly than for other aerial survey methods. We do recognize, however, that the analytical techniques are complex, particularly the bootstrap modeling required to estimate confidence intervals (Griffin et al., 2013). To date, data analysis has been developed specifically for each study and requires an experienced statistical analyst. Development of reusable software to facilitate analyses of this type is an important area for future work.