Analytic approximations to non-linear third order jerk equations via modified global error minimization method

Gamal M. Ismail; Hanaa Abu-Zinadah

doi:10.1016/j.jksus.2020.10.016

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

01 2020

:33;

101219

doi:

10.1016/j.jksus.2020.10.016

Analytic approximations to non-linear third order jerk equations via modified global error minimization method

Gamal M. Ismail^{^a,^b,⁎}, Hanaa Abu-Zinadah^{^c}

a Department of Mathematics, Faculty of Science, Sohag University, Sohag 82524, Egypt

b Department of Mathematics, Faculty of Science, Islamic University of Madinah, Madinah 42351, Saudi Arabia

c Department of Statistics, College of Science, University of Jeddah, Jeddah, Saudi Arabia

⁎Corresponding author at: Department of Mathematics, Faculty of Science, Sohag University, Sohag 82524, Egypt. gamal@science.sohag.edu.eg (Gamal M. Ismail)

Received: 2020-7-10, Accepted: 2020-10-9,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this paper, a modified version of the global error minimization method (GEMM) is presented for solving non-linear third order jerk equations by obtaining the unknown parameters up to third order. Two illustrative examples are given to demonstrate the implementation and validity of the present method. The obtained analytical results are compared and simulated with the known solutions and the exact numerical one, which reveal that the current method are very effective and provides an efficient alternative to the known previously existing methods and can be used for other nonlinear applications arising in engineering and sciences. The analytical and numerical results are presented through Tables and graphs.

Keywords

Nonlinear third order jerk equations

Analytical solutions

Global error minimization method

Numerical solution

Periodic solutions

Show Related Articles from PubMed

1 Introduction

Mathematical modeling in many engineering systems often leads to non-linear differential equations that have attracted the attention of the research community during the last decade. Nonlinear differential equations has many real applications in different fields of science and engineering, for examples, plasma physics, nonlinear optics, fluid dynamics, bioengineering, biology and other different scientific fields.

Recently, various powerful analytical and numerical approximate techniques have been suggested for dealing with differential equations and fractional differential equations. We may mention, for example (Singh, 2020a, 2020b; Singh et al., 2019, 2020; Yadav et al., 2019; Kumar et al., 2020a, 2020b, 2020c; Veeresha et al., 2020; Alshabanat et al., 2020; Ismail et al., 2020a ).

There are a large numbers of analytical methods used for the solution of nonlinear oscillatory differential equations such as, Linstedt-Poincare (Casal and Freedman, 1980; Nayfeh, 1973), multiple scales (Nayfeh and Mook, 1979; Ahmadian and Azizi, 2010), homotopy perturbation (He, 1999) and so on (He, 2010; Navarro and Cveticanin, 2016; Ismail et al., 2019, 2020b; Hosen et al., 2020; Cveticanin and Ismail, 2019; El-Naggar and Ismail, 2016 ).

Nowadays, due to the importance of knowledge of the analytical solutions of the jerk problems, we find that many scientists focused on the study of like this problems, they have done great efforts to modify or find new methods to solve this type of problems so several distinct techniques have been proposed such as (Gottlieb, 2004) used the method of harmonic balance up to first order (HB). Wu et al., 2006 presented the harmonic balance approach up to third approximations to solve jerk equations. Ma et al., 2008 used the homotopy perturbation method and (Hu, 2008) applied the parameter perturbation method to obtain high-order analytic solutions for the nonlinear jerk equations. Hu et al., 2010 generalized the Mickens iteration method to obtain the periodic solutions for nonlinear jerk equation. Ramos, 2010 used Linstedt-Poincare methods to obtained analytical solutions to some jerk equations. Leung and Guo (2011) applied the residue harmonic balance method while (Karahan, 2017) applied the multiple scales Lindstedt-Poincare (MSLP) method to solve the current problems. Recently, (Rahman and Hasan, 2018) used the modified harmonic balance method for solving the same problems.

The GEM method see (Yazdi and Tehrani, 2016; Farzaneh and Tootoonchi, 2010; Mirzabeigy et al., 2012 ) is one of the most widely used techniques for dealing with the solution of nonlinear differential equations as it gives more accurate result than the other known methods.

Our aim in current paper is to extend the global error minimization method to obtain analytic approximations up to third order for the non-linear jerk equations due to increasing importance in various physical problems modeling. Amplitude-frequency relationship is obtained in an analytical form. Further, the obtained analytical and numerical results are presented in the form of Tables and Figures. Also the analytical results are compared with some known methods from the literature.

The remnant of this study is described according to the following: In Section 2, we demonstrate briefly discuss the description of the modified global error minimization method. Applications of the MGEMM to study two nonlinear jerk equations with cubic nonlinearity have been shown in Section 3. The results of the current study are summarized in Section 4. Finally, conclusion remarks are descried in Section 5.

2 The modified global error minimization method

In this section, we explain the basic idea of MGEMM by consider the following nonlinear differential equation:

(1)

\overset{⃛}{x} + f (x, \dot{x}, \ddot{x}) = 0, x (0) = 0, \dot{x} (0) = A, \ddot{x} (0) = 0 .

Following (Gottlieb, 2004), the general nonlinear third order jerk equation has the form

(2)

\overset{⃛}{x} = - γ \dot{x} - α {\dot{x}}^{3} - β x^{2} \dot{x} + δ x \dot{x} \ddot{x} - ε \dot{x} {\ddot{x}}^{2},

with the initial conditions

(3)

x (0) = 0, \dot{x} (0) = A, \ddot{x} (0) = 0,

where the parameters

α, β, γ, δ

and

ε

are constants and at least one of them should be non-zero.

Defining a functional as follows:

(4)

E (x) = \int_{0}^{T} {(\overset{⃛}{x} + f (x, \dot{x}, \ddot{x}))}^{2} d t, T = \frac{2 π}{ω} .

The function $x (t)$ of Eq. (2) can be determine by the next trial solutions,

(5)

x (t) = \sum_{n = 0}^{\infty} (\frac{a_{(2 n + 1)}}{(2 n + 1) ω} s i n (2 n + 1) ω t),

where

a_{(2 n + 1)}, (n = 0, 1, \dots)

are unknown coefficients satisfying the initial conditions in (2) so that

(6)

\sum_{n = 0}^{\infty} a_{(2 n + 1)} = A .

The unknown parameters (i.e., $a_{(2 n + 1)}$ & $ω$ ) can be finding through the conditions:

(7)

\frac{\partial E (x)}{\partial ω} = 0, \frac{\partial E (x)}{\partial a_{(2 n + 1)}} = 0, f o r n \geq 1 .

In order to demonstrate the practicality and effectiveness of the modified global error minimization method, the nonlinear jerk equations are taken into consideration in this study.

3 Examples

In this segment, MGEM method is presented to solve two different cases of nonlinear jerk equations with cubic nonlinearity see (Gottlieb, 2004):

3.1

3.1 Jerk function of displacement time's velocity times acceleration and velocity

The first special case of the nonlinear third order jerk equation is considered. Namely, for $γ = δ = 1, α = β = ε = 0,$ in the form:

(8)

\overset{⃛}{x} + \dot{x} - x \dot{x} \ddot{x} = 0, x (0) = 0, \dot{x} (0) = A, \ddot{x} (0) = 0 .

3.1.1

3.1.1 First order approximation

For the first order approximation, assume new trial function is:

(9)

x_{1} (t) = \frac{a_{1}}{ω} \sin ω t .

Substituting (9) in (4) yields:

(10)

E (x) = \int_{0}^{2 π / ω} {(\overset{⃛}{x} + \dot{x} - x \dot{x} \ddot{x})}^{2} d t .

Choosing $a_{1} = A,$ and performing the integration we have

(11)

E (x) = \frac{A^{2} π}{ω} + \frac{A^{4} π}{2 ω} + \frac{A^{6} π}{8 ω} - 2 A^{2} π ω - \frac{1}{2} A^{4} π ω + A^{2} π ω^{3} .

Applying $\partial E (x) / \partial ω = 0,$ the approximate frequency is obtained as:

(12)

ω_{1} = \sqrt{\frac{4 + A^{2} + \sqrt{64 + 32 A^{2} + 7 A^{4}}}{12} .}

3.1.2

3.1.2 Second order approximations

To improve the analytical approximation and illustrate the capacity of the (GEMM), the second order approximation is applied to jerk equation, by using the following new trial solution.

(13)

x_{2} (t) = \frac{a_{1}}{ω} \sin ω t + \frac{a_{3}}{3 ω} \sin 3 ω t,

where

(14)

{A = a_{1} + a}_{3} .

Substituting Eq. (13) in Eq. (4), we obtain

(15)

E (x) = \frac{π a_{1}^{2}}{ω} - 2 π ω a_{1}^{2} + π ω^{3} a_{1}^{2} + \frac{π a_{1}^{4}}{2 ω} - \frac{1}{2} π ω a_{1}^{4} + \frac{π a_{1}^{6}}{8 ω} + \frac{2 π a_{1}^{3} a_{3}}{3 ω} + \frac{10}{3} π ω a_{1}^{3} a_{3} + \frac{π a_{1}^{5} a_{3}}{24 ω} + \frac{π a_{3}^{2}}{ω} - 18 π ω a_{3}^{2} + 81 π ω^{3} a_{3}^{2} + \frac{2 π a_{1}^{2} a_{3}^{2}}{ω} - 10 π ω a_{1}^{2} a_{3}^{2} + \frac{145 π a_{1}^{4} a_{3}^{2}}{72 ω} - \frac{29 π a_{1}^{3} a_{3}^{3}}{36 ω} + \frac{π a_{3}^{4}}{2 ω} - \frac{9}{2} π ω a_{3}^{4} + \frac{145 π a_{1}^{2} a_{3}^{4}}{72 ω} + \frac{π a_{3}^{6}}{8 ω} .

Setting $\partial E (x) / \partial ω = 0,$ and $\partial E (x) / \partial a_{3} = 0$ yields to:

(16)

- 2 π a_{1}^{2} - \frac{π a_{1}^{2}}{ω^{2}} + 3 π ω^{2} a_{1}^{2} - \frac{π a_{1}^{4}}{2} - \frac{π a_{1}^{4}}{2 ω^{2}} - \frac{π a_{1}^{6}}{8 ω^{2}} + \frac{10}{3} π a_{1}^{3} a_{3} - \frac{2 π a_{1}^{3} a_{3}}{3 ω^{2}} - \frac{π a_{1}^{5} a_{3}}{24 ω^{2}} - 18 π a_{3}^{2} - \frac{π a_{3}^{2}}{ω^{2}} + 243 π ω^{2} a_{3}^{2} - 10 π a_{1}^{2} a_{3}^{2} - \frac{2 π a_{1}^{2} a_{3}^{2}}{ω^{2}} - \frac{145 π a_{1}^{4} a_{3}^{2}}{72 ω^{2}} + \frac{29 π a_{1}^{3} a_{3}^{3}}{36 ω^{2}} - \frac{9 π a_{3}^{4}}{2} - \frac{π a_{3}^{4}}{2 ω^{2}} - \frac{145 π a_{1}^{2} a_{3}^{4}}{72 ω^{2}} - \frac{π a_{3}^{6}}{8 ω^{2}} = 0,

(17)

\frac{2 π a_{1}^{3}}{3 ω} + \frac{10}{3} π ω a_{1}^{3} + \frac{π a_{1}^{5}}{24 ω} + \frac{2 π a_{3}}{ω} - 36 π ω a_{3} + 162 π ω^{3} a_{3} + \frac{4 π a_{1}^{2} a_{3}}{ω} - 20 π ω a_{1}^{2} a_{3} + \frac{145 π a_{1}^{4} a_{3}}{36 ω} - \frac{29 π a_{1}^{3} a_{3}^{2}}{12 ω} + \frac{2 π a_{3}^{3}}{ω} - 18 π ω a_{3}^{3} + \frac{145 π a_{1}^{2} a_{3}^{3}}{18 ω} + \frac{3 π a_{3}^{5}}{4 ω} = 0 .

After applying the condition ${A = a_{1} + a}_{3}$ and solving Eqs. (16) and (17) the parameters of $a_{1},$ $a_{3}$ and the angular frequency $ω$ can be determined for a known amplitude.

3.1.3

3.1.3 Third-order approximations

The accuracy of results will be further improved by consider the following equation as the response of the system

(18)

x_{2} (t) = \frac{a_{1}}{ω} \sin ω t + \frac{a_{3}}{3 ω} \sin 3 ω t + \frac{a_{5}}{5 ω} \sin 5 ω t,

where

(19)

{A = a_{1} + a}_{3} + a_{5} .

Substituting Eq. (18) in Eq. (4), we obtain

(20)

E (x) = \frac{π a_{1}^{2}}{ω} - 2 π ω a_{1}^{2} + π ω^{3} a_{1}^{2} + \frac{π a_{1}^{4}}{2 ω} - \frac{1}{2} π ω a_{1}^{4} + \frac{π a_{1}^{6}}{8 ω} + \frac{2 π a_{1}^{3} a_{3}}{3 ω} + \frac{10}{3} π ω a_{1}^{3} a_{3} + \frac{π a_{1}^{5} a_{3}}{24 ω} + \frac{π a_{3}^{2}}{ω} - 18 π ω a_{3}^{2} + 81 π ω^{3} a_{3}^{2} + \frac{2 π a_{1}^{2} a_{3}^{2}}{ω} - 10 π ω a_{1}^{2} a_{3}^{2} + \frac{145 π a_{1}^{4} a_{3}^{2}}{72 ω} - \frac{29 π a_{1}^{3} a_{3}^{3}}{36 ω} + \frac{π a_{3}^{4}}{2 ω} - \frac{9}{2} π ω a_{3}^{4} + \frac{145 π a_{1}^{2} a_{3}^{4}}{72 ω} + \frac{π a_{3}^{6}}{8 ω} - \frac{21 π a_{1}^{5} a_{5}}{40 ω} + \frac{2 π a_{1}^{2} a_{3} a_{5}}{ω} + \frac{166}{5} π ω a_{1}^{2} a_{3} a_{5} + \frac{13 π a_{1}^{4} a_{3} a_{5}}{30 ω} + \frac{2 π a_{1} a_{3}^{2} a_{5}}{ω} - \frac{158}{5} π ω a_{1} a_{3}^{2} a_{5} + \frac{973 π a_{1}^{3} a_{3}^{2} a_{5}}{180 ω} - \frac{51 π a_{1}^{2} a_{3}^{3} a_{5}}{20 ω} + \frac{23 π a_{1} a_{3}^{4} a_{5}}{10 ω} + \frac{π a_{5}^{2}}{ω} - 50 π ω a_{5}^{2} + 625 π ω^{3} a_{5}^{2} + \frac{2 π a_{1}^{2} a_{5}^{2}}{ω} - 26 π ω a_{1}^{2} a_{5}^{2} + \frac{801 π a_{1}^{4} a_{5}^{2}}{200 ω} - \frac{647 π a_{1}^{3} a_{3} a_{5}^{2}}{150 ω} + \frac{2 π a_{3}^{2} a_{5}^{2}}{ω} - 34 π ω a_{3}^{2} a_{5}^{2} + \frac{1109 π a_{1}^{2} a_{3}^{2} a_{5}^{2}}{90 ω} - \frac{167 π a_{1} a_{3}^{3} a_{5}^{2}}{300 ω} + \frac{2281 π a_{3}^{4} a_{5}^{2}}{1800 ω} - \frac{511 π a_{1}^{2} a_{3} a_{5}^{3}}{100 ω} + \frac{3809 π a_{1} a_{3}^{2} a_{5}^{3}}{900 ω} + \frac{π a_{5}^{4}}{2 ω} - \frac{25}{2} π ω a_{5}^{4} + \frac{801 π a_{1}^{2} a_{5}^{4}}{200 ω} + \frac{2281 π a_{3}^{2} a_{5}^{4}}{1800 ω} + \frac{π a_{5}^{6}}{8 ω}

Setting $\partial E (x) / \partial ω = 0,$ $\partial E (x) / \partial a_{3} = 0$ and $\partial E (x) / \partial a_{5} = 0$ yields to:

(21)

- 2 π a_{1}^{2} - \frac{π a_{1}^{2}}{ω^{2}} + 3 π ω^{2} a_{1}^{2} - \frac{π a_{1}^{4}}{2} - \frac{π a_{1}^{4}}{2 ω^{2}} - \frac{π a_{1}^{6}}{8 ω^{2}} + \frac{10}{3} π a_{1}^{3} a_{3} - \frac{2 π a_{1}^{3} a_{3}}{3 ω^{2}} - \frac{π a_{1}^{5} a_{3}}{24 ω^{2}} - 18 π a_{3}^{2} - \frac{π a_{3}^{2}}{ω^{2}} + 243 π ω^{2} a_{3}^{2} - 10 π a_{1}^{2} a_{3}^{2} - \frac{2 π a_{1}^{2} a_{3}^{2}}{ω^{2}} - \frac{145 π a_{1}^{4} a_{3}^{2}}{72 ω^{2}} + \frac{29 π a_{1}^{3} a_{3}^{3}}{36 ω^{2}} - \frac{9 π a_{3}^{4}}{2} - \frac{π a_{3}^{4}}{2 ω^{2}} - \frac{145 π a_{1}^{2} a_{3}^{4}}{72 ω^{2}} - \frac{π a_{3}^{6}}{8 ω^{2}} + \frac{21 π a_{1}^{5} a_{5}}{40 ω^{2}} + \frac{166}{5} π a_{1}^{2} a_{3} a_{5} - \frac{2 π a_{1}^{2} a_{3} a_{5}}{ω^{2}} - \frac{13 π a_{1}^{4} a_{3} a_{5}}{30 ω^{2}} - \frac{158}{5} π a_{1} a_{3}^{2} a_{5} - \frac{2 π a_{1} a_{3}^{2} a_{5}}{ω^{2}} - \frac{973 π a_{1}^{3} a_{3}^{2} a_{5}}{180 ω^{2}} + \frac{51 π a_{1}^{2} a_{3}^{3} a_{5}}{20 ω^{2}} - \frac{23 π a_{1} a_{3}^{4} a_{5}}{10 ω^{2}} - 50 π a_{5}^{2} - \frac{π a_{5}^{2}}{ω^{2}} + 1875 π ω^{2} a_{5}^{2} - 26 π a_{1}^{2} a_{5}^{2} - \frac{2 π a_{1}^{2} a_{5}^{2}}{ω^{2}} - \frac{801 π a_{1}^{4} a_{5}^{2}}{200 ω^{2}} + \frac{647 π a_{1}^{3} a_{3} a_{5}^{2}}{150 ω^{2}} - 34 π a_{3}^{2} a_{5}^{2} - \frac{2 π a_{3}^{2} a_{5}^{2}}{ω^{2}} - \frac{1109 π a_{1}^{2} a_{3}^{2} a_{5}^{2}}{90 ω^{2}} + \frac{167 π a_{1} a_{3}^{3} a_{5}^{2}}{300 ω^{2}} - \frac{2281 π a_{3}^{4} a_{5}^{2}}{1800 ω^{2}} + \frac{511 π a_{1}^{2} a_{3} a_{5}^{3}}{100 ω^{2}} - \frac{3809 π a_{1} a_{3}^{2} a_{5}^{3}}{900 ω^{2}} - \frac{25 π a_{5}^{4}}{2} - \frac{π a_{5}^{4}}{2 ω^{2}} - \frac{801 π a_{1}^{2} a_{5}^{4}}{200 ω^{2}} - \frac{2281 π a_{3}^{2} a_{5}^{4}}{1800 ω^{2}} - \frac{π a_{5}^{6}}{8 ω^{2}} = 0,

(22)

\frac{2 π a_{1}^{3}}{3 ω} + \frac{10}{3} π ω a_{1}^{3} + \frac{π a_{1}^{5}}{24 ω} + \frac{2 π a_{3}}{ω} - 36 π ω a_{3} + 162 π ω^{3} a_{3} + \frac{4 π a_{1}^{2} a_{3}}{ω} - 20 π ω a_{1}^{2} a_{3} + \frac{145 π a_{1}^{4} a_{3}}{36 ω} - \frac{29 π a_{1}^{3} a_{3}^{2}}{12 ω} + \frac{2 π a_{3}^{3}}{ω} - 18 π ω a_{3}^{3} + \frac{145 π a_{1}^{2} a_{3}^{3}}{18 ω} + \frac{3 π a_{3}^{5}}{4 ω} + \frac{2 π a_{1}^{2} a_{5}}{ω} + \frac{166}{5} π ω a_{1}^{2} a_{5} + \frac{13 π a_{1}^{4} a_{5}}{30 ω} + \frac{4 π a_{1} a_{3} a_{5}}{ω} - \frac{316}{5} π ω a_{1} a_{3} a_{5} + \frac{973 π a_{1}^{3} a_{3} a_{5}}{90 ω} - \frac{153 π a_{1}^{2} a_{3}^{2} a_{5}}{20 ω} + \frac{46 π a_{1} a_{3}^{3} a_{5}}{5 ω} - \frac{647 π a_{1}^{3} a_{5}^{2}}{150 ω} + \frac{4 π a_{3} a_{5}^{2}}{ω} - 68 π ω a_{3} a_{5}^{2} + \frac{1109 π a_{1}^{2} a_{3} a_{5}^{2}}{45 ω} - \frac{167 π a_{1} a_{3}^{2} a_{5}^{2}}{100 ω} + \frac{2281 π a_{3}^{3} a_{5}^{2}}{450 ω} - \frac{511 π a_{1}^{2} a_{5}^{3}}{100 ω} + \frac{3809 π a_{1} a_{3} a_{5}^{3}}{450 ω} + \frac{2281 π a_{3} a_{5}^{4}}{900 ω} = 0,

(23)

- \frac{21 π a_{1}^{5}}{40 ω} + \frac{2 π a_{1}^{2} a_{3}}{ω} + \frac{166}{5} π ω a_{1}^{2} a_{3} + \frac{13 π a_{1}^{4} a_{3}}{30 ω} + \frac{2 π a_{1} a_{3}^{2}}{ω} - \frac{158}{5} π ω a_{1} a_{3}^{2} + \frac{973 π a_{1}^{3} a_{3}^{2}}{180 ω} - \frac{51 π a_{1}^{2} a_{3}^{3}}{20 ω} + \frac{23 π a_{1} a_{3}^{4}}{10 ω} + \frac{2 π a_{5}}{ω} - 100 π ω a_{5} + 1250 π ω^{3} a_{5} + \frac{4 π a_{1}^{2} a_{5}}{ω} - 52 π ω a_{1}^{2} a_{5} + \frac{801 π a_{1}^{4} a_{5}}{100 ω} - \frac{647 π a_{1}^{3} a_{3} a_{5}}{75 ω} + \frac{4 π a_{3}^{2} a_{5}}{ω} - 68 π ω a_{3}^{2} a_{5} + \frac{1109 π a_{1}^{2} a_{3}^{2} a_{5}}{45 ω} - \frac{167 π a_{1} a_{3}^{3} a_{5}}{150 ω} + \frac{2281 π a_{3}^{4} a_{5}}{900 ω} - \frac{1533 π a_{1}^{2} a_{3} a_{5}^{2}}{100 ω} + \frac{3809 π a_{1} a_{3}^{2} a_{5}^{2}}{300 ω} + \frac{2 π a_{5}^{3}}{ω} - 50 π ω a_{5}^{3} + \frac{801 π a_{1}^{2} a_{5}^{3}}{50 ω} + \frac{2281 π a_{3}^{2} a_{5}^{3}}{450 ω} + \frac{3 π a_{5}^{5}}{4 ω} = 0 .

Combining Eqs. (22) and (23) and applying the conditions ${A = a_{1} + a}_{3} + a_{5},$ the parameter $a_{1},$ $a_{3},$ $a_{5}$ and the angular frequency $ω$ can be obtained for a known amplitude.

3.2

3.2 Jerk function of velocity times acceleration-squared, and velocity

The second case of the nonlinear third order jerk equation is considered. Namely, for $γ = ε = 1, α = β = δ = 0,$ in the form:

(24)

\overset{⃛}{x} + \dot{x} + \dot{x} {\ddot{x}}^{2} = 0, x (0) = 0, \dot{x} (0) = A, \ddot{x} (0) = 0 .

3.2.1

3.2.1 First-order approximation

Assume the trial function for the first-order approximation is

(25)

x_{1} (t) = \frac{a_{1}}{ω} \sin ω t .

Inserting Eq. (25) in Eq. (4) yields:

(26)

E (x) = \int_{0}^{2 π / ω} {(\overset{⃛}{x} + \dot{x} + \dot{x} {\ddot{x}}^{2})}^{2} d t .

Choosing $A = a_{1}$ and performing the integration we have

(27)

E (x) = \frac{A^{2} π}{ω} - 2 A^{2} π ω + \frac{1}{2} A^{4} π ω + A^{2} π ω^{3} - \frac{1}{2} A^{4} π ω^{3} + \frac{1}{8} A^{6} π ω^{3} .

Applying $\partial E (x) / \partial ω = 0,$ the approximate frequency is obtained as:

(28)

ω = \sqrt{\frac{8 - {2 A}^{2} + 2 \sqrt{64 - 32 A^{2} + 7 A^{4}}}{24 - 12 A^{2} + 3 A^{4}}}

Using the previously mentioned procedure as in the application 3.1 the solution in the second and third approximation are calculated and the results were displayed in Fig. 2 and Table 2.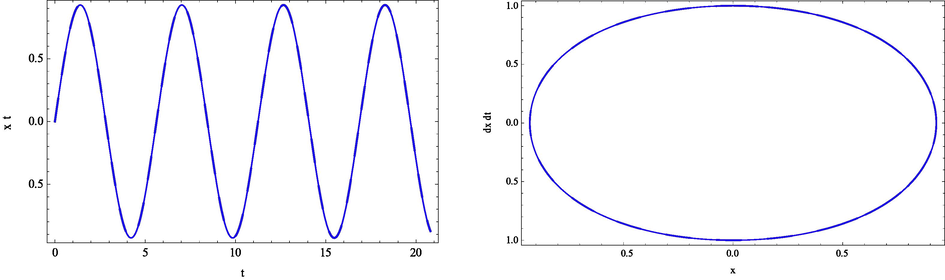

Comparison of the R-K solution (solid line) and approximate solution (dashed line) for Eq. (8) at A = 1 .

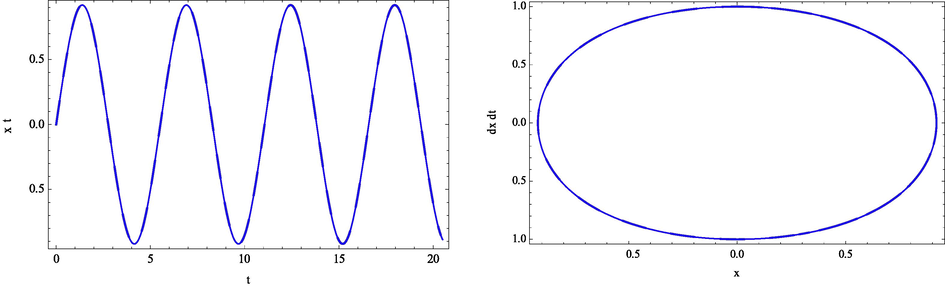
Comparison of the R-K solution (solid line) and approximate solution (dashed line) for Eq. (24) at A = 1 .

Table 1 Comparison of the exact and approximate periods for Eq. (8).

$A$	$T_{e}$	Current $T_{3}$	Karahan (2017)	Leung and Guo (2011)	Ma et al. (2008)	Ramos (2010)	Gottlieb (2004)	Rahman and Hasan (2018)
0.1	6.275347	6.275347	6.2753468	6.275346837	6.27534684	6.275348	6.275346	6.275346837
0.2	6.252016	6.252016	6.2520158	6.25201599	6.25201599	6.252028	6.252003	6.25201599
0.5	6.096061	6.096061	6.0960246	6.09606050	6.09605904	6.096491	6.095585	6.096060516
1	5.626007	5.62602	5.6245487	5.62599289	5.62579479	5.630343	5.619852	5.62599937
2	4.491214	4.47661	4.4664554	4.49012538	4.48208113	4.509311	4.442883	4.49112308

Table 2 Comparison of the exact and approximate periods for Eq. (24).

$A$	$T_{e}$	Current $T_{3}$	Karahan (2017)	Leung and Guo (2011)	Ma et al. (2008)	Ramos (2010)	Gottlieb (2004)	Rahman and Hasan (2018)
0.1	6.2753338	6.27533378	6.27533378	6.2753338	6.27533377	6.275329	6.2753264	6.275333785
0.2	6.251809	6.25180898	6.25180884	6.25180911	6.25182078	6.251740	6.251690	6.25180897
0.5	6.088449	6.08845017	6.08841902	6.08848374	6.08815979	6.085649	6.083668	6.088450
1	5.527200	5.527656919	5.52576588	5.52994105	5.50818960	5.477174	5.441398	5.527497
1.5	4.690247	4.7771790	4.68572454	4.72603111	4.44735707	4.412733	4.155936	4.68326934

4 Numerical results and discussion

In comparison our results obtained from the MGEM method with others different methods and exact numerical one, Tables 1 and 2 give a comparison of the third approximate period $T_{3}$ for the two examples with the known exact period and other existing results. It can be seen that the approximate solutions obtained by MGEM method provides the better result than that others known method. Also it shows excellent agreement between numerical and analytical ones, it is clear that the results of MGEM method are more precise.

Figs. 1 and 2 show the comparison of the MGEMM and corresponding numerical solutions of Eqs. (8) and (24) for $A = 1$ , up to third order analytical approximations. It can be seen form Figs. 1 and 2 that the approximation of the solution using the present method agree with the numerical solution, also the approximate frequencies give excellent agreement with the corresponding exact solutions, this means that usage of the MGEMM with higher order provides realistic results.

5 Conclusion

In this present paper, an extended version of the global error minimization method is developed to solve the nonlinear third order jerk equations up to third order. Two special cases of (3.1) and (3.2) are investigated and compared with numerically and other known analytically results to demonstrate the powerfulness of the present method. In the two cases, MGEMM produced analytical approximate solutions and periods with excellent agreement with the known exact periods and numerical solutions for non-linear jerk equations. The comparison between analytical and numerical results shows that the two solutions are very close. Mathematica software programs have been used in obtaining analytical and numerical solutions. The proposed technique can be applied to other nonlinear mathematical models.

The suggested research work in this direction has several opportunities with the higher order nonlinear differential equations and fractional differential equations. We can developing several analytical methods conformable with nonlinear and fractional differential equations and simulate the results using others known analytical and numerical methods.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Ahmadian H., Azizi H., . Stability analysis of a nonlinear jointed beam under distributed follower force. J. Vib. Control. 2010;17:27-38.
[Google Scholar]
Alshabanat A., Jleli M., Kumar S., Samet B., . Generalization of Caputo-Fabrizio fractional derivative and applications to electrical circuits. Front. Phys.. 2020;8:64.
[Google Scholar]
Casal A., Freedman M., . A Poincare-Lindstedt approach to bifurcation problems for differential-delay equations. IEEE Trans. Autom. Control. 1980;25:967-973.
[Google Scholar]
Cveticanin L., Ismail G.M., . Higher-order approximate periodic solution for the oscillator with strong nonlinearity of polynomial type. Euro. Phys. J. Plus. 2019;134:266.
[Google Scholar]
El-Naggar A.M., Ismail G.M., . Analytical solution of strongly nonlinear Duffing oscillators. Alexandria Eng. J.. 2016;55:1581-1585.
[Google Scholar]
Farzaneh Y., Tootoonchi A.A., . Global error minimization method for solving strongly nonlinear oscillator differential equations. Comput. Math. Appl.. 2010;59:2887-2895.
[Google Scholar]
Gottlieb H.P.W., . Harmonic balance approach to periodic solution of nonlinear jerk equation. J. Sound Vib.. 2004;271:671-683.
[Google Scholar]
He J.H., . Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng.. 1999;178:257-262.
[Google Scholar]
He J.H., . Hamiltonian approach to nonlinear oscillators. Phys. Lett. A. 2010;374:2312-2314.
[Google Scholar]
Hosen M.A., Ismail G.M., Yildirim A., Kamal M.A.S., . A modified energy balance method to obtain higher-order approximations to the oscillators with cubic and harmonic restoring force. J. Appl. Comput. Mech.. 2020;6:320-331.
[Google Scholar]
Hu H., . Perturbation method for periodic solutions of nonlinear jerk equations. Phys. Lett. A. 2008;372:4205-4209.
[Google Scholar]
Hu H., Zheng M.Y., Guo Y.J., . Iteration calculations of periodic solutions to nonlinear jerk equations. Acta Mech.. 2010;209:269-274.
[Google Scholar]
Ismail G.M., Abul-Ez M., Farea N.M., Saad N., . Analytical approximations to nonlinear oscillation of nanoelectro-mechanical resonators. Euro. Phys. J. Plus. 2019;134:47.
[Google Scholar]
Ismail G.M., Abdl-Rahim H.R., Abdel-Aty A., Kharabsheh R., Alharbi W., Abdel-Aty M., . An analytical solution for fractional oscillator in a resisting medium. Chaos, Solitons Fractals. 2020;130:109395
[Google Scholar]
Ismail G.M., Abul-Ez M., Farea N.M., . An accurate analytical solution to strongly nonlinear differential equations. Appl. Math. Inf. Sci.. 2020;14:141-149.
[Google Scholar]
Karahan M.M.F., . Approximate solutions for the nonlinear third-order ordinary differential equations. Z. Naturforschung A 2017
[CrossRef] [Google Scholar]
Kumar S., Kumar R., Cattani C., Samet B., . Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons Fractals. 2020;135:109811.
[CrossRef] [Google Scholar]
Kumar S., Kumar A., Abbas S., Al Qurashi M., Baleanu D., . A modified analytical approach with existence and uniqueness for fractional Cauchy reaction–diffusion equations. Adv. Differ. Equ.. 2020;2020(1)
[CrossRef] [Google Scholar]
Kumar S., Ghosh S., Lotayif M.S.M., Samet B., . A model for describing the velocity of a particle in Brownian motion by Robotnov function based fractional operator. Alexandria Eng. J.. 2020;59(3):1435-1449.
[CrossRef] [Google Scholar]
Leung A.Y.T., Guo Z.J., . Residue harmonic balance approach to limit cycles of nonlinear jerk equations. Int. J. Non-linear Mech.. 2011;46:898-906.
[Google Scholar]
Ma X.Y., Wei L.P., Guo Z.J., . He’s homotopy perturbation method to periodic solutions of nonlinear jerk equations. J. Sound Vib.. 2008;314:217-227.
[Google Scholar]
Mirzabeigy A., Yazdi M.K., Yildirim A., . Analytical approximations for a conservative nonlinear singular oscillator in plasma physics. J. Egypt. Math. Soc.. 2012;20:163-166.
[Google Scholar]
Navarro H.A., Cveticanin L., . Amplitude-frequency relationship obtained using Hamiltonian approach for oscillators with sum of non-integer order nonlinearities. Appl. Math. Comput.. 2016;291:162-171.
[Google Scholar]
Nayfeh A.H., . Perturbation Methods. New York: J. Wiley; 1973.
Nayfeh A.H., Mook D.H., . Nonlinear Oscillations. John Wiley & Sons; 1979.
Rahman M.S., Hasan A.S.M.Z., . Modified harmonic balance method for the solution of nonlinear jerk equations. Results Phys.. 2018;8:893-897.
[Google Scholar]
Ramos J.I., . Approximate methods based on order reduction for the periodic solutions of nonlinear third-order ordinary differential equations. Appl. Math. Comput.. 2010;215:4304-4319.
[Google Scholar]
Singh H., . Analysis for fractional dynamics of Ebola virus model. Chaos, Solitons Fractals. 2020;138:109992.
[CrossRef] [Google Scholar]
Singh H., . Numerical simulation for fractional delay differential equations. Int. J. Dyn. Control 2020
[CrossRef] [Google Scholar]
Singh H., Pandey R.K., Srivastava H.M., . Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics. 2019;7:224.
[Google Scholar]
Singh H., Akhavan Ghassabzadeh F., Tohidi E., Cattani C., . Legendre spectral method for the fractional Bratu problem. Math. Meth. Appl. Sci.. 2020;43(9):5941-5952.
[CrossRef] [Google Scholar]
Veeresha P., Prakasha D.G., Kumar S., . A fractional model for propagation of classical optical solitons by using nonsingular derivative. Math. Methods Appl. Sci. 2020
[CrossRef] [Google Scholar]
Wu B.S., Lim C.W., Sun W.P., . Improved harmonic balance approach to periodic solutions of non-linear jerk equations. Phys. Lett. A. 2006;354:95-100.
[Google Scholar]
Yadav S.L., Kumar S.D., Singh A.K., . Magnetohydrodynamic flow in flow in horizontal concentric cylinders. Int. J. Ind. Math.. 2019;11:89-98.
[Google Scholar]
Yazdi M.K., Tehrani P.H., . Frequency analysis of nonlinear oscillations via the global error minimization. Nonlinear Eng., DE GRUYTER. 2016
[CrossRef] [Google Scholar]

Introduction

The modified global error minimization method

Examples

Jerk function of displacement time's velocity times acceleration and velocity
Jerk function of velocity times acceleration-squared, and velocity

Numerical results and discussion

Conclusion

Fulltext Views
36

PDF downloads
29

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Ahmadian H., Azizi H., . Stability analysis of a nonlinear jointed beam under distributed follower force. J. Vib. Control. 2010;17:27-38.
[Google Scholar]

[2] Alshabanat A., Jleli M., Kumar S., Samet B., . Generalization of Caputo-Fabrizio fractional derivative and applications to electrical circuits. Front. Phys.. 2020;8:64.
[Google Scholar]

[3] Casal A., Freedman M., . A Poincare-Lindstedt approach to bifurcation problems for differential-delay equations. IEEE Trans. Autom. Control. 1980;25:967-973.
[Google Scholar]

[4] Cveticanin L., Ismail G.M., . Higher-order approximate periodic solution for the oscillator with strong nonlinearity of polynomial type. Euro. Phys. J. Plus. 2019;134:266.
[Google Scholar]

[5] El-Naggar A.M., Ismail G.M., . Analytical solution of strongly nonlinear Duffing oscillators. Alexandria Eng. J.. 2016;55:1581-1585.
[Google Scholar]

[6] Farzaneh Y., Tootoonchi A.A., . Global error minimization method for solving strongly nonlinear oscillator differential equations. Comput. Math. Appl.. 2010;59:2887-2895.
[Google Scholar]

[7] Gottlieb H.P.W., . Harmonic balance approach to periodic solution of nonlinear jerk equation. J. Sound Vib.. 2004;271:671-683.
[Google Scholar]

[8] He J.H., . Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng.. 1999;178:257-262.
[Google Scholar]

[9] He J.H., . Hamiltonian approach to nonlinear oscillators. Phys. Lett. A. 2010;374:2312-2314.
[Google Scholar]

[10] Hosen M.A., Ismail G.M., Yildirim A., Kamal M.A.S., . A modified energy balance method to obtain higher-order approximations to the oscillators with cubic and harmonic restoring force. J. Appl. Comput. Mech.. 2020;6:320-331.
[Google Scholar]

[11] Hu H., . Perturbation method for periodic solutions of nonlinear jerk equations. Phys. Lett. A. 2008;372:4205-4209.
[Google Scholar]

[12] Hu H., Zheng M.Y., Guo Y.J., . Iteration calculations of periodic solutions to nonlinear jerk equations. Acta Mech.. 2010;209:269-274.
[Google Scholar]

[13] Ismail G.M., Abul-Ez M., Farea N.M., Saad N., . Analytical approximations to nonlinear oscillation of nanoelectro-mechanical resonators. Euro. Phys. J. Plus. 2019;134:47.
[Google Scholar]

[14] Ismail G.M., Abdl-Rahim H.R., Abdel-Aty A., Kharabsheh R., Alharbi W., Abdel-Aty M., . An analytical solution for fractional oscillator in a resisting medium. Chaos, Solitons Fractals. 2020;130:109395
[Google Scholar]

[15] Ismail G.M., Abul-Ez M., Farea N.M., . An accurate analytical solution to strongly nonlinear differential equations. Appl. Math. Inf. Sci.. 2020;14:141-149.
[Google Scholar]

[16] Karahan M.M.F., . Approximate solutions for the nonlinear third-order ordinary differential equations. Z. Naturforschung A 2017
[CrossRef] [Google Scholar]

[17] Kumar S., Kumar R., Cattani C., Samet B., . Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons Fractals. 2020;135:109811.
[CrossRef] [Google Scholar]

[18] Kumar S., Kumar A., Abbas S., Al Qurashi M., Baleanu D., . A modified analytical approach with existence and uniqueness for fractional Cauchy reaction–diffusion equations. Adv. Differ. Equ.. 2020;2020(1)
[CrossRef] [Google Scholar]

[19] Kumar S., Ghosh S., Lotayif M.S.M., Samet B., . A model for describing the velocity of a particle in Brownian motion by Robotnov function based fractional operator. Alexandria Eng. J.. 2020;59(3):1435-1449.
[CrossRef] [Google Scholar]

[20] Leung A.Y.T., Guo Z.J., . Residue harmonic balance approach to limit cycles of nonlinear jerk equations. Int. J. Non-linear Mech.. 2011;46:898-906.
[Google Scholar]

[21] Ma X.Y., Wei L.P., Guo Z.J., . He’s homotopy perturbation method to periodic solutions of nonlinear jerk equations. J. Sound Vib.. 2008;314:217-227.
[Google Scholar]

[22] Mirzabeigy A., Yazdi M.K., Yildirim A., . Analytical approximations for a conservative nonlinear singular oscillator in plasma physics. J. Egypt. Math. Soc.. 2012;20:163-166.
[Google Scholar]

[23] Navarro H.A., Cveticanin L., . Amplitude-frequency relationship obtained using Hamiltonian approach for oscillators with sum of non-integer order nonlinearities. Appl. Math. Comput.. 2016;291:162-171.
[Google Scholar]

[24] Nayfeh A.H., . Perturbation Methods. New York: J. Wiley; 1973.

[25] Nayfeh A.H., Mook D.H., . Nonlinear Oscillations. John Wiley & Sons; 1979.

[26] Rahman M.S., Hasan A.S.M.Z., . Modified harmonic balance method for the solution of nonlinear jerk equations. Results Phys.. 2018;8:893-897.
[Google Scholar]

[27] Ramos J.I., . Approximate methods based on order reduction for the periodic solutions of nonlinear third-order ordinary differential equations. Appl. Math. Comput.. 2010;215:4304-4319.
[Google Scholar]

[28] Singh H., . Analysis for fractional dynamics of Ebola virus model. Chaos, Solitons Fractals. 2020;138:109992.
[CrossRef] [Google Scholar]

[29] Singh H., . Numerical simulation for fractional delay differential equations. Int. J. Dyn. Control 2020
[CrossRef] [Google Scholar]

[30] Singh H., Pandey R.K., Srivastava H.M., . Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics. 2019;7:224.
[Google Scholar]

[31] Singh H., Akhavan Ghassabzadeh F., Tohidi E., Cattani C., . Legendre spectral method for the fractional Bratu problem. Math. Meth. Appl. Sci.. 2020;43(9):5941-5952.
[CrossRef] [Google Scholar]

[32] Veeresha P., Prakasha D.G., Kumar S., . A fractional model for propagation of classical optical solitons by using nonsingular derivative. Math. Methods Appl. Sci. 2020
[CrossRef] [Google Scholar]

[33] Wu B.S., Lim C.W., Sun W.P., . Improved harmonic balance approach to periodic solutions of non-linear jerk equations. Phys. Lett. A. 2006;354:95-100.
[Google Scholar]

[34] Yadav S.L., Kumar S.D., Singh A.K., . Magnetohydrodynamic flow in flow in horizontal concentric cylinders. Int. J. Ind. Math.. 2019;11:89-98.
[Google Scholar]

[35] Yazdi M.K., Tehrani P.H., . Frequency analysis of nonlinear oscillations via the global error minimization. Nonlinear Eng., DE GRUYTER. 2016
[CrossRef] [Google Scholar]

Analytic approximations to non-linear third order jerk equations via modified global error minimization method

Abstract

Keywords

Nonlinear third order jerk equations

Analytical solutions

Global error minimization method

Numerical solution

Periodic solutions

1 Introduction

2 The modified global error minimization method

3 Examples

3.1 Jerk function of displacement time's velocity times acceleration and velocity

3.1.1 First order approximation

3.1.2 Second order approximations

3.1.3 Third-order approximations

3.2 Jerk function of velocity times acceleration-squared, and velocity

3.2.1 First-order approximation

4 Numerical results and discussion

5 Conclusion

Declaration of Competing Interest

References

Suggested read for related articles: