Analysis of Al₂O₃-Cu nanofluid flow behaviour over a permeable moving wedge with convective surface boundary conditions

1 Introduction

Boundary layer flow over a wedge has become a trending subject in fluid mechanics nowadays due to its thermal engineering applications, for example, thermal insulation heat exchangers, geothermal systems, crude oil extraction, the storage of nuclear waste, etc. The flow configuration on the wedge was first initiated by Falkner and Skan (1931). Since then, the investigations on wedge were made by a lot of researchers and they obtained lots of valuable results, such as Yih (1999), Sattar (2011), Turkyilmazoglu (2015), Raju and Sandeep (2016), Kudenatti et al. (2017), Awaludin et al. (2018) and many more. The problem of boundary layer flow over a wedge embedded in porous media filled with nanofluid with MHD and viscous dissipation effect have been investigated by Ibrahim and Tulu (2019) numerically by employing spectral quasilinearization method. Recently, Bano et al. (2020) have study the stretching wedge of Casson fluid with various effect analytically. Waini et al. (2020a) explored the non-unique solutions on stretching and shrinking wedge with the presence of magnetohydrodynamic in a hybrid nanofluid. They found that duality exist for the case of shrinking wedge and confirmed that the first solution is stable.

Due to the limited ability of regular heat transfer, base fluids (water, oil and ethylene glycol) are not sufficient to satisfy today's demands. Thus, the latest form of high-potential heat transfer fluids which referred to nanofluids are introduced and implemented in the industrial sector. Nanofluid is a combination of nano-sized particles (<100 nm) in regular fluids which demonstrate greater heat dissipation than ordinary fluids (Choi and Eastman (1995)). Some interesting studies on the nanofluid flow for various physical conditions and effects can be found in the papers of Muthtamilselvan and Renuka (2018), Al-Amri and Muthtamilselvan (2020), Doh et al. (2020) and Renuka et al. (2020). However, in these recent days, a new type of hybrid nanofluid have been extensively explored by many scientists due to its extraordinary thermal conductivities. Hybrid nanofluid is the mixture of two different nanoparticle into the base fluid. Suresh et al. (2011,2012) proposed the concept of hybrid nanofluid, which was demonstrated through experiments and numerical solutions. Anuar et al. (2019) highlighted an exponentially shrinking sheet flow of hybrid nanofluid in the stagnation region with suction/injection effect. Nadeem et al. (2020) analysed the Cu-Al₂O₃/water nanofluid past an exponentially stretching curved surface. They claimed that hybrid nanofluid gains larger heat transfer rate than nanofluid. In addition, the flow of hybrid nanofluid have also been discussed in the literature of Dinarvand (2019), Khashi’ie et al. (2020), Hanif et al. (2020) and Aminian et al. (2020).

The idea to use convective boundary condition was first proposed by Aziz (2009) in analysing the Blasius flow. Afterwards, several authors such as Subhashini et al. (2011), Uddin et al. (2012), Hayat et al. (2016), Rashad (2017) and Zeeshan et al. (2018) used this type of boundary condition to study convective phenomena. Rashad and Nabwey (2019) carried out the study over a circular cylinder containing motile gyrotactic micro-organisms with convective boundary conditions. Jha and Samaila (2020) in their research presented on the impact of thermal radiation and convective boundary condition on the flat plate and conclude that the temperature distribution intensify with Biot number. Recently, the non-unique solutions of inclined stretching/shrinking surface in micropolar nanofluid with convective boundary condition was investigated by Lund et al. (2020a).

In several boundary layer flow problems, the existence of dual solutions is another interesting flow phenomenon. The occurrence of non-unique solution is due to several physical parameters’ impacts, such as mixed convection parameter, suction parameter, shrinking parameter and moving (opposing flow to the free stream) parameter. Due to the different behaviour of the dual branches in velocity and temperature profiles, the stability analysis of the dual solutions has gained considerable attention among researchers. A stability analysis is needed to determine a stable solution when a non-unique solution occurs. It should be noted that Merkin (1986), Weidman et al. (2006), Harris et al. (2009), Awaludin et al. (2018), Anuar et al. (2019,2020), Khashi’ie et al. (2020), Lund et al. (2020a), Lund et al. (2020b), Waini et al. (2020a), Waini et al. (2020b) and among others have found non-unique solution and performed the stability analysis to various flow problems. In this regard, researchers claimed that only a stable solution has a physical significance which means that only a stable solution can be used in practical applications. Therefore, non-unique solution was considered in this study along with their stability analysis.

The present study deals with the boundary layer flow of hybrid nanofluid in a permeable moving wedge with convective boundary conditions. To the best of authors awareness, this kind of flow has not been studied yet. The objective of current study is to extend the research done by Yacob et al. (2011) to the case of hybrid nanofluid with an additional impact of convective boundary condition. In this study, a model of Tiwari and Das (2007) is used to deal with governing equations by including hybrid nanoparticles, namely copper (Cu) and alumina (Al₂O₃), with water as a base fluid. In addition, we also performed stability analysis since Yacob et al. (2011) did not consider this analysis in their studies. Utilizing the similarity transformation method, the governing PDEs are converted into ODEs and solved numerically using bvp4c in Matlab software. Variation of velocity and temperature together with local skin friction and Nusselt number for different governing parameter are shown graphically. Further, to identify a stable and physically reliable solution, we performed a stability analysis.

2 Flow modelling

A steady boundary layer flow embedded in Al₂O₃-Cu/water nanofluid flowing through a moving wedge is physically displayed as in Fig. 1. The $x-$ axis is considered along the surface of the wedge and $y-$ axis is considered normal to it. The wedge moves with a velocity $U_w=u_w{x}^m$ in the same or opposite direction to the free stream velocity $U_e=u_e{x}^m$ . The wedge surface is retained by convective heat transfer $T_f$ . Meanwhile the temperature $T_{\infty }$ is the ambient fluid temperature.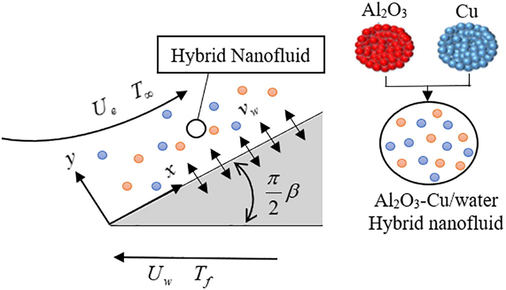

Close

Fig. 1

Schematic diagram.

Export to PPT

Under the above assumptions, we have (Yacob et al. (2011), Khan and Pop (2013)):

here, $\left(u,v\right)$ is the components of velocity along $\left(x,y\right)$ direction, respectively. $\mu ,\rho$ and $\alpha$ denote the dynamic viscosity, density and thermal diffusivity in which subscript ${}^{\prime }hn{f}^{\prime }$ represents by “hybrid nanofluid”. These terms are given by (Devi and Devi (2016)):

Note that the subscript ${}^{\prime }{f}^{\prime },{}^{\prime }s{1}^{\prime }$ and ${}^{\prime }s{2}^{\prime }$ represent the “fluid”, “alumina nanoparticle” and “copper nanoparticle”. Here, $\phi ,\rho C_p,$ and $k$ denote the nanoparticle volume fraction, heat capacity and thermal conductivity, respectively. Thermophysical properties of these nanofluids are given in Table 1.

The accompanying conditions are:

here, the mass transfer velocity $v_w$ are given by $-\sqrt{\frac{\left(m+1\right){\nu }_f{U}_e}{2x}}s$ ; where ${\nu }_f$ is the kinematic viscosity and $s$ is a positive constant which indicates a suction parameter. Meanwhile, $h_f=c\sqrt{\left(m+1\right)x^{m-1}}$ is the convective heat transfer coefficient arises from convective boundary conditions where $c$ is a constant.

The following stream function $\psi$ and similarity variable $\eta$ are applied to the system of Eqs. (1)–(3).

with $f$ and $\theta$ is the dimensionless stream and temperature function. $u$ and $v$ in this study are defined as $\partial \psi /\partial y$ and $-\partial \psi /\partial x$ , respectively. Hence, this leads us to:

with conditions:

in which $m$ is a constant wedge parameter, $\mathit{Bi}$ and $\lambda$ are the Biot number and velocity ratio parameter, respectively, while $Pr$ is the Prandtl number which expressed as:

where Hartree pressure gradient parameter is denoted by $\beta$ . Note that $\lambda >0$ and $\lambda <0$ correspond to the wedge moves with the same direction and opposing direction to the free stream. Meanwhile, $\lambda =0$ indicates the static wedge.

The local skin friction and Nusselt number which represent by $C_f$ and $N{u}_x$ are defined by:

applying variable (6) into (11), we can write:

where ${Re}_x=U_{e}x/{\nu }_f$ is the local Reynolds number. Note that, local Nusselt number is a dimensionless parameter that shows how much heat transfer from a surface to a moving fluid and indicative of the ratio of heat transfer by convection to conduction across a fluid layer.

3 Numerical results

To demonstrate the influence of hybrid nanofluid in moving wedge, the system of ODEs (7) and (8) along with conditions (9) are solved numerically via Matlab’s built in function (bvp4c). The direct comparison of results from the previous researchers (Yacob et al. (2011), Khan and Pop (2013), Khan et al. (2015)) also has been done for some special cases in a way to confirm the accuracy of the present study. We have tabulated Table 2 for the validation values of $f^{″}\left(0\right)$ for the case of static wedge $\left(\lambda =0\right)$ and neglecting the effect of suction $\left(s=0\right)$ and nanoparticle $\left({\phi }_1={\phi }_2=0\right)$ . The results are observed to be in a good agreement which confirm our numerical computation. In addition, this section will discuss the graphical results of velocity and temperature profile together with local skin friction and Nusselt number for selected governing parameter, i.e. wedge $m$ , suction $s$ , moving $\lambda$ , Biot number $\mathit{Bi}$ and nanoparticle volume fraction parameters ${\phi }_1,{\phi }_2$ . Since the base fluid is water and following the works of Oztop and Abu-Nada (2008), the value of Prandtl number in this study is adopted to $6.2$ which is in accordance with room temperature of nearly 295.15 K. The designated hybrid nanofluid are produced by suspending the Al₂O₃ nanoparticle into the Cu-water/nanofluid. Therefore, ${\phi }_1$ represent Cu nanoparticle while ${\phi }_2$ corresponds to Al₂O₃ nanoparticle. The values of nanoparticle volume fraction parameter are investigated in the range of 0–0.2 (Oztop and Abu-Nada (2008)). The wedge parameter is varied in the range of 0 – 1 where $m=0$ indicates horizontal plate, $0<m<1$ refer to wedge surface and $m=1$ corresponds to stagnation point flow. The suction parameter is considered in the range of $s>0.3$ because the existence of two solutions is found in this region $\left(0.3<s<1\right)$ . Meanwhile, Biot number is considered for three different values, 0.1, 0.5 and 1 where the Biot number of 0.1 represents a weak convective heating situation. In addition, the constant temperature results were recovered by using a value of $\mathit{Bi}=\infty$ in the third boundary condition in Equation (9) which then gives the condition $\theta \left(0\right)=1$ (isothermal condition).

3.1

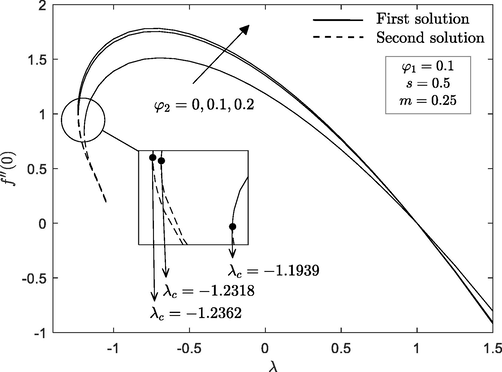
3.1 Impact of wedge parameter, $m$

The velocity $f^{\prime }\left(\eta \right)$ and temperature $\theta \left(\eta \right)$ profiles for various value of wedge parameter $\left(m=0.3,0.4,0.5\right)$ are illustrated in Figs. 2 and 3. From these figures, it is seen that the dimensionless profiles asymptotically fulfil the boundary conditions and there is exist non-unique solutions (dual solutions). In this paper, solid lines refer to the first solution, while the dash lines represent the second solution. The momentum and thermal boundary layer are observed to decrease during the increment of wedge parameter $m$ for first solution, but opposite trend is seen for second solution. This is due to the fact that an increment of wedge angle causes the fluid moves much slower. We have also found that the second solution displays a greater thickness (boundary layer) than the first solution. The existence of non-unique solutions in the previous profiles encourages us to examine which of the governing parameters may contribute to a non-unique solution. Figs. 4 and 5 reveal the influence of wedge parameter $m$ on reduced skin friction $f^{″}\left(0\right)$ and heat transfer $-{\theta }^{\prime }\left(0\right)$ for Al₂O₃-Cu/water nanofluid. It is remarkable that these figures show an increment trend as $m$ parameter increase. Additionally, the presence of non-unique solutions is observed when the wedge moves in the opposite direction ${\lambda }_c<\lambda <0$ , whereas a unique solution is observed for assisting flow $\lambda >0$ . Eventually, no solution is found as $\lambda <{\lambda }_c$ in which ${\lambda }_c$ is the critical value where the first and second solution connected. One can see from these figures that the range of duality to exist also depends on the values of $m$ itself. Furthermore, the range of dual solutions exist when $m=0$ are in the range of $\left(-0.7651⩽\lambda ⩽0\right),$ while as $m=0.5$ and $1$ , the range of dual solutions are $\left(-1.4111⩽\lambda ⩽-1\right)$ and $\left(-1.5563⩽\lambda ⩽-1\right)$ , respectively. Also, the range of $\lambda$ for which the solutions to exist is larger for wedge surface $\left(m=0.5\right)$ compared to horizontal plate $\left(m=0\right)$ . This means that wedge parameter acts in postponing the boundary layer separation. To analysed the impact of wedge parameter $m$ on the local skin friction $C_f{Re}_x^{1/2}$ and Nusselt number $N{u}_x{Re}_x^{-1/2}$ , we plot Figs. 6 and 7 for the case of moving wedge in the assisting flow $\lambda =0.5.$ As expected, the wedge parameter $m$ is an increasing function of $C_f{Re}_x^{1/2}$ and $N{u}_x{Re}_x^{-1/2}$ . Further, it should be mentioned that the existence of hybrid nanofluid increase the magnitude of $C_f{Re}_x^{1/2}$ and $N{u}_x{Re}_x^{-1/2}$ . Hence, thermal conductivity of nanoparticles is bound to increases as more particles are suspended in it.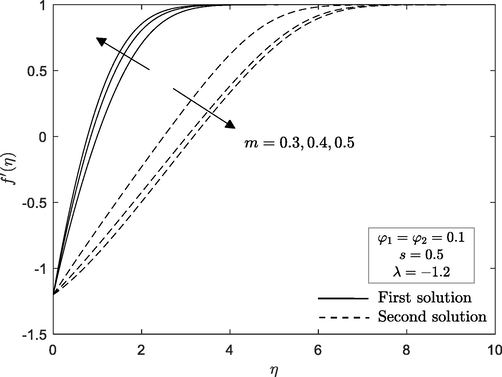

Close

Fig. 2

Velocity profile for different $m$

Export to PPT

Close

Fig. 3

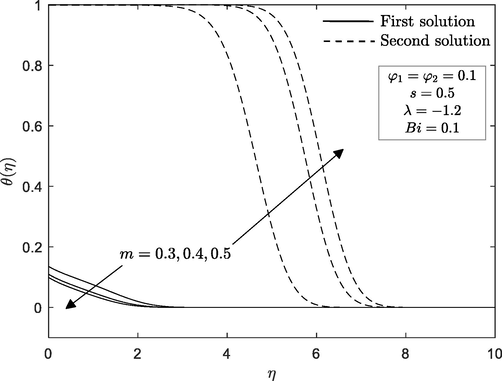
Temperature profile for different $m$

Export to PPT

Close

Fig. 4

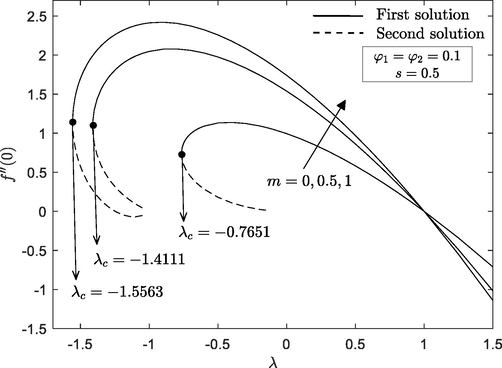
Reduced skin friction for some values of $m$

Export to PPT

Close

Fig. 5

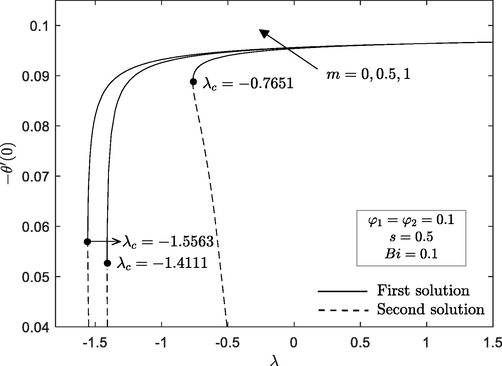
Reduced heat transfer for some values of $m$

Export to PPT

Close

Fig. 6

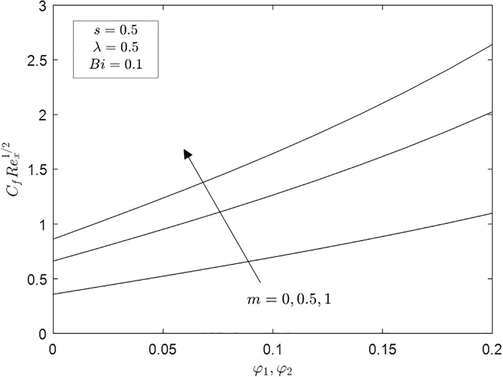
Local skin friction with hybridity for different values of $m$

Export to PPT

Close

Fig. 7

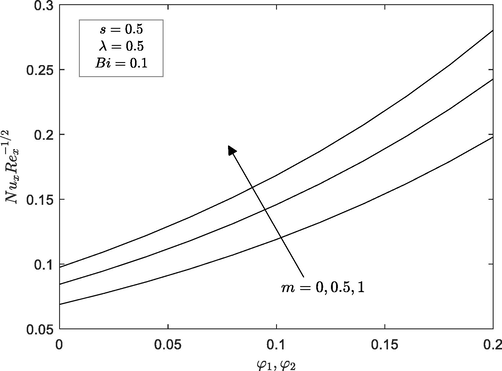
Local Nusselt number with hybridity for different values of $m$

Export to PPT

3.2

3.2 Impact of suction parameter, $s$

Figs. 8 and 9 illustrated the velocity and temperature profiles for different value of suction parameter $s$ in the case of wedge moving in opposing direction $\lambda =-1.2$ . The values of suction adopted in these profiles are $0.5,0.7$ and $0.9$ . It is important to point out that the presence of dual solutions is observed in these profiles. Moreover, the thickness of both momentum and thermal boundary layer for the first solution decreases with the increase of $s$ , meanwhile the second solution shows a reverse effect. Consequently, the act of suction that allows the fluid molecules to fill the wedge surface triggers the heat from the surface of the wedge to increase. Hence, the thinner thermal boundary layer thickness will affect the temperature gradient to be steeper as suction increases and hence supports the heat transfer enhancement.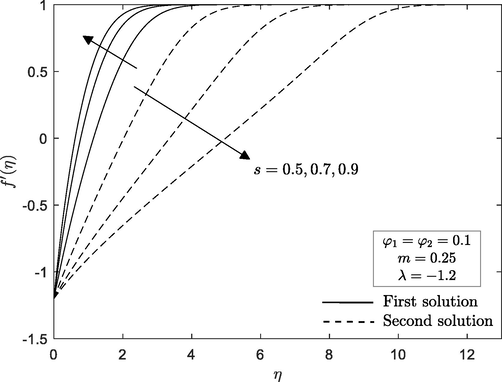

Close

Fig. 8

Velocity profile for various $s$

Export to PPT

Close

Fig. 9

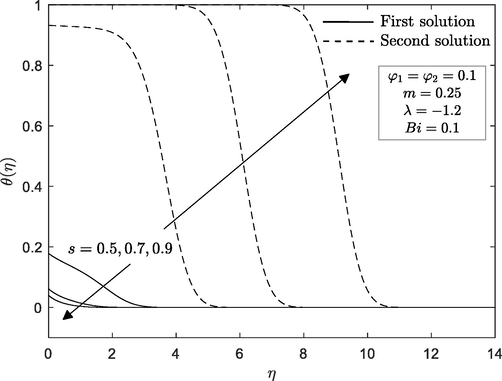
Temperature profile for different $s$

Export to PPT

3.3

3.3 Impact of nanoparticle volume fraction, ${\phi }_2$

The effect of Al₂O₃ nanoparticle volume fraction ${\phi }_2$ on the reduced skin friction $f^{″}\left(0\right)$ and heat transfer $-{\theta }^{\prime }\left(0\right)$ with suction parameter $s$ and moving wedge parameter $\lambda$ are presented in Figs. 10 – 13. For the fixed value of ${\phi }_1=0.1$ , the flow is corresponding to the Cu/water nanofluid when ${\phi }_2=0$ , meanwhile as the values of ${\phi }_2$ increase to $0.1$ and $0.2$ , the flow is corresponds to the Al₂O₃-Cu/water hybrid nanofluid. As can be observed from earlier profiles (Figs. 8 and 9), the selected suction value is critical in deciding the presence of non-unique solutions. Hence, Figs. 10 and 11 are plotted in order to identify the range of similarity solutions for some values of nanoparticle volume fraction ${\phi }_2$ when $\lambda =-1.15$ . The dual solutions are up to only a certain value of suction which given by $s_c$ such that $s_c=0.4363,0.3947$ and $0.3905$ for ${\phi }_2=0,0.1$ and $0.2$ , respectively. In addition, a unique solution is noticed when $s⩾1$ and no solution when $s<s_c$ . The same trend are seen for the reduced skin friction $f^{″}\left(0\right)$ and heat transfer $-{\theta }^{\prime }\left(0\right)$ with moving wedge $\lambda$ as presented in Figs. 12 and 13. In addition, the presence of dual solutions is observed when the wedge surface moves in the opposite direction with the free stream, ${\lambda }_c<\lambda <-1$ . It is apparent that the value of $\left|{\lambda }_c\right|$ for Al₂O₃-Cu/water hybrid nanofluid $\left({\phi }_1=0.1,{\phi }_2=0.1,0.2\right)$ are higher than Cu/water nanofluid $\left({\phi }_1=0.1,{\phi }_2=0\right)$ . Therefore, it is concluded that an increment of Al₂O₃ nanoparticle volume fraction ${\phi }_2$ causes the region of solutions to expand. It should be noted that $f^{″}\left(0\right)$ is found to be higher for larger volume fraction of nanoparticle ${\phi }_2$ , while a reverse trend is observed for $-{\theta }^{\prime }\left(0\right)$ . In the present work, the values of $-{\theta }^{\prime }\left(0\right)$ may decrease as a result of the higher value of $s$ . Therefore, other researchers can manipulate the appropriate value of physical parameters from the current investigation to obtain the optimum heat transfer rate.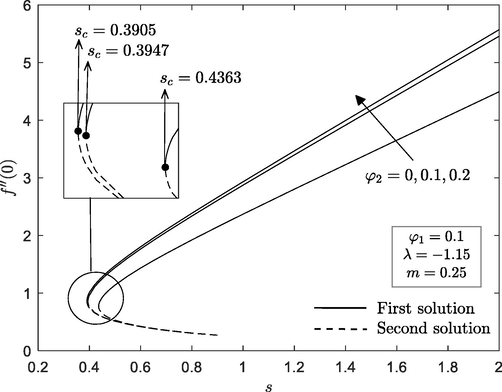

Close

Fig. 10

Reduced skin friction with $s$ for different ${\phi }_2$

Export to PPT

Close

Fig. 11

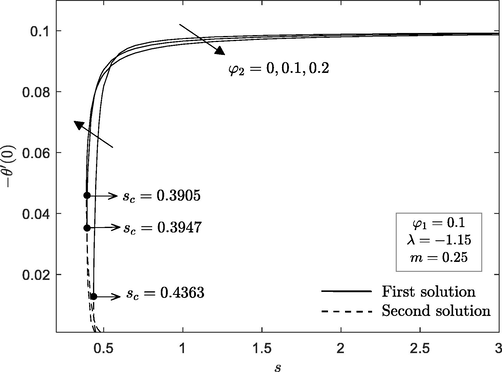
Reduced heat transfer with $s$ for various ${\phi }_2$

Export to PPT

Close

Fig. 12

Reduced skin friction for various ${\phi }_2$

Export to PPT

Close

Fig. 13

Reduced heat transfer for various ${\phi }_2$

Export to PPT

3.4

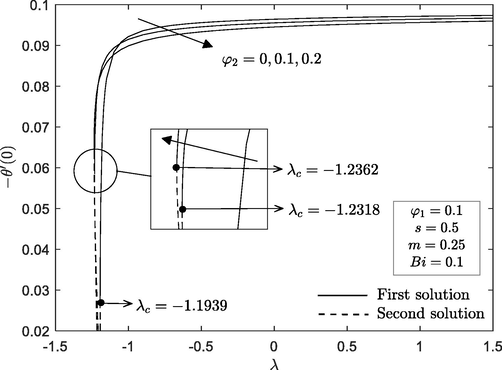
3.4 Impact of Biot number, $\mathit{Bi}$

Figs. 14 and 15 exhibit the temperature profile $\theta \left(\eta \right)$ and local Nusselt number $N{u}_x{Re}_x^{-1/2}$ towards hybrid nanoparticle ${\phi }_1,{\phi }_2$ within specific range of Biot number $\mathit{Bi}$ . As expected, the increased convective heating which associated with increasing values of $\mathit{Bi}$ results in thickening of thermal boundary layer thickness for both solutions, increase the fluid temperature and causing the thermal effect to penetrate deeper into the quiescent fluid. The effect of $\mathit{Bi}$ on local Nusselt number $N{u}_x{Re}_x^{-1/2}$ has exactly the same increasing behaviour (see Figs. 6 and 7). It is shown that local Nusselt number $N{u}_x{Re}_x^{-1/2}$ is an increasing function of hybrid nanoparticle $\left({\phi }_1,{\phi }_2\right)$ as well as Biot number $\mathit{Bi}$ . The thermal conductivity of hybrid nanofluids is enhanced due to a rise in the volume of nanoparticles. As a result, an increase in the thermal conductivity of hybrid nanofluids has a positive effect on the fluid temperature as it increases with an increase in the nanoparticle volume fraction.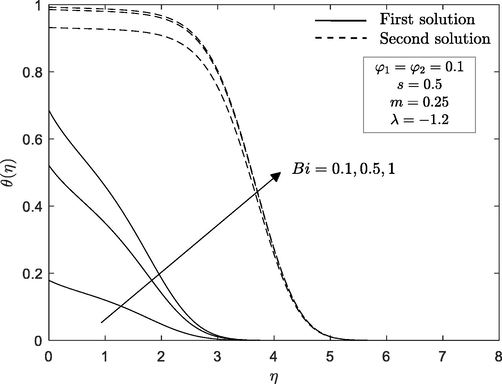

Close

Fig. 14

Temperature profile for various $\mathit{Bi}$

Export to PPT

Close

Fig. 15

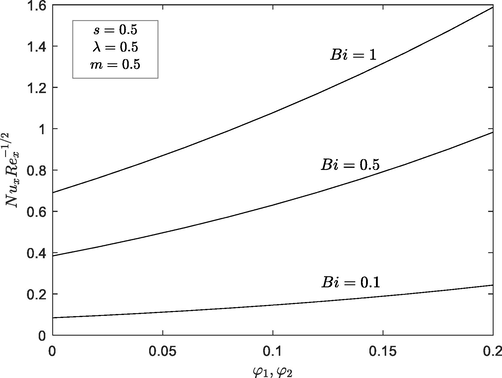
Local Nusselt number with hybridity $\left({\phi }_1,{\phi }_2\right)$ for various $\mathit{Bi}$

Export to PPT

4 Stability analysis of solutions

Non-unique solutions for some governing parameter are found to exist from the previous section. Therefore, a stability analysis is needed in order to identify which of these solutions are stable solutions. Merkin's work (1986) was used for this approach where time-dependent problem is taken into consideration. So, the unsteady case for the current problem is:

along with the respected conditions:

By applying the Equation (16) into Equations (13)–(15), the reduced system will be:

associated with conditions:

The behaviour of stability on the steady flow solutions $f\left(\eta \right)=f_0\left(\eta \right)$ and $\theta \left(\eta \right)={\theta }_0\left(\eta \right)$ can be identified by implementing the work done by Weidman et al. (2006):

Here, $F\left(\eta ,\tau \right)$ and $H\left(\eta ,\tau \right)$ are approximately small compared to $f_0\left(\eta \right)$ and ${\theta }_0\left(\eta \right)$ , while $\gamma$ is an unknown eigenvalues parameter. Substitute Equation (20) into Equations (17)–(19) and let $\tau \to 0$ , in which $F\left(\eta \right)=F_0\left(\eta \right)$ and $H\left(\eta \right)=H_0\left(\eta \right)$ , thereby we have:

together with conditions:

The conditions $F_0^{\prime }\left(\eta \right)\to 0$ as $\eta \to \infty$ need to be relax as recommended by Harris et al. (2009) and can be replaced by $F_0^{″}\left(0\right)=1$ . Therefore, together with new boundary conditions, we solve the system of equations (21)–(23) using built-in function (bvp4c) in Matlab software.

The system of equations (21)–(23) provides an infinite range of eigenvalues $\gamma$ . When $\gamma <0$ , the flow has an initial growth of disturbance that can disrupt the flow and thereby make the flow unstable. In the meantime, as $\gamma >0$ , there is only an initial decay of disturbance in the fluid, thus indicates the stable flow. Table 3 shows the smallest eigenvalues $\gamma$ for selected values of wedge parameter $m$ , nanoparticle volume fraction ${\phi }_1,{\phi }_2$ and moving parameter $\lambda$ . It is clearly seen that the first and second solutions display a positive and negative value of $\gamma$ , respectively. Further, these smallest eigenvalues tend to approach zeros as it is approaching its own critical value ${\lambda }_c.$ As a result, we can therefore confirm that the first solution is physically stable.

5 Conclusions

Numerical analysis of steady Al₂O₃-Cu/water nanofluid flow on the moving wedge with convective condition effect is investigated. The key findings on the present work are listed as bellow:

• The presence of dual solutions is noticed when the wedge surface moves in the opposing flow with the free stream $\left({\lambda }_c<\lambda <0\right)$ and no solution when $\lambda <{\lambda }_c$ .

• The skin friction and Nusselt number gradually increase as the nanoparticle volume fraction $\left({\phi }_1,{\phi }_2\right)$ and wedge parameter $m$ increase.

• The similarity solutions can be widened with an increase in Al₂O₃ nanoparticle volume fraction ${\phi }_2$ and wedge parameter $m$ , therefore postponing the boundary layer separation.

• Dual solution only visible with the certain range of suction parameter $\left(0.3<s<1\right)$ .

• Larger values of Biot number show an increasing behaviour for temperature and local Nusselt number.

• Analysis on the stability of solutions proves that the first solution is a stable solution, while the second solution is unstable.