An efficient semi-analytical method for solving the generalized regularized long wave equations with a new fractional derivative operator

H.M. Srivastava; Sinan Deni̇z; Khaled M. Saad

doi:10.1016/j.jksus.2021.101345

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

03 2021

:33;

101345

doi:

10.1016/j.jksus.2021.101345

An efficient semi-analytical method for solving the generalized regularized long wave equations with a new fractional derivative operator

H.M. Srivastava^{^a,^b,^c}, Sinan Deni̇z^{^d}, Khaled M. Saad^{^e,^f,⁎}

a Department of Mathematics and Statistics, University of Victoria, Victoria, British Columbia V8W 3R4, Canada

b Department of Medical Research, China Medical University Hospital, China Medical University, Taichung 40402, Taiwan, Republic of China

c Department of Mathematics and Informatics, Azerbaijan University, 71 Jeyhun Hajibeyli Street, AZ1007 Baku, Azerbaijan

d Department of Mathematics, Faculty of Art and Sciences, Manisa Celal Bayar University, 45140 Manisa, Turkey

e Department of Mathematics, College of Arts and Sciences, Najran University, Kingdom of Saudi Arabia

f Department of Mathematics, Faculty of Applied Science, Taiz University, Taiz, Yemen

⁎Corresponding author. khaledma_sd@hotmail.com (Khaled M. Saad)

Received: 2020-11-12, Accepted: 2021-1-2,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this work, the newly developed optimal perturbation iteration technique with Laplace transform is applied to the generalized regularized long wave equations with a new fractional operator to obtain new approximate solutions. We transform the classical generalized regularized long wave equations to fractional differential form by using the Atangana-Baleanu fractional derivative which is defined with the Mittag-Leffler function. To show the efficiency of the proposed method, a numerical example is given for different values of physical parameters.

Keywords

Optimal perturbation iteration method

Generalized regularized long wave equations

Atangana-Baleanu derivative

Convergence

26A33

34A08

91B76

1 Introduction

Partial differential equations, especially nonlinear ones, have been used to model many scientific phenomena in applied mathematics and engineering. The importance of getting approximate solutions of them either numerically or analytically has always been emphasized. From the early 2000s onwards, many researchers have constructed a variety of techniques to analyze the solutions of nonlinear partial differential equations, such as the sine-Gordon expansion method (Baskonus et al., 2017), the extended sinh-Gordon equation expansion method (Cattani et al., 2018), Bernoulli sub-equation function method (Baskonus and Bulut, 2016), homotopy analysis method (Liao, 2004), modified simple equation method (Khan et al., 2016), homotopy perturbation method (HPM) (Dubey et al., 2016) and Adomian decomposition method (Deniz and Bildik, 2014). Due to the inability of these methods for many works, researchers have proposed new methods such as perturbation iteration method (Aksoy and Pakdemirli, 2010; Aksoy et al., 2012), optimal homotopy asymptotic method (Bildik and Deniz, 2020a; Marinca and Herisanu, 2008; Bildik and Deniz, 2018a; Iqbal et al., 2010 ) and optimal perturbation iteration method (OPIM) (Deniz and Bildik, 2017a,b, 2018; Deniz, 2017; Bildik and Deniz, 2017a,b, 2018b,c ) to deeply analyze nonlinear models.

One of the most important nonlinear partial differential equations is the generalized regularized long wave (GRLW) equation which can be given as

(1.1)

u_{t} + u_{x} + γ {(u^{p})}_{x} - β u_{xxt} = 0, (x, t) \in (a, b) \times (0, T)

where

γ, β

are positive constants and p is a positive integer. The Eq. (1.1) was initially used by Peregrine for presenting small-amplitude long-waves on the surface of water in a channel (Peregrine, 1996). Besides that, GRLW equations are used for describing a variety of physical phenomena such as longitudinal dispersive waves in elastic rods, rotating flow down a tube and pressure waves in liquid–gas bubble mixtures. The nonlinear term

γ {(u^{p})}_{x}

in Eq. (1.1) causes steepening of the wave form. Also, the last term

β u_{xxt}

is named as dispersion effect term and this term is used to make the wave form spread. The solitons emerge by virtue of the balance between dispersion and nonlinearity (Mohammadi and Mokhtari, 2011). These solitons exist in many types of systems from sky to laboratory (Bhardwaj and Shankar, 2000). Many researchers have also demonstrated that GRLW equation is superior to the KdV equation and can be used instead of KdV equation in many nonlinear systems (Bona et al., 1983).

The Eq. (1.1) can be modified to the regularized long wave equation (RLW) for $p = 1$ or to the modified regularized long wave (MRLW) equation for $p = 2$ . The development of an undular bore can be described by the RLW and MRLW equations. The constants $γ, β$ in the Eq. (1.1) characterise the behavior of an undular bore. In many fields of mathematics and engineering such as magneto-hydrodynamics waves in plasma, lossless propagation of shallow water waves, rotating flow down a tube, longitudinal dispersive waves in elastic rods, ion-acoustic waves in plasma,pressure waves in liquid–gas bubble mixture and thermally excited phonon packets in low temperature nonlinear crystals, RLW and MRLW equations play a pivotal role (Mirzaei and Dehghan, 2011; Dehghan and Salehi, 2011).

It is widely known that any dynamical system defined with the help of fractional order differential operators has a memory effect. In other words, the future state of a physical system depends on the present as well as the past states (Kumar et al., 2017, 2018; Singh et al., 2017; Singh and Srivastava, 2020; Srivastava et al., 2019a,b, 2020a ). Therefore, it is reasonable to transform any differential equations to fractional ones to deeply analyze the solutions. Many problems have been reconsidered via fractional derivatives and newly developed techniques. Numerical solution of Caputo-Fabrizio time fractional distributed order reaction–diffusion equation has been obtained via quasi wavelet based numerical method (Kumar and Gómez-Aguilar, 2020). Shifted Chebyshev collocation of the fourth kind with convergence analysis has been used for solving the space–time fractional advection–diffusion equation (Safdari et al., 2020). Modified fractional derivatives with non-singular kernel have been analyzed via Laplace variational- iteration method (Yépez-Martínez and Gómez-Aguilar, 2020). Numerical solutions of the fractional Fisher’s type equations have been obtained by using spectral collocation methods (Saad et al., 2019a). Laplace homotopy analysis method has been applied for solving linear partial differential equations using a fractional derivative (Morales-Delgado et al., 2016). Many other papers can also be seen in Pandey et al. (2020), Bhangale et al. (2020), Dwivedi et al. (2020), Bonyah et al. (2021) and Deniz (2020a)).

In 2016, Baleanu and Atangana came up with new operators, namely AB operators, with fractional order based upon the well-known Mittag–Leffler function to come through the kernel problems of the Caputo-Fabrizio and Caputo-Riemann–Liouville derivatives (Atangana and Baleanu, 2016). AB operators have all the utilities of those of past counterpasts apart from all these; the kernel of the operator is nonsingular and nonlocal. Additionally, AB fractional integral is the fractional average of the Riemann–Liouville (RL) fractional integral of the function. These new prospective ideas on fractional operators have drawn attention of many researchers. A lot of manuscripts have been written in only 4–5 years. One can see the most effective ones in Saad (2018), Algahtani (2016), Gómez-Aguilar (2018), Bildik and Deniz (2019), Saad et al. (2018, 2019b), Jajarmi and Baleanu (2018), Kilbas et al. (2006), Srivastava (2020a,b), Srivastava et al. (2019c, 2020b) and references therein.

In this research paper, we aim to extend the GRLW equations by interchanging the derivative with a newly constructed AB – derivative to get

(1.2)

_{0}^{ABC} D_{t}^{α} u + u_{x} + γ {(u^{p})}_{x} - β u_{xxt} = 0, (x, t) \in (a, b) \times (0, T), 0 < α ⩽ 1

and additionally to exhibit the approximate solutions of the modified fractional GRLW equations with the help of optimal perturbation iteration technique and Laplace technique.

2 Preliminaries and some definitions

In this current part, we present some important preliminaries and results of AB derivative. One can see Atangana and Baleanu (2016) for much more information.

Definition 1

The Atangana-Baleanu (AB) time-fractional derivative in the Caputo sense is given as

(2.1)

_{a}^{ABC} D_{t}^{α} f (t) = \frac{B (α)}{1 - α} \int_{a}^{t} f' (τ) E_{α} [- \frac{α {(t - τ)}^{α}}{1 - α}] d τ

where

B (α)

holds the property that

B (0) = B (1) = 1, f \in L_{1} (a, b)

α \in [0, 1]

and

E_{α} (z) = \sum_{k = 0}^{\infty} \frac{z^{k}}{Γ (α k + 1)}

is Mittag-Leffler function.

Definition 2

The Atangana-Baleanu (AB) time-fractional derivative in the RL sense is given as (Atangana and Baleanu, 2016)

(2.2)

_{a}^{ABR} D_{t}^{α} f (t) = \frac{B (α)}{1 - α} \frac{d}{dt} \int_{a}^{t} f (τ) E_{α} [- \frac{α {(t - τ)}^{α}}{1 - α}] d τ

where

α \in [0, 1], f \in L_{1} (a, b)

and not differentiable.

Definition 3

The Laplace transform of the AB fractional derivative in the Caputo sense ${_{a}}^{ABC} D_{t}^{α} f (t)$ has the form

(2.3)

L \{_{a}^{ABC} D_{t}^{α} f (t)\} (s) = \frac{B (α)}{1 - α} \frac{s^{α} Lf (t) (s) - s^{α - 1} f (0)}{s^{α} + \frac{α}{1 - α}} .

Definition 4

The Laplace transform of the AB fractional derivative in the RL sense ${_{a}}^{ABR} D_{t}^{α} f (t)$ has the form

(2.4)

L \{_{a}^{ABR} D_{t}^{α} f (t)\} (s) = \frac{B (α)}{1 - α} \frac{s^{α} Lf (t) (s)}{s^{α} + \frac{α}{1 - α}} .

3 Analysis of fractional GRLW equations via OPIM

Optimal perturbation iteration method (OPIM) is first constructed by Bildik and Deniz by using the ideas of perturbation iteration (Aksoy and Pakdemirli, 2010; Aksoy et al., 2012) and optimal homotopy asymptotic methods (Marinca and Herisanu, 2008; Bildik and Deniz, 2018a; Iqbal et al., 2010 ). Many different types of problems have been solved by using this techniques (Deniz, 2020b,c; Agarwal et al., 2020; Deniz, 2020d; Bildik et al., 2020; Deniz et al., 2020; Bildik and Deniz, 2020b,c ). In this section, we use OPIM and Laplace transform to obtain approximate solutions of the extended fractional GRLW equations.

Let us consider the Eq. (1.2) with the initial condition $u (x, 0) = A$ . Then, by applying the Laplace transform to the Eq. (1.2) and with the help of the definitions in the previous section, one can get

(3.1)

L [u] - \frac{1}{s} A + \frac{α (- 1 + s^{- α}) + 1}{B (α)} L [F (u_{xxt}, u_{x}, u)] = 0

where

(3.2)

F = F (u_{xxt}, u_{x}, u, ε) = u_{x} + γ {(u^{p})}_{x} - β u_{xxt}

is a nonlinear term. Now, we use OPIM to decompose the nonlinear term. The following formulation can be used to summarize the technique:

(a) The perturbation parameter can be artificially embedded into (3.2) as

(3.3)

F (u_{xxt}, u_{x}, u, ε) = 0

to handle with nonlinear terms. For instance, in our case,

ε = 1

can be inserted into the Eq. (3.2) as:

(3.4)

F = u_{x} + ε γ {(u^{p})}_{x} - β u_{xxt} = 0 .

(b) One can take an approximate solution with one correction term in the perturbation expansion as follows:

(3.5)

u_{n + 1} = u_{n} + ε {(u_{c})}_{n}

where

n \in N

. Upon substitution of (3.5) into (3.4), expanding in a Taylor series with first derivatives only gives the following algorithm:

(3.6)

F + F_{u} {(u_{c})}_{n} ε + F_{u_{x}} {({(u_{c})}_{n})}_{x} ε + F_{u_{xxt}} {({(u_{c})}_{n})}_{xxt} ε + F_{ε} ε = 0

where

F_{u} = \frac{\partial F}{\partial u}, F_{u_{x}} = \frac{\partial F}{\partial u_{x}}, F_{u_{xxt}} = \frac{\partial F}{\partial u_{xxt}}, F_{ε} = \frac{\partial F}{\partial ε} .

Using the Eq. (3.1) and computing all derivatives, functions at $ε = 0$ gives

(3.7)

L [u_{n}] - \frac{1}{s} A + \frac{α (- 1 + s^{- α}) + 1}{B (α)} L [{({(u_{c})}_{n})}_{x} + β {(u_{n})}_{xxt} - {(u_{n})}_{x} - {({(u_{c})}_{n})}_{xxt}] = 0 .

(3.7) is an iteration procedure for OPIM algorithms of fractional GRLW Eqs. (1.2). One can begin to iterate by picking a first trial function $u_{0}$ which should satisfy the prescribed conditions. By doing that, first correction term ${(u_{c})}_{0}$ can be obtained from the algorithm (3.7) by using $u_{0}$ and condition(s).

c) In order to enhance the accuracy of the results and effectiveness of the method, we offer to use the following formula

(3.8)

u_{n + 1} = u_{n} + P_{n} {(u_{c})}_{n}

where

P_{0}, P_{1}, P_{2}, \dots

are convergence control parameters which alters us to adjust the convergence.

Performing the calculations for $n = 0, 1, \dots$ , one can get more approximate solutions as follows:

(3.9)

\begin{matrix} u_{1} = u (x, t; P_{0}) = u_{0} + P_{0} {(u_{c})}_{0} \\ u_{2} (x, t; P_{0}, P_{1}) = u_{1} + P_{1} {(u_{c})}_{1} \\ ⋮ \\ u_{m} (x, t; P_{0}, \dots, P_{m - 1}) = u_{m - 1} + P_{m - 1} {(u_{c})}_{m - 1} \end{matrix}

d) Substituting the approximate solution $u_{m}$ into the Eq. (1.2), the general problem is transformed to the following residual:

(3.10)

Re (x, t; P_{0}, \dots, P_{m - 1}) = F ({(u_{m})}_{xxt}, {(u_{m})}_{x}, {(u_{m})}_{t}, (u_{m}))

Undoubtedly, if $Re (x, t; P_{0}, \dots, P_{m - 1}) = 0$ then the approximation $u_{m} (x, t; P_{0}, \dots, P_{m - 1})$ is the exact solution. However, this case doesn’t usually arise in nonlinear differential equations, but the functional can be minimized as:

(3.11)

J (P_{0}, \dots, P_{m - 1}) = \int_{0}^{T} \int_{a}^{b} {Re}^{2} (x, t; P_{0}, \dots, P_{m - 1}) dxdt

where

a, b

and T are taken from the domain of the problem. Optimal values of

P_{0}, P_{1}, \dots

can be received from the conditions

(3.12)

\frac{\partial J}{\partial P_{0}} = \frac{\partial J}{\partial P_{1}} = \dots = \frac{\partial J}{\partial P_{m - 1}} = 0 .

If the Eq. (3.12) may be very difficult to solve or it can take too much CPU time. In that case, the constants $P_{0}, P_{1}, \dots$ may be obtained from

(3.13)

Re (x_{0}, t_{0}; P_{i}) = Re (x_{1}, t_{1}; P_{i}) = \dots = Re (x_{m - 1}, t_{m - 1}; P_{i}) = 0, i = 0, 1, \dots, m - 1

where

x_{i}, t_{i} \in (a, b) \times (0, T)

. As it is known, this method is called collocation technique. There is no general theorem for selecting collocation points. For more information about obtaining these constants, readers may refer to Marinca and Herisanu (2008), Iqbal et al. (2010) and Deniz and Sezer (2020).

4 Convergence analysis of the proposed technique

In this section, convergence analysis of the optimal perturbation iteration technique is investigated by using Banach fixed-point theorem. To achieve that, we first reorganize the approximate solutions with different indexes such as:

(4.1)

\begin{matrix} u_{0} = ϒ_{0}, \\ P_{n} {(u_{c})}_{n} = ϒ_{n + 1} \end{matrix}

and correspondingly one can get

(4.2)

\begin{matrix} u_{0} = ϒ_{0} \\ u_{1} = u (x, t; P_{0}) = u_{0} + P_{0} {(u_{c})}_{0} = ϒ_{0} + ϒ_{1} \\ u_{2} = u (x, t; P_{0}, P_{1}) = u_{1} + P_{1} {(u_{c})}_{1} = ϒ_{0} + ϒ_{1} + ϒ_{2} \\ ⋮ \\ u_{n} = u (x, t; P_{0}, \dots, P_{n - 1}) = ϒ_{0} + ϒ_{1} + \dots + ϒ_{n} \end{matrix}

Thereby, the n-th order OPIM solution may be represnted as:

(4.3)

u_{n} (x, t; P_{0}, \dots, P_{n - 1}) = ϒ_{0} (x, t) + \sum_{j = 1}^{n} ϒ_{j} (x, t; P_{0}, \dots P_{j - 1}) .

Theorem 1

Let $B$ be a Banach space denoted by a norm $‖.‖$ over which the series (4.3) is given. In addition to that, we assume that the initial function $u_{0} = ϒ_{0}$ falls into the ball of the desired solution. (4.3) converges if there is a $β$ such that

(4.4)

‖ϒ_{n + 1}‖ ⩽ β ‖ϒ_{n}‖ .

Proof

At first, a sequence may be constructed as:

(4.5)

\begin{matrix} R_{0} = ϒ_{0} \\ R_{1} = ϒ_{0} + ϒ_{1} \\ R_{2} = ϒ_{0} + ϒ_{1} + ϒ_{2} \\ ⋮ \\ R_{n} = ϒ_{0} + ϒ_{1} + ϒ_{2} + \dots + ϒ_{n} . \end{matrix}

Secondly, it is required to show that ${\{A_{n}\}}_{n = 0}^{\infty}$ is a Cauchy sequence in $B$ . To do that, let us consider

(4.6)

‖R_{n + 1} - R_{n}‖ = ‖ϒ_{n + 1}‖ ⩽ β ‖ϒ_{n}‖ ⩽ β^{2} ‖ϒ_{n - 1}‖ ⩽ \dots ⩽ β^{n + 1} ‖ϒ_{0}‖ .

For every $n, k \in N, n ⩾ k$ , one can get

(4.7)

\begin{matrix} ‖R_{n} - R_{k}‖ = ‖(R_{n} - R_{n - 1}) + (R_{n - 1} - R_{n - 2}) + \dots + (R_{k + 1} - R_{k})‖ \\ ⩽ ‖R_{n} - R_{n - 1}‖ + ‖R_{n - 1} - R_{n - 2}‖ + \dots + ‖R_{k + 1} - R_{k}‖ \\ ⩽ β^{n} ‖ϒ_{0}‖ + β^{n - 1} ‖ϒ_{0}‖ + \dots + β^{k + 1} ‖ϒ_{0}‖ = \frac{1 - β^{n - k}}{1 - β} β^{k + 1} ‖ϒ_{0}‖ \end{matrix}

Since, it is given that $0 < β < 1$ , one may obtain from (4.7) that

(4.8)

\lim_{n, k \to \infty} ‖R_{n} - R_{k}‖ = 0 .

Consequently, ${\{R_{n}\}}_{n = 0}^{\infty}$ is a Cauchy sequence in $B$ and this implies that approximate solution (4.3) is convergent.

Theorem 2

Let us suppose that the starting function $u_{0} = ϒ_{0}$ falls into the ball of the solution $u (x, t)$ . Then, $R_{n} = \sum_{i = 0}^{n} ϒ_{i}$ also stays inside the ball of the solution.

Proof

Let us assume that

(4.9)

ϒ_{0} \in B_{r} (u)

where

(4.10)

B_{r} (u) = \{ϒ \in R| ‖u - ϒ‖ < r\}

denoted the ball of the solution

u (x, t)

. From the hypothesis

u = \lim_{n \to \infty} R_{n} = \sum_{i = 0}^{\infty} ϒ_{i}

and from Theorem 1, we have

(4.11)

‖u - R_{n}‖ ⩽ β^{n + 1} ‖ϒ_{0}‖ < ‖ϒ_{0}‖ < r

where

n \in N

and

β \in (0, 1)

It should be emphasized here that the selection of the starting function directly affects convergence of the approximations. However, there is no general theorem about the election of the initial function.

5 Numerical example

In the current part, we solve the following fractional GRLW equation with $p = 8, γ = β = 1$ as follows:

(5.1)

_{0}^{ABC} D_{t}^{α} u + u_{x} + {(u^{8})}_{x} - u_{xxt} = 0

with the initial condition

(5.2)

u (x, 0) = \sqrt[7]{18} {sech}^{\frac{2}{7}} (\frac{7 (x + 1)}{\sqrt{5}}) .

One can initiate the procedures by taking the Eq. (5.2) as an initial function $u_{0}$ . Then by applying Laplace transform, we have

(5.3)

L [u] - \frac{\sqrt[7]{18} {sech}^{\frac{2}{7}} (\frac{7 (x + 1)}{\sqrt{5}})}{s} + \frac{α (- 1 + s^{- α}) + 1}{B (α)} L [F (u_{xxt}, u_{x}, u)] = 0

and correspondingly

(5.4)

L [u] - \frac{\sqrt[7]{18} {sech}^{\frac{2}{7}} (\frac{7 (x + 1)}{\sqrt{5}})}{s} + \frac{α (- 1 + s^{- α}) + 1}{B (α)} L [u_{x} + {(u^{8})}_{x} - u_{xxt}] = 0

Now, by using the iterative formula, one can obtain

(5.5)

{(u_{1})}_{OPIM} = \sqrt[7]{18} {sech}^{\frac{2}{7}} (\frac{7 (x + 1)}{\sqrt{5}}) + P_{0} t [\begin{matrix} \frac{2 \sqrt{23} \sinh (\frac{7 (x + 1)}{\sqrt{5}}) {sech}^{\frac{9}{7}} (\frac{7 (x + 1)}{\sqrt{5}})}{\sqrt{5}} + \\ \frac{288 \sqrt{23} \sinh (\frac{7 (x + 1)}{\sqrt{5}}) {sech}^{\frac{23}{7}} (\frac{7 (x + 1)}{\sqrt{5}})}{\sqrt{5}} \end{matrix}] (1 - α + \frac{α t^{α}}{Γ (α + 1)})

(5.6)

{(u_{2})}_{OPIM} = - \frac{7}{5} \sqrt{23} P_{0} t^{2} {sech}^{\frac{2}{7}} (\frac{7 (x + 1)}{\sqrt{5}}) - \frac{1008}{5} \sqrt{23} P_{1} t^{2} {sech}^{\frac{16}{7}} (\frac{7 (x + 1)}{\sqrt{5}}) + P_{0} P_{1} [\begin{matrix} - 12694 \cosh (\frac{28 (x + 1)}{\sqrt{5}}) + 4313 \cosh (\frac{42 (x + 1)}{\sqrt{5}}) + \\ - 28850 \cosh (\frac{28 (x + 1)}{\sqrt{5}}) + 8331 \cosh (\frac{42 (x + 1)}{\sqrt{5}}) \\ - 4316 \sqrt{5} \cosh (\frac{28 (x + 1)}{\sqrt{5}}) {sech}^{\frac{2}{7}} (\frac{7 (x + 1)}{\sqrt{5}}) \\ + 2051 \sqrt{7} \cosh (\frac{52 (x + 1)}{\sqrt{17}}) {sech}^{\frac{5}{7}} (\frac{13 (x + 1)}{\sqrt{19}}) \\ + 18051 \sqrt{17} \cosh (\frac{29 (x + 1)}{\sqrt{22}}) {sech}^{\frac{15}{7}} (\frac{21 (x + 1)}{\sqrt{101}}) + \\ \dots \end{matrix}] (1 - α + \frac{α t^{α}}{Γ (α + 1)})

and so on.

It can be easily deduced that as the number of iterations increase, the approximate solution becomes more tortuous and the use of the symbolic computer program becomes indispensable. Mathematica 9.0 is used to handle the complex calculations in this paper.

One can prefer to use the collocation method to get the parameters $P_{0}, P_{1}, \dots$ . For third order OPIM solutions, we reach the values $P_{0} = 0.80635, P_{1} = 0.40536, P_{2} = 0.10589$ for $α = 0.5$ and $P_{0} = 0.96302, P_{1} = 0.09965, P_{2} = 0.85012$ for $α = 0.8$ . Tables 1 and 2 display the absolute residual error for approximate OPIM solutions of fractional GRLW equation for different $α$ ’s at some constants x. Additionally, Figs. 1–4 demonstrate the different behaviour of the OPIM solutions for different $α$ ’s.

Table 1 Absolute residual errors of the third and fourth order OPIM solutions at

x = 30

t	$Third Order, α = 0.5$	$Third Order, α = 0.8$	$Fourth Order, α = 0.5$	$Fourth Order, α = 0.8$
0.1	$2.0850 \times 10^{- 12}$	$5.1034 \times 10^{- 12}$	$6.0147 \times 10^{- 15}$	$8.0125 \times 10^{- 16}$
0.2	$4.0293 \times 10^{- 12}$	$2.2231 \times 10^{- 12}$	$5.2066 \times 10^{- 15}$	$8.8804 \times 10^{- 16}$
0.3	$6.4350 \times 10^{- 12}$	$5.7742 \times 10^{- 13}$	$3.0156 \times 10^{- 15}$	$8.9034 \times 10^{- 16}$
0.4	$2.9716 \times 10^{- 12}$	$8.1069 \times 10^{- 12}$	$9.088 \times 10^{- 14}$	$8.111 \times 10^{- 17}$
0.5	$5.1784 \times 10^{- 12}$	$2.7072 \times 10^{- 12}$	$5.0124 \times 10^{- 14}$	$5.3307 \times 10^{- 16}$
0.6	$7.7258 \times 10^{- 12}$	$8.0142 \times 10^{- 12}$	$3.052 \times 10^{- 14}$	$7.0125 \times 10^{- 16}$
0.7	$7.4391 \times 10^{- 12}$	$5.138 \times 10^{- 12}$	$6.077 \times 10^{- 14}$	$2.1055 \times 10^{- 16}$
0.8	$9.5418 \times 10^{- 12}$	$1.0054 \times 10^{- 13}$	$1.0452 \times 10^{- 14}$	$7.1104 \times 10^{- 16}$
0.9	$1.2037 \times 10^{- 12}$	$8.7924 \times 10^{- 12}$	$3.7434 \times 10^{- 14}$	$6.022 \times 10^{- 16}$
1.	$3.3024 \times 10^{- 12}$	$9.9602 \times 10^{- 12}$	$6.9985 \times 10^{- 14}$	$1.4457 \times 10^{- 16}$

Table 2 Absolute residual errors of the third and fourth order OPIM solutions at

x = 100

t	$Third Order, α = 0.5$	$Third Order, α = 0.8$	$Fourth Order, α = 0.5$	$Fourth Order, α = 0.8$
0.1	$1.0124 \times 10^{- 10}$	$2.0564 \times 10^{- 14}$	$8.1051 \times 10^{- 14}$	$9.5099 \times 10^{- 15}$
0.2	$2.1112 \times 10^{- 10}$	$7.1051 \times 10^{- 10}$	$9.8222 \times 10^{- 14}$	$9.0441 \times 10^{- 15}$
0.3	$5.3224 \times 10^{- 9}$	$6.9901 \times 10^{- 11}$	$1.3655 \times 10^{- 13}$	$7.4301 \times 10^{- 15}$
0.4	$7.7758 \times 10^{- 9}$	$7.0201 \times 10^{- 11}$	$2.0215 \times 10^{- 12}$	$1.7893 \times 10^{- 16}$
0.5	$6.0447 \times 10^{- 10}$	$8.3069 \times 10^{- 10}$	$5.2217 \times 10^{- 14}$	$1.4520 \times 10^{- 17}$
0.6	$6.1044 \times 10^{- 9}$	$7.0132 \times 10^{- 12}$	$9.6321 \times 10^{- 15}$	$3.5714 \times 10^{- 17}$
0.7	$2.0057 \times 10^{- 9}$	$5.0433 \times 10^{- 11}$	$1.0635 \times 10^{- 14}$	$1.4223 \times 10^{- 18}$
0.8	$9.0291 \times 10^{- 10}$	$8.7852 \times 10^{- 11}$	$5.5524 \times 10^{- 14}$	$7.0211 \times 10^{- 17}$
0.9	$1.2552 \times 10^{- 8}$	$7.1717 \times 10^{- 11}$	$2.1105 \times 10^{- 13}$	$6.3336 \times 10^{- 17}$
1.	$7.1046 \times 10^{- 9}$	$1.0012 \times 10^{- 10}$	$9.0307 \times 10^{- 14}$	$4.5503 \times 10^{- 17}$

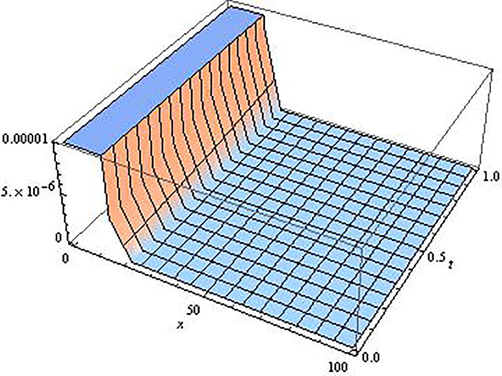
Third order OPIM approximate solution of the Eq. (5.1) for α = 0.5 .

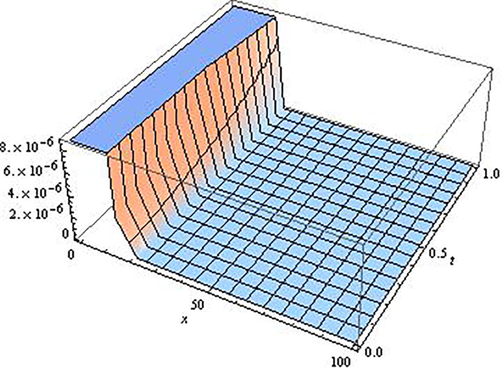
Third order OPIM approximate solution of the Eq. (5.1) for α = 0.8 .

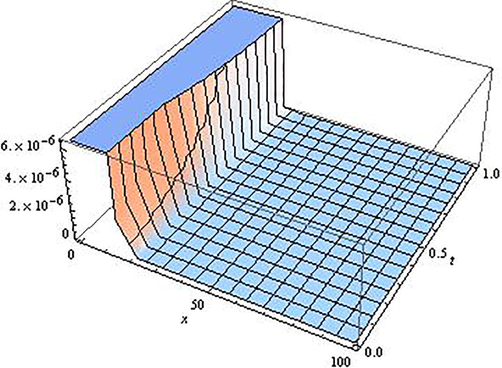
Fourth order OPIM approximate solution of the Eq. (5.1) for α = 0.5 .

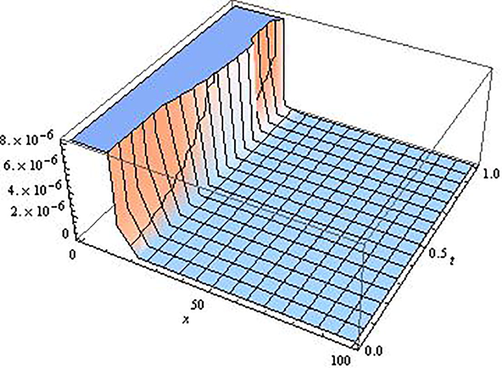
Fourth order OPIM approximate solution of the Eq. (5.1) for α = 0.8 .

6 Conclusion

In this research, we first aim to reconstruct the generalized regularized long wave equations with a new fractional operator. Then, optimal perturbation iteration technique has been implemented to get the approximate solutions of the extended version of the GRLW. Laplace transform is also used to form the OPIM algorithms. We can say that the most important portion of the present study is the usage of the AB fractional derivative instead of integer order derivative in generalized regularized long wave equations to examine the nature of displacement of ion acoustic plasma waves and shallow water waves.Numerical results also show that the suggested scheme is highly methodical and can be used to investigate nonlinear partial fractional mathematical models modeling natural phenomena. It can be also deduced that the use of fractional derivative brings the new paradigms in the area of mathematics or engineering. Future studies can be carried out by using another fractional operators or integral equations with the proposed technique.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Agarwal, Praveen, Deniz, S., Jain, Shilpi. Alderremy, Aisha Abdullah, Aly, Shaban, 2020. A new analysis of a partial differential equation arising in biology and population genetics via semi analytical techniques. Physica A: Statistical Mechanics and its Applications 542, 122769.
Aksoy Yigit, Pakdemirli Mehmet, . New perturbation-iteration solutions for Bratu-type equations. Computers & Mathematics with Applications. 2010;59(8):2802-2808.
[Google Scholar]
Aksoy Y., Pakdemirli M., Abbasbandy S., Boyaci H., . New perturbation-iteration solutions for nonlinear heat transfer equations. International Journal of Numerical Methods for Heat & Fluid Flow 2012
[Google Scholar]
Algahtani, Obaid Jefain Julaighim, 2016. Comparing the Atangana-Baleanu and Caputo-Fabrizio derivative with fractional order: Allen Cahn model. Chaos, Solitons & Fractals 89, 552–559.
Atangana, Abdon, Baleanu, Dumitru, 2016. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. arXiv preprint arXiv:1602.03408.
Baskonus Haci Mehmet, Bulut Hasan, . Exponential prototype structures for (2+1)-dimensional Boiti-Leon-Pempinelli systems in mathematical physics. Waves in Random and Complex Media. 2016;26(2):189-196.
[Google Scholar]
Baskonus Haci Mehmet, Bulut Hasan, Sulaiman Tukur Abdulkadir, . Investigation of various travelling wave solutions to the extended (2+1)-dimensional quantum ZK equation. The European Physical Journal Plus. 2017;132(11):1-8.
[Google Scholar]
Bhangale Nikita, Kachhia Krunal B., Gómez-Aguilar J.F., . A new iterative method with ρ-Laplace transform for solving fractional differential equations with Caputo generalized fractional derivative. Engineering with Computers 2020:1-14.
[Google Scholar]
Bhardwaj D., Shankar R., . A computational method for regularized long wave equation. Computers & Mathematics with Applications. 2000;40(12):1397-1404.
[Google Scholar]
Bildik N., Deniz S., . A new efficient method for solving delay differential equations and a comparison with other methods. The European Physical Journal Plus. 2017;132(1):51.
[Google Scholar]
Bildik, N., Deniz, S., 2017. A practical method for analytical evaluation of approximate solutions of Fisher’s equations. ITM Web of Conferences, 13 (Article Number: 01001).
Bildik N., Deniz S., . Comparative study between optimal homotopy asymptotic method and perturbation-iteration technique for different types of nonlinear equations. Iranian Journal of Science and Technology Transactions A: Science. 2018;42(2):647-654.
[Google Scholar]
Bildik N., Deniz S., . New analytic approximate solutions to the generalized regularized long wave equations. Bulletin of the Korean Mathematical Society. 2018;55(3):749-762.
[Google Scholar]
Bildik N., Deniz S., . Solving the Burgers’ and regularized long wave equations using the new perturbation iteration technique. Numerical Methods for Partial Differential Equations. 2018;34(5):1489-1501.
[Google Scholar]
Bildik N., Deniz S., . A new fractional analysis on the polluted lakes system. Chaos, Solitons & Fractals. 2019;122:17-24.
[Google Scholar]
Bildik N., Deniz S., . New approximate solutions to electrostatic differential equations obtained by using numerical and analytical methods. Georgian Mathematical Journal. 2020;27(1):23-30.
[Google Scholar]
Bildik N., Deniz S., . New approximate solutions to the nonlinear Klein-Gordon equations using perturbation iteration techniques. Discrete and Continuous Dynamical Systems Series S. 2020;13(03):503-518.
[Google Scholar]
Bildik N., Deniz S., . Optimal iterative perturbation technique for solving Jeffery-Hamel flow with high magnetic field and nanoparticle. Journal of Applied Analysis and Computation. 2020;10(6):2476-2490.
[CrossRef] [Google Scholar]
Bildik N., Deniz S., Saad K.M., . A comparative study on solving fractional cubic isothermal auto-catalytic chemical system via new efficient technique. Chaos, Solitons & Fractals. 2020;132
[Google Scholar]
Bona J.L., Pritchard W.G., Scott L.R., . A comparison of solutions of two model equations for long waves. In: Lebovitz N.R., ed. Fluid Dynamics in Astrophysics and Geophysics, Lectures in Appl. Math.. 1983. p. :235-267.
[Google Scholar]
Bonyah, Ebenezer, Sagoe, Ato Kwamena, Kumar, Devendra, Deniz, S., 2021. Fractional optimal control dynamics of coronavirus model with Mittag-Leffler Law. Ecological Complexity 45, 100880.
Cattani Carlo, . On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Optical and Quantum Electronics. 2018;50(3):138.
[Google Scholar]
Dehghan Mehdi, Salehi Rezvan, . The solitary wave solution of the two-dimensional regularized long-wave equation in fluids and plasmas. Computer Physics Communications. 2011;182(12):2540-2549.
[Google Scholar]
Deniz, S., 2017. Optimal perturbation iteration method for solving nonlinear heat transfer equations, Journal of Heat Transfer-ASME, 139 (7), 074503-1.
Deniz, S., 2020. On the stability analysis of the time-fractional variable order Klein-Gordon equation and a numerical simulation. Communications Faculty of Sciences University of Ankara Series A1: Mathematics and Statistics, 69 (1), 981–992.
Deniz S., . Semi-analytical investigation of modified Boussinesq-Burger equations. Journal of BAUN Institute of Science and Technology. 2020;22(1):327-333.
[Google Scholar]
Deniz S., . Modification of coupled Drinfel’d-Sokolov-Wilson Equation and approximate solutions by optimal perturbation iteration method. Afyon Kocatepe University Journal of Science and Engineering. 2020;20(1):35-40.
[Google Scholar]
Deniz S., . Iterative perturbation technique for solving a special magnetohydrodynamics problem. Celal Bayar University Journal of Science. 2020;16(1):69-74.
[Google Scholar]
Deniz S., Bildik N., . Comparison of Adomian decomposition method and Taylor matrix method in solving different kinds of partial differential equations. International Journal of Modelling and Optimization. 2014;4(4):292-298.
[Google Scholar]
Deniz S., Bildik N., . Applications of optimal perturbation iteration method for solving nonlinear differential equations. AIP Conf. Proc.. 2017;1798:020046
[Google Scholar]
Deniz S., Bildik N., . A new analytical technique for solving Lane - Emden type equations arising in astrophysics. Bulletin of the Belgian Mathematical Society – Simon Stevin. 2017;24(2):305-320.
[Google Scholar]
Deniz S., Bildik N., . Optimal perturbation iteration method for Bratu-type problems. Journal of King Saud University – Science. 2018;30(1):91-99.
[Google Scholar]
Deniz S., Sezer M., . Rational Chebyshev collocation method for solving nonlinear heat transfer equations. International Communications in Heat and Mass Transfer. 2020;114:104595
[Google Scholar]
Deniz S., Konuralp A., De la Sen M., . Optimal perturbation iteration method for solving fractional model of damped Burgers’ equation. Symmetry-Basel. 2020;12(6):958.
[Google Scholar]
Dubey R.S., Belgacem F.B.M., Goswami P., . Homotopy perturbation approximate solutions for Bergman’s Minimal Blood Glucose-Insulin Model. Journal of Fractal Geometry and Nonlinear Analysis in Medicine and Biology (FGNAMB). 2016;2(3):1-6.
[Google Scholar]
Dwivedi Kushal Dhar, Das S., Gomez-Aguilar José Francisco, . Finite difference/collocation method to solve multi term variable-order fractional reaction-advection-diffusion equation in heterogeneous medium. Numerical Methods for Partial Differential Equations 2020
[Google Scholar]
Gómez-Aguilar J.F., . Chaos in a nonlinear Bloch system with Atangana-Baleanu fractional derivatives. Numerical Methods for Partial Differential Equations. 2018;34(5):1716-1738.
[Google Scholar]
Iqbal S., . Some solutions of the linear and nonlinear Klein-Gordon equations using the optimal homotopy asymptotic method. Applied Mathematics and Computation. 2010;216(10):2898-2909.
[Google Scholar]
Jajarmi Amin, Baleanu Dumitru, . A new fractional analysis on the interaction of HIV with CD4+ T-cells. Chaos, Solitons & Fractals. 2018;113:221-229.
[Google Scholar]
Khan M.A., Akbar M.A., Belgacem F.B.M., . Solitary wave solutions for the Boussinesq and Fisher equations by the modified simple equation method. Mathematics Letters. 2016;2(1):1-18.
[Google Scholar]
Kilbas A.A., Srivastava H.M., Trujillo J.J., . Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies. Vol vol. 204. Amsterdam, London and New York: Elsevier (North-Holland) Science Publishers; 2006.
Kumar Sachin, Gómez-Aguilar José Francisco, . Numerical solution of Caputo-Fabrizio time fractional distributed order reaction-diffusion equation via quasi wavelet based numerical method. Journal of Applied and Computational Mechanics. 2020;6(4):848-861.
[Google Scholar]
Kumar Devendra, Singh Jagdev, Baleanu Dumitru, . A new analysis for fractional model of regularized long wave equation arising in ion acoustic plasma waves. Mathematical Methods in the Applied Sciences. 2017;40(15):5642-5653.
[Google Scholar]
Kumar Devendra, Singh Jagdev, Baleanu Dumitru, . Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Physica A: Statistical Mechanics and its Applications. 2018;492:155-167.
[Google Scholar]
Liao Shijun, . On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation. 2004;147(2):499-513.
[Google Scholar]
Marinca Vasile, Herisanu Nicolae, . Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. International Communications in Heat and Mass Transfer. 2008;35(6):710-715.
[Google Scholar]
Mirzaei D., Dehghan M., . MLPG method for transient heat conduction problem with MLS as trial approximation in both time and space domains. Computer Modeling in Engineering and Sciences, CMES. 2011;72:185-210.
[Google Scholar]
Mohammadi Maryam, Mokhtari Reza, . Solving the generalized regularized long wave equation on the basis of a reproducing kernel space. Journal of Computational and Applied Mathematics. 2011;235(14):4003-4014.
[Google Scholar]
Morales-Delgado Victor Fabian, . Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Advances in Difference Equations. 2016;2016(1):1-17.
[Google Scholar]
Pandey Prashant, . An efficient technique for solving the space-time fractional reaction-diffusion equation in porous media. Chinese Journal of Physics. 2020;68:483-492.
[Google Scholar]
Peregrine D.H., . Calculations of the development of an undular bore. Journal of Fluid Mechanics. 1996;25:321-330.
[Google Scholar]
Saad K.M., . Comparing the Caputo, Caputo-Fabrizio and Atangana-Baleanu derivative with fractional order: Fractional cubic isothermal auto-catalytic chemical system. The European Physical Journal Plus. 2018;133(3):94.
[Google Scholar]
Saad Khaled M., . Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2019;29(2):023116
[Google Scholar]
Saad Khaled M., Atangana Abdon, Baleanu Dumitru, . New fractional derivatives with non-singular kernel applied to the Burgers equation. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2018;28(6):063109
[Google Scholar]
Saad K.M., Deniz S., Baleanu D., . On the new fractional analysis of Nagumo equation. International Journal of Biomathematics. 2019;12(03):1950034.
[Google Scholar]
Safdari H., Esmaeelzade Aghdam Y., Gómez-Aguilar J.F., . Shifted Chebyshev collocation of the fourth kind with convergence analysis for the space-time fractional advection-diffusion equation. Engineering with Computers 2020:1-12.
[Google Scholar]
Singh, H., Srivastava, H.M., 2020. Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Applied Science 10 (Article ID 2850).
Singh H., Srivastava H.M., Kumar D., . A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons & Fractals. 2017;103:131-138.
[Google Scholar]
Srivastava H.M., . Fractional-order derivatives and integrals: introductory overview and recent developments. Kyungpook Mathematical Journal. 2020;60:73-116.
[Google Scholar]
Srivastava H.M., . Diabetes and its resulting complications: mathematical modeling via fractional calculus. Public Health Open Access. 2020;4(3):1-5. (Article ID 2)
[Google Scholar]
Srivastava H.M., Günerhan H., Ghanbari B., . Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity. Mathematical Methods in the Applied Sciences. 2019;42:7210-7221.
[Google Scholar]
Srivastava H.M., Shah F.A., Abass R., . An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation. Russian Journal of Mathematical Physics. 2019;26:77-93.
[Google Scholar]
Srivastava H.M., Dubey R.S., Jain M., . A study of the fractional-order mathematical model of diabetes and its resulting complications. Mathematical Methods in the Applied Sciences. 2019;42:4570-4583.
[Google Scholar]
Srivastava, H.M., Baleanu, D., Machado, J.A.T., Osman, M.S., Rezazadeh, H., Arshed, S., Günerhan, H., 2020. Traveling wave solutions to nonlinear directional couplers by modified Kudryashov method. Physica Scripta 95 (Article ID 75217).
Srivastava H.M., Saad K.M., Khader M.M., . An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals. 2020;140:1-7. (Article ID 110174)
[Google Scholar]
Yépez-Martínez Huitzilín, Gómez-Aguilar José Francisco, . Laplace variational iteration method for modified fractional derivatives with non-singular kernel. Journal of Applied and Computational Mechanics. 2020;6(3):684-698.
[Google Scholar]

Introduction

Preliminaries and some definitions

Analysis of fractional GRLW equations via OPIM

Convergence analysis of the proposed technique

Numerical example

Conclusion

Declaration of Competing Interest

Fulltext Views
34

PDF downloads
30

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Agarwal, Praveen, Deniz, S., Jain, Shilpi. Alderremy, Aisha Abdullah, Aly, Shaban, 2020. A new analysis of a partial differential equation arising in biology and population genetics via semi analytical techniques. Physica A: Statistical Mechanics and its Applications 542, 122769.

[2] Aksoy Yigit, Pakdemirli Mehmet, . New perturbation-iteration solutions for Bratu-type equations. Computers & Mathematics with Applications. 2010;59(8):2802-2808.
[Google Scholar]

[3] Aksoy Y., Pakdemirli M., Abbasbandy S., Boyaci H., . New perturbation-iteration solutions for nonlinear heat transfer equations. International Journal of Numerical Methods for Heat & Fluid Flow 2012
[Google Scholar]

[4] Algahtani, Obaid Jefain Julaighim, 2016. Comparing the Atangana-Baleanu and Caputo-Fabrizio derivative with fractional order: Allen Cahn model. Chaos, Solitons & Fractals 89, 552–559.

[5] Atangana, Abdon, Baleanu, Dumitru, 2016. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. arXiv preprint arXiv:1602.03408.

[6] Baskonus Haci Mehmet, Bulut Hasan, . Exponential prototype structures for (2+1)-dimensional Boiti-Leon-Pempinelli systems in mathematical physics. Waves in Random and Complex Media. 2016;26(2):189-196.
[Google Scholar]

[7] Baskonus Haci Mehmet, Bulut Hasan, Sulaiman Tukur Abdulkadir, . Investigation of various travelling wave solutions to the extended (2+1)-dimensional quantum ZK equation. The European Physical Journal Plus. 2017;132(11):1-8.
[Google Scholar]

[8] Bhangale Nikita, Kachhia Krunal B., Gómez-Aguilar J.F., . A new iterative method with ρ-Laplace transform for solving fractional differential equations with Caputo generalized fractional derivative. Engineering with Computers 2020:1-14.
[Google Scholar]

[9] Bhardwaj D., Shankar R., . A computational method for regularized long wave equation. Computers & Mathematics with Applications. 2000;40(12):1397-1404.
[Google Scholar]

[10] Bildik N., Deniz S., . A new efficient method for solving delay differential equations and a comparison with other methods. The European Physical Journal Plus. 2017;132(1):51.
[Google Scholar]

[11] Bildik, N., Deniz, S., 2017. A practical method for analytical evaluation of approximate solutions of Fisher’s equations. ITM Web of Conferences, 13 (Article Number: 01001).

[12] Bildik N., Deniz S., . Comparative study between optimal homotopy asymptotic method and perturbation-iteration technique for different types of nonlinear equations. Iranian Journal of Science and Technology Transactions A: Science. 2018;42(2):647-654.
[Google Scholar]

[13] Bildik N., Deniz S., . New analytic approximate solutions to the generalized regularized long wave equations. Bulletin of the Korean Mathematical Society. 2018;55(3):749-762.
[Google Scholar]

[14] Bildik N., Deniz S., . Solving the Burgers’ and regularized long wave equations using the new perturbation iteration technique. Numerical Methods for Partial Differential Equations. 2018;34(5):1489-1501.
[Google Scholar]

[15] Bildik N., Deniz S., . A new fractional analysis on the polluted lakes system. Chaos, Solitons & Fractals. 2019;122:17-24.
[Google Scholar]

[16] Bildik N., Deniz S., . New approximate solutions to electrostatic differential equations obtained by using numerical and analytical methods. Georgian Mathematical Journal. 2020;27(1):23-30.
[Google Scholar]

[17] Bildik N., Deniz S., . New approximate solutions to the nonlinear Klein-Gordon equations using perturbation iteration techniques. Discrete and Continuous Dynamical Systems Series S. 2020;13(03):503-518.
[Google Scholar]

[18] Bildik N., Deniz S., . Optimal iterative perturbation technique for solving Jeffery-Hamel flow with high magnetic field and nanoparticle. Journal of Applied Analysis and Computation. 2020;10(6):2476-2490.
[CrossRef] [Google Scholar]

[19] Bildik N., Deniz S., Saad K.M., . A comparative study on solving fractional cubic isothermal auto-catalytic chemical system via new efficient technique. Chaos, Solitons & Fractals. 2020;132
[Google Scholar]

[20] Bona J.L., Pritchard W.G., Scott L.R., . A comparison of solutions of two model equations for long waves. In: Lebovitz N.R., ed. Fluid Dynamics in Astrophysics and Geophysics, Lectures in Appl. Math.. 1983. p. :235-267.
[Google Scholar]

[21] Bonyah, Ebenezer, Sagoe, Ato Kwamena, Kumar, Devendra, Deniz, S., 2021. Fractional optimal control dynamics of coronavirus model with Mittag-Leffler Law. Ecological Complexity 45, 100880.

[22] Cattani Carlo, . On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Optical and Quantum Electronics. 2018;50(3):138.
[Google Scholar]

[23] Dehghan Mehdi, Salehi Rezvan, . The solitary wave solution of the two-dimensional regularized long-wave equation in fluids and plasmas. Computer Physics Communications. 2011;182(12):2540-2549.
[Google Scholar]

[24] Deniz, S., 2017. Optimal perturbation iteration method for solving nonlinear heat transfer equations, Journal of Heat Transfer-ASME, 139 (7), 074503-1.

[25] Deniz, S., 2020. On the stability analysis of the time-fractional variable order Klein-Gordon equation and a numerical simulation. Communications Faculty of Sciences University of Ankara Series A1: Mathematics and Statistics, 69 (1), 981–992.

[26] Deniz S., . Semi-analytical investigation of modified Boussinesq-Burger equations. Journal of BAUN Institute of Science and Technology. 2020;22(1):327-333.
[Google Scholar]

[27] Deniz S., . Modification of coupled Drinfel’d-Sokolov-Wilson Equation and approximate solutions by optimal perturbation iteration method. Afyon Kocatepe University Journal of Science and Engineering. 2020;20(1):35-40.
[Google Scholar]

[28] Deniz S., . Iterative perturbation technique for solving a special magnetohydrodynamics problem. Celal Bayar University Journal of Science. 2020;16(1):69-74.
[Google Scholar]

[29] Deniz S., Bildik N., . Comparison of Adomian decomposition method and Taylor matrix method in solving different kinds of partial differential equations. International Journal of Modelling and Optimization. 2014;4(4):292-298.
[Google Scholar]

[30] Deniz S., Bildik N., . Applications of optimal perturbation iteration method for solving nonlinear differential equations. AIP Conf. Proc.. 2017;1798:020046
[Google Scholar]

[31] Deniz S., Bildik N., . A new analytical technique for solving Lane - Emden type equations arising in astrophysics. Bulletin of the Belgian Mathematical Society – Simon Stevin. 2017;24(2):305-320.
[Google Scholar]

[32] Deniz S., Bildik N., . Optimal perturbation iteration method for Bratu-type problems. Journal of King Saud University – Science. 2018;30(1):91-99.
[Google Scholar]

[33] Deniz S., Sezer M., . Rational Chebyshev collocation method for solving nonlinear heat transfer equations. International Communications in Heat and Mass Transfer. 2020;114:104595
[Google Scholar]

[34] Deniz S., Konuralp A., De la Sen M., . Optimal perturbation iteration method for solving fractional model of damped Burgers’ equation. Symmetry-Basel. 2020;12(6):958.
[Google Scholar]

[35] Dubey R.S., Belgacem F.B.M., Goswami P., . Homotopy perturbation approximate solutions for Bergman’s Minimal Blood Glucose-Insulin Model. Journal of Fractal Geometry and Nonlinear Analysis in Medicine and Biology (FGNAMB). 2016;2(3):1-6.
[Google Scholar]

[36] Dwivedi Kushal Dhar, Das S., Gomez-Aguilar José Francisco, . Finite difference/collocation method to solve multi term variable-order fractional reaction-advection-diffusion equation in heterogeneous medium. Numerical Methods for Partial Differential Equations 2020
[Google Scholar]

[37] Gómez-Aguilar J.F., . Chaos in a nonlinear Bloch system with Atangana-Baleanu fractional derivatives. Numerical Methods for Partial Differential Equations. 2018;34(5):1716-1738.
[Google Scholar]

[38] Iqbal S., . Some solutions of the linear and nonlinear Klein-Gordon equations using the optimal homotopy asymptotic method. Applied Mathematics and Computation. 2010;216(10):2898-2909.
[Google Scholar]

[39] Jajarmi Amin, Baleanu Dumitru, . A new fractional analysis on the interaction of HIV with CD4+ T-cells. Chaos, Solitons & Fractals. 2018;113:221-229.
[Google Scholar]

[40] Khan M.A., Akbar M.A., Belgacem F.B.M., . Solitary wave solutions for the Boussinesq and Fisher equations by the modified simple equation method. Mathematics Letters. 2016;2(1):1-18.
[Google Scholar]

[41] Kilbas A.A., Srivastava H.M., Trujillo J.J., . Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies. Vol vol. 204. Amsterdam, London and New York: Elsevier (North-Holland) Science Publishers; 2006.

[42] Kumar Sachin, Gómez-Aguilar José Francisco, . Numerical solution of Caputo-Fabrizio time fractional distributed order reaction-diffusion equation via quasi wavelet based numerical method. Journal of Applied and Computational Mechanics. 2020;6(4):848-861.
[Google Scholar]

[43] Kumar Devendra, Singh Jagdev, Baleanu Dumitru, . A new analysis for fractional model of regularized long wave equation arising in ion acoustic plasma waves. Mathematical Methods in the Applied Sciences. 2017;40(15):5642-5653.
[Google Scholar]

[44] Kumar Devendra, Singh Jagdev, Baleanu Dumitru, . Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Physica A: Statistical Mechanics and its Applications. 2018;492:155-167.
[Google Scholar]

[45] Liao Shijun, . On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation. 2004;147(2):499-513.
[Google Scholar]

[46] Marinca Vasile, Herisanu Nicolae, . Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. International Communications in Heat and Mass Transfer. 2008;35(6):710-715.
[Google Scholar]

[47] Mirzaei D., Dehghan M., . MLPG method for transient heat conduction problem with MLS as trial approximation in both time and space domains. Computer Modeling in Engineering and Sciences, CMES. 2011;72:185-210.
[Google Scholar]

[48] Mohammadi Maryam, Mokhtari Reza, . Solving the generalized regularized long wave equation on the basis of a reproducing kernel space. Journal of Computational and Applied Mathematics. 2011;235(14):4003-4014.
[Google Scholar]

[49] Morales-Delgado Victor Fabian, . Laplace homotopy analysis method for solving linear partial differential equations using a fractional derivative with and without kernel singular. Advances in Difference Equations. 2016;2016(1):1-17.
[Google Scholar]

[50] Pandey Prashant, . An efficient technique for solving the space-time fractional reaction-diffusion equation in porous media. Chinese Journal of Physics. 2020;68:483-492.
[Google Scholar]

[51] Peregrine D.H., . Calculations of the development of an undular bore. Journal of Fluid Mechanics. 1996;25:321-330.
[Google Scholar]

[52] Saad K.M., . Comparing the Caputo, Caputo-Fabrizio and Atangana-Baleanu derivative with fractional order: Fractional cubic isothermal auto-catalytic chemical system. The European Physical Journal Plus. 2018;133(3):94.
[Google Scholar]

[53] Saad Khaled M., . Numerical solutions of the fractional Fisher’s type equations with Atangana-Baleanu fractional derivative by using spectral collocation methods. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2019;29(2):023116
[Google Scholar]

[54] Saad Khaled M., Atangana Abdon, Baleanu Dumitru, . New fractional derivatives with non-singular kernel applied to the Burgers equation. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2018;28(6):063109
[Google Scholar]

[55] Saad K.M., Deniz S., Baleanu D., . On the new fractional analysis of Nagumo equation. International Journal of Biomathematics. 2019;12(03):1950034.
[Google Scholar]

[56] Safdari H., Esmaeelzade Aghdam Y., Gómez-Aguilar J.F., . Shifted Chebyshev collocation of the fourth kind with convergence analysis for the space-time fractional advection-diffusion equation. Engineering with Computers 2020:1-12.
[Google Scholar]

[57] Singh, H., Srivastava, H.M., 2020. Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Applied Science 10 (Article ID 2850).

[58] Singh H., Srivastava H.M., Kumar D., . A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons & Fractals. 2017;103:131-138.
[Google Scholar]

[59] Srivastava H.M., . Fractional-order derivatives and integrals: introductory overview and recent developments. Kyungpook Mathematical Journal. 2020;60:73-116.
[Google Scholar]

[60] Srivastava H.M., . Diabetes and its resulting complications: mathematical modeling via fractional calculus. Public Health Open Access. 2020;4(3):1-5. (Article ID 2)
[Google Scholar]

[61] Srivastava H.M., Günerhan H., Ghanbari B., . Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity. Mathematical Methods in the Applied Sciences. 2019;42:7210-7221.
[Google Scholar]

[62] Srivastava H.M., Shah F.A., Abass R., . An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation. Russian Journal of Mathematical Physics. 2019;26:77-93.
[Google Scholar]

[63] Srivastava H.M., Dubey R.S., Jain M., . A study of the fractional-order mathematical model of diabetes and its resulting complications. Mathematical Methods in the Applied Sciences. 2019;42:4570-4583.
[Google Scholar]

[64] Srivastava, H.M., Baleanu, D., Machado, J.A.T., Osman, M.S., Rezazadeh, H., Arshed, S., Günerhan, H., 2020. Traveling wave solutions to nonlinear directional couplers by modified Kudryashov method. Physica Scripta 95 (Article ID 75217).

[65] Srivastava H.M., Saad K.M., Khader M.M., . An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals. 2020;140:1-7. (Article ID 110174)
[Google Scholar]

[66] Yépez-Martínez Huitzilín, Gómez-Aguilar José Francisco, . Laplace variational iteration method for modified fractional derivatives with non-singular kernel. Journal of Applied and Computational Mechanics. 2020;6(3):684-698.
[Google Scholar]

An efficient semi-analytical method for solving the generalized regularized long wave equations with a new fractional derivative operator

Abstract

Keywords

Optimal perturbation iteration method

Generalized regularized long wave equations

Atangana-Baleanu derivative

Convergence

26A33

34A08

91B76

1 Introduction

2 Preliminaries and some definitions

3 Analysis of fractional GRLW equations via OPIM

4 Convergence analysis of the proposed technique

5 Numerical example

6 Conclusion

Declaration of Competing Interest

References

Suggested read for related articles: