An efficient local meshless approach for solving nonlinear time-fractional fourth-order diffusion model

O. Nikan; Z. Avazzadeh; J.A. Tenreiro Machado

doi:10.1016/j.jksus.2020.101243

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

01 2020

:33;

101243

doi:

10.1016/j.jksus.2020.101243

An efficient local meshless approach for solving nonlinear time-fractional fourth-order diffusion model

O. Nikan^{^a}, Z. Avazzadeh^{^b,⁎}, J.A. Tenreiro Machado^{^c}

a School of Mathematics, Iran University of Science and Technology, Narmak, Tehran, Iran

b Department of Applied Mathematics, Xi’an Jiaotong-Liverpool University, Suzhou 215123, China

c Department of Electrical Engineering, ISEP-Institute of Engineering, Polytechnic of Porto, Porto, Portugal

⁎Corresponding author at: Department of Applied Mathematics, Xi’an Jiaotong-Liverpool University, Suzhou 215123, China. zakieh.avazzadeh@xjtlu.edu.cn (Z. Avazzadeh),

Received: 2020-8-2, Accepted: 2020-11-16,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

This paper adopts an efficient meshless approach for approximating the nonlinear fractional fourth-order diffusion model described in the Riemann–Liouville sense. A second-order difference technique is applied to discretize temporal derivatives, while the radial basis function meshless generated the finite difference scheme approximates the spatial derivatives. One key advantage of the local collocation method is the approximation of the derivatives via the finite difference formulation, for each local-support domain, by deriving the basis functions expansion. Another advantage of this method is that it can be applied in problems with non-regular geometrical domains. For the proposed time discretization, the unconditional stability is examined and an error bound is obtained. Numerical results illustrate the applicability and validity of the scheme and confirm the theoretical formulation.

Keywords

Nonlinear time-fractional fourth-order diffusion problem

Radial basis function

Finite difference scheme

Convergence and stability

Show Related Articles from PubMed

1 Introduction

Fractional calculus (FC) generalizes integrals and derivatives leads to non-integer orders. Many problems in physical science, including general transport theory, electrochemistry, diffusion, and electromagnetism, have a more comprehensive description when adopting the viewpoint of FC (Oldham and Spanier, 1974; Podlubny, 1998). In fact, the FC makes use of nonlocal operators, describing more clearly the behavior of physical systems with long range memory effects. Fractional order equations became popular in the modeling of phenomena in fields as diverse as wave propagation, anomalous diffusion, chemistry, mechanics, physics, continuous-time random walk (CTRW), control, and engineering applications, see (Singh, 2017; Singh et al., 2020; Singh and Srivastava, 2020; Singh et al., 2019; Zaky et al., 2020; Zaky and Machado, 2020; Zaky, 2018; Zaky and Machado, 2017; Zaky, 2018 ).

Hereafter, we focus on an efficient meshless numerical method for seeking accurate solutions of the nonlinear time fractional fourth-order diffusion problem (NTF4DP)

(1)

\frac{\partial v (x, t)}{\partial t} - \frac{\partial^{β} Δ v (x, t)}{\partial t^{β}} - Δ v (x, t) + Δ^{2} v (x, t) = f (x, t) + G (v), x \in Ω \subset R^{2}, 0 < t ⩽ T,

The initial condition is considered as

(2)

v (x, 0) = g (x), x \in \overline{Ω},

together with the boundary conditions

(3)

v (x, t) = Δ v (x, t) = 0, x \in \partial Ω, t > 0,

where

0 < β < 1, x = (x, y)

stands for space variable,

\partial Ω

is the closed curve bounding the region,

\overline{Ω} = Ω \cup \partial Ω

represents the space domain,

f (x, t)

is the forcing term with sufficient smoothness and

g (x)

is a given continuous function. The symbols

Δ

and

Δ^{2}

denote the Laplacian and double Laplacian operators corresponding to the space directions, respectively. The fractional diffusion term

\frac{\partial^{β} Δ v (x, t)}{\partial t^{β}}

reflects the anomalous subdiffusion behavior of diffusion processes. The nonlinear source term

G (v)

fulfills the assumed conditions:

G (v)

is the polynomial of u or

∣ G (v) ∣ ⩽ C_{} ∣ v ∣

and

∣ G^{'} (v) ∣ ⩽ C_{}

, where

C_{}

is a positive constant. The fractional operator

\partial^{β} z (x, t) / \partial t^{β}

represents the Riemann–Liouville (R-L) fractional derivative with respect to time variable t, given by

\frac{\partial^{β} z (x, t)}{\partial t^{β}} = \frac{1}{Γ (1 - β)} \frac{\partial}{\partial t} \int_{0}^{t} \frac{z (x, s)}{{(t - s)}^{β}} d s,

where

Γ (\cdot)

is the Gamma function. To the author’s best knowledge, only a few numerical schemes have been proposed to approximate the NTF4DP. Du et al. (2017) developed proposed a local discontinuous Galerkin scheme. Liu et al. (2014) formulated a finite element (FE) technique. Liu et al. (2015) presented a two-grid mixed finite element method. Liu et al. (2015) applied also finite difference (FD) and FE schemes in the temporal and space directions, respectively. Liu et al. (2018) adopted the mixed FE Galerkin technique in combination with a time second-order discrete approach.

Partial differential equations (PDEs) are commonly solved using numerical techniques, such as the finite element, finite difference, pseudo spectral, and finite volume algorithms (FE, FD, PS, and FV algorithms, respectively); but, the majority of them are based on pre-defined meshes/grid. This means that the mesh generation is often required in the computations, posing a high load and representing a time consuming process. In addition, these approaches reveal a lower accuracy in complex domains and non-smooth since the solution is available only at the nodes. In order to solve these issues meshless techniques were developed. In general, meshless techniques have two advantages (Liu and Gu, 2005) because they: (i) do not require a prior knowledge of the relationship between the nodes in order to interpolate or approximate the unknown functions of the field variable when solving a PDE, (ii) can handle arbitrary high dimensional geometries without the need for a mesh.

A mesh-free technique, based on radial basis functions (RBF), capable of solving these challenging problems was proposed. Unlike mesh generating methods, the RBF does not reveal difficulties for calculating inter-nodal distances in case of an increase in the number of dimensions. In other words, the RBF technique can readily be applied to high-dimensional problems since it poses a limited computational burden. Hardy (1971) first introduced the RBF methodology as a result of research on a topological application on quadric surfaces. He also proposed the multiquadric (MQ) approximation technique. Franke (1982) not only applied the modified Maude and the Foley’s methods, but also considered other techniques such as the global basis function type, finite element, inverse distance weighted, and rectangle-based blending to scattered data interpolation. Franke (1987) evaluated these methods based on various parameters such as storage memory, accuracy, and required computational time, leading to the conclusion that the MQ RBF was the best approach. Micchelli (1984) developed the RBF further and provided the proof that it is always possible to solve the MQ surface interpolation. Kansa (1990) addressed the MQ RBF and introduced the so-called the Kansa method, a globally supported interpolant that can be used for solving a PDE. Buhmann et al. (1992) and Chui et al., 1996 shown that the RBF are related to the prewavelets. The attainable error and the condition number of the interpolation cannot be both kept small (Schaback, 1995). This inverse relationship is widely known as the trade off (uncertainty) principle (Schaback, 1995). Buhmann (2003) and Madych and Nelson (1990) shown the exponential convergence property of the MQ interpolation. The RBF interpolation in terms of convergence and existence, uniqueness properties was investigated in (Franke and Schaback, 1998; Micchelli, 1984; Madych and Nelson, 1990 ). In the present paper, we assume that for the problem (1)-(3) we have a unique solution that has sufficiently smooth properties according to $v (x, t) \in Ω \times [0, T]$ . We can determine the solvability of the method using the Leray–Schauder fixed point theorem (Vong and Wang, 2015). Furthermore, we assume that $v (x, 0)$ and $f (x, t)$ are sufficiently smooth for the current theoretical analysis and that $\frac{\partial^{2} v}{\partial t^{2}}$ is continuous on $Ω \times [0, T]$ .

This article proposes a local approach based on the RBF to obtain the approximate solution of the NTF4DP. Stemming from these ideas, the article is organized as follows. Section 2 describes a time-discrete scheme for the approximate solution of NTF4DP. Moreover, the unconditionally stability analysis and the error estimation of the time-discrete formulation are provided. Section 3 presents the LRBF-FD for discretizing the spatial derivative terms. Section 4 shows the ability of LRBF-FD technique on the solution of two problems involving regular and irregular points. Finally, Section 5 reviews the conclusions and remarks.

2 Time-discrete formulation

For formulating the numerical scheme in the time variable, let us define $τ = T / M$ as a uniform time step size with grid points $t_{k} = k τ, 0 ⩽ k ⩽ M$ .

We now introduce the necessary notations and lemmas about the integer and fractional derivatives in time (Gao et al., 2015; Wang et al., 2016; Tian et al., 2015 ).

Lemma 1

Following Gao et al. (2015), for approximating $\frac{\partial v (x, t)}{\partial t}$ , we have the discrete formula

(4)

\frac{\partial v (x, t_{k - \frac{β}{2}})}{\partial t} = \{\begin{matrix} P_{t}^{β} v^{k - \frac{β}{2}} + O (τ^{2}), k ⩾ 2, \\ P_{t} v^{1} + O (τ), k = 1, \end{matrix}

where

P_{t}^{β} v^{k - \frac{β}{2}} = \frac{(3 - β) v^{k} - (4 - 2 β) v^{k - 1} + (1 - β) v^{k - 2}}{τ}

and

P_{t} v^{1} = \frac{v^{1} - v^{0}}{τ} \cdot

Lemma 2

Considering the Tian et al. (2015), Gao et al. (2015) and Liu et al. (2018), the R-L fractional derivative can be approximated by

(5)

\frac{\partial^{β} Δ v (x, t_{k - \frac{β}{2}})}{\partial t^{β}} = τ^{- β} \sum_{j = 0}^{k} ω_{j}^{β} Δ v^{k - j} + O (τ^{2}) = τ^{- β} \sum_{j = 0}^{k} ω_{j}^{β} Δ v^{k - j - \frac{β}{2}} + O (τ^{2}),

where

ω_{0}^{(β)} = 1

and

ω_{j}^{(β)} = (1 - \frac{β + 1}{j}) ω_{j - 1}^{(β)}, j ⩾ 1

Lemma 3

Following Gao et al. (2015) and Wang et al. (2016), we obtain two equalities at time $t_{k - \frac{β}{2}}$ , namely $\begin{matrix} f (x, t_{k - \frac{β}{2}}) = (1 - \frac{β}{2}) f^{k} + \frac{β}{2} f^{k - 1} + O (τ^{2}), \\ G (v (x, t_{k - \frac{β}{2}})) = (2 - \frac{β}{2}) G (v^{k - 1}) - (1 - \frac{β}{2}) G (v^{k - 2}) + O (τ^{2}) . \end{matrix}$

Based on the above notations, the semi-discrete formulation at time $t_{k - \frac{β}{2}}$ will be derived as:

(6)

\frac{\partial v (x, t)}{\partial t} |_{t = t_{k - \frac{β}{2}}} - \frac{\partial^{β} Δ u}{\partial t^{β}} |_{t = t_{k - \frac{β}{2}}} - Δ v (x, t) |_{t = t_{k - \frac{β}{2}}} + Δ^{2} v (x, t) |_{t = t_{k - \frac{β}{2}}} = f (x, t) |_{t = t_{k - \frac{β}{2}}} + G (v (x, t)) |_{t = t_{k - \frac{β}{2}}},

so that

v^{k} = v (x, y, t_{k})

stands for the solution at the kth time level.

(7)

\{\begin{matrix} P_{t} v^{1} - τ^{- β} \sum_{j = 0}^{1} λ_{j} Δ v^{1 - j - \frac{β}{2}} - Δ v^{1 - \frac{β}{2}} + Δ^{2} v^{1 - \frac{β}{2}} = f^{1 - \frac{β}{2}} + G (v^{0}) + R_{}^{1 - \frac{β}{2}}, & k = 1, \\ P_{t}^{β} v^{k - \frac{β}{2}} - τ^{- β} \sum_{j = 0}^{k} λ_{j} Δ v^{k - j - \frac{β}{2}} - Δ v^{k - \frac{β}{2}} + Δ^{2} v^{k - \frac{β}{2}} = f^{k - \frac{β}{2}} + G (v^{k - \frac{β}{2}}) + R_{}^{k - \frac{β}{2}}, & k ⩾ 2, \end{matrix}

in which

R_{}^{1 - \frac{β}{2}} = O (τ)

and

R_{}^{k - \frac{β}{2}} = O (τ^{2})

represent the truncation errors.

By neglecting the truncation error terms of the above equation, the semi-discrete scheme is formulated by:

(8)

\{\begin{matrix} P_{t} V^{1} - τ^{- β} \sum_{j = 0}^{1} λ_{j} Δ V^{1 - j - \frac{β}{2}} - Δ V^{1 - \frac{β}{2}} + Δ^{2} V^{1 - \frac{β}{2}} = f^{1 - \frac{β}{2}} + G (V^{0}), & k = 1, \\ P_{t}^{β} V^{k - \frac{β}{2}} - τ^{- β} \sum_{j = 0}^{k} λ_{j} Δ V^{k - j - \frac{β}{2}} - Δ V^{k - \frac{β}{2}} + Δ^{2} V^{k - \frac{β}{2}} = f^{k - \frac{β}{2}} + G (V^{k - \frac{β}{2}}), & k ⩾ 2 . \end{matrix}

where

V^{k} = V (x, t_{k})

is approximation solution of

v^{k} = v (x, t_{k})

Remark 1

The study of high-order approximation methods as applied to fractional derivatives is key relevance. This research attempts to obtain high-order convergence along the temporal direction following the WSGD operator concept (Tian et al., 2015; Gao et al., 2015; Liu et al., 2018 ), subject to certain conditions, for approximating the R-L fractional derivatives. To use the WSGD operator for approximating the Caputo time-fractional derivative provided that $0 < β < 1$ (Liu et al., 2015; Liu et al., 2015), one needs to take into account the relationship between Caputo and R-L derivatives based on some regularity assumptions. Moreover, an initial value of zero, i.e., $v (x, 0) = 0$ , must be assumed (Li and Cai, 2019) [page 72]. Otherwise, one needs only to perform the change of variable $u (x, t) = v (x, t) - v (x, 0)$ . Further information about a comprehensive analysis of the role of $β$ ( $0 < β < 1$ ) in using the WSGD operator concept to approximate the Caputo time-fractional derivative can be found in (Liu et al., 2015; Liu et al., 2015).

Remark 2

In practical computations, we need only to take into account the value at $t_{1}$ , rather than that at $t_{1 - \frac{β}{2}}$ in order to determine the approximate solution $V^{1}$ .

2.1

2.1 Error estimation

Let us consider three following functional spaces that are equipped with the standard norm for the theoretical analysis of the semi-discrete formulation: $\begin{matrix} H_{}^{1} (Ω) = \{v \in L^{2} (Ω), \frac{d v}{d x} \in L^{2} (Ω)\}, \\ H_{0}^{1} (Ω) = \{v \in H^{1} (Ω), v_{|_{\partial Ω}} = 0\}, \\ H^{m} (Ω) = \{v \in L^{2} (Ω), D^{β} v \in L^{2} (Ω), for all | β | ⩽ m\}, \end{matrix}$ where $L^{2} (Ω)$ represents the space of measurable functions in the bounded and open domain $Ω$ and $β = (β_{1}, \dots, β_{d})$ with $| β | = \sum_{i = 1}^{d} β_{i}$ . Moreover, let us define the operator $D^{β} v = \frac{\partial^{| β |} v}{\partial x_{1}^{β} \partial x_{2}^{β} \dots \partial x_{d}^{β}} \cdot$

The symbol $H^{m} (Ω)$ is Hilbert space with norm $∥ v ∥_{H^{m} (Ω)} = {(\sum_{| β | ⩽ m} ∥ D^{β} v ∥_{L^{2} (Ω)}^{2})}^{\frac{1}{2}} .$

In what follows, we introduce some useful notations concerning the stability and convergence of the numerical procedure.

Definition 1

(Liu et al., 2012) A finite difference algorithm is called to be stable for the norm $‖\cdot‖$ , if there exist two constants $C_{1} > 0$ and $C_{2} > 0$ , independent of $δ t$ , such that when $δ t$ approaches zero:

(9)

‖V^{k}‖ ⩽ C_{1} ‖V^{0}‖ + C_{2} ‖f‖,

where f and

V^{0}

represent the source term and the initial data, respectively.

Lemma 4

(Gao et al., 2015.) For the sequence ${V^{k}}$ ( $n ⩾ 2$ ) and $V^{k} \in L^{2} (Ω)$ , the following inequality holds: $\begin{matrix} F (V^{k}) = (3 - β) ∥ V^{k} ∥^{2} - (1 - β) ∥ V^{k - 1} ∥^{2} + (2 - \frac{β}{2}) (1 - β) ∥ V^{k} - V^{k - 1} ∥^{2} ⩾ \frac{2}{2 - β} ∥ V^{k} ∥^{2}, k ⩾ 2, \\ 〈 P_{t} V^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 ⩾ \frac{1}{4 τ} (F (V^{k}) - F (V^{k - 1})) . \end{matrix}$

Lemma 5

(Gao et al., 2015). If ${λ_{j}}_{j = 0}^{\infty}$ is introduced in the approximation (5), for any mesh series ${V^{j}}_{j = 0}^{M}$ , then we have

(10)

\sum_{k = 0}^{M} \sum_{j = 0}^{k} λ_{j} 〈V^{k - j}, V^{k}〉 ⩾ 0 .

Theorem 1

For $V^{k} \in H_{0}^{1} (Ω)$ , we have $∥ V^{k} ∥^{2} ⩽ C (∥ V^{0} ∥_{}^{2} + T \max_{0 ⩽ j ⩽ k} ∥ f^{j} ∥^{2}),$ where $C \in R^{+}$ .

Proof

Taking the inner product of Eq. (8) by $ν$ on domain $Ω$ , the variational weak formulation can be represented as:

(11)

\begin{matrix} 〈 P_{t}^{β} V^{k - \frac{β}{2}}, ν 〉 - τ^{- β} \sum_{j = 0}^{k} λ_{j} 〈 Δ V^{k - j - \frac{β}{2}}, ν 〉 - 〈 Δ V^{k - \frac{β}{2}}, ν 〉 + 〈 Δ^{2} V^{k - \frac{β}{2}}, ν 〉 \\ = 〈 f^{k - \frac{β}{2}}, ν 〉 + 〈 G (V^{k - \frac{β}{2}}), ν 〉 \cdot \end{matrix}

Using the divergence theorem, the aforesaid relation can be rewritten as follows:

(12)

\begin{matrix} 〈 P_{t}^{β} V^{k - \frac{β}{2}}, ν 〉 + τ^{- β} \sum_{j = 0}^{k} λ_{k} 〈 \nabla V^{k - j - \frac{β}{2}}, \nabla ν 〉 + 〈 \nabla V^{k - \frac{β}{2}}, \nabla ν 〉 + 〈 Δ V^{k - \frac{β}{2}}, Δ ν 〉 \\ = 〈 f^{k - \frac{β}{2}}, ν 〉 + 〈 G (V^{k - \frac{β}{2}}), ν 〉 \cdot \end{matrix}

Choosing $ν = τ V^{k - \frac{β}{2}}$ in Eq. (12), we get

(13)

\begin{matrix} τ 〈 P_{t}^{β} V^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 + τ^{- β + 1} \sum_{j = 0}^{k} λ_{j} 〈 \nabla V^{k - j - \frac{β}{2}}, \nabla V^{k - \frac{β}{2}} 〉 + τ 〈 \nabla V^{k - \frac{β}{2}}, \nabla V^{k - \frac{β}{2}} 〉 + τ 〈 Δ V^{k - \frac{β}{2}}, Δ V^{k - \frac{β}{2}} 〉 \\ = τ 〈 f^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 + τ 〈 G (V^{k - \frac{β}{2}}), V^{k - \frac{β}{2}} 〉 \cdot \end{matrix}

Summing relation (13) from $k = 0$ to M yields

(14)

\begin{matrix} τ \sum_{k = 0}^{M} 〈 P_{t}^{β} V^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 + τ^{- β + 1} \sum_{k = 0}^{M} \sum_{j = 0}^{k} λ_{j} 〈 \nabla V^{k - j - \frac{β}{2}}, \nabla V^{k - \frac{β}{2}} 〉 + τ \sum_{k = 0}^{M} 〈 \nabla V^{k - \frac{β}{2}}, \nabla V^{k - \frac{β}{2}} 〉 \\ + τ \sum_{k = 0}^{M} 〈 Δ V^{k - \frac{β}{2}}, Δ V^{k - \frac{β}{2}} 〉 = τ \sum_{k = 0}^{M} 〈 f^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 + τ \sum_{k = 0}^{M} 〈 G (V^{k - \frac{β}{2}}), V^{k - \frac{β}{2}} 〉 \cdot \end{matrix}

Applying Lemma 4, the relation (14) can be rewritten as

(15)

\begin{matrix} \frac{1}{4} [∥ V^{M} ∥^{2} - ∥ V^{0} ∥^{2}] + τ^{- β + 1} \sum_{k = 0}^{M} \sum_{j = 0}^{k} λ_{j} 〈 \nabla V^{k - j - \frac{β}{2}}, \nabla V^{k - \frac{β}{2}} 〉 + τ \sum_{k = 0}^{M} ∥ \nabla V^{k - \frac{β}{2}} ∥^{2} + τ \sum_{k = 0}^{M} ∥ Δ V^{k - \frac{β}{2}} ∥^{2} \\ = τ \sum_{k = 0}^{M} 〈 f^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 + τ \sum_{k = 0}^{M} 〈 G (V^{k - \frac{β}{2}}), V^{k - \frac{β}{2}} 〉 \cdot \end{matrix}

Meanwhile, by applying Lemma 5, we know that

(16)

τ^{- β + 1} \sum_{k = 0}^{M} \sum_{j = 0}^{k} λ_{j} 〈 \nabla V^{k - j - \frac{β}{2}}, \nabla V^{k - \frac{β}{2}} 〉 ⩾ 0 \cdot

The use of both Schwarz and Yang inequalities on the right hand side of Eq. (15) yields the following relation

(17)

\begin{matrix} τ \sum_{k = 0}^{M} 〈 f^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 + τ \sum_{k = 0}^{M} 〈 G^{k - \frac{β}{2}}, V^{k - \frac{β}{2}} 〉 ⩽ τ \sum_{k = 0}^{M} ∥ G (V^{k - \frac{β}{2}}) ∥ ∥ V^{k - \frac{β}{2}} ∥ + τ \sum_{k = 0}^{M} ∥ f^{k - \frac{β}{2}} ∥ ∥ V^{k - \frac{β}{2}} ∥ \\ ⩽ C τ [\sum_{k = 2}^{M} (∥ V^{k - 1} ∥^{2} + ∥ V^{k - 2} ∥^{2}) + \sum_{k = 2}^{M} (∥ f^{k} + f^{k - 1} ∥^{2})] \cdot \end{matrix}

Substituting inequality (17) into Eq. (15), considering the discrete Gronwall inequality, and dropping the nonnegative terms on the left hand side of Eq. (15), we arrive at $∥ V^{M} ∥^{2} ⩽ C (∥ V^{0} ∥^{2} + τ \sum_{k = 0}^{M} ∥ f^{k} ∥^{2}),$ that switching notation from M to k gives $\begin{matrix} ∥ V^{k} ∥^{2} ⩽ C (∥ V^{0} ∥^{2} + τ \sum_{j = 0}^{k} ∥ f^{j} ∥^{2}) ⩽ C (∥ V^{0} ∥_{}^{2} + k τ \max_{0 ⩽ j ⩽ k} ∥ f^{j} ∥^{2}) \\ ⩽ C (∥ V^{0} ∥_{}^{2} + T \max_{0 ⩽ j ⩽ k} ∥ f^{j} ∥^{2}) . \end{matrix}$

The proof is completed.

The next theorem concludes the convergence.

Theorem 2

Assume that $v^{k} \in H_{0}^{1} (Ω)$ and $V^{k} \in H_{0}^{1} (Ω)$ represent the analytic and approximate solutions of (7) and (8), respectively. Then time-discrete formulation (8) is convergent as the convergence rate is $O (τ^{2})$ .

Proof

Let us set $ρ^{k} = v^{k} - V^{k}$ at $t = t_{k}, k = 0, 1, \dots, M$ . Then, we can obtain the following weak formulation correspond to Eqs. (7) and (8) by:

(18)

\begin{matrix} 〈 P_{t}^{β} v^{k - \frac{β}{2}}, ν 〉 - τ^{- β} \sum_{j = 0}^{k} λ_{j} 〈 Δ v^{k - j - \frac{β}{2}}, ν 〉 - 〈 Δ v^{k - \frac{β}{2}}, ν 〉 + 〈 Δ^{2} v^{k - \frac{β}{2}}, ν 〉 = 〈 f^{k - \frac{β}{2}}, ν 〉 \\ + 〈 G (v^{k - \frac{β}{2}}), ν 〉 + 〈 R^{k - \frac{β}{2}}, ν 〉 \end{matrix}

and

(19)

\begin{matrix} 〈 P_{t}^{β} V^{k - \frac{β}{2}}, ν 〉 - τ^{- β} \sum_{j = 0}^{k} λ_{j} 〈 Δ V^{k - j - \frac{β}{2}}, ν 〉 - 〈 Δ V^{k - \frac{β}{2}}, ν 〉 + 〈 Δ^{2} V^{k - \frac{β}{2}}, ν 〉 = 〈 f^{k - \frac{β}{2}}, ν 〉 \\ + 〈 G (V^{k - \frac{β}{2}}), ν 〉 . \end{matrix}

Subtracting relation (18) from (19) yields

\begin{matrix} 〈 P_{t}^{β} ρ^{k - \frac{β}{2}}, ν 〉 - τ^{- β} \sum_{j = 0}^{k} λ_{j} 〈 Δ ρ^{k - j - \frac{β}{2}}, ν 〉 - 〈 Δ ρ^{k - \frac{β}{2}}, ν 〉 + 〈 Δ^{2} ρ^{k - \frac{β}{2}}, ν 〉 = 〈 G (v^{k - \frac{β}{2}}) - G (V^{k - \frac{β}{2}}), ν 〉 \\ + 〈 R^{k - \frac{β}{2}}, ν 〉 . \end{matrix}

If we set

ν = τ ρ^{k - \frac{1}{2}}

, then

(20)

\begin{matrix} τ 〈 P_{t}^{β} ρ^{k - \frac{β}{2}}, τ ρ^{k - \frac{1}{2}} 〉 - τ^{- β + 1} \sum_{j = 0}^{k} λ_{j} 〈 Δ ρ^{k - j - \frac{β}{2}}, τ ρ^{k - \frac{1}{2}} 〉 - τ 〈 Δ ρ^{k - \frac{β}{2}}, τ ρ^{k - \frac{1}{2}} 〉 + τ 〈 Δ^{2} ρ^{k - \frac{β}{2}}, τ ρ^{k - \frac{1}{2}} 〉 \\ = τ 〈 G (v^{k - \frac{β}{2}}) - G (V^{k - \frac{β}{2}}), τ ρ^{k - \frac{1}{2}} 〉 + τ 〈 R^{k - \frac{β}{2}}, τ ρ^{k - \frac{1}{2}} 〉 . \end{matrix}

In virtue of Theorem 1 and Eq. (20), and noticing that

ρ^{0} = 0

, we obtain

∥ ρ^{k} ∥^{2} ⩽ C τ \sum_{k = 0}^{M} ∥ R^{k - \frac{β}{2}} ∥^{2} = CT ∥ R^{k - \frac{β}{2}} ∥^{2} .

Therefore, we have

(21)

∥ ρ^{k} ∥ ⩽ C τ^{2} .

This finishes the proof.

3 The LRBF-FD methodology

By considering a distribution of N centers $X_{C} = {x_{1}^{c}, \dots, x_{N}^{c}} \subseteq R^{d}$ , the approximation solution of the unknown function $v (x)$ using a combination basis functions can be represented as:

(22)

v (x) ≃ S (x) = \sum_{j = 1}^{N} α_{j} ϕ_{j} (x, ε),

where

ε

denotes shape parameter and

ϕ_{j} (x, ε) = ϕ (‖ x - x_{j}^{c} ‖_{2}, ε), j = 1, \dots, N

, is a RBF corresponding the

j^{th}

center. The unknown linear combination coefficients

{α_{j}}_{j = 1}^{N}

, can be specified by exerting the interpolation conditions

S (x_{i}^{c}) = u_{i}^{c}, i = 1, \dots, N

. For special choices of radial basis function, it has been proved that the corresponding interpolation matrix

ϕ

is always nonsingular (Buhmann, 2003).

For approximating $L v (x)$ in a center node $x_{i}$ , Kansa (1990) adopted the linear partial differential operator on (22), so that

(23)

L v (x_{i}) ≃ \sum_{j = 1}^{N} α_{j} L ϕ_{j} (x_{i}, ε) .

The relation (23) implements a global RBF (GRBF) approximation since one needs all the domain points in order to approximate $L$ at one of the points. A local version of the technique was introduced more recently using the FD method. A disadvantage of the GRBF meshfree technique is the resulting ill-conditioned and dense matrices where each corresponds to a collocation point. In fact, the adoption of the GRBF is unfeasible because the corresponding matrices are dense for large problems. To solve this issue, several researchers proposed a novel technique named the LRBF-FD (Tolstykh and Shirobokov, 2003; Shu et al., 2003; Wright and Fornberg, 2006 ). The LRBF-FD is constructed by combining the RBF and FD methods. The LRBF-FD consists of a local meshfree approach, where the domain is discretized by computing a set of local differentiation matrices and joining them into a sparse system instead of inverting a full matrix. One considers only the neighbor nodes to obtain the differentiation matrix at each node. For this purpose, it is required to solve a small system of linear algebraic equation in each stencil with conditionally positive definite coefficient matrix.

We presume that $Ξ = {x_{1}, \dots, x_{N}} \subseteq R^{d}$ be a set of arbitrary points (centers) in the computational domain $Ω$ and the subset $S^{I} = {x_{1}^{(i)}, \dots, x_{N_{I}}^{(i)}} \subseteq Ξ$ be local-support domain involving $N_{I} - 1$ nearest neighboring centers, and define it as a stencil for every point $x_{(i)}$ . One must specify the index corresponding to the $N_{I}$ nearest neighbors for every point to determine the weighting coefficients needed to approximate an operator $L$ . The operator $L$ is evaluated at a center $x_{i}$ by using a weighted combination of the function values $v (x_{j}^{(i)})$ at all points within stencil of $x_{i}$ :

(24)

L v (x_{i}) ≃ \sum_{j = 1}^{N_{I}} w_{j}^{(i)} v (x_{j}^{(i)}) .

The LRBF-FD weights, ${w_{j}^{(i)}}_{j = 1}^{N_{I}}$ , is obtained by enforcing the linear constraint (24) and the RBF ${ϕ_{j} (x, ε)}_{j = 1}^{N_{I}}$ , centered at the stencil point locations $S^{I}$ (Tolstykh and Shirobokov, 2003; Shu et al., 2003; Wright and Fornberg, 2006 ), resulting

(25)

L ϕ_{k} (x_{i}, ε) = \sum_{j = 1}^{N_{I}} w_{j}^{(i)} ϕ_{j} (x_{k}, ε), k = 1, \dots, N_{I} .

This concludes to a the $N_{I} \times N_{I}$ linear system in the matrix form:

(26)

Φ w^{I} = {[L Φ]}^{I},

where

ϕ_{kj} = ϕ_{j} (x_{k}, ε), k, j = 1, \dots, N_{I}

, are the entries of the coefficient matrix

Φ

, the coefficients

w_{N_{I} \times 1}^{I} = {w_{j}^{(i)}}_{j = 1}^{N_{I}}

denotes the LRBF-FD stencil weights, and

{[L Φ]}_{N_{I} \times 1}^{I}

has the entries

L ϕ_{k} (x_{i}, ε), k = 1, \dots, N_{I}

. The LRBF-FD weights

w^{I}

at each stencil are determined as

(27)

w^{I} = Φ^{- 1} {[L Φ]}^{I} .

The concept of the LRBF-FD technique is similar to the one for the classical FD approximation. Nevertheless, one can employ the LRBF-FD technique for scattered points in more than one space dimensions. One calculates the FD weights ${w_{j}^{(i)}}_{j = 1}^{N_{I}}$ by polynomial basis functions, while in the LRBF-FD, one obtains the weights by applying an RBF interpolant to $N_{I}$ local support nodes for the neighbor of $x_{i}$ . Generally, the kd-tree can be achieved using the knnsearch function of the MATLAB. The calculation of the differential weight and the search of nearest-neighbor are the other two pre-processing operations required by the LRBF-FD.

4 Numerical illustration

This section implements the LRBF-FD in two prototype problems and examines the influence of several numerical values of the temporal and spatial steps. The temporal order of convergence $C_{τ}$ is computed with the help of the following formula $C_{τ} = \log_{2} (\frac{∥ L_{\infty} (2 τ, h) ∥}{∥ L_{\infty} (τ, h) ∥}),$ in which $L_{\infty} = \max_{1 ⩽ j ⩽ N - 1} | v (x_{j}, T) - v (x_{j}, T) |$ is the absolute error norm. The technique developed using Sarra (2012) is employed to calculate an optimal shape parameter.

The computational regions containing the uniform and Halton distribution (Fasshauer, 2007) displayed in Fig. 1 are considered in the follow-up. The domain $Ω_{1} = {[0, 1]}^{2}$ represents the rectangular domain with uniform nodes. The circumference of the domains $Ω_{2}$ and $Ω_{3}$ is formulated via $r (θ) = 1 + 1.2 \cos (θ) \sin^{2} (θ)$ and $r (θ) = \frac{1}{10} (8 + (\sin (6 θ) + \sin (3 θ))), 0 ⩽ θ ⩽ 2 π$ , with uniform and Halton nodes, respectively. The inner and outer boundaries of the domain $Ω_{4}$ are $r (θ) = \frac{1}{4}$ and $r (θ) = \frac{1}{2}$ including Halton nodes, respectively.

Example 1

We consider the following NTF4DP (Liu et al., 2015):

(28)

\begin{matrix} \frac{\partial v (x, y, t)}{\partial t} - \frac{\partial^{β} Δ v (x, y, t)}{\partial t^{β}} - Δ v (x, y, t) + Δ^{2} v (x, y, t) = - v^{2} (x, y, t) + [2 t + 8 π^{2} t^{2} + 64 π^{4} t^{2} \\ + \frac{16 π^{2} t^{2}}{Γ (3 - β)}] \sin (2 π x) \sin (2 π y) + t^{4} \sin^{2} (2 π x) \sin^{2} (2 π y), 0 < t ⩽ T (x, y) \in Ω, \end{matrix}

that has exact solution

v (x, y, t) = t^{2} \sin (2 π x) \sin (2 π y)

. The boundary and initial conditions can be achieved from it.

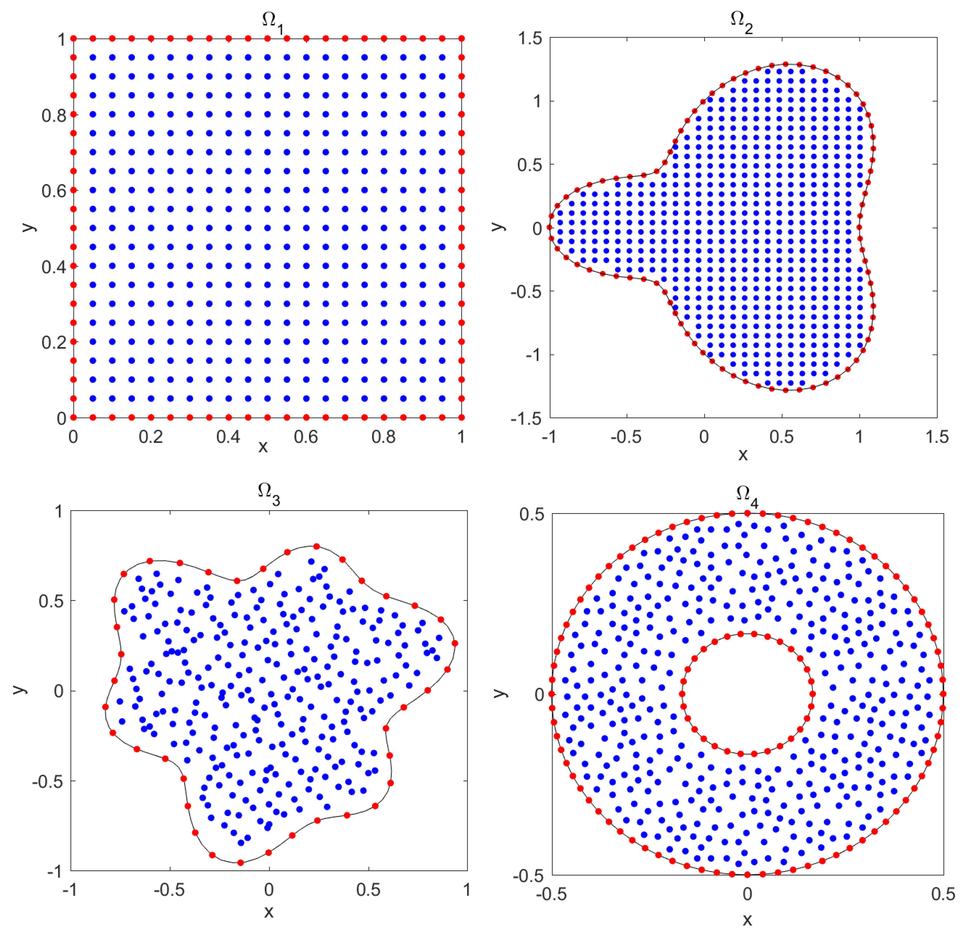
The used computational regions Ω 1 , Ω 2 , Ω 3 , Ω 4 .

The results are summarized in Tables 1–3 and Figs. 2–5 for different values of $τ, β$ and h on the regular and irregular domains. Table 1 illustrates the rate of convergence in the temporal direction and computational time (in seconds) at $T = 1$ on $Ω_{1}$ , and coincides with the outcome of Theorem 2. Table 2 shows the computational errors achieved using the proposed method on the considered domains with $τ = 1 / 200$ at various final times. Table 3 compares the errors $L_{2}$ of the proposed method with those obtained for other methods. These results confirm that the proposed method is in agreement with the method proposed in (Liu et al., 2015). Fig. 2 portraits the numerical solutions and computational errors considering $τ = 1 / 100, N = 256$ and $N_{I} = 81$ when $T \in {1, 3}$ on $Ω_{1}$ . Fig. 3 plots numerical solutions and computational errors by choosing $N = 325, N_{I} = 57$ and $τ = 1 / 400$ for $β \in {0.25, 0.95}$ when $T = 1$ on $Ω_{2}$ . Fig. 4 depicts the numerical solutions and computational errors by considering $τ = 1 / 400$ and $N = 381, N_{I} = 63$ for $β \in {0.45, 0.85}$ , when $T = 1$ on $Ω_{3}$ . Finally, Fig. 5 plots numerical solutions and computational errors by taking $β = 0.95, τ = 1 / 500$ and $N = 401, N_{I} = 97$ when $T \in {1, 3}$ on $Ω_{4}$ . From Figs. 3-5, we see clearly that the LRBF-FD is efficient in the case of irregular domains with uniform and non-uniform nodes.

Example 2

We consider the following NTF4DP:

(29)

\frac{\partial v (x, y, t)}{\partial t} - \frac{\partial^{β} Δ v (x, y, t)}{\partial t^{β}} - Δ v (x, y, t) + Δ^{2} v (x, y, t) - \sin (u) = 0,

with the initial and boundary conditions

(30)

v (x, y, 0) = 0, (x, y) \in Ω,

(31)

v (x, y, t) = Δ v (x, y, t) = 0, (x, y) \in \partial Ω, t > 0,

Table 1 Numerical convergence orders in time variable by letting

N = 256

Ω_{1} .

$τ$	$β = 0.6$		$β = 0.3$
	$L_{\infty}$	$C_{τ}$	$L_{\infty}$	$C_{τ}$	CPU (seconds)
$1 / 5$	$4.2354 e - 02$	–	$1.3711 e - 02$	–	$0.1817$
$1 / 10$	$1.3224 e - 02$	$1.6793$	$4.2069 e - 03$	$1.7797$	$0.2764$
$1 / 20$	$3.8415 e - 03$	$1.7834$	$1.1791 e - 03$	$1.8418$	$0.3210$
$1 / 40$	$1.1014 e - 04$	$1.8023$	$3.3160 e - 04$	$1.8479$	$0.4639$
$1 / 80$	$3.1040 e - 04$	$1.8271$	$9.1232 e - 05$	$1.9181$	$0.4705$
$1 / 160$	$8.1963 e - 05$	$1.9211$	$2.5165 e - 05$	$1.9288$	$0.7378$
$1 / 320$	$2.1125 e - 05$	$1.9560$	$6.4638 e - 06$	$1.9004$	$1.8255$
$1 / 640$	$5.3548 e - 06$	$1.9800$	$1.6513 e - 06$	$1.9422$	$3.5196$

Table 2 The error

L_{\infty}

by choosing

N = 225, N_{I} = 71

and

τ = 1 / 200

on the considered domains.

$β$	$T$	$Ω_{2}$	$Ω_{3}$	$Ω_{4}$
$0.55$
	$0.25$	$1.6446 e - 04$	$2.1025 e - 04$	$5.6209 e - 03$
	$0.50$	$2.5958 e - 04$	$4.2075 e - 04$	$1.3459 e - 02$
	$0.75$	$3.5230 e - 04$	$6.8986 e - 04$	$2.5360 e - 02$
	$1.00$	$4.4692 e - 04$	$8.0193 e - 04$	$4.0560 e - 02$

$0.45$
	$0.25$	$1.2212 e - 04$	$1.6237 e - 04$	$3.3032 e - 03$
	$0.50$	$1.6936 e - 04$	$3.1939 e - 04$	$1.0038 e - 02$
	$0.75$	$1.7577 e - 04$	$5.0395 e - 04$	$2.0519 e - 02$
	$1.00$	$1.9101 e - 04$	$7.1760 e - 04$	$3.4685 e - 02$

Table 3 Comparison between the error values

L_{2}

for scheme (Liu et al., 2015) and the LRBF-FD with

M = 2000

T = 0.1

Ω_{1} .

$β$	$h$	Liu et al. (2015)	LRBF-FD	CPU (seconds)
$0.01$
	$1 / 10$	$5.4985 e - 06$	$5.6147 e - 06$	$10.1668$
	$1 / 16$	$2.0573 e - 06$	$4.2664 e - 06$	$19.1081$
	$1 / 20$	$1.3019 e - 06$	$1.3970 e - 06$	$27.8290$

$0.3$
	$1 / 10$	$8.1459 e - 06$	$9.4420 e - 06$	$10.1668$
	$1 / 16$	$3.1715 e - 06$	$3.7221 e - 06$	$19.1081$
	$1 / 20$	$2.0283 e - 06$	$2.8510 e - 06$	$27.8290$

$0.99$
	$1 / 10$	$3.6315 e - 05$	$3.9164 e - 05$	$10.1668$
	$1 / 16$	$1.6353 e - 05$	$1.6504 e - 05$	$19.1081$
	$1 / 20$	$1.1427 e - 05$	$1.8008 e - 05$	$27.8290$

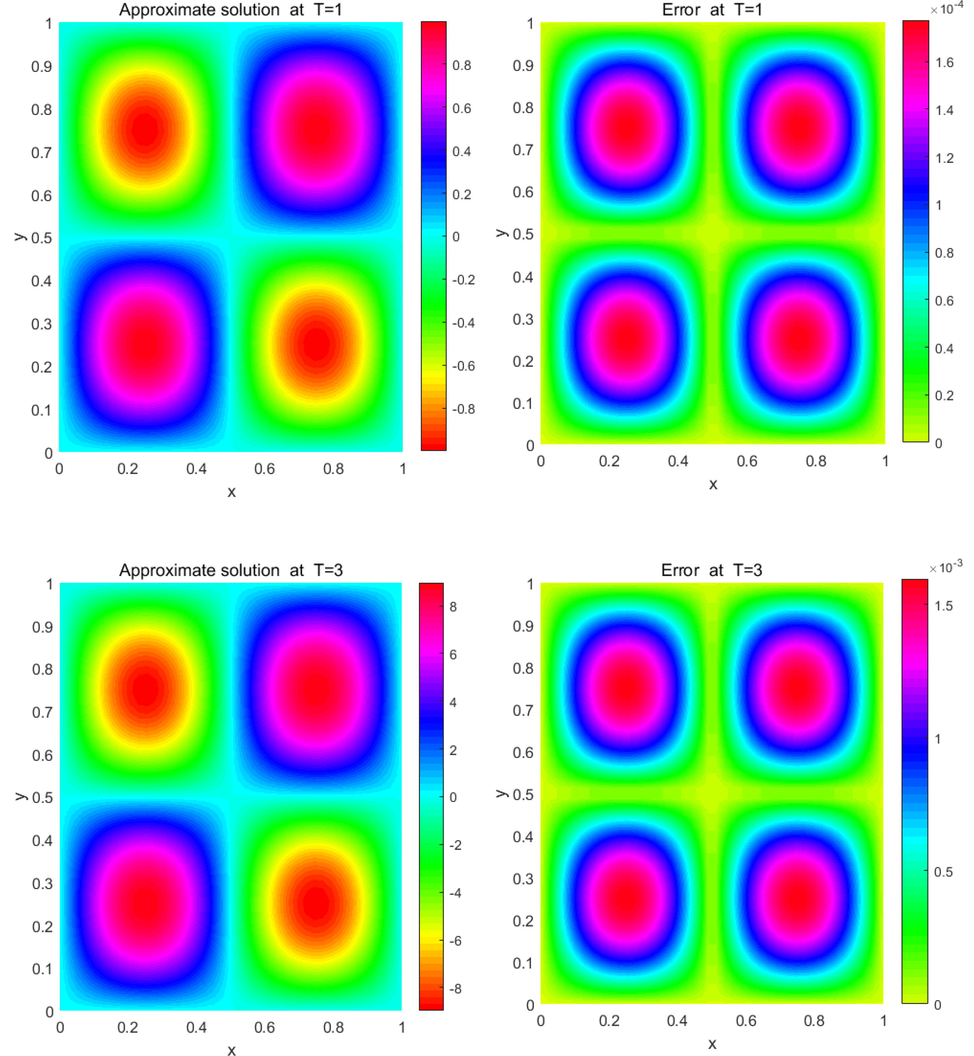
The numerical solutions of (28) and resulting errors on Ω 1 .

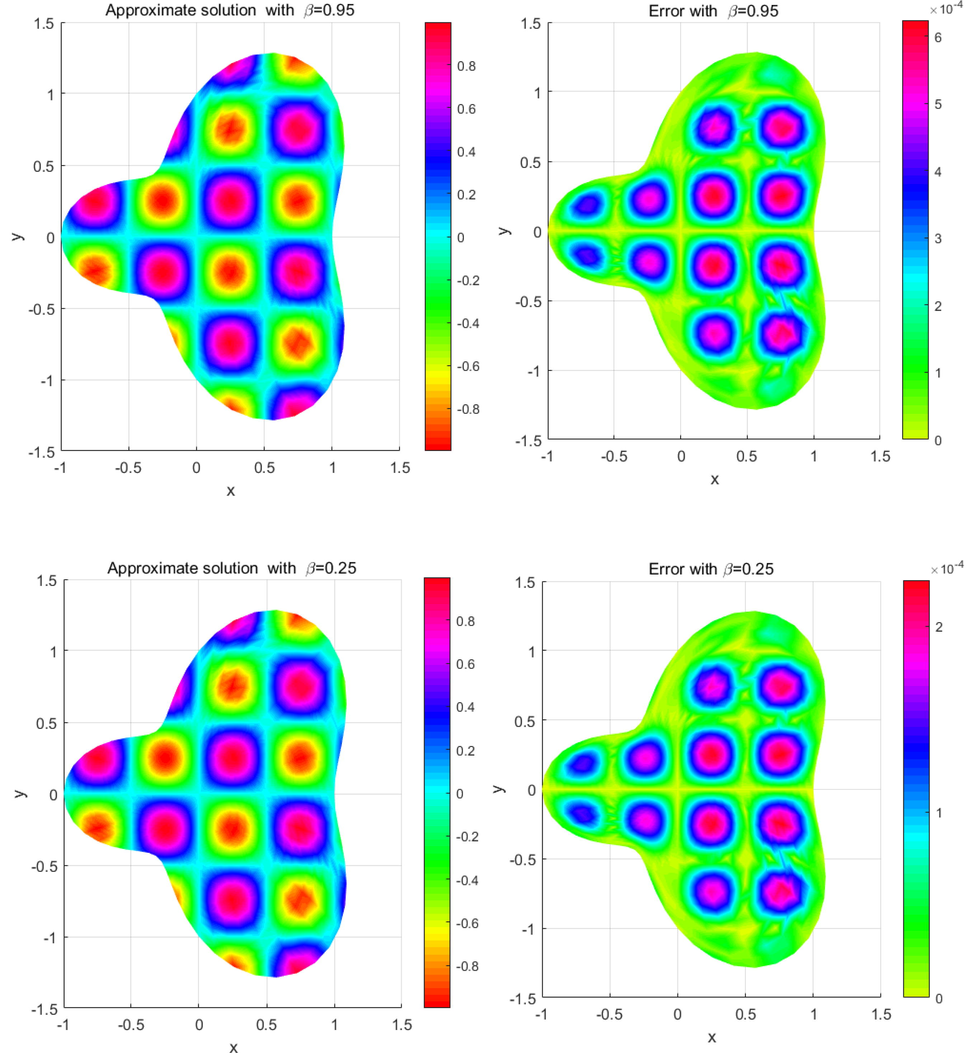
The numerical solutions of (28) and the resulting errors on Ω 2 .

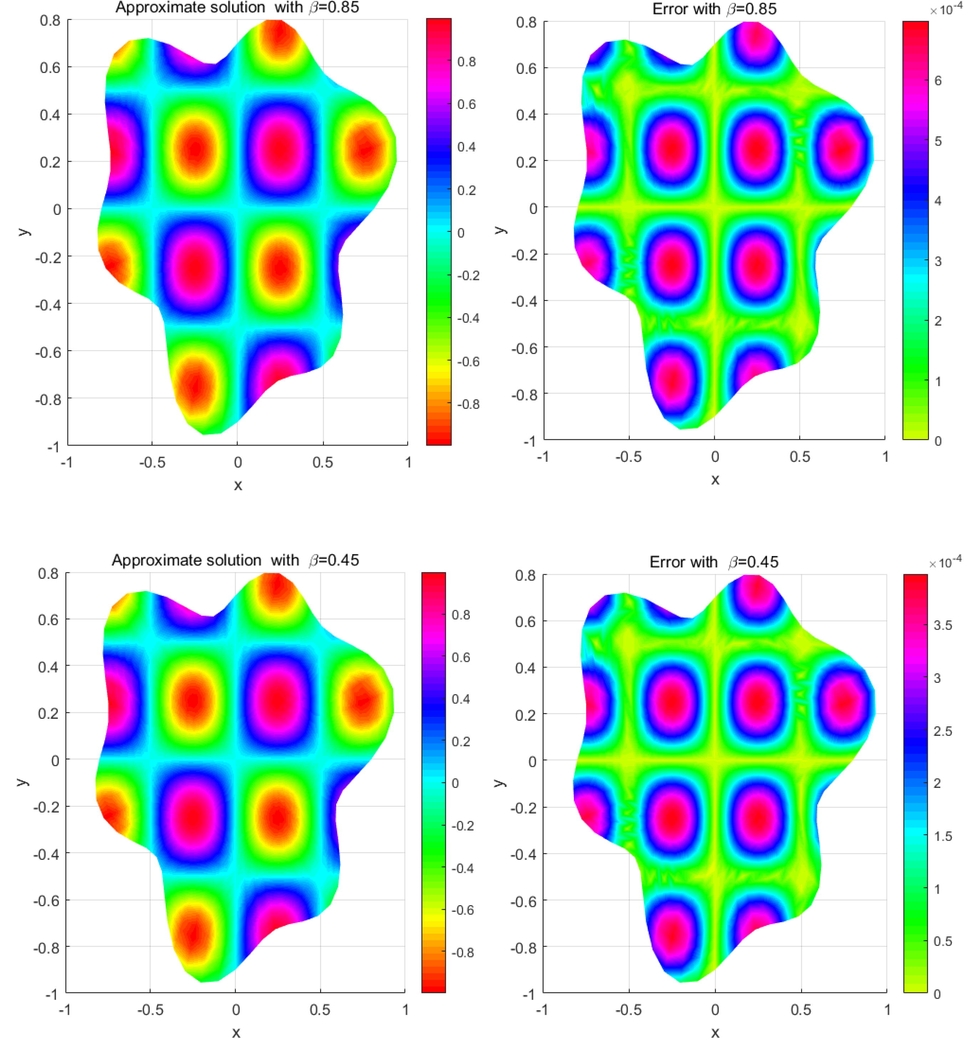
The numerical solutions of (28) and the resulting errors on Ω 3 .

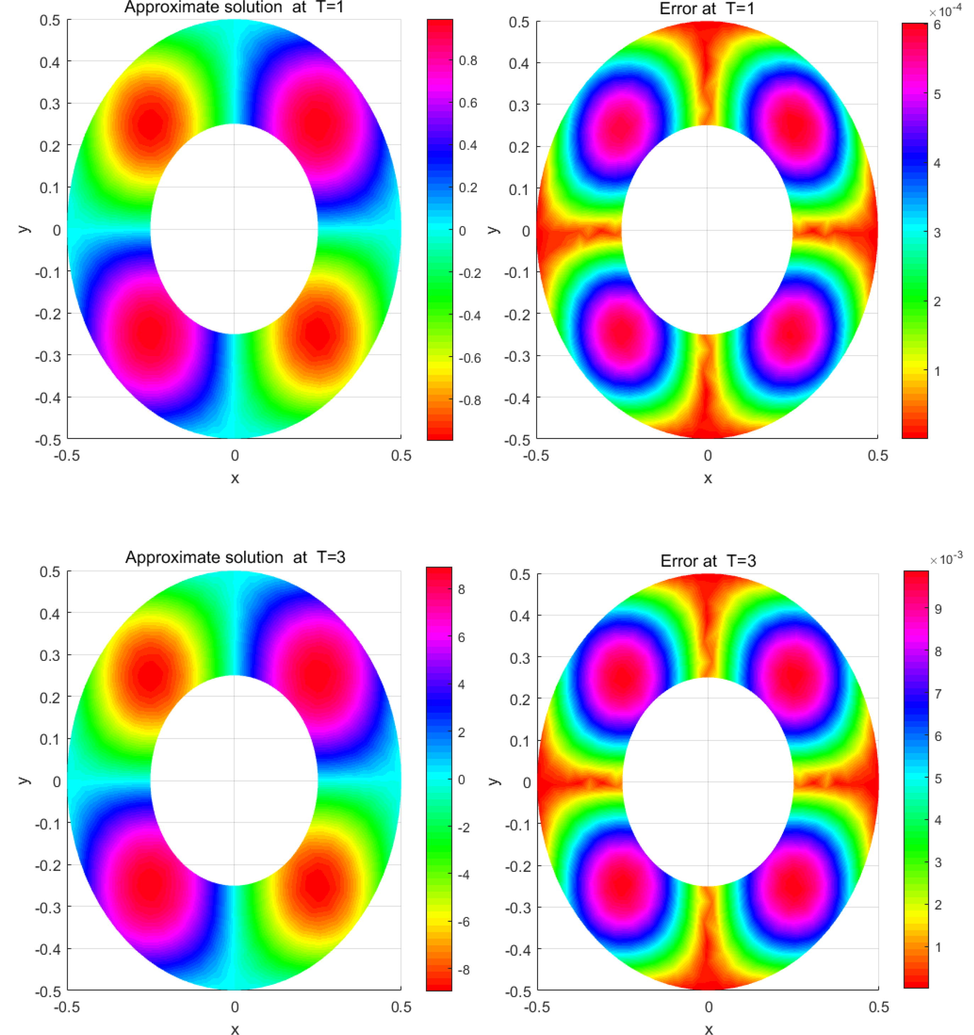
The numerical solutions of (28) and the resulting errors on Ω 4 .

We do not know the exact solution of (29). Hence, we use the relation proposed by (Tatari et al., 2011) for the convergence criterion of the solution:

(32)

E_{V}^{k} = \frac{∥ V^{k + 1} - V^{k} ∥}{∥ V^{k + 1} ∥} \cdot

Here, we evaluate the error at $τ$ as the difference between the solutions $V_{τ}$ and $V_{2 τ}$ at time steps $τ$ and $2 τ$ , which expressed by $E_{τ} = ∥ V_{τ} - V_{2 τ} ∥$ . The predictor–corrector procedure is used to determine the error in the spatial variable

(33)

E_{h_{1}, h_{2}} = ∥ V_{h_{1}} - V_{h_{2}} ∥,

where

V_{h_{1}}

and

V_{h_{2}}

are the approximate solutions corresponding to

h_{1}

and

h_{2}

, respectively. We calculate the spatial convergence rate as follows:

(34)

C_{h} = \log_{2} (\frac{E_{h, h / 2}}{E_{h / 2, h / 4}}),

with

E_{h, h / 2}

and

E_{h / 2, h / 4}

representing the absolute errors between the solutions with the size of mesh

\{h, h / 2\}

and

\{h / 2, h / 4\}

, respectively. Table 4 lists the error of

E_{V}^{k}

, the time convergence order and the computational time (in seconds). Table 5 shows the error of

E_{h_{1}, h_{2}}

, the computational time (in seconds) and the spatial convergence order by the predictor–corrector procedure.

Table 4 Numerical errors

E_{V}^{k}

and time convergence order

C_{τ}

by letting

h = 1 / 15

Ω_{1}

T = 1 .

$τ$	$β = 0.85$		$β = 0.15$
	$E_{V}^{k}$	$C_{τ}$	$E_{V}^{k}$	$C_{τ}$	CPU (seconds)
$1 / 10$	$5.1849 e - 01$	–	$1.7713 e - 01$	–	0.4022
$1 / 20$	$1.4048 e - 01$	$1.3059$	$7.9959 e - 02$	$1.1475$	0.8435
$1 / 40$	$3.5152 e - 02$	$1.3854$	$2.8839 e - 03$	$1.4712$	1.0435
$1 / 80$	$8.1838 e - 03$	$1.4575$	$1.0589 e - 03$	$1.4455$	1.5236

Table 5 Numerical errors

E_{h_{1}, h_{2}}

and spatial convergence order

C_{h}

with

τ = 1 / 50

Ω_{1}

T = 1 .

$h$	$β = 0.75$		$β = 0.25$
	$E_{h_{1}, h_{2}}$	$C_{h}$	$E_{h_{1}, h_{2}}$	$C_{h}$	CPU (seconds)
$2 / 4, 2 / 8$	$2.0543 e - 01$	–	$1.2121 e - 01$	–	1.1217
$2 / 8, 2 / 16$	$8.5635 e - 02$	$1.2624$	$6.0682 e - 02$	$0.9982$	1.9749
$2 / 16, 2 / 32$	$2.6329 e - 02$	$1.7015$	$2.1378 e - 02$	$1.5051$	3.1690

5 Conclusion

This paper considered a local meshless RBF to obtain the approximate solution of the NTF4DP. Some computational approaches have an high-order numerical accuracy, but they cannot be implemented on complex domains. For handling that case, one can use a number of these approaches for complex domains, but they do not have good accuracy. Given these facts, we present a local meshfree technique based on LRBF-FD. This technique has good accuracy and can be adopted in the case of domains with complex shapes. The new approach includes of two phases. First, a weighted discrete algorithm implementing a second-order formulation is applied to approximate the temporal derivative terms. Second, the LRBF-FD discretization is applied to discrete space. The time-discrete scheme is unconditionally stable and convergent. The numerical results illustrate the good performance of the LRBF-FD proving to be consistent with the theoretical formulation. In the future, the approximation solution for the nonlinear modified time-factional fourth-order diffusion equation will be developed and analyzed.

Acknowledgements

The authors are very grateful to the anonymous referees and the editor for useful comments that led to a great improvement of the paper.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Buhmann M.D., . Radial basis functions: theory and implementations. Vol vol. 12. Cambridge University Press; 2003.
Buhmann M.D., Micchelli C.A., . Multiquadric interpolation improved. Comput. Math. Appl.. 1992;24(12):21-25.
[Google Scholar]
Chui C.K., Stöckler J., Ward J.D., . Analytic wavelets generated by radial functions. Adv. Comput. Math.. 1996;5(1):95-123.
[Google Scholar]
Du Y., Liu Y., Li H., Fang Z., He S., . Local discontinuous Galerkin method for a nonlinear time-fractional fourth-order partial differential equation. J. Comput. Phys.. 2017;344:108-126.
[Google Scholar]
Fasshauer G.E., . Meshfree Approximation Methods with Matlab. Vol vol. 6. World Scientific Publishing Company; 2007.
Franke C., Schaback R., . Convergence order estimates of meshless collocation methods using radial basis functions. Adv. Comput. Math.. 1998;8(4):381-399.
[Google Scholar]
Franke R., . Scattered data interpolation: tests of some methods. Math. Comput.. 1982;38(157):181-200.
[Google Scholar]
Franke R., . Recent advances in the approximation of surfaces from scattered data. In: Topics in multivariate approximation. Elsevier; 1987. p. :79-98.
[Google Scholar]
Gao G.H., Sun H.W., Sun Z.Z., . Stability and convergence of finite difference schemes for a class of time-fractional sub-diffusion equations based on certain superconvergence. J. Comput. Phys.. 2015;280:510-528.
[Google Scholar]
Hardy R.L., . Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res.. 1971;76(8):1905-1915.
[Google Scholar]
Kansa E.J., . Multiquadrics–a scattered data approximation scheme with applications to computational fluid-dynamics–i surface approximations and partial derivative estimates. Comput. Math. Appl.. 1990;19(8–9):127-145.
[Google Scholar]
Li C., Cai M., . Theory and numerical approximations of fractional integrals and derivatives. SIAM; 2019.
Liu F., Zhuang P., Burrage K., . Numerical methods and analysis for a class of fractional advection–dispersion models. Comput. Math. Appl.. 2012;64(10):2990-3007.
[Google Scholar]
Liu G.R., Gu Y.T., . An introduction to meshfree methods and their programming. Springer Science & Business Media; 2005.
Liu N., Liu Y., Li H., Wang J., . Time second-order finite difference/finite element algorithm for nonlinear time-fractional diffusion problem with fourth-order derivative term. Comput. Math. Appl.. 2018;75(10):3521-3536.
[Google Scholar]
Liu Y., Du Y., Li H., He S., Gao W., . Finite difference/finite element method for a nonlinear time-fractional fourth-order reaction–diffusion problem. Comput. Math. Appl.. 2015;70(4):573-591.
[Google Scholar]
Liu Y., Du Y., Li H., Li J., He S., . A two-grid mixed finite element method for a nonlinear fourth-order reaction–diffusion problem with time-fractional derivative. Comput. Math. Appl.. 2015;70(10):2474-2492.
[Google Scholar]
Liu Y., Fang Z., Li H., He S., . A mixed finite element method for a time-fractional fourth-order partial differential equation. Appl. Math. Comput.. 2014;243:703-717.
[Google Scholar]
Madych W., Nelson S., . Multivariate interpolation and conditionally positive definite functions. ii. Math. Comput.. 1990;54(189):211-230.
[Google Scholar]
Micchelli C.A., . Interpolation of scattered data: distance matrices and conditionally positive definite functions. In: Approximation theory and spline functions. Springer; 1984. p. :143-145.
[Google Scholar]
Oldham K.B., Spanier J., . The Fractional Calculus 1974 111 of Mathematics in science and engineering
Podlubny I., . Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Vol vol. 198. Elsevier; 1998.
Sarra S.A., . A local radial basis function method for advection–diffusion–reaction equations on complexly shaped domains. Appl. Math. Comput.. 2012;218(19):9853-9865.
[Google Scholar]
Schaback R., . Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math.. 1995;3(3):251-264.
[Google Scholar]
Shu C., Ding H., Yeo K., . Local radial basis function-based differential quadrature method and its application to solve two-dimensional incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng.. 2003;192(7–8):941-954.
[Google Scholar]
Singh H., . Operational matrix approach for approximate solution of fractional model of Bloch equation. J. King Saud Univ.-Sci.. 2017;29(2):235-240.
[Google Scholar]
Singh H., Akhavan Ghassabzadeh F., Tohidi E., Cattani C., . Legendre spectral method for the fractional Bratu problem. Math. Methods Appl. Sci.. 2020;43(9):5941-5952.
[Google Scholar]
Singh H., Pandey R.K., Srivastava H.M., . Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics. 2019;7(3):224.
[Google Scholar]
Singh H., Srivastava H., . Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl. Sci.. 2020;10(8):2850.
[Google Scholar]
Tatari M., Kamranian M., Dehghan M., . The finite point method for reaction-diffusion systems in developmental biology. Comput. Modeling Eng. Sci. (CMES). 2011;82(1):1-27.
[Google Scholar]
Tian W., Zhou H., Deng W., . A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput.. 2015;84(294):1703-1727.
[Google Scholar]
Tolstykh A., Shirobokov D., . On using radial basis functions in a finite difference mode with applications to elasticity problems. Comput. Mech.. 2003;33(1):68-79.
[Google Scholar]
Vong S., Wang Z., . A high-order compact scheme for the nonlinear fractional Klein-Gordon equation. Numer. Methods Partial Differ. Eqs.. 2015;31(3):706-722.
[Google Scholar]
Wang Y., Liu Y., Li H., Wang J., . Finite element method combined with second-order time discrete scheme for nonlinear fractional cable equation. Eur. Phys. J. Plus. 2016;131(3):61.
[Google Scholar]
Wright G.B., Fornberg B., . Scattered node compact finite difference-type formulas generated from radial basis functions. J. Comput. Phys.. 2006;212(1):99-123.
[Google Scholar]
Zaky M.A., . A Legendre spectral quadrature tau method for the multi-term time-fractional diffusion equations. Comput. Appl. Math.. 2018;37(3):3525-3538.
[Google Scholar]
Zaky M.A., . An improved tau method for the multi-dimensional fractional Rayleigh-Stokes problem for a heated generalized second grade fluid. Comput. Math. Appl.. 2018;75(7):2243-2258.
[Google Scholar]
Zaky M.A., Hendy A.S., Macías-Díaz J.E., . Semi-implicit Galerkin-Legendre spectral schemes for nonlinear time-space fractional diffusion–reaction equations with smooth and nonsmooth solutions. J. Sci. Comput.. 2020;82(1):1-27.
[Google Scholar]
Zaky M.A., Machado J.T., . On the formulation and numerical simulation of distributed-order fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul.. 2017;52:177-189.
[Google Scholar]
Zaky M.A., Machado J.T., . Multi-dimensional spectral tau methods for distributed-order fractional diffusion equations. Comput. Math. Appl.. 2020;79(2):476-488.
[Google Scholar]

Introduction

Time-discrete formulation

Error estimation

The LRBF-FD methodology

Numerical illustration

Conclusion

Fulltext Views
32

PDF downloads
30

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Buhmann M.D., . Radial basis functions: theory and implementations. Vol vol. 12. Cambridge University Press; 2003.

[2] Buhmann M.D., Micchelli C.A., . Multiquadric interpolation improved. Comput. Math. Appl.. 1992;24(12):21-25.
[Google Scholar]

[3] Chui C.K., Stöckler J., Ward J.D., . Analytic wavelets generated by radial functions. Adv. Comput. Math.. 1996;5(1):95-123.
[Google Scholar]

[4] Du Y., Liu Y., Li H., Fang Z., He S., . Local discontinuous Galerkin method for a nonlinear time-fractional fourth-order partial differential equation. J. Comput. Phys.. 2017;344:108-126.
[Google Scholar]

[5] Fasshauer G.E., . Meshfree Approximation Methods with Matlab. Vol vol. 6. World Scientific Publishing Company; 2007.

[6] Franke C., Schaback R., . Convergence order estimates of meshless collocation methods using radial basis functions. Adv. Comput. Math.. 1998;8(4):381-399.
[Google Scholar]

[7] Franke R., . Scattered data interpolation: tests of some methods. Math. Comput.. 1982;38(157):181-200.
[Google Scholar]

[8] Franke R., . Recent advances in the approximation of surfaces from scattered data. In: Topics in multivariate approximation. Elsevier; 1987. p. :79-98.
[Google Scholar]

[9] Gao G.H., Sun H.W., Sun Z.Z., . Stability and convergence of finite difference schemes for a class of time-fractional sub-diffusion equations based on certain superconvergence. J. Comput. Phys.. 2015;280:510-528.
[Google Scholar]

[10] Hardy R.L., . Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res.. 1971;76(8):1905-1915.
[Google Scholar]

[11] Kansa E.J., . Multiquadrics–a scattered data approximation scheme with applications to computational fluid-dynamics–i surface approximations and partial derivative estimates. Comput. Math. Appl.. 1990;19(8–9):127-145.
[Google Scholar]

[12] Li C., Cai M., . Theory and numerical approximations of fractional integrals and derivatives. SIAM; 2019.

[13] Liu F., Zhuang P., Burrage K., . Numerical methods and analysis for a class of fractional advection–dispersion models. Comput. Math. Appl.. 2012;64(10):2990-3007.
[Google Scholar]

[14] Liu G.R., Gu Y.T., . An introduction to meshfree methods and their programming. Springer Science & Business Media; 2005.

[15] Liu N., Liu Y., Li H., Wang J., . Time second-order finite difference/finite element algorithm for nonlinear time-fractional diffusion problem with fourth-order derivative term. Comput. Math. Appl.. 2018;75(10):3521-3536.
[Google Scholar]

[16] Liu Y., Du Y., Li H., He S., Gao W., . Finite difference/finite element method for a nonlinear time-fractional fourth-order reaction–diffusion problem. Comput. Math. Appl.. 2015;70(4):573-591.
[Google Scholar]

[17] Liu Y., Du Y., Li H., Li J., He S., . A two-grid mixed finite element method for a nonlinear fourth-order reaction–diffusion problem with time-fractional derivative. Comput. Math. Appl.. 2015;70(10):2474-2492.
[Google Scholar]

[18] Liu Y., Fang Z., Li H., He S., . A mixed finite element method for a time-fractional fourth-order partial differential equation. Appl. Math. Comput.. 2014;243:703-717.
[Google Scholar]

[19] Madych W., Nelson S., . Multivariate interpolation and conditionally positive definite functions. ii. Math. Comput.. 1990;54(189):211-230.
[Google Scholar]

[20] Micchelli C.A., . Interpolation of scattered data: distance matrices and conditionally positive definite functions. In: Approximation theory and spline functions. Springer; 1984. p. :143-145.
[Google Scholar]

[21] Oldham K.B., Spanier J., . The Fractional Calculus 1974 111 of Mathematics in science and engineering

[22] Podlubny I., . Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Vol vol. 198. Elsevier; 1998.

[23] Sarra S.A., . A local radial basis function method for advection–diffusion–reaction equations on complexly shaped domains. Appl. Math. Comput.. 2012;218(19):9853-9865.
[Google Scholar]

[24] Schaback R., . Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math.. 1995;3(3):251-264.
[Google Scholar]

[25] Shu C., Ding H., Yeo K., . Local radial basis function-based differential quadrature method and its application to solve two-dimensional incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng.. 2003;192(7–8):941-954.
[Google Scholar]

[26] Singh H., . Operational matrix approach for approximate solution of fractional model of Bloch equation. J. King Saud Univ.-Sci.. 2017;29(2):235-240.
[Google Scholar]

[27] Singh H., Akhavan Ghassabzadeh F., Tohidi E., Cattani C., . Legendre spectral method for the fractional Bratu problem. Math. Methods Appl. Sci.. 2020;43(9):5941-5952.
[Google Scholar]

[28] Singh H., Pandey R.K., Srivastava H.M., . Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics. 2019;7(3):224.
[Google Scholar]

[29] Singh H., Srivastava H., . Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl. Sci.. 2020;10(8):2850.
[Google Scholar]

[30] Tatari M., Kamranian M., Dehghan M., . The finite point method for reaction-diffusion systems in developmental biology. Comput. Modeling Eng. Sci. (CMES). 2011;82(1):1-27.
[Google Scholar]

[31] Tian W., Zhou H., Deng W., . A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput.. 2015;84(294):1703-1727.
[Google Scholar]

[32] Tolstykh A., Shirobokov D., . On using radial basis functions in a finite difference mode with applications to elasticity problems. Comput. Mech.. 2003;33(1):68-79.
[Google Scholar]

[33] Vong S., Wang Z., . A high-order compact scheme for the nonlinear fractional Klein-Gordon equation. Numer. Methods Partial Differ. Eqs.. 2015;31(3):706-722.
[Google Scholar]

[34] Wang Y., Liu Y., Li H., Wang J., . Finite element method combined with second-order time discrete scheme for nonlinear fractional cable equation. Eur. Phys. J. Plus. 2016;131(3):61.
[Google Scholar]

[35] Wright G.B., Fornberg B., . Scattered node compact finite difference-type formulas generated from radial basis functions. J. Comput. Phys.. 2006;212(1):99-123.
[Google Scholar]

[36] Zaky M.A., . A Legendre spectral quadrature tau method for the multi-term time-fractional diffusion equations. Comput. Appl. Math.. 2018;37(3):3525-3538.
[Google Scholar]

[37] Zaky M.A., . An improved tau method for the multi-dimensional fractional Rayleigh-Stokes problem for a heated generalized second grade fluid. Comput. Math. Appl.. 2018;75(7):2243-2258.
[Google Scholar]

[38] Zaky M.A., Hendy A.S., Macías-Díaz J.E., . Semi-implicit Galerkin-Legendre spectral schemes for nonlinear time-space fractional diffusion–reaction equations with smooth and nonsmooth solutions. J. Sci. Comput.. 2020;82(1):1-27.
[Google Scholar]

[39] Zaky M.A., Machado J.T., . On the formulation and numerical simulation of distributed-order fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul.. 2017;52:177-189.
[Google Scholar]

[40] Zaky M.A., Machado J.T., . Multi-dimensional spectral tau methods for distributed-order fractional diffusion equations. Comput. Math. Appl.. 2020;79(2):476-488.
[Google Scholar]

An efficient local meshless approach for solving nonlinear time-fractional fourth-order diffusion model

Abstract

Keywords

Nonlinear time-fractional fourth-order diffusion problem

Radial basis function

Finite difference scheme

Convergence and stability

1 Introduction

2 Time-discrete formulation

2.1 Error estimation

3 The LRBF-FD methodology

4 Numerical illustration

5 Conclusion

Acknowledgements

Declaration of Competing Interest

References

Suggested read for related articles: