An efficient approach for fractional nonlinear chaotic model with Mittag-Leffler law
⁎Corresponding authors at: Department of Physics, College of Sciences, University of Bisha, P.O. Box 344, Bisha 61922, Saudi Arabia (A.–H. Abdel-Aty). amabdelaty@ub.edu.sa (Abdel-Haleem Abdel-Aty), skiitbhu28@gmail.com (Sunil Kumar)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this work, we exemplify the behaviour of the nonlinear model of arbitrary order differential equations by adopting
Keywords
Homotopy analysis method
AB derivative
Chaotic system
Laplace transform
Fixed point theorem
1 Introduction
The theory and applications of arbitrary order derivative recently magnetise the attention of many young researchers even though it was originated in Newton’s time. Fractional calculus is the most influential apparatus from the last few decades to examine and exemplify the nonlinear complex phenomena, due to the auspicious assets namely, memory effect, nonlocality, analyticity and hereditary. Within the frame of FC, the most simulating leaps in science, technology and their associated areas have been arises. The fractional differential operators accomplished to exemplify the necessary development of the nonlinear phenomena having a diffusion mechanism. Many scholars begin to investigate on the FC with fundamentals and its applications due to the progress of a mathematical algorithm. The diverse definitions are anticipated by numerous pioneering for fractional calculus, and which prearranged the groundwork for FC (Liouville, 1832; Riemann, 1896; Caputo, 1969; Miller and Ross, 1993; Podlubny, 1999; Kilbas et al., 2006). The fundamental theory and applications of FC are widely illustrated in various aspects with emerging phenomena like nanotechnology (Baleanu et al., 2010), chaos theory (Esen et al., 2018), human diseases (Veeresha et al., 2019), optics (Baleanu et al., 2017), and other fields (Veeresha et al., 2019a, 2020b, 2019c; Gao, 2020). Particularly, mathematical models exemplifying diverse phenomena are analysed by the aid of notions and fundamentals of FC, for instance authors in (Singh and Srivastava, 2020) studied Liénard and D uffing equation arising in oscillating circuit theory and presented the numerical stimulation within the frame of arbitrary order calculus, the epidemiological model of the Ebola virus is analysed by Srivastava et al. in (Srivastava et al., 2020) with the help of spectral collocation technique, the behaviour of the solution achieved for arbitrary-order Drinfeld-Sokolov-Wilson system is captured by authors in (Srivastava and Saad, 2020), Singh and his co-authors derived numerical solution for arbitrary-order Bloch equation by adopting the Jacobi polynomials (Singh and Srivastava, 2020), the overview and recent developments are effectively illustrated by senior and emeritus scholar in (Srivastava, 2020), new mathematical models of the human immune against IAV infection is nurtured within the frame of arbitrary order calculus by authors in (Srivastava et al., 2020), and researchers in (Izadi and Srivastava, 2020) presented few stimulating results with respect to nonlinear arbitrary order logistic equation by using an discretization approach.
Nowadays, there is a tremendous fascination towards the study of nonlinear dynamics, particularly chaos and fractals. Dynamics is the subject that deals with changes and systems that evolve in time. This subject originated in the mid of 1600s when Newton invented DEs. Particularly, the theory of chaos magnetized the attention of many scientists and engineers due to the discovery of the Lorenz attractor (Lorenz, 1963) and the innovation of high-speed computers. In has been proven that, chaotic signal play a vibrant role in the chaos-based information systems, and is used for the control processing and secure communication. In addition to this, authors in (Grigorenko and Grigorenko, 2003; Hammouch and Mekkaoui, 2014; Baskonus et al., 2015) demonstrated the essence of fractional order with chaos system in order to study the various physical phenomena and capture the behaviour of nature in an effective and systematic manner.
The chaotic nature of the systems is the emerging and interesting topic in the recent era. It has been studied and analysed by many senior scholars in order to illustrate the many interesting and emerging consequences arisen in diverse areas. In connection with this, authors in (Owolabi and Atangana, 2018) capture the chaotic behaviour of some fractional-order system, authors in (Bhalekar et al., 2012) illustrated the chaotic nature of Bloch equations which address the key issue in NMR relaxation problem, authors in Daftardar-Gejji et al. (2012) presented the chaotic dynamics of Chen system having fractional order.
Many nonlinear interesting phenomena arisen in related fields of science and engineering are systematically and effectively demonstrated using fractional calculus. Many pioneers defined the diverse notions for arbitrary order differential and integral. However, each definition has its own limitation. The Riemann–Liouville derivative fails to define the importance of the ICs, the Liouville-Caputo fractional operator is not related to describe singular kernel. Later Caputo and Fabrizio in 2015 overcome these limitations (Caputo and Fabrizio, 2015), and soon after many researchers applied to analyse and illustrate some stimulating nature for complex models. Recently, some authors raised some issues associated with important properties exemplifying the behaviour of nonlinear problems like non-singular kernel and non-local. In 2016, Atangana and Baleanu proposed definition with the assist of Mittag–Leffler functions, namely Atangana-Baleanu (AB) derivative (Atangana and Baleanu, 2016) and which get huge attention of the research community.
We assume the model of the equation which described the chaotic nature studied by Hammouch and Mekkaoui (Hammouch and Mekkaoui, 2018):
Authors in (Hammouch and Mekkaoui, 2018) suggested the simulation for the arbitrary order system with Caputo derivative which poses the interesting chaotic behaviour by the aid of Adams–Bashforth–Moulton scheme and also they demonstrated the circuit design. In this work, we consider with AB derivative to include non-singular kernel and non-local, and which as follows
In the last few decades, many advanced methods are proposed by mathematicians and physicist to examine the differential and integral equations. In this connection, Liao Shijun defined the homotopy analysis technique (Liao, 1997, 1998). It has advantageously and efficiently considered evaluating the solution for nonlinear problems. But, there is an essence of the amalgamation of this algorithm and classical transform methods. Since this method requires more computer memory and huge time for calculation work.
In this present investigation, we exemplified and evaluate the solution for the arbitrary order system describes the interesting chaotic behaviour by the help of
The suggested algorithm will reduce vast mathematical computations. The projected solution procedure is recently many researchers considered in to exemplify the behaviour of many classes of nonlinear and complex systems (Srivastava et al., 2017; Veeresha et al., 2020, 2019; Gao, 2020; Veeresha and Prakasha, 2019, 2020; Kumar et al., 2018; Prakasha and Veeresha, 2020; Kiran, 2020). Moreover, it cogently encompasses the consequences of various classical techniques such as HPM, RDTM, Adomian decomposition method and
2 Preliminaries
We present the essential definitions of Laplace transform (LT) and FC (Singh et al., 2018; Veeresha et al., 2020; Atangana and Alkahtani, 2015, 2016; Prakasha et al., 2020).
For a function
For a
The arbitrary order AB integral presented as
The Laplace transform (LT) with AB operator is described as
For the Riemann-Liouville and AB derivatives, the subsequent Lipschitz conditions respectively satisfy (Grigorenko and Grigorenko, 2003)
and
The arbitrary order DEs
3 Solution for considered system with suggested method
In this segment, we illustrate the efficiency of the suggested algorithm to find the solution for a considered arbitrary-order nonlinear chaotic system. Moreover, we capture the behaviour of the achieved results. Now, we have by the aid of Eq. (2), we have
associated to
Using the Eq. (11) after applying LT on Eq. (10), one can have
Now,
At
where
The Eq. (14) simplifies after employing inverse LT, as follows
On clarifying the Eq. (16) with
4 Existence of solutions
Now, we consider the system (10) to illustrate the existence of the solution as follows:
By the help of Theorem 2, the above model transformed to the Volterra integral equation and we have
The kernel
Now, we consider
where
Therefore, the Lipschitz condition is attained for
The recursive form of Eq. (19) described as follows
The associated initial conditions are
The successive difference between the terms is described as
Clearly
By using Eq. (21) after employing the norm on the
In the same manner, we have
With the assist of forgoing theorem, we find the following result:
If we have particular
for
Let
Therefore, which show the existence and continuity for the attained solutions. In order to verify the system (29) is a solution for the model (10), we begin with
Now, we consider
Similarly at
From Eq. (32) we can observer that, as
Now, we present the uniqueness of the obtained solution. Suppose
the Eq. (33) reduces with the assist of the norm, to
With the assist of the above relation, one can get
By the aid of forgoing relation, we can see that
Hence, Eq. (53) evidences our essential result.
5 Results and discussion
In this paper, we applied an analytical technique in order to capture the chaotic nature of the projected fractional dynamical system using
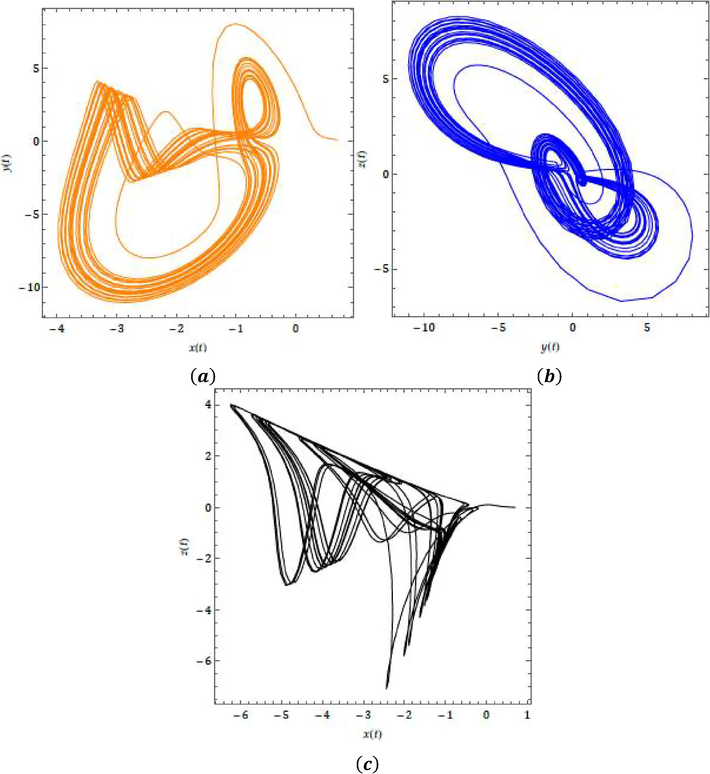
- Chaotic nature of the suggested model
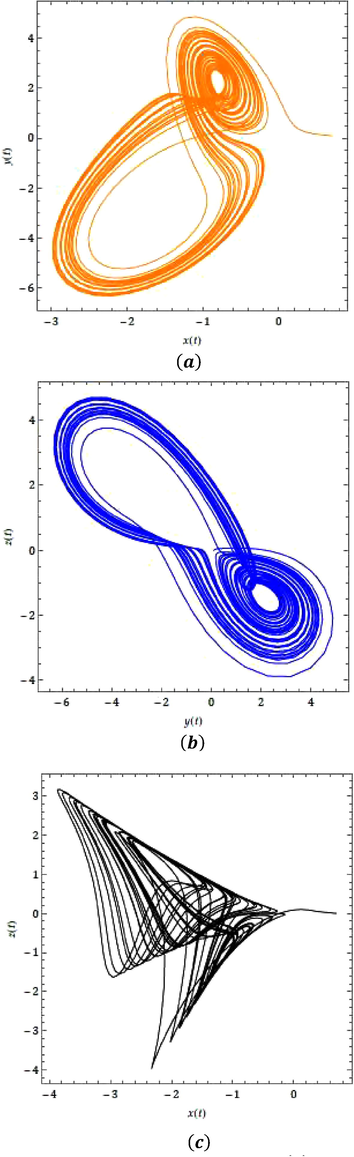
- Chaotic nature of the suggested model
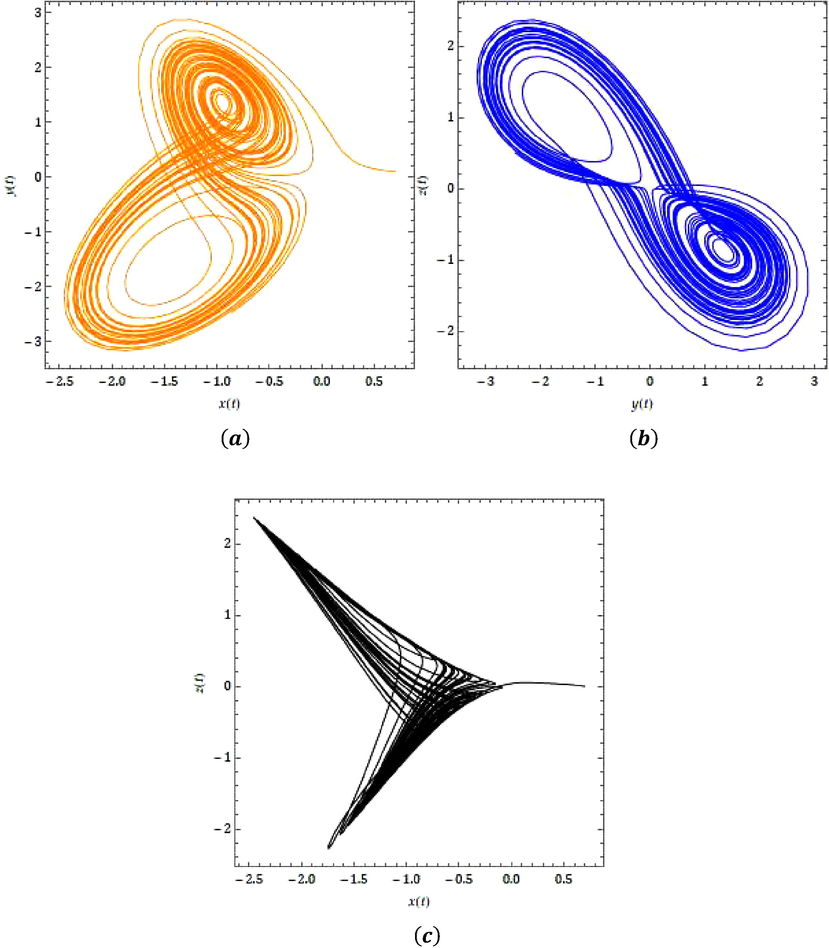
- Chaotic nature for the suggested model
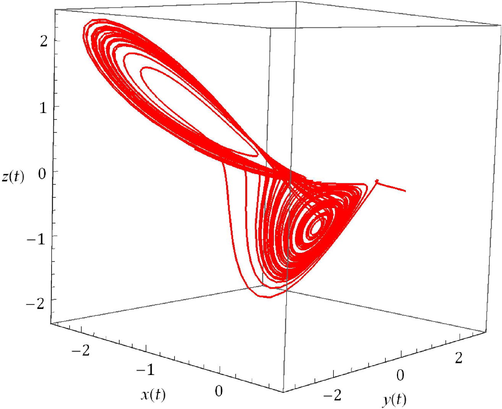
- Chaotic nature of the suggested model at
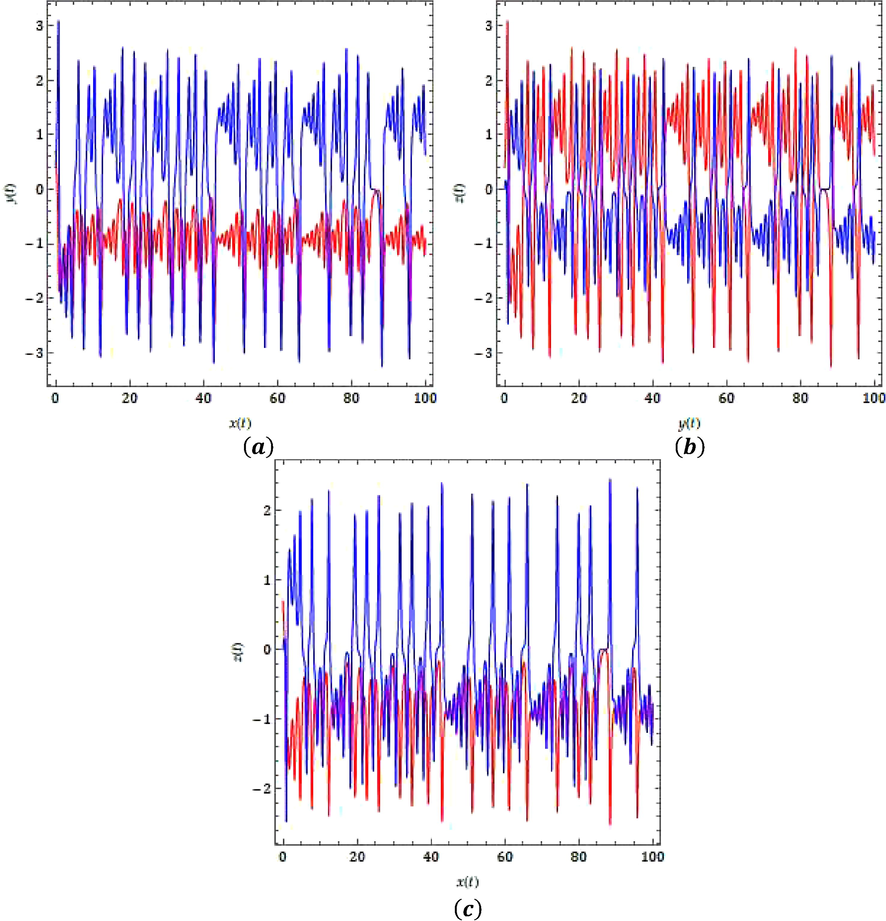
- Behaviour of the time series for the suggested model
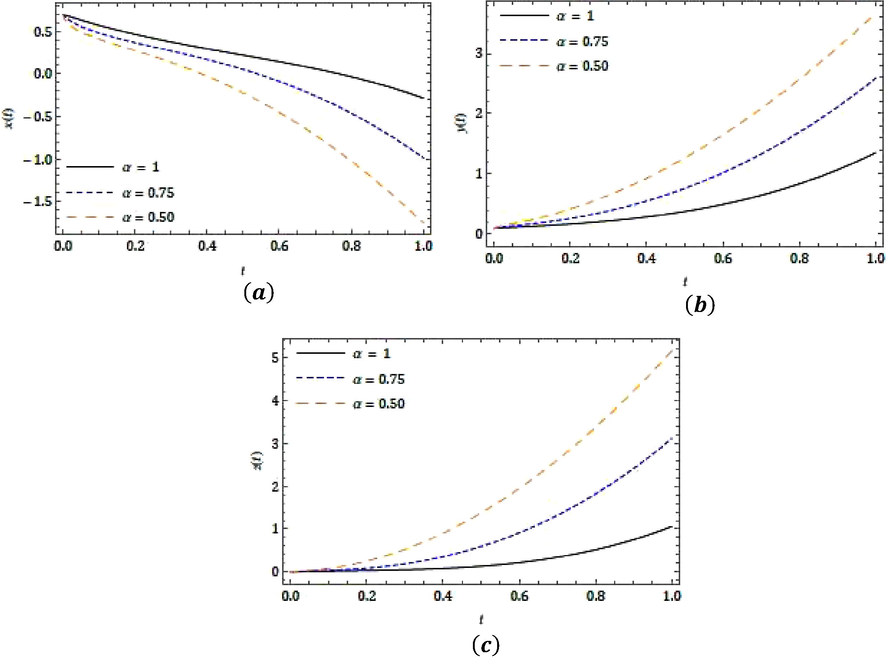
- Nature of the attained result for
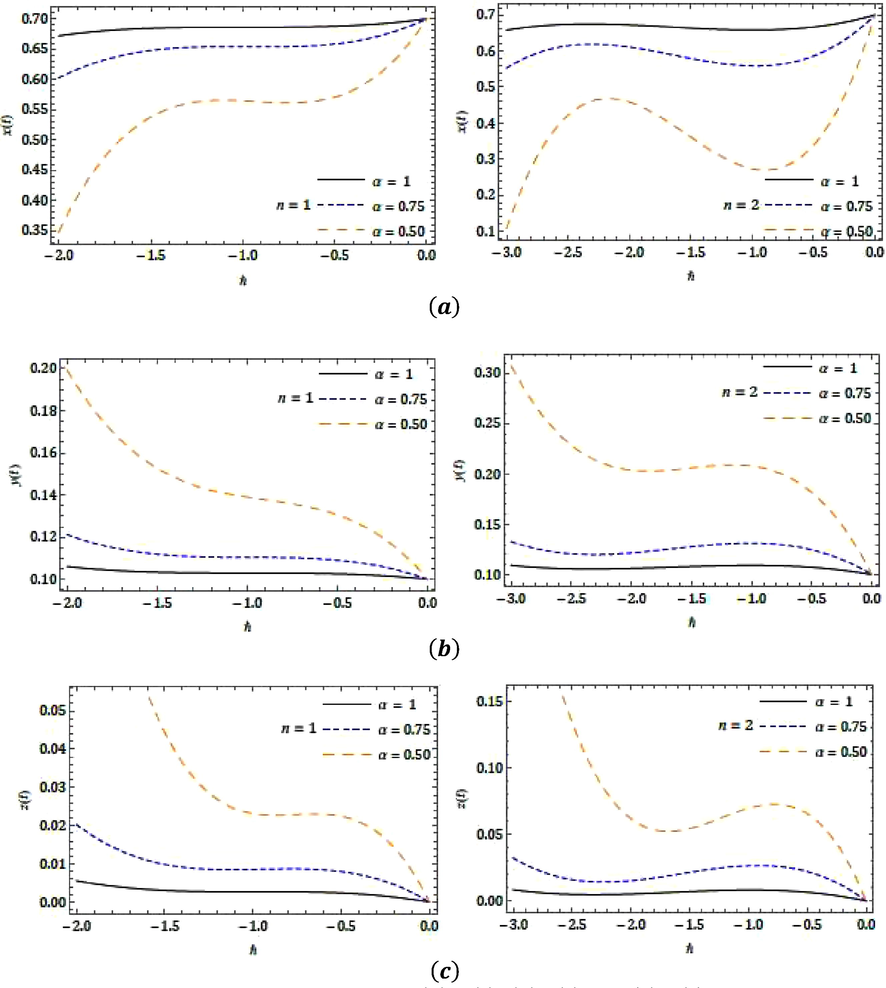
- ℏ-curves for the attained result of
6 Conclusion
In this paper, we examined and capture the chaotic nature of the projected arbitrary order model. In the present framework, we illuminate the effeteness of the projected AB derivative and since this derivative proposed by the assist of generalized Mittag-Leffler function. We presented the existence and uniqueness for the achieved results with the help of fixed point theorem. More preciously, the considered scheme offered the solution for the considered model without necessitating any discretization, conversion or perturbation. As associated with consequences accessible in the literature, the results acquired by the projected solution procedure are more stimulating. The present investigation illuminates, the projected chaotic system highly be contingent on the time history and the time instant, and these phenomena can be effectively exemplified will be aid of the concept of fractional calculus. Lastly, the present study ensures considered solution procedure is very accurate, more effective and extremely methodical, and it can be employed to describe the distinct classes of the dynamical system.
Acknowledgements
Taif University Researchers Supporting Project number (TURSP-2020/20), Taif University, Taif, Saudi Arabia.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Analysis of the Keller-Segel model with a fractional derivative without singular kernel. Entropy. 2015;17:4439-4453.
- [Google Scholar]
- Analysis of non-homogenous heat model with new trend of derivative with fractional order. Chaos Solitons Fractals. 2016;89:566-571.
- [Google Scholar]
- New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model. Thermal Sci.. 2016;20:763-769.
- [Google Scholar]
- New Trends in Nanotechnology and Fractional Calculus Applications. London New York: Springer Dordrecht Heidelberg; 2010.
- Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals. 2017;102:99-105.
- [Google Scholar]
- Active control of a chaotic fractional order economic system. Entropy. 2015;17(8):5771-5783.
- [Google Scholar]
- Transient chaos in fractional Bloch equations. Comput. Math. Appl.. 2012;64:3367-3376.
- [Google Scholar]
- A new definition of fractional derivative without singular kernel. Prog. Fract. Diff. Appl.. 2015;1(2):73-85.
- [Google Scholar]
- Caputo, M. 1969. Elasticita e Dissipazione, Bologna: Zanichelli.
- Dynamics of fractional-ordered Chen system with delay. Pramana J. Phy.. 2012;79(1):61-69.
- [Google Scholar]
- The q-homotopy analysis method (q-HAM) Int. J. Appl. Math. Mech.. 2012;8(15):51-75.
- [Google Scholar]
- Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik. 2018;167:150-156.
- [Google Scholar]
- New numerical results for the time-fractional Phi-four equation using a novel analytical approach. Symmetry. 2020;12(3)
- [CrossRef] [Google Scholar]
- Iterative method applied to the fractional nonlinear systems arising in thermoelasticity with Mittag-Leffler kernel. Fractals 2020
- [CrossRef] [Google Scholar]
- Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett.. 2003;91(3)
- [CrossRef] [Google Scholar]
- Chaos synchronization of a fractional nonautonomous system. Nonauton Dyn. Syst.. 2014;1:61-71.
- [Google Scholar]
- Circuit design and simulation for the fractional-order chaotic behaviour in a new dynamical system. Complex Intell. Syst.. 2018;4:251-260.
- [Google Scholar]
- A discretization approach for the nonlinear fractional logistic equation. Entropy. 2020;22(11)
- [CrossRef] [Google Scholar]
- Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier; 2006.
- A mathematical analysis of ongoing outbreak COVID-19 in India through nonsingular derivative. Numer. Meth. Partial. Differ. Equ. 2020
- [CrossRef] [Google Scholar]
- A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math.. 2018;399:405-413.
- [Google Scholar]
- Homotopy analysis method and its applications in mathematics. J. Basic Sci. Eng.. 1997;5(2):111-125.
- [Google Scholar]
- Homotopy analysis method: A new analytic method for nonlinear problems. Appl. Math. Mech.. 1998;19:957-962.
- [Google Scholar]
- Memoire surquelques questions de geometrieet de mecanique, et sur un nouveau genre de calcul pour resoudreces questions. J. Ecole. Polytech.. 1832;13:1-69.
- [Google Scholar]
- An Introduction to Fractional Calculus and Fractional Differential Equations. New York: A Wiley; 1993.
- Chaotic behaviour in system of noninteger-order ordinary differential equations. Chaos Solitons Fractals. 2018;115:362-370.
- [Google Scholar]
- Fractional Differential Equations. New York: Academic Press; 1999.
- New approach for fractional Schrödinger-Boussinesq equations with Mittag-Leffler kernel. Math. Meth. Appl. Sci.. 2020;43:9654-9670.
- [Google Scholar]
- Analysis of Lakes pollution model with Mittag-Leffler kernel. J. Ocean Eng. Sci.. 2020;5(4):310-322.
- [Google Scholar]
- Riemann, G.F.B. 1896. Versuch Einer Allgemeinen Auffassung der Integration und Differentiation, Gesammelte Mathematische Werke, Leipzig.
- Numerical solution of time- and space-fractional coupled Burgers’ equations via homotopy algorithm. Alexandria Eng. J.. 2016;55(2):1753-1763.
- [Google Scholar]
- A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput.. 2018;316:504-515.
- [Google Scholar]
- Numerical investigation of the fractional-order Liénard and Duffing equation arising in oscillating circuit theory. Front. Phys.. 2020;8
- [CrossRef] [Google Scholar]
- Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl. Sci.. 2020;10
- [CrossRef] [Google Scholar]
- Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J.. 2020;60:73-116.
- [Google Scholar]
- Some new mathematical models of the fractional-order system of human immune against IAV infection. Math. Biosci. Eng.. 2020;17(5):4942-4969.
- [Google Scholar]
- Some new and modified fractional analysis of the time-fractional Drinfeld-Sokolov-Wilson system. Chaos. 2020;30
- [CrossRef] [Google Scholar]
- An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model.. 2017;45:192-204.
- [Google Scholar]
- An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals. 2020;140
- [CrossRef] [Google Scholar]
- Novel approach for modified forms of Camassa-Holm and Degasperis-Procesi equations using fractional operator. Commun. Theor. Phys.. 2020;72(10)
- [CrossRef] [Google Scholar]
- Analysis of fractional Swift-Hohenberg equation using a novel computational technique. Math. Meth. Appl. Sci.. 2019;43(4):1970-1987.
- [Google Scholar]
- New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos. 2019;29(013119)
- [CrossRef] [Google Scholar]
- Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci.. 2019;13(2):115-128.
- [Google Scholar]
- Novel simulations to the time-fractional Fisher’s equation. Math. Sci.. 2019;13(1):33-42.
- [CrossRef] [Google Scholar]
- Solution for fractional Zakharov-Kuznetsov equations by using two reliable techniques. Chin. J. Phys.. 2019;60:313-330.
- [Google Scholar]
- An efficient technique for fractional coupled system arisen in magneto-thermoelasticity with rotation using Mittag-Leffler kernel. J. Comput Nonlinear Dynam.. 2020;16(1)
- [CrossRef] [Google Scholar]
- Fractional Klein-Gordon-Schrödinger equations with Mittag-Leffler memory. Chinese J. Phys.. 2020;68:65-78.
- [Google Scholar]
- An efficient approach for the model of thrombin receptor activation mechanism with Mittag-Leffler function, nonlinear analysis: Problems. Appl. Comput. Methods 2020:44-60.
- [CrossRef] [Google Scholar]







