An effective modification of the homotopy perturbation method for MHD viscous flow over a stretching sheet

M. Fathizadeh; M. Madani; Yasir Khan; Naeem Faraz; Ahmet Yıldırım; Serap Tutkun

doi:10.1016/j.jksus.2011.08.003

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original Article

25 (

); 107-113

doi:

10.1016/j.jksus.2011.08.003

An effective modification of the homotopy perturbation method for MHD viscous flow over a stretching sheet

M. Fathizadeh^a, M. Madani^a, Yasir Khan^b,*, Naeem Faraz^c, Ahmet Yıldırım^d, Serap Tutkun^d

a Chemical Engineering Department, Amirkabir University of Technology, No. 424, Hafez Ave., Tehran, Iran

b Department of Mathematics, Zhejiang University, Hangzhou 310027, China

c Modern Textile Institute, Donghua University, 1882 Yan'an Xilu Road, Shanghai 200051, China

d Ege University, Science Faculty, Department of Mathematics, 35100 Bornova, İzmir, Turkey

*Corresponding author. Tel.: +8657187996214 yasirmath@yahoo.com (Yasir Khan),

Received: 2011-7-27, Accepted: 2011-8-12, Published: 2011-04-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 22 August 2011

Peer review under responsibility of King Saud University.

Abstract

In this paper, we propose a powerful modification of the homotopy perturbation method that will accelerate the rapid convergence of series solution. The modified method is employed to solve the MHD boundary-layer equations. The viscous fluid is electrically conducting in the presence of a uniform applied magnetic field and the induced magnetic field is neglected for small magnetic Reynolds number. Similarity solutions of ordinary differential equation resulting from the momentum equation are obtained. Finally, some numerical comparisons among the new modified homotopy perturbation method, the standard homotopy perturbation, the Exact Solution and the Shooting method have been made, which manifest that the modified method is a very accurate and effective algorithm to solve the two-dimensional MHD viscous flow over a stretching sheet.

Keywords

New modified homotopy perturbation method

Similarity transforms

MHD viscous flow

Show Related Articles from PubMed

1 Introduction

The steady two-dimensional laminar flow of an incompressible, viscous fluid past a stretching sheet has become a classical problem in fluid dynamics as it admits an unusually simple closed form solution, first discovered by Crane (1970). Gupta and Gupta (1977) added surface suction (and injection) which models condensation (and evaporation), a uniform transverse magnetic field, when the fluid is electrically conducting, by Andersson (1992). The uniqueness of Crane's solution is also shown (Mcleod and Rajagopal, 1987; Troy et al., 1987). For general values of the parameter the solution was derived by Ariel (1995), though these solutions have been shown to be unstable. The joint effect of viscoelasticity and magnetic field on Crane's problem has been investigated by Ariel (1994). The flow past a stretching sheet need not be necessarily two-dimensional because the stretching of the sheet can take place in a variety of ways. It can be three-dimensional, axisymmetric when the stretching is radial and for this problem there is no closed form exact analytical solution. The three-dimensional case was solved by Wang (1984). The effects of viscoelasticity on the axisymmetric flow past a stretching sheet have been analyzed by Ariel for an elastico-viscous fluid (Ariel, 1992) and a second grade fluid (Ariel, 2001). A non-iterative solution for the MHD flow has been given by Ariel (2004) using the technique of Samuel and Hall (1973), Ariel et al. (2006) and Ariel (2009) applied HPM and extended HPM to derive the analytical solution to the axisymmetric flow past a stretching sheet.

Magnetohydrodynamics (MHD) is the study of the interaction of conducting fluids with electromagnetic phenomena. The flow of an electrically conducting fluid in the presence of a magnetic field is of importance in various areas of technology and engineering such as MHD power generation, MHD flow meters, MHD pumps, etc. Most boundary-layer models can be reduced to systems of nonlinear ordinary differential equations which are usually solved by numerical methods. It is however interesting to find approximate analytical solutions to boundary layer problems. Analytical methods have significant advantages over numerical methods in providing analytic, verifiable, rapidly convergent approximation. Various powerful analytical techniques such as Similarity solutions (Banks, 1983; Chaim, 1995), Adomian decomposition method (Wazwaz, 1997, 2006; Awang Kechil and Hashim, 2007, 2008; Hayat et al., 2009; Noor et al., 2010; Ganji and Ganji, 2010 ), Laplace decomposition method (Khan, 2009; Khan and Faraz, 2010, 2011; Khan and Austin, 2010 ), homotopy analysis method (Sajid and Hayat, 2009; Sajid et al., 2008), differential transform method (Rashidi, 2009) and variational iteration method (Mirgolbabaei et al., 2009; Noor and Mohyud-Din, 2009; Mohyud-Din et al., 2010; Ganji et al., 2010b ) have been proposed for obtaining exact and approximate analytic solutions. Most of these techniques encounter the inbuilt deficiencies and involve huge computational work. He (He, 1999, 2000, 2004, 2006a, 2008; Yıldırım and Berberler, 2010; Mustafa Inc., 2010 ) developed and formulated homotopy perturbation method (HPM) by merging the standard homotopy and perturbation. The He's homotopy perturbation method (HPM) proved to be compatible with the versatile nature of the physical problems and has been to a wide class of functional equations; see (Ganji et al., 2009, 2010a; Fathizadeh and Rashidi, 2009; Kelleci and Yıldırım, 2011; Raftari and Yıldırım, 2010; Ates and Yıldırım, 2010; Yıldırım and Sezer, 2010; Xu, 2007; Madani and Fathizadeh, 2010 ) and the references therein. It is worth mentioning that the HPM is applied without any discretization, restrictive assumption or transformation and is free from round off errors. Unlike the method of separation of variables that requires initial and boundary conditions, the homotopy perturbation method (HPM) provides an analytical solution by using the initial conditions only. The fact that HPM solves nonlinear problems without using Adomian's polynomials can be considered as a clear advantage of this technique over the decomposition method.

The basic motivation of this paper is to propose a new modification of this reliable technique (HPM) for solving MHD boundary-layer equations for stretching sheet problem. Although the modified technique needs only a slight variation from the standard homotopy perturbation method, but the proposed modification will accelerate the rapid convergence of the series solution if compared with the standard HPM, and therefore provides a major progress. While this slight variation is rather simple, it does demonstrate the reliability and the power of the proposed modification. It is important to note that the modified technique works effectively independent of other phenomena in some cases. To the best of our knowledge no attempt has been made to exploit this method to solve MHD boundary layer equation. Also our aim in this article is to compare the results with solutions to the standard HPM, exact and shooting method.

2 A new modified homotopy perturbation method

In order to elucidate the solution procedure of the homotopy perturbation method, we consider the following nonlinear differential equation:

(1)

L (u) + N (u) = f (r), r \in Ω

with boundary condition

(2)

B (u, \partial u / \partial n) = 0, r \in Γ,

where L is any linear integral or differential operator while N is non-linear differential operator B, Γ is the boundary of the domain Ω and f(r) is a known analytic function. In view of HPM (He, 1999, 2000, 2004, 2006a, 2008; Yıldırım and Berberler, 2010; Mustafa Inc., 2010 ) was introduced by He, we can construct a homotopy for Eq. (1) as follows:

(3)

H (v, p) = (1 - p) [L (v) - L (u_{0})] + p [L (v) + N (v) - f (r)] = 0,

(4)

H (v, p) = L (v) - L (u_{0}) + pL (u_{0}) + p [N (v) - f (r)] = 0,

where p ∈ [0, 1] is an embedding parameter. If p = 0 Eqs. (3) and (4) become

L (v) - L (u_{0}) = 0,

and when p = 1 both Eqs. (3) and (4) turn out to be the original nonlinear differential equation (1). The Homotopy perturbation method (He, 1999, 2000, 2004, 2006a, 2008; Yıldırım and Berberler, 2010; Mustafa Inc., 2010 ) admits a solution in the form

(5)

v (x, t) = p^{0} v_{0} (t) + p^{1} v_{1} (t) + p^{2} v_{2} (t) + \dots

The convergence of the above series is discussed in He (2006b) and the asymptotic behavior of the series is illustrated in He (2006c). Setting p = 1 results in the solution of Eq. (5) we get

(6)

v (x, t) = v_{0} (t) + v_{1} (t) + v_{2} (t) + \dots

For the nonlinear term in (1), let us set N(u) = h(u). Invoking Eq. (5) into Eq. (4) and collecting the terms with the same powers of p, we can obtain a series of equations of the following form:

(7)

\begin{matrix} p^{0} : L (v_{0}) = L (u_{0}), \\ p^{1} : L (v_{1}) = h_{1} (u_{0}) - f (r), \\ p^{2} : L (v_{2}) = h_{1} (u_{0}, u_{1}), \\ p^{3} : L (v_{2}) = h_{1} (u_{0}, u_{1}), \\ ⋮ \end{matrix}

and so on, where the function u₁, u₂, u₃, …, satisfies the following equation:

h (u_{0} + {pu}_{1} + p^{2} u_{2} + \dots) = h_{1} (u_{0}) + {ph}_{2} (u_{0}, u_{1}) + p^{2} h_{3} (u_{0}, u_{1}, u_{2}) + \dots

A new modified form of the HPM can be established based on the assumption that we decompose u₀ into two parts:

(8)

u_{0} = H_{0} + H_{1},

Instead of the iteration procedure, Eq. (7), we suggest the following modification

(9)

\begin{matrix} p^{0} : v_{0} = H_{0}, \\ p^{1} : v_{1} = H_{1} + L^{- 1} [h_{1} (u_{0}) - f (r)], \\ p^{2} : L (v_{2}) = h_{1} (u_{0}, u_{1}), \\ p^{3} : L (v_{2}) = h_{1} (u_{0}, u_{1}, u_{2}), \\ ⋮ \end{matrix}

The solution through the new modified homotopy perturbation method highly depends upon the choice of H₀(x, t) and H₁(x, t). We will show how to suitably choose H₀(x, t) and H₁(x, t) by example. This suggestion will facilitate the calculations of the terms u₀, u₁, u₂, … and hence accelerate the rapid convergence of the series solution.

3 Governing equations

The MHD boundary layer flow over a flat plate is governed by the continuity and the Navier–Stokes equations for an incompressible viscous fluid. The fluid is electrically conducting under the influence of an applied magnetic field B(x) normal to the stretching sheet. The induced magnetic field is neglected. The resulting boundary-layer equations are:

(10)

\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,

(11)

u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = ν \frac{\partial^{2} u}{\partial y^{2}} - σ \frac{B^{2} (x)}{ρ} u,

where u and v are the velocity components in the x and y directions, respectively. Also

v

, ρ and σ are the kinematic viscosity, density and electrical conductivity of the fluid. There is B(x) equal to

B (x) = B_{0} x^{n - 1 / 2}

The boundary conditions are given below:

(12)

u (x, 0) = {cx}^{n}, v (x, 0) = 0, and u (x, \infty) = 0 .

To solve the problem, momentum and energy equations are firstly nondimensionalized by introducing the following dimensionless variables:

(13)

η = \sqrt{\frac{c (n + 1)}{2 ν}} x^{\frac{n - 1}{2}} y,

(14)

u = {cx}^{n} f^{'} (η),

(15)

v = - \sqrt{\frac{c ν (n + 1)}{2}} x^{\frac{n - 1}{2}} [f (η) + \frac{η - 1}{η + 1} η f^{'} (η)] .

Using Eqs. (13)–(15), the governing equations can be reduced to non-linear differential equation where f is a function of the similarity variable (η):

(16)

f^{‴} + {ff}^{″} - β f^{' 2} - {Mf}^{'} = 0, f (0) = 0, f^{'} (0) = 1 and f^{'} (\infty) = 0,

where

(17)

β = \frac{2 n}{n + 1}, M = \frac{2 σ β_{0}^{2}}{ρ c (1 + n)} .

4 Application

To demonstrate the effectiveness of the proposed modification and to compare the new modification of the HPM with the standard HPM, we have chosen MHD boundary layer equation (16). In view of the homotopy (3), we construct the homotopy

(18)

\begin{matrix} (1 - p) (f^{‴} - f_{0}^{‴}) + p (f^{‴} + {ff}^{″} - β f^{'^{2}} - {Mf}^{'}) = 0, \\ f (0) = 0, f^{'} (0) = 1, f^{″} (0) = α . \end{matrix}

Substituting (5) and the initial conditions into the homotopy (18) and equating the terms with identical powers of p we obtain the following set of linear differential equations:

(19)

\begin{matrix} p^{0} : f_{0}^{‴} = 0, \\ f_{0} (0) = 0, f_{0}^{'} (0) = 1, f_{0}^{″} (0) = α, \end{matrix}

(20)

\begin{matrix} p^{1} : f_{1}^{‴} + f_{0}^{‴} - {Mf}_{0}^{'} + f_{0} f_{0}^{″} - β f_{0}^{' 2} = 0, \\ f_{1} (0) = 0, f_{1}^{'} (0) = 0, f_{1}^{″} (0) = 0, \end{matrix}

(21)

\begin{matrix} p^{2} : f_{2}^{‴} - {Mf}_{1}^{'} - 2 β f_{0}^{'} f_{1}^{'} + f_{1} f_{0}^{″} + f_{0} f_{1}^{″} = 0, \\ f_{2} (0) = 0, f_{2}^{'} (0) = 0, f_{2}^{″} (0) = 0, \end{matrix}

(22)

\begin{matrix} p^{3} : f_{3}^{‴} - {Mf}_{2}^{'} - β (f_{1}^{' 2} + 2 f_{0}^{'} f_{2}^{'}) + f_{1} f_{1}^{″} + f_{0} f_{2}^{″} + f_{2} f_{0}^{″} = 0, \\ f_{3} (0) = 0, f_{3}^{'} (0) = 0, f_{3}^{″} (0) = 0, \end{matrix}

(23)

\begin{matrix} p^{4} : f_{4}^{‴} - {Mf}_{3}^{'} - 2 β (f_{3}^{'} f_{0}^{'} + f_{1}^{'} f_{2}^{'}) + f_{3} f_{0}^{″} + f_{0} f_{3}^{″} + f_{1} f_{2}^{″} + f_{2} f_{1}^{″} = 0, \\ f_{4} (0) = 0, f_{4}^{'} (0) = 0, f_{4}^{″} (0) = 0, \end{matrix}

by solving Eqs. (19)–(23):

(24)

f_{0} = \frac{1}{2} α η^{2} + η,

(25)

f_{1} = \frac{(2 β - 1)}{120} α^{2} η^{5} + \frac{(M - 1 + 2 β)}{24} α η^{4} + \frac{(M + β)}{6} η^{3},

(26)

f_{2} = \frac{(20 β^{2} - 40 β - 11)}{40320} α^{3} η^{8} + \frac{(11 + 10 M β + 20 β^{2} - 8 M - 32 β)}{5040} α^{2} η^{7} + \frac{(3 - 12 β - 8 M + 10 β^{2} + 10 M β + M^{2})}{720} α η^{6} + \frac{(M^{2} + 2 β^{2} - 2 β - 2 M + 3 M β)}{120} η^{2},

(27)

f_{3} = \frac{(600 β^{3} - 1596 β^{2} - 1398 β - 375)}{39916800} α^{4} η^{11} + \frac{(4800 β^{3} - (12868 - 2400 M) β^{2} + (11184 - 4368 M) β - 3000 + 1944 M)}{5040} α^{3} η^{10} + \frac{(16800 β^{3} - (39760 - 16800 M) β^{2} + (30688 - 30576 M + 2352 M^{2}) β - 7222 + 13608 M - 2184 M^{2})}{20321280} α^{2} η^{9} + \frac{(26880 β^{3} - (55776 - 40320 M) β^{2} + (34608 - 65856 M + 14112 M^{2}) β - 5040 + 26880 M - 13104 M^{2})}{13547520} α η^{8} + \frac{(16800 β^{3} - (26880 - 33600 M) β^{2} + (13440 - 43680 M + 18480 M^{2}) β)}{8467200} η^{7},

(28)

\begin{matrix} f = f_{0} + f_{1} + f_{2} + f_{3} + \dots, \\ p \to 1 . \end{matrix}

To select

f^{″} (0) = α

and η_∞, we begin with some initial guess value of α and draw f′. The solution process is repeated with another value of α until f′ receive to zero. Also, η_∞ is obtained from highest value of η in f′. According to the new modified homotopy perturbation method, we first set

(29)

f_{0} = \frac{1}{2} α η^{2} + η .

As suggested before we split zeroth iteration f₀ into two parts

(30)

H_{0} (η) = η

and

(31)

H_{1} (η) = \frac{1}{2} α η^{2} .

According to the iteration algorithm, Eq. (9), we obtain

(32)

f_{0} = η,

(33)

f_{1} = \frac{1}{2} α η^{2} + \frac{1}{6} (M + β) η^{3},

(34)

f_{2} = \frac{1}{120} (M^{2} + 3 M β + 2 β^{2} - 2 M - 2 β) η^{5} + \frac{1}{48} (2 M - 2 + 4 β) α η^{4},

(35)

f_{2} = (\frac{M^{3}}{5040} - \frac{M^{2}}{504} - \frac{M}{630} - \frac{13 M β}{2520} + \frac{11 M^{2} β}{5040} + \frac{M β^{2}}{252} - \frac{β^{2}}{315} + \frac{β}{630}) η^{7} + (\frac{M^{2}}{720} - \frac{M}{90} + \frac{M β}{72} + \frac{β^{2}}{72} - \frac{β}{60} + \frac{1}{240}) α η^{6} + (\frac{β}{60} - \frac{1}{120}) α^{2} η^{5},

(36)

\begin{matrix} f = f_{0} + f_{1} + f_{2} + f_{3} + \dots, \\ p \to 1 . \end{matrix}

5 Results and discussion

Eq. (16) were solved analytically using the new modified HPM, standard HPM and numerically using the shooting method. It was shown in Figs. 1–3 the analytical, the exact solution and the numerical solution of f for different values of M and β. Furthermore, the comparison between the MHPM and the standard HPM solutions of f′ was performed (Fig. 4). A very good agreement was illustrated between the results obtained by the new modified HPM, HPM, exact solution and the numerical results for all values of η. The result of modified HPM has better than HPM in large amount of M.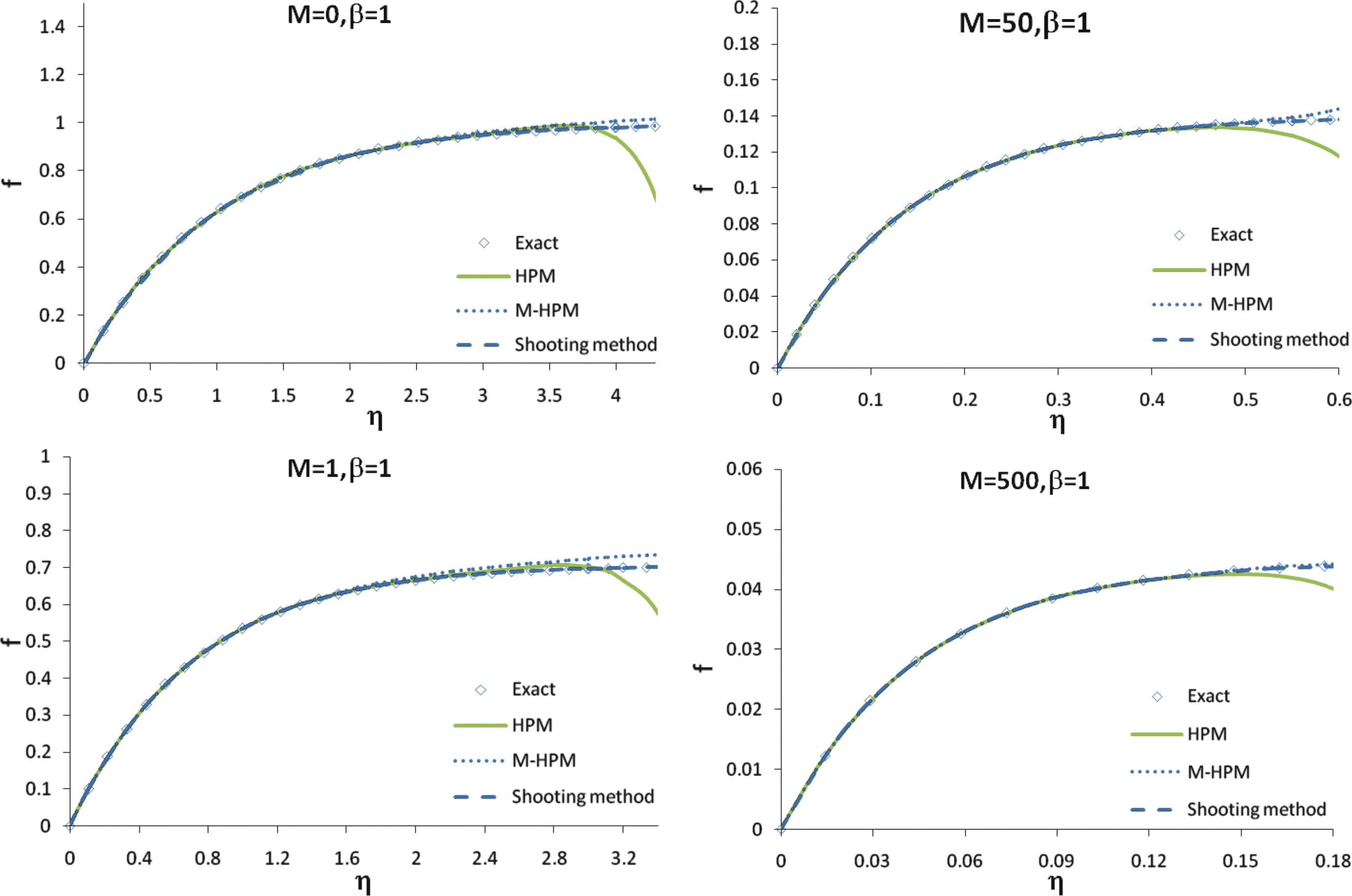

The results of f obtained for employing HPM and modified HPM as well as the numerical method suggested by shooting method.

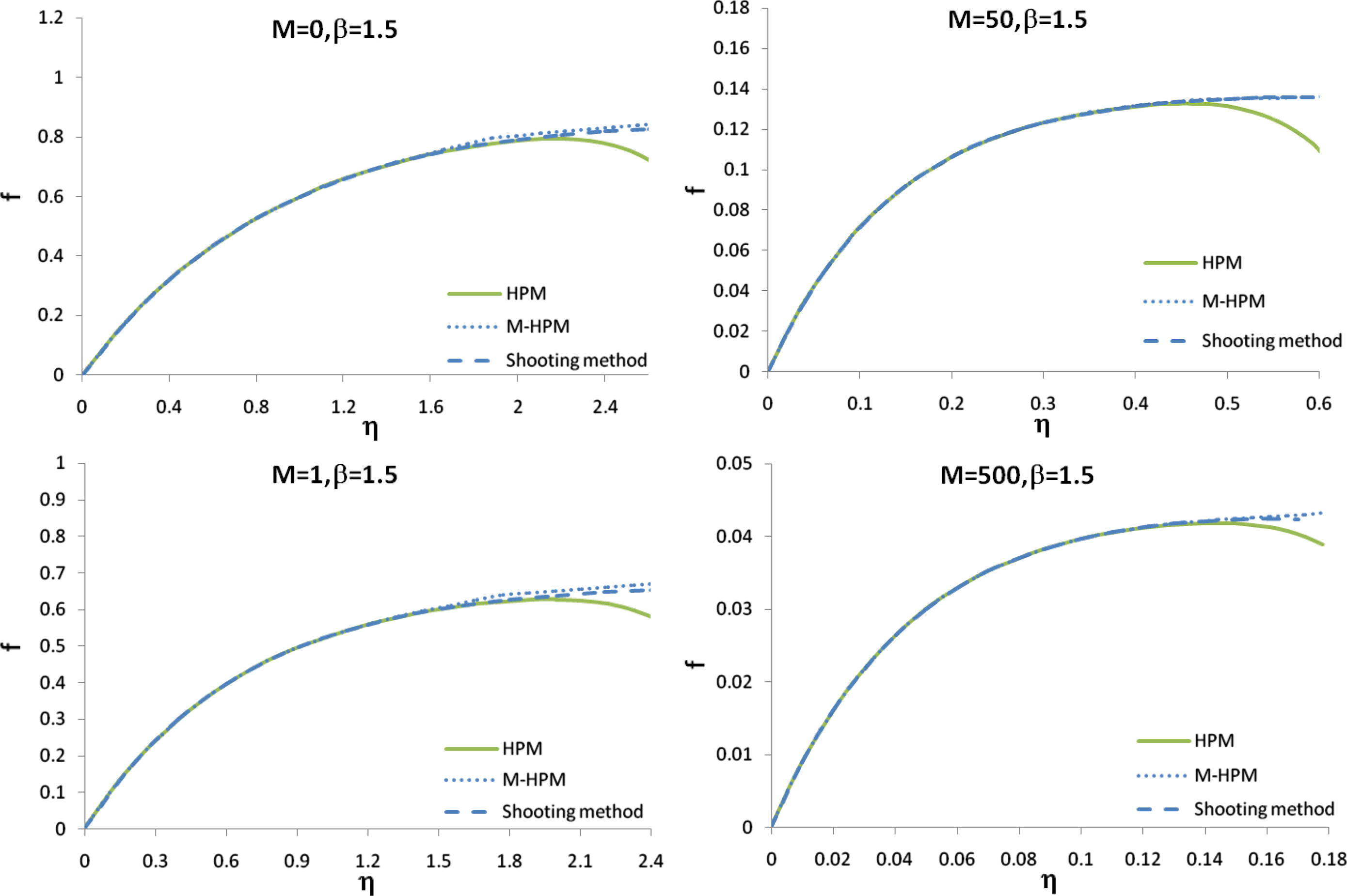
The variation of f for different values of M and β = 1.5 approximated by HPM, modified HPM and shooting method.

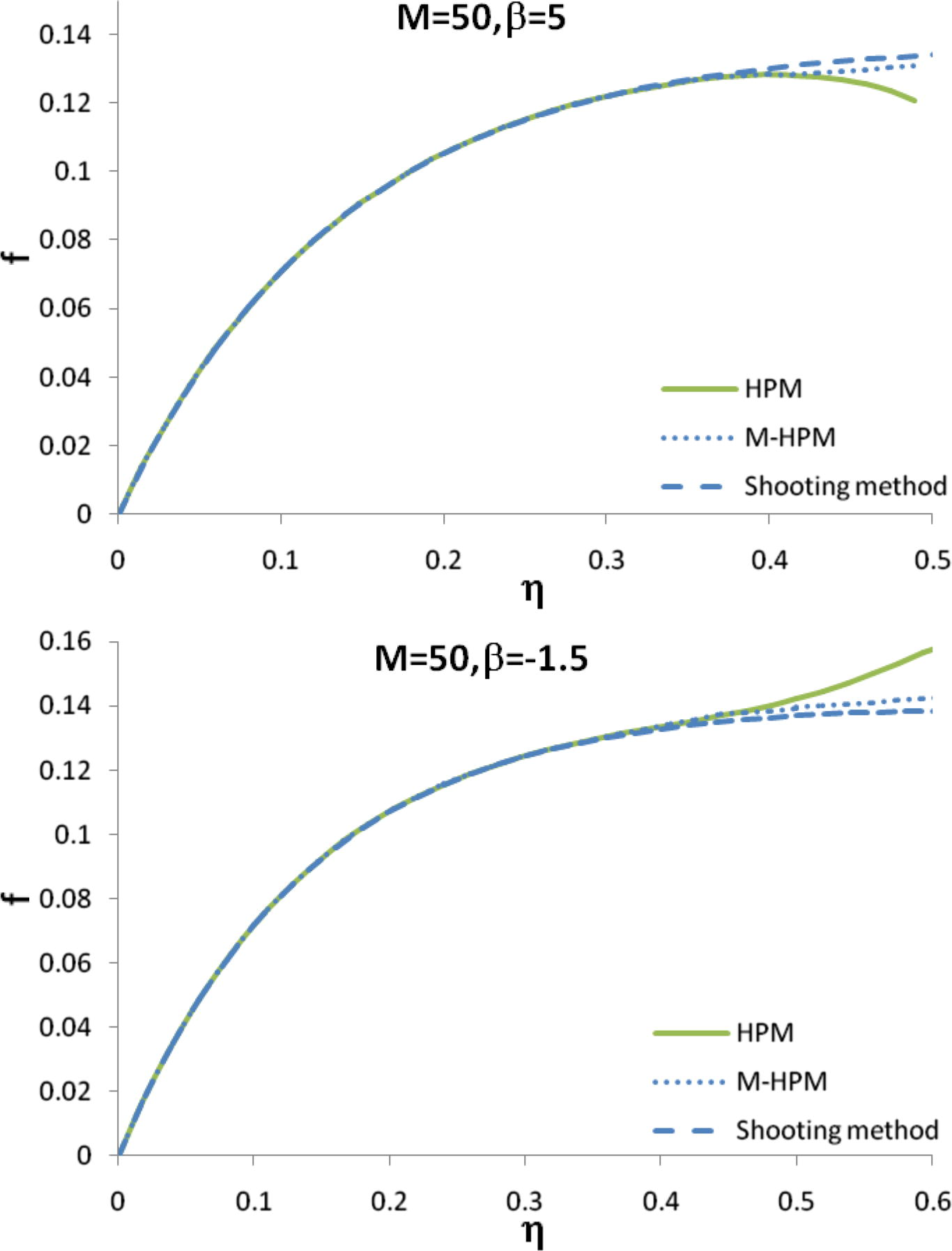
The variation of f for different values of β and M = 50 approximated by HPM, modified HPM and shooting method.

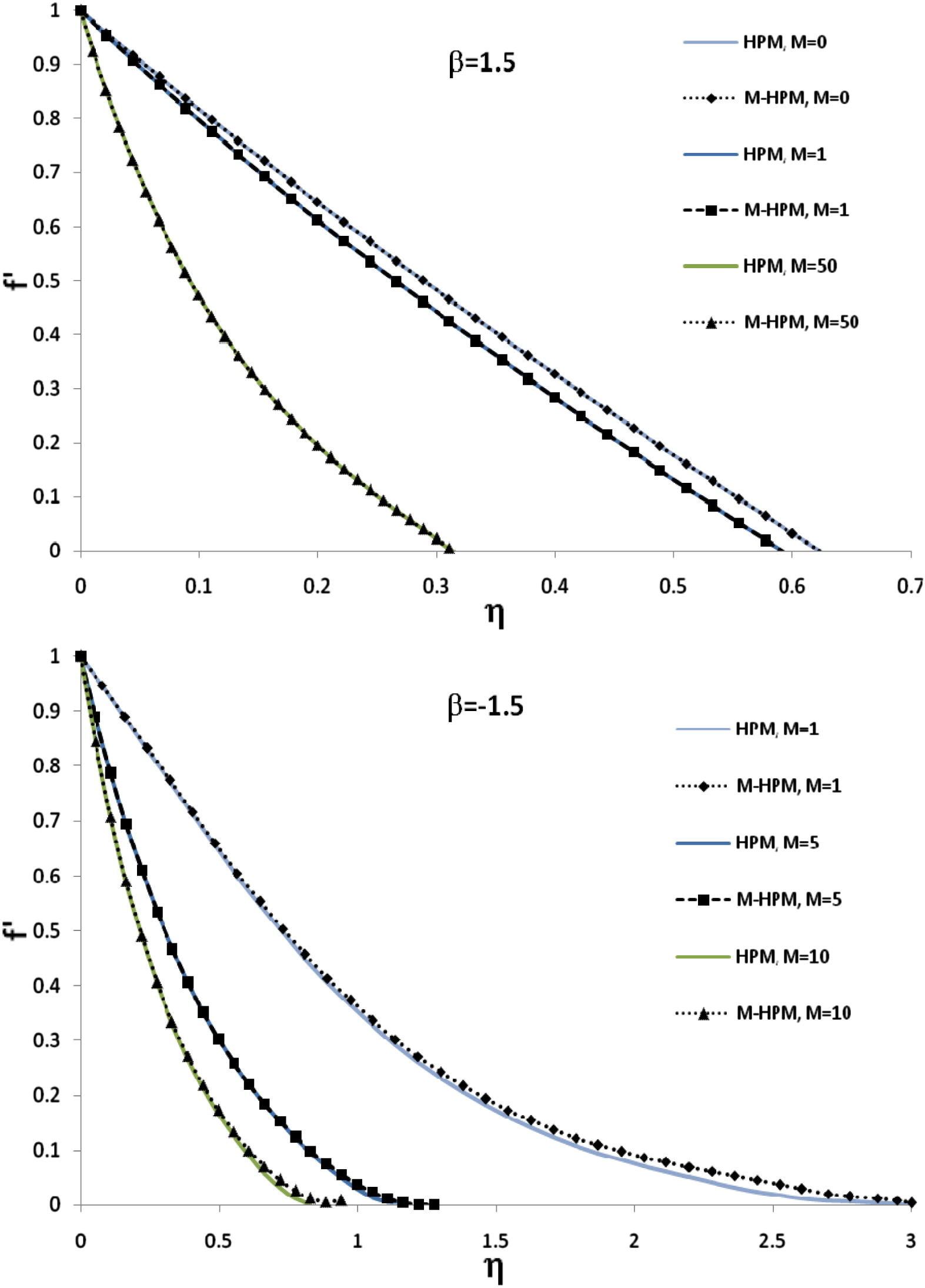
Comparison of the solution (f′) obtained by a new modified HPM and the standard HPM solution for different values of M and β.

Tables 1 and 2 clearly elucidate that present solution method namely modified HPM shows excellent agreement with the exact solution, standard HPM and numerical method and more convergent as compared with standard HPM. This analysis shows that MHPM suits for MHD viscous flow problems.

Table 1 Comparison of the values of f″(0) obtained by HPM, the modified HPM and the exact solution.

β	M	HPM	M-HPM	Exact solution
1	0	−1	−1	−1
	1	−1.41421	−1.41421	−1.41421
	5	−2.44948	−2.44948	−2.44948
	10	−3.31662	−3.31662	−3.31662
	50	−7.14142	−7.14142	−7.14142
	100	−10.0499	−10.0499	−10.04987
	500	−22.383	−22.383	−22.38302
	1000	−31.6386	−31.6386	−31.63858

Table 2 Variation in f″(0) at the different values of β and M obtained by HPM, modified HPM and shooting method.

β	M	HPM	M-HPM	Shooting method	β	M	HPM	M-HPM	Shooting method
1.5	0	−1.1486	−1.1547	−1.1547	5	0	−1.9025	−1.9098	−1.9098
	1	−1.5252	−1.5252	−1.5252		1	−2.1529	−2.1528	−2.1528
	5	−2.5161	−2.5161	−2.5161		5	−2.9414	−2.9414	−2.9414
	10	−3.3663	−3.3663	−3.3663		10	−3.6956	−3.6956	−3.6956
	50	−7.1647	−7.1647	−7.1647		50	−7.3256	−7.3256	−7.3256
	100	−10.0664	−10.0776	−10.0776		100		−10.1816	−10.1816
	500	−22.3901	−22.3904	−22.3904		500		−22.4425	−22.4425
	1000	−31.6432	−31.6438	−31.6438		1000		−31.6806	−31.6806

6 Concluding remarks

In this work, we carefully proposed an efficient modification of the HPM that accelerate the rapid convergence of series solution. A newly modified HPM was used to find analytical solutions of magnetohydrodynamics boundary-layer equation. Comparison of the present solution is made with the HPM, exact and shooting method solutions. An excellent agreement is achieved. The proposed method is employed without using linearization, discretization or transformation. It may be concluded that the MHPM is very powerful and efficient in finding the analytical solutions for a wide class of boundary value problems. The method gives more realistic series solutions that converge very rapidly in physical problems.

References

Andersson H.I., . MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech.. 1992;95:227-230.
[Google Scholar]
Ariel P.D., . Computation of flow of viscoelastic fluids by parameter differentiation. Int. J. Numer. Methods Fluids. 1992;15:1295-1312.
[Google Scholar]
Ariel P.D., . MHD flow of a viscoelastic fluid past a stretching sheet with suction. Acta Mech.. 1994;105:49-56.
[Google Scholar]
Ariel P.D., . On the second solution of flow of viscoelastic fluid over a stretching sheet. Quart. Appl. Math.. 1995;53:629-632.
[Google Scholar]
Ariel P.D., . Axisymmetric flow of a second grade fluid past a stretching sheet. Int. J. Eng. Sci.. 2001;39:529-553.
[Google Scholar]
Ariel P.D., . Extended homotopy perturbation method and computation of flow past a stretching sheet. Comput. Math. Appl.. 2009;58:2402-2409.
[Google Scholar]
Ariel, P.D., 2004. Computation of MHD flow due to moving boundary. Technical Report MCS-2004-01, Department of Mathematical Sciences, Trinity Western University.
Ariel P.D., Hayat T., Asghar S., . Homotopy perturbation method and axisymmetric flow over a stretching sheet. Int. J. Nonlinear Sci. Numer. Simul.. 2006;7:399-406.
[Google Scholar]
Ates Inan, Yıldırım Ahmet, . Comparison between variational iteration method and homotopy perturbation method for linear and nonlinear partial differential equations with the nonhomogeneous initial conditions. Numer. Methods Partial Differ. Eq.. 2010;26:1581-1593.
[Google Scholar]
Awang Kechil S., Hashim I., . Non-perturbative solution of free-convection boundary-layer equation by Adomian decomposition method. Phys. Lett. A. 2007;363:110-114.
[Google Scholar]
Awang Kechil S., Hashim I., . Series solution of flow over nonlinearly stretching sheet with chemical reaction and magnetic field. Phys. Lett. A. 2008;372:2258-2263.
[Google Scholar]
Banks W.H.H., . Similarity solutions of the boundary layer equations for a stretching wall. J. Mech. Theor. Appl.. 1983;2:375-392.
[Google Scholar]
Chaim T.C., . Hydromagnetic flow over a surface stretching with a power law velocity. Int. J. Eng. Sci.. 1995;33:429-435.
[Google Scholar]
Crane L.J., . Flow past a stretching plate. Z. Angew. Math. Phys.. 1970;21:645-647.
[Google Scholar]
Fathizadeh M., Rashidi F., . Boundary layer convective heat transfer with pressure gradient using homotopy perturbation method (HPM) over a flat plate. Chaos Solitons Fract.. 2009;42:2413-2419.
[Google Scholar]
Ganji Z.Z., Ganji D.D., . Analytical solution of viscous flow in porous media using ADM and comparison with the numerical Runge–Kutta method. Transp. Porous Med.. 2010;81:527-546.
[Google Scholar]
Ganji D.D., Gorji M., Alipanah M., Farnad E., . Analytical solutions to nonlinear equations arising in heat transfer by variational iteration, homotopy perturbation, and Adomian decomposition methods. Numer. Methods Partial Differ. Eq. 2009 doi:10.1002/num.20503
[Google Scholar]
Ganji D.D., Ganji S.S., Karimpour S., Ganji Z.Z., . Numerical study of homotopy-perturbation method applied to Burgers equation in fluid. Numer. Methods Partial Differ. Eq.. 2010;26:917-930.
[Google Scholar]
Ganji Davood Domiri, Safari Mehdi, Ghayor Reza, . Application of He's variational iteration method and Adomian's decomposition method to Sawada–Kotera–Ito seventh-order equation. Numer. Methods Partial Differ. Eq.. 2010;26:1463-1475.
[Google Scholar]
Gupta P.S., Gupta A.S., . Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng.. 1977;55:744-746.
[Google Scholar]
Hayat T., Hussain Q., Javed T., . The modified decomposition method and Pade approximants for the MHD flow over a non-linear stretching sheet. Nonlinear Anal.: Real World Appl.. 2009;10:966-973.
[Google Scholar]
He J.H., . Homotopy perturbation technique. Comput. Math. Appl. Mech. Eng. 1999:178-257.
[Google Scholar]
He J.H., . A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J. Nonlinear Mech.. 2000;35(1):115-123.
[Google Scholar]
He J.H., . Comparison of homotopy perturbation method and homotopy analysis method. Appl. Math. Comput.. 2004;156:527-539.
[Google Scholar]
He J.H., . Homotopy perturbation method for solving boundary value problems. Phys. Lett. A. 2006;350:87-88.
[Google Scholar]
He J.H., . Strongly Nonlinear Problems, Dissertation. Berlin: de-Verlag im Internat GmbH; 2006.
He J.H., . New interpretation of homotopy perturbation method. Int. J. Modern Phys. B. 2006;20:1-7.
[Google Scholar]
He J.H., . Recent developments of the homotopy perturbation method. Top. Methods Nonlinear Anal.. 2008;31:205-209.
[Google Scholar]
Kelleci Alev, Yıldırım Ahmet, . An efficient numerical method for solving coupled Burgers’ equation by combining homotopy perturbation and Pade techniques. Numer. Methods Partial Differ. Eq.. 2011;27:982-995.
[Google Scholar]
Khan Yasir, . An effective modification of the Laplace decomposition method for nonlinear equations. Int. J. Nonlinear Sci. Numer. Simul.. 2009;10(11–12):1373-1376.
[Google Scholar]
Khan Yasir, Austin Francis, . Application of the Laplace decomposition method to nonlinear homogeneous and non-homogeneous advection equations. Z. Naturforsch.. 2010;65a:849-853.
[Google Scholar]
Khan Yasir, Faraz Naeem, . A new approach to differential difference equations. J. Adv. Res. Differ. Eq.. 2010;2(2):1-12.
[Google Scholar]
Khan Yasir, Faraz Naeem, . Application of modified Laplace decomposition method for solving boundary layer equation. J. King. Saud Univ. Sci.. 2011;23(1):115-119.
[Google Scholar]
Madani M., Fathizadeh M., . Homotopy perturbation algorithm using Laplace transformation. Nonlinear Sci. Lett. A. 2010;1(3):263-267.
[Google Scholar]
Mcleod J.B., Rajagopal K.R., . On the uniqueness of flow of a Navier–Stokes fluid due to a stretching boundary. Arch. Ration. Mech. Anal.. 1987;98:386-393.
[Google Scholar]
Mirgolbabaei H., Ganji D.D., Etghani M.M., Sobati A., . Adapted variational iteration method and axisymmetric flow over a stretching sheet. World J. Model. Simul.. 2009;5:307-314.
[Google Scholar]
Mohyud-Din S.T., Yıldırım A., Sezer S.A., Usman M., . Modified variational iteration method for free-convective boundary-layer equation using Padé approximation. Math. Probl. Eng.. 2010;2010:1-11. (Article ID 318298)
[Google Scholar]
Mustafa Inc., 2010. He's homotopy perturbation method for solving Korteweg–de Vries Burgers equation with initial condition. Numer. Methods Partial Differ. Eq. 26, 1224–1235.
Noor M.A., Mohyud-Din S.T., . Modified variational iteration for a boundary layer problem in unbounded domain. Int. J. Nonlinear Sci.. 2009;7(4):426-430.
[Google Scholar]
Noor N.F.M., Awang Kechil S., Hashim I., . Simple non-perturbative solution for MHD viscous flow due to a shrinking sheet. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:144-148.
[Google Scholar]
Raftari B., Yıldırım A., . The application of homotopy perturbation method for MHD flows of UCM fluids above porous stretching sheets. Comput. Math. Appl.. 2010;59:3328-3337.
[Google Scholar]
Rashidi M.M., . The modified differential transform method for solving MHD boundary-layer equations. Comput. Phys. Commun.. 2009;180:2210-2217.
[Google Scholar]
Sajid M., Hayat T., . The application of homotopy analysis method for MHD viscous flow due to a shrinking sheet. Chaos Solitons Fract.. 2009;39:1317-1323.
[Google Scholar]
Sajid M., Javed T., Hayat T., . MHD rotating flow of a viscous fluid over a shrinking surface. Nonlinear Dyn.. 2008;51:259-265.
[Google Scholar]
Samuel T.D.M.A., Hall I.M., . On the series solution to the laminar boundary layer with stationary origin on a continuous moving porous surface. Proc. Camb. Philos. Soc.. 1973;73:223-229.
[Google Scholar]
Troy W., Overman E.A. II, Ermentrout G.B., Keener J.P., . Uniqueness of flow of a second-order fluid past a stretching sheet. Quart. Appl. Math.. 1987;44:753-755.
[Google Scholar]
Wang C.Y., . The three-dimensional flow due to a stretching surface. Phys. Fluids. 1984;27:1915-1917.
[Google Scholar]
Wazwaz A.M., . A study on a boundary-layer equation arising in an incompressible fluid. Appl. Math. Comput.. 1997;87:199-204.
[Google Scholar]
Wazwaz A.M., . The modified decomposition method and Padé approximants for a boundary layer equation in unbounded domain. Appl. Math. Comput.. 2006;177:737-744.
[Google Scholar]
Xu L., . He's homotopy perturbation method for a boundary layer equation in unbounded domain. Comput. Math. Appl.. 2007;54:1067-1070.
[Google Scholar]
Yıldırım Ahmet, Berberler Murat Ersen, . Homotopy perturbation method for numerical solutions of KdV–Burger's and Lax's seventh-order KdV equations. Numer. Methods Partial Differ. Eq.. 2010;26:1040-1053.
[Google Scholar]
Yıldırım A., Sezer S.A., . Non-perturbative solution of the MHD flow over a non-linear stretching sheet by HPM-Padé technique. Z. Naturforsch. A: J. Phys. Sci.. 2010;65:1106-1110.
[Google Scholar]

Introduction

A new modified homotopy perturbation method

Governing equations

Application

Results and discussion

Concluding remarks

Fulltext Views
5

PDF downloads
3

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Andersson H.I., . MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech.. 1992;95:227-230.
[Google Scholar]

[2] Ariel P.D., . Computation of flow of viscoelastic fluids by parameter differentiation. Int. J. Numer. Methods Fluids. 1992;15:1295-1312.
[Google Scholar]

[3] Ariel P.D., . MHD flow of a viscoelastic fluid past a stretching sheet with suction. Acta Mech.. 1994;105:49-56.
[Google Scholar]

[4] Ariel P.D., . On the second solution of flow of viscoelastic fluid over a stretching sheet. Quart. Appl. Math.. 1995;53:629-632.
[Google Scholar]

[5] Ariel P.D., . Axisymmetric flow of a second grade fluid past a stretching sheet. Int. J. Eng. Sci.. 2001;39:529-553.
[Google Scholar]

[6] Ariel P.D., . Extended homotopy perturbation method and computation of flow past a stretching sheet. Comput. Math. Appl.. 2009;58:2402-2409.
[Google Scholar]

[7] Ariel, P.D., 2004. Computation of MHD flow due to moving boundary. Technical Report MCS-2004-01, Department of Mathematical Sciences, Trinity Western University.

[8] Ariel P.D., Hayat T., Asghar S., . Homotopy perturbation method and axisymmetric flow over a stretching sheet. Int. J. Nonlinear Sci. Numer. Simul.. 2006;7:399-406.
[Google Scholar]

[9] Ates Inan, Yıldırım Ahmet, . Comparison between variational iteration method and homotopy perturbation method for linear and nonlinear partial differential equations with the nonhomogeneous initial conditions. Numer. Methods Partial Differ. Eq.. 2010;26:1581-1593.
[Google Scholar]

[10] Awang Kechil S., Hashim I., . Non-perturbative solution of free-convection boundary-layer equation by Adomian decomposition method. Phys. Lett. A. 2007;363:110-114.
[Google Scholar]

[11] Awang Kechil S., Hashim I., . Series solution of flow over nonlinearly stretching sheet with chemical reaction and magnetic field. Phys. Lett. A. 2008;372:2258-2263.
[Google Scholar]

[12] Banks W.H.H., . Similarity solutions of the boundary layer equations for a stretching wall. J. Mech. Theor. Appl.. 1983;2:375-392.
[Google Scholar]

[13] Chaim T.C., . Hydromagnetic flow over a surface stretching with a power law velocity. Int. J. Eng. Sci.. 1995;33:429-435.
[Google Scholar]

[14] Crane L.J., . Flow past a stretching plate. Z. Angew. Math. Phys.. 1970;21:645-647.
[Google Scholar]

[15] Fathizadeh M., Rashidi F., . Boundary layer convective heat transfer with pressure gradient using homotopy perturbation method (HPM) over a flat plate. Chaos Solitons Fract.. 2009;42:2413-2419.
[Google Scholar]

[16] Ganji Z.Z., Ganji D.D., . Analytical solution of viscous flow in porous media using ADM and comparison with the numerical Runge–Kutta method. Transp. Porous Med.. 2010;81:527-546.
[Google Scholar]

[17] Ganji D.D., Gorji M., Alipanah M., Farnad E., . Analytical solutions to nonlinear equations arising in heat transfer by variational iteration, homotopy perturbation, and Adomian decomposition methods. Numer. Methods Partial Differ. Eq. 2009 doi:10.1002/num.20503
[Google Scholar]

[18] Ganji D.D., Ganji S.S., Karimpour S., Ganji Z.Z., . Numerical study of homotopy-perturbation method applied to Burgers equation in fluid. Numer. Methods Partial Differ. Eq.. 2010;26:917-930.
[Google Scholar]

[19] Ganji Davood Domiri, Safari Mehdi, Ghayor Reza, . Application of He's variational iteration method and Adomian's decomposition method to Sawada–Kotera–Ito seventh-order equation. Numer. Methods Partial Differ. Eq.. 2010;26:1463-1475.
[Google Scholar]

[20] Gupta P.S., Gupta A.S., . Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng.. 1977;55:744-746.
[Google Scholar]

[21] Hayat T., Hussain Q., Javed T., . The modified decomposition method and Pade approximants for the MHD flow over a non-linear stretching sheet. Nonlinear Anal.: Real World Appl.. 2009;10:966-973.
[Google Scholar]

[22] He J.H., . Homotopy perturbation technique. Comput. Math. Appl. Mech. Eng. 1999:178-257.
[Google Scholar]

[23] He J.H., . A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J. Nonlinear Mech.. 2000;35(1):115-123.
[Google Scholar]

[24] He J.H., . Comparison of homotopy perturbation method and homotopy analysis method. Appl. Math. Comput.. 2004;156:527-539.
[Google Scholar]

[25] He J.H., . Homotopy perturbation method for solving boundary value problems. Phys. Lett. A. 2006;350:87-88.
[Google Scholar]

[26] He J.H., . Strongly Nonlinear Problems, Dissertation. Berlin: de-Verlag im Internat GmbH; 2006.

[27] He J.H., . New interpretation of homotopy perturbation method. Int. J. Modern Phys. B. 2006;20:1-7.
[Google Scholar]

[28] He J.H., . Recent developments of the homotopy perturbation method. Top. Methods Nonlinear Anal.. 2008;31:205-209.
[Google Scholar]

[29] Kelleci Alev, Yıldırım Ahmet, . An efficient numerical method for solving coupled Burgers’ equation by combining homotopy perturbation and Pade techniques. Numer. Methods Partial Differ. Eq.. 2011;27:982-995.
[Google Scholar]

[30] Khan Yasir, . An effective modification of the Laplace decomposition method for nonlinear equations. Int. J. Nonlinear Sci. Numer. Simul.. 2009;10(11–12):1373-1376.
[Google Scholar]

[31] Khan Yasir, Austin Francis, . Application of the Laplace decomposition method to nonlinear homogeneous and non-homogeneous advection equations. Z. Naturforsch.. 2010;65a:849-853.
[Google Scholar]

[32] Khan Yasir, Faraz Naeem, . A new approach to differential difference equations. J. Adv. Res. Differ. Eq.. 2010;2(2):1-12.
[Google Scholar]

[33] Khan Yasir, Faraz Naeem, . Application of modified Laplace decomposition method for solving boundary layer equation. J. King. Saud Univ. Sci.. 2011;23(1):115-119.
[Google Scholar]

[34] Madani M., Fathizadeh M., . Homotopy perturbation algorithm using Laplace transformation. Nonlinear Sci. Lett. A. 2010;1(3):263-267.
[Google Scholar]

[35] Mcleod J.B., Rajagopal K.R., . On the uniqueness of flow of a Navier–Stokes fluid due to a stretching boundary. Arch. Ration. Mech. Anal.. 1987;98:386-393.
[Google Scholar]

[36] Mirgolbabaei H., Ganji D.D., Etghani M.M., Sobati A., . Adapted variational iteration method and axisymmetric flow over a stretching sheet. World J. Model. Simul.. 2009;5:307-314.
[Google Scholar]

[37] Mohyud-Din S.T., Yıldırım A., Sezer S.A., Usman M., . Modified variational iteration method for free-convective boundary-layer equation using Padé approximation. Math. Probl. Eng.. 2010;2010:1-11. (Article ID 318298)
[Google Scholar]

[38] Mustafa Inc., 2010. He's homotopy perturbation method for solving Korteweg–de Vries Burgers equation with initial condition. Numer. Methods Partial Differ. Eq. 26, 1224–1235.

[39] Noor M.A., Mohyud-Din S.T., . Modified variational iteration for a boundary layer problem in unbounded domain. Int. J. Nonlinear Sci.. 2009;7(4):426-430.
[Google Scholar]

[40] Noor N.F.M., Awang Kechil S., Hashim I., . Simple non-perturbative solution for MHD viscous flow due to a shrinking sheet. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:144-148.
[Google Scholar]

[41] Raftari B., Yıldırım A., . The application of homotopy perturbation method for MHD flows of UCM fluids above porous stretching sheets. Comput. Math. Appl.. 2010;59:3328-3337.
[Google Scholar]

[42] Rashidi M.M., . The modified differential transform method for solving MHD boundary-layer equations. Comput. Phys. Commun.. 2009;180:2210-2217.
[Google Scholar]

[43] Sajid M., Hayat T., . The application of homotopy analysis method for MHD viscous flow due to a shrinking sheet. Chaos Solitons Fract.. 2009;39:1317-1323.
[Google Scholar]

[44] Sajid M., Javed T., Hayat T., . MHD rotating flow of a viscous fluid over a shrinking surface. Nonlinear Dyn.. 2008;51:259-265.
[Google Scholar]

[45] Samuel T.D.M.A., Hall I.M., . On the series solution to the laminar boundary layer with stationary origin on a continuous moving porous surface. Proc. Camb. Philos. Soc.. 1973;73:223-229.
[Google Scholar]

[46] Troy W., Overman E.A. II, Ermentrout G.B., Keener J.P., . Uniqueness of flow of a second-order fluid past a stretching sheet. Quart. Appl. Math.. 1987;44:753-755.
[Google Scholar]

[47] Wang C.Y., . The three-dimensional flow due to a stretching surface. Phys. Fluids. 1984;27:1915-1917.
[Google Scholar]

[48] Wazwaz A.M., . A study on a boundary-layer equation arising in an incompressible fluid. Appl. Math. Comput.. 1997;87:199-204.
[Google Scholar]

[49] Wazwaz A.M., . The modified decomposition method and Padé approximants for a boundary layer equation in unbounded domain. Appl. Math. Comput.. 2006;177:737-744.
[Google Scholar]

[50] Xu L., . He's homotopy perturbation method for a boundary layer equation in unbounded domain. Comput. Math. Appl.. 2007;54:1067-1070.
[Google Scholar]

[51] Yıldırım Ahmet, Berberler Murat Ersen, . Homotopy perturbation method for numerical solutions of KdV–Burger's and Lax's seventh-order KdV equations. Numer. Methods Partial Differ. Eq.. 2010;26:1040-1053.
[Google Scholar]

[52] Yıldırım A., Sezer S.A., . Non-perturbative solution of the MHD flow over a non-linear stretching sheet by HPM-Padé technique. Z. Naturforsch. A: J. Phys. Sci.. 2010;65:1106-1110.
[Google Scholar]