A reliable numerical method for solving fractional reaction-diffusion equations
⁎Corresponding author. devendra.maths@gmail.com (Devendra Kumar),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The present work aims to solve the fractional reaction–diffusion equation (RDE) using an effective and powerful hybrid analytical scheme, namely q-HASTM. The suggested technique is the combination of Sumudu transform (ST) and HAM technique. The definition of Caputo's fractional derivative has used. The numerical procedure reveals that only few iterations are needed for better approximation of the solution which illustrate the competence and sincerity of the suggested scheme. The impact of the reaction term in the solution of the problem explained through the graph.
Keywords
Caputo fractional derivative
Reaction-diffusion equation
q-HAM
Sumudu transform
1 Introduction
The word diffusion had been consequent of the Latin word “diffundere,” which indicates diffused of a substance concerning area of high concentration to low concentration.
It is also well-known as Brownian motion. It was noticed by the Brownian who was the botanist and investigating that the movement of pollen grains under a microscope, and observing their unpredictable jitter in water (Brown, 1828). In 1905, Einstein established the relation between the traditional diffusion equation and Brownian motion.
The process of diffusion may be described in one of two ways, via Langevin's equation (Langevin and Acad, 1908) or a continuum approach. In 1885, Adolf Fick introduced Fick's first and second laws of diffusion (Philbert, 2005). The first law of diffusion describes the relationship between the flux of particles J and the spatial derivative of the probability distribution function of the particles. Fick's second law relates the time and special derivative of the probability density function (
PDF) and flux respectively.
The standard diffusion equation
The RDEs are significant type of parabolic equations emerge in many scientific and engineering problems
We know that this equation straightforwardly solved when
FDEs have been new applications in areas of science and technology. Some essential results interrelated to solving differential equations with derivatives of fractional order (FO) may be initiate in Kilbas et al. (2006) have provided a very reliable and relevant discussion expressly on the subject of fractional calculus. The fractional differential equations became popular because the FO system eventually converges to the response system of integer-order. During past years the fractional reaction diffusion equations have been proved to be a decent model especially for numerous systems in the several streams of science, engineering and biology due to their practical relevance. The RDEs naturally express the various evolving problems in the physical realm: chemistry, physics, biomechanics, and other fields of knowledge. Generally, the nonlinear problems do not have an exact solution; substantially difficult to get it for the nonlinear problems with fractional order derivatives. So, approximate analytical methods will help determine these kinds of equations. Mainardi et al. (2001) explained the significant solution of time and space fractional diffusion equation. Wazwaz (2001) used the ADM to determine the diffusion equation's solution in the nonlinear case. Hao et al. (2013) examined the Helmholtz and diffusion equations on the Cantor sets involving local fractional derivative operators.
Yang et al. (2015) have been presented the non-differentiable diffusion equation by the local fractional similarity solution. Yang et al. (2016) employed a two-dimensional extended differential transform method for solving the local fractional diffusion equation.
Gao et al. (2016) proposed the coupling of the variational iteration method with the Sumudu transform through the local fractional calculus operator to solve the local fractional diffusion equation in one-dimensional fractal space.
Zhukovsky and Srivastava (2017) implemented an operational method, coupled with integral transforms and extended forms of orthogonal polynomials to achieve exact analytical solutions for heat diffusion equations beyond the Fourier model.
Yang et al. (2017) studied the Riemann-Liouville and Liouville-Caputo fractional time anomalous diffusion models with non-singular power-law kernel.
Mahto et al. (2019) investigated the approximate controllability of an impulsive system's fractional sub-diffusion equation by employing a unique continuation property.
Schot et al. (2007) obtained a solution of the diffusion equation approximately in terms of Fox H-function. Zahran (2009) have derived an exact solution of the generalized linear fractional reaction–diffusion equation in the form of Fox H-function. Silva et al. (2007) and Lenzi et al. (2009) solved a nonlinear diffusion equation that comprises spatial derivatives with fractional order. Das (2009) investigated the fractional diffusion equation's analytical solution in the appearance of outside force via VIM. Das and Gupta (2010) discussed the fractional diffusion equation in the presence of a reaction term and outside force via HPM. Singh et al. (2012) performed HPTM for handling fractional order RDEs. Kumar et al. (Kumar et al., 2015) analyzed the fractional-order multi-dimensional diffusion equations by the Laplace transform approach. Tripathi et al. (2016) obtained a solution of higher-order fractional time derivative RDE. In 2017, Tiwana et al. (2017) solved the Lotka-Volterra type fractional non-linear reaction diffusion system via HPTM. Zheng et al. (2017) solved numerically fractional order RDE with moving boundary conditions for the first time. Das et al. (2018) determined the numerical explication for the fractional-order advection-reaction diffusion equation. Saad et al. (2020) used the numerical method based upon the Lagrange polynomial interpolation to estimate the approximate solutions to the fractional-order quadratic autocatalysis model with linear inhibition.
Singh et al. (2017) proposed a numerical algorithm for the fractional vibration equation solution.
Srivastava et al. (2019) proposed an appropriate novel method based on the Gegenbauer wavelet expansion, coupling with operational matrices of fractional integral and block-pulse functions to solve the Bagley–Torvik equation.
Srivastava et al. (2020) applied the Chebyshev spectral collocation method for approximate solutions of the Ebola virus model with fractional Liouville-Caputo derivative.
Singh and Srivastava (2020) studied numerical Simulation for fractional-order Bloch equation in nuclear magnetic resonance using the Jacobi polynomials.
Srivastava and Saad (2020a) investigated the numerical solutions of the fractal-fractional Ebola virus in the sense of three different kernels based on the power law, the exponential decay, and the generalized Mittag-Leffler function.
Srivastava and Saad (2020b) employed the spectral collocation method with the shifted Legendre polynomials, the two-stage fractional Runge–Kutta method, and the four-stage fractional Runge–Kutta method to find the numerical solutions of the fractional-order clock chemical model.
Das et al. (2011) discussed the explication of a fractional reaction-diffusion equation via HPM. S. J. Liao (Liao, 1995, 2003, 2004) proposed and developed an approximate analytical scheme HAM by adopting the concept of homotopy, which methodically studies the differential equations of nonlinear characteristics. The approach of various nonlinear problems applying HAM confirms its efficiency and effectiveness (Mohyud-Din et al., 2011; Onyejek, 2014; Song and Zhang, 2007; Tan and Abbasbandy, 2008).
Integral transform technique is extensively used and a lot of work has been done. In 1993, the Sumudu transform was developed by Watugala (1993) and applied to solve of ODE in control engineering problems. The fundamental properties of Sumudu transform are deliberate in Belgacem and Karaballi (2006), Chaurasia and Singh (2010).
The fusion scheme q-HASTM has been proposed by Singh et al. (2017). This scheme is a combination of Sumudu transform and q-HAM. El-Tawil and Huseen (2012, 2013) proposed the method q-HAM, the improvement in HAM with the simplification of the embedding parameter
In this article the powerful mathematical tool q-HASTM is successfully applied to solve fractional order reaction diffusion equation in existence of reaction term
2 Preliminaries and notations
This section defines the essential definition and characteristics of fractional derivatives, integrals and the ST operator.
Definition 2.1. (Kilbas et al., 2006)
A function
Liouvile-Caputo derivative of fractional order
we have
The operator
we have
Consider a set of functions
where ST described as,
The ST of derivative of fractional order in Caputo’ form is
and
3 Solution of problem by q-HASTM
Applying ST operator on Eq. (1), and employing fractional derivative of ST, we obtain
On simplifying Eq. (3), we obtain
Now, we state an operator in nonlinear form
Now, construct the homotopy as
where
hence
Now expansion
We can control convergence of above series by adjusting value of
Define the vectors
Differentiating equation (6)
Operating inverse ST in Eq. (10) and setting
So,
Where,
Now, we obtain the solution of Eq. (11) is
Thus,
Proceeding, other iterations of
Conclusively, we get the solution of
The preceding series solution usually converges very quickly.
4 Numerical results and discussion
Numerical consequences of the chemical concentration
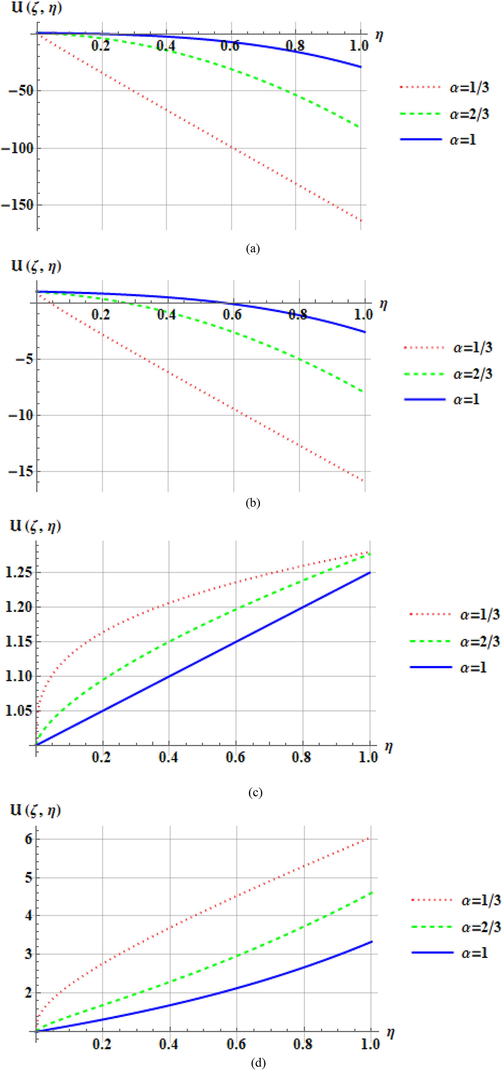
- Plots of
- Plots of
- Plots of
- Plots of
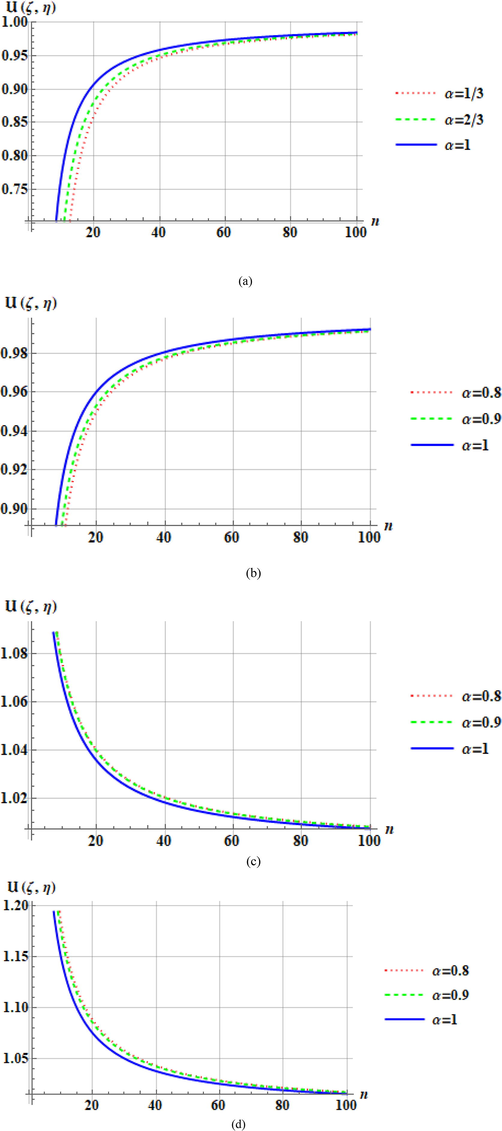
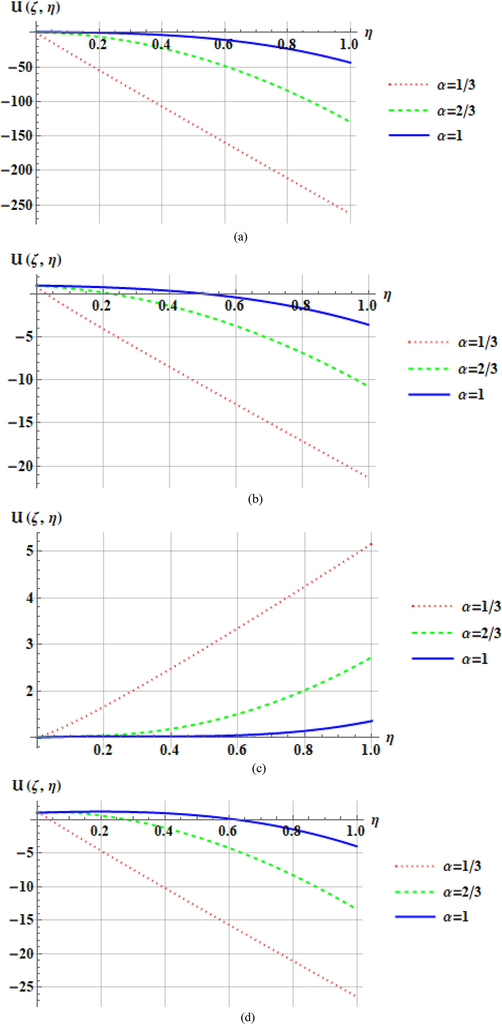
- Plots of
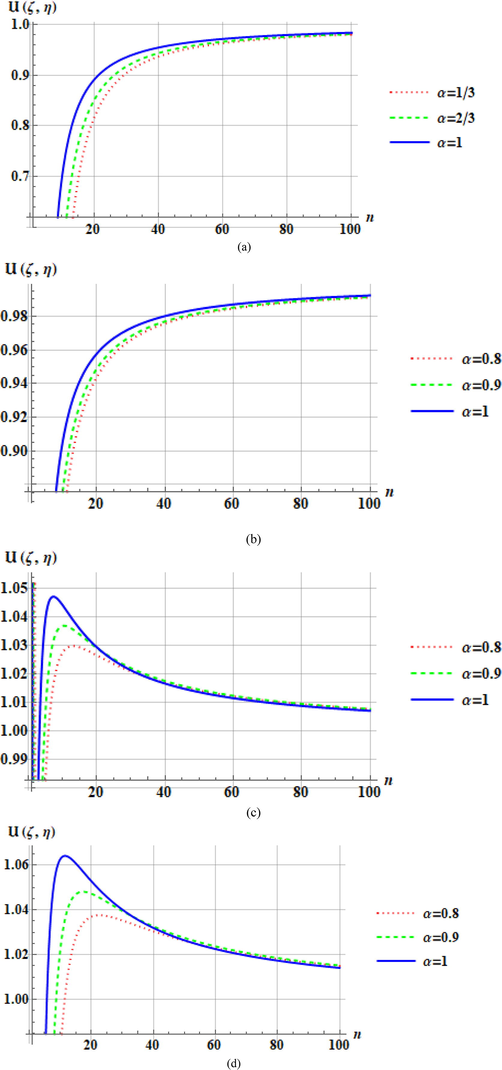
- Plots of
From Fig. 2 when reaction term is absent i.e.
Figs. 3 and 4, demonstrate the variation of
It is detected that in Fig. 3,
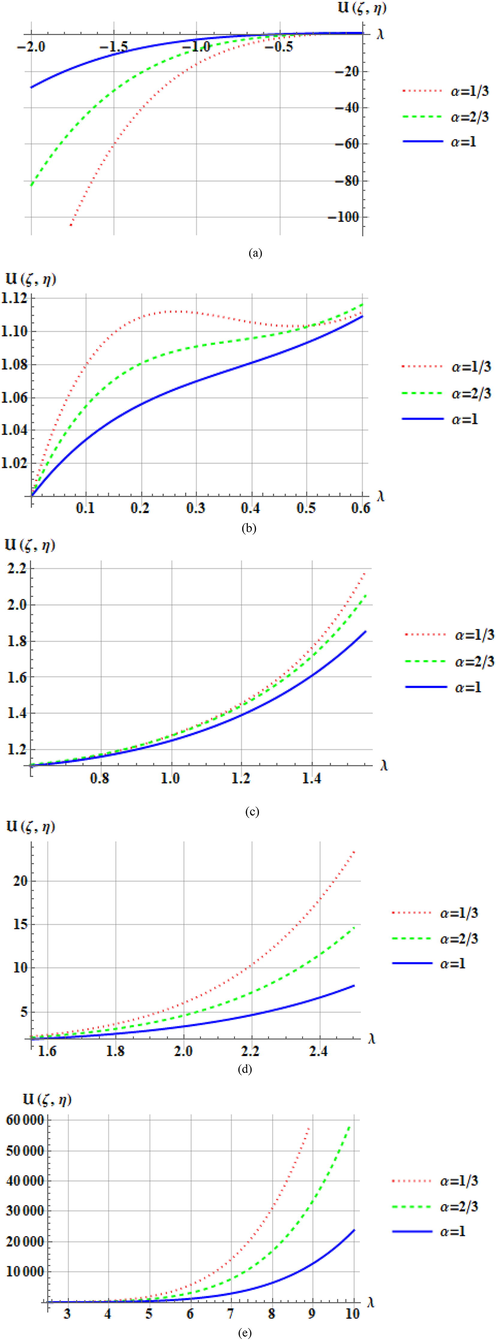
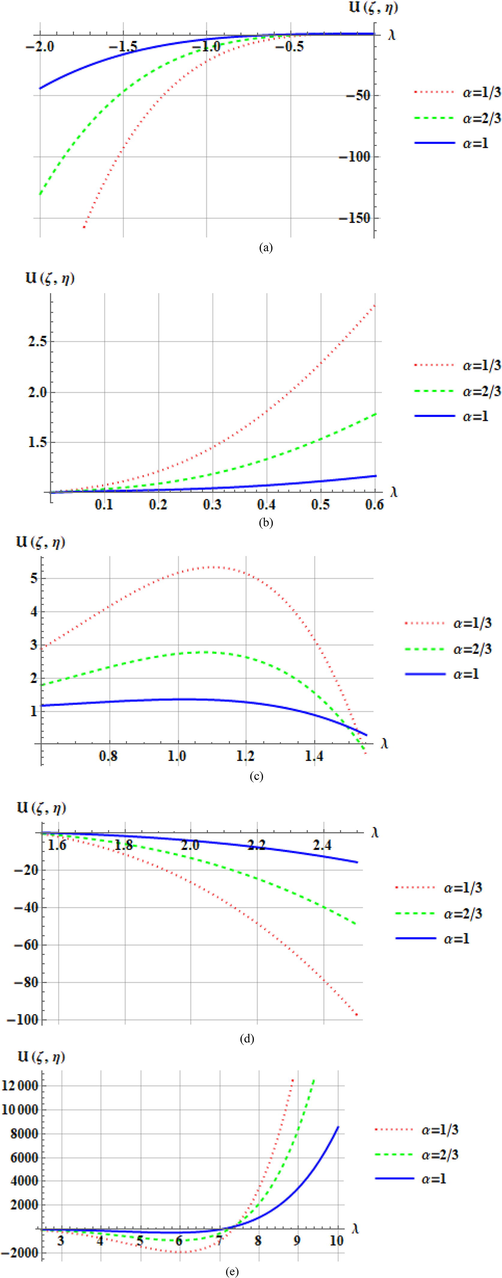
Figs. 5 and 6 plots of
5 Conclusion
The present study exhibits the prosperous purpose of q-HATM to achieve solutions of a reaction-diffusion equation with fractional time derivatives approximately. The q-HATM gives quantitatively reliable outcomes with fewer computational effort and adequately selecting the control parameters and gives a more accurate approximate solution. The study's significant part is the presentation graphically of the consequence of the reaction part on the nonlinear fractional diffusion equation solution. The prominent characteristic of the projected work is the demonstration of the considered fractional-order equation's stochastic nature. The article effectively demonstrates the consequence of damping with the occurrence of reaction term.
The effect of reaction term in the range
CRediT authorship contribution statement
Supriya Yadav: Conceptualization, Formal analysis, Methodology, Writing - review & editing. Devendra Kumar: Conceptualization, Formal analysis, Investigation, Writing - original draft, Writing - review & editing. Kottakkaran Sooppy Nisar: Conceptualization, Formal analysis, Investigation, Methodology, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Sumudu transform fundamental properties investigation and applications. J. Appl. Math. Stochastic Anal. 2006:1-23.
- [Google Scholar]
- Philos. Mag.. 1828;4:161.
- Application of Sumudu transform in Schrödinger equation occurring in quantum mechanics. Appl. Math. Sci.. 2010;4(57):2843-2850.
- [Google Scholar]
- A note on fractional diffusion equation. Chaos, Solitons & Fractals.. 2009;42:2074-2079.
- [Google Scholar]
- Das S, Gupta PK. An approximate analytical solution of the fractional diffusion equation with absorbent term and external force by homotopy perturbation method. Z. Fur Naturforsch Sec A, 2009.
- An approximate solution of nonlinear fractional reaction–diffusion equation. Appl. Math. Model.. 2011;35(8):4071-4076.
- [CrossRef] [Google Scholar]
- Numerical solution of fractional order advection-reaction diffusion equation. Therm. Sci.. 2018;22(Suppl. 1):309-316.
- [CrossRef] [Google Scholar]
- Travelling wave behavior for a porous-Fisher equation. Eur. J. Appl. Math.. 1998;9:285-304.
- [Google Scholar]
- The balance between strong reaction and slow diffusion. Commun. Part. Differ. Equat.. 1990;15(2):159-183.
- [CrossRef] [Google Scholar]
- Travelling waves and finite propagation in a reaction-diffusion equation. J. Different. Equat.. 1991;93(1):19-61.
- [CrossRef] [Google Scholar]
- The q-homotopy analysis method (q- HAM) Int. J. Appl. Math. Mech.. 2012;8(15):51-75.
- [Google Scholar]
- On convergence of the q-homotopy analysis method. Int. J. Conte. Math. Sci.. 2013;8(10):481-497.
- [Google Scholar]
- Travelling waves to a reaction-diffusion equation. Discrete Continuous Dyn. Syst.. 2007;Supplement:382-1290.
- [Google Scholar]
- Ann. Eugenics. 1937;7:355.
- Feng Gao, H. M. Srivastava, Ya-Nan Gao, Xiao-Jun Yang, A coupling method involving the Sumudu transform and the variational iteration method for a class of local fractional diffusion equations J. Nonlinear Sci. Appl. 9 (2016), 5830 5835.
- Helmholtz and diffusion equations associated with local fractional derivative operators involving the cantorian and cantor-type cylindrical coordinates. Adv. Math. Phys.. 2013;2013:1-5.
- [CrossRef] [Google Scholar]
- Theory and applications of fractional differential equations. North-Holland mathematical studies. Vol 204. Amsterdam, London and New York: Elsevier (North-Holland) Science Publishers; 2006.
- D. Kumar, J. Singh, S. Kumar, Analytical modelling for fractional multi-dimensional diffusion equations by using Laplace transform, Commu. Numer. Anal., 16-29, 2015.
- Sci. (Paris). 1908;146:530.
- Lenzi EK, Lenzi MK, Evangelista LR, Malacarne LC, Mendes RS. Solutions for a fractional nonlinear diffusion equation with external force and absorbent term. J. Stat. Mech., P02048, 2009.
- Approximate solution technique not depending on small parameters: a special example. Int. J. Nonlinear Mech.. 1995;30(3):371-380.
- [Google Scholar]
- Beyond Perturbation: Introduction to Homotopy Analysis Method. Boca Raton: Chapman and Hall/CRC Press; 2003.
- On the homotopy analysis method for nonlinear problems. Appl. Math. Comput.. 2004;147(2):499-513.
- [CrossRef] [Google Scholar]
- L. Mahto, S. Abbas, M. Hafayed and H. M. Srivastava, Approximate Controllability of Sub-Diffusion Equation with Impulsive Condition, Mathematics 2019, 7, 190; doi:10.3390/math7020190.
- The fundamental solution of the space time fractional diffusion equation. Fract. Calc. Appl. Anal.. 2001;4:153-192.
- [Google Scholar]
- Homotopy analysis method for fractional partial differential equations. Inter. J. Phys. Sci.. 2011;6(1):136-145.
- [Google Scholar]
- Solutions of some parabolic inverse problems by homotopy analysis method. Inter. J. Appl. Math. Res.. 2014;3(1):81-87.
- [Google Scholar]
- Diffusion Fundamantals. 2005;2:1.
- A Fractional Quadratic autocatalysis associated with chemical clock reactions involving linear inhibition. Chaos Solitons Fractals. 2020;132:109557
- [Google Scholar]
- Fractional diffusion equation with an absorbent term and a linear external force: Exact solution. Phys. Lett. A. 2007;366:346-350.
- [Google Scholar]
- Fractional nonlinear diffusion equation, solutions and anomalous diffusion. Physica A: Stat. Mech. Appl.. 2007;375(1):65-71.
- [CrossRef] [Google Scholar]
- H. Singh and H. M. Srivastava, Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials, Appl. Sci. 2020, 10, 2850; doi:10.3390/app10082850.
- J. Singh, D. Kumar, Sushila, Application of homotopy perturbation transform method to linear and nonlinear space-time fractional reaction diffusion equations, J. Math. Comput. Sci. 5 (1), 40-52, 2012.
- A novel numerical approach for a nonlinear fractional dynamic model of interpersonal and romantic relationships. Entropy. 2017;19(7):1-17.
- [Google Scholar]
- A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons Fractals. 2017;103:131-138.
- [CrossRef] [Google Scholar]
- Application of homotopy analysis method to fractional KdV–Burgers–Kuramoto equation. Phys. Lett. A. 2007;367(1-2):88-94.
- [CrossRef] [Google Scholar]
- H. M. Srivastava and K. M. Saad, Numerical Simulation of the Fractal-Fractional Ebola Virus, Fractal Fract. 2020, 4, 49; doi:10.3390/fractalfract4040049.
- H. M. Srivastava and K. M. Saad, A Comparative Study of the Fractional-Order Clock, Chemical Model, Mathematics 2020, 8, 1436; doi:10.3390/math8091436.
- An application of the gegenbauer wavelet method for the numerical solution of the fractional bagley-torvik equation. Russ. J. Math. Phys.. 2019;26(1):77-93.
- [CrossRef] [Google Scholar]
- An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals. 2020;140:110174
- [Google Scholar]
- Homotopy analysis method for quadratic Riccati differential equation. Commun. Nonlinear Sci. Numer. Simul.. 2008;13(3):539-546.
- [CrossRef] [Google Scholar]
- An alternative approach to the Epstein-Hubbel integral for the energy behaviour study of a class of nuclear reaction products. Radiat. Phys. Chem.. 1997;49(3):319-326.
- [Google Scholar]
- Homotopy perturbation Laplace transform solution of fractional non-linear reaction diffusion system of Lotka-Volterra type differential equation. Eng. Sci. Technol. Int. J.. 2017;20(2):672-678.
- [CrossRef] [Google Scholar]
- N. K. Tripathi, S. Das, S. H. Ong, H. Jafari, et al., Solution of higher order nonlinear time fractional reaction diffusion equation, Entropy, 1-11, 2016.
- Sumudu transform: A new integral transform to solve differential equations and control engineering problems. Int. J. Math. Educ. Sci. Technol.. 1993;24(1):35-43.
- [CrossRef] [Google Scholar]
- Exact solutions to nonlinear diffusion equations obtained by the decomposition method. Appl. Math. Comput.. 2001;123(1):109-122.
- [CrossRef] [Google Scholar]
- An asymptotic solution for traveling waves of a nonlinear-diffusion Fisher's equation. J. Math. Biol.. 1994;33(1):1-16.
- [CrossRef] [Google Scholar]
- A new numerical technique for solving the local fractional diffusion equation: Two-dimensional extended differential transform approach. Appl. Math. Comput.. 2016;274:143-151.
- [Google Scholar]
- Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett.. 2015;47:54-60.
- [CrossRef] [Google Scholar]
- General fractional-order anomalous diffusion with non-singular power-law kernel. Therm. Sci.. 2017;21(suppl. 1):1-9.
- [CrossRef] [Google Scholar]
- On the derivation of fractional diffusion equation with an absorbent term and a linear external force. Appl. Math. Model.. 2009;33(7):3088-3092.
- [CrossRef] [Google Scholar]
- Numerical solution of time fractional reaction-diffusion equation with a moving boundary. J. Comput. Phys.. 2017;338:493-510.
- [Google Scholar]
- Analytical solutions for heat diffusion beyond Fourier law. Appl. Math. Comput.. 2017;293:423-437.
- [CrossRef] [Google Scholar]







