A novel pixel’s fractional mean-based image enhancement algorithm for better image splicing detection

2.1 Preprocessing

In the proposed model, we rely on preprocessing to ensure a better features extraction process which will improve the accuracy of the algorithm later on.

2.1.1

2.1.1 Chroma space

In this step, the input RGB image is converted to the YCbCr color space. The RGB space is the most popular and widely used color space in digital imaging. It simply represents the intensities of the red, green, and blue colors. Although RGB has its own advantages over the other color spaces, it is not suitable for use with splicing detection because in RGB, the correlation between red, green, and blue colors is very high, and the chromatic and achromatic information cannot be differentiated. We previously demonstrated the advantage of using the YCbCr color space in forgery detection through another algorithm (Moghaddasi et al., 2014; Subramaniam et al., 2019). In short, the YCbCr represents the luminance (Y), blue difference (Cb) and red difference (Cr) chrominance components, respectively. We chose Cb in our present study. Fig. 3 shows an RGB image and its YCbCr counterpart with the corresponding channels.

Close

Fig. 3

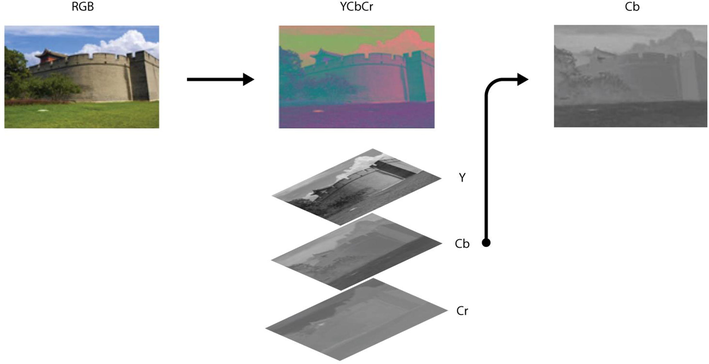
Illustration of preprocessing of a sample RGB image from the reference dataset. The obtained Cb images are subsequently enhanced by PFM and are then used for feature extraction.

Export to PPT

2.1.2

2.1.2 Proposed image enhancement algorithm

Here, we explore new fractional operators to enhance and preserve the fine details of the images for the purpose of image splicing detection. The fractional operator is one of the significant approaches in fractional analysis, which is utilized to measure the fractional structures of images. This approach is widely utilized for resolving complex problems in image processing (Jalab, 2021; Jalab et al., 2017; Jalab et al., 2019). We obtain the generalized fractional image enhancement method by using the fractional operator (Ibrahim, 2011) as follows: $$\begin{array}{c}{\mathrm{\Delta }}_{\varkappa }^{v,\omega }\vartheta \left(\varkappa \right):=\frac{1}{N}\frac{{\left(\omega +1\right)}^v}{\mathrm{\Gamma }\left(1-v\right)}\frac{d}{d\varkappa }{\int }_0^{\varkappa }\frac{{\varkappa }^{\omega }\vartheta \left(\varkappa \right)}{{\left({\varkappa }^{\omega +1}-{\varkappa }^{\omega +1}\right)}^v}d\varkappa ;v∊\left(0,1\right];\omega \ge 0\#\left(1\right)\end{array}$$ where ν,ω are the fractional operators.

Because the dimension in image processing is commonly considered to be two dimensions, it is convenient to use the two-dimensional parmetric operator as specified in Eq (1). More than, we consider the sample mean which is the arithmetic average of the values of pixels in an image. By applying the discrete formula of Eq. (1), we obtain the following expression for pixel’s fraction mean $\mathrm{\Delta }\left(\varkappa \right)$ :

For a function ϰ in a fractional set, and v, and ω > 1 then, the mean of image pixels (Δ (ϰ)) satisfies the following: $$\begin{array}{c}\mathrm{\Delta }\left(\varkappa \right)=\frac{1}{N}{\sum }_{n=1}^N\frac{{\left(1+\omega \right)}^{v-1}\mathrm{\Gamma }\left(1+\frac{n}{1+\omega }\right)}{\mathrm{\Gamma }\left(1+\frac{n}{1+\omega }-v\right)}{\varkappa }^{\left(1-v\right)\left(1+\omega \right)}\#\left(2\right)\end{array}$$

$\varkappa$ is the image’s pixel probability, N is the total number of image pixels, and $\mathrm{\Delta }\left(\varkappa \right)$ is the fractional mean parameter for input image pixels.

The image enhanced by the proposed FOIE (Ien) will be the result of the multiplication of the input image I with the mean parameter Δ, as follows: $$\begin{array}{c}\mathit{Ien}=Ix\mathrm{\Delta }\left(\varkappa \right)\#\left(3\right)\end{array}$$

The effects attained by the proposed PFM for a set of sample images are shown in Fig. 4 (C). It is noted from Fig. 4(B) that one may not be able to directly notice the abrupt changes caused by the splicing operation. However, when applying the PFM for enhancement as shown in Fig. 4 (C), the spliced regions become clearer and brighter. It can be seen that the proposed PFM enhances the details and the structure of tampered objects despite the overall noise and blur that affect the images.

Close

Fig. 4

The enhancement results of the proposed PFM. (A) The original spliced images, (B) the Cb converted images, (C) the PFM-enhanced images.

Export to PPT

The enhancement of the low visibility regions in the input images is attributed to the ability of PFM to dynamically extract the illumination values from the pixels of the input image. The logic behind using PFM in image enhancement lies in its capability to capture the details of the image according to the pixel’s probability, as well as to capture the high frequency details of an image, irrespective of noise, blur, and distortion created by the forgery operations. This signifies the contribution of PFM in this work. It can be concluded that PFM helps to widen the differences between the pixel values between authentic and tampered images.

In the preprocessing step, the image is broken up into several non-overlapping blocks with size of 16 × 16, and then the pixel intensity occurrences number is calculated. The algorithm for extracting the PFM for each block is based on Eq. (2) and is presented in Algorithm 1.

Algorithm 1: Pixel’s fractional mean (PFM)
Initialization: I = Input image, set the fractional power ω = 1.6
For each Input image I
[k1, k2, …, kn] split I into non-overlapped blocks size of r × r pixels
For i = 1 to n
${\mathit{PFM}}_{v,w}\leftarrow$ I // PFM is calculated as defined in Eq. (2)
EndFor
EndFor

In the proposed PFM, the two fractional operators (ω and v) play a vital role in achieving better enhancement results. To determine the optimal values that can give the best results across different datasets, 500 random samples were chosen from all the categories of the dataset and NIQE was calculated for ω when v = 1.5, as shown in Fig. 5. The ω value has been selected experimentally as illustrated in Fig. 5. It can be seen that when ω value is 1.6, the proposed method reaches the best NIQE score (lower is better and when ω = 1.6, NIQE is at its lowest). Therefore, the value of ω has been set to 1.6 across all of the experiments mentioned in this study. NIQE was utilized because it is a no-reference image quality score for measuring the quality of images that are affected by arbitrary distortions.

Close

Fig. 5

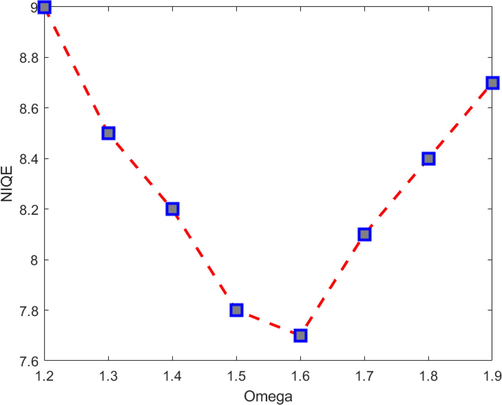
Showing the relationship between NIQE and ω. The value of the parameter ω is determined based on the lowest NIQE score.

Export to PPT

2.2 Feature extraction

Our proposed model is based on the extraction of low dimension features for the detection of image splicing. We primarily deal with the image artifacts that manifest as inconsistencies which can be seen in the tampered image. Specifically, we are concerned with the texture of the image which is altered as a result of the splicing process.

For this study, we considered the effect of the textural features of the tampered regions in forged images, which are represented by the individual pixel’s statistical properties such as the mean, variance, skewness, and kurtosis, in addition to the relation between pixels. For this, we considered the following: “Histogram of Oriented Gradient” (HOG) and “Gray-Level Co-Occurrence Matrix” (GLCM) (Dalal and Triggs, 2005).

1. HOG allows the measurement of the histograms of gradient directions (Dalal and Triggs, 2005). It describes the distribution of the directions of the local pixel intensities in each region of the image. This is done by dividing the image into smaller regions and creating 1-D gradient orientation histogram for each region. The direction and magnitude of the gradient, which are later used to obtain the HOG, are determined from the pixels found inside the given region. 13824 HOG textural features are obtained in total for every Cb image.

2. GLCM characterizes the texture of an image by considering the spatial relationship of pixels. It describes the frequency at which pixel pairs of certain values and spatial relationships occur in a grey-level image via a statistical measure. We used GLCM in the proposed work in four directions which indicate the offset between a pair of pixels. These directions are expressed as degrees (0°, 45°, 90°, 135°) where each one represents the neighborhood of the pixel i. In the present model, the offset is calculated by a pixel-long distance expressed as [0 1; −1 1; −1 0; −1–1] for all of the four directions. Fundamentally, for each element (i,j) in the GLCM matrix, the occurrence of the pixel with value ‘i’ in the direction to the pixel with value ‘j’ in image P is given. We employed GLCM to obtain a measure of the following features: contrast, correlation, energy, and homogeneity, which are described as follows:

The product of Eq. (4) represents the contrast between the given pixel and its neighborhood in the whole image, where it is equal to 0 if the image is constant. $$\begin{array}{c}\mathit{Correlation}=\sum \frac{\left(i-\mu i\right)\left(j-\mu j\right)p\left(i,j\right)}{{\sigma }_i{\sigma }_j}\#\left(5\right)\end{array}$$

The correlation represents the joint probability occurrence of the given pairs of pixels as formulated in Eq. (5), where µ and σ represent the mean and standard deviation of pixel i and pixel j respectively. The product of the equation specifies the extent to which two neighbors are perfectly correlated. Correlation is always expressed as values within the range of [−1,1] where a completely positively-correlated image has a correlation of +1, and a completely negatively-correlated image has a correlation of −1. $$\begin{array}{c}\mathit{Energy}=\sum {p\left(i,j\right)}^2\#\left(6\right)\end{array}$$

Energy measures the angular second moment of an image. The equation in Eq. (6) represents the sum of squared elements in the GLCM. The values of energy range from 0 to 1, where the energy is equal to 1 if the image is constant. $$\begin{array}{c}\mathit{Homogeneity}=\sum \frac{p\left(i,i\right)}{1+\left|i-j\right|}\#\left(7\right)\end{array}$$

Homogeneity provides a measure of how close the diagonal distribution of elements is in GLCM. Given in Eq. (7), the homogeneity values range from 0 to 1.

Overall, we extract (4 × 4) GLCM texture features by applying the aforementioned equations. Therefore, 1536 textural features from every Cb image are extracted from the GLCM for the purpose of splicing detection.

As mentioned previously, textural features are directly affected by the splicing operation such that any disturbances can be detected by the splicing detection algorithm. The distribution of textural features provides a quantitative basis to discriminate between authentic and spliced images. This behavior is illustrated in the scatter plot shown Fig. 6, in terms of the mean and standard deviation. Such plot allows us to demonstrate that the classification classes (i.e., authentic, and tampered) are distinctive, and can indeed be separated. From the figure, it can be noticed that the features are divided into two categories: “authentic” and “tampered”.

Close

Fig. 6

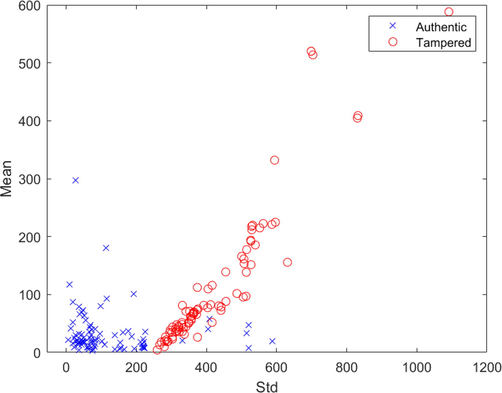
The feature distribution of authentic and spliced images from the reference database.

Export to PPT

2.3 Dimension reduction

Reducing the dimensionality of features is needed to be implemented to reduce the computational overhead and resources allocation. This ensures that the algorithm is operating at optimal and efficient settings, which leads to performance gains during the training and testing phases. Dimension reduction is carried out by removing non-essential features from the feature vector. The resulting feature vector would contain only essential features that give the best representation of the image.

In the present work, the mean, variance, and skewness are used to reduce the dimensionality of the data where these values are calculated for each feature set extracted by HOG and GLCM. At the end of feature reduction, the final feature vector would comprise sets of 28 features (12 from HOG and 16 from GLCM). The former is subsequently used by the SVM classifier to conduct the classification step

2.4 The classification

The proposed work employs the SVM classifier which is a well-known and is applied in different applications, such as pattern recognition and classification. The code for this classifier is accessible through MATLAB R2021b (The Mathworks (2021). “Matlab”.).

The SVM is a binary classifier works to divide images into two classes based on a kernel function (RBF). The SVM classification includes the split of the image’s dataset into training and testing.

In this study, 5-fold cross-validation is implemented. The dataset is divided into 5 subsets, and the main method is repeated 5 times, where in each iteration, 70% of the images are used for training, and the remaining 30% are used for testing. Additionally, for each iteration, one of the five subsets is used for testing while the rest are used for training. The setting ensures that every image is used for training and testing, thus eliminating any possible bias that could arise due to manual selection of data.

3.1 Image dataset

We used the publicly-available “CASIA V2.0” dataset in our present study (CASIA Tampered Image Detection Evaluation Database (CASIA TIDE v2.0)). This dataset is widely used in splicing detection. The dataset contains 12,614 images in total, of which 7491 (60%) are authentic, and 5123 (40%) are spliced. The images are classified into several categories and are offered in JPG, TIF, BMP image formats.

3.2 Evaluation metrics

Accuracy, true positive rate (TPR), and true negative rate (TNR) metrics were used to evaluate the performance of the proposed model. These metrics were calculated as follows: $$\begin{array}{c}\mathit{TPR}=\frac{\mathit{TP}}{\mathit{TP}+FN}\#\left(8\right)\end{array}$$ $$\begin{array}{c}\mathit{TNR}=\frac{\mathit{TN}}{\mathit{TN}+FP}\#\left(9\right)\end{array}$$ $$\begin{array}{c}\mathit{Accuracy}=\frac{\mathit{TP}+TN}{\mathit{TP}+TN+FN+FP}\#\left(10\right)\end{array}$$ where TP (“True Positive”) and TN (“True Negative”) indicate the number of spliced and original images that have been appropriately classified, whereas FN (“False Negative”) and FP (“False Positive”) represent the number of spliced and original images that are mistakenly labeled.

The results reveal that the proposed method is capable of achieving TPR, TNR, and accuracy rates of 98.80%, 98%, and 98.40% respectively with 28-D vector obtained from the CASIA V2.0 dataset (see Table 1). Another way to validate the classification results is using the “reception operating characteristic” (ROC) curve and its score (“area under the curve” AUC). This curve presents the classification performance at all thresholds by plotting the TP and FP rates. We constructed an ROC curve for the proposed model with the CASIA V2.0 dataset as shown in Fig. 7. From the figure, the AUC is equal to 0.99 (higher is better), which indicates better and improved separation of the classification classes.

Close

Fig. 7

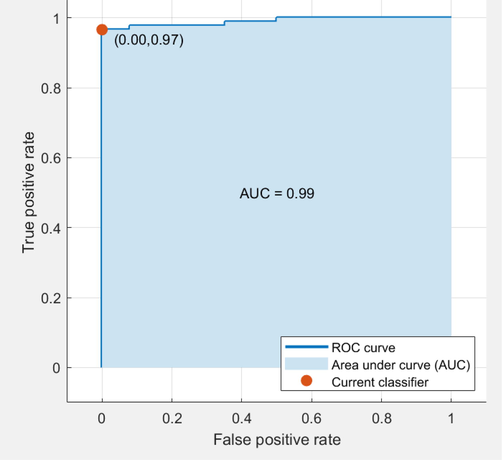
The ROC curve for the proposed model using the CASIA V2.0.

Export to PPT

3.3 Comparison with other image splicing detection algorithms

The proposed algorithm's performance was compared to those of similar state-of-the-art splicing detection approaches to verify its robustness. These include the following: Moghaddasi et al (2014) applied the “run length run number” algorithm along with PCA and kernel PCA for feature reduction to detect image splicing. This method achieved an accuracy rate of 93.80% with 100-D feature vector. Jaiprakash et al (2020) utilized image statistics and pixel correlation obtained from DCT and DWT domains to detect splicing and copy-move forgeries. The achieved accuracy by this method was 89.5% with 212-D feature vector. Li et al. (2017) employed Markov feature vector in quaternion discrete cosine transform to detect image splicing through the use of SVM. Their method achieved an accuracy rate of 92.38% with feature dimension of 972. El-Latif et al. (2019) proposed an algorithm for the detection of image splicing using deep learning with 1024-D vector for an automated generation of features from colored images. Despite the high accuracy of the method, which is comparable to ours, deep learning requires large overhead and thorough datasets, with limited hardware support. This can be considered as a disadvantage when aiming to develop an efficient algorithm.

Table 1 shows the results of the relative comparison between our method and the referenced state-of-the-art methods (El-Latif et al., 2019; Jaiprakash et al., 2020; Li et al., 2017; Moghaddasi et al., 2014; Subramaniam et al., 2019).

The experimental results showed that the proposed method achieved the highest splicing detection results, which showed how good the proposed method in detecting the spliced and authentic images. Moreover, the (Subramaniam et al., 2019) achieved the second highest accuracy among the five other methods.

The results shown in the table confirm that the proposed method achieves the highest accuracy with the lowest number of feature dimensions. This attest to the efficacy and reliability of the method, and further proves the benefit of using fractional calculus in image processing.