Translate this page into:
A new modified deflected subgradient method
⁎Corresponding author. belgacemrachid02@yahoo.fr (Rachid Belgacem),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
A new deflected subgradient algorithm is presented for computing a tighter lower bound of the dual problem. These bounds may be useful in nodes evaluation in a Branch and Bound algorithm to find the optimal solution of large-scale integer linear programming problems. The deflected direction search used in the present paper is a convex combination of the Modified Gradient Technique and the Average Direction Strategy. We identify the optimal convex combination parameter allowing the deflected subgradient vector direction to form a more acute angle with the best direction towards an optimal solution. The modified algorithm gives encouraging results for a selected symmetric travelling salesman problem (TSPs) instances taken from TSPLIB library.
Keywords
90C26
90C10
90C27
90C06
Integer linear programming
Subgradient method
Nonsmooth optimization
Travelling salesman problem

1 Introduction
In this paper we consider the following integer linear program:
It is easy to prove that
for all
(weak duality (Bazaraa et al., 2006)). The best choice for
would be the optimal solution of the following problem, called the dual problem:
With some suitable assumptions, the dual optimal value
is equal to
(strong duality (Bazaraa et al., 2006)). In general,
provides a tighter lower bound of
. These bounds may be useful in nodes evaluation in exact methods such as Branch and Bound algorithm to find the optimal solution of
. The function
is continuous and concave but non-smooth. The most widely adopted method for solving the dual problem is the subgradient optimization, see for instance Polyak (1967), Shor (1985), Nedic and Bertsekas (2010), Nesterov (2014) and Hu et al. (2015). The pure subgradient optimization method is an iterative procedure that can be used to solve the problem of maximizing (minimizing) a non-smooth concave (convex) function
on a closed convex set
. This procedure is summarized in Algorithm 1, and it is used in various fields in science and engineering (Sra et al., 2012). Choose an initial point
. Construct a sequence of points
which eventually converges to an optimal solution using the rule
, where
is a projection operator on the set
and
is a positive scalar called step length such that
Replace k by
and repeat the process until some stopping criteria.
Algorithm 1 (Based Subgradient Algorithm).
In the context of Lagrangian relaxation, computing the subgradient direction and the projection is a relatively easy problem. Since the subgradient is not necessarily a descent direction, the step-length rule (4) differs from those given in the area of descent methods. In fact, this choice assures the decreasing of the subsequence as well as the convergence of to . However, it is impossible to know in advance the value of for most problems. To this end, the most effective way is to use the variable target value methods developed in Kim et al. (1990), Fumero (2001) and Sherali et al. (2000).
Another challenge in subgradient optimization is the choice of direction search that affects the computational performance of the algorithm. It is known that choosing the subgradient direction
, leads to the zigzagging phenomenon that might cause slow the procedure to crawl towards optimality (Bazaraa et al., 2006). To overcome this situation, in the spirit of conjugate gradient method (Nocedal and Wright, 2006; Fletcher and Reeves, 1964), we can adopt a direction search that deflects the subgradient pure direction. Accordingly, the direction search
at
is computed as:
Some promising deflection algorithms of this type are the Modified Gradient Technique (MGT) (Camerini et al., 1975) and the Average Direction Strategy (ADS) (Sherali and Ulular, 1989). The MGT method was found to be superior to the pure subgradient method when used in concert with a specially designed step-length selection rule. The deflection parameter
is computed according to:
The ADS strategy recommends to make the deflection at each iteration point by choosing the direction search which simply bisects the angle between the current subgradient
and the previous direction search
. To get this direction, the deflection parameter is computed according to:
With this choice of the deflection parameter, the direction becomes:
Nowadays, the deflected subgradient method remains an important tool for nonsmooth optimization problems, especially for linear integer programming, due to its simple formulation and low storage requirement. In this paper, we present a new deflected direction search as a convex combination of the direction (8) and the direction (10). Our main result is the identification of the convex combination parameter which forces the algorithm to have a better deflection search than those given in the pure subgradient, MGT and ADS. For a numerical comparison of our approach and the two concurrent techniques MGT and ADS, we opted for the Travelling Salesman Problem (TSP) where its importance comes from the richness of its application and the fact that it is a typical of other problems of combinatorial optimization (Diaby and Karwan, 2016; El-Sherbeny, 2010).
The remainder of the paper is organized as follows: in Section 2, we describe our deflected subgradient method with convergence analysis. The computational tests, conducted on the Lagrangian relaxation of TSP of different sizes are described in Section 3. In Section 4 we conclude the paper.
2 A new modified deflected subgradient method
In this section, we present a new modified deflected subgradient method
which determines the direction search as follows:
We then obtain the following deflection parameter:
(Initialization): Choose a starting point
, let
and
. Determine a subgradient
and compute
where
is given by relation (12) and
will be specified later. Replace k by
if a stopping condition is not yet met and return to step 2.
Algorithm 2 (The Deflected Subgradient Algorithm).
Consider the deflected subgradient method algorithm given in Algorithm 2. The following proposition extends important properties of the subgradient vector and the deflected subgradient direction to the new deflected subgradient direction (11). With a best choice of the parameter make an acute angle with and . We also get the decreasing of the subsequence .
Let
,
be the new deflected subgradient direction given by (11) and (12) and let
be the sequence of iterations generated by the deflected subgradient scheme. If we take
and the stepsize
to satisfy
-
(14)
-
(15)
-
-
The proof is established by induction on k. Since we start with , the case is trivial. Now, assume that we have
(16)and let us establish (14) at iteration k. Using the definition of , we obtain thatFurthermore, from the concavity of the function , the induction hypothesis (16) and the inequalities in (13), we get
(17)Since the vector is perpendicular to the supporting hyperplane of at , the angle at is obtuse (see Fig. 1). We deduce that which is equivalent to
(18) -
We have
From the concavity of w, the inequalities in (13) and by applying (14) in Proposition 1, we get the following relations, respectively:
It follows, that
Consequently,
-
If then and hence the claim follows. Thus, consider the case . we have then
This completes the prove. □
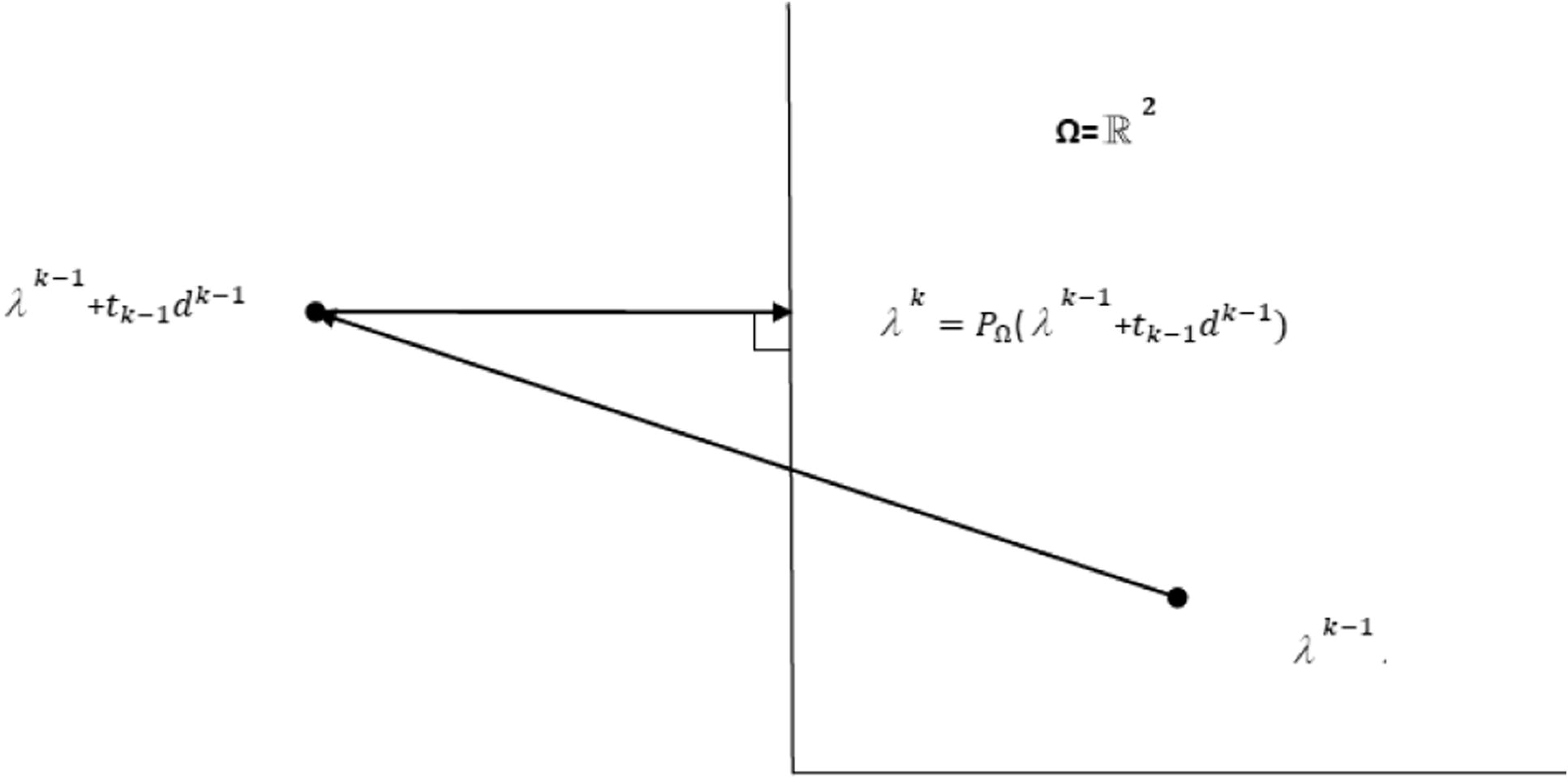
- Illustration in a two-dimensional case.
The importance of Proposition 1 lies on the fact that choosing the deflection parameter using the rule (12) with forces the current deflected subgradient direction to form always an acute angle with the previous step direction and hence, this method eliminates the zigzagging of the pure subgradient procedure. Note that the choice of the vector of deflected direction is always at least as good as the direction of the subgradient vector . If , then (Camerini et al., 1975).
The theorem below shows that with a particular choice of the convex combination parameter and the parameter , the deflected subgradient vector direction is always at least as good as the direction in a sense that can form a more acute angle with the best direction towards an optimal solution than does (see Fig. 2), which enhances the speed of convergence. The two lemmas below are necessary for the proof of our principal result.
Let
and set
if
. With the assumption in (13) and letting
Using (8), (10) and (11) we obtain the following relation:
From (7) and (9) it follows that:
Using the last equality and applying Proposition 1 we get (21). □
Under the same hypothesis of Lemma 1, we have
If then and hence (23) obviously holds and one simply has . In the case where , then:
Since one finds:
By the choice of such that we obtain
Under the same hypothesis of Lemma 1, we have
(i)
(24)(ii) If the vectors and form an angle and , respectively, with the vector , then
Direct consequence of the previous lemmas. □
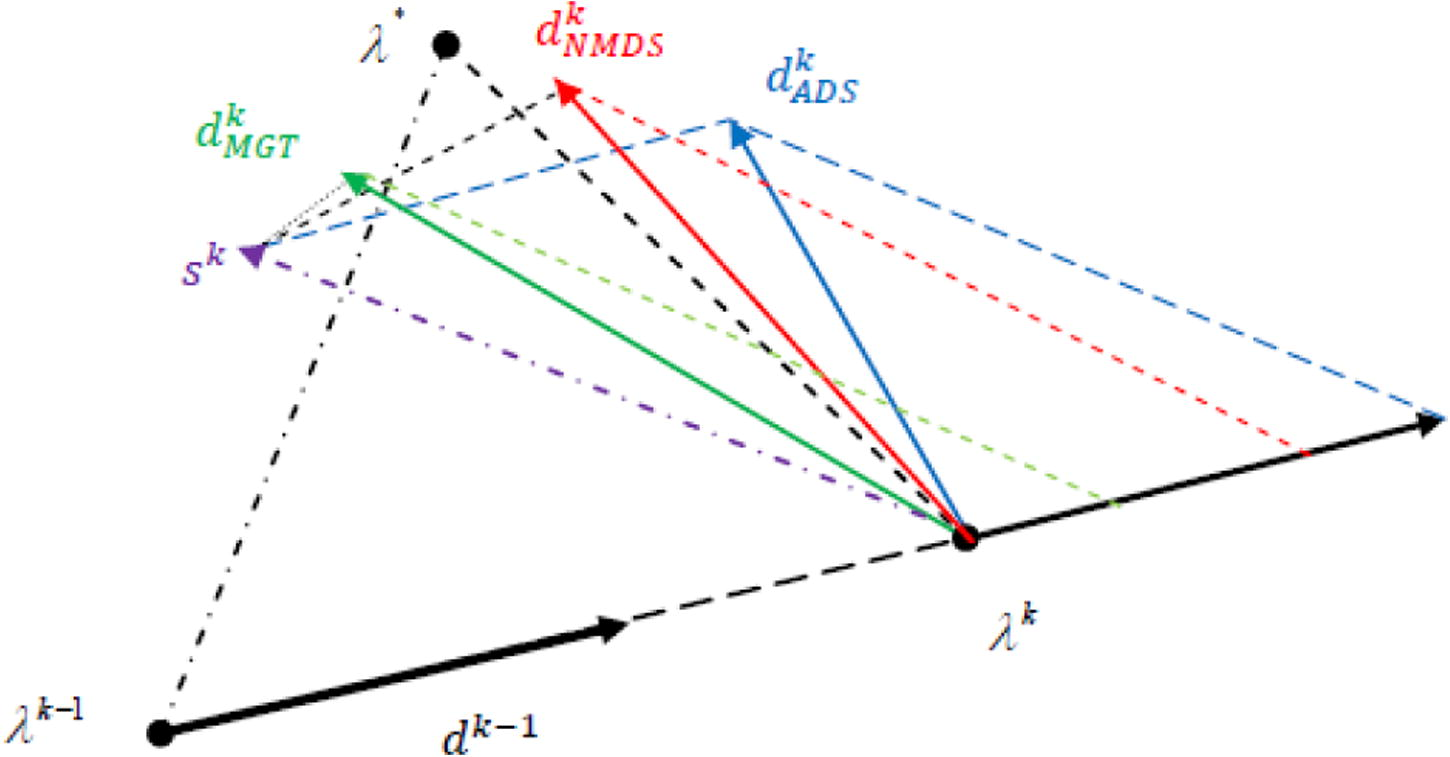
- Case where
is deflected since it has formed an obtuse angle with
and the direction
is better as compared to other directions
and
.
3 Computational results
The proposed algorithm has been applied to one of the standard integer linear programming problems in the field of operational research, namely the symmetric travelling salesman problem (TSPs). The travelling salesman problem is a classical NP-Hard combinatorial optimization problem (Garey and Johnson, 1990). It can be formulated as follows: giving a set of cities, and distances between them, the goal is to find the shortest tour visiting every city only once and returning to the starting city. More details on this problem may be found in Lawler et al., 1985. The TSPs can be stated as follows (where
is the cost of link
):
From this, one obtains the following dual function, which has to be maximized:
Given a vector
, if
optimizes
, then a vector
whose
component
To validate the feasibility and effectiveness of the proposed approach, we have applied it on some TSPs instances taken from TSPLIB.1 The proposed algorithm, MGT and ADS were implemented in Matlab and executed on an Intel(R) Core(TM) i517U CPU @ 1.70 GHz 1.70 GHz RAM 4.00GO.
For all symmetric instances and for a fair comparison between the three algorithms, the following parameter settings were chosen:
-
The same initial multiplier was used for the three algorithms.
-
The stop conditions are the maximum number of iteration , or , where is a small tolerance .
-
The step size is defined according to formula (4).
-
The parameter follows the Held et al. (1974) suggestion, that makes , beginning with . If after 20iterations not increases, is updated to .
-
For MGT algorithm, as mentioned in Camerini et al. (1975), the use of is recommended and its intuitive justification together with computational results are also given, which indicates that in practise, the performance of MGT strategy is superior to that of the pure subgradient algorithm.
-
For our algorithm the value of depends on the optimal convex combination parameter as indicated in Lemma 1, where if . We used , where is an arbitrary small value.
Table 1 shows the experimental results obtained by: MGT strategy, ADS strategy and by applying our NMDS algorithm proposed in this paper with 11 symmetric benchmark instances between n = 6 and n = 101 vertices taken from TSPLIB. For the three strategies, the duality GAP for these 11 examples is null. However, always NMDS algorithm outperforms the others in number of iterations and execution time. Table 2 gives the computational results for 19 symmetric benchmark instances between 131 and 3056 vertices. This table also shows that our algorithm gives near optimal results for several instances. The column headers are as follows:
-
Name: Indicate the instance name.
-
n: Indicate the problem size.
-
: The best known optimal solution.
-
LB: The best value (lower bound) obtained by each strategy.
-
Iter: Number of iterations at which the best value LBis obtained (limited to 1000).
-
.
-
CPU: Total computer time, in second for calculating the best value LBobtained by each strategy.
| Name | n | Strategy | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Our method | ADS strategy | MGT strategy | ||||||||||||
| LB | GAP | Iter | CPU | LB | GAP | Iter | CPU | LB | GAP | Iter | CPU | |||
| tsp6 | 6 | 207 | 207 | 0 | 2 | 0.027862 s | 207 | 0 | 2 | 0.032690 s | 207 | 0 | 2 | 0.028533 s |
| tsp7 | 7 | 106.4 | 106.4 | 0 | 3 | 0.028651 s | 106.4 | 0 | 3 | 0.028819 s | 106.4 | 0 | 3 | 0.029059 s |
| tsp8 | 8 | 100 | 100 | 0 | 3 | 0.032122 s | 100 | 0 | 3 | 0.032360 s | 100 | 0 | 3 | 0.033069 s |
| tsp10 | 10 | 378 | 10 | 0 | 3 | 0.077130 s | 378 | 0 | 18 | 0.085784 s | 378 | 0 | 15 | 0.099755 s |
| ulysses16 | 16 | 68.59 | 68.59 | 0 | 16 | 0.077255 s | 68.59 | 0 | 30 | 0.099056 s | 68.59 | 0 | 26 | 0.090043 s |
| gr21 | 21 | 2707 | 2707 | 0 | 19 | 0.077098 s | 2707 | 0 | 26 | 0.086654 s | 2707 | 0 | 22 | 0.080609 s |
| ulysses22 | 22 | 70.13 | 70.13 | 0 | 21 | 0.219532 s | 70.13 | 0 | 70 | 0.467253 s | 70.13 | 0 | 28 | 0.253197 s |
| tsp33 | 33 | 10861 | 10861 | 0 | 18 | 0.27955 s | 10861 | 0 | 19 | 0.303524 s | 10861 | 0 | 22 | 0.304997 s |
| eil76 | 76 | 538 | 538 | 0 | 12 | 0.728258 s | 538 | 0 | 23 | 1.285156 s | 538 | 0 | 18 | 1.071510 s |
| rat99 | 99 | 1211 | 1211 | 0 | 19 | 1.817552 s | 1211 | 0 | 20 | 1.902072 s | 1211 | 0 | 34 | 3.111573 s |
| eil101 | 101 | 629 | 629 | 0 | 13 | 1.253360 s | 629 | 0 | 16 | 1.523116 s | 629 | 0 | 15 | 1.422569 s |
| Name | n | Strategy | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Our method | ADS strategy | MGT strategy | ||||||||||||
| LB | GAP | Iter | CPU | LB | GAP | Iter | CPU | LB | GAP | Iter | CPU | |||
| xq131 | 131 | 564 | 555.96 | 0.0159 | 350 | 38.134934 s | 555.52 | 0.0167 | 350 | 39.009219 s | 555.64 | 0.0165 | 350 | 42.417376 s |
| ch150 | 150 | 6528 | 6498.3 | 0.0045 | 193 | 57.562539 s | 6463.2 | 0.0099 | 200 | 58.301731 s | 6490.4 | 0.0057 | 202 | 59.548258 s |
| tsp237 | 237 | 1019 | 1004.8 | 0.0139 | 190 | 76.942993 s | 1002.4 | 0.0162 | 200 | 79.046667 s | 1003.9 | 0.0148 | 197 | 77.288710 s |
| a280 | 280 | 2579 | 2569.8 | 0.0035 | 251 | 128.401733 s | 2568.3 | 0.0041 | 251 | 134.245723 s | 2569.8 | 0.0035 | 251 | 129.376815 |
| linhp318 | 318 | 41345 | 41345 | 0 | 188 | 135.792252 s | 41330 | 0.0003 | 200 | 148.125054 s | 41337 | 0.0001 | 195 | 140.734334 s |
| pbk411 | 411 | 1343 | 1443 | 0 | 250 | 328.562376 s | 1338.3 | 0.0034 | 250 | 376.626413 s | 1338.6 | 0.0032 | 250 | 235.626147 s |
| pbn423 | 423 | 1365 | 1365 | 0 | 251 | 344.519801 s | 1360.3 | 0.0034 | 251 | 349.933052 s | 1361.5 | 0.0025 | 251 | 370.504702 s |
| pbm436 | 436 | 1443 | 1423.9 | 0.0132 | 207 | 241.663478 s | 1422.3 | 0.0143 | 251 | 334.741944 s | 1421.4 | 0.0149 | 207 | 255.055079 s |
| rat575 | 575 | 6773 | 6721.2 | 0.0076 | 350 | 1287.476161 s | 6716 | 0.0084 | 350 | 1266.572875 s | 6718.9 | 0.0079 | 350 | 1138.613357 s |
| rbx711 | 711 | 3115 | 3099.6 | 0.0049 | 500 | 1648.379114 s | 3094.3 | 0.0066 | 500 | 1668.377875 s | 3096.2 | 0.0060 | 500 | 1701.099452 s |
| rat783 | 783 | 8806 | 8652.2 | 0.0197 | 121 | 496.527482 s | 8609.5 | 0.0223 | 180 | 744.089813 s | 8642.8 | 0.0185 | 131 | 592.200505 s |
| dkg813 | 813 | 3199 | 3164.7 | 0.0107 | 200 | 126.290411 s | 3147.5 | 0.0203 | 200 | 129.330427 s | 3154.7 | 0.0138 | 200 | 138.698584 s |
| pbd984 | 984 | 2797 | 2797 | 0 | 500 | 2216.458302,s | 2772 | 0.0089 | 500 | 4059.009584 s | 2774.3 | 0.0081 | 500 | 3394.524016,s |
| xit1083 | 1083 | 3558 | 3551.1 | 0.0019 | 550 | 3394.524016 s | 3525.1 | 0.0092 | 600 | 3394.524016 s | 3549.6 | 0.0023 | 600 | 3726.7668 s |
| dka1376 | 1376 | 4666 | 4666 | 0 | 500 | 7321.695698 s | 4659.6 | 0.0013 | 500 | 14632.080221 s | 4662 | 0.0008 | 500 | 14704.797585 s |
| dja1436 | 1436 | 5257 | 5194.2 | 0.0437 | 500 | 10959.322745 s | 5189.4 | 0.0128 | 500 | 12014.302471 s | 5184.4 | 0.0138 | 500 | 11486.802618 s |
| dcc1911 | 1911 | 6396 | 6367.9 | 0.0043 | 500 | 10602.013548 s | 6338.3 | 0.0097 | 500 | 11742.144423 s | 6357.2 | 0.0060 | 500 | 11127.0759858 s |
| djb2103 | 2103 | 6197 | 6197 | 0 | 430 | 13566.845650 s | 6133.8 | 0.0101 | 500 | 14954.211430 s | 6169.3 | 0.0044 | 500 | 15955.063763 s |
| pia3056 | 3056 | 8285 | 8285 | 0 | 500 | 51124.513213 s | 8192 | 0.0112 | 500 | 59123.013454 s | 8228.2 | 0.0068 | 500 | 58072.083303 s |
4 Conclusion
By identifying the optimal convex combination parameter, a new deflected direction is given as convex combination of the deflected direction of MGT and ADS. This direction, at each iteration reduces the zigzagging phenomenon and hence getting closer and faster to the optimal solution. The analysis studies are consistent with the numerical experiments. Moreover, this method can be used to improve convergence in the area of deflected subgradient method using augmented Lagrangian duality (Burachik and Kaya, 2010) and dual subgradient methods (Gustavsson et al., 2015). One can also follow Lim and Sherali (2006) and combine this method with a variable target technique in order to have a good performance. Finally, the subgradient method is usually used as subroutine in exact, heuristic and metaheuristic optimization, which justifies the large spectrum of applications of our approach.
Acknowledgements
The authors wish to express their sincere thanks to the editor and the reviewers for their constructive comments, which are very useful for improving this paper.
References
- On the choice of step sizes in subgradient optimization. Eur. J. Oper. Res.. 1981;7:380-388.
- [Google Scholar]
- Bazaraa, M.S., Sherali, H.D., Shetty, C.M., 2006. Non Linear Programming: Theory and Algorithms. Wiley-Interscience Series in Discrete Mathematics and Optimization.
- A deflected subgradient method using a general augmented Lagrangian duality with implications on penalty methods. In: Burachik R., Yao J.C., eds. Variational Analysis and Generalized Differentiation in Optimization and Control. Springer Optimization and Its Applications. Vol vol. 47. New York, NY: Springer; 2010.
- [Google Scholar]
- On improving relaxation methods by modified gradient techniques. In: Balinski M.L., Wolfe P., eds. Nondifferentiable Optimization. Math. Program. Studies. Vol vol. 3. Berlin, Heidelberg: Springer; 1975.
- [Google Scholar]
- Diaby, M., Karwan, M.H., 2016. Advances in combinatorial optimization: linear programming formulation of the travelling salesman and other hard combinatorial optimization problems.
- Vehicle routing with time windows: An overview of exact, heuristic and metaheuristic methods. J. King Saud Univ. Sci.. 2010;22:123-131.
- [Google Scholar]
- A modified subgradient algorithm for Lagrangian relaxation. Comput. Oper. Res.. 2001;28:33-52.
- [Google Scholar]
- Computers and Intractability: A Guide to the Theory of NP Completeness. New York, NY, USA: W. H. Freeman & Co.; 1990.
- Primal convergence from dual subgradient methods for convex optimization. Math. Program.. 2015;150:365-390.
- [Google Scholar]
- The travelling salesman problem and minimum spanning trees. Oper. Res.. 1970;18:1138-1162.
- [Google Scholar]
- Inexact subgradient methods for quasi-convex optimization problems. Eur. J. Oper. Res.. 2015;240:315-327.
- [Google Scholar]
- The Travelling Salesman Problem: A Guided Tour of Combinatorial Optimization. John Wiley & Sons Inc; 1985.
- Convergence and computational analyses for Some variable target value and subgradient deflection methods. Comput. Optim. Appl.. 2006;34:409-428.
- [Google Scholar]
- The effect of deterministic noise in subgradient methods. Math. Program.. 2010;125:75-99.
- [Google Scholar]
- Subgradient methods for huge-scale optimizations problems. Math. Program.. 2014;146:275-297.
- [Google Scholar]
- Nocedal, J., Wright, S.J., 2006. Numerical Optimization. Springer Series in Operations Research.
- A primal-dual conjugate subgradient algorithm for specially structured linear and convex programming problems. Appl. Math. Optim.. 1989;20:193-221.
- [Google Scholar]
- A Variable target value method for nondifferentiable optimization. Oper. Res. Lett.. 2000;26:1-8.
- [Google Scholar]
- Minimization Methods for Non-Differentiable Functions. Berlin: Springer; 1985.
- Optimization For Machine Learning. MIT Press; 2012.






