A Liu-Storey-type conjugate gradient method for unconstrained minimization problem with application in motion control

1 Introduction

In this paper, we present alternative nonlinear conjugate gradient (CG) method for solving unconstrained optimization problems.

Conjugate gradient methods are preferable among other optimization methods because of low storage requirements (Hager and Zhang, 2006). Based on these, a considerable amount of research articles have been published, most of these articles considered global convergence of the conjugate gradient methods that are previously difficult to globalize (see, for example, Zhang et al., 2006; Gilbert and Nocedal, 1992; Al-Baali, 1985; Dai et al., 2000). In other perspective, some articles considered widening the applicability as well as improving the numerical performance of the existing conjugate gradient methods (see for example Yuan et al., 2019; Yuan et al., 2020; Hager and Zhang, 2013; Ding et al., 2010; Xie et al., 2009; Xie et al., 2010; Abubakar et al., 2021; Abubakar et al., 2021; Malik et al., 2021).

Consider the unconstrained optimization problem

The parameter ${\alpha }_k>0$ is the steplength obtained by either the standard Wolfe line search conditions (Sun and Yuan, 2006), namely,

The scalar ${\beta }_k$ is known as the conjugate gradient parameter. Some notable parameters are; the Hestenes-Stiefel (HS) (Hestenes and Stiefel, 1952), Polak-Ribiére-Polyak (PRP) (Polak and Ribiere, 1969; Polyak, 1969) and Liu-Storey (LS) (Liu and Storey, 1991). They are defined as follows: $${\beta }_k^{\mathit{HS}}=\frac{g_k^T{y}_{k-1}}{d_{k-1}^T{y}_{k-1}}{\beta }_k^{\mathit{PRP}}=\frac{g_k^T{y}_{k-1}}{\Vert g_{k-1}{\Vert }^2},{\beta }_k^{\mathit{LS}}=\frac{g_k^T{y}_{k-1}}{-g_{k-1}^T{d}_{k-1}}\text{.}$$ where $g_k=g\left(x_k\right),y_{k-1}=g_k-g_{k-1}$ .

It can be observed that the HS, PRP, and LS method have similarity in their numerator, this similarity makes them have some common features in terms of computational performance. There exists many works on the development of the HS and PRP methods (see, for example, Zhang et al., 2007; Dong et al., 2017; Yu et al., 2008; Saman and Ghanbari, 2014; Andrei, 2011; Yuan et al., 2021), however, as noticed by Hager and Zhang (2006) in their review article, the research on the LS method is rare. Nevertheless, some works on the LS parameter have been presented in the references (Shi and Shen, 2007; Tang et al., 2007; Zhang, 2009; Liu and Feng, 2011; Li and Feng, 2011. In Shi and Shen, 2007; Tang et al., 2007; Liu and Feng, 2011), the authors proposed a new form of Armijo-like line search strategy and used it to investigate the global convergence of the LS method. Zhang (2009), developed a new descent LS-type method based on the memoryless BFGS update and proved the global convergence of the method for general function using the Grippo and Lucidi (1997) line search. Li and Feng (2011), remarked that because of the similarity of the HS, PRP, and LS conjugate parameters, the techniques applied to the HS and PRP can be applied to the LS method to improve its convergence and computational performance. In this regard, Li and Feng, proposed a modification of the LS method similar to the well-known Hager and Zhang CG-DESCENT (Hager and Zhang, 2005).

Noticing the above development, in this paper, we seek another alternative LS-type method following the modifications of the HS and PRP methods by Liang et al. (2015) and Aminifard and Saman (2019), respectively. Motivated by the above proposals and the similarity of the LS CG parameter with HS and PRP parameters, we present an efficient descent LS-type method for nonconvex functions. The direction satisfy the sufficient descent property without any line search requirement and the method is globally convergent under the standard Wolfe line search as well as the Armijo-like line search. The rest of the paper is organized as follows. In Section 2 we provide the algorithm of the descent LS -type method together with its convergence result. In Section 3, we present the numerical experiments, and conclusions are given in Section 4. Unless otherwise stated, throughout this paper we denote $g_k=g(x_k)$ .

2 Algorithm and theoretical results

Recently, some proposals have been made to modify the HS and PRP methods. The proposal to modify the HS method was done by Liang et al. (2015) and that to modify the PRP (named as NMPRP method) was done by Aminifard and Saman (2019). In Liang et al. (2015), some CG methods with a descent direction was presented. Moreover, the conjugacy condition given by Dai and Liao (2001) was extended. Likewise in Aminifard and Saman (2019), a descent extension of the PRP method was presented and the global convergence was shown under the Wolfe and Armijo-like line search, respectively. In this section, we build on the analysis given in Liang et al. (2015) and Aminifard and Saman (2019) on the LS method to guarantee a sufficient descent direction (3).

Note that if ${\beta }_k^{\mathit{LS}}⩾0$ , then condition (3) is satisfied when $g_k^T{d}_{k-1}⩽0$ . Now, our interest is to consider the case where $g_k^T{d}_{k-1}>0$ and the direction satisfies (3). To achieve this, we attach a scaling parameter ${\gamma }_k$ to the term $-g_k$ in (2) and propose the following search direction

It is worth noting that if the exact line search is used, the parameter ${\beta }_k^{\mathit{MLS}}$ reduces to ${\beta }_k^{\mathit{LS}}$ . If $g_k^T{y}_{k-1}⩽0$ the direction $d_k^{\prime }$ defined in (7) may not necessarily be descent, in this case we set $d_k^{\prime }=-g_k$ . Therefore, we defined the proposed direction by

It can be observed that a restart process for the CG method with direction $d_k^{\prime }$ defined by (7) occur when $g_k^T{y}_{k-1}⩽0$ .

Below we give the algorithm flow framework of the proposed scheme.

Algorithm 1: New Modified LS method (NMLS)

Next, we prove the convergence of Algorithm 1 under the standard Wolfe line search conditions (4)-(5). In addition, we employ the following assumptions.

Assumptions 2.3 and 2.4 implies that for all $x\in \mathcal{H}$ there exists $c_1,c_2>0$ such that;

• $\Vert x\Vert ⩽c_1$ .

• $\Vert g(x)\Vert ⩽c_2$ .

• $\{x_k\}\in \mathcal{H}$ as $\{f(x_k)\}$ is decreasing.

In what follows, we prove the convergence result of Algorithm 1 under the Armijo-like condition (6).

Since $\{f(x_k)\}$ is nonincreasing, using (6) we have $${\displaystyle \sum _{k=0}^{\infty }}{\alpha }_k^2\Vert d_k{\Vert }^2<+\infty ,$$ which further implies that

3 Numerical examples

This section demonstrates the numerical performance of Algorithm 1. Algorithm 1 is named as NMLS method. Based on the number of iteration (NOI), the number of function evaluations (NOF), and central processing unit (CPU) time, we compare the performance of the NMLS method with the NMPRP method (Aminifard and Saman, 2019). Fifty-six (56) test functions suggested by Andrei (2017) and Jamil (2013) are selected for testing the computational performance of each method. For each test function, we run two problems with different starting points or variation dimensions of 2, 4, 8, 10, 50, 100, 500, 1000, 5000, 10000, 50000 and 100000. The list of test functions is given in Table 1. The algorithm was coded in MATLAB R2019a and compiled on a PC with specification: processor Intel Core i7, operating system Windows 10 pro 64 bit, and 16 GB RAM. We stop the algorithm when $\Vert g_k\Vert ⩽{10}^{-6}$ , and the numerical results are said to fail (use “–” to report the failure), if one of the conditions is satisfied: the NOI is more than 10,000 or the problem fail to attained the optimum value.

In this section, we compare the proposed NMLS method with NMPRP method using the strong Wolfe and Armijo-like line searches. This is done as a fair comparison adapted to the NMPRP method in Aminifard and Saman (2019). We use the strong Wolfe conditions comprises of (4) and the following stronger version of (5): $$|g_{k+1}^T{d}_k|⩽-\sigma g_k^T{d}_k\text{.}$$

To obtain the step-size ${\alpha }_k$ by using strong Wolfe line search in the NMLS method, the parameters are selected as $\sigma =0.05$ and $\vartheta =0.0001$ . Meanwhile, under the Armijo-like line search, we use the parameters $\rho =0.25$ and $\delta =0.00003$ . For good performance, we choose the parameter $t=0.1$ for evaluating ${\beta }_k^{\mathit{MLS}}$ . In the NMPRP method, we still maintain all the parameter values according to the article (Aminifard and Saman, 2019). All numerical results under the strong Wolfe line search are shown in Table 2 and under Armijo-like line search are given in Table 3. The items in each table have the following meanings: Funct.: the test function, Dim.: dimension, and IP: arbitrary initial points. From the numerical results in Tables 2 and 3, we can see that the NMLS method in this paper is promising.

On the other hand, we use the performance profile introduced by Dolan and Moré (2002) to compare and evaluate the performance of NMLS and the NMPRP methods. The performance profile of each method is depicted by a segment of each problem to obtain a profile curve. From the profile curve, the method that top the curve has the best performance.

Figs. 1–3 present the performance profile with respect to the three metrics; NOI, NOF and CPU time of the two methods, respectively. From Fig. 1a, Fig. 1b, Fig. 2a, Fig. 2b, Fig. 3a, and Fig. 3b, the proposed NMLS method has the best performance based on all metrics under strong Wolfe line search and Armijo-like line search.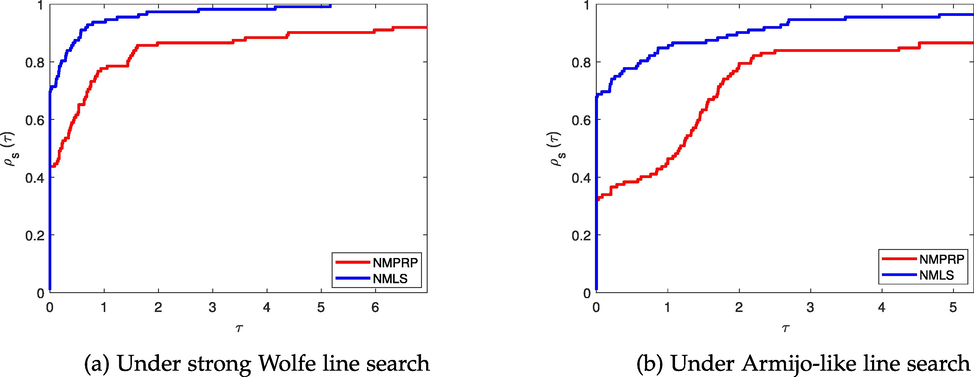

Close

Fig. 1

Performance profile based on NOI.

Export to PPT

Close

Fig. 2

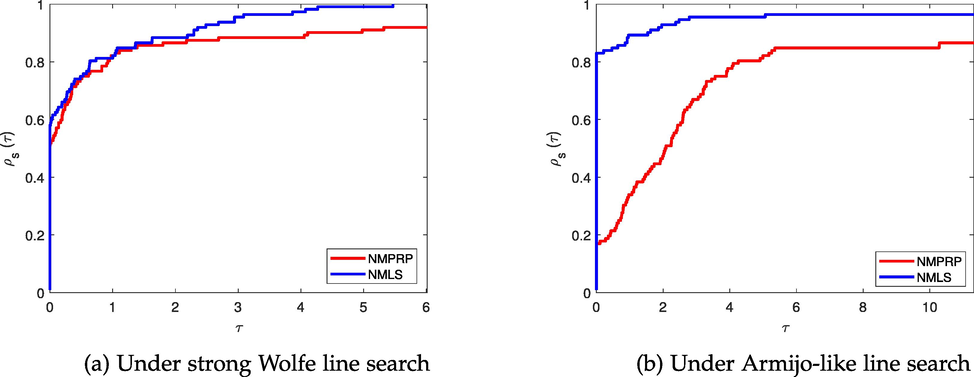
Performance profile based on NOF.

Export to PPT

Close

Fig. 3

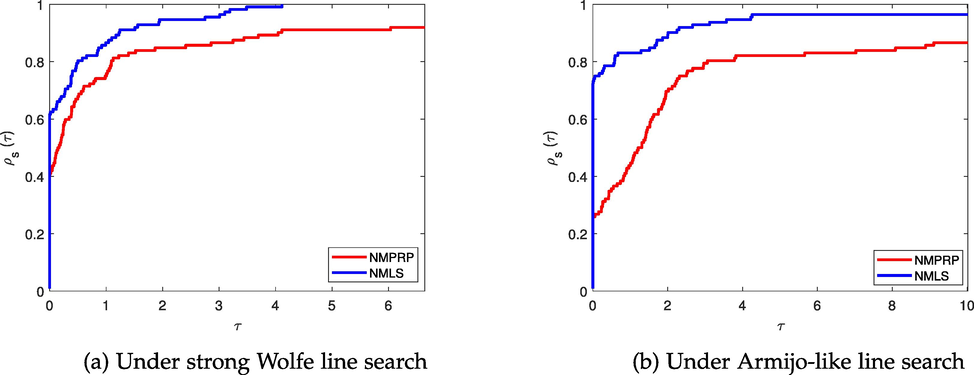
Performance profile based on CPU time.

Export to PPT

3.1

3.1 Application in motion control

This subsection test the efficiency of Algorithm 1 in solving motion control problem. Algorithm 1 (NMLS method) is implemented using the Armijo-like line search (6), in which we set $\rho =0.6,t={10}^{-14}$ and $\vartheta =0.018$ . We begin with a brief background on motion control problems (Zhang et al., 2019; Sun et al., 2020). Here we look only at the motion control of two-joint planar robot manipulator. Given the path of the vector desired $r_{\mathit{dk}}\in {\mathcal{R}}^2$ at time instant $t_k\in [0,t_f]$ , the discrete-time kinematics equation is: finding ${\theta }_k\in {\mathcal{R}}^2$ such that $$f({\theta }_k)=r_{\mathit{dk}}\text{.}$$

f is a mapping given by $$f(\theta )=\left[\begin{array}{c}{l}_1{c}_1+l_2{c}_2\hfill \\ l_1{s}_1+l_2{s}_2\hfill \end{array}\right],$$ where $c_1=\cos ({\theta }_1),s_1=\sin ({\theta }_1),c_2=\cos ({\theta }_1+{\theta }_2),s_2=\sin ({\theta }_1+{\theta }_2)$ , and $l_i$ denote the i-th rod length. Obviously, this problem can be described as a minimization problem

(21)

$${\displaystyle \underset{{\theta }_k\in {\mathcal{R}}^2}{\min }}\frac{1}{2}\Vert f({\theta }_k)-r_{\mathit{dk}}{\Vert }^2\text{.}$$

For simplicity, we set $l_i=1(i=1,2)$ and the end-effector is controlled to track the following Lissajous curve (Zhang et al., 2019) $$r_{\mathit{dk}}=\left[\begin{array}{c}1.5+0.2\sin (\pi t_k/5)\hfill \\ \sqrt{3}/2+0.2\sin (2\pi t_k/5+\pi /3)\hfill \end{array}\right]\text{.}$$

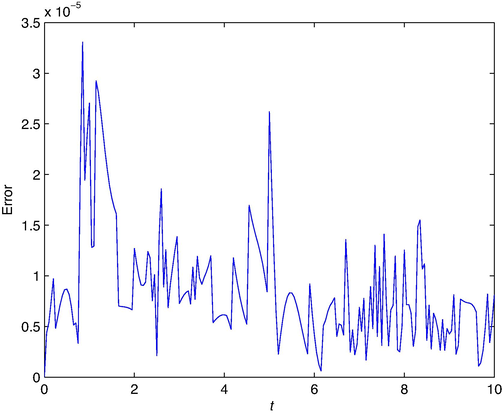
The starting point of the initial problem is ${\theta }_0={[0,\pi /3]}^{\top }$ , and that of any i-th problem is the approximate solution to the $i-1$ -th problem ( $i=2,3,\cdots$ ). Furthermore the time for the task is $[0,10]$ , and divided equally into 200 pieces. The outcomes obtained by NMLS are presented in Fig. 4, which shows that NMLS algorithm effectively accomplished the task. More specifically, synthesization of the trajectories of the robot using the NMLS algorithm is plotted in Fig. 4a, and trajectory of end-effector as well as the path desired are plotted in Fig. 4b. Figs. 4c and 4d show the error generated by the NMLS method on x-axis and y-axis, respectively. It is not easy to see the variation of the generated end-effector trajectory and desired path from Fig. 4a and 4b. Actually, Fig. 4c and 4d depict that the errors are not above ${10}^{-5}$ . In addition, to show the absolute error generated by NMLS, we show their Euclidean distance of end-effector trajectory and desired path in Fig. 5, from which we find that the absolute error is always smaller than $3.5\times {10}^{-5}$ . This shows that NMLS completes the task with high precision. In Fig. 4a there is one broken line that is far from other broken lines, which indicates that there is some sudden shift of the manipulator. This may cause damage to the manipulator. Therefore, in addition to the unconstrained optimization model (21), we need to design some new mathematical model of this motion control, which can generate continuous and repetitive motion control. This is one of our further research topics.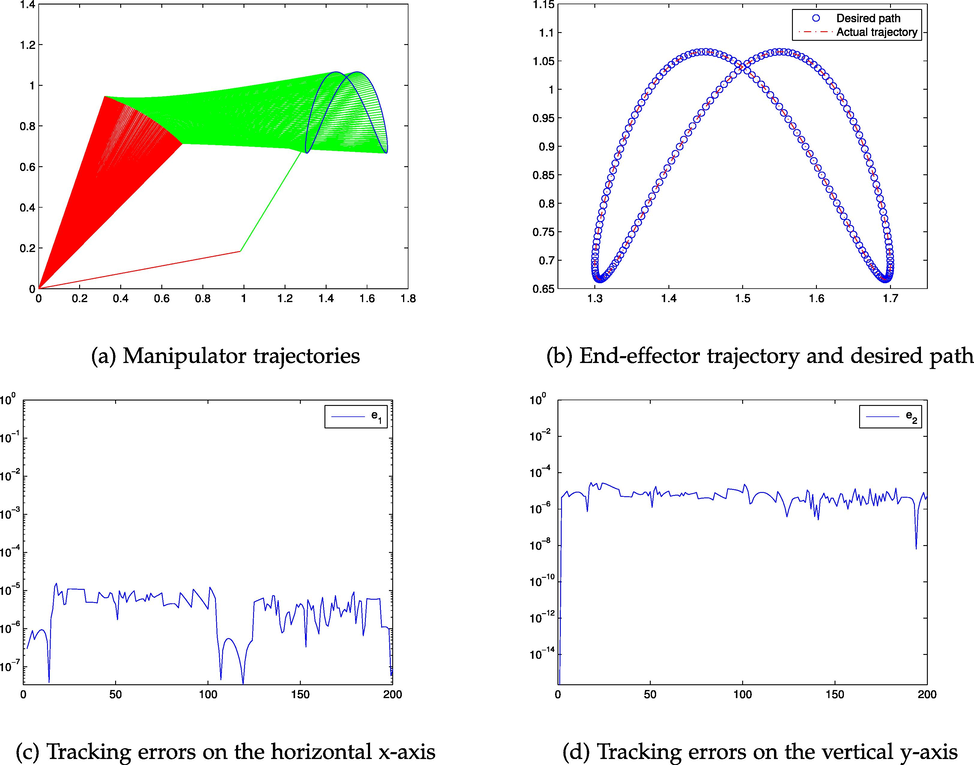

Close

Fig. 4

Numerical results generated by NMLS.

Export to PPT

Close

Fig. 5

Absolute error generated by NMLS.

Export to PPT

4 Conclusions

In this article, we have presented a Liu-Storey type conjugate gradient method that guarantees sufficient descent condition independent of the line search. Using the Wolfe and Armijo-like line search conditions, we proved that the NMLS method converges globally. Moreover, the presented method can inherit a built-in self-restarting mechanism of the LS method. Based on our numerical findings, we conclude that the proposed method is the most efficient and promising.