Translate this page into:
A four-step implicit block method with three generalized off-step points for solving fourth order initial value problems directly
⁎Corresponding author. rafatshaab@yahoo.com (Ra’ft Abdelrahim),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
The existing hybrid methods for solving ordinary differential equations were only derived using specific off-step points. Thus, this paper proposes a new four-step block method with three generalized off-step points for solving initial value problems of fourth order ordinary differential equations directly. The strategy employed to develop this method is interpolating the basis function at and collocating the fourth derivative of the basis function at all points within the selected interval. The implementation of this method in a block-by-block fashion can overcome the setbacks of applying starting values and predictors which are created in predictor-corrector approach. The convergence analysis of the developed method is performed and the accuracy of the method is tested on several problems. The numerical results indicate that the new method outperforms the existing ones in terms of errors. In addition, the new method does not require much computation when compared with previous methods.
Keywords
Block method
Hybrid block method
Fourth order ordinary differential equations
Collocation and interpolation
Three off-step points
1 Introduction
In this paper, we consider the numerical solution of the fourth order IVPs of the form
Eq. (1) arises in wide fields of science and engineering. This equation can be solved by converting it into system of four equations of first-order IVPs and then suitable numerical methods for first order is employed (see Henrici, 1962; Lambert, 1973). However, this approach increases the number of equations and therefore some researchers have opted hybrid block methods for solving Eq. (1) directly, for instance, among of these researchers are (Yap and Ismail, 2015; Abdelrahim and Omar, 2015; Hussain et al., 2015; Omar and Abdelrahim, 2016; Jator, 2008; Awoyemi, 2005). In hybrid block methods, not only the numerical approximation can be computed at more than one point in the same time, but computational burden and zero stability barrier can also be avoided, see Adesanya et al. (2012) and Kayode (2008). However, the existing hybrid block methods only focus on the specific off step points. Hence, the aim of this work is to generalize three off step points of four step block method. As a results, the new method will be more robust and flexible.
2 Derivation of the method
This section shows the derivation of a four-step hybrid block method with three generalized off-step points and for solving (1).
Consider the polynomial of the form:
The next step in the derivation of the hybrid block method involves differentiating (2) four times to give
Interpolating the approximate solution (2) at and collocating Eq. (3) at all points in the selected interval produces twelve equations which can be written as a system in matrix form , where
The unknown values of
can be obtained by matrix inverse approach, where
. The values obtained are then substituted back into Eq. (2) to produce a continuous implicit scheme of the form
Differentiating (4) once, twice and thrice gives
Eq. (4) is evaluated at the non-interpolating point
while Eqs. (5) is evaluated at
to give the discrete schemes and its derivatives at
. The discrete schemes and its derivatives at
are combined in a matrix form as below
The elements of and are given in A.
Multiplying Eq. (6) by the inverse of A gives a four-step hybrid block method (main block) with three generalized off-step points of the form
In order to get the derivatives (first, second and third) of the block, the value of the block at and are substituted into the first, second and third derivatives of the discrete schemes and this produces first, second and third derivatives of the block.
3 Analysis of the Method
3.1 Order of the Method
In finding order of the new block method (7), we define the linear difference operator L associated with (7)
Expanding
and
components in Taylors series respectively and collecting their terms in powers of h yields
The hybrid block method (7) and its linear operator (8) are said to have order p, if and with error constants vector .
Expanding (8) about using Taylor series gives the orders of all integrators in the main block method which are . Therefore, the new hybrid block method is consistent since each integrator has order greater than one.
3.2 Zero stability
Following Fatunla(1991), the zero stability of the method will obtain by finding the roots of the first characteristic function as given below, where I is identity matrix and is coefficients matrix of ,
Solving yields . Hence, our method is zero stable since having roots such that , and when , the multiplicity of doesn’t exceed four.
3.3 Convergence
.
Theorem 3.2 Henrici, 1962
Consistency and zero stability are sufficient conditions for a linear multistep method to be convergent.
Following the theorem in the above the developed method (7) is convergent since it is zero stable and consistent.
3.4 Implementation of the method
The developed method is implemented by combining all the hybrid integrators for IVPs simultaneously without additional method to predict the starting values. We continue by explicitly obtaining initial conditions at x, using the computed values over subintervals . For example, using (7), where its first, second and third derivatives are simultaneously obtained over the subinterval as are known from the IVP (1), for with its derivatives are simultaneously obtained over the subinterval as are known from the previous block and so on. Hence, the method is applied over non overlapping subintervals and the solutions derived are more accurate than those obtained in the existing method. We remind that, the system of these equations has a unique solution since the determinant of its matrix when . We also note that, for linear problems, we solve (7) directly from the start with Gaussian elimination using partial pivoting and for nonlinear problems, we use a modified Newton–Raphson method.
4 Numerical results
In this section, the following IVPs available in previous literatures which are solved to special case of the new method when
and
(chosen arbitrarily) in order to compare the performance of new method with the existing ones in [3,4–9]. It is worth noting that the block method proposed is in a generalized form and hence can take varying off-step point values which gives room for flexibility. The absolute errors at different value of end point x with several h were carried out using flexible Matlab code as depicted in Tables 1,2,3,4.
h
Method
at x = 2.
Steps
New method
5
Yap and Ismail (2015)
5
0.1
Adams
Jator
20
New method
10
Yap and Ismail (2015)
10
0.05
Adams
Jator
40
New method
20
Yap and Ismail (2015)
20
0.025
Adams
Jator
80
h
Method
at x = 1.01325
Steps.
New method
80
0.003125
Kayode (2008)
320
New method
3
0.103125
Awoyemi et al. (2015)
2
h
at x = 1
New method
3
0.1
Adesanya et al (2012)
2
x
AE in new method
AE in Yap (2015).
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
x
AE in Kayode (2008)
AE in Awoyemi et al. (2015)
AE in new method.
0.103125
0.206250
0.306250
0.406250
0.506250
0.603125
0.703125
0.803125
0.903125
1.003125
The following notations are used in the tables.
h:step size.
Step: total number of steps taken to obtain solution.
: magnitude of the maximum error of the computed solution.
AE: absolute error.
In general, the results from Tables 1, show that the performance of four-step hybrid block methods for solving fourth order ODEs directly using three specific hybrids points is better than existing methods in terms of error. These are demonstrated in (Figs. 1 and 2).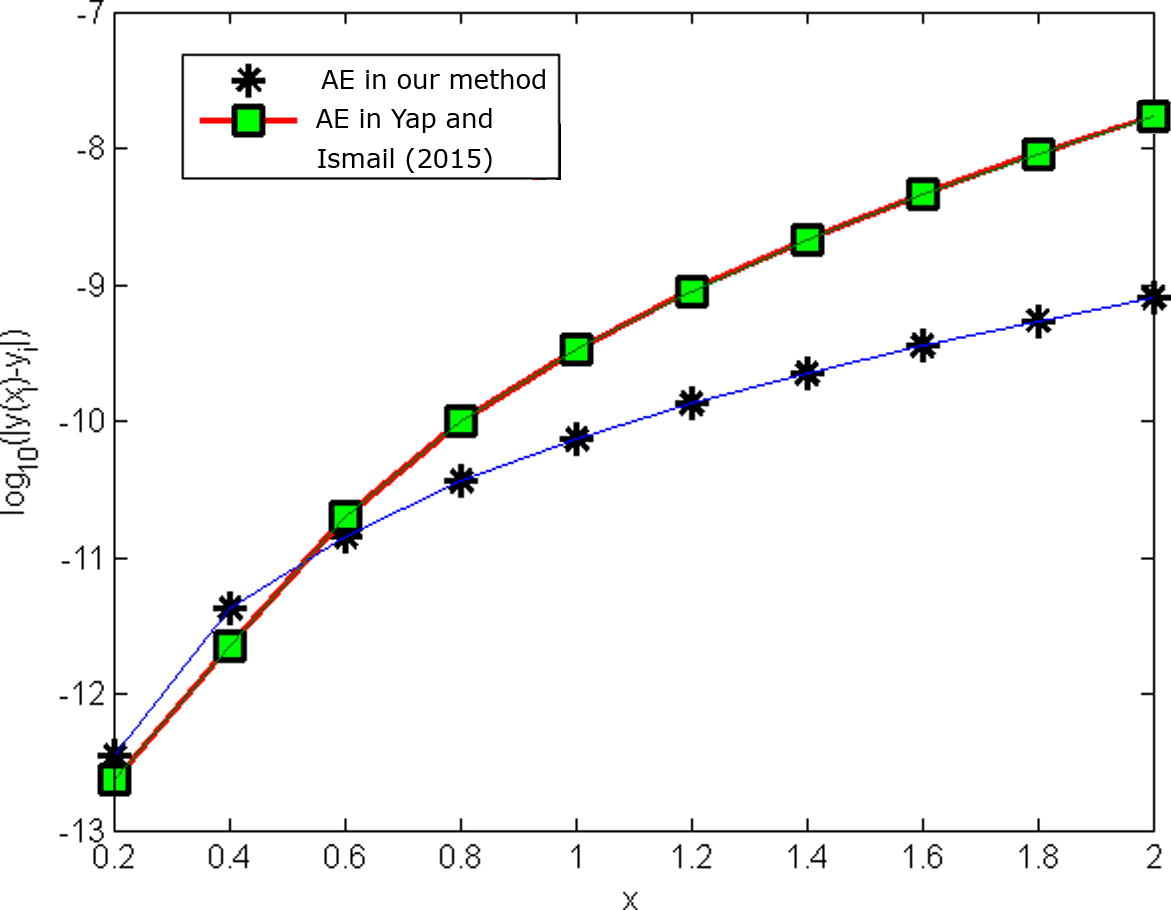
Showing error in Problem 1.
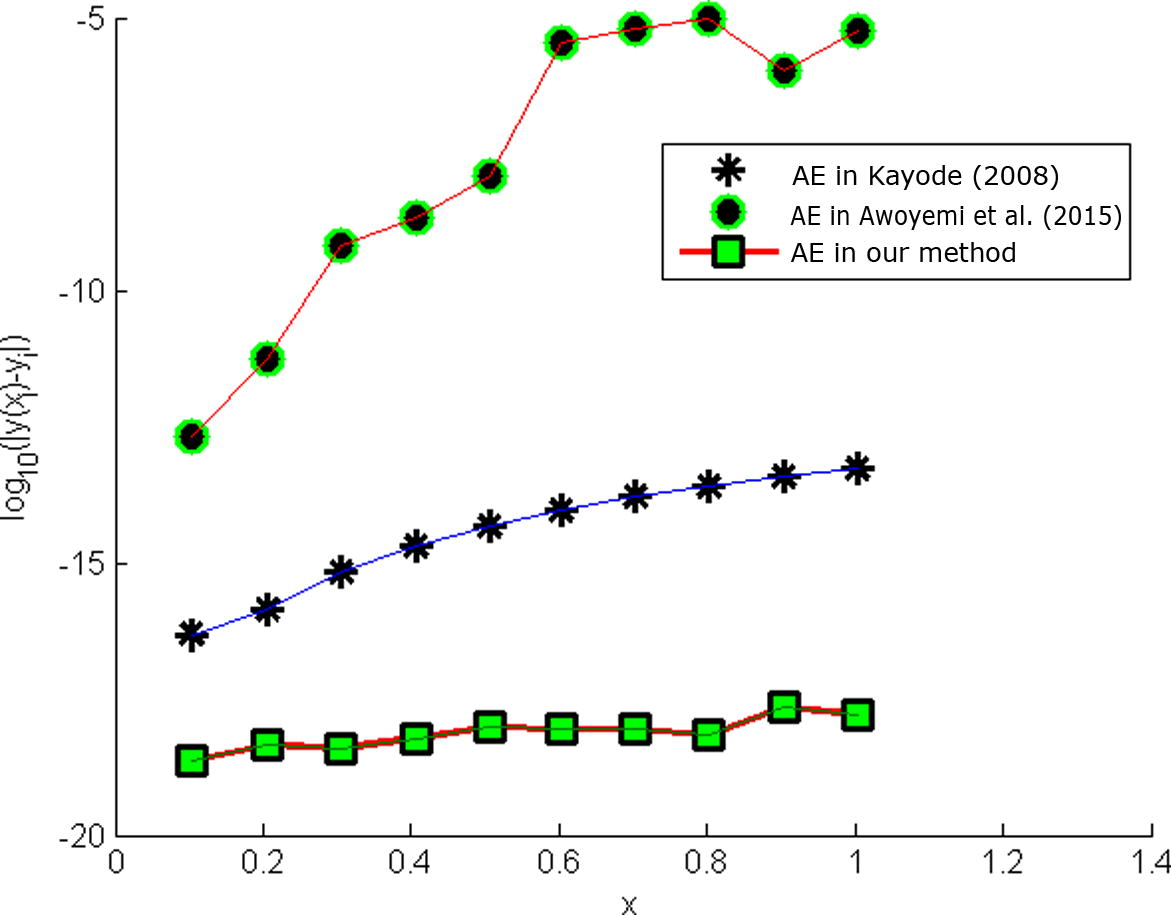
Showing error in Problem 1.
Application:
The new developed method is applied for solving physical problem occurs in ship dynamics. In particular, this problem has been studied and solved numerically by Twizell (1988) and Cortell (1993) which describes how the sinusoidal wave of frequency
passes along a ship or offshore structure to lead to fourth order differential equation relates the fluids action with time x as below
The comparison of the new method with Twizell (1988) and Cortell (1993) has been made at the end point
in terms of accuracy (refer to Table 5), where
and
.
h
Method
Error at x = 15.
New method
0.25
Yap and Ismail (2015)
Twizell
New method
0.1
Yap and Ismail (2015)
Cortell
The block method (7) is self-starting and applied without the use of predictors which can reduce the accuracy of the method as well as increase programming time.
5 Conclusion
We have developed a four-step block method with three generalized off step points for the solution of fourth order initial value problems which was applied without the use of predictors that reduce the accuracy of the method. The properties of the developed block method which include: zero stability, order, consistency and convergence are established. The existing four-step hybrid block methods only focus on the specific off step points. Since the new method works for any three off-step points, it is therefore more flexible and robust. The application of the developed method was then made to several fourth order initial value problems. In general, the benefit of using the four-step hybrid block method for solving IVPs of fourth order ODEs is obvious. The new method displays its superiority by producing less error if compared to the present methods as shown in Tables 1 and 2. In addition, the developed method does not require much computation when compared with predictor corrector methods.
Author Contributions
Both authors equally contributed to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Solving third order ordinary differential equations using hybrid block method of order five. Int. J. Appl. Eng. Res. 2015;10:44307-44310.
- [Google Scholar]
- Five steps block method for the solution of fourth order ordinary differential equations. Int. J. Eng. Res. Appl.. 2012;2:991-998.
- [Google Scholar]
- Algorithmic collocation approach for direct solution of fourth-order initial-value problems of ordinary differential equations. Int. J. Comput. Math.. 2005;47:321-329.
- [Google Scholar]
- A Six-step continuous multistep method for the solution of general fourth order initial value problems of ordinary differential equations. J. Nat. Sci. Res.. 2015;5:131-138.
- [Google Scholar]
- Application of the fourth-order Runge-Kutta method for the solution of high-order general initial value problems. Comput. Struct.. 1993;49:897-900.
- [Google Scholar]
- Discrete Variable Methods in Ordinary Differential Equations. New York, NY, USA: John Wiley & Sons; 1962.
- Runge-Kutta type methods for directly solving special fourth-order ordinary differential equations. Math. Prob. Eng. 2015
- [Google Scholar]
- Numerical integrators for fourth order initial and boundary value problems. Int. J. Pure Appl. Math.. 2008;47:563-576.
- [Google Scholar]
- An order six zero-stable method for direct solution of fourth order ordinary differential equations. Am. J. Appl. Sci.. 2008;5:1461-1466.
- [Google Scholar]
- Lambert, J.D. 1973. Computational methods in ordinary differential equations.
- Application of single step with three generalized hybrid points block method for solving third order ordinary differential equations. Int. J. Appl. Eng. Res.. 2016;9:2705-2717.
- [Google Scholar]
- A family of numerical methods for the solution of high-order general initial value problems. Comput. Methods Appl. Mech. Eng.. 1988;67:15-25.
- [Google Scholar]
- Block hybrid collocation method with application to fourth order differential equations. Math. Prob. Eng.. 2015;2015:1-6.
- [Google Scholar]
Appendix A
Appendix B







