Translate this page into:
A criterion for the global convergence of conjugate gradient methods under strong Wolfe line search
⁎Corresponding author. mogtaba.m@mu.edu.sa (Mogtaba A.Y. Mohammed),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
From 1952 until now, the sufficient descent property and the global convergence of conjugate gradient (CG) methods have been studied extensively. However, the sufficient descent property and the global convergence of some CG methods such as the method of Polak, Ribière, and Polyak (PRP) and the method of Hestenes and Stiefel (HS) have not been established yet under the strong Wolfe line search. In this paper, based on Yousif (Yousif, 2020) we present a criterion that guarantees the generation of descent search directions property and the global convergence of CG methods when they are applied under the strong Wolfe line search. Moreover, the PRP and the HS methods are restricted in order to satisfy the presented criterion, so new modified versions of PRP and HS are proposed. Finally, to support the theoretical proofs, a numerical experiment is done.
Keywords
Unconstrained optimization problems
Conjugate gradient methods
Strong Wolfe line search
Sufficient descent property
Global convergence
1 Introduction
Unconstrained optimization problems usually arise in various fields of science, engineering, and economics. They are mathematically formulated as
Such that
represents the step length that is a CG method takes in each step toward the search direction
. Strong Wolfe line search is one of the most used methods in practical computations for computing
, in which
satisfies
Such that
represents the gradient of the nonlinear function
at the value
and
and
is the search direction given by:
Such that is the factor that determines how the conjugate gradient methods differ. Some of the very well-known formulas attributed to Hestenes-Stiefel (HS) (Hestenes and Stiefel, 1952), Fletcher-Reeves (FR) (Fletcher and Reeves, 1964) and Polak-Ribière-Polyak (PRP) (Polyak, 1969; Polak and Ribière, 1969). These formulas are given by
respectively. Other formulas are conjugate descent (CD) (Fletcher, 1987), Liu-Storey (LS) (Liu and Storey, 1992), and Dai-Yuan (DY) (Dai and Yuan, 2000). For more formulas for the coefficient see (Abubakar et al., 2022; Yuan and Lu, 2009; Zhang, 2009; Rivaie et al., 2012; Hager and Zhang, 2005; Dai, 2002; Yuan and Sun, 1999; Salleh et al., 2022; Dai, 2016; Wei et al., 2006, Wei et al., 2006).
To guarantee that every search direction generated by a CG method is descent, the sufficient descent property
, (1.6)
is needed.
The global convergence and descent directions property of the FR method are established using both exact (Zoutendijk and Abadie, 1970) and strong Wolfe line search (Al-Baali, 1985) on general functions. The PRP and the HS methods with exact line search can cycle infinitely without approaching a solution which implies that they both do not have global convergence for general functions (Powell, 1984). Nevertheless, the good performance of the PRP and the HS in practice, that is, due to self-restarting property, both methods are preferred to the FR method. To establish the convergence of them with the strong Wolfe line search, Powell (Powell, 1986) suggested restricting them to be non-negative. Motivated by Powell’s suggestion (Powell, 1986), Gilbert and Nocedal (Gilbert and Nocedal, 1992) conducted an elegant analysis and established that they are globally convergent if they are restricted to be non-negative and the step length satisfies the sufficient descent condition. Further studies on global convergence properties of CG methods are of Hu and Storey (Hu and Storey, 1991), Liu et al (Zoutendijk and Abadie, 1970), and Touati-Ahmed and Storey (Touati-Ahmed and Storey, 1990) among others.
Recently, Yousif (Yousif, 2020) gave detailed proof for the sufficient descent property and the global convergence of the modified method of Rivaie; Mamat, Ismail, and Leong (RMIL + ) (Rivaie et al., 2012). In this author’s work, the coefficient is given by
The proof is based on the inequality
In the above setting the RMIL + method generated and under the application of strong Wolfe line search in the case of .
In this paper, inspired by Yousif (Yousif, 2020), we present a criterion that guarantees the descent property and the global convergence of each CG method satisfying this criterion. This is presented in Sections 2. In Section 3, based on this criterion, we propose modified versions of PRP and HS methods. Finally, in Section 4, to show the efficiency of the proposed modified methods in practical computation, they are compared with PRP, HS, FR, and RMIL + methods.
2 A new criterion guarantees sufficient descent and global convergence
In this section, we firstly show that for every CG method whose coefficient
satisfies
the inequality (1.8) holds true. Secondly, we prove the sufficient descent property and the global convergence of any CG method whose coefficient satisfies (2.1) under the application of strong Wolfe line search in the case of .
2.1 The sufficient descent property
Before we prove the desired property, we first note that for every-two positive real numbers
and
, we have
Theorem 2.1: Assume that and are generated by a CG method such that satisfies (2.1) under the application of strong Wolfe line search in the case of . Then (1.8) holds.
Proof: We follow the induction argument. For , (1.5) shows that (1.8) is satisfied. Now , suppose that (1.8) is true for , rewrite equation (1.5) for and multiply the resulting equation by , we get
Applying the triangle inequality, we get
Using the condition (1.4), we obtain
Substitute (2.1) for
and use C—S inequality, we get
Dividing both sides of (2.3) by and then applying the induction hypothesis (1.8), we come to
which leads to
Since and (see (2.2)), we come to
thus, the proof is complete.
Now, we are able to establish the sufficient descent property (1.6) under the condition (2.1). This is the topic of the following theorem
Theorem 2.2: Assume that and are generated by a CG method such that satisfies (2.1) under the application of strong Wolfe line search in the case of . Then the sufficient descent property (1.6) holds true.
Proof: For the result is clear by using (1.5). Consider the case .
From (1.5), we have
Applying the strong Wolfe condition (1.4), we get
Using Cauchy-Schwartz inequality and then substituting (2.1) and (1.8), we come to
which means
2.2 The global convergence
Now, based on the following assumption on the objective function , we establish the global convergence under strong Wolfe line search with of every CG method whose coefficient satisfies (2.1).
Assumption 2.1
-
Define and assume that is bounded for all initial points .
-
Let be a neighborhood of and assume that ) such that for some
-
‖g(x)-g(y)‖ ≤l ‖x-y‖, ∀ x,y ∈ N.
Under this assumption, Zoutendijk (Zoutendijk and Abadie, 1970) proved the following results.
Lemma 2.1 Let Assumption 2.1 is given. The for any conjugate gradient method in the forms (1.2)-(1.5) such that α_k is computed according to strong Wolfe line search. Then
From (2.4), we get
for all
which leads to
From (2.5) and (2.6) together, we come to.
Therefore, based on Assumption 2.1, we deduce that if the sequences and are generated by a CG method with coefficient satisfying (2.1) when it is applied under the strong Wolfe line search with , then (2.7) holds.
The following lemma will be used in the proof of the global convergence
Lemma 2.2: Suppose that
and
are generated by any CG method such that
satisfies (2.1) under the application of the strong Wolfe line search with
. Then there exists a positive constant
such that
Proof: Multiplying (1.5) by and then applying the triangle inequality, we obtain
Substituting (2.1) and applying the strong Wolfe condition (1.4) and using inequality (1.8), we get
which means where and this completes the proof.
Theorem 2.3: Suppose that Assumption 2.1 holds. Any CG method with a coefficient
satisfying (2.1) is globally convergent when it is applied under the strong Wolfe line search with
, that is,
Proof: The proof is by contradiction. It assumes that the opposite of (2.9) holds, that is, there exists a constant
and an integer
such that
which leads to
From (1.5), by squaring both sides of
, we get
Using (2.8), we obtain
which means
where .
Substituting (2.1) and dividing both sides by , we get
Since
(see (1.8)), then
Combining (2.11) and (2.13) together, we come to
This means
Then
Since
and
We come to
This contradicts (2.7). Therefore, the proof is completed.
3 Modified versions of the PRP and the HS methods
In this section, since the sufficient descent property and the global convergence of the well-known PRP and HS methods are not established under strong Wolfe line search, then motivated by the results in Section 2, we propose modified versions of PRP and HS methods, that is, by restricting the coefficients
and
in order to satisfy (2.1) as follows
and
We call these modified versions OPRP and OHS respectively, where the letter “O” stands for Osman.
Of course, both of the modified versions of PRP and HS satisfy (2.1), so that they generate descent directions at each iteration and globally convergent when they are applied under strong Wolfe line search with . Note that, in (3.1) and (3.2) when , then and and also tends to zero. Therefore, for a sufficiently large value of , the OPRP and the OHS methods can be considered as good approximations to both PRP and HS methods.
We also note, like PRP and HS methods, OPRP and OHS methods perform a restart when they encounter a bad direction, i.e., when approaches , then both and approach zero, so that approaches . Hence, we expect that they perform better than FR method in practice. Also, the sufficient descent property and the global convergence of both OPRP and OHS methods qualified them to be better than both PRP and HS theoretically, but it remains to show their performance in practical computations and this will be shown in the next section.
4 Numerical experiment
In this section, to show the efficiency and robustness and to support the theoretical proofs in Section 2, numerical experiments based on comparing the proposed OPRP and OHS when
with PRP, HS, FR, and RMIL + methods are done. To accomplish the comparison, a MATLAB coded program for these methods when they are all implemented under strong Wolfe line search with
and
is run. We stop the program if
. The test problems are unconstrained and most of them are from (Andrei, 2008). To show the robustness, test problems are implemented under low, medium, and high dimensions, namely, 2, 3, 4, 10, 50, 100, 500, 1000, and 10000. Furthermore, for each dimension, two different initial points are used, one of them is the initial point, which is suggested by Andrei (Andrei, 2008) and the other point is chosen arbitrarily. The comparison is based on the number of iterations (NI), the number of function evaluations (NF), and the number of gradient evaluations (NG). The numerical results are in Table 1. In Table 1, a method is considered to have failed, and we report “Fail” if the number of iterations exceeds
, or the search direction is not descent.
NI/NF/NG
NI/NF/NG
NI/NF/NG
NI/NF/NG
NI/NF/NG
NI/NF/NG
1
GENERALIZED WHITE & HOLST (Andrei, 2008)
2
49/233/127
74/307/17715/113/47
16/111/5315/98/47
Fail14/89/49
18/112/6214/89/45
18/115/6420/113/59
24/141/80
2
THREE-HUMP (Molga and Smutnicki, 2005)
2
14/397/85
Fail26/750/93
26/770/12211/293/48
14/347/14326/750/93
19/530/13811/293/48
15/385/8614/387/99
20/547/175
3
SIX-HUMP (Molga and Smutnicki, 2005)
2
13/44/30
10/54/285/19/13
8/47/235/19/13
8/47/255/19/13
7/40/225/19/13
8/45/245/19/13
8/50/26
4
TRECANNI (Zhu, 2004)
2
10/40/25
9/32/205/26/16
4/17/105/26/16
Fail5/26/16
5/20/125/26/16
5/19/115/26/16
Fail
13
EXTENDED WOOD (Andrei, 2008)
4
6897/33847/16150
1115/5012/2624123/481/282
167/736/401106/428/243
157/697/38351/225/128
74/397/20057/250/142
85/458/233118/406/254
245/982/581
14
FREUDENSTEIN & ROTH (Andrei, 2008)
4
24/88/53
194/85/47Fail
7/41/197/39/19
10/52/257/35/18
7/45/207/36/19
9/52/258/40/20
9/52/25
15
GENERALIZED TRIDIAGONAL 2 (Andrei, 2008)
4
5/16/13
Fail4/13/11
10/51/344/13/11
10/49/334/13/11
12/61/434/13/11
12/61/434/13/11
12/61/43
16
QP1 (Andrei, 2008)
4
205/69/45
17/74/436/24/14
10/54/277/27/16
8/43/227/27/16
10/52/297/27/16
10/52/297/28/17
11/55/31
17
FLETCHER (Andrei, 2008)
10
1203/5826/2809
2443/1202/58756/256/134
73/344/17356/256/134
73/348/17456/256/134
66/380/17556/256/134
51/300/13774/307/171
105/502/253
18
GENERALIZED TRIDIAGONAL 1 (Andrei, 2008)
10
27/88/58
43/164/10323/76/50
27/112/6823/76/50
27/112/6823/76/50
27/112/6823/76/50
27/112/6822/73/48
27/109/66
19
HAGER (Andrei, 2008)
10
11/34/31
97/314/21512/37/32
17/60/5112/37/32
17/60/5112/37/32
17/60/5112/37/32
17/60/5112/37/32
18/65/57
20
ARWHEAD (Andrei, 2008)
10
7/27/17
13/70/365/22/14
8/52/245/22/14
9/55/265/22/14
9/58/285/22/14
8/55/265/22/14
9/58/28
21
GENERALIZED QUARTIC (Andrei, 2008)
10
11/222/58
47/1065/8688/89/57
17/335/1028/93/59
16/320/1317/69/39
14/223/1158/93/59
15/236/1476/48/17
12/154/76
22
POWER (Andrei, 2008)
10
10/30/20
103/30/2010/30/20
10/30/2010/30/20
10/30/2010/30/20
10/30/2010/30/20
10/30/20104/312/208
122/366/244
23
GENERALIZED ROSENBROCK (Andrei, 2008)
10
Fail
Fail437/1702/1000
361/1540/868480/1847/1103
449/1840/1054642/2271/1431
962/3409/21241805/5798/3804
1211/4135/26151173/3915/2505
1691/5709/3598
24
RAYDAN 1 (Andrei, 2008)
10
102
19/90/76
2806/9964/6278
949/484/197
880/3806/191017/80/67
Fail
74/287/152
170/723/37317/80/67
Fail
75/314/157
169/694/37117/80/67
36/199/166
74/287/152
130/559/29417/80/67
36/196/168
75/314/157
130/565/29320/96/81
37/200/171
86/266/179
153/587/353
25
EXTENDED DENSHENB (Andrei, 2008)
10
102
9/31/22
17/65/42
18/68/44
9/44/235/19/14
8/34/21
8/34/21
9/51/275/19/14
8/34/21
8/34/21
10/48/265/19/14
9/37/23
9/37/23
9/44/235/19/14
9/37/23
9/37/23
9/44/235/19/14
10/45/29
10/45/29
10/47/25
26
EXTENDED PENALTY (Andrei, 2008)
10
102
12/52/31
17/64/38
238/4732/506
2830/11510/430945/162/106
10/49/29
17/97/51
15/96/4929/106/67
11/52/33
Fail
Fail16/63/39
9/40/23
13/78/40
12/71/3715/60/37
9/40/23
13/81/42
12/71/3714/57/36
8/37/22
23/144/78
13/75/39
27
QP2 (Andrei, 2008)
102
283/3487/737
2482/3295/64921/219/74
27/285/8823/244/77
24/256/8435/322/114
31/294/10036/325/116
32/308/10433/301/105
30/287/97
28
DIXON3DQ (Andrei, 2008)
50
25/79/55
25/79/5525/79/55
25/79/5525/79/55
25/79/5525/79/55
25/79/5525/79/55
25/79/55123/376/262
127/392/275
29
QF2 (Andrei, 2008)
50
116/394/285
73/299/16870/244/160
66/272/15070/244/160
65/269/14870/244/160
66/272/15070/244/160
65/269/14878/274/181
74/305/177
30
QF1 (Andrei, 2008)
50
50038/114/76
40/120/80
131/393/262
137/411/27438/114/76
40/120/80
131/393/262
137/411/27438/114/76
40/120/80
131/393/262
137/411/27438/114/76
40/120/80
131/393/262
137/411/27438/114/76
40/120/80
13/393/262
137/411/27469/207/138
78/234/156
162/486/325
198/594/397
31
HIMMELH (Andrei, 2008)
500
13/79/29
11/64/235/15/10
5/15/105/15/10
5/15/106/32/13
6/18/126/32/13
6/18/125/15/10
6/18/12
32
QUARTC (Andrei, 2008)
500
3/31/26
4/43/33Fail
Fail2/24/23
Fail3/31/26
3/26/163/31/26
3/26/163/31/26
3/26/16
33
EXTENDED TRIDIAGONAL 1 (Andrei, 2008)
500
103
340/1190/1035
14/68/58
399/1396/1212
518/1813/156114/71/60
7/42/35
14/71/60
7/43/2514/72/58
11/63/53
14/72/58
14/83/6112/61/50
8/47/38
12/61/51
13/78/5512/61/50
8/47/38
12/61/50
13/77/5512/60/50
8/47/38
12/60/50
7/44/24
34
DIAGONAL 4 (Andrei, 2008)
500
103
2/6/5
2/6/5
2/6/5
2/6/52/6/5
2/6/5
2/6/5
2/6/52/6/5
2/6/5
2/6/5
2/6/52/6/5
2/6/5
2/6/5
2/6/52/6/5
2/6/5
2/6/5
2/6/52/6/5
2/6/5
2/6/5
2/6/5
35
EXTENDED WHITE & HOLST (Andrei, 2008)
500
103
57/257/143
282/3749/859
572/257/143
1231/1608/37215/113/47
50/585/212
15/113/47
35/297/13515/98/47
49/548/207
15/98/47
35/292/12815/95/50
50/432/195
15/95/50
48/371/16815/95/50
50/432/194
15/95/50
49/376/17022/121/65
52/436/199
22/121/65
120/914/418
36
EXTENDED ROSENBROCK (Andrei, 2008)
103
104
68/530/182
260/2899/718
71/539/188
715/6694/176419/120/58
23/176/70
19/120/58
17/115/5321/134/67
25/183/72
21/134/67
18/117/5428/168/90
33/219/102
28/168/90
18/105/5728/167/88
32/215/99
28/167/88
18/105/5731/181/99
27/185/88
31/181/99
45/301/148
37
EXTENDED HIMMELBLAU (Andrei, 2008)
103
104
15/54/34
11/51/27
22/127/55
17/72/387/29/17
9/48/24
9/44/23
10/52/248/32/19
9/43/22
9/44/23
Fail8/32/19
7/39/19
10/47/25
9/47/218/32/19
7/39/19
9/44/23
9/47/217/30/18
7/39/19
9/39/22
9/48/22
38
STRAIT (Mishra, 2005)
103
104
35/146/91
88/682/269
35/147/92
109/774/34817/86/48
19/148/59
18/90/51
20/129/5917/86/48
19/150/60
18/90/51
20/127/6015/80/44
19/179/71
15/80/44
19/185/7115/80/44
18/172/63
15/80/44
18/184/6820/96/55
22/193/78
20/97/55
23/167/71
39
SHALLOW (Issam, 2005)
103
104
18/63/48
179/605/390
46/144/97
19/71/497/27/21
13/63/42
8/28/20
9/38/267/17/21
14/66/39
8/28/20
10/41/287/28/22
12/62/39
9/35/26
10/49/327/28/22
12/62/39
9/35/26
10/49/327/28/22
15/70/46
8/33/25
10/47/31
40
EXTENDED BEALE (Andrei, 2008)
103
104
75/242/159
80/254/170
88/285/187
86/272/18210/48/31
10/42/29
9/41/26
10/42/2913/67/41
11/45/31
9/41/24
11/45/3111/52/33
12/52/39
10/48/31
12/52/3914/72/46
12/52/39
9/43/26
12/52/3914/62/43
13/53/40
6/30/18
13/53/40
According to Table 1, we show the performance of OPRP, OHS, HS, PRP, FR, and RMIL + methods in Figs. 1-3 relative to the number of iterations, number of function evaluations, and number of gradient evaluations respectively. We used the performance profile introduced by Dolan and More (Dolan and More, 2002) which provides solver efficiency, robustness, and probability of success. In Dolan and More performance profile, we plot the percentage P of the test questions where a method falls within the best t-factor. Obviously, in the performance profile table, the curved shape at the top of the method is the winner. Furthermore, plot correctness is a measure of the robustness of the method.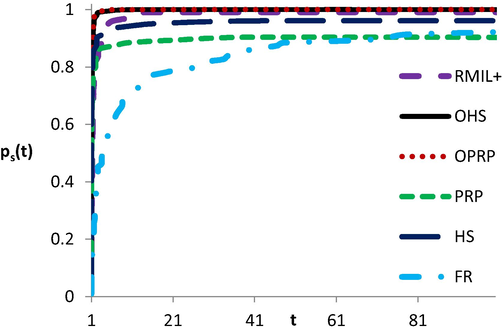
The performance based on NI.
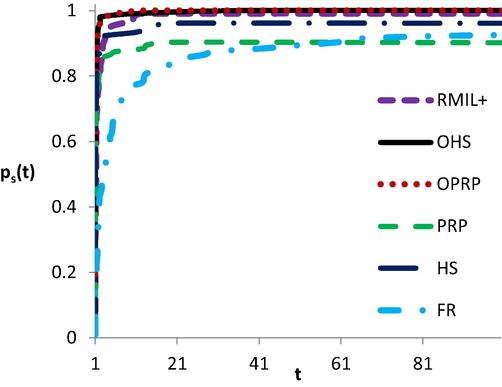
The performance based on NF.
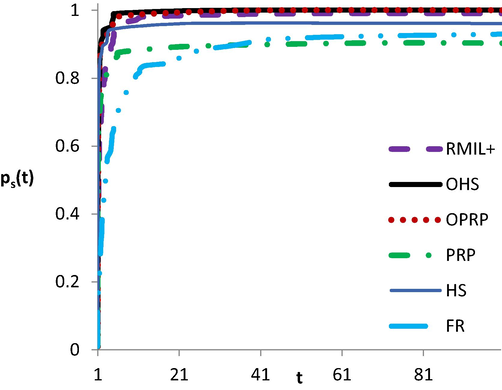
The performance based on NG.
Clearly, from Figs. 1-3, OPRP and OHS solve all test problems and therefore, reach 100 % percentage, whereas, FR, HS, PRP, and RMIL + solve about 94 %, 96 %, 90 %, and 99 % respectively. Furthermore, the left sides of all figures show that OPRP, OHS, PRP, and HS almost have the same highest probability of being the optimal solvers. In general, since the curves of both OPRP and OHS are above all other curves in most cases, then their performance is better than of the other methods.
5 Conclusions
In this paper, under the strong Wolfe line search, with , , we established the sufficient descent property and global convergence of CG methods with their coefficient satisfying for all . At the same time, we have proposed new modified versions of both PRP and HS methods called OPRP and OHS respectively. To show the efficiency and robustness and to support the theoretical proofs which establish the sufficient descent property and the global convergence, numerical experiments based on comparing OPRP and OHS with HS, PRP, FR, and RMIL+ have been done. Based on Dolan and More performance profile, it has been found that the new modified versions perform better than the other methods.
Funding
This research is supported by the deanship of scientific research in Majmaah University under the project number R-2022-230.
Declaration of Competing Interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Mogtaba Mohammed - Majamaah University, Osman Yousif - University of Gezera, Mohammed Saleh - Qassim University, Murtada Elbashir - Jouf University.
References
- A Liu-Storey-type conjugate gradient method for unconstrained minimization problem with application in motion control. J. King Saud Univ. Sci.. 2022;34(4):101923
- [Google Scholar]
- Descent property and global convergence of the Fletcher-Reeves method with inexact line search. IMA J. Numer. Anal.. 1985;5:121-124.
- [Google Scholar]
- An unconstrained optimization test functions collection. Adv. Model. Pptimizat.. 2008;10(1):147-161.
- [Google Scholar]
- A nonmonotone conjugate gradient algorithm for unconstrained optimization. J. Syst. Sci. Complex.. 2002;15(2):139-145.
- [Google Scholar]
- Comments on a new class of nonlinear conjugate gradient coefficients with global convergence properties. Appl. Math. Comput. 2016;276:297-300.
- [Google Scholar]
- A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim.. 2000;10:177-182.
- [Google Scholar]
- Benchmarking optimization software with performance profile. Math. Prog.. 2002;91:201-213.
- [Google Scholar]
- Global convergence properties of conjugate gradient methods for optimization. SIAM. J. Optim.. 1992;2:21-42.
- [Google Scholar]
- A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM. J. Optim.. 2005;16(1):170-192.
- [Google Scholar]
- Methods of conjugate gradients for solving linear systems. J. Research Nat. Bur. Standards.. 1952;49:409-436.
- [Google Scholar]
- Global convergence result for conjugate gradient methods. J. Optim. Theory Appl.. 1991;71:399-405.
- [Google Scholar]
- Minimization of extended quadratic functions with inexact line searches. J. Korean Soc. Indust. Appl. Math.. 2005;9(1):55-61.
- [Google Scholar]
- Efficient generalized conjugate gradient algorithms. Part 1: Theory. J. Optimiz. Theory Appl.. 1992;69:129-137.
- [Google Scholar]
- Some New Test Functions for Global Optimization and Performance of Repulsive Particle Swam Method. India: North-Eastern Hill University; 2005.
- M. Molga and C. Smutnicki, Test Functions for Optimization Needs, www.zsd.ict.pwr.wroc.p1/files/docs/functions.pdf, 2005.
- Note sur la convergence de directions conjuguée. Rev. Francaise Informat Recherche Operationelle, 3e Année. 1969;16:35-43.
- [Google Scholar]
- The conjugate gradient method in extremem problems. USSR Comp. Math. Math. Phys.. 1969;9:94-112.
- [Google Scholar]
- Nonconvex Minimization Calculations And The Conjugate Gradient Method In Lecture Notes In Mathematics, 1066. Berlin: Springer-Verlag; 1984. p. :122-141.
- Convergence properties of algorithms for nonlinear optimization. SIAM Rev.. 1986;28:487-500.
- [Google Scholar]
- A new class of nonlinear conjugate gradient coefficient with global convergence properties. Appl. Math. Comput.. 2012;218:11323-11332.
- [Google Scholar]
- Two efficient modifications of AZPRP conjugate gradient method with sufficient descent property. J. Inequal. Appl.. 2022;1:1-21.
- [Google Scholar]
- Efficient hybrid conjugate gradient techniques. J. Optim. Theory Appl.. 1990;64:379-397.
- [Google Scholar]
- New nonlinear conjugate gradient formulas for large-scale unconstrained optimization problems. Appl. Math. Comput. 2006;179(2):407-430.
- [Google Scholar]
- The convergence properties of some new conjugate gradient methods. Appl. Math. Compu.. 2006;183(2):1341-1350.
- [Google Scholar]
- The convergence properties of RMIL+ conjugate gradient method under strong Wolfe line search. Appl. Math. Compu.. 2020;367:124777
- [Google Scholar]
- Theory and Methods of Optimization. Beijing, China: Science Press of China; 1999.
- An improved Wei-Yao-Liu nonlinear conjugate gradient method for optimization computation. Appl. Math. Comput.. 2009;215:2269-2274.
- [Google Scholar]
- A Class of Filled Functions irrelevant to the Number of Local Minimizers for Global Optimization. J. Syst. Sci. Math. Sci.. 2004;22(4):406-413.
- [Google Scholar]
- Nonlinear programming, computational methods. In: Abadie J., ed. Integer and Nonlinear Programming. Amsterdam: North- Holland; 1970. p. :37-86.
- [Google Scholar]







