A counting problem on lattice points in two-, three- and four-dimensional spaces

1 Introduction

In molecular dynamics simulations, the coordination shells around an atom are often considered, such as in pairwise potentials (Kittel, 2005), the Van der Waals interactions (Mittemeijer, 2010), the embedded atom potentials (Daw and Baskes, 1984; Finnis and Sinclair, 1984; Duan and Liu, 2020) and the radial distribution function (Callister, 2001). Mirjalili and Vahdati-Khaki (2008) calculated the melting point of nano-particles by introducing and using the mean coordination number. Peresypkina and Blatov (1999) and Peresypkina and Blatov (2000) considered the molecular coordination numbers in crystal structures of simple substances and organic compounds. Wang et al. (2010) investigated the coordination numbers and geometrical conformation of rare earth metal. In Duan et al. (2020), computational problems of multilayered coordination radii and coordination numbers in cubic crystals were considered, respectively for simple cubic, body-centered cubic and face-centered cubic crystals. These problems were solved by modelling the enumeration of lattice points in 3-dimensional space by means of the Diophantine equations and generating functions.

The calculation problem of coordination numbers of cubic crystals, especially the simple cubic crystals, may be modeled as counting of lattice points in the Cartesian coordinate system. In a 2-dimensional space, the calculation of lattice points within a circle is related to an ancient puzzle, known as the Gauss’s circle problem (Hardy and Landau, 1924; Berndt et al., 2018), which is still an open problem (Berndt et al., 2018) the resolution of which involves the application of advanced number theory and special functions (Andrews, 2015; Travaglini, 2015; Grosswald, 1985). Its counterpart in 3-dimensional space has been considered in (Grosswald, 1985; Fraser and Gotlieb, 1962; Arkhipova, 2008; Fomenko, 2014). Further, a new field, the geometry on the integer lattices, was developed in Maehara and Martini (2018). Owing to the complicacy of computation problem on lattices, the lattice theory has been applied to the field of cryptography (Micciancio et al., 2011; Wang et al., 2016).

In this article, we consider a counting problem on lattice points in the n-dimensional space with the Cartesian rectangular coordinate system. Lattice points are all the points with the integer coordinates. The following notations are used:

n: the dimension of space under consideration.

r: the distance to the origin O of the Cartesian rectangular coordinate system.

$r_{n,k}$ : the distances from lattice points to the origin O in n-dimensional rectangular coordinate system, ordered from small to large as $r_{n,0}<r_{n,1}<r_{n,2}<\dots$ , where $r_{n,0}=0$ means the distance of the origin O to itself. So $r_{n,k}^2$ is just the $(k+1)$ th non-negative integer in natural order that may be expressed as sum of n square numbers.

$N_{n,k}$ : the number of lattice points on the spherical surface with the radius $r_{n,k},k=0,1,\dots$ .

$L_{n,k}$ : the total of lattice points on or inside the spherical surface with the radius $r_{n,k},k=0,1,\dots$ .

$\mathbb{Z}$ : the set of all the integers.

In the next section, we discuss the properties of the sequence $r_{n,k}$ and express $N_{n,k}$ as the number of integer solutions of a quadratic indefinite equation. Further, we derive the generating function for the sequences $N_{n,k}$ and $r_{n,k}^2,k=0,1,\dots$ , in terms of the elliptic theta functions. So convenient computing methods for $N_{n,k}$ and $r_{n,k}^2$ are obtained. In Section 3, we consider the properties of the sequences $N_{n,k}$ and $L_{n,k},k=0,1,\dots$ , especially focused on the cases of $n=2,3$ and 4.

2 Sequences $r_{n,k}$ and $N_{n,k},k=0,1,\dots$ , and the generating function

We consider the lattice points in n-dimensional space with rectangular coordinate system. Suppose the basis vectors of the unit orthogonal basis to be ${\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_n$ . Then, every lattice point A may uniquely be represented as a vector

The set of all possible values of $r^2$ is countable, assumed to be $r_{n,k}^2,k=0,1,2,\dots$ , and $$r_{n,0}<r_{n,1}<r_{n,2}<\dots \text{.}$$

All of the number $r_{n,k}^2,k=0,1,2,\dots$ , are exactly the set of all of the sums of n square numbers. It is obvious that

In 2-dimensional case, $r_{2,k}^2$ cannot equal 3, i.e. the first positive integer which cannot be represented as the quadratic sum of two integers is 3. In 3-dimensional case, $r_{3,k}^2$ cannot equal 7.

Whether a given positive integer can be represented into a quadratic sum of two, three or four integers is a classical and attractive problem. We list the related results in the following three theorems (Andrews, 2015; Travaglini, 2015; Grosswald, 1985; Feng, 2011).

If a positive integer m can be expressed as a sum of p square numbers, then m can be expressed as a sum of more than p square numbers either because some terms in the sum are already sum of squares or by trivially adding as many zeros squared as one wants. It can be derived that the sequence $\left\{r_{2,k}^2\right\}$ is a subsequence of $\left\{r_{3,k}^2\right\}$ , and the sequence $\left\{r_{3,k}^2\right\}$ is a subsequence of $\left\{r_{4,k}^2\right\}$ . From Theorem 3, if $n⩾4$ , then the sequence $\left\{r_{n,k}^2\right\}$ is just all the nonnegative integers, i.e.

We notice that for the higher dimensional cases, $n⩾4$ , the sequence $\left\{r_{n,k}^2\right\}$ is very simple. But for the 2-dimensional and 3-dimensional cases, namely $n=2,3$ , it is difficult to find a general term formula or recurrence relation for the sequence $\left\{r_{n,k}^2\right\}$ . By means of the software MATHEMATICA 8.0, the plots of $r_{n,k}^2$ versus k for $k=0,1,\dots ,49$ are shown in Fig. 1, where n is taken as 2, 3 and 4, respectively.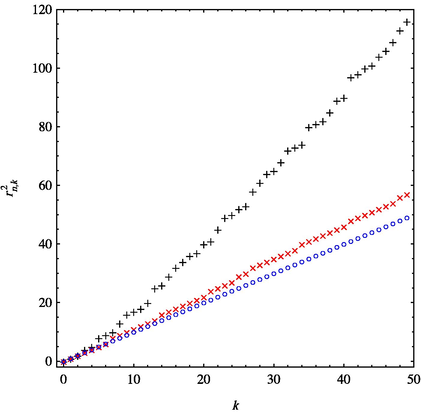

Close

Fig. 1

Plots of $r_{n,k}^2$ versus k for $k=0,1,\dots ,49$ (+: $n=2,\times :n=3,\circ :n=4$ ).

Export to PPT

The plots of $r_{n,k}^2$ versus k for $k=1$ through $k=20000$ were examined visually for $n=2$ and 3, and we found that for $n=3$ , the plot is almost a straight line, while for $n=2$ , the plot appears to be slightly concave. By linear fitting, the obtained results are

We also examined the fitting effects by adding a nonlinear term in the form of $\mathit{ak}+b+{\mathit{ck}}^d$ , and find that for the case of $n=3$ , the fitting result nearly does not change and $d=1$ again, while for the case of $n=2$ , the fitting result is ${\widehat{r}}_{2,k}^2=-2.1113k-119.88+4.3433k^{1.0366}$ .

For any nonnegative integer k, the number of lattice points, $N_{n,k}$ , on the spherical surface $\left|{\mathit{r}}_A\right|=r_{n,k}$ , introduced in the last section, is just the number of the n-tuples, $(x_1,x_2,\dots ,x_n)\in {\mathbb{Z}}^{\mathbb{n}}$ , the integer solutions of the quadratic indefinite equation

Next, we consider the generating function $G_n\left(t\right)$ of the sequence $N_{n,k},k=0,1,2,\dots$ , starting from the equation

Considering Eq. (7), combining the terms with same powers on the left hand side of Eq. (8) forms a power series on t, which is just in the form of ${\sum }_{k=0}^{\infty }{N}_{n,k}{t}^{r_{n,k}^2}$ . So we obtain the generating function for the sequences $N_{n,k}$ and $r_{n,k}^2,k=0,1,2,\dots$ , as

We can resort to a computer software to expand the power of the elliptic theta function in Eq. (9) into power series to obtain the values of $r_{n,k}^2$ and $N_{n,k}$ . We note that the elliptic theta function is built-in in MATHEMATICA 8.0. Let $L_{n,k}={\sum }_{i=0}^k{N}_{n,i}$ . In Table 1, the first ten values of the sequences $\left\{r_{n,k}^2\right\},\left\{N_{n,k}\right\}$ and $\left\{L_{n,k}\right\}$ for $n=2,3,4$ are listed.

3 Properties of sequences $N_{n,k}$ and $L_{n,k},k=0,1,2,\dots$

In this section, we investigate properties of the sequence $N_{n,k}$ and $L_{n,k},k=0,1,2,\dots$ , especially for the cases of $n=2,3$ and 4.

In the following we show that all of $l_i$ for $i=1,\dots ,n$ are even.

(i) If $n=2$ , then $l_1$ and $l_2$ in Eq. (11) are both even. In fact, it is obvious that there cannot be exactly one even. Suppose both $l_1$ and $l_2$ are odd, then $$l_1^2+l_2^2={(2u+1)}^2+{(2v+1)}^2=2(2u^2+2u+2v^2+2v+1),$$ where $u,v$ are integers. Eq. (11) cannot hold.

If $n=3$ , Eq. (11) implies evidently that $l_1,l_2$ and $l_3$ cannot be all odd, nor exactly one odd. Suppose there are exactly two being odd, then we have

Hence if $n=2$ or 3, all $l_i$ in Eq. (11) are even. Thus $(l_1/2,\dots ,l_n/2)$ is an integer solution of the equation ${\sum }_{i=1}^n{x}_i^2=r_{n,k}^2$ . It follows that $N_{n,k}⩾N_{n,s}$ .

(ii) If $n=4$ , Eq. (11) implies obviously that among $l_1,l_2,l_3$ and $l_4$ , there cannot be exactly one or three being odd. If there were exactly two being odd, a counterpart with Eq. (12) would derived. So Eq. (11) cannot hold. If all the four were odd, then

This is contradictory to Eq. (13). Hence if $n=4$ , all $l_i$ in Eq. (11) are even. Thus $(l_1/2,\dots ,l_4/2)$ is an integer solution for the equation ${\sum }_{i=1}^4{x}_i^2=r_{n,k}^2$ . It follows that $N_{n,k}⩾N_{n,s}$ . The proof is completed. $\blacksquare$ .

Theorem 5 indicates that for the 2-dimensional or 3-dimensional cases, the numbers of lattice points on the spherical surfaces remain the same when the radius doubles; for the 4-dimensional case, if the square of the radius is even, then as the radius doubles, the number of lattice points on the spherical surface remains unchanged. For the 4-dimensional case, if the square of the radius is odd, such invariant property cannot hold by the following theorem.

In Fig. 2, plots of $N_{n,k}$ versus k for $k=1$ through 260 are shown for $n=2$ , 3 and 4, respectively. From Theorem 5, for the 2-dimensional or 3-dimensional cases, for any $s⩾1$ , there are infinitely many terms in the sequence $\left\{N_{n,k}\right\}$ taking the same value with $N_{n,s}$ . This properties are reflected in Figs. 2a and 2b.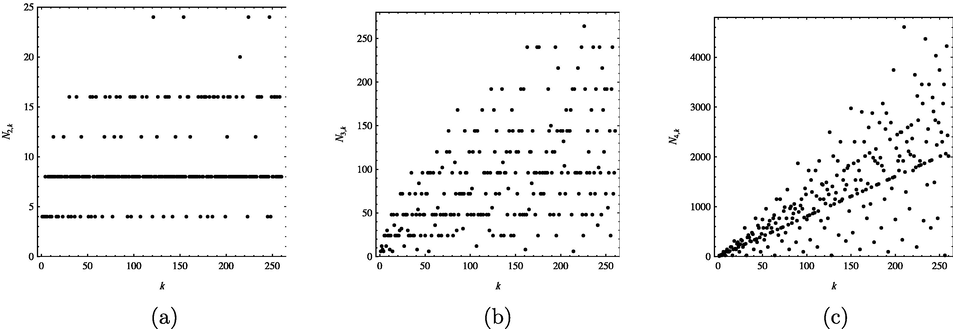

Close

Fig. 2

Plots of $N_{n,k}$ versus k for $k=1$ through 260 ((a) $n=2$ , (b) $n=3$ , (c) $n=4$ ).

Export to PPT

By using Eq. (4), the results in Theorems 5 (ii) and 6 mean

Because one lattice point occupies one n-dimensional unit cube and the n-dimensional sphere with the radius r has the volume $V_n\left(r\right)=\frac{{\pi }^{n/2}{r}^n}{\mathrm{\Gamma }(\frac{n}{2}+1)}$ ,where $\mathrm{\Gamma }(·)$ is the gamma function, so we have the asymptotic behavior for the sequence $L_{n,k}$ as

This means

We checked the results for $n=2,3$ and 4, and the data are plotted in Fig. 3.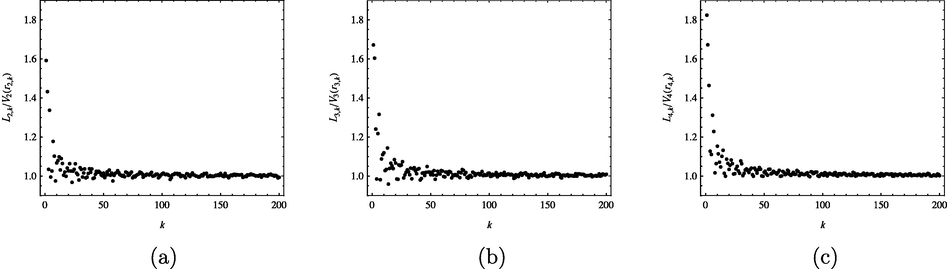

Close

Fig. 3

Plots of $L_{n,k}/V_n\left(r_{n,k}\right)$ versus k for $k=1$ through 200 ((a) $n=2$ , (b) $n=3$ , (c) $n=4$ ).

Export to PPT

Unlike the sequence $L_{n,k},k=0,1,2,\dots$ ,in Eqs. (22) and (23), the sequence $N_{n,k},k=0,1,2,\dots$ ,does not have an asymptotic behavior for our considered cases $n=2,3$ and 4. Instead, we may consider the sequence of mean values

From Eq. (22), it has the asymptotic behavior

For the case of $n=4$ , a simple result may be derived considering Eq. (4) as ${\bar{N}}_{4,k}\sim \frac{{\pi }^{2}k}{2},k\to \infty$ .For the cases of $n=2$ and $n=3$ , we only have ${\bar{N}}_{2,k}\sim \frac{\pi r_{2,k}^2}{k}$ and ${\bar{N}}_{3,k}\sim \frac{4\pi r_{3,k}^3}{3k}$ as $k\to \infty$ , since we do not know the asymptotic behaviors of the sequences $\left\{r_{2,k}\right\}$ and $\left\{r_{3,k}\right\}$ .

4 Conclusions

Lattice points in n-dimensional space scatter on a series of concentric spherical surfaces with the center O and the radii $r_{n,k}$ , where $0=r_{n,0}<r_{n,1}<r_{n,2}<\dots$ . All of the number $r_{n,k}^2,k=0,1,2,\dots$ , are exactly the set of all of the sums of n square numbers. If $n⩾4$ , the sequence $\left\{r_{n,k}^2\right\}$ is just the sequence of all the nonnegative integers, i.e. $r_{n,k}^2=k,k=0,1,2,\dots$ .The number of lattice points, $N_{n,k}$ , on the spherical surface with the radius $r_{n,k}$ equals the number of integer solutions of the quadratic indefinite equation ${\sum }_{i=1}^n{x}_i^2=r_{n,k}^2$ . The generating function is derived as $G_n\left(t\right)={\sum }_{k=0}^{\infty }{N}_{n,k}{t}^{r_{n,k}^2}={\left({\theta }_3\right(0,t\left)\right)}^n$ in terms of the elliptic theta functions for convenient calculation of $r_{n,k}$ and $N_{n,k}$ .

We proved that for the 2-dimensional or 3-dimensional cases, the numbers of lattice points on the spherical surfaces, $N_{n,k}$ , remain the same when the radius doubles; for the 4-dimensional case, if the square of the radius is even, then as the radius doubles, the number of lattice points on the spherical surface remains unchanged, while if the square of the radius is odd, such invariant property does not hold.

For the 2-dimensional case, for every $h,h=0,1,2,\dots$ , there exists a positive integer s, such that $r_{2,s}^2=2^h$ and $N_{2,s}=4$ .For the 3-dimensional case, for every $h,h=0,1,2,\dots$ , there exists a positive integer s, such that $r_{3,s}^2=4^h$ and $N_{3,s}=6$ . For the 4-dimensional case, for every $h,h=1,2,\dots$ , the equalities $N_{4,2^h}=24$ hold and 24 is the least value of $N_{4,k}$ for $k⩾2$ . Finally, the asymptotic behaviors of the sequences $L_{n,k}$ and ${\bar{N}}_{n,k}$ are given.