Translate this page into:
Influence of dipole interaction on the quantum correlation detection and teleportation in a qubit-field system
⁎Corresponding author at: Department of Mathematics, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia. eiedkhalil@tu.edu.sa (E.M. Khalil)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
This study examines the analysis of the teleportation process in a two-qubit state, particularly scrutinizing the interplay of atomic dipole coupling interaction, the detuning parameter, photon count, and the surrounding environment. Our investigation assumes the existence of a teleportation channel comprising two-qubit systems interacting with a photon field enveloped by the dephasing environment. Within this framework, we closely examine the quantum correlations exhibited by the teleported state, encompassing dimensions of entanglement, steering, and non-locality. Our results underscore the pivotal role played by the initial state of the atomic and field subsystems in shaping quantum relations. The dipole coupling has a profound impact, significantly enhancing the three quantifiers. Particularly, the entanglement changes from a de-entangled state to a partially entangled state. On the other hand, the detuning parameter introduces distortion in the quantum correlations, a phenomenon that can be effectively mitigated by controlling the dipole coupling.
Keywords
Dipole interaction
Teleportation
Steering
Entanglement
Non-locality
1 Introduction
Realistic experiments demonstrate that open quantum systems inevitably exchange energy with their surrounding environment during interactions. This energy exchange gradually erodes the system’s quantum properties, even at specific instances, potentially hindering their exploitation for practical applications (Yu and Eberly, 2009; Almeida et al., 2007). The detrimental effects of decoherence are particularly pronounced in the context of independent qubits, each embedded in its environment, which is essential for implementing quantum communication and information protocols with distant, individually addressable particles (Ladd et al., 2010; Abd-Rabboul et al., 2021). In response to the detrimental effects of decoherence on quantum correlations, researchers are exploring the possibility of designing effective and feasible quantum models that can safeguard these delicate correlations from the harmful influence of noise (Gisin and Thew, 2007). Conversely, significant attention has been devoted to Markovian designs, which involve crafting appropriate quantum systems capable of preserving quantum memory effects (Man et al., 2018). The non-Markovian systems exhibit fundamental characteristics that are essential for reviving quantum entanglement, regardless of whether they possess a bosonic or fermionic quantum nature (Fanchini et al., 2010; Rahman et al., 2023) or a classical nature (e.g., random noise, random field, noisy phase laser) (Abd-Rabbou et al., 2023c). In quantum systems, the presence of a thermal environment, characterized by its temperature, poses a significant challenge as it can induce decoherence, ultimately leading to the degradation of quantum correlations (Bellomo et al., 2008; Yan and Yue, 2013). This phenomenon has garnered considerable attention in recent research efforts, particularly in understanding its impact on entanglement dynamics. Moreover, the entanglement of multi-qubit quantum systems under the influence of both thermal and dephasing environments has been a subject of investigation (Hu et al., 2009; Hu, 2012). Additionally, quantum systems are often subjected to various noisy channels, such as amplitude damping, depolarizing, and phase damping channels, which disrupt quantum correlations, leading to information loss and diminished entanglement (Abd-Rabbou et al., 2019, 2023a). Therefore, this paper aims to explore the effects of the thermal environment and common dephasing environment on entanglement dynamics, particularly in the presence of n-sequential sin -pulse shapes (Abd-Rabbou et al., 2023b).
Quantum information theory was adopted to study the entanglement of quantum systems because of its key role in knowing the main characteristics in the interaction process between parts of the system, such as quantum encryption (Bouwmeester et al., 2013), quantum computations, geometric quantum computation (Wang, 2009; Guo et al., 2019), and dense cryptography (Hiroshima, 2001). Quantum correlations underpin the fundamental principles of quantum information processing. These correlations, including entanglement, nonlocality, steering, and discord, arise from interactions between parts of complex quantum systems (Abd-Rabbou et al., 2022; Youssef et al., 2023). Attention has been paid to studying the features of quantum correlations in encryption and teleportation on a large scale, both theoretically and experimentally (Mirmasoudi and Ahadpour, 2018). Using the previous quantum entanglement in which the sender and receiver participated, quantum teleportation and dense cryptography were implemented (Omri et al., 2022; Abd-Rabbou and Khalil, 2022). Therefore, many different quantum models have been designed to generate quantum correlation theoretically and experimentally. For example, a surface polariton-supporting method has been proposed to generate dually entangled electrons (Asban and García de Abajo, 2021). A shared phonon tank was designed to form non-classical correlations between two excited qubits (Krzywda and Roszak, 2016). The entanglement and discord periods generated from an unbound system when exposed to a combined thermal or pressurized tank are investigated in Gallego et al. (2012). A laboratory-viable scheme for generating a multi-mode quantum light source using a non-degenerate four-wave mixing procedure in a thermally controlled atomic vapor cell was designed in Cao et al. (2017). In addition, another practical scheme has been proposed, therefore, to generate quantum correlations and experimentally control the parameters of the quantum system to study entanglement periods (Ding et al., 2012).
The central aim of this study is to explore the viability of teleporting a pair of quantum qubits through an atom-field interaction within a dephasing environment. Teleported qubits undergo instantaneous exposure to various effects originating from the teleportation channel, encompassing factors such as the channel’s initial state, photon count, detuning, dipole coupling, and the decay rate of the dephasing environment. These factors can exert either augmenting or diminishing influences on the teleported quantum correlations. Prior research has indicated that dipole coupling has the potential to enhance quantum correlations (Khalil and Abd-Rabbou, 2022; Abd-Rabbou and Khalil, 2022). Our objective is to ascertain whether this enhancement extends to teleported quantum correlations and whether it can ameliorate the adverse effects of the dephasing environment and detuning. To address these inquiries, we will scrutinize the entanglement, steering, and nonlocality of the teleported state. This paper is structured as follows: Section 2 introduces the Hamiltonian model of the quantum channel and its density operator, incorporating the effects of the dephasing environment. Sections 3 and 4 provide a concise overview of the teleportation process and quantum correlation quantifiers, including entanglement, steering, and nonlocality. Section 5 presents our results, exploring the impact of teleportation channel parameters on quantum correlations. Finally, Section 6 summarizes our findings and concludes the paper.
2 Physical model of channel
Consider two partners, referred to as Jon in lab (a) and Rob in lab (b), who share a quantum channel comprising a two-qubit system with a frequency
. These qubits are coupled to each other through the coupling parameter,
, and simultaneously interact with a single mode of an ideal bosonic cavity with a frequency denoted as
. The system is described in Fig. 1. Mathematically, the Hamiltonian model of the quantum channel, under the rotating wave approximation, can be expressed as follows (Abd-Rabbou et al., 2024)
Now, we direct our focus toward determining the dynamic operators governing the current system. To achieve this, the application of well-established principles, such as the Heisenberg equations of motion, becomes imperative
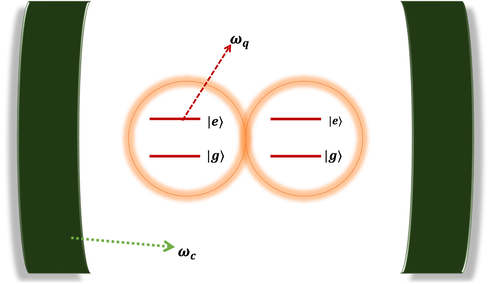
A Sketch of a two-qubit system located inside a cavity field. Here,
, and
are the frequencies of the quantized cavity field, and the two-qubit system.
To get
of the channel between Jon and Rob, we can employ the master equation, which is expressed as (Manzano, 2020)
According to Eqs. (5) and (6), we can get the following system of ordinary differential equations (ODE)
3 Teleportation process
The phenomenon of teleporting an entangled state between two distinct labs through a quantum channel has been introduced in the work of Lee and Kim (2000). Our methodology involves the utilization of the decayed density operator
as a communication channel, for transferring the state
between two key participants: Jon and Rob. In this collaborative effort, they both share the state (9) as their communication conduit, and the output state can be obtained by (Abd-Rabboul et al., 2021)
Hereinafter, we employ the concurrence, 3-steering, and Bell non-locality to examine the quantum correlation of the teleported state.
4 Quantum correlation measure
The fundamental concepts of quantum entanglement, steering, and non-locality are presented in this section as potent expressions of quantum correlations. States demonstrating entanglement and steerability can be quantified via metrics like concurrence and 3-steering, respectively. Notably, states that transgress Bell inequalities exemplify the most formidable correlations, signifying inherent non-locality between qubits when subjected to optimal measurement procedures.
4.1 Entanglement by concurrence
The degree of entanglement existing between two qubits can be effectively quantified through a well-established metric known as concurrence (Coffman et al., 2000). Concurrence serves as a reliable indicator of the entanglement strength within the quantum system, offering valuable insights into the interconnection between qubits. This quantification enables a more precise assessment of the quantum correlations and their potential impact on the system’s overall behavior. The quantification of entanglement, whether in pure or mixed quantum states, is conducted through the evaluation of eigenvalues (
) of the matrix
. Here,
which is derived from the hermitian conjugate of original density operator
and through the tensor product with Pauli spin matrices,
. The concurrence metric is formally defined as follows
4.2 Steering
In quantum information theory, 3-steering represents a concept that delves into the phenomenon of steering, which is a manifestation of quantum correlations. Steering involves the possibility of one quantum system indirectly influencing the state of another. In terms of three observable measurements on the two qubits (a) and (b), say
and
, the steering inequality can be expressed by (Costa and Angelo, 2016)
4.3 Bell non-locality
For deep investigation, we shall use the Bell non-locality, which is a phenomenon wherein entangled states correlations that cannot be elucidated by any local hidden variable theory (Clauser et al., 1970). This concept provides us with profound insights into the intricate nature of quantum correlations. In the case of a two-qubit state with X-shaped, the Bell non-locality is given by
5 Results and discussion
Fig. 2 provides a comprehensive visualization of the quantum correlations characterizing the teleported state through a damped atomic-field channel. In this study, we consider two distinct initial scenarios for the channel, one with
and the other with
, while the channel parameters are set at
and
, with the field initially in the vacuum state (
). By varying the dipole coupling (e.g.
and
), the discernible hierarchy among quantum correlations emerges, with the general order being maximum entanglement
steering
non-locality. This hierarchy illustrates the interplay of quantum correlations and underscores that the teleported information through the channel adheres to a distinct hierarchy of quantum correlations. In the first scenario, represented by
(as depicted in the left panels), and with variations in the coupling parameter
. All three quantifiers commence from their respective maximum values, which are one. Fig. 2(a) shows that these three correlations exhibit oscillatory behavior characterized by periods of sudden decline and resurgence, each subsequent phase displaying a lower maximum value than the preceding one. However, as time progresses, this pattern undergoes a reversal, leading to an eventual increase in the maximum values of these correlations. By increasing the parameter value of
to
in Fig. 2(c), it is evident that the quantum correlations undergo a noteworthy enhancement. Initially, at the onset of the scaled temporal evolution, quantum entanglement and steering exhibit an equivalence in their magnitudes, while the lower bounds of non-locality
are reduced. However, as time progresses, all three quantifiers exhibit a decreasing trend, which can be attributed to the influence of the decay rate
. Notably, non-locality experiences a more rapid decrease toward zero compared to steering and entanglement. Subsequently, upon further increasing
to 30, as depicted in Fig. 2(e), we observe a more pronounced enhancement in the three quantifiers and an increase in the number of oscillations. Notably, the entanglement curve
becomes distinct from the steering curve
as time advances, with steering converging to zero while entanglement tends toward a residual value.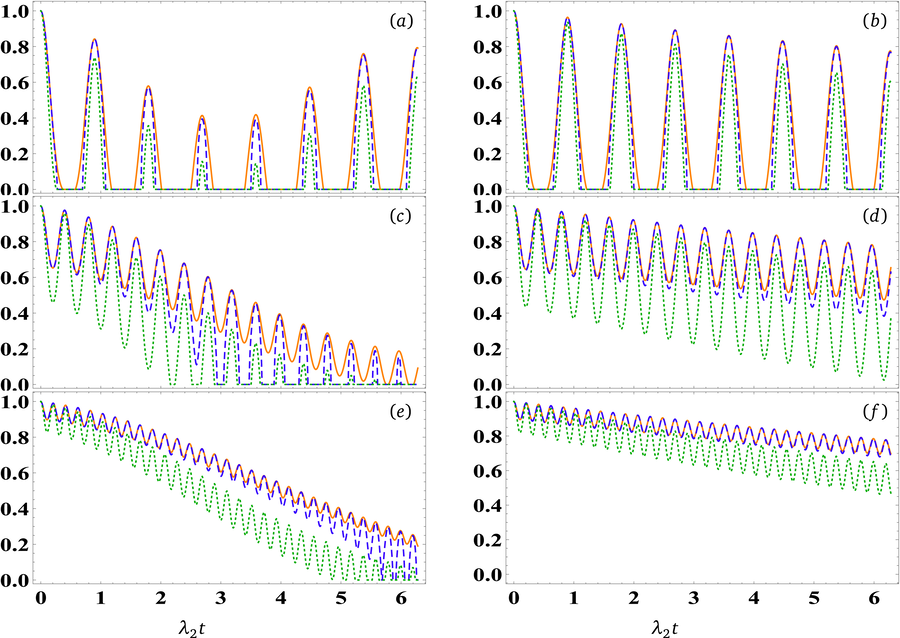
The temporal evolution of quantum correlations
(solid-orange-curve),
(dashed-blue-curve), and
(dotted-green-curve) against the scaled time
, where
,
,
and
. In the Left panels:
, (a)
, (c)
, (e)
. In the right panels: (b, d, f) are the same as (a, c, e), but
.
In the context of the second scenario, where (right panel), and keeping the conditions consistent with those presented in Figs. 2 (a, c, e), a distinct overall behavior is observed for the three quantifiers. At , these three functions exhibit corresponding oscillations at their maximum values. However, the presence of a decay rate diminishes the quantum correlations. Increasing reveals a convergence of the maximum bounds for steering and entanglement, while their minimum bounds diverge. Non-locality exhibits similar oscillatory behavior, consistently remaining below the bounds observed for steering and entanglement. Upon further increasing to 30, the steering and entanglement tend to exhibit greater similarity over time. A comparison of Figs. 2 (c, e) with Figs. 2 (d, f) reveals that in the first scenario ( = 1), the three quantifiers reach zero more rapidly than in the second scenario ( = 0). In the second scenario, steering and entanglement exhibit a stronger relationship with each other than in the first scenario. Consequently, it becomes evident that enhancing the dipole coupling strength, and thus the robustness of quantum correlations, at = 0 surpasses the scenario where = 1.
The impact of varying detuning parameter
and dipole coupling parameter
on the dynamics of the three quantum quantifiers of the two initial atomic scenarios is displayed in Fig. 3. We have set the initial field in the vacuum state n = 0, with
, and
. For the first scenario, characterized by
with
and
, Fig. 3(a) underscores how the detuning parameter influences the overall behavior of quantum correlations. It deformed the general behavior of quantum correlations, and non-locality is observed at specific intervals. However, under identical conditions but with
, Fig. 3(b) reveals a chaotic behavior exhibited by the three quantifiers. Notably, the maximally entangled state of the teleported state transitions into a partially entangled state. Over time, the oscillations in steering and non-locality tend to converge to zero. With an elevation in the detuning parameter (
), with
and
, Fig. 3(c) provides insights into the behavior of quantum correlations. As
increases, we observe a corresponding augmentation in the number of oscillations. The entangled teleported state through our channel undergoes oscillations between a partially entangled state and a de-entangled state. Consequently, the dynamics of steering and non-locality mirror this oscillatory pattern. In the case of
, while maintaining
, and
, Fig. 3(d) demonstrates the input teleported entangled state, due to its interaction with the channel, turns into a partially entangled state over time. Notably, non-locality oscillates between zero and partial non-locality, while steering does not reach zero until a certain time has elapsed. Fig. 3(e) shows the dynamics of teleported quantum correlations with
, influenced by the increase of the detuning parameter
and dipole coupling
. An enhancement is observed across the three quantifiers because of increasing
, where there are increases in the maximum bounds, and reducing in periods of de-entanglement. This positive trend is enhanced in the case of
, where the three quantifiers tend to a maximally correlated state. The presence of the decay factor in the dephasing environment induces an apparent decay in the system’s overall behavior over time. However, the dipole coupling counteracts this detrimental effect by reorganizing the inherent randomness and decay arising from the detuning parameter. In essence, the dipole coupling plays a crucial role in enhancing quantum correlations, ultimately leading to an increase in the maximum bounds achievable.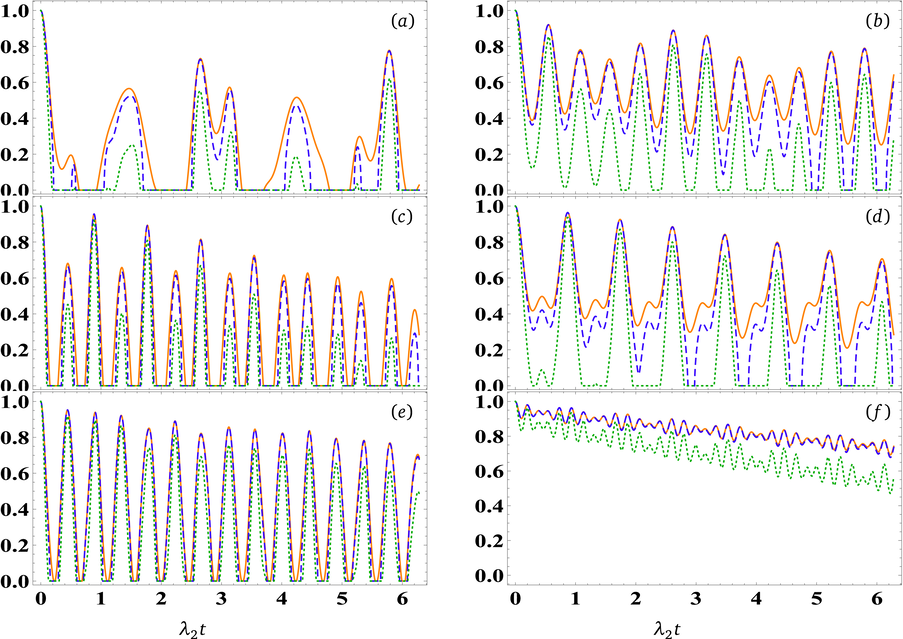
The temporal evolution of quantum correlations
(solid-orange-curve),
(dashed-blue-curve), and
(dotted-green-curve) against the scaled time
, where
,
, and
. In the Left panels:
, (a)
,
(b)
,
. (c)
,
. In the right panels: (b, d, f) are the same as (a, c, e), but
.
Fig. 4 exhibits the influence of increasing the number of photons (
) on the teleported quantum correlations under varying dipole coupling (
) conditions. When
,
, and
, Fig. 4(a) illustrates that the number of oscillations amplifies with the growing photon count. Notably, entanglement and steering exhibit a nearly identical trend at their maximum values, while the minimum bounds of steering diminish more rapidly than those of entanglement. The minimum bounds of non-locality approach zero, while the maximum bounds exhibit a non-monotonic behavior, initially decreasing and then increasing again. Interestingly, under identical conditions but with
(as shown in Fig. 4(b)), entanglement persists over time, whereas both steering and non-locality vanish completely. Upon raising the photon count to
, with
, both scenarios,
and
, displayed in Figs. 4(c) and (d), exhibit similar behaviors. They share nearly identical maximum bounds and a comparable number of oscillations. This suggests that the photon count plays a mitigating role in negating the influence of initial state parameters. Based on elevating the dipole coupling value to
, while keeping
, Figs. 4 (e), and (b) illustrate a notable augmentation in the number of oscillations and the amplification of maximum bounds. In this context, the minimum bounds exhibit enhancement but do not reach zero as readily. This decay over time can be attributed to the interaction with the dephasing environment.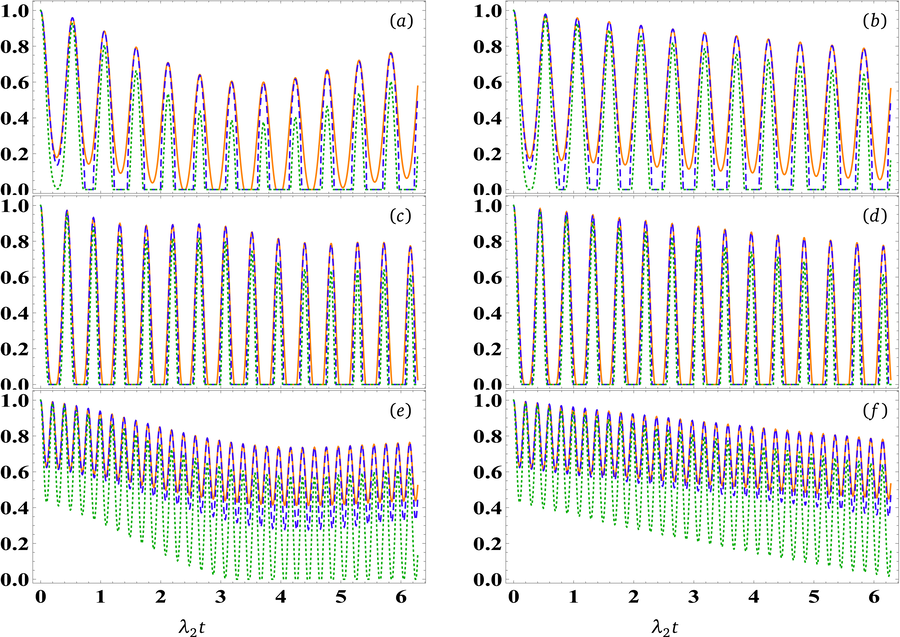
The temporal evolution of quantum correlations
(solid-orange-curve),
(dashed-blue-curve), and
(dotted-green-curve) against the scaled time
, where
,
, and
. In the Left panels:
, (a) n=1,
(b)
,
. (c)
,
. In the right panels: (b, d, f) are the same as (a, c, e), but
.
Fig. 5 depicts the impact of the dephasing environment, characterized by
, on the three quantum quantifiers and how the coupling dipole contributes to the augmentation of maximum bounds in quantum correlations. Figs. 5(a) and (b) shed light on how the initial state can sustain quantum correlations. However, it is worth noting that when the initial states are maximally entangled, the three phenomena for
exhibit greater resilience to the effects of the dephasing environment compared to the case of
, where the maximum bounds are notably higher at
(Figs. 5 (c) and (d)). It becomes evident that with an increase in the dipole coupling strength to
, there is a clear enhancement in the maximum bounds of the three quantum measures, accompanied by an increase in the number of oscillations. Although non-locality and steering diminish over time, entanglement does not reach zero within the measured time-frame. The strength of entanglement depends on the initial state of the system. This highlights the crucial role played by the initial state of the channel in shaping the dynamics of instantaneously transmitted quantum correlations, while the dipole coupling enhances entanglement and mitigates the impact of the surrounding thermal environment on the teleported state’s entanglement.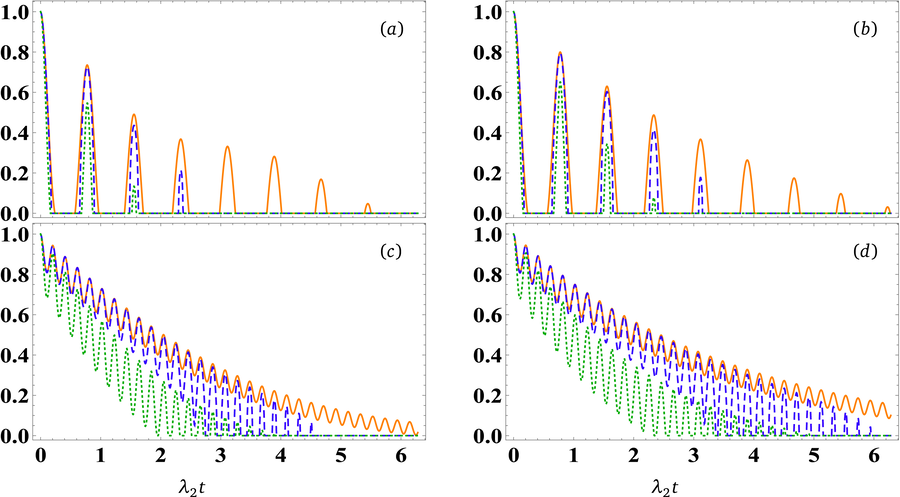
The temporal evolution of quantum correlations
(solid-orange-curve),
(dashed-blue-curve), and
(dotted-green-curve) against the scaled time
, where
,
,
, and
. In the Left panels:
, (a)
(b)
. In the right panels: (b, d) are the same as (a, c), but
.
6 Conclusion
This paper has examined the teleportation process of a pair of entangled qubits traversing a channel composed of interacting atoms immersed in a quantum field, all within the confines of a dephasing environment. The primary focus of our investigation revolved around the comprehensive analysis of entanglement, steering, and non-locality exhibited by the teleported state, particularly concerning the channel parameters. The key factors under scrutiny encompassed the dipole coupling, detuning, photon number, and the influence exerted by the surrounding dephasing environment. Notably, our study has been grounded in the assumption that the channel atoms commence with a state of maximal entanglement, following two distinct scenarios, while the quantum field remains in a number state.
Our results showed that the initial state of the channel system has a clear effect on the state to be teleported and its associated quantum correlations. Furthermore, a noteworthy enhancement in quantum correlations has been observed with the escalation of dipole coupling. This amplification has been particularly evident in the transformation of the teleported state, transitioning from a de-entangled state to a partially entangled state. The minima of steering and non-locality have also experienced elevation in response to heightened coupling levels.
As we increased the detuning parameter, we observed the distortion of quantum correlations, accompanied by heightened oscillations. Notably, increasing the dipole coupling reconfigured these oscillations and mitigated the adverse effects resulting from detuning. Furthermore, the increase in the photon number amplified the oscillations, making the teleported state less reliant on the initial atomic state. Coupling this heightened photon count with the double coupling effect led to a marked enhancement in the maximum values of quantum correlations. Conversely, the interaction of our system with the dephasing environment diminished the strength of quantum correlations in the teleported state. However, the dipole coupling played a significant role in mitigating this interaction’s influence.
CRediT authorship contribution statement
Hanaa Abu-Zinadah: Writing – original draft, Methodology, Conceptualization. E.M. Khalil: Writing – review & editing, Writing – original draft, Software, Methodology, Investigation, Conceptualization.
Acknowledgments
This work was funded by the University of Jeddah, Jeddah, Saudi Arabia under grant No. (UJ-23-DR-220). Therefore, the authors thanks the University of Jeddah for its technical and financial support.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Detraction of decoherence that arises from the acceleration process. J. Opt. Soc. Am. B. 2023;40(3):585-593.
- [Google Scholar]
- Dense coding and quantum memory assisted entropic uncertainty relations in a two-qubit state influenced by dipole and symmetric cross interactions. Ann. Phys. (Berl.). 2022;534(9):2200204
- [Google Scholar]
- Noise-based damping of chaotic entanglement in pulsed driven two-qubit system. Ann. Phys. (Berlin) 20232300423
- [Google Scholar]
- Probing teleported quantum correlations in a two-qubit system inside a coherent field. Optik. 2024;296:171551
- [Google Scholar]
- Suppressing the information losses of accelerated qubit–qutrit system. Int. J. Quantum Inf.. 2019;17(04):1950032
- [Google Scholar]
- Improving the bidirectional steerability between two accelerated partners via filtering process. Modern Phys. Lett. A. 2022;37(22):2250143
- [Google Scholar]
- Non-classical correlations of accelerated observers interacting with a classical stochastic noise beyond the single mode approximation. Opt. Quantum Elect.. 2023;55(8):715.
- [Google Scholar]
- Quantum Fisher information of a teleported state in heisenberg XYZ chain with magnetic field and Kaplan–Shekhtman–Entin-Wohlman–Aharony interaction. IEEE Access. 2021;9:51325-51331.
- [Google Scholar]
- Generation, characterization, and manipulation of quantum correlations in electron beams. npj Quantum Inf.. 2021;7(1):42.
- [Google Scholar]
- Entanglement dynamics of two independent qubits in environments with and without memory. Phys. Rev. A. 2008;77:032342
- [Google Scholar]
- The Physics of Quantum Information: Quantum Cryptography, Quantum Teleportation, Quantum Computation. Springer Science & Business Media; 2013.
- Experimental observation of quantum correlations in four-wave mixing with a conical pump. Opt. Lett.. 2017;42(7):1201-1204.
- [Google Scholar]
- Proposed experiment to test local hidden variable theories. Phys. Rev. Lett.. 1970;24:549.
- [Google Scholar]
- Quantification of Einstein-Podolsky-Rosen steering for two-qubit states. Phys. Rev. A. 2016;93:020103
- [Google Scholar]
- Generation of non-classical correlated photon pairs via a ladder-type atomic configuration: Theory and experiment. Opt. Express. 2012;20(10):11433-11444.
- [Google Scholar]
- Constraint relation between steerability and concurrence for two-qubit states. Ann. Phys.. 2021;533(8):2100098
- [Google Scholar]
- Generation of quantum correlations for two qubits through a common reservoir. Phys. Scr.. 2012;2012(T147):014012
- [Google Scholar]
- Teleportation of quantum Fisher information under decoherence channels with memory. Laser Phys. Lett.. 2019;16(9):095203
- [Google Scholar]
- Optimal dense coding with mixed state entanglement. J. Phys. A: Math. Gen.. 2001;34(35):6907.
- [Google Scholar]
- Disentanglement, bell-nonlocality violation and teleportation capacity of the decaying tripartite states. Ann. Phys., NY. 2012;327(9):2332-2342.
- [Google Scholar]
- Thermal and phase decoherence effects on entanglement dynamics of the quantum spin systems. Physica B: Cond. Matt.. 2009;404(20):3499-3506.
- [Google Scholar]
- Robustness of a teleported state influenced by dipole interaction and magnetic field under intrinsic decoherence. Optik. 2022;267:169703
- [Google Scholar]
- Phonon-mediated generation of quantum correlations between quantum dot qubits. Sci. Rep.. 2016;6(1):23753.
- [Google Scholar]
- Temperature effects on quantum non-Markovianity via collision models. Phys. Rev. A. 2018;97(6):062104
- [Google Scholar]
- Dynamics of super quantum discord and optimal dense coding in quantum channels. J. Phys. A. 2018;51(34):345302
- [Google Scholar]
- Witnessing quantum correlations in two coupled quantum dots under intrinsic decoherence. Alex. Eng. J.. 2023;69:521-527.
- [Google Scholar]
- Thermal information and teleportation in two-qutrit Heisenberg XX chain model. Alex. Eng. J.. 2022;61(10):8335-8342.
- [Google Scholar]
- Two-qubit steerability, nonlocality, and average steered coherence under classical dephasing channels. Ann. Phys. (Berl.). 2023;535(4):2200523
- [Google Scholar]
- Geometric quantum computation and dynamical invariant operators. Phys. Rev. A. 2009;79(2):024304
- [Google Scholar]
- Dynamics of quantum and classical correlations of a two-atom system in thermal reservoirs. Chaos Solit. Fractals. 2013;57:117-122.
- [Google Scholar]
- Exploring quantum correlations of two-qubit heisenberg chain model influenced by magnetic dipole–dipole, magnetic field, and a symmetric cross interaction. Quantum Inf. Process.. 2023;22(6):229.
- [Google Scholar]







