Explicit and traveling wave solutions of the non-linear couple Drinfeld-Sokolov-Wilson dynamical system arising in shallow water waves

Aly R. Seadawy; David Yaro; Hanadi Zahed

doi:10.1016/j.jksus.2020.101276

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

03 2020

:33;

101276

doi:

10.1016/j.jksus.2020.101276

Explicit and traveling wave solutions of the non-linear couple Drinfeld-Sokolov-Wilson dynamical system arising in shallow water waves

Aly R. Seadawy^{^a,⁎}, David Yaro^{^b}, Hanadi Zahed^{^a}

a Department of Mathematics, Faculty of Science, Taibah University, Al-Madinah Al-Munawarah, Saudi Arabia

b Faculty of Science, Jiangsu University, ZhenJiang, JiangSu 212013, PR China

⁎Corresponding author. aly742001@yahoo.com (Aly R. Seadawy)

Received: 2020-2-6, Accepted: 2020-11-27,

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Abstract

We efficaciously extended the ansatz in the Riccati equation rational expansion technique to a new broad form and is used to attain some new exact wave solutions for the couple non-linear Drinfeld-Sokolov-Wilson (DSW) system. This system arises in water waves, quantum mechanics, fluid mechanics, biology, chemistry etc. Several of the attained solutions which is in the shape of rational solitary wave solutions and periodic wave solutions are entirely new and could be vital for researchers to appreciate. Certain selected solutions are graphically verified by precise values allocated to constant parameters. This technique with the current ansatz can be implemented with a broader range of applicability to handle various other forms of non-linear evolution systems (NLES).

Keywords

Riccati equation rational expansion method

Non-linear Drinfeld-Sokolov-Wilson (DSW) system

Solitary wave solutions

Non-linear evolution systems

Show Related Articles from PubMed

1 Introduction

Of late, it is well observing that several attentions have been focused by researchers on the proliferation of finding the exact solitary wave solutions for coupled non-linear evolution systems (NLES), which play a crucial part in characterizing non-linear problems in mathematical physics and sciences. The coupled non-linear systems have many applications and are often used to exemplify many of the problems in physical sciences, for instance, material science, chemistry, biology, ocean waves, fluid dynamics, optical fiber, plasma physics etc. (Li et al., 2019; Li and Viglialoro, 2018; Abdou and Soliman, 2005; Abdou, 2007a; Abdou, 2007b; Seadawy and Alamri, 2018; Aljahdaly et al., 2019; Arshad et al., 2019; Lu et al., 2019b; Yaro et al., 2019 ). Attaining numerical and exact solutions for coupled NLES exhibits indispensable task in the investigation of tangible occurrence and has become a vigorous and important task. However, attaining the exact solution of problems involving coupled NLES can aid researchers understand these occurrences well as compare to the numerical solutions (Apeanti et al., 2019a; Seadawy et al., 2018; Nasreen et al., 2019; Ahmed et al., 2019; Cheemaa et al., 2019; Lu et al., 2019a; Apeanti et al., 2019b; Iqbal et al., 2019 ). Hence, the research of the exact wave solutions of coupled NLES exhibits a significant role in the investigation of these tangible phenomena and numerous controlling techniques already proposed to attain the exact solutions, for example, extended tanh technique, Painlev $\overset{́}{e}$ technique, extended mapping technique, homogeneous balance technique, homotopy perturbation technique, Exp-function technique, finite difference technique, F-expansion technique, Adomian decomposition technique, various Tanh technique, auxiliary equation technique, rational expansion technique and so on (Agarwal et al., 2020; Agarwal et al., 2017; Wen, 2010; Zenga and Wang, 2009; Selima et al., 2016; Seadawy and El-Rashidy, 2013; Yue et al., 2016; Arshad et al., 2016; Wen, 2011; Wang et al., 2012; Lin et al., 2011; Qin, 2008; Liu and Li, 2016 ). Several authors (Abdullah and Wang, 2017; Arshad et al., 2017) have investigated the structure and the exact solitary wave solutions for the non-linear Drinfeld–Sokolov–Wilson (DSW) system.

In the meantime the aforementioned method have numerous advantages over the other methods, the easiness and the accessibility of softwares which can smooths the tedious algebraic calculations motivated us to implement the RERE method to ascertain new exact solutions for the DSW system via new ansatz. For this current paper, the ansatz equation is extended to a new general form in the Riccati equation rational expansion (RERE) technique (Wang et al., 2005) to attain successions of solutions for the non-linear coupled DSW system. Therefore, more or less new and versatile exact traveling wave solutions have been constructed.

The remaining work arrangements are as follows: The Section 2 outlined the RERE technique. In Section 3, this technique is implemented to obtain a new series of solutions for DSW systems. In Section 4, some of the solutions attained are presented graphically to describe the evolutionary shape of the solutions. Section 5 represents the results and discussions. Section 6 points out the conclusion.

2 Summary of the technique

In this aspect, the analytical technique of how the Riccati equation rational technique is used to attain the traveling wave solution of NLES. Most importantly, we check the technique when implementing the NLES defined problems, which has two non-dependent variables, a space (x) dimension and time (t) dimension. Given the subsequent non-linear evolution equation of which we attain traveling wave solutions:

(1)

P_{j} (m_{j}, m_{jt}, m_{jx}, m_{jtt}, m_{jxt}, m_{jxx}, \dots) = 0,

where

m (ξ) = m (x, t)

is an unidentified function,

P_{j}

is a polynomial of

m (x, t)

and its partial derivatives as well as the maximum order derivative and non-linear terms. Consequently, we introduce the significant steps for this technique: Step 1. In joining the cases

ξ, ∊

and

ζ

into a variable

ξ = β x - δ t

, we suggest

(2)

m_{j} (x, t) = M_{j} (ξ), ξ = β x - δ t,

where

β

and

δ

are unknowns which will be attained later. Eq. (2) allows us to simplify Eq. (1) to the succeeding ordinary differential equation (ODE):

(3)

Q_{j} (M_{j}, M_{j}^{'}, M_{j}^{″}, \dots) = 0,

where

Q_{j}

is the polynomial in

M_{j} (ξ)

and its derivatives, whereas

M_{j}^{'} = \frac{dM}{d ξ}, M_{j}^{″} = \frac{d^{2} M}{d ξ^{2}}

, etc.

Step 2. We can now suggest that equation (3) has a well founded solution

(4)

M_{j} (ξ) = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} {(ψ (ξ))}^{k} + λ_{j} {(ψ (ξ))}^{j - 1} ψ^{'} (ξ)}{{(α ψ (ξ) + 1)}^{j}} + \sum_{j = 2}^{n} μ_{j} {(ψ (ξ))}^{j - 2} ψ^{'} (ξ) + \sum_{j = 1}^{n} γ_{j} {(\frac{ψ^{'} (ξ)}{ψ (ξ)})}^{j},

where

ψ = ψ (ξ)

fulfill the equation

(5)

ψ^{'} (ξ) = k_{1} + k_{2} ψ {(ξ)}^{2},

with

α, k_{1}, k_{2}, σ_{0}, σ_{j}, λ_{j}, μ_{j}

and

γ_{j} (j = 1, 2, \dots, n)

are unknowns which will be obtained later.

Step 3. The basic systems of a succession of essential solutions, like polynomial exponential, Jacobi, rational solitary waves, and triangular periodic are the diverse special effects of varying waveforms in various non-linear systems, hence, dispersion, dissolution and non-linearity (either in combination or in used) can be balanced. We apply $D [M_{j} (ξ)] = n_{j}$ to signify the degree for $M_{j} (ξ)$ and that of the other terms as:

(6)

D [M_{j}^{(η)}] = n_{j} + η, D [M_{j}^{η} {(M_{l}^{(κ)})}^{ν}] = n_{j} κ + (η + n_{l}) ν .

Step 4. Now by putting (4) in (3) together with (5) and then by setting all coefficients of $ψ^{j} (ξ), (j = 1, 2, \dots)$ of the numerator of the obtained system’s to zero, the system of non-linear algebraic equations about $β, α, σ_{0}, σ_{j}, λ_{j}, μ_{j}$ and $γ_{j} (j = 1, 2, \dots, n)$ can be determined.

Step 5. Applying software (ie. Mathematica or Maple) to find the non-linear algebraic expressions in Step 4, then we obtain the clear solution for the terms $β, α, σ_{0}, σ_{j}, λ_{j}, μ_{j}$ and $γ_{j} (j = 1, 2, \dots, n)$ .

Stage 6. Lastly, (5) has the subsequent validated solutions:

I. For $k_{1} = \frac{1}{2}$ and $k_{2} = - \frac{1}{2}$ ,

(7)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} {(\tanh (ξ) \pm isech (ξ))}^{j} + λ_{j} {(\tanh (ξ) \pm isech (ξ))}^{j - 1} ({sech}^{2} (ξ) \mp isech (ξ) \tanh (ξ))}{{(α (\tanh (ξ) \pm isech (ξ)) + 1)}^{j}} + \sum_{j = 2}^{n} μ_{j} {(\tanh (ξ) \pm isech (ξ))}^{j - 2} ({sech}^{2} (ξ) \mp isech (ξ) \tanh (ξ)) + \sum_{j = 1}^{n} γ_{j} {(\frac{{sech}^{2} (ξ) \mp isech (ξ) \tanh (ξ)}{\tanh (ξ) \pm isech (ξ)})}^{j},

(8)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} {(\coth (ξ) \pm csch (ξ))}^{j} - λ_{j} {(\coth (ξ) \pm csch (ξ))}^{j - 1} ({csch}^{2} (ξ) \pm csch (ξ) \coth (ξ))}{{(α (\coth (ξ) \pm icsch (ξ)) + 1)}^{j}} - \sum_{j = 2}^{n} μ_{j} {(\coth (ξ) \pm csch (ξ))}^{j - 2} ({csch}^{2} (ξ) \pm csch (ξ) (\coth (ξ))) + \sum_{j = 1}^{n} γ_{j} {(\frac{- ({csch}^{2} (ξ) \pm csch (ξ) \coth (ξ))}{\coth (ξ) \pm csch (ξ)})}^{j},

II. For $k_{1} = k_{2} = \pm \frac{1}{2}$ ,

(9)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} {(\sec (ξ) \pm \tan (ξ))}^{j} + λ_{j} {(\sec (ξ) \pm \tan (ξ))}^{j - 1} (\sec (ξ) \tan (ξ) \pm \sec^{2} (ξ))}{{(α (\sec (ξ) \pm \tan (ξ)) + 1)}^{j}} + \sum_{j = 2}^{n} μ_{j} {(\sec (ξ) \pm \tan (ξ))}^{j - 2} (\sec (ξ) \tan (ξ) \pm \sec^{2} (ξ)) + \sum_{j = 1}^{n} γ_{j} {(\frac{\sec (ξ) \tan (ξ) \pm \sec^{2} (ξ)}{\sec (ξ) \pm \tan (ξ)})}^{j},

(10)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} {(\csc (ξ) \pm \cot (ξ))}^{j} - λ_{j} {(\csc (ξ) \pm \cot (ξ))}^{j - 1} (\csc (ξ) \cot (ξ) \pm \csc^{2} (ξ))}{{(α (\csc (ξ) \pm \cot (ξ)) + 1)}^{j}} - \sum_{j = 2}^{n} μ_{j} {(\csc (ξ) \pm \cot (ξ))}^{j - 2} (\csc (ξ) \cot (ξ) \pm \csc^{2} (ξ)) + \sum_{j = 1}^{n} γ_{j} {(\frac{- (\csc (ξ) \cot (ξ) \pm \csc^{2} (ξ))}{\csc (ξ) \pm \cot (ξ)})}^{j},

III. For $k_{1} = 1$ and $k_{2} = - 1$ ,

(11)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} \tanh^{j} (ξ) + λ_{j} \tanh^{j - 1} (ξ) {sech}^{2} (ξ)}{{(α \tanh (ξ) + 1)}^{j}} + \sum_{j = 2}^{n} μ_{j} {(\tanh (ξ))}^{j - 2} {sech}^{2} (ξ) + \sum_{j = 1}^{n} γ_{j} {(\frac{{sech}^{2} (ξ)}{\tanh (ξ)})}^{j},

(12)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} \coth^{j} (ξ) - λ_{j} \coth^{j - 1} (ξ) {csch}^{2} (ξ)}{{(α \coth (ξ) + 1)}^{j}} - \sum_{j = 2}^{n} μ_{j} {(\coth (ξ))}^{j - 2} {csch}^{2} (ξ) + \sum_{j = 1}^{n} γ_{j} {(\frac{- {csch}^{2} (ξ)}{\coth (ξ)})}^{j},

IV. For $k_{1} = k_{2} = 1$ ,

(13)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} \tan^{j} (ξ) + λ_{j} \tan^{j - 1} (ξ) \sec^{2} (ξ)}{{(α \tan (ξ) + 1)}^{j}} + \sum_{j = 2}^{n} μ_{j} {(\tan (ξ))}^{j - 2} \sec^{2} (ξ) + \sum_{j = 1}^{n} γ_{j} {(\frac{\sec^{2} (ξ)}{\tan (ξ)})}^{j},

V. For $k_{1} = k_{2} = - 1$ ,

(14)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} \cot^{j} (ξ) - λ_{j} \cot^{j - 1} (ξ) \csc^{2} (ξ)}{{(α \cot (ξ) + 1)}^{j}} - \sum_{j = 2}^{n} μ_{j} {(\cot (ξ))}^{j - 2} \csc^{2} (ξ) + \sum_{j = 1}^{n} γ_{j} {(\frac{- \csc^{2} (ξ)}{\cot (ξ)})}^{j},

VI. For $k_{1} = 0$ and $k_{2} \neq 0$ ,

(15)

m_{j} = σ_{0} + \sum_{j = 1}^{n} \frac{σ_{j} {(k_{2} ξ + f_{0})}^{j} - λ_{j} k_{2} {(k_{2} ξ + f_{0})}^{j - 1}}{{(α (k_{2} ξ + f_{0}) + {(k_{2} ξ + f_{0})}^{2})}^{j}} - \sum_{j = 2}^{n} μ_{j} k_{2} {(k_{2} (ξ) + f_{0})}^{j - 2} + \sum_{j = 1}^{n} γ_{j} {(\frac{- k_{2}}{k_{2} (ξ) + f_{0}})}^{j},

where

ξ = β x - δ t, i = \sqrt{- 1}

and

f_{0}

is constant.

Remark. Notice that the ansatz suggested in this paper is new and different from the one suggested by Wang et al. (2005).

3 Implementation

3.1

3.1 The non-linear Drinfeld–Sokolov–Wilson (DSW) system

Here, we take into consideration the couple non-linear DSW system given in the form

(16)

\begin{matrix} m_{t} + {(r^{2})}_{x} = 0, \\ r_{t} - r_{xxx} + 3 {rm}_{x} + 3 {mr}_{x} = 0 . \end{matrix}

The non-linear coupled DSW system have been studied by several researchers (Arshad et al., 2017). By implementing (2) on (16) we attain

(17)

\begin{matrix} - δ M^{'} + β {(R^{2})}^{'} = 0, \\ - δ R^{'} - β^{3} R^{‴} + 3 β {RM}^{'} + 3 β {MR}^{'} = 0 . \end{matrix}

Now by ignoring the integral constant after integrating the first equation in (17), we get

(18)

δ M = β R^{2} .

By putting Eq. (18) into the second equation of (17), we get

(19)

δ^{2} R + β^{3} δ R^{″} - 3 β^{2} R^{3} = 0 .

Now from (19) and by implementing the homogeneous balance principle gives $n = 1$ . Therefore,(19) tends to

(20)

R (ξ) = σ_{0} + \frac{σ_{1} ψ (ξ) + λ_{1} ψ^{'} (ξ)}{α ψ (ξ) + 1} + γ_{1} \frac{ψ^{'} (ξ)}{ψ (ξ)},

where

ψ (ξ)

satisfies (5).

Substituting (20) alongside (5), results in a polynomial of $ψ^{j} (ξ) (j = 0, 1, \dots)$ . By setting the coefficients of the terms $ψ^{j} (ξ)$ to zero, gives a set of algebraic equation systems. Solving this set of systems for $σ_{0}, σ_{1}, λ_{1}, γ_{1}, α$ and $β$ with the aid of software gives the subsequent values.

Family 1: $k_{1} = \frac{1}{2}$ and $k_{2} = - \frac{1}{2}$ , $σ_{0} = 0, σ_{1} = 0, λ_{1} = 0, γ_{1} = \pm i \sqrt{\frac{2}{3}} δ^{2 / 3}, α = 0, β = - \sqrt[3]{δ},$ $σ_{0} = \pm \frac{δ^{2 / 3}}{4 \sqrt{3}}, σ_{1} = \pm \frac{δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3, β = 2 \sqrt[3]{δ},$ $\begin{matrix} σ_{0} = & \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}}, σ_{1} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3, \\ β = & - \sqrt[3]{- 2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, α = 0, \\ β = - \sqrt[3]{- 2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{4 \sqrt{3}}, σ_{1} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3, \\ β = - 2 \sqrt[3]{- 1} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, α = 0, \\ β = - \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{\sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{\sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, α = 0, \\ β = \frac{\sqrt[3]{δ}}{\sqrt[3]{2}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}}, σ_{1} = \pm \frac{δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3, \\ β = \sqrt[3]{2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{2^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, α = 0, \\ β = \sqrt[3]{2} \sqrt[3]{δ} . \end{matrix}$

Family 2: $k_{1} = k_{2} = \pm \frac{1}{2}$ , $\begin{matrix} σ_{0} = 0, σ_{1} = 0, λ_{1} = 0, γ_{1} = \pm \sqrt{\frac{2}{3}} δ^{2 / 3}, α = 0, β = \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 0, β = \sqrt[3]{- 2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{\sqrt[6]{- 1} 2^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, α = 0, \\ β = \sqrt[3]{- 2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{i \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{i \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, α = 0, β = - \frac{\sqrt[3]{δ}}{\sqrt[3]{2}}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{i δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{i 2^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, α = 0, β = - \sqrt[3]{2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{2 \sqrt{3} \sqrt[3]{4 - 3 i}}, σ_{1} = \pm \frac{\sqrt[6]{4 - 3 i} δ^{2 / 3}}{\sqrt{6}}, λ_{1} = 0, γ_{1} = 0, α = 3 i, \\ β = \sqrt[3]{4 - 3 i} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{2 \sqrt{3} \sqrt[3]{4 + 3 i}}, σ_{1} = \pm \frac{\sqrt[6]{4 + 3 i} δ^{2 / 3}}{\sqrt{6}}, λ_{1} = 0, γ_{1} = 0, α = - 3 i, \\ β = \sqrt[3]{4 + 3 i} \sqrt[3]{δ} . \end{matrix}$

Family 3: $k_{1} = 1$ and $k_{2} = - 1$ , $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{2 δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{δ^{2 / 3}}{\sqrt{3}}, α = 0, β = \frac{\sqrt[3]{δ}}{2}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}}, σ_{1} = \pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3, \\ β = - \sqrt[3]{- 2} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{2 {(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, α = 0, \\ β = - \frac{1}{2} \sqrt[3]{- 1} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2^{2 / 3} \sqrt{3}}, σ_{1} = \pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3, \\ β = - \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{2^{2 / 3} \sqrt{3}}, σ_{1} = \pm \frac{\sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3, β = \frac{\sqrt[3]{δ}}{\sqrt[3]{2}}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{\sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{\sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, α = 0, β = \frac{\sqrt[3]{δ}}{\sqrt[3]{2}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}}, σ_{1} = \pm \frac{2^{2 / 3} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3, β = \sqrt[3]{2} \sqrt[3]{δ} . \end{matrix}$

Family 4: $k_{1} = k_{2} = 1$ , $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{2 i δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{i δ^{2 / 3}}{\sqrt{3}}, α = 0, β = - \frac{\sqrt[3]{δ}}{2}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{2 \sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}}, α = 0, β = \frac{1}{2} \sqrt[3]{- 1} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{\sqrt[6]{- 1} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 0, β = \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{\sqrt{3} \sqrt[3]{8 - 6 i}}, σ_{1} = \pm \frac{\sqrt[6]{8 - 6 i} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3 i, \\ β = \frac{\sqrt[3]{4 - 3 i} \sqrt[3]{δ}}{2^{2 / 3}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3} \sqrt[3]{8 - 6 i}}, σ_{1} = \pm \frac{(3 - i) δ^{2 / 3}}{\sqrt[3]{- 8 + 6 i} \sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3 i, \\ β = - \frac{\sqrt[3]{- 4 + 3 i} \sqrt[3]{δ}}{2^{2 / 3}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3} \sqrt[3]{8 + 6 i}}, σ_{1} = \pm \frac{\sqrt[3]{- 3 - i} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3 i, \\ β = \frac{{(- 1)}^{2 / 3} \sqrt[3]{4 + 3 i} \sqrt[3]{δ}}{2^{2 / 3}} . \end{matrix}$

Family 5: $k_{1} = k_{2} = - 1$ , $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{2 i δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{i δ^{2 / 3}}{\sqrt{3}}, α = 0, β = - \frac{\sqrt[3]{δ}}{2}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{2 \sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}}, α = 0, β = \frac{1}{2} \sqrt[3]{- 1} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{\sqrt[6]{- 1} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 0, β = \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ}, \end{matrix}$ $\begin{matrix} σ_{0} = 0, σ_{1} = \pm \frac{i \sqrt[3]{- 2} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = \pm \frac{i \sqrt[3]{- 2} δ^{2 / 3}}{\sqrt{3}}, α = 0, β = - \frac{{(- 1)}^{2 / 3} \sqrt[3]{δ}}{\sqrt[3]{2}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{\sqrt{3} \sqrt[3]{8 - 6 i}}, σ_{1} = \pm \frac{\sqrt[6]{8 - 6 i} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = 3 i, \\ β = \frac{\sqrt[3]{4 - 3 i} \sqrt[3]{δ}}{2^{2 / 3}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ^{2 / 3}}{\sqrt{3} \sqrt[3]{8 + 6 i}}, σ_{1} = \pm \frac{\sqrt[6]{8 + 6 i} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3 i, \\ β = \frac{\sqrt[3]{4 + 3 i} \sqrt[3]{δ}}{2^{2 / 3}}, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3} \sqrt[3]{8 + 6 i}}, σ_{1} = \pm \frac{{(- 1)}^{2 / 3} \sqrt[6]{8 + 6 i} δ^{2 / 3}}{\sqrt{3}}, λ_{1} = 0, γ_{1} = 0, α = - 3 i, \\ β = - \frac{\sqrt[3]{- 1} \sqrt[3]{4 + 3 i} \sqrt[3]{δ}}{2^{2 / 3}} . \end{matrix}$

Family 6: $k_{1} = 0$ and $k_{2} \neq 0$ , $\begin{matrix} σ_{0} = 0, σ_{1} = - k_{2} γ_{1}, λ_{1} = 0, γ_{1} = γ_{1}, α = 0, β = β, \end{matrix}$ $\begin{matrix} σ_{0} = \pm \frac{δ}{\sqrt{3} β}, σ_{1} = - k_{2} γ_{1}, λ_{1} = 0, γ_{1} = γ_{1}, α = 0, β = β . \end{matrix}$

As indicated in Family 1, (16) obtain the following solutions:

(21)

r_{11} = \pm \frac{i \sqrt{\frac{2}{3}} δ^{2 / 3} ({sech}^{2} (ξ) \mp itanh (ξ) sech (ξ))}{\tanh (ξ) \pm isech (ξ)},

(22)

m_{11} = - \frac{1}{δ^{2 / 3}} {(\pm \frac{i \sqrt{\frac{2}{3}} δ^{2 / 3} ({sech}^{2} (ξ) \mp itanh (ξ) sech (ξ))}{\tanh (ξ) \pm isech (ξ)})}^{2},

(23)

r_{12} = - \frac{i \sqrt{\frac{2}{3}} δ^{2 / 3} ({csch}^{2} (ξ) \pm \coth (ξ) csch (ξ))}{\coth (ξ) \pm csch (ξ)},

(24)

m_{12} = - \frac{1}{δ^{2 / 3}} {(- \frac{i \sqrt{\frac{2}{3}} δ^{2 / 3} ({csch}^{2} (ξ) \pm \coth (ξ) csch (ξ))}{\coth (ξ) \pm csch (ξ)})}^{2},

where

ξ = - \sqrt[3]{δ} x - δ t

and

δ

is constant,

(25)

r_{13} = \pm \frac{δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{δ^{2 / 3}}{\sqrt{3}} (\tanh (ξ) \pm isech (ξ))}{3 (\tanh (ξ) \pm isech (ξ)) + 1},

(26)

m_{13} = \frac{2}{δ^{2 / 3}} {(\pm \frac{δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{δ^{2 / 3}}{\sqrt{3}} (\tanh (ξ) \pm isech (ξ))}{3 (\tanh (ξ) \pm isech (ξ)) + 1})}^{2},

(27)

r_{14} = \pm \frac{δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{δ^{2 / 3}}{\sqrt{3}} (\coth (ξ) \pm csch (ξ))}{3 (\coth (ξ) \pm icsch (ξ)) + 1},

(28)

m_{14} = \frac{2}{δ^{2 / 3}} {(\pm \frac{δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{δ^{2 / 3}}{\sqrt{3}} (\coth (ξ) \pm csch (ξ))}{3 (\coth (ξ) \pm icsch (ξ)) + 1})}^{2},

where

ξ = 2 \sqrt[3]{δ} x - δ t

and

δ

is constant,

(29)

r_{15} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\tanh (ξ) \pm isech (ξ))}{1 - 3 (\tanh (ξ) \pm isech (ξ))},

(30)

m_{15} = - \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\tanh (ξ) \pm isech (ξ))}{1 - 3 (\tanh (ξ) \pm isech (ξ))})}^{2},

(31)

r_{16} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\coth (ξ) \pm csch (ξ))}{1 - 3 (\coth (ξ) \pm icsch (ξ))},

(32)

m_{16} = - \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\coth (ξ) \pm csch (ξ))}{1 - 3 (\coth (ξ) \pm icsch (ξ))})}^{2},

where

ξ = - \sqrt[3]{- 2} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(33)

r_{17} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\tanh (ξ) \pm isech (ξ)) \pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3} ({sech}^{2} (ξ) \mp itanh (ξ) sech (ξ))}{\sqrt{3} (\tanh (ξ) \pm isech (ξ))},

(34)

m_{17} = - \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\tanh (ξ) \pm isech (ξ)) \pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3} ({sech}^{2} (ξ) \mp itanh (ξ) sech (ξ))}{\sqrt{3} (\tanh (ξ) \pm isech (ξ))})}^{2},

(35)

r_{19} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} (\tanh (ξ) \pm isech (ξ))}{3 (\tanh (ξ) \pm isech (ξ)) + 1},

(36)

m_{19} = - \frac{2 \sqrt[3]{- 1}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} (\tanh (ξ) \pm isech (ξ))}{3 (\tanh (ξ) \pm isech (ξ)) + 1})}^{2},

(37)

r_{110} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} (\coth (ξ) \pm csch (ξ))}{3 (\coth (ξ) \pm icsch (ξ)) + 1},

(38)

m_{110} = - \frac{2 \sqrt[3]{- 1}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{4 \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} (\coth (ξ) \pm csch (ξ))}{3 (\coth (ξ) \pm icsch (ξ)) + 1})}^{2},

where

ξ = - 2 \sqrt[3]{- 1} \sqrt[3]{δ} x - δ t

and

δ

is constant.

Remark. Not all the solutions of Family 1 cases listed are attained.

As indicated in Family 2, (16) obtain the following solutions:

(39)

r_{21} = \pm \frac{\sqrt{\frac{2}{3}} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sec (ξ) \pm \tan (ξ)},

(40)

m_{21} = \frac{1}{δ^{2 / 3}} {(\pm \frac{\sqrt{\frac{2}{3}} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sec (ξ) \pm \tan (ξ)})}^{2},

(41)

r_{22} = - \frac{\sqrt{\frac{2}{3}} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\csc (ξ) \pm \cot (ξ)},

(42)

m_{22} = \frac{1}{δ^{2 / 3}} {(- \frac{\sqrt{\frac{2}{3}} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\csc (ξ) \pm \cot (ξ)})}^{2},

where

ξ = \sqrt[3]{δ} x - δ t

and

δ

is constant,

(43)

r_{23} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\sec (ξ) \pm \tan (ξ)),

(44)

m_{23} = \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\sec (ξ) \pm \tan (ξ)))}^{2},

(45)

r_{24} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\csc (ξ) \pm \cot (ξ)),

(46)

m_{24} = \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\csc (ξ) \pm \cot (ξ)))}^{2},

where

ξ = \sqrt[3]{- 2} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(47)

r_{25} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\sec (ξ) \pm \tan (ξ)) \pm \frac{\sqrt[6]{- 1} 2^{2 / 3} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sqrt{3} (\sec (ξ) \pm \tan (ξ))},

(48)

m_{25} = \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\sec (ξ) \pm \tan (ξ)) \pm \frac{\sqrt[6]{- 1} 2^{2 / 3} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sqrt{3} (\sec (ξ) \pm \tan (ξ))})}^{2},

(49)

r_{26} = \pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\csc (ξ) \pm \cot (ξ)) - \frac{\sqrt[6]{- 1} 2^{2 / 3} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\sqrt{3} (\csc (ξ) \pm \cot (ξ))},

(50)

m_{26} = \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{\sqrt[6]{- 1} δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\csc (ξ) \pm \cot (ξ)) \pm - \frac{\sqrt[6]{- 1} 2^{2 / 3} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\sqrt{3} (\csc (ξ) \pm \cot (ξ))})}^{2},

where

ξ = \sqrt[3]{- 2} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(51)

\begin{matrix} r_{27} & = \pm \frac{i \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} (\sec (ξ) \pm \tan (ξ)) \pm \frac{i \sqrt[3]{2} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sqrt{3} (\sec (ξ) \pm \tan (ξ))}, \end{matrix}

(52)

m_{27} = - \frac{1}{\sqrt[3]{2} δ^{2 / 3}} {(\pm \frac{i \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} (\sec (ξ) \pm \tan (ξ)) \pm \frac{i \sqrt[3]{2} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sqrt{3} (\sec (ξ) \pm \tan (ξ))})}^{2},

(53)

r_{28} = \pm \frac{i \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} (\csc (ξ) \pm \cot (ξ)) - \frac{i \sqrt[3]{2} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\sqrt{3} (\csc (ξ) \pm \cot (ξ))},

(54)

m_{28} = - \frac{1}{\sqrt[3]{2} δ^{2 / 3}} {(\pm \frac{i \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} (\csc (ξ) \pm \cot (ξ)) - \frac{i \sqrt[3]{2} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\sqrt{3} (\csc (ξ) \pm \cot (ξ))})}^{2},

where

ξ = - \frac{\sqrt[3]{δ}}{\sqrt[3]{2}} x - δ t

and

δ

is constant,

(55)

r_{29} = \pm \frac{i δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\sec (ξ) \pm \tan (ξ)) \pm \frac{i 2^{2 / 3} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sqrt{3} (\sec (ξ) \pm \tan (ξ))},

(56)

m_{29} = - \frac{\sqrt[3]{2}}{δ^{2 / 3}} {(\pm \frac{i δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\sec (ξ) \pm \tan (ξ)) \pm \frac{i 2^{2 / 3} δ^{2 / 3} (\tan (ξ) \sec (ξ) \pm \sec^{2} (ξ))}{\sqrt{3} (\sec (ξ) \pm \tan (ξ))})}^{2},

(57)

r_{210} = \pm \frac{i δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\csc (ξ) \pm \cot (ξ)) - \frac{i 2^{2 / 3} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\sqrt{3} (\csc (ξ) \pm \cot (ξ))},

(58)

m_{210} = - \frac{\sqrt[3]{2}}{δ^{2 / 3}} {(\pm \frac{i δ^{2 / 3}}{\sqrt[3]{2} \sqrt{3}} (\csc (ξ) \pm \cot (ξ)) - \frac{i 2^{2 / 3} δ^{2 / 3} (\cot (ξ) \csc (ξ) \pm \csc^{2} (ξ))}{\sqrt{3} (\csc (ξ) \pm \cot (ξ))})}^{2},

where

ξ = - \sqrt[3]{2} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(59)

r_{211} = \frac{\pm \frac{\sqrt[6]{4 - 3 i} δ^{2 / 3}}{\sqrt{6}} (\sec (ξ) \pm \tan (ξ))}{1 + 3 i (\sec (ξ) \pm \tan (ξ))} \pm \frac{δ^{2 / 3}}{2 \sqrt{3} \sqrt[3]{4 - 3 i}},

(60)

m_{211} = \frac{\sqrt[3]{4 - 3 i}}{δ^{2 / 3}} {(\frac{\pm \frac{\sqrt[6]{4 - 3 i} δ^{2 / 3}}{\sqrt{6}} (\sec (ξ) \pm \tan (ξ))}{1 + 3 i (\sec (ξ) \pm \tan (ξ))} \pm \frac{δ^{2 / 3}}{2 \sqrt{3} \sqrt[3]{4 - 3 i}})}^{2},

Remark. Not all the solutions of Family 2 cases listed are attained.

As indicated in Family 3, (16) obtain the following solutions:

(61)

r_{31} = \pm \frac{2 δ^{2 / 3}}{\sqrt{3}} \tanh (ξ) \pm \frac{δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}},

(62)

m_{31} = \frac{1}{2 δ^{2 / 3}} {(\pm \frac{2 δ^{2 / 3}}{\sqrt{3}} \tanh (ξ) \pm \frac{δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}})}^{2},

(63)

r_{32} = \pm \frac{2 δ^{2 / 3}}{\sqrt{3}} \coth (ξ) - \frac{δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}},

(64)

m_{32} = \frac{1}{2 δ^{2 / 3}} {(\pm \frac{2 δ^{2 / 3}}{\sqrt{3}} \coth (ξ) - \frac{δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}})}^{2},

where

ξ = \frac{\sqrt[3]{δ}}{2} x - δ t

and

δ

is constant,

(65)

r_{33} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{\pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} \tanh (ξ)}{3 \tanh (ξ) + 1},

(66)

m_{33} = - \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{\pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} \tanh (ξ)}{3 \tanh (ξ) + 1})}^{2},

(67)

r_{34} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{(\pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}) \coth (ξ)}{3 \coth (ξ) + 1},

(68)

m_{34} = - \frac{\sqrt[3]{- 2}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2 \sqrt[3]{2} \sqrt{3}} + \frac{(\pm \frac{{(- 2)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}}) \coth (ξ)}{3 \coth (ξ) + 1})}^{2},

where

ξ = - \sqrt[3]{- 2} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(69)

r_{35} = \pm \frac{2 {(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} \tanh (ξ) \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}},

(70)

m_{35} = - \frac{\sqrt[3]{- 1}}{2 δ^{2 / 3}} {(\pm \frac{2 {(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} \tanh (ξ) \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}})}^{2},

(71)

r_{36} = \pm \frac{2 {(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} \coth (ξ) - \frac{{(- 1)}^{2 / 3} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}},

(72)

m_{36} = - \frac{\sqrt[3]{- 1}}{2 δ^{2 / 3}} {(\pm \frac{2 {(- 1)}^{2 / 3} δ^{2 / 3}}{\sqrt{3}} \coth (ξ) - \frac{{(- 1)}^{2 / 3} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}})}^{2},

where

ξ = - \frac{1}{2} \sqrt[3]{- 1} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(73)

r_{37} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2^{2 / 3} \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} \tanh (ξ)}{1 - 3 \tanh (ξ)},

(74)

m_{37} = - \frac{\sqrt[3]{- \frac{1}{2}}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2^{2 / 3} \sqrt{3}} + \frac{\pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} \tanh (ξ)}{1 - 3 \tanh (ξ)})}^{2},

(75)

r_{38} = \pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2^{2 / 3} \sqrt{3}} + \frac{(\pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}) \coth (ξ)}{1 - 3 \coth (ξ)},

(76)

m_{38} = - \frac{\sqrt[3]{- \frac{1}{2}}}{δ^{2 / 3}} {(\pm \frac{{(- 1)}^{2 / 3} δ^{2 / 3}}{2^{2 / 3} \sqrt{3}} + \frac{(\pm \frac{{(- 1)}^{2 / 3} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}}) \coth (ξ)}{1 - 3 \coth (ξ)})}^{2},

where

ξ = - \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(77)

r_{39} = \pm \frac{i \sqrt[6]{2} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}},

(78)

m_{39} = - \frac{1}{2^{2 / 3} δ^{2 / 3}} {(\pm \frac{i \sqrt[6]{2} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}})}^{2},

(79)

r_{310} = - \frac{i \sqrt[6]{2} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}},

(80)

m_{310} = - \frac{1}{2^{2 / 3} δ^{2 / 3}} {(- \frac{i \sqrt[6]{2} δ^{2 / 3} csch (ξ) sech (ξ)}{\sqrt{3}})}^{2},

where

ξ = - \frac{\sqrt[3]{δ}}{2^{2 / 3}} x - δ t

and

δ

is constant.

Remark. Not all the solutions of Family 3 cases listed are attained.

As indicated in Family 4, (16) obtain the following solutions:

(81)

r_{41} = \pm \frac{2 i δ^{2 / 3}}{\sqrt{3}} \tan (ξ) \pm \frac{i δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(82)

m_{41} = - \frac{1}{2 δ^{2 / 3}} {(\pm \frac{2 i δ^{2 / 3}}{\sqrt{3}} \tan (ξ) \pm \frac{i δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = - \frac{\sqrt[3]{δ}}{2} x - δ t

and

δ

is constant,

(83)

r_{42} = \pm \frac{2 \sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}} \tan (ξ) \pm \frac{\sqrt[6]{- 1} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(84)

m_{42} = \frac{\sqrt[3]{- 1}}{2 δ^{2 / 3}} {(\pm \frac{2 \sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}} \tan (ξ) \pm \frac{\sqrt[6]{- 1} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = \frac{1}{2} \sqrt[3]{- 1} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(85)

r_{43} = \pm \frac{\sqrt[6]{- 1} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} \tan (ξ),

(86)

m_{43} = \frac{\sqrt[3]{- \frac{1}{2}}}{δ^{2 / 3}} {(\pm \frac{\sqrt[6]{- 1} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} \tan (ξ))}^{2},

where

ξ = \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(87)

r_{44} = \pm \frac{\sqrt[6]{2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(88)

m_{44} = \frac{1}{2^{2 / 3} δ^{2 / 3}} {(\pm \frac{\sqrt[6]{2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = \frac{\sqrt[3]{δ}}{2^{2 / 3}} x - δ t

and

δ

is constant,

(89)

r_{45} = \pm \frac{i \sqrt[6]{- 2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(90)

m_{45} = - \frac{\sqrt[3]{- 1}}{2^{2 / 3} δ^{2 / 3}} {(\pm \frac{i \sqrt[6]{- 2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = - \frac{\sqrt[3]{- 1} \sqrt[3]{δ}}{2^{2 / 3}} x - δ t

and

δ

is constant.

Remark. Not all the solutions of Family 4 cases listed are attained.

As indicated in Family 5, (16) obtain the following solutions:

(91)

r_{51} = \pm \frac{2 i δ^{2 / 3}}{\sqrt{3}} \cot (ξ) - \frac{i δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(92)

m_{51} = - \frac{1}{2 δ^{2 / 3}} {(\pm \frac{2 i δ^{2 / 3}}{\sqrt{3}} \cot (ξ) - \frac{i δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = - \frac{\sqrt[3]{δ}}{2} x - δ t

and

δ

is constant,

(93)

r_{52} = \pm \frac{2 \sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}} \cot (ξ) - \frac{\sqrt[6]{- 1} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(94)

m_{52} = \frac{\sqrt[3]{- 1}}{2 δ^{2 / 3}} {(\pm \frac{2 \sqrt[6]{- 1} δ^{2 / 3}}{\sqrt{3}} \cot (ξ) - \frac{\sqrt[6]{- 1} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = \frac{1}{2} \sqrt[3]{- 1} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(95)

r_{53} = \pm \frac{\sqrt[6]{- 1} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} \cot (ξ),

(96)

m_{53} = \frac{\sqrt[3]{- \frac{1}{2}}}{δ^{2 / 3}} {(\pm \frac{\sqrt[6]{- 1} \sqrt[3]{2} δ^{2 / 3}}{\sqrt{3}} \cot (ξ))}^{2},

where

ξ = \sqrt[3]{- \frac{1}{2}} \sqrt[3]{δ} x - δ t

and

δ

is constant,

(97)

r_{54} = - \frac{\sqrt[6]{2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(98)

m_{54} = \frac{1}{2^{2 / 3} δ^{2 / 3}} {(- \frac{\sqrt[6]{2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = \frac{\sqrt[3]{δ}}{2^{2 / 3}} x - δ t

and

δ

is constant,

(99)

r_{55} = - \frac{i \sqrt[6]{- 2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}},

(100)

m_{55} = - \frac{\sqrt[3]{- 1}}{2^{2 / 3} δ^{2 / 3}} {(- \frac{i \sqrt[6]{- 2} δ^{2 / 3} \csc (ξ) \sec (ξ)}{\sqrt{3}})}^{2},

where

ξ = - \frac{\sqrt[3]{- 1} \sqrt[3]{δ}}{2^{2 / 3}} x - δ t

and

δ

is constant.

Remark. Not all the solutions of Family 5 cases listed are attained.

As indicated in Family 6, (16) obtain the following solutions:

(101)

r_{61} = - \frac{2 γ_{1} k_{2}}{f_{0} + k_{2} ξ},

(102)

m_{61} = \frac{β}{δ} {(- \frac{2 γ_{1} k_{2}}{f_{0} + k_{2} ξ})}^{2},

(103)

r_{62} = \pm \frac{δ}{\sqrt{3} β} - \frac{2 γ_{1} k_{2}}{f_{0} + k_{2} ξ},

(104)

m_{62} = \frac{β}{δ} {(\pm \frac{δ}{\sqrt{3} β} - \frac{2 γ_{1} k_{2}}{f_{0} + k_{2} ξ})}^{2},

where

ξ = β x - δ t, δ, β, γ_{1}, f_{0}

are constants and

k_{2} \neq 0

4 Graphical depiction for some of the solutions acquired

In this section, graphically displays for some of the acquired solutions in the preceding section is represented. The numerous acquired solutions are achieved via allocating a constant value to each parameter. The physical nature is presented within the interval $- 2 ⩽ x, t ⩽ 2$ . The graphs are plotted by taking the values at constants $δ = 2, γ_{1} = 1, κ_{2} = 1.5, β = 1.5$ and $f_{0} = 1.5$ . The nature of the graphs depict how significance the solutions attained for the non-linear coupled DSW system is introduced as system of water waves. Below are some of the plotted figures, thus, Figs. 1–5 .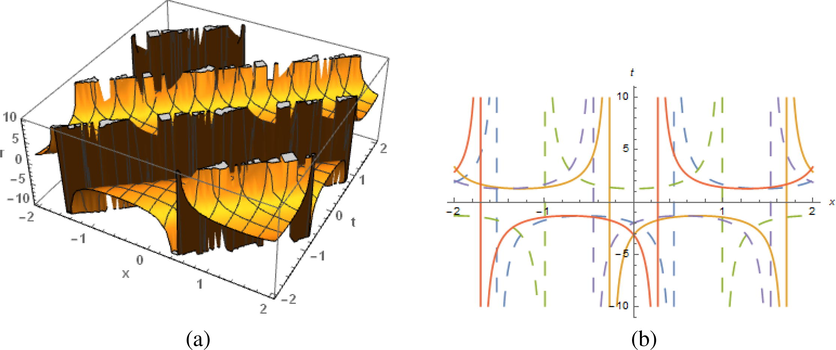

The results of (39) display from the figures with diverse plotted natures at δ = 2 in the range - 2 ⩽ x , t ⩽ 2 : (a) periodic solitary wave and (b) represent 2–dimensional nature.

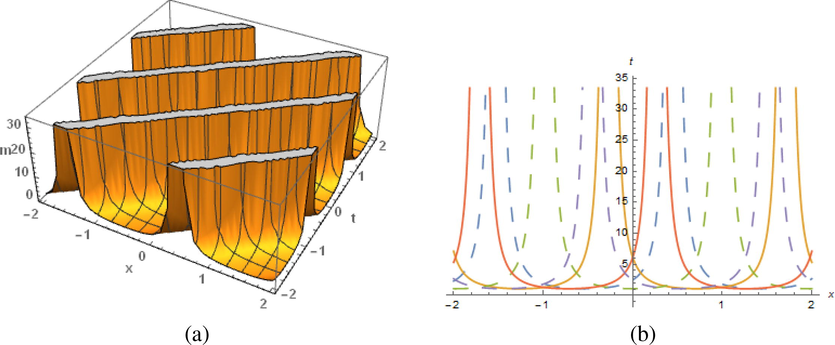
The results of (40) display from the figures with diverse plotted natures at δ = 2 in the range - 2 ⩽ x , t ⩽ 2 : (a) periodic solitary wave and (b) represent 2–dimensional nature.

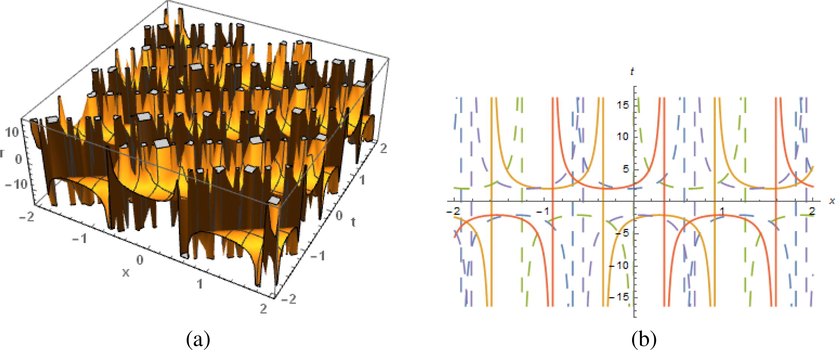
The results of (87) display from the figures with diverse plotted natures at δ = 2 in the range - 2 ⩽ x , t ⩽ 2 : (a) periodic solitary wave and (b) represent 2–dimensional nature.

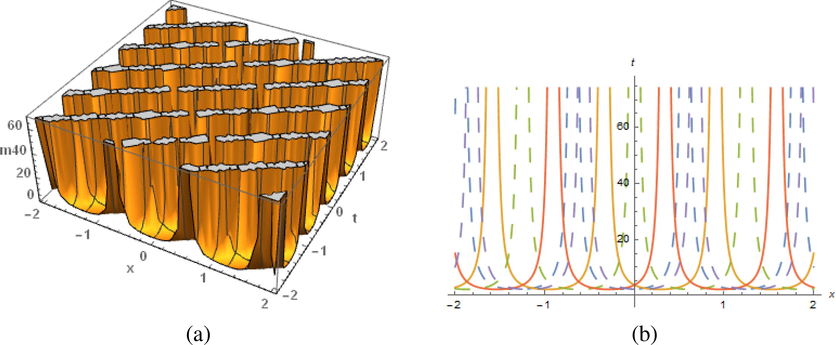
The results of (88) display from the figures with diverse plotted natures at δ = 2 in the range - 2 ⩽ x , t ⩽ 2 : (a) periodic solitary wave and (b) represent 2–dimensional nature.

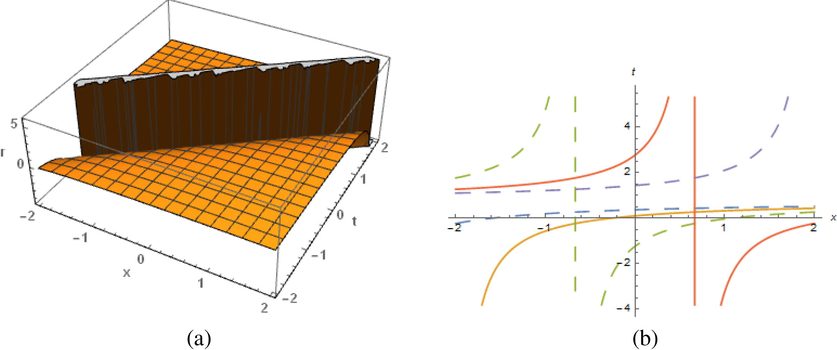
The results of (103) display from the figures with diverse plotted natures at δ = 2 , γ 1 = 1 , k 2 = 1.5 , β = 1.5 and f 0 = 1.5 in the range - 2 ⩽ x , t ⩽ 2 : (a) solitary wave and (b) represent 2–dimensional nature.

5 Results and discussion

In this paper, we confirm that several of the attained solutions are new by comparing the results acquired with the results of other different works using different techniques. The merits and validity of our technique over other techniques are discussed below:

5.1

5.1 Merits

A key advantage of our technique applied over other techniques is, it offers a further flexible and amusing genuine wave solution with several practical parameters. The accurate solution of NLES is of excessive worth for enlightening the essential machinery of cumbersome actual phenomena. In addition to the actual implementation, the approximation solution of NLES aids numerical solvers compare the effectiveness of their solution and contribute to their stability studies.

5.2

5.2 Validity

In Arshad et al. (2017) studied the traveling wave solutions of (16) by implementing the modified extended direct algebraic technique. Consequently, they attained various explicit solutions like solitary wave solutions, periodic wave solutions, Jacobi elliptic solutions and Weierstrass elliptic function. It is important to note that most of the results acquired in this paper are comparable to the results attained in Arshad et al. (2017). In addition, the rest of the results are new and valuable for researchers to know more about this technique.

Furthermore, in Khan et al. (2015) K. Khan et al. studied the exact analytical solutions for the (16) by implementing the enhanced $(\frac{G}{G^{'}})$ –expansion technique. Therefore, they were able to deduce abundant of traveling wave solutions comprising of hyperbolic solutions. It is important to note that some of the results acquired in this paper are comparable to the results attained in Khan et al. (2015), but the rest of our attained solutions are new and is useful for researchers (Lu et al., 2018a; Lu et al., 2018b; Iqbal et al., 2018; Helal et al., 2014; Ali et al., 2018; Iqbal et al., 2020; Seadawy et al., 2019; Ozkan et al., 2020; Ahmad et al., 2020 ).

Thus, it is proved that the RERE technique with the current ansatz provides a commanding and essential mathematical tool for finding non-linear evolutionary systems in mathematical physics and sciences. Hence, this new technique is dependable and suggests a diversity of solitary wave solutions that can be applied to numerous other NLES.

6 Conclusion

In this paper, we have efficaciously extended the ansatz in the RERE technique to new and generalized form and attained some new exact traveling wave solutions for (16). Some selected solutions with different physical profiles of (16) are constructed in this paper. Several of the attained solutions which is in the form of rational solitary wave solutions and periodic wave solutions are entirely new and could be vital for researchers to appreciate. The results show that the proposed technique has a broader implementation and is more real than other techniques. Therefore, the technique can be applied to study various NLES that normally seem in scientific real-time applications like mathematics, physics and engineering. In addition, it is essential to investigate the stability of some NLES by using the current formal ansatz applied in this paper which could be useful for researchers.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Abdou M.A., . The extended F-expansion method and its application for a class of non-linear evolution equations. Chaos, Solitons Fractals. 2007;31(1):95-104.
[Google Scholar]
Abdou M.A., . The extended tanh method and its applications for solving non-linear physical models. Appl. Math. Comput.. 2007;190(1):988-996.
[Google Scholar]
Abdou M.A., Soliman A.A., . Variational iteration method for solving Burger’s and coupled Burger’s equations. J. Comput. Appl.. 2005;181(2):245-251.
[Google Scholar]
Abdullah Aly Seadawy, Wang Jun, . Mathematical methods and solitary wave solutions of three-dimensional Zakharov-Kuznetsov-Burgers equation in dusty plasma and its applications. Results Phys.. 2017;7:4269-4277.
[Google Scholar]
Agarwal P., Jain S., Mansour T., . Further extended Caputo fractional derivative operator and its applications. Russ. J. Math. Phys.. 2017;24(4):415-425.
[Google Scholar]
Agarwal P., Hyder Abd-Allah, Zakarya M., . Well-posedness of stochastic modified Kawahara equation. Adv. Diff. Eqs.. 2020;1:1-10.
[Google Scholar]
Ahmad Hijaz, Seadawy Aly R., Khan Tufail A., Thounthong Phatiphat, . Analytic approximate solutions Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. Taibah University J. Sci.. 2020;14(1):346-358.
[Google Scholar]
Ahmed I., Seadawy A.R., Lu D., . Kinky breathers, W-shaped and multi-peak solitons interaction in (2 + 1)-dimensional non-linear Schrdinger equation with Kerr law of non-linearity. Eur. Phys. J. Plus. 2019;134:120.
[CrossRef] [Google Scholar]
Ali Asghar, Seadawy Aly R., Dianchen Lu., . Computational methods and traveling wave solutions for the fourth-Order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications. Open Phys. J.. 2018;16:219-226.
[Google Scholar]
Aljahdaly N.H., Seadawy A.R., Albarakati W.A., . Applications of dispersive analytical wave solutions of non-linear seventh order Lax and Kaup-Kupershmidt dynamical wave equations. Results Phys.. 2019;14
[CrossRef] [Google Scholar]
Apeanti W.O., Lu D., Yaro D., Akuamoah S.W., . Dispersive traveling wave solutions of non-linear optical wave dynamical models, Modern. Phys. Lett. B. 2019;30pages
[CrossRef] [Google Scholar]
Apeanti W.O., Seadawy A.R., Lu D., . Complex optical solutions and modulation instability of hyperbolic Schrodinger dynamical equation. Results Phys.. 2019;12:2091-2097.
[CrossRef] [Google Scholar]
Arshad M., Seadawy A.R., Lu D., Wang J., . Travelling wave solutions of generalized coupled zakharov-Kuznetsov and dispersive long wave equations. Res Phys.. 2016;6:1136.
[Google Scholar]
Arshad M., Seadawy A.R., Lu Dianchen, Wang Jun, . Travelling wave solutions of Drinfel’d-Sokolov-Wilson, Whitham-Broer-Kaup and (2+1)-dimensional Broer-Kaup-Kupershmit equations and their applications. Chinese J. Phys. 2017:1-18.
[Google Scholar]
Arshad M., Seadawy A.R., Lu D., . Study of soliton solutions of higher-order non-linear Schrdinger dynamical model with derivative non-Kerr non-linear terms and modulation instability analysis. Results Phys.. 2019;13
[CrossRef] [Google Scholar]
Cheemaa N., Seadawy A.R., Chen S., . Some new families of solitary wave solutions of the generalized Schamel equation and their applications in plasma physics. Eur. Phys. J. Plus. 2019;134:117.
[CrossRef] [Google Scholar]
Dianchen Lu., Seadawy Aly R., Ali Asghar, . Applications of Exact Traveling wave solutions of Modified Liouville and the Symmetric Regularized Long Wave equations via two new techniques. Results Phys.. 2018;9:1403-1410.
[Google Scholar]
Dianchen Lu., Seadawy Aly R., Ali Asghar, . Dispersive traveling wave solutions of the Equal-Width and Modified Equal-Width equations via mathematical methods and its applications. Results Phys.. 2018;9:313-320.
[Google Scholar]
Helal M.A., Seadawy A.R., Zekry M.H., . Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation. Appl. Math. Comput.. 2014;232:1094-1103.
[Google Scholar]
Iqbal Mujahid, Seadawy Aly R., Dianchen Lu., . Construction of solitary wave solutions to the nonlinear modified Kortewege-de Vries dynamical equation in unmagnetized plasma via mathematical methods. Mod. Phys. Lett. A. 2018;33(32):1850183.
[Google Scholar]
Iqbal M., Seadawy A.R., Lu D., . Applications of non-linear longitudinal wave equation in a magneto-electro-elastic circular rod and new solitary wave solutions. Modern Phys. Lett. B. 2019;33(18):17.
[CrossRef] [Google Scholar]
Iqbal Mujahid, Seadawy Aly R., Khalil Omer H., Dianchen Lu., . Propagation of long internal waves in density stratified ocean for the (2+1)-dimensional nonlinear Nizhnik-Novikov-Vesselov dynamical equation. Results Phys.. 2020;16:102838
[Google Scholar]
Khan K., Akbar M.A., Koppelaar H., . Study of coupled non-linear partial differential equations for finding exact analytical solutions. R. Soc. Open Sci.. 2015;2:140406
[CrossRef] [Google Scholar]
Li Tongxing, Viglialoro Giuseppe, . Analysis and explicit solvability of degenerate tensorial problems. Boundary Value Problems. 2018;2018 Article number 2
[Google Scholar]
Li Tongxing, Pintus Nicola, Viglialoro Giuseppe, . Properties of solutions to porous medium problems with different sources and boundary conditions. Z. Angew. Math. Phys.. 2019;70:1-18. Art. 86
[Google Scholar]
Lin G.D., Gao Y.T., Wang L., Minh D.X., Yu X., . Elastic-inelastic-interaction coexistence and double wronskian solutions for the Whitham-Broer-Kaup shallow-water-wave model. Commun. Nonlinear Sci. Numer. Simulat.. 2011;16:3090.
[Google Scholar]
Liu Y.-K., Li B., . Nonlocal symmetry and exact solutions of the (2+1)-dimensional gardner equation. Chin. J. Phys.. 2016;54:718.
[Google Scholar]
Lu D., Seadawy A.R., Ali A., . Dispersive analytical wave solutions of three non-linear dynamical water waves models via modified mathematical method. Results Phys.. 2019;13
[CrossRef] [Google Scholar]
Lu D., Seadawy A., Yaro D., . Analytical wave solutions for the non-linear three-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov and two-dimensional Kadomtsev-Petviashvili-Burgers equations. Results Phys.. 2019;12:2164-2168.
[CrossRef] [Google Scholar]
Nasreen N., Seadawy A.R., Lu D., Arshad M., . Construction of modulation instability analysis and optical soliton solutions of pertubed non-linear Schrdinger dynamical equation with power law non-linearity in non-kerr medium. Results Phys.. 2019;13
[CrossRef] [Google Scholar]
Ozkan Yesim Glam, Yasar Emrullah, Seadawy Aly, . A third-order nonlinear Schrodinger equation: the exact solutions, group-invariant solutions and conservation laws. J. Taibah University Sci.. 2020;14(1):585-597.
[Google Scholar]
Qin Z.X., . An improved f-expension method and its application to coupled Drinfl’d-Sokolov-Wilson equation. Commnicat. Theor. Phys.. 2008;50:309.
[Google Scholar]
Seadawy A.R., Alamri S.Z., . Mathematical methods via the non-linear two-dimensional water waves of Olver dynamical equation and its exact solitary wave solutions. Results Phys.. 2018;8:286-291.
[Google Scholar]
Seadawy A.R., El-Rashidy K., . Traveling wave solutions for some coupled non-linear evolution equations by using the direct algebraic method. Math. Comput. Model.. 2013;57:1371.
[Google Scholar]
Seadawy A.R., Kumar D., Chakrabarty A.K., . Dispersive optical soliton solutions for the hyperbolic and cubic-quintic non-linear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur. Phys. J. Plus 2018:133-183.
[CrossRef] [Google Scholar]
Seadawy Aly R., Iqbal Mujahid, Lu Dianchen, . Nonlinear wave solutions of the Kudryashov-Sinelshchikov dynamical equation in mixtures liquid-gas bubbles under the consideration of heat transfer and viscosity. J. Taibah University Sci.. 2019;13(1):1060-1072.
[Google Scholar]
Selima Ehab S., Seadawy Aly R., Yao Xiaohua, . The non-linear dispersive Davey-Stewartson system for surface waves propagation in shallow water and its stability. Eur. Phys. J. Plus. 2016;131:425.
[Google Scholar]
Wang Q., Chen Y., Zhang H., . A new Riccati equation rational expansion method and its application to (2+1)–dimensional Burgers equation. Chaos, Solitons Fractals. 2005;25:1019-1028.
[Google Scholar]
Wang L., Gao Y.T., Gai X.L., . Gauge transformation, elastic and inelastic interactions for the Whitham-Broer-Kaup shallow-water model. Commun. Nonlinear Sci. Numer. Simulat.. 2012;17:2833.
[Google Scholar]
Wen X.Y., . Construction of new exact rational form non-traveling wave solutions to the (2+1)-dimensional generalized Broer-Kaup system. Appl. Math. Comput.. 2010;217:1367.
[Google Scholar]
Wen X.Y., . N-soliton solutions and localized structures for the (2 + 1)-dimensional Broer-Kaup-Kupershmidt system. Nonlinear Anal.. 2011;12:3346.
[Google Scholar]
Yaro D., Seadawyb A.R., Lu D., Apeanti W.O., Akuamoaha S.W., . Dispersive wave solutions of the non-linear fractional Zakhorov-Kuznetsov-Benjamin-Bona-Mahony equation and fractional symmetric regularized long wave equation. Results Phys.. 2019;12:1971-1979.
[CrossRef] [Google Scholar]
Yue C., Seadawy A., Lu D., . Stability analysis of the soliton solutions for the generalized quintic derivative non-linear Schrdinger equation. Res. Phys.. 2016;6:911.
[Google Scholar]
Zenga X., Wang D.S., . A generalized extended rational expansion method and its application to (1+1)-dimensional dispersive long wave equation. App. Math. Comput.. 2009;212:296.
[Google Scholar]

Introduction

Summary of the technique

Implementation

The non-linear Drinfeld–Sokolov–Wilson (DSW) system

Graphical depiction for some of the solutions acquired

Results and discussion

Merits
Validity

Conclusion

Fulltext Views
36

PDF downloads
26

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abdou M.A., . The extended F-expansion method and its application for a class of non-linear evolution equations. Chaos, Solitons Fractals. 2007;31(1):95-104.
[Google Scholar]

[2] Abdou M.A., . The extended tanh method and its applications for solving non-linear physical models. Appl. Math. Comput.. 2007;190(1):988-996.
[Google Scholar]

[3] Abdou M.A., Soliman A.A., . Variational iteration method for solving Burger’s and coupled Burger’s equations. J. Comput. Appl.. 2005;181(2):245-251.
[Google Scholar]

[4] Abdullah Aly Seadawy, Wang Jun, . Mathematical methods and solitary wave solutions of three-dimensional Zakharov-Kuznetsov-Burgers equation in dusty plasma and its applications. Results Phys.. 2017;7:4269-4277.
[Google Scholar]

[5] Agarwal P., Jain S., Mansour T., . Further extended Caputo fractional derivative operator and its applications. Russ. J. Math. Phys.. 2017;24(4):415-425.
[Google Scholar]

[6] Agarwal P., Hyder Abd-Allah, Zakarya M., . Well-posedness of stochastic modified Kawahara equation. Adv. Diff. Eqs.. 2020;1:1-10.
[Google Scholar]

[7] Ahmad Hijaz, Seadawy Aly R., Khan Tufail A., Thounthong Phatiphat, . Analytic approximate solutions Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. Taibah University J. Sci.. 2020;14(1):346-358.
[Google Scholar]

[8] Ahmed I., Seadawy A.R., Lu D., . Kinky breathers, W-shaped and multi-peak solitons interaction in (2 + 1)-dimensional non-linear Schrdinger equation with Kerr law of non-linearity. Eur. Phys. J. Plus. 2019;134:120.
[CrossRef] [Google Scholar]

[9] Ali Asghar, Seadawy Aly R., Dianchen Lu., . Computational methods and traveling wave solutions for the fourth-Order nonlinear Ablowitz-Kaup-Newell-Segur water wave dynamical equation via two methods and its applications. Open Phys. J.. 2018;16:219-226.
[Google Scholar]

[10] Aljahdaly N.H., Seadawy A.R., Albarakati W.A., . Applications of dispersive analytical wave solutions of non-linear seventh order Lax and Kaup-Kupershmidt dynamical wave equations. Results Phys.. 2019;14
[CrossRef] [Google Scholar]

[11] Apeanti W.O., Lu D., Yaro D., Akuamoah S.W., . Dispersive traveling wave solutions of non-linear optical wave dynamical models, Modern. Phys. Lett. B. 2019;30pages
[CrossRef] [Google Scholar]

[12] Apeanti W.O., Seadawy A.R., Lu D., . Complex optical solutions and modulation instability of hyperbolic Schrodinger dynamical equation. Results Phys.. 2019;12:2091-2097.
[CrossRef] [Google Scholar]

[13] Arshad M., Seadawy A.R., Lu D., Wang J., . Travelling wave solutions of generalized coupled zakharov-Kuznetsov and dispersive long wave equations. Res Phys.. 2016;6:1136.
[Google Scholar]

[14] Arshad M., Seadawy A.R., Lu Dianchen, Wang Jun, . Travelling wave solutions of Drinfel’d-Sokolov-Wilson, Whitham-Broer-Kaup and (2+1)-dimensional Broer-Kaup-Kupershmit equations and their applications. Chinese J. Phys. 2017:1-18.
[Google Scholar]

[15] Arshad M., Seadawy A.R., Lu D., . Study of soliton solutions of higher-order non-linear Schrdinger dynamical model with derivative non-Kerr non-linear terms and modulation instability analysis. Results Phys.. 2019;13
[CrossRef] [Google Scholar]

[16] Cheemaa N., Seadawy A.R., Chen S., . Some new families of solitary wave solutions of the generalized Schamel equation and their applications in plasma physics. Eur. Phys. J. Plus. 2019;134:117.
[CrossRef] [Google Scholar]

[17] Dianchen Lu., Seadawy Aly R., Ali Asghar, . Applications of Exact Traveling wave solutions of Modified Liouville and the Symmetric Regularized Long Wave equations via two new techniques. Results Phys.. 2018;9:1403-1410.
[Google Scholar]

[18] Dianchen Lu., Seadawy Aly R., Ali Asghar, . Dispersive traveling wave solutions of the Equal-Width and Modified Equal-Width equations via mathematical methods and its applications. Results Phys.. 2018;9:313-320.
[Google Scholar]

[19] Helal M.A., Seadawy A.R., Zekry M.H., . Stability analysis of solitary wave solutions for the fourth-order nonlinear Boussinesq water wave equation. Appl. Math. Comput.. 2014;232:1094-1103.
[Google Scholar]

[20] Iqbal Mujahid, Seadawy Aly R., Dianchen Lu., . Construction of solitary wave solutions to the nonlinear modified Kortewege-de Vries dynamical equation in unmagnetized plasma via mathematical methods. Mod. Phys. Lett. A. 2018;33(32):1850183.
[Google Scholar]

[21] Iqbal M., Seadawy A.R., Lu D., . Applications of non-linear longitudinal wave equation in a magneto-electro-elastic circular rod and new solitary wave solutions. Modern Phys. Lett. B. 2019;33(18):17.
[CrossRef] [Google Scholar]

[22] Iqbal Mujahid, Seadawy Aly R., Khalil Omer H., Dianchen Lu., . Propagation of long internal waves in density stratified ocean for the (2+1)-dimensional nonlinear Nizhnik-Novikov-Vesselov dynamical equation. Results Phys.. 2020;16:102838
[Google Scholar]

[23] Khan K., Akbar M.A., Koppelaar H., . Study of coupled non-linear partial differential equations for finding exact analytical solutions. R. Soc. Open Sci.. 2015;2:140406
[CrossRef] [Google Scholar]

[24] Li Tongxing, Viglialoro Giuseppe, . Analysis and explicit solvability of degenerate tensorial problems. Boundary Value Problems. 2018;2018 Article number 2
[Google Scholar]

[25] Li Tongxing, Pintus Nicola, Viglialoro Giuseppe, . Properties of solutions to porous medium problems with different sources and boundary conditions. Z. Angew. Math. Phys.. 2019;70:1-18. Art. 86
[Google Scholar]

[26] Lin G.D., Gao Y.T., Wang L., Minh D.X., Yu X., . Elastic-inelastic-interaction coexistence and double wronskian solutions for the Whitham-Broer-Kaup shallow-water-wave model. Commun. Nonlinear Sci. Numer. Simulat.. 2011;16:3090.
[Google Scholar]

[27] Liu Y.-K., Li B., . Nonlocal symmetry and exact solutions of the (2+1)-dimensional gardner equation. Chin. J. Phys.. 2016;54:718.
[Google Scholar]

[28] Lu D., Seadawy A.R., Ali A., . Dispersive analytical wave solutions of three non-linear dynamical water waves models via modified mathematical method. Results Phys.. 2019;13
[CrossRef] [Google Scholar]

[29] Lu D., Seadawy A., Yaro D., . Analytical wave solutions for the non-linear three-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov and two-dimensional Kadomtsev-Petviashvili-Burgers equations. Results Phys.. 2019;12:2164-2168.
[CrossRef] [Google Scholar]

[30] Nasreen N., Seadawy A.R., Lu D., Arshad M., . Construction of modulation instability analysis and optical soliton solutions of pertubed non-linear Schrdinger dynamical equation with power law non-linearity in non-kerr medium. Results Phys.. 2019;13
[CrossRef] [Google Scholar]

[31] Ozkan Yesim Glam, Yasar Emrullah, Seadawy Aly, . A third-order nonlinear Schrodinger equation: the exact solutions, group-invariant solutions and conservation laws. J. Taibah University Sci.. 2020;14(1):585-597.
[Google Scholar]

[32] Qin Z.X., . An improved f-expension method and its application to coupled Drinfl’d-Sokolov-Wilson equation. Commnicat. Theor. Phys.. 2008;50:309.
[Google Scholar]

[33] Seadawy A.R., Alamri S.Z., . Mathematical methods via the non-linear two-dimensional water waves of Olver dynamical equation and its exact solitary wave solutions. Results Phys.. 2018;8:286-291.
[Google Scholar]

[34] Seadawy A.R., El-Rashidy K., . Traveling wave solutions for some coupled non-linear evolution equations by using the direct algebraic method. Math. Comput. Model.. 2013;57:1371.
[Google Scholar]

[35] Seadawy A.R., Kumar D., Chakrabarty A.K., . Dispersive optical soliton solutions for the hyperbolic and cubic-quintic non-linear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur. Phys. J. Plus 2018:133-183.
[CrossRef] [Google Scholar]

[36] Seadawy Aly R., Iqbal Mujahid, Lu Dianchen, . Nonlinear wave solutions of the Kudryashov-Sinelshchikov dynamical equation in mixtures liquid-gas bubbles under the consideration of heat transfer and viscosity. J. Taibah University Sci.. 2019;13(1):1060-1072.
[Google Scholar]

[37] Selima Ehab S., Seadawy Aly R., Yao Xiaohua, . The non-linear dispersive Davey-Stewartson system for surface waves propagation in shallow water and its stability. Eur. Phys. J. Plus. 2016;131:425.
[Google Scholar]

[38] Wang Q., Chen Y., Zhang H., . A new Riccati equation rational expansion method and its application to (2+1)–dimensional Burgers equation. Chaos, Solitons Fractals. 2005;25:1019-1028.
[Google Scholar]

[39] Wang L., Gao Y.T., Gai X.L., . Gauge transformation, elastic and inelastic interactions for the Whitham-Broer-Kaup shallow-water model. Commun. Nonlinear Sci. Numer. Simulat.. 2012;17:2833.
[Google Scholar]

[40] Wen X.Y., . Construction of new exact rational form non-traveling wave solutions to the (2+1)-dimensional generalized Broer-Kaup system. Appl. Math. Comput.. 2010;217:1367.
[Google Scholar]

[41] Wen X.Y., . N-soliton solutions and localized structures for the (2 + 1)-dimensional Broer-Kaup-Kupershmidt system. Nonlinear Anal.. 2011;12:3346.
[Google Scholar]

[42] Yaro D., Seadawyb A.R., Lu D., Apeanti W.O., Akuamoaha S.W., . Dispersive wave solutions of the non-linear fractional Zakhorov-Kuznetsov-Benjamin-Bona-Mahony equation and fractional symmetric regularized long wave equation. Results Phys.. 2019;12:1971-1979.
[CrossRef] [Google Scholar]

[43] Yue C., Seadawy A., Lu D., . Stability analysis of the soliton solutions for the generalized quintic derivative non-linear Schrdinger equation. Res. Phys.. 2016;6:911.
[Google Scholar]

[44] Zenga X., Wang D.S., . A generalized extended rational expansion method and its application to (1+1)-dimensional dispersive long wave equation. App. Math. Comput.. 2009;212:296.
[Google Scholar]

Explicit and traveling wave solutions of the non-linear couple Drinfeld-Sokolov-Wilson dynamical system arising in shallow water waves

Abstract

Keywords

Riccati equation rational expansion method

Non-linear Drinfeld-Sokolov-Wilson (DSW) system

Solitary wave solutions

Non-linear evolution systems

1 Introduction

2 Summary of the technique

3 Implementation

3.1 The non-linear Drinfeld–Sokolov–Wilson (DSW) system

4 Graphical depiction for some of the solutions acquired

5 Results and discussion

5.1 Merits

5.2 Validity

6 Conclusion

Declaration of Competing Interest

References

Suggested read for related articles: