Translate this page into:
Existence result and approximate solutions for quadratic integro-differential equations of fractional order
⁎Corresponding author. hsharbi@taibahu.edu.sa (Hind Al-badrani)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University
Abstract
This research outlines a reliable strategy for finding a solutions of nonlinear quadratic integro-differential equation of fractional order (FQIDEs). Local and global existence theorems of solutions of the FQIDEs have been obtained by using Schauder’s and Tychonoff fixed point theorems. The fractional derivative is described in the Caputo sense. The Laplace decomposition method (LDM) and modified Adomian decomposition method (MADM) are described to be fast and accurate. Illustrative examples are included to demonstrate the efficiency and reliability of presented techniques.
1 Introduction
The fractional calculus deals with derivatives and integrals to an arbitrary orders (real or complex order). The fractional calculus is applied to model the frequency-dependent damping behaviour of many viscoelastic materials (Bagley and Torvik, 1983), continuum and statistical mechanics (Mainardi, 2012), control theory (Bohannan, 2008), bioengineering (Magin, 2004).
This is one of the reason of why fractional calculus has become more and more popular, and it is described as something which is realistic.
Some of the problems that exist in the real world are being modelled by using fractional derivative and integral terms and such equations are known as the fractional integro-differential equations (FIDEs). FIDEs are found in the fields of signal prossing (Diethelm, 2010), mechanics (Rossikhin and Shitikova, 1997), econometrics (Baillie, 1996), fluid dynamics (Kilbas et al., 2006), unclear reactor dynamics, a coustic waves (Oldham and Spanier, 1974) and electromagnetics (Tarasov, 2009) etc.
There are many authors who have investigated the analytic results on existence and uniqueness of problems solutions to FIDEs such as Momani (2000) has got the local and global existence and uniqueness solution of the integro-differential equation. Karthikeyan and Trujillo (2012) studied the existence and uniqueness of FIDEs with boundary value conditions. Most of nonlinear FIDEs has not had the exact analytic solution. So approximation and numerical techniques must be used. Recently, several numerical methods are applied for solving fractional differential equations and fractional integro-differential equations. Momani and Noor (2006) applied Adomian polynomials to solve FIDEs. The authors in Pandey et al. (2009), obtained the approximate solution of Abel’s integral equations by using homotopy perturbation method (HPM) and it’s modification, also, by using Adomian decomposition method and it’s modification. Zhang et al. (2011) produced the homotopy analysis method for higher-order FIDEs. Collocation method is introduced in Eslahchi et al. (2014), Saadatmandi and Dehghan (2011), Zhao et al. (2014) for solving the FIDEs with weakly singular kernels and linear and nonlinear integro-differential equations of fractional orders with Volterra type.
In Mohammed (2014), Mohammed investigated the numerical solution of linear FIDEs by least squares method shifted chebyshev polynomials. More recently in 2017, Kumar and co-authors (Kumar et al., 2017) presented a comparative study three numerical schemes such as linear, Quadratic and Quadratic-Linear for the FIDEs. Wang and Zhu (2017) used the wavelet numerical method to solve nonlinear Volterra FIDEs.
In this paper we negotiate the local and global existence of the solution for the following FQIDEs
We present a comparative study between two methods LDM and the MADM for solving FQIDEs. Several analytical and numerical methods such as LDM were used to solve nonlinear ordinary, partial and integral equation. Yang and Hou (Yang and Hou, 2013) used this method to solve nonlinear FIDEs. The reliable modification of ADM has been done by Wazwaz (1999), this computational method leads to find the analytical solutions and has certain advantages over standard numerical methods. The previous method shows that there is no sign for the rounding of errors in it. As it does not involve discretization and does not require large computer obtained memory of power. The main purpose of this paper is applying LDM and MADM to solve nonlinear FQIDEs because there is no attempt have been made to solve this kind of equations.
The paper is organized as follows. It is started by introducing some necessary definitions and mathematical preliminaries of the fractional calculus theory which are required for establishing our results. In Section 3, local and global existence of FQIDEs is proved by using Schauder’s and Tychonoff fixed point theorems. In Section 4, we extend the application of LDM and MADM to construct our analytical approximate solution to nonlinear FQIDEs. In Section 5, we present two examples that show the efficiency of the methods.
2 Basic information about the fractional calculus
Here, we intend to introduce some basic definitions and properties of fractional calculus theory see (Kilbas et al., 2006;Podlubny, 1998; Samko et al., 1993).
A real function is said to be in space if there exists a real number , such that , where , and it is said to be in the space if and only if .
The Riemann-Liouville fractional integral operator of order
of a function
, is defined as
-
,
-
,
-
.
The fractional derivative of
in the caputo sense is defined as
The Laplace transform of the Caputo derivative is defined as
If , the following two properties hold:
-
,
-
.
3 Local and Global Existence Solutions
This section is devoted to the study of the initial value problem (IVP) for FQIDEs of the type
Theorem 3.1 Schauder (Zeidler, 1995)
If E is a closed, bounded, convex subset of a Banach space B and is completely continuous then T has a fixed point.
Assume that
-
for
-
-
-
then the (IVP) (3.1) has at least one solution on , for some .
Consider the set
and let
on D. Choose
and let
where
and
. Clearly the set
is closed, convex and bounded. For any
define the operator Tx by
To show that T is a continuous map, let us take an and in , it follows, using uniform continuity of f and K that for any there exists such that Since f and K is uniformly continuous for the above , there exist such that , by using (ii)-(iv) we have
We shall next discuss a global existence result for IVP(3.1) using Tychonoff’s fixed point theorem, which we state in the following form.
Theorem 3.3 Tychonoff (Zeidler, 1995)
Let B be a complete, locally convex, linear space and a closed convex subset of B. Let the mapping be a continuous and if the closure of is compact then Thas a fixed point in .
Assume that
(i) is monotone nondecreasing in u for each and
(ii) is monotone nondecreasing in u for each and
(iii)
Let us consider the real vector space B of all continuous functions from into , the topology on B being that induced by the family of pseudo-norms where for . A fundamental system of neighborhoods is the given by , where under this topology, B is a complete, locally convex linear space.
Now define a subset of B as follows: where is a solution of (3.5) existing for . It is clear that in the topology of is closed convex and bounded. Consider the integral operator defined by (3.3) whose fixed point corresponds to a solution of (3.1), evidently, the operator T is compact in the topology of B, and hence the closure of is compact. In view of the boundedness of . Now to prove , observe that for any , Using the monotonicity of g and G, the definition of , and the fact is a solution of (3.5), therefore , which implies .
Hence by Tychonoff’s fixed point theorem, T has a fixed point in , which completes the proof of the theorem.
4 Numerical methods to solve the fractional quadratic integro-differential equations
4.1 Laplace decomposition method
Firstly, we consider the FQIDEs (1) and apply the Laplace transform first on both sides of (1)
4.2 Modified Adomian decomposition method
we consider the FQIDEs (1) and apply the operator
, the inverse of the operator
to both sides of (1) yields
5 Numerical examples
In this section, we present some numerical examples of solutions of the FQIDEs via the LDM and MADM.
Tables 1, 2 presents the approximate solution for different values of , we have noticed that the accuracy is improving by computing more terms of the approximate solutions (see Fig. 1).
| t | ||||
|---|---|---|---|---|
| 0.10 | 0.00003306 | 0.00001760 | 0.00000854 | 0.00000393 |
| 0.20 | 0.00006887 | 0.00004630 | 0.00002766 | 0.00001542 |
| 0.30 | 0.00010211 | 0.00007925 | 0.00005394 | 0.00003391 |
| 0.40 | 0.00013495 | 0.00011479 | 0.00008569 | 0.00005879 |
| 0.50 | 0.00017335 | 0.00015398 | 0.00012242 | 0.00008971 |
| 0.60 | 0.00022680 | 0.00020067 | 0.00016515 | 0.00012687 |
| 0.70 | 0.00030859 | 0.00026180 | 0.00021683 | 0.00017138 |
| 0.80 | 0.00043603 | 0.00034789 | 0.00028290 | 0.00022580 |
| 0.90 | 0.00063071 | 0.00047350 | 0.00037189 | 0.00029462 |
| 1.00 | 0.00091880 | 0.00065781 | 0.00049606 | 0.00038493 |
| t | ||||
|---|---|---|---|---|
| 0.10 | 0.00003306 | 0.00001760 | 0.00000854 | 0.00000393 |
| 0.20 | 0.00006887 | 0.00004627 | 0.00002765 | 0.00001542 |
| 0.30 | 0.00010146 | 0.00007907 | 0.00005389 | 0.00003389 |
| 0.40 | 0.00013261 | 0.00011402 | 0.00008545 | 0.00005872 |
| 0.50 | 0.00016694 | 0.00015166 | 0.00012162 | 0.00008945 |
| 0.60 | 0.00021225 | 0.00019489 | 0.00016298 | 0.00012609 |
| 0.70 | 0.00027948 | 0.00024930 | 0.00021177 | 0.00016944 |
| 0.80 | 0.00038294 | 0.00032352 | 0.00027235 | 0.00022147 |
| 0.90 | 0.00054051 | 0.00042959 | 0.00035172 | 0.00028583 |
| 1.00 | 0.00077391 | 0.00058345 | 0.00046007 | 0.00036840 |
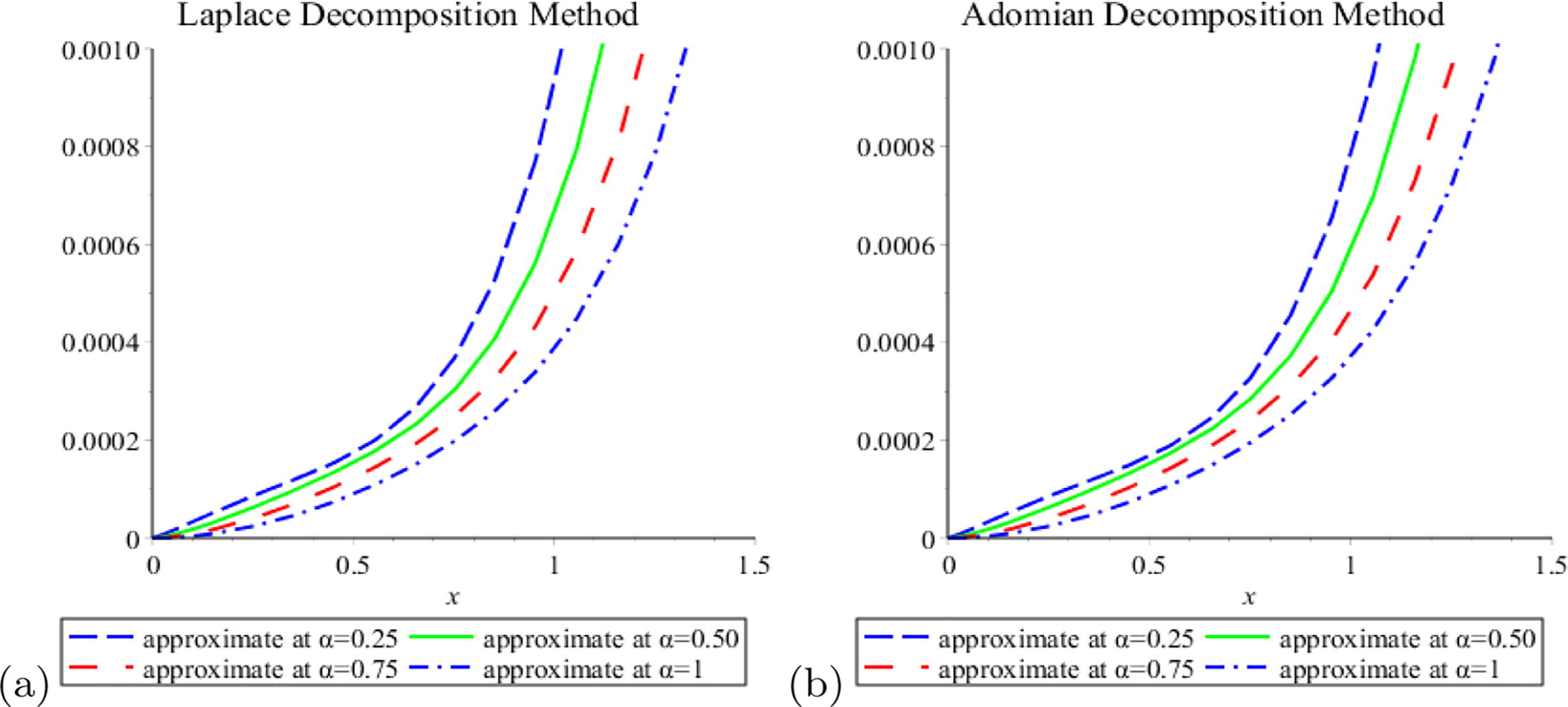
- Approximate solutions by using (LDM) and (ADM).
| t | ||||
|---|---|---|---|---|
| 0.10 | 0.36765557 | 0.18953458 | 0.09364270 | 0.04465906 |
| 0.20 | 0.64992844 | 0.39965869 | 0.23491078 | 0.13300533 |
| 0.30 | 0.91632907 | 0.62512154 | 0.40768544 | 0.25566171 |
| 0.40 | 1.17989872 | 0.86293000 | 0.60610126 | 0.40930681 |
| 0.50 | 1.45649193 | 1.11417053 | 0.82680896 | 0.59157564 |
| 0.60 | 1.77042701 | 1.38614601 | 1.06939284 | 0.80089138 |
| 0.70 | 2.15749580 | 1.69486410 | 1.33799321 | 1.03724849 |
| 0.80 | 2.66751254 | 2.06790583 | 1.64365154 | 1.30364112 |
| 0.90 | 3.36681803 | 2.54769945 | 2.00732460 | 1.60814543 |
| 1.00 | 4.34085479 | 3.19522247 | 2.46360149 | 1.96674225 |
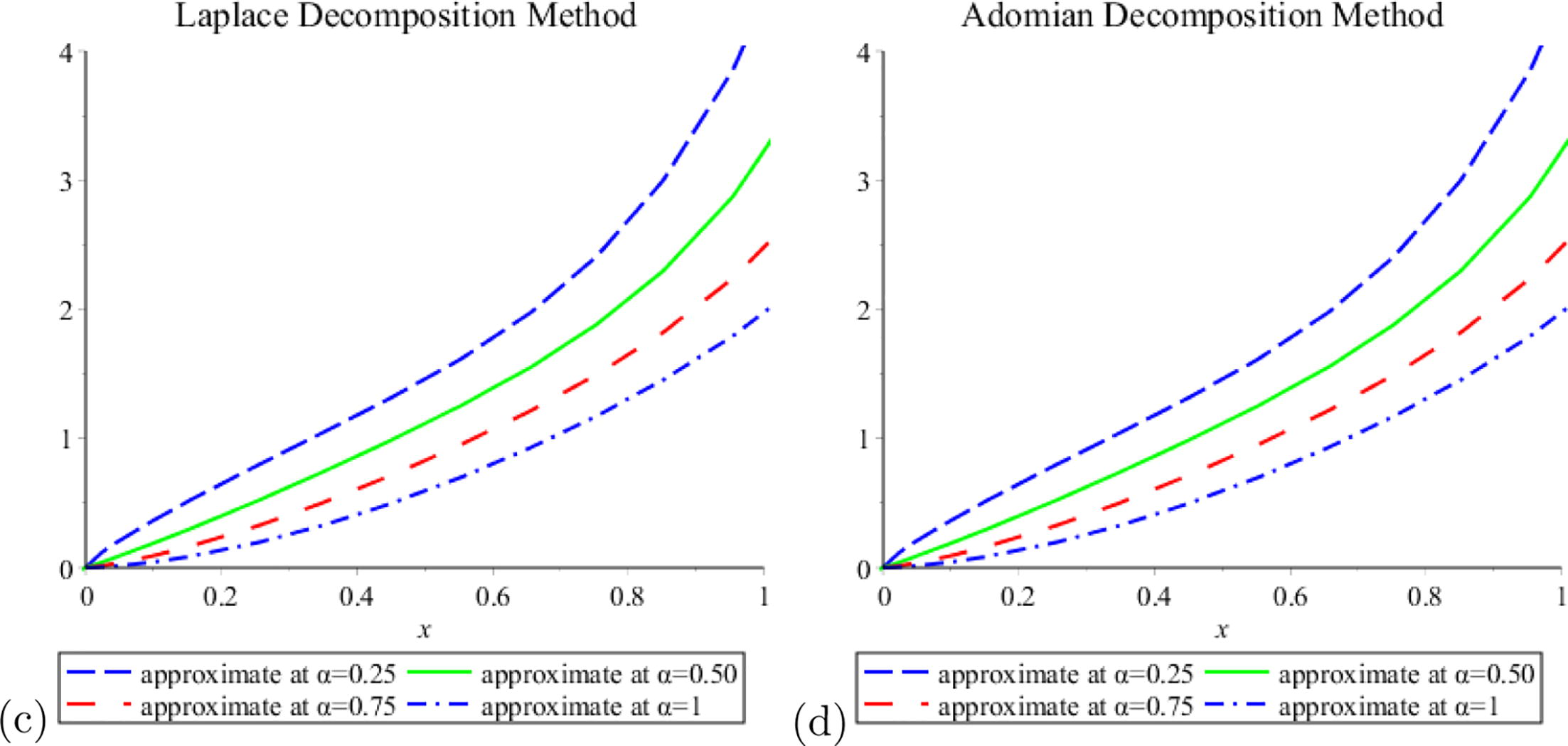
- Approximate solutions by using (LDM) and (ADM).
6 Conclusion
In this paper, we have proved the local and global existence of solutions. Also we have applied the LDM and MADM to find the solution of nonlinear initial value problems of FQIDEs for the first order. Actually, these methods do not require any linearization, perturbation or restrictive assumptions. In our research we have observed that the LDM and MADM is a very effective and powerful tool for finding the solutions for any problems in this field. We use the Maple package (2015) in calculations.
References
- Solving Frontier Problems of Physics: The Decomposition Method. Boston, MA: Kluwer; 1994.
- A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol.. 1983;27:201-210.
- [Google Scholar]
- Long memory processes and fractional integration in econometrics. J. Econ.. 1996;73(1):5-59.
- [Google Scholar]
- Analog fractional order controller in temperature and motor control applications. J. Vib. Control. 2008;14:1487-1498.
- [Google Scholar]
- Decomposition methods: a new proof of convergence. Math. Computer Modell.. 1993;18:103-106.
- [Google Scholar]
- The Analysis of Fractional Differential Equations. Berlin, Germany: Springer-Verlag; 2010.
- Application of the collocation method for solving nonlinear fractional integro-differential equations. J. Comput. Appl. Math.. 2014;257:105-128.
- [Google Scholar]
- Existence and uniqueness results for fractional integro differential equations with boundary value conditions. Commun. Nonlinear Sci. Numer. Simul.. 2012;17:4037-4043.
- [Google Scholar]
- Kilbas, A.A., Srivastava, H.M, Trujillo, J.J., 2006. Theory and Applications of Fractional Differential Equations, North-Holland Mathematics studies, 204. Elsevier Science B.V., Amsterdam.
- Comparative study of three numerical schemes for fractional integro-differential equations. J. Comput. Appl. Math.. 2017;315:287-302.
- [Google Scholar]
- Mainardi, F., 2012. Fractional calculus: some basic problems in continuum and statistical mechanics. arXiv preprint arXiv:1201.0863.
- Miller, K. S., Ross, B., 1993. An introduction to the fractional calculus and fractional differential equations.
- Numerical solution of fractional integro-differential equations by least squares method and shifted Chebyshev polynomial. Math. Problems Eng.. 2014;2014
- [Google Scholar]
- Local and global existence theorems on fractional integro-differential equations. J. Fract. Calc. 2000;18:81-86.
- [Google Scholar]
- Numerical methods for fourth-order fractional integro-differential equations. Appl. Math. Comput.. 2006;182:754-760.
- [Google Scholar]
- Fractional Calculus: Theory and Applications, Differentiation and Integration to Arbitrary Order. New York/London, UK: Academic Press; 1974.
- Efficient algorithms to solve singular integral equations of Abel type. Comput. Math. Appl.. 2009;57:664-676.
- [Google Scholar]
- Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications. Vol vol. 198. Academic press; 1998.
- Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev.. 1997;50:15-67.
- [Google Scholar]
- A Legendre collocation method for fractional integro-differential equations. J. Vib. Control. 2011;17(13):2050-2058.
- [Google Scholar]
- Fractional Integrals and Derivatives. Theory and Applications. Yverdon: Gordon and Breach; 1993.
- Fractional integro-differential equations for electromagnetic waves in dielectric media. Theor. Math. Phys.. 2009;158(3):355-359.
- [Google Scholar]
- Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method. Adv. Diff. Eq.. 2017;2017(1):27.
- [Google Scholar]
- A reliable modification of Adomian decomposition method. Appl. Math. Comput.. 1999;102(1):77-86.
- [Google Scholar]
- Numerical solution of integro-differential equations of fractional order by Laplace decomposition method. J. Wseas Trans. Math.. 2013;12:1173-2880.
- [Google Scholar]
- Zeidler, E., 1995. Applied Functional Analysis: Applications to Mathematical Physics (Applied Mathematical Sciences)(v. 108).
- Homotopy analysis method for higher-order fractional integro-differential equations. Comput. Math. Appl.. 2011;62:3194-3203.
- [Google Scholar]
- Collocation methods for fractional integro-differential equations with weakly singular kernels. Numer. Algorithms. 2014;65(4):723-743.
- [Google Scholar]






