Predicting the effective viscosity of nanofluids based on the rheology of suspensions of solid particles

Dilan S. Udawattha; Mahinsasa Narayana; Uditha P.L. Wijayarathne

doi:10.1016/j.jksus.2017.09.016

View/Download PDF

Buy Reprints

PDF

Translate this page into:

31 (

); 412-426

doi:

10.1016/j.jksus.2017.09.016

Predicting the effective viscosity of nanofluids based on the rheology of suspensions of solid particles

Dilan S. Udawattha^⁎, Mahinsasa Narayana, Uditha P.L. Wijayarathne

Department of Chemical and Process Engineering, University of Moratuwa, Sri Lanka

⁎Corresponding author at: University of Moratuwa, Moratuwa, Sri Lanka. iamdilansanjaya@gmail.com (Dilan S. Udawattha),

Received: 2017-7-26, Accepted: 2017-9-21, Published: 2017-07-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Abstract

The development of nanofluid as an innovative class of thermal fluid subsequently inspired use in their engineering applications. As a result, the necessity of experimental work to determine the thermophysical properties of nanofluids affecting heat transfer such as specific heat capacity, viscosity, thermal conductivity and density. Theoretical models are used in numerical studies of engineering applications to calculate thermophysical properties. This study intends to develop a new correlation for calculating the effective viscosity of nanofluids. In the model, we considered an effect of interfacial layer on the nanoparticle, the interfacial layer on nanoparticle works as a solid like layer in between the base fluid and nanoparticle surface. When nanoparticles are suspended in the base fluid, Brownian motion occurs due to the relative velocity of the base fluid and nanoparticles, which is also incorporated in this model. The correlation developed successfully express in outcome advance the viscosity of a variety of nanofluids, (Al₂O₃, Fe, hexagonal boron nitride (hBN), ZnO)-Ethylene Glycol, (Al₂O₃, hBN, SiC)-Ethylene Glycol Water mixture, (CuO, Al₂O₃, Fe₃O₄, TiO₂, hBN, Graphite, Single-wall carbon nanotube (SWCNT))-water, (Fe₃O₄)-Toluene. The new correlation was derived from 501 viscosity values of nanofluid, 75% of them are within the correlation coefficient 0.78–1 and mean deviation less than 5%.

Nomenclature

$h_{s}$: inter particle spacing (m)
$d_{p}$: diameter of a particle (m)
$r$: radius of a nanoparticle (m)
$h$: thickness of a nanolayer (m)
$V_{B}$: Brownian velocity
$T$: temperature
$N_{A}$: Avogadro constant
$r_{p}$: radius of a particle
$r_{r}$: relative radius
$M_{p}$: mass of a particle
$A_{p}$: area of a particle
$C_{f}$: correction factor
$c$: constant
$Z$: linear equation 1
$A$: factor
$B$: linear equation 2
$k_{B}$: Boltzmann constant

$μ_{nf}$: dynamic viscosity of nano fluid
$μ_{bf}$: $μ_{enf}$
$ρ_{p}$: particle density (kg m³)
$ρ_{l}$: liquid density (kg m³)
$\emptyset_{m \cdot}$: maximum particle volume (m³)
$μ_{ST}$: static part of viscosity of nanofluid
$μ_{DY}$: dynamic part of effective viscosity of nanofluids
$μ_{BM}$: viscosity due to Brownian motion
$ϕ_{m}$: mass fraction
$ϕ_{e}$: effective volume fraction
$\emptyset$: volume fraction
$δ$: distance between the nanoparticles (m)
$ρ$: density (kgm³)
$μ_{enf}$: experimental dynamic viscosity of nanofluid
$α_{n}, β_{n}, γ_{n}$: functions

$nf$: nano fluid
$bf$: base fluid
$p$: particle
$l$: liquid

$EG$: Ethylene glycol
$BM$: Brownian motion
$Re$: Reynolds number
$EM$: Einstein model
$DY$: dynamic
$ST$: static

1 Introduction

Nanofluid is a novel class of fluid, which is developed by dispersing nano-sized particles in base fluid (Kasaeian et al., 2015; Nkurikiyimfura et al., 2013; Angayarkanni and Philip, 2015; Raja et al., 2016 ). The heat transfer and fluid flow processes consist of active roles in chemical processors, automotive, air conditioning and power generation (Mar et al., 2015; Zhai et al., 2015; Sheremet et al., 2015; Ghanbarpour et al., 2015; Mahian et al., 2013; Alawi and Sidik, 2015 ). Base fluids such as engine oil, ethylene glycol or water were extensively used as heat transferring fluids in many industries (Esfe et al., 2015). Stephan U.S. Choi invented that high thermal conductivity nanofluid, such as engine oil, water or ethylene glycol, can be formed by dispersing nanosize particles into some conventional heat transfer fluids (Choi and Eastman, 1995).

There are four theoretical models related to fluid namely viscosity, thermal conductivity, density and specific heat capacity. The viscosity and rheological properties of nanofluids are also crucial for their thermal and energy applications. In fact, pumping power in energy and heat systems is related to nanofluids viscosity, and pressure drop in flow systems is directly linked to viscosity. Moreover, viscosity influences heat transfer enhancement of nanofluids from forced convection and natural convection and appear in many dimensionless numbers and coefficients such as Prandtl number, Brinkman number, Reynolds number, Rayleigh number, and Colburn j factor used in thermal and fluids sciences (Murshed and Estellé, 2017).

The most important thermo-physical property of nanofluid is viscosity, which is mainly affected by convective heat transfer and the pumping power requirement. It is evident that convective heat transfer coefficient increases with an increment of nanoparticle volume fraction. Moreover, the pumping power requirement reduces with nanoparticle loading. Hence precise figures on the effective viscosity of nanofluids are critical for industrial applications of nanofluids (Yang et al., 2012).

Einstein (1906), Brinkman (1952) and Batchelor (1977) developed analytical models to estimate viscosity values of composites and mixtures at the beginning of the twentieth century. Those analytical models were failed dramatically predicting viscosity of nanofluid, which are based on a well-established theory of colloid including particles of the order of micrometer or millimeter. Thus new models based on the viscosity of nanofluid have been proposed. They mainly considered interfacial layer on the nanoparticle (Avsec and Oblak, 2007). One of them based on Brownian motion of nanoparticle in the base fluid (Masoumi et al., 2009).

It has been proven beyond doubt that the liquid molecules are arranged themselves into an ordered layer at the solid-liquid interface (Yu et al., 2000), so that the thermal conductivity in that ordered layer is smaller than a thermal conductivity of the solid particles but larger than that of the base fluid. This interfacial layer is a solid-like structure, and it is referred to as nanolayer. This hypothetical nanometre size layer is considered as a thermal layer between the solid particle surface and the base fluid. Nanolayer is one of the likely mechanisms behind thermal conductivity enhancement and has been proposed by many research groups (Leong et al., 2006; Wang et al., 2003; Yu and Choi, 2003; Murshed et al., 2009 ). Yu and Choi suggested a renovated Maxwell correlation, which was considered the effect of the nanolayer. They have demonstrated that existence of even a thin nanolayer could considerably boost the thermal conductivity of nanofluids, mainly when the particle diameter is smaller than 10 nm (Yu and Choi, 2003). Tso et al. proposed an exponential decay equation for the nanolayer thickness and the nanoparticle radius for different types of nanofluids (Tso et al., 2014).

It can be argued that the reason for extra energy transport of nanoparticles is due to result of Brownian motion. The relative motion between nanoparticles and base fluid molecules generates micro-convection (Shukla et al., 2016). Jang and Choi proposed an initial model based on the convection, which affects by Brownian motion of the particles (Jang and Choi, 2004). However, Ravi Prasher showed that the correlation proposed by Jang and Choi is incorrect and he developed a new correlation for effective thermal conductivity of nanofluid based on Brownian motion (Prasher et al., 2006; Prasher et al., 2005). Masoumi et al. have presented improved correlation for viscosity of nanofluid with the foundation of Ravi Prasher correlation for thermal conductivity of nanofluid (Masoumi et al., 2009). Koo and Kleinstreuer proposed a correlation for the viscosity of nanofluid employing the same concept to develop thermal conductivity of nanofluid, which is based on Brownian motion of nanoparticle (Koo and Kleinstreuer, 2005). Keblinski et al. contended that the motion as a result of Brownian motion is negligible (Phillpot and Eastman, 2016).

Yang et al. found the temperature impact over the viscosity of nanofluid. They have used graphene as the nanomaterial in experiments. They showed that the viscosity declines with the increase of temperature (Yang et al., 2005). Chen et al. studied the same effect of MWCNT-distilled water nanofluid for 278 K–338 K and showed that viscosity ratio increases expressively with temperature after 338 K (Chen et al., 2008).

He et al. showed that experimental values of nanofluid viscosity increase with intense the size of the particle (He et al., 2007). However, Lu and Fan discovered that viscosity of nanofluid declines with increases of a radius of the particle (Lu and Fan, 2008). Chevalier et al. investigated the experimental viscosity values of SiO₂-Ethanol nanofluid for different particle radius such as 17, 47, 95 nm and revealed that viscosity rises with the decreasing the diameter of the particle (Chevalier et al., 2007). Prasher et al. found that nanofluid viscosity is not depending on nanoparticle diameter (Prasher et al., 2006).

Chevalier et al. experimentally found that viscosity abnormally increases when an increase in volume concentrations (Chevalier et al., 2007). Lu and Fan discovered that experimental viscosity values of nanofluids evolve into advanced as the volume fraction rises (Lu and Fan, 2008). Chen et al. found that viscosity increases after a 0.4% of volume fraction (Chen et al., 2008). Phuoc and Massoudi discovered Fe₂O₃-deionized water nanofluids experimental viscosity values rises with increasing particle volume concentration (Phuoc and Massoudi, 2009). Nguyen et al. found in their study of Al₂O₃-water 530 percentage increment in viscosity when volume fraction increases from 0 to 12% (Nguyen et al., 2008).

Garg et al. discovered a fourfold advancement in experimentally viscosity values when compare the Einstein model (Garg et al., 2008). Mahbubul et al. cited as no correlation can forecast the experimental viscosity values exactly in a broad range of particle volume concentration (Mahbubul et al., 2012). Murshed et al. discussed that the well-established models such as Einstein (1906), Krieger and Dougherty (1959) and Batchelor (1977) could not forecast the experimental viscosity values in an exact way (Murshed et al., 2008).

In previous studies, many models were developed to evaluate effective viscosity of nanofluids by considering Brownian motion. The aim of the present work is to develop a new correlation for the effective viscosity of nanofluids while considering the interfacial layer on nanoparticle and Brownian motion. The current model compared with the classical model of Einstein (1906) and predictions of Wang et al. (1999) with the selected experimental results of nanofluids as a function of the parameters such as a material of nanoparticle, nanoparticle size, volume fraction, and temperature.

2 Theoretical models

Presently, various theoretical correlations have been introduced to model the dependence of nanofluid viscosity with the fluid characteristics.

2.1

2.1 Einstein model

Einstein derived the applicable first theoretical formula for the estimation of viscosity values of composites or mixtures in 1906. This model developed while assuming linear viscous fluid including suspensions of rigid and spherical particles. Einstein’s model is valid for very low volume fraction (∅ < 0.02) Einstein, 1906.

(1)

μ_{EM nf} = μ_{bf} (1 + 2.5 \emptyset)

(2)

ϕ = \frac{ρ_{l} ϕ_{m}}{ρ_{l} ϕ_{m} + ρ_{p} (1 - ϕ_{m})}

2.2

2.2 Brinkman model

Brinkman modified Einstein’s model for used with average particle volume fraction up to 4% (Brinkman, 1952).

(3)

μ_{nf} = μ_{bf} (\frac{1}{{(1 - \emptyset)}^{2.5}})

2.3

2.3 Batchelor model

Batchelor reformed Einstein’s theoretical model by presenting Brownian motion effect (Batchelor, 1977).

(4)

μ_{nf} = μ_{bf} (1 + 2.5 \emptyset + 6.5 \emptyset^{2})

2.4

2.4 Graham model

Graham has proposed a generalization of Batchelor model. His formula is agreed well with Einstein’s model for volume fraction lower than 0.02. Graham’s model is as follows (Mori and Ototake, 1956).

(5)

μ_{nf} = μ_{bf} (1 + 2.5 \emptyset + 4.5 [\frac{1}{(\frac{h_{s}}{d_{p}}) [2 + (\frac{h_{s}}{d_{p}})] {[1 + (\frac{h_{s}}{d_{p}})]}^{2}}])

2.5

2.5 Wang et al. model

Wang et al. found a model to predict viscosity of nanofluid as follows (Wang et al., 1999).

(6)

μ_{nf} = μ_{bf} (1 + 7.3 \emptyset + 123 \emptyset^{2})

2.6

2.6 Avsec and Oblak model

Avsec and Oblak cited as renewed Ward model as follows (Avsec and Oblak, 2007).

(7)

μ_{nf} = μ_{bf} (1 + 2.5 ϕ_{e} + {(2.5 ϕ_{e})}^{2} + \dots)

(8)

ϕ_{e} = ϕ {(1 + \frac{h}{r})}^{3}

(9)

μ_{nf} = μ_{bf} (\frac{1}{1 - 2.5 ϕ_{e}})

2.7

2.7 Masoumi et al. model

Masoumi et al. suggested a new viscosity correlation by considering Brownian motion of nanoparticle in nanofluid (Masoumi et al., 2009).

(10)

μ_{nf} = μ_{bf} (1 + \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times δ \times C})

(11)

V_{B} = \sqrt{\frac{18 \times R \times T}{π \times N_{A} \times ρ_{p} \times d_{p}^{3}}}

(12)

δ = \sqrt[3]{\frac{π \times d_{p}^{3}}{6 \times \emptyset}}

(13)

C = {(- 1.133 \times d_{p} - 2.771) \emptyset + (0.09 \times d_{p} - 0.393)} \times 10^{- 6}

3 Methodology

3.1

3.1 Experimental database

The primary goal of the current work is to present an advance model, which is capable of predicting the effective viscosity for different size of nanofluids. The current model was developed based on an extensive range of experimental values of nanofluid viscosity, which were acquired from following literature (Table 1). Various types of base fluids, such as water, ethylene glycol, ethylene glycol-water mixture and toluene containing different types of particles nanomaterial, like Al₂O₃, Fe, hBN, ZnO, SiC, CuO, Fe₃O₄, TiO₂, Graphite, and SWCNT were used for making this model (Table 2). The experimental database, which is used in this study, is shown in Table 1.

Table 1 Summary of experimental data of viscosity of nanofluids from different researches.

No	Base fluid	Nano particle type	Particle size (nm)	Volume fractions (%)	Temperatures (K)	Reference	Data points
1	EG	Al₂O₃	43	0.5,1,1.5,2.1,3.1,4.8,6.6	283.15,288.15,293.15,298.15,303.15,308.15,313.15,323.15	Pastoriza-Gallego et al. (2011a)	56
2	EG	Al₂O₃	8	0.5,1,1.5,2.1,3.1	283.15,288.15,293.15,298.15,303.15,308.15,313.15,323.15	Pastoriza-Gallego et al. (2011a)	40
3	Water	CuO	33	*wt(%)1,1.74,2.5,3.5,5,7,10	283.15,288.15,293.15,298.15,303.15,308.15,313.15,323.15	Pastoriza-Gallego et al. (2011b)	56
4	Water	CuO	11	*wt(%)1,2.5,3.5,5,7,10	283.15,288.15,293.15,298.15,303.15,308.15,313.15,323.15	Pastoriza-Gallego et al. (2011b)	48
5	Water	Graphite	8	0.5,1,1.5,2	293,303,313,323,333	Dalkilic et al. (2016)	20
6	Water	Al₂O₃	25	0.5,1,2,3,4	283,288,293, *298 (0.5,1,2)	Mena et al. (2013)	18
7	EG:Water = 20:80	Al₂O₃	36	0.3,0.6,0.8,1	293	Syam Sundar et al. (2014)	4
8	Water	TiO₂	21	0.2,0.6,1,1.5,2	288,298,308	Duangthongsuk and Wongwises (2010)	15
9	EG	Fe	40	0.125,0.25,0.5,1	299,308,318,328	Hemmat Esfe et al. (2014)	16
10	EG	Fe	70	0.125,0.25,0.5,1	299,308,318,328	Hemmat Esfe et al. (2014)	16
11	EG	Fe	100	0.125,0.25,0.5,1	299,308,318,328	Hemmat Esfe et al. (2014)	16
12	Water	CNT	9	0.0554,0.277,0.554,1.1,2.8,4.2,5.6	273,283,293,303,313	Halelfadl et al. (2013)	35
13	Water	hBN	70	0.5,1,2,3	298	İlhan et al. (2016)	4
14	Water: EG = 50:50	hBN	70	0.5,1,2,3	298	İlhan et al. (2016)	4
15	EG	hBN	70	0.5,1,2,3	298	İlhan et al., 2016	4
16	Water	TiO₂	95	0.25,0.6,1.2	298	He et al. (2007)	3
17	Water	SWCNT	45	1.25,2.5,5,7.5	303,308,313,318,323,328,333	Baratpour et al. (2016)	28
18	Toluene	Fe₃O₄	10	0.19,0.31,0.4,0.5	298,308,318,328,338	Singh et al. (2015)	20
19	Water: EG = 60:40	SiC	30	0.2,0.4,0.6,0.8,1	283.15,288.15,293.15,298.15,303.15,308.15	Li and Zou (2016)	30
20	EG	ZnO	100	0.5,1,2,3,4	293,308,323,338,353	Lee et al. (2012)	25
21	Water	Nano-diamond (ND)	12	0.2,0.4,0.6,0.8,1	293,303,313,323,333	Sundar et al. (2016)	25
22	Water	Fe₃O₄	25	0.1,0.2,0.4,1,2,3	293,298,308	Toghraie et al. (2016)	18
23	Coconut oil	CuO	40	*wt(%)0.5,1,1.5,2,2.5	308,318,328	Nabeel Rashin and Hemalatha (2013a)	15
24	Coconut oil	ZnO	40	*wt(%)0.5,1,1.5,2,2.5	308,318,328	Nabeel Rashin and Hemalatha (2013b)	15
25	EG	AlN	43	*wt(%) 0.05,0.1,0.15,0.2	293.6	Żyła and Fal (2016)	4

Table 2 Summary of nanofluids.

No	Type	Description	Data points
1	Base fluids	Water, EG, (Water:EG)-50:50, (Water:EG)-80:20, (Water:EG)-40:60 and Toluene, Coconut oil	7
2	Nanoparticle materials	Al₂O₃, CuO, Graphite, TiO₂, Fe, Fe₃O₄, hBN, SWCNT, SiC, ZnO, AlN	11
3	Nanofluids	Based on nanomaterial and base fluid	25
4	Fluids	Based on volume fractions	128
5	Experimental data points	Based on volume fractions into temperatures	535

3.2

3.2 Factors consider in the new correlation

The Einstein model well predicts viscosity values of the suspension containing particles volume fraction less than 0.02. Therefore Einstein model can be applicable for nanofluid. However, Garg et al. discovered that experimental results higher than viscosity values of nanofluid predicted by the Einstein model (Garg et al., 2008). Moreover, Hemmat Esfe et al. (2014) observed the effective viscosity of nanofluid depends on particle size. That implies the effective viscosity of nanofluid depends on some other factors other than volume fraction. Brownian velocity is introduced due to Brownian motion of nanoparticles within the base fluid. Masoumi et al. (2009) developed a theoretical model for effective viscosity of nanofluid by considering Brownian motion effect.

4 Description of the new correlation

4.1

4.1 Development of the model

Brownian motion of nanoparticles was contemplated together with the outcome of fluid particles moving beside nanoparticles situated on sides of them (Koo and Kleinstreuer, 2005). Masoumi et al. developed a model for the viscosity of nanofluids by adding base fluid viscosity and effective viscosity due to Brownian motion (Masoumi et al., 2009).

(14)

μ_{nf} = μ_{bf} (1 + \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times δ \times C})

(15)

V_{B} = \sqrt{\frac{18 \times R \times T}{π \times N_{A} \times ρ_{p} \times d_{p}^{3}}}

(16)

δ = \sqrt[3]{\frac{π \times d_{p}^{3}}{6 \times \emptyset}}

(17)

C = {(- 1.133 \times d_{p} - 2.771) \emptyset + (0.09 \times d_{p} - 0.393)} \times 10^{- 6}

Brownian motion part of Masoumi et al. model as follows (Masoumi et al., 2009),

(18)

μ_{BM} = \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times C_{f} \times δ}

Correction factor ( $C_{f}$ )

(19)

\frac{μ_{BM}}{μ_{bf}} = \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times C_{f} \times δ \times μ_{bf}}

(20)

Z = C_{f} \times μ_{bf}

(21)

Z = A \emptyset^{- B}

When the particle size in micrometer, $μ_{BM} = \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times C_{f} \times δ} \approx 0$

Hence, $d_{p} > 1 μ m$ $μ_{s} \approx μ_{bf} (1 + 0)$ $μ_{s} \approx μ_{bf}$

According to the rheology of suspensions of solid particles when the particle size in micrometer viscosity of the suspension is higher than the base fluid. Hence there should be a part related to volume fraction.

Einstein in 1906 has derived the applicable first theoretical formula for the estimation of viscosity values of composites or mixtures (Einstein, 1906).

(22)

μ_{EM nf} = μ_{bf} (1 + 2.5 \emptyset)

Viscosity effect due to nanolayer

(23)

μ_{NL nf} = μ_{bf} (2.5 ϕ_{e}) - μ_{bf} (2.5 \emptyset)

(24)

μ_{ST} = μ_{EM nf} + μ_{NL nf}

This part consider as a static part,

(25)

μ_{ST} = μ_{bf} (1 + 2.5 ϕ_{e})

Finally model as follows,

(26)

μ_{nf} = μ_{bf} (1 + 2.5 ϕ_{e} + \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times C_{f} \times δ})

By analyzing several experimental results, an equation for Z obtained as follows.

(27)

Z = T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}

(28)

C_{f} = μ_{bf}^{- 1} [T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}]

The Brownian motion part consider as a dynamic part,

(29)

μ_{DY} = μ_{bf} (\frac{ρ_{p} V_{B} d_{p}^{2}}{72 δ [T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}]})

4.2

4.2 The new correlation

The effective viscosity is combination of static and dynamic parts of nanofluid viscosity, and then it can be stated as follows,

(30)

\{\begin{matrix} Effective \\ Viscosity of \\ nanofluid \end{matrix}\} = \{\begin{matrix} Static part \\ of the effective \\ viscosity of nanofluid \end{matrix}\} + \{\begin{matrix} Dynamic part \\ of the effective \\ viscosity of nanofluid \end{matrix}\} μ_{nf} = μ_{ST} + μ_{DY}

(31)

μ_{nf} = μ_{bf} (1 + 2.5 ϕ_{e} + \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times δ \times [T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}]})

5 Results and discussion

5.1

5.1 Statically analysis

The present model was validated by using experimental data. In the statical evaluation authors used two statistical indicators median deviation (MD) and correlation coefficient (R²). The mean deviation specifies that how much two groups of data are correlated. The correlation coefficient shows that how much closer to one group of data set with another group of data set.

(32)

MD = \frac{1}{n} \sum_{1}^{n} \{ABS (\frac{μ_{ef} - μ_{nf}}{μ_{ef}}) \times 100\}

(33)

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(μ_{Enf} - μ_{nf})}^{2}}{\sum_{i = 1}^{n} {(μ_{Enf} - μ_{Enf})}^{2}}

The present model suits with the 501 viscosity values with mean deviations lower than 5% and 75% of them are within the correlation coefficient 0.78–1.

5.2

5.2 Present model comparison with existing theoretical models

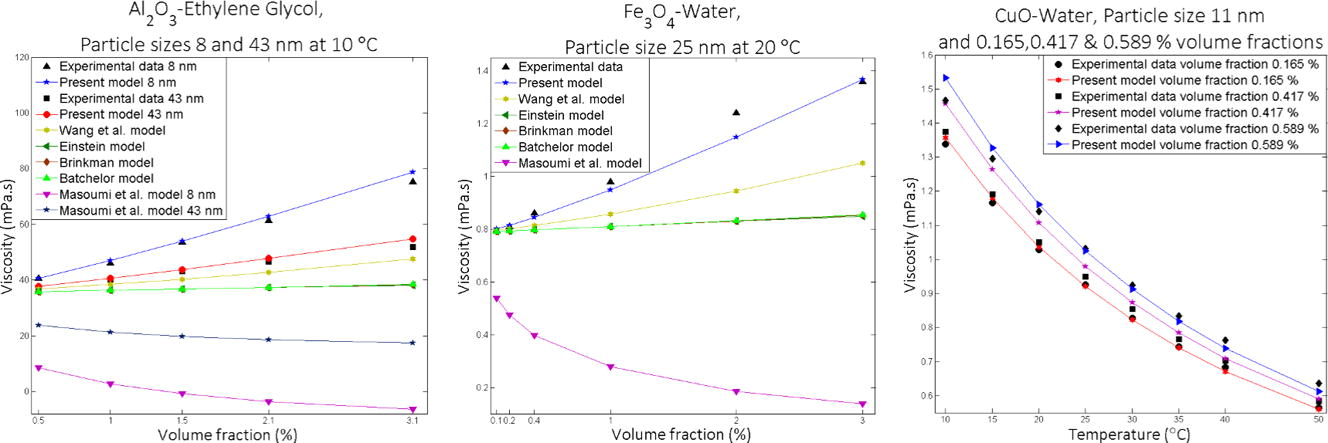
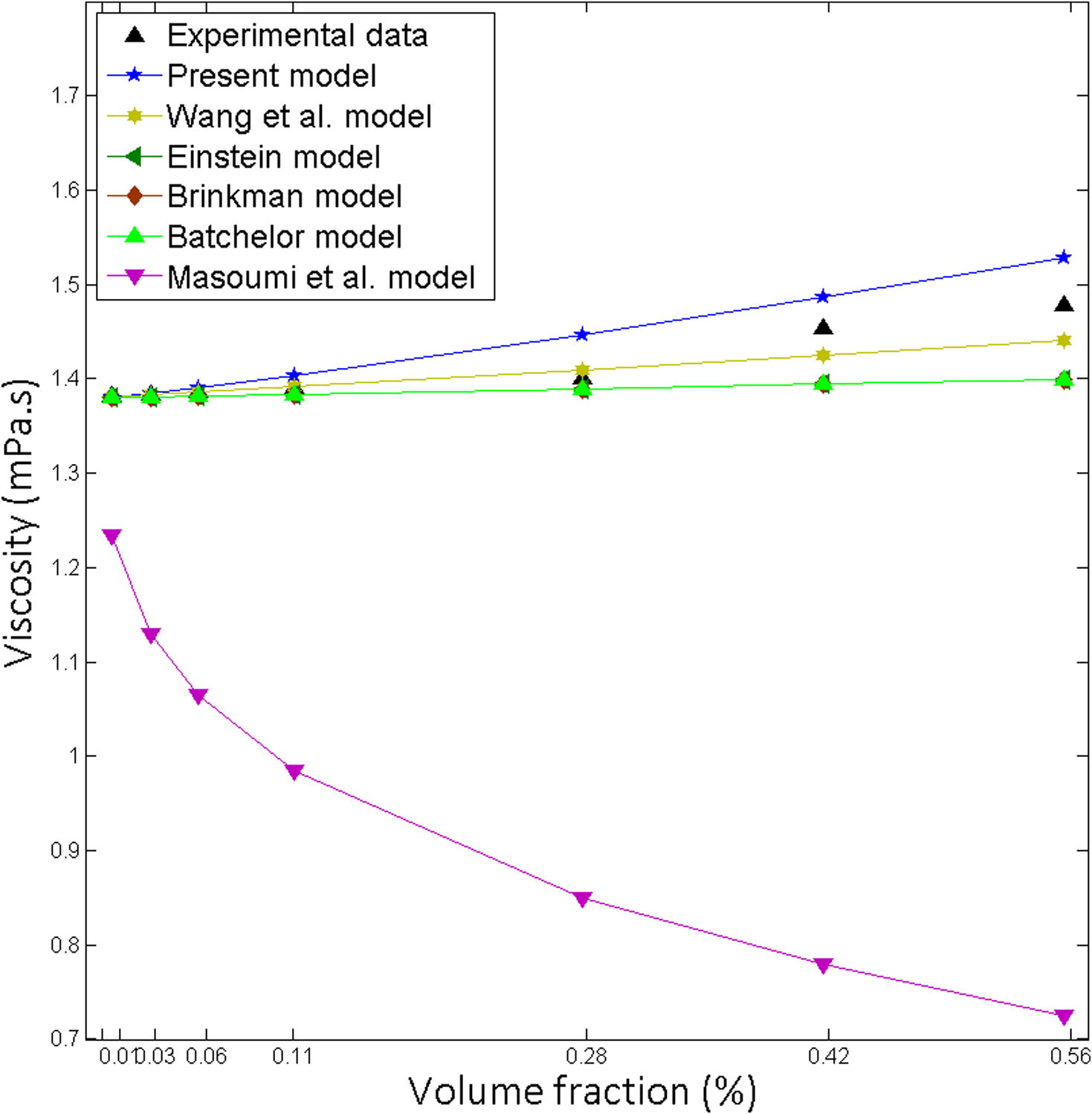
Existing models Einstein (1906), Brinkman (1952), Batchelor (1977), Wang et al. (1999) and Masoumi et al. (2009), are expressively underpredicted the experimental data (Figs. 1–5 ). The developed model is in excellent agreement with the experimental data (Table 3). It was found that Masoumi et al. (2009) model predicts viscosity lower than base fluid, which is due to its correction factor. Masoumi et al. model (Masoumi et al., 2009) valid only for the following conditions (Eq. 41).

(34)

\emptyset < \frac{(0.09 \times d_{p} - 0.393)}{(1.133 \times d_{p} + 2.771)}

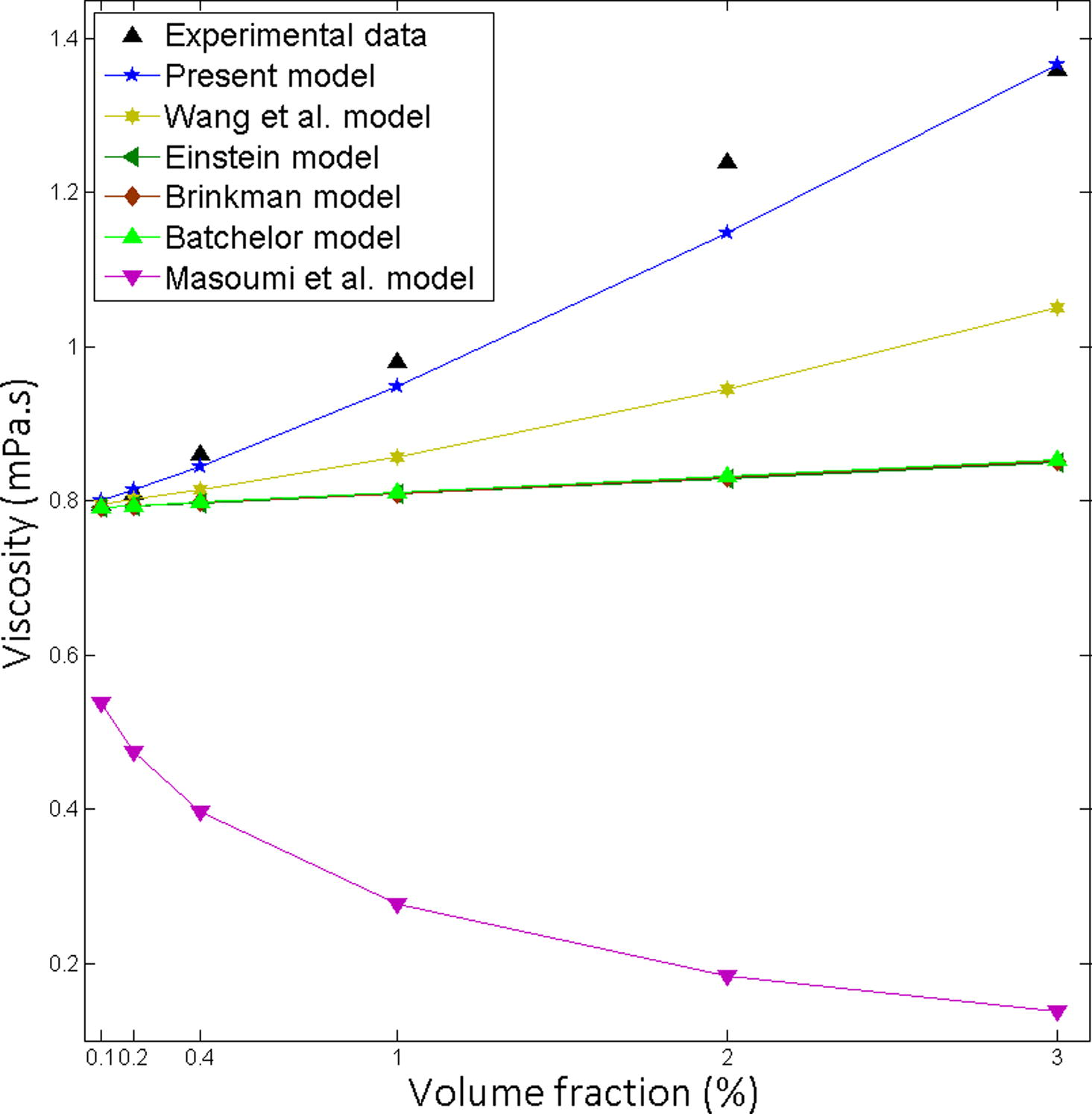
Comparison of the theoretical predictions with the experimental results for Fe3O4-Water, Particle size 25 nm at 20 °C.

Comparison of the theoretical predictions with the experimental results for Carbon Nanotube-Water, Particle size 9 nm at 10 °C.

Comparison of the theoretical predictions with the experimental results for Al2O3-Water, Particle size 36 nm at 20 °C.

Comparison of the theoretical predictions with the experimental results for SiC-EG: Water = 40:60, Particle size 30 nm at 10 °C.

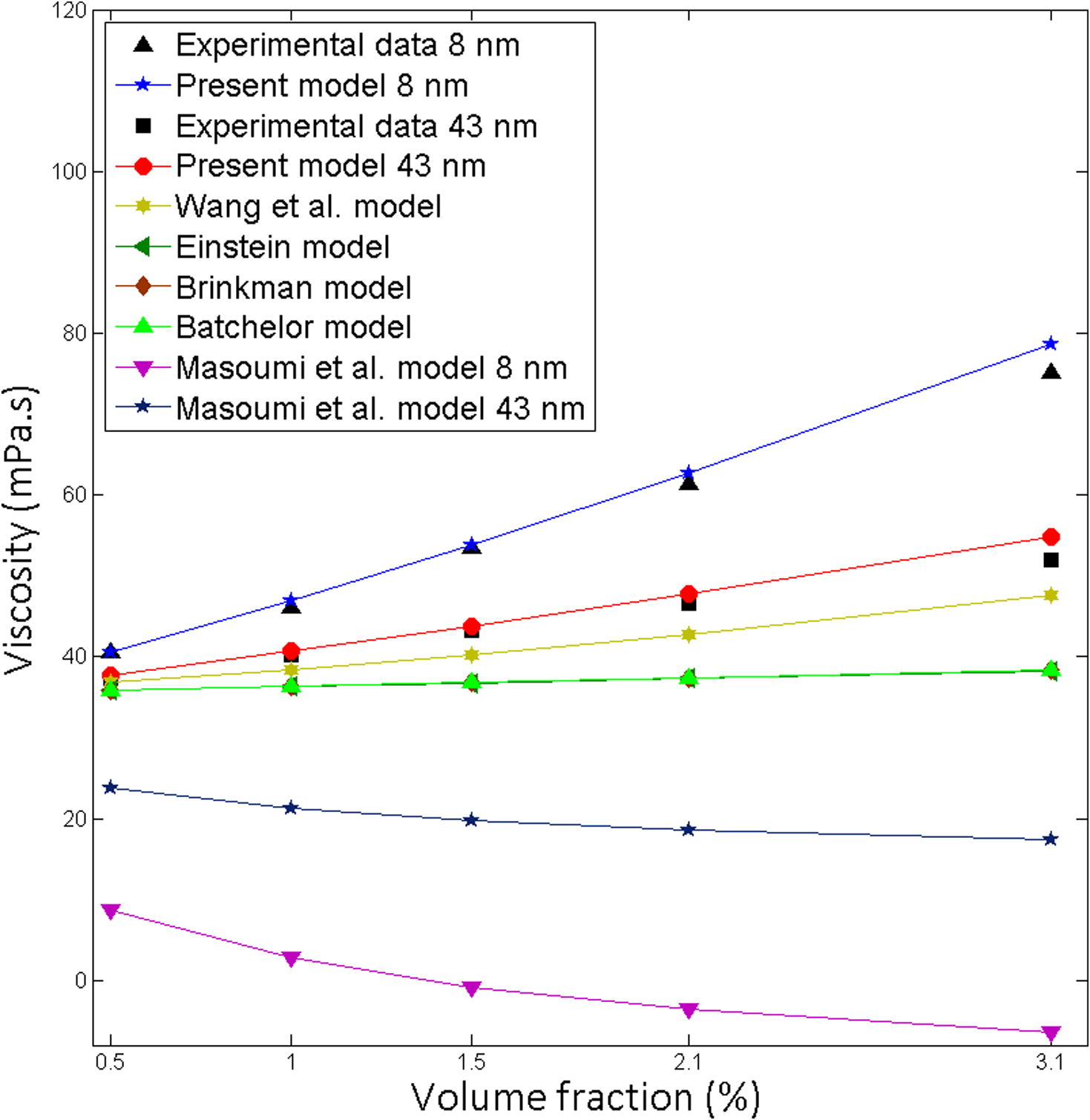
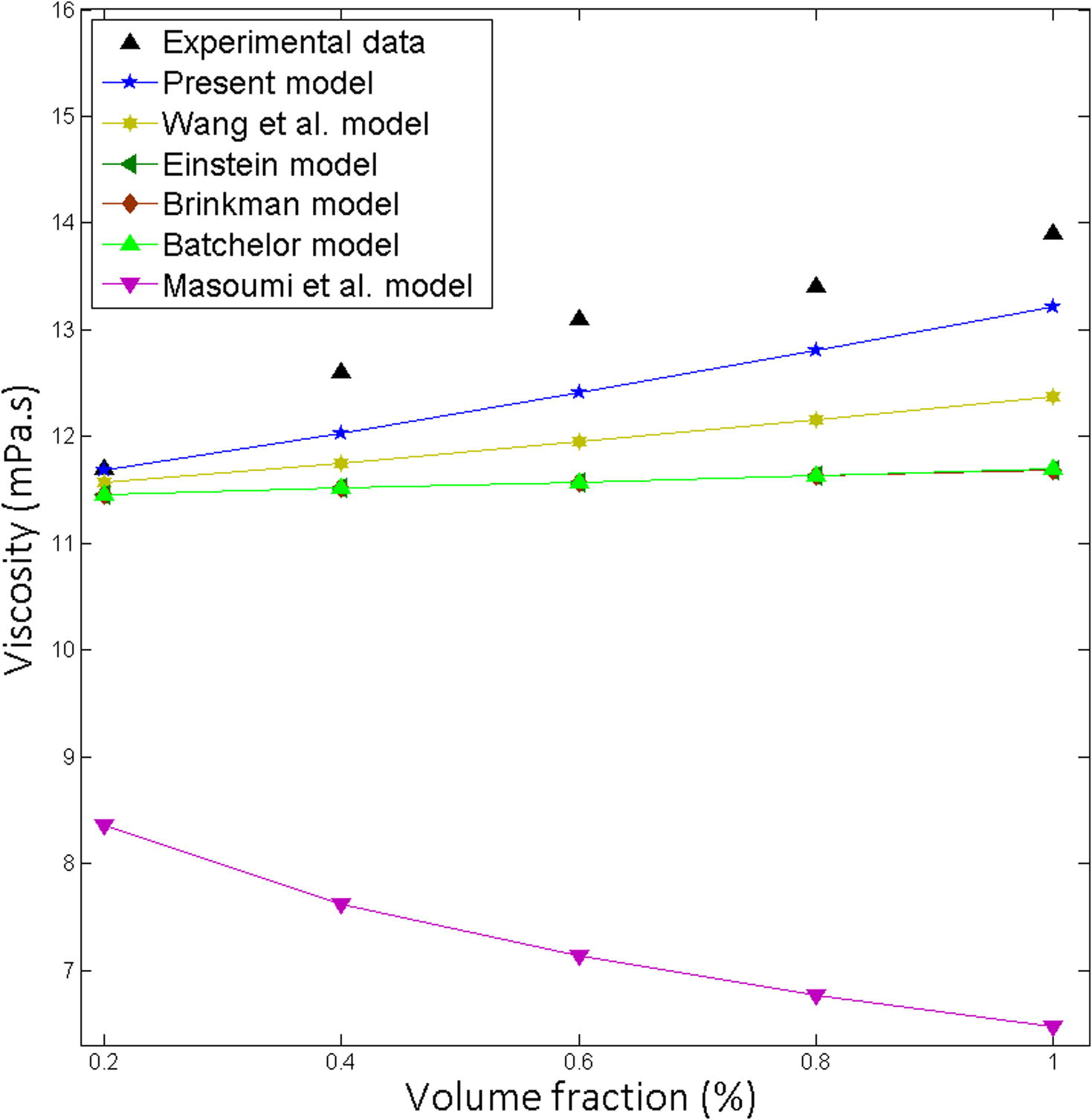
Comparison of the theoretical predictions with the experimental results for Al2O3-EG, Particle size 43, 8 nm at 10 °C.

Table 3 Comparison of the theoretical predictions with the experimental results.

Figure	Nanomaterial	Base fluid	Particle size (nm)	MD%	R²	Experimental Data
Fig. 1	Fe₃O₄	Water	25	3.2	0.95	Toghraie et al. (2016)
Fig. 2	CNT	Water	N/A	1.4	0.83	Halelfadl et al. (2013)
Fig. 3	Al₂O₃	Water	36	1.7	0.78	Syam Sundar et al. (2014)
Fig. 4	SiC	Ethylene Glycol	30	3.8	0.43	Li and Zou (2016)
Fig. 5	Al₂O₃	Ethylene Glycol	8	2	0.95	Pastoriza-Gallego et al. (2011a)
Fig. 5	Al₂O₃	Ethylene Glycol	43	1.4	0.99	Pastoriza-Gallego et al. (2011a)

5.3

5.3 Effective parameters on the effective viscosity of nanofluid

5.3.1

5.3.1 Effect of particle size

Al₂O₃–ethylene glycol (Pastoriza-Gallego et al., 2011a) nanofluids exhibit that the smaller particles improve the viscosity compared with larger particles. Fe-Ethylene glycol (Dalkilic et al., 2016), CuO-water (Pastoriza-Gallego et al., 2011b) show a similar pattern (Fig. 6). The new correlation exhibits viscosity’s declining trend with increasing particle size. Particle size effect associated with both the static part and the dynamic part. Then the effect of particle size on the new correlation as follows,

(35)

μ_{nf} = γ_{1} + α_{1} (\frac{1}{d_{p}^{3}}) + β_{1} (\frac{1}{d_{p}^{\frac{1}{2}}})

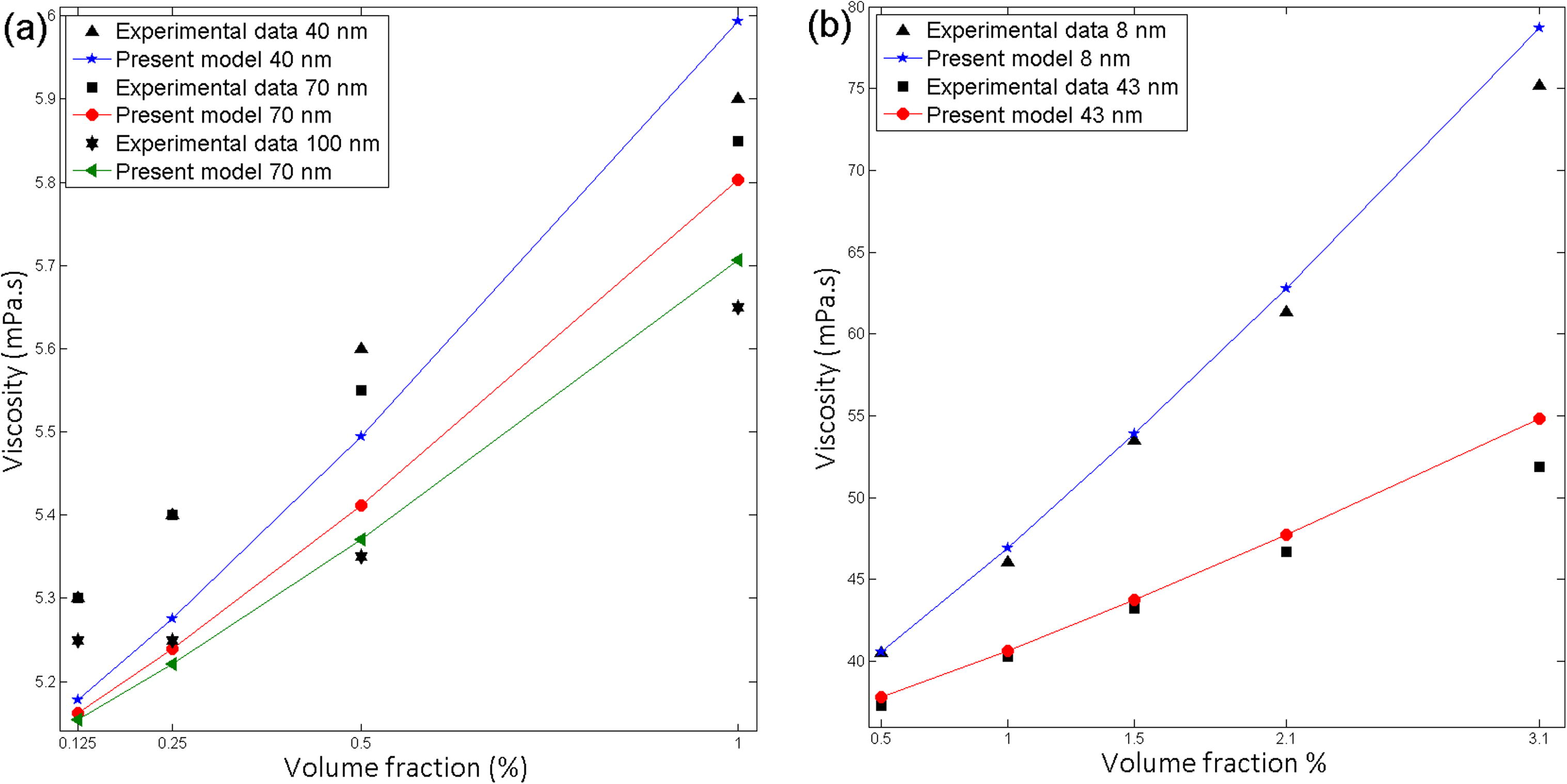
Effect of volume fraction on viscosity for (a) Fe-EG, particle size 40, 70,100 nm at 55 °C (b) Al2O3-EG, particle size 43, 8 nm at 10 °C.

5.3.2

5.3.2 Effect of temperature

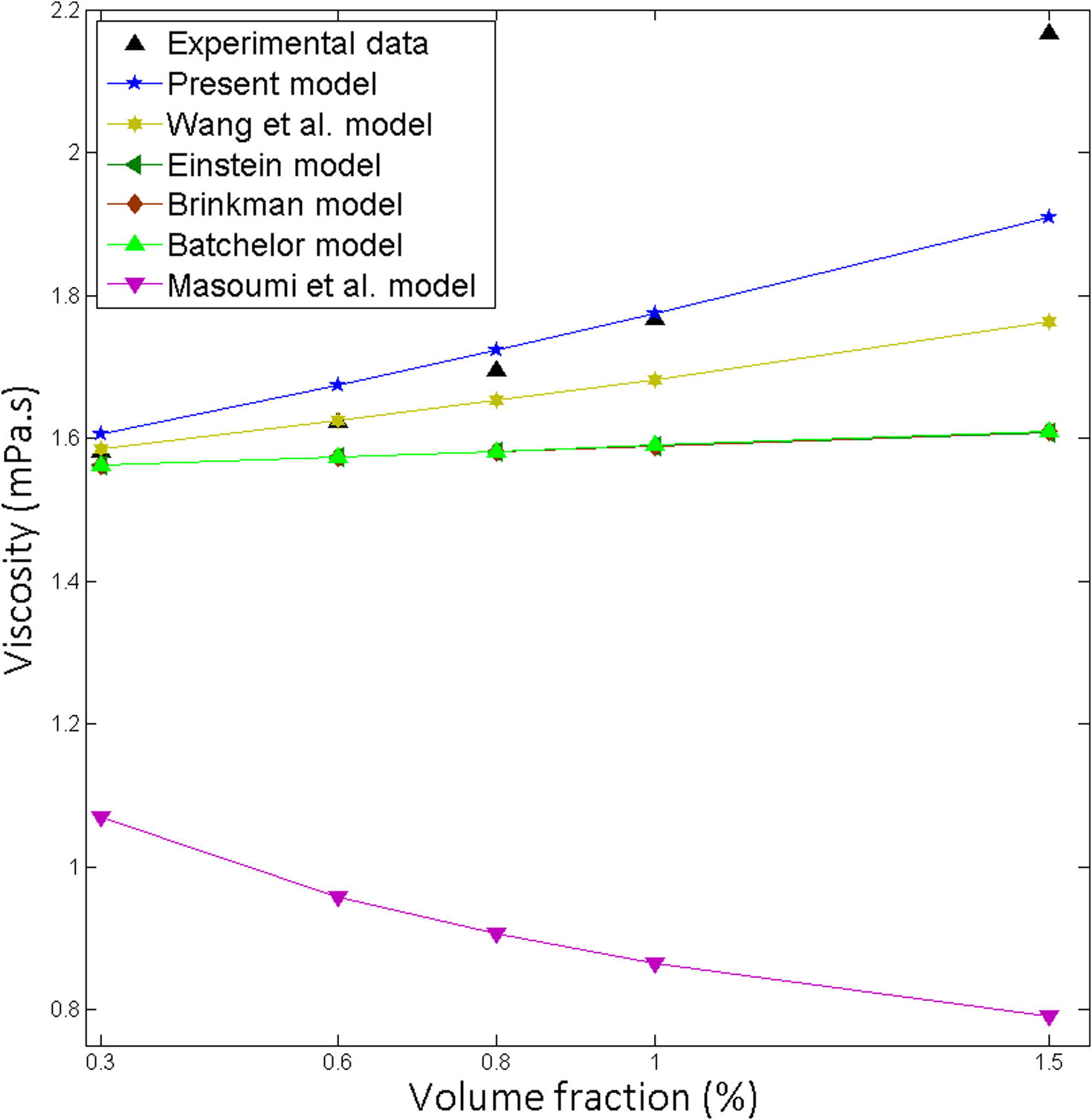
Mena et al. experimentally measured temperature effect of Al₂O₃-Water nanofluid viscosity for a temperature range of 283 K–298 K. They experimentally found that dynamic viscosity declines with the increase of temperature (Pastoriza-Gallego et al., 2011a). Pastoriza-Gallego et al. showed the temperature effect of CuO-water nanofluid for eight temperatures (283.15, 288.15, 293.15, 298.15, 303.15, 308.15, 313.15, and 323.15 K) and indicated that relative viscosity decreases with increase of temperature (Pastoriza-Gallego et al., 2011b) (Fig. 7).

(36)

μ_{nf} = γ_{2} + α_{2} + β_{2} (\frac{1}{\sqrt{T} \times \emptyset^{- AT}})

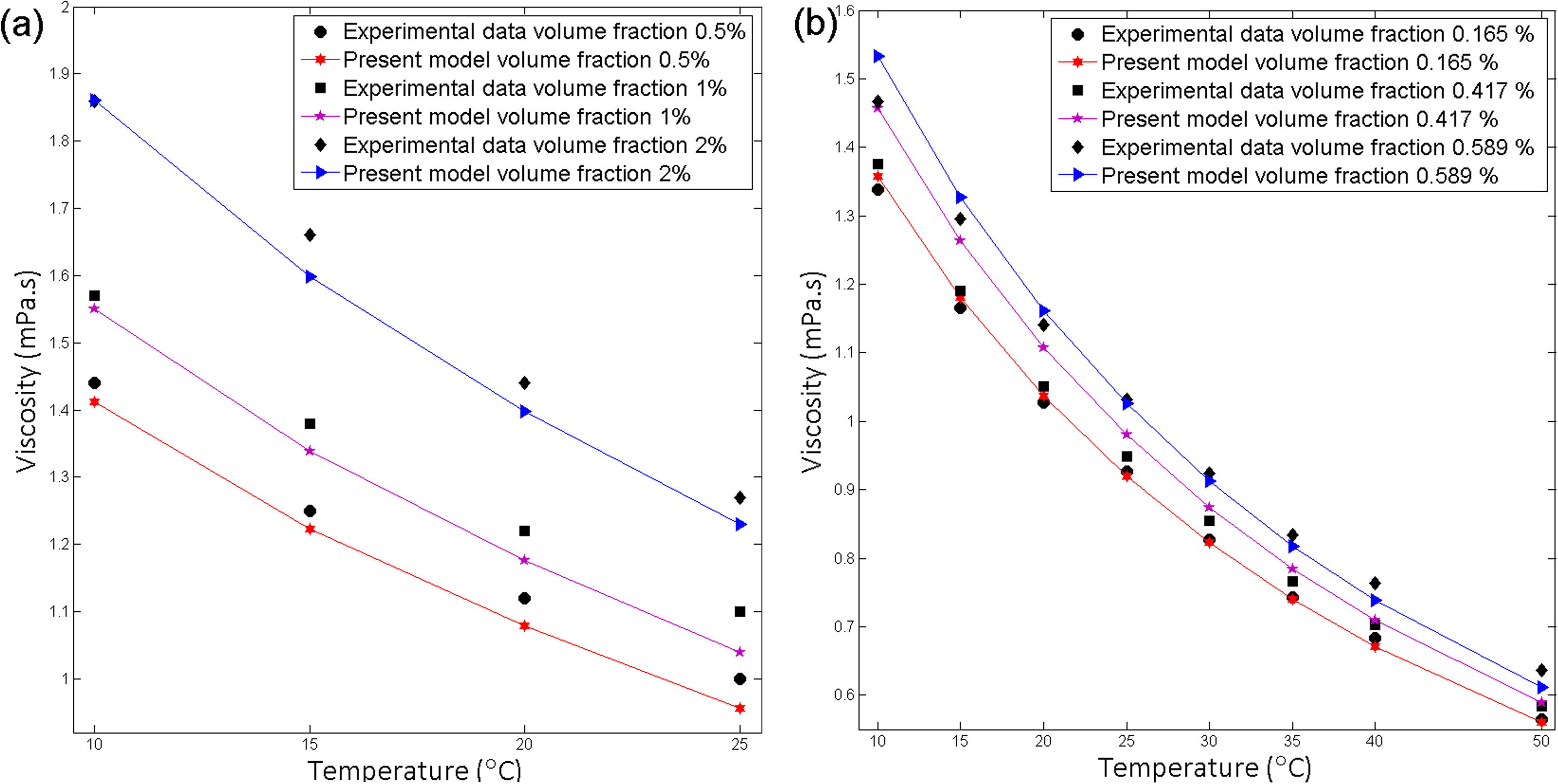
Effect of volume fraction on viscosity for (a) Al2O3-water, Particle size 25 and 0.5, 1 and 2% volume fractions (b) CuO-water, Particle size 11 nm and 0.165, 0.417, 0.589% volume fractions.

5.3.3

5.3.3 Effect of volume concentration

Dalkilic et al. (2016) and Pastoriza-Gallego et al. (2011a) found that viscosity of nanofluid increased with rising the particle volume fraction (Fig. 8). The present model complies with viscosity’s increasing trend with increasing volume concentration. Volume concentration effect consists of both static part and dynamic part. The effect of volume concentration on the present model as follows,

(37)

μ_{nf} = γ_{3} + α_{3} (\emptyset) + β_{3} (\frac{1}{\emptyset^{A}})

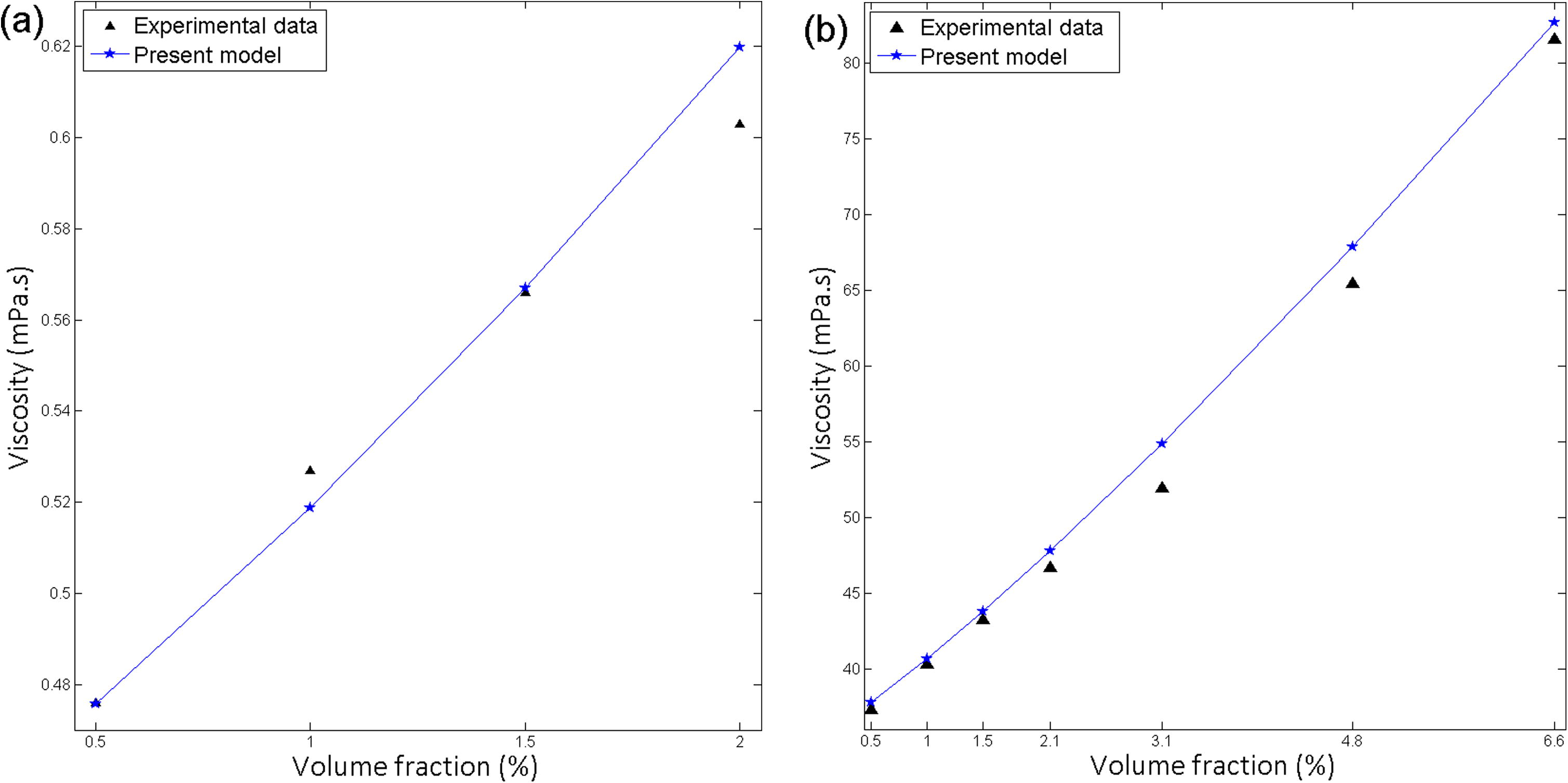
Effect of volume fraction on viscosity for (a) graphene-water, particle size 8 nm at 60 °C (b) Al2O3-EG, particle size 43 nm at 10 °C.

It is evident that nanofluid must exhibit base fluid properties at the point of volume fraction is zero. The present model shows viscosity of the base fluid at the point volume fraction is zero. One can obtain the same result for Einstein (1906), Batchelor (1977), Brinkman (1952), Wang et al. (1999), Masoumi et al. (2009), models except for Graham model (Mori and Ototake, 1956).

5.3.4

5.3.4 Effect of nanoparticle material

There is no considerable generic model to evaluate effects of nanoparticle material on nanofluid viscosity. The combination of Mena et al. (2013) and Toghraie et al. (2016) findings come into view that viscosity of nanofluid increases with nanoparticle material density (Fig. 9).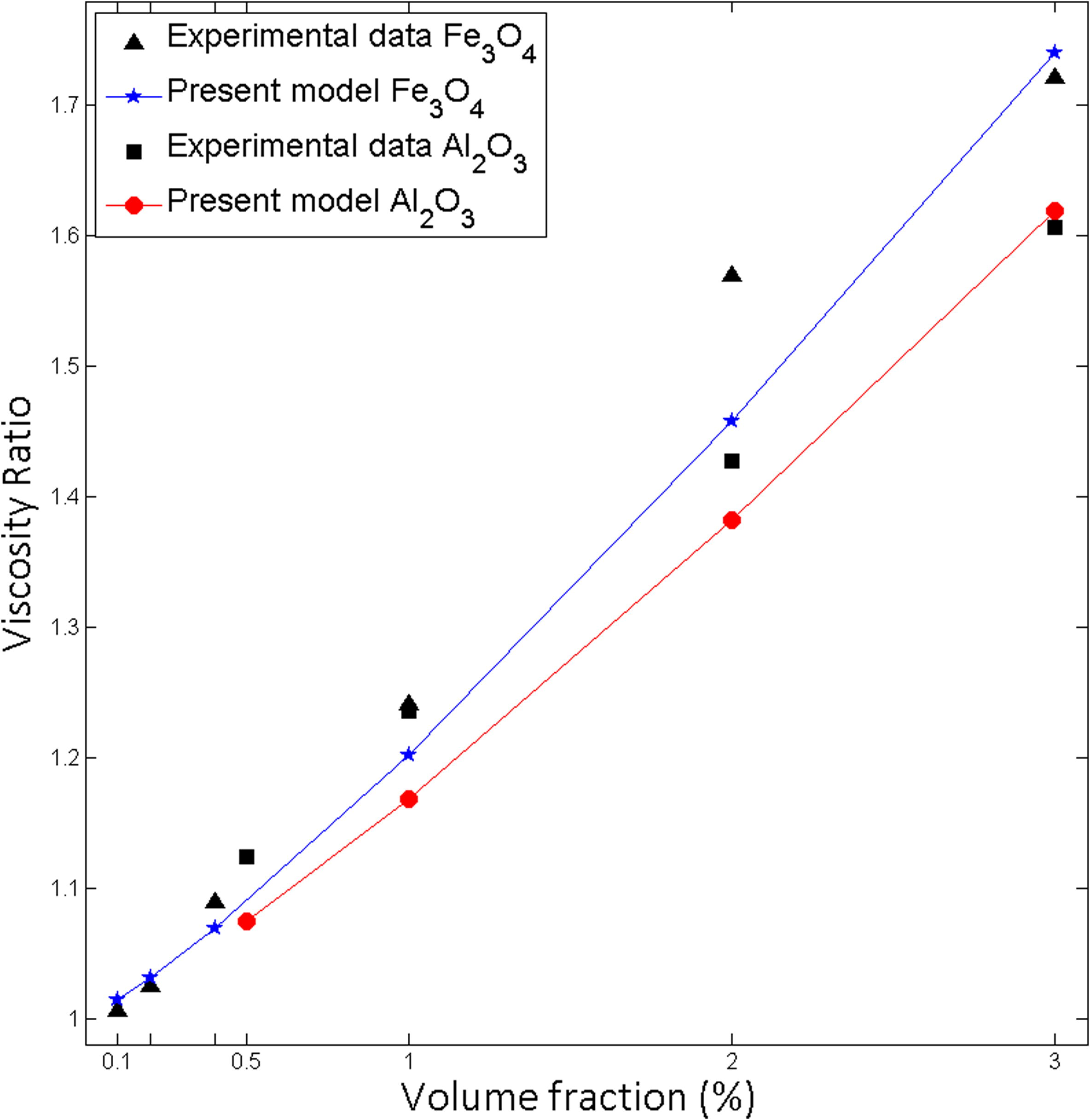

Effect of volume fraction on viscosity for Al2O3-water, Fe3O4-water particle size 25 nm at 25 °C.

The present model exhibits viscosity’s increasing trend with increasing nanomaterial density. Nanomaterial density depends on the only dynamic part. The present model expresses the effect of Nanomaterial density as follows,

(38)

μ_{nf} = γ_{4} + α_{4} + β_{4} (\sqrt{ρ_{p}})

5.3.5

5.3.5 Effect of particle shape

The Present model developed while assuming nanoparticles are rigid and spherical. Carbon nanotubes are cylindrical with dimensions: radius in nanometer and length in micrometer. As an example, Sundra L.S. et al. cited their research paper Multi-walled carbon nanotubes (MWCNT) outer diameter of 10–30 nm and length of 0.5–500 μm (Sundar et al., 2014) (Fig. 10).

Effect of volume fraction on viscosity for carbon nanotube-water, particle size 9.2 nm at 20 °C.

5.4

5.4 Comparison of dynamic and static parts

Numerous authors have suggested semi-empirical models described the relative viscosity of concentrated suspensions, as a function of the volume concentration and compared with the Einstein model (Einstein, 1906). The present model consists of two parts namely the static part and the dynamic part. The static part is a function of volume fractions and ratio of nanolayer thickness to nanoparticle radius. It may be a debatable point to consider, where the dynamic viscosity part is negligible. Fig. 11 shows the experimental viscosity values of Pastoriza-Gallego et al. (2011a) and Pastoriza-Gallego et al. (2011b) (Fig. 11). It can be concluded as the effect of the dynamic part in viscosity ratio increased with increasing the particle concentration. Furthermore, the proportion of dynamic part in viscosity ratio depends on nanoparticle size, nanofluid temperature and density of nanomaterial.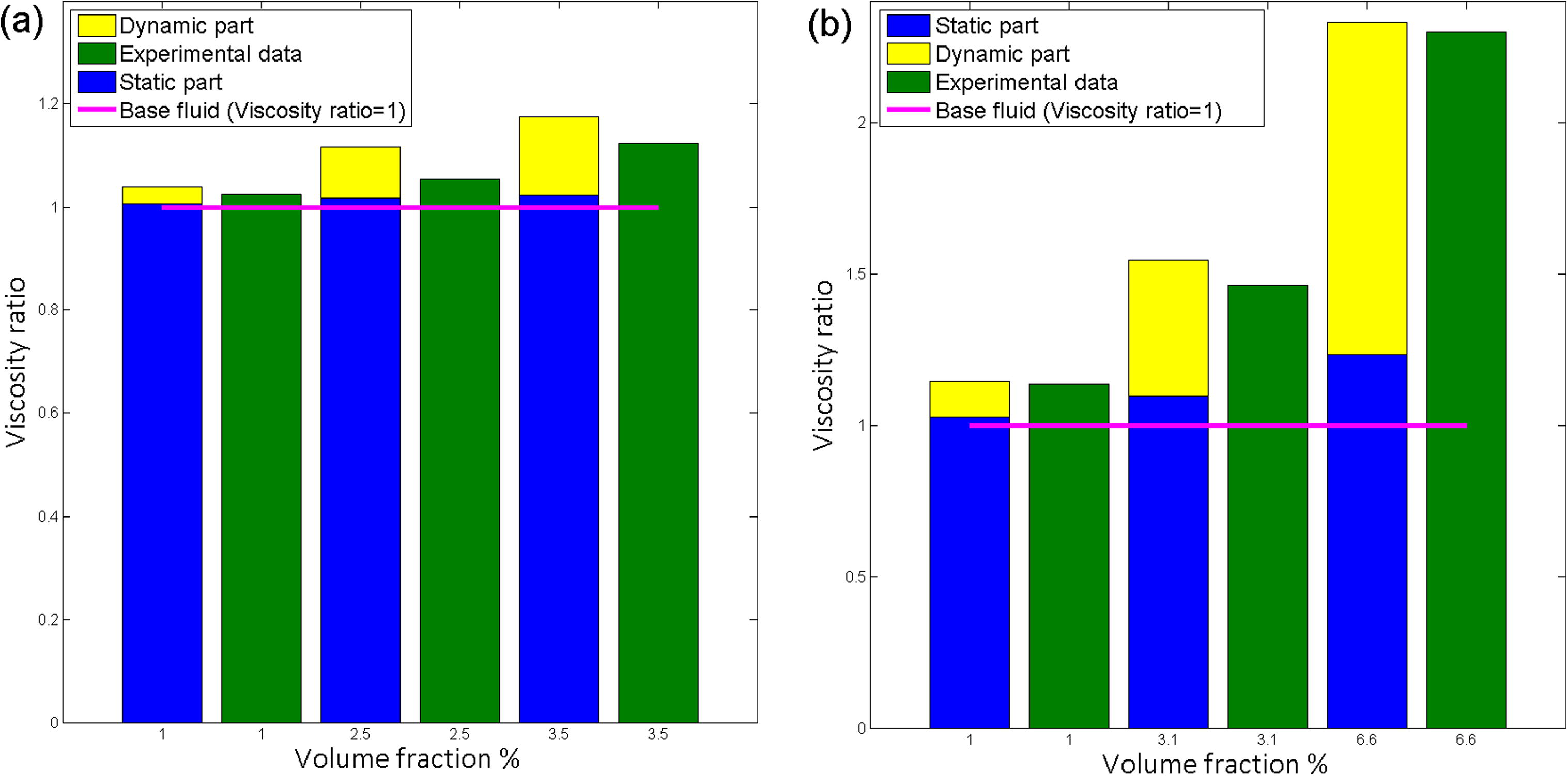

Effect of volume fraction on viscosity for (a) CuO-water, particle size 11 nm at 10 oC (b) Al2O3-EG, particle size 43 nm at 10 °C.

5.5

5.5 Particle size in micrometer

The nanofluid considers as a fluid, which is dispersing nano-sized particles in the base fluid. Einstein model based on the well-established theory of colloid including particles in size of micrometer or millimeter. Experimental results of Pastoriza-Gallego et al. (2011a) used to compare particle size of micrometer and nanometer (Fig. 12).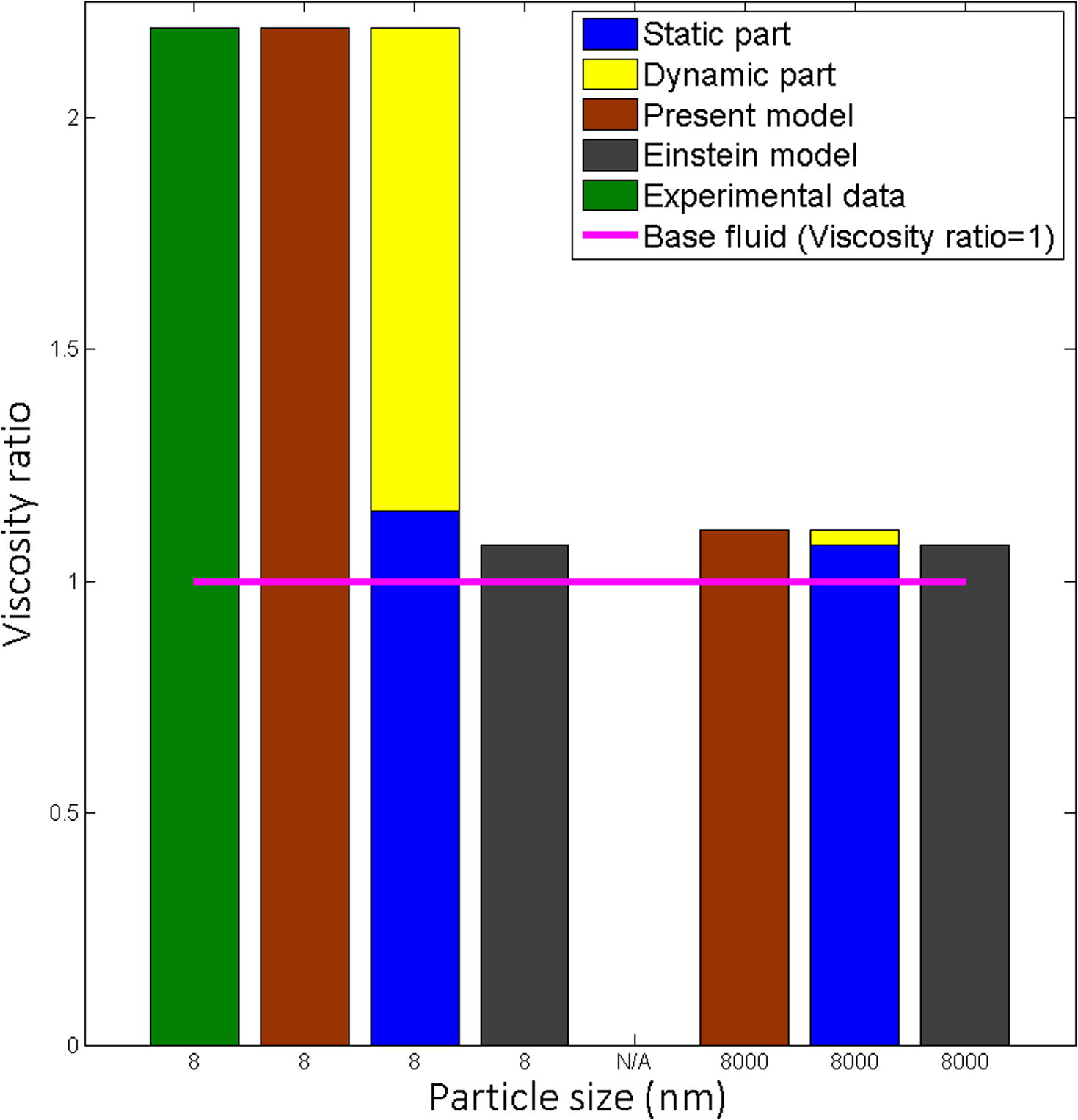

Effect of particle size on viscosity for Al2O3-water, volume fraction 3.1% at 10 °C.

When particle size in micrometer,

The dynamic part $(\frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times δ \times [T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}]}) \approx 0$

Nanolayer thickness to particle radius ratio $\frac{h}{r} \approx 0$

The static part $(1 + 2.5 ϕ_{e}) \approx (1 + 2.5 \emptyset)$

That implies, present model turned into the Einstein model for the effective viscosity of nanofluid at particle size higher than 1 micrometer. $d_{p} > 1 μ m$ $μ_{nf} = μ_{bf} (1 + 2.5 ϕ_{e} + \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times δ \times [T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}]}) \approx μ_{bf} (1 + 2.5 \emptyset)$

5.6

5.6 Non-Newtonian nanofluid

The many tunable parameters in nanofluids lead to the wide variations in the properties of nanofluids, such as non-Newtonian rheological properties. Based on experimental results, authors have mentioned that nanofluid exhibits shear-thinning non-Newtonian behavior. To conclude, the present model is not valid for non-Newtonian nanofluid (Table 4).

(39)

μ_{nf} = μ_{bf} (1 + 2.5 ϕ_{e} + \frac{ρ_{p} \times V_{B} \times d_{p}^{2}}{72 \times δ \times [Z_{r}]})

Table 4 Comparison of Shear rate vs Z equation.

Experimental data	Nanomaterial	Basefluid	Particle size (nm)	Shear rate	Z equation
Żyła and Fal (2016)	AlN	Ethylene Glycol	20	5.94	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.284}$
				14.56	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.385}$
				244.2	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.63}$
				494.2	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.68}$
				790.6	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.71}$
				1000	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.73}$
Nabeel Rashin and Hemalatha (2013a)	CuO	Coconut oil	20	14.28	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.04}$
Nabeel Rashin and Hemalatha (2013b)	ZnO	Coconut oil	20	14.28	$T \times 10^{- 10} \times \emptyset^{- 0.002 T - 0.001}$

The Z equations for Aluminum Nitride-Ethylene glycol, CuO-Coconut oil, and ZnO-Coconut oil same shear rate (14 s⁻¹) are different from each other. Finally, more experimental results in non-Newtonian nanofluid are needed for build a relationship between shear rate and correction factor.

5.7

5.7 Viscosity and nanofluid stability

Surfactants and dispersants are mostly applied to nanofluid as a stabilizer. The addition of surfactants take down the surface tension of host fluids and adds the immersion of particle. Surfactants are normally used to stabilize the nanofluid (Mukherjee and Paria, 2013). Colangelo et al. discovered surfactants effect for nanofluid viscosity (Colangelo et al., 2016). Even though the present model is developed based on assumption nanoparticles are well immersed, it uses experimental data with unstable nanofluids to derive correction factor.

5.8

5.8 Hybrid nanofluids

Researchers and engineers have carried out experiments for hybrid nanofluids, which are immersed nanoparticles consists of two or more dissimilar materials in the base fluid (Botha et al., 2011; Munkhbayar et al., 2013; Nine et al., 2013; Chen et al., 2014 ). This study suggested a model that determine the viscosity of hybrid nanofluids are as follows. Furthermore, this model can be expanded for three or four materials. Researchers could perform experimental studies for the viscosity of hybrid nanofluid and develop a general empirical equation.

(40)

μ_{hnf} = μ_{bf} (1 + 2.5 ϕ_{e 1} + \frac{ρ_{p 1} \times V_{B 1} \times d_{p 1}^{2}}{72 \times δ_{1} \times [T \times 10^{- 10} \times \emptyset_{1}^{- 0.002 T - 0.284}]} + 2.5 ϕ_{e 2} + \frac{ρ_{p 2} \times V_{B 2} \times d_{p 2}^{2}}{72 \times δ_{2} \times [T \times 10^{- 10} \times \emptyset_{2}^{- 0.002 T - 0.284}]})

6 Future works

The present correlation is derived from a wide range of experimental data of the effective viscosity of nanofluids. In most of the experimental studies reported in the literature, just the effects of two or three relevant parameters have been investigated. Therefore, for future works, the researchers would perform experimental studies by considering all of the important factors including temperature, nanoparticle size, nanoparticle material, non-Newtonian nanofluid, type of base fluid, which would lead to generating more accurate correlations to predict the effective viscosity of nanofluid.

7 Conclusions

A novel analytical model to determine the effective viscosity of fluid containing homogeneously dispersed rigid and spherical nanoparticles was presented. The effective viscosity of nanofluids is consists of two parts namely static and dynamic. The static part of the viscosity of nanofluid is a combination of Einstein model and viscosity effect due to nanolayer. Viscosity effect due to nanolayer was developed as one nanolayer is around a nanoparticle and its thickness is 1 nm. The dynamic part consists of viscosity effect due to Brownian motion of nanoparticles. Viscosity effect due to Brownian motion was included correction factor. Power function was used to derive correction factor. It depends on temperature and volume fraction. Using numerous experimental results correction factor was developed.

The new correlation was tested with 22 different nanofluids. It was used 501 experimental viscosity values to test the new model, and 75% of them are within the correlation coefficient 0.78–1. The new correlation performed well with experimental results when they are under variations of base fluid, nanoparticle size, volume fraction, temperature, and nanomaterial. It was found the new correlation isn’t valid for non-Newtonian nanofluid. The model has been tested with numerous experimental results containing one type of nanomaterial. It is evident that the present model isn’t valid for hybrid nanofluids. One model has been proposed to predict to the effective viscosity of hybrid nanofluid.

Acknowledgment

The authors would like to express their sincere gratitude for the University of Moratuwa.

Conflict of interest

None declared.

References

Alawi O.A., Sidik N.A.C., . The effect of temperature and particles concentration on the determination of thermo and physical properties of SWCNT-nanorefrigerant. Int. Commun. Heat Mass Transfer. 2015;67:8-13.
[Google Scholar]
Angayarkanni S.A., Philip J., . Review on thermal properties of nanofluids: recent developments. Adv. Colloid Interface Sci.. 2015;225:146-176.
[Google Scholar]
Avsec J., Oblak M., . The calculation of thermal conductivity, viscosity and thermodynamic properties for nanofluids on the basis of statistical nanomechanics. Int. J. Heat Mass Transfer. 2007;50(21–22):4331-4341.
[Google Scholar]
Baratpour M., Karimipour A., Afrand M., Wongwises S., . Effects of temperature and concentration on the viscosity of nanofluids made of single-wall carbon nanotubes in ethylene glycol. Int. Commun. Heat Mass Transfer. 2016;74:108-113.
[Google Scholar]
Batchelor G.K., . The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech.. 1977;83(1):97.
[Google Scholar]
Botha S.S., Ndungu P., Bladergroen B.J., . Physicochemical properties of oil-based nanofluids containing hybrid structures of silver nanoparticles supported on silica. Ind. Eng. Chem. Res.. 2011;50(6):3071-3077.
[Google Scholar]
Brinkman H.C., . The viscosity of concentrated suspensions and solutions. J. Chem. Phys.. 1952;20(4):571-581.
[Google Scholar]
Chen L., Xie H., Li Y., Yu W., . Nanofluids containing carbon nanotubes treated by mechanochemical reaction. Thermochim. Acta. 2008;477(1–2):21-24.
[Google Scholar]
Chen L.F., Cheng M., Yang D.J., Yang L., . Enhanced thermal conductivity of nanofluid by synergistic effect of multi-walled carbon nanotubes and Fe₂O₃ nanoparticles. Appl. Mech. Mater.. 2014;548:118-123.
[Google Scholar]
Chevalier J., Tillement O., Ayela F., . Rheological properties of nanofluids flowing through microchannels. Appl. Phys. Lett.. 2007;91(23):1-4.
[Google Scholar]
Yu W., Choi S.U.S., . The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated maxwell model. J. Nanopart. Res.. 2003;5:167.
[Google Scholar]
Choi S.U.S., Eastman J.A., . Enhancing Thermal Conductivity of Fluids With Nanoparticles. Mater. Sci.. 1995;231:99-105.
[Google Scholar]
Colangelo G., Favale E., Miglietta P., Milanese M., de Risi A., . Thermal conductivity, viscosity and stability of Al₂O₃-diathermic oil nanofluids for solar energy systems. Energy. 2016;95:124-136.
[Google Scholar]
Dalkilic A.S., Çebi A., Celen A., Yildiz O., Acikgoz O., Jumpholkul C., Bayrak M., Surana K., Wongwises S., . Prediction of graphite nanofluids’ dynamic viscosity by means of artificial neural networks. Int. Commun. Heat Mass Transfer. 2016;73:33-42.
[Google Scholar]
Duangthongsuk W., Wongwises S., . An experimental study on the heat transfer performance and pressure drop of TiO₂-water nanofluids flowing under a turbulent flow regime. Int. J. Heat Mass Transfer. 2010;53(1–3):334-344.
[Google Scholar]
Einstein A., . Eine neue Bestimmung der Molekul-dimensionen. Ann. d. Phys.. 1906;19:289-306.
[Google Scholar]
Esfe M.H., Yan W., Akbari M., Karimipour A., Hassani M., . Evaluation of thermal conductivity of COOH-functionalized MWCNTs/water via temperature and solid volume fraction by using experimental data and ANN methods. J. Therm. Anal. Calorim.. 2015;121(3):1273-1278.
[Google Scholar]
Garg J., Poudel B., Chiesa M., Gordon J.B., Ma J.J., Wang J.B., Ren Z.F., Kang Y.T., Ohtani H., Nanda J., McKinley G.H., Chen G., . Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid. J. Appl. Phys.. 2008;103(7)
[Google Scholar]
Ghanbarpour M., Nikkam N., Khodabandeh R., Toprak M.S., . Thermal performance of inclined screen mesh heat pipes using silver nanofluids. Int. Commun. Heat Mass Transfer. 2015;67:14-20.
[Google Scholar]
Halelfadl, S., Estell, P., Aladag, B., Doner, N., Mar, T., Halelfadl, S., Estell, P., Aladag, B., Doner, N., Mar, T., 2013. Viscosity of carbon nanotubes water based nanofluids: Influence of concentration and temperature to cite this version.
He Y., Jin Y., Chen H., Ding Y., Cang D., Lu H., . Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transfer. 2007;50(11–12):2272-2281.
[Google Scholar]
Hemmat Esfe M., Saedodin S., Mahian O., Wongwises S., . Efficiency of ferromagnetic nanoparticles suspended in ethylene glycol for applications in energy devices: effects of particle size, temperature, and concentration. Int. Commun. Heat Mass Transfer. 2014;58:138-146.
[Google Scholar]
İlhan B., Kurt M., Ertürk H., . Experimental investigation of heat transfer enhancement and viscosity change of hBN nanofluids. Exp. Therm. Fluid Sci.. 2016;77:272-283.
[Google Scholar]
Jang S.P., Choi S.U.S., . Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett.. 2004;84(21):4316-4318.
[Google Scholar]
Kasaeian A., Eshghi A.T., Sameti M., . A review on the applications of nanofluids in solar energy systems. Renew. Sustain. Energy Rev.. 2015;43:584-598.
[Google Scholar]
Koo J., Kleinstreuer C., . Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transfer. 2005;48(13):2652-2661.
[Google Scholar]
Krieger I.M., Dougherty T.J., . A mechanism for non-newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol.. 1959;3(1):137-152.
[Google Scholar]
Lee G.J., Kim C.K., Lee M.K., Rhee C.K., Kim S., Kim C., . Thermal conductivity enhancement of ZnO nanofluid using a one-step physical method. Thermochim. Acta. 2012;542:24-27.
[Google Scholar]
Leong K.C., Yang C., Murshed S.M.S., . A model for the thermal conductivity of nanofluids – the effect of interfacial layer. J. Nanoparticle Res.. 2006;8(2):245-254.
[Google Scholar]
Li X., Zou C., . International Journal of Heat and Mass Transfer Thermo-physical properties of water and ethylene glycol mixture based SiC nanofluids: an experimental investigation. Int. J. Heat Mass Transf.. 2016;101:412-417.
[Google Scholar]
Lu W.Q., Fan Q.M., . Study for the particle’s scale effect on some thermophysical properties of nanofluids by a simplified molecular dynamics method. Eng. Anal. Bound. Elem.. 2008;32(4):282-289.
[Google Scholar]
Mahbubul I.M., Saidur R., Amalina M.A., . Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transfer. 2012;55(4):874-885.
[Google Scholar]
Mahian O., Kianifar A., Kalogirou S.A., Pop I., Wongwises S., . A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transfer. 2013;57(2):582-594.
[Google Scholar]
Mar T., Halelfadl S., Van Vaerenbergh S., Estell?? P., . Unexpected sharp peak in thermal conductivity of carbon nanotubes water-based nanofluids. Int. Commun. Heat Mass Transfer. 2015;66:80-83.
[Google Scholar]
Masoumi N., Sohrabi N., Behzadmehr A., . A new model for calculating the effective viscosity of nanofluids. J. Phys. D Appl. Phys.. 2009;42(5):55501.
[Google Scholar]
Mena J.B., Ubices De Moraes A.A., Benito Y.R., Ribatski G., Parise J.A.R., . Extrapolation of Al₂O₃-water nanofluid viscosity for temperatures and volume concentrations beyond the range of validity of existing correlations. Appl. Therm. Eng.. 2013;51(1–2):1092-1097.
[Google Scholar]
Mori Y., Ototake N., . On the viscosity of suspensions. Chem. Eng.. 1956;20(9):488-494.
[Google Scholar]
Mukherjee S., Paria S., . Preparation and stability of nanofluids-a review. IOSR J. Mech. Civ. Eng.. 2013;9(2):63-69.
[Google Scholar]
Munkhbayar B., Tanshen M.R., Jeoun J., Chung H., Jeong H., . Surfactant-free dispersion of silver nanoparticles into MWCNT-aqueous nanofluids prepared by one-step technique and their thermal characteristics. Ceram. Int.. 2013;39(6):6415-6425.
[Google Scholar]
Murshed S.M.S., Estellé P., . A state of the art review on viscosity of nanofluids. Renew. Sustain. Energy Rev.. 2017;76(March):1134-1152.
[Google Scholar]
Murshed S.M.S., Leong K.C., Yang C., . Thermophysical and electrokinetic properties of nanofluids – a critical review. Appl. Therm. Eng.. 2008;28(17–18):2109-2125.
[Google Scholar]
Murshed S.M.S., Leong K.C., Yang C., . A combined model for the effective thermal conductivity of nanofluids. Appl. Therm. Eng.. 2009;29(11–12):2477-2483.
[Google Scholar]
Nabeel Rashin M., Hemalatha J., . Viscosity studies on novel copper oxide-coconut oil nanofluid. Exp. Therm. Fluid Sci.. 2013;48:67-72.
[Google Scholar]
Nabeel Rashin M., Hemalatha J., . Synthesis and viscosity studies of novel ecofriendly ZnO-coconut oil nanofluid. Exp. Therm. Fluid Sci.. 2013;51:312-318.
[Google Scholar]
Nguyen C.T., Desgranges F., Galanis N., Roy G., Mar?? T., Boucher S., Angue Mintsa H., . Viscosity data for Al₂O₃-water nanofluid-hysteresis: is heat transfer enhancement using nanofluids reliable? Int. J. Therm. Sci.. 2008;47(2):103-111.
[Google Scholar]
Nine M.J., Munkhbayar B., Rahman M.S., Chung H., Jeong H., . Highly productive synthesis process of well dispersed Cu2O and Cu/Cu2O nanoparticles and its thermal characterization. Mater. Chem. Phys.. 2013;141(2–3):636-642.
[Google Scholar]
Nkurikiyimfura I., Wang Y., Pan Z., . Heat transfer enhancement by magnetic nanofluids – a review. Renew. Sustain. Energy Rev.. 2013;21:548-561.
[Google Scholar]
Pastoriza-Gallego M.J., Lugo L., Legido J.L., Piñeiro M.M., . Thermal conductivity and viscosity measurements of ethylene glycol-based Al₂O₃ nanofluids. Nanoscale Res. Lett.. 2011;6(1):221.
[Google Scholar]
Pastoriza-Gallego M.J., Casanova C., Legido J.L., Piñeiro M.M., . CuO in water nanofluid: Influence of particle size and polydispersity on volumetric behaviour and viscosity. Fluid Phase Equilib.. 2011;300(1–2):188-196.
[Google Scholar]
Phillpot, S., Eastman, J.A., 2002. Mechanisms of heat flow in suspensions of nano-sized particles (nano fluids), 45, 2002, 855–863.
Phuoc T.X., Massoudi M., . Experimental observations of the effects of shear rates and particle concentration on the viscosity of Fe2O3-deionized water nanofluids. Int. J. Therm. Sci.. 2009;48(7):1294-1301.
[Google Scholar]
Prasher R., Bhattacharya P., Phelan P.E., . Thermal conductivity of nanoscale colloidal solutions (nanofluids) Phys. Rev. Lett.. 2005;94(2):3-6.
[Google Scholar]
Prasher R., Bhattacharya P., Phelan P.E., . Brownian-motion-based convective-conductive model for the effective thermal conductivity of nanofluids. J. Heat Transfer. 2006;128(6):588.
[Google Scholar]
Prasher R., Song D., Wang J., Phelan P., . Measurements of nanofluid viscosity and its implications for thermal applications. Appl. Phys. Lett.. 2006;89(13):67-70.
[Google Scholar]
Raja M., Vijayan R., Dineshkumar P., Venkatesan M., . Review on nanofluids characterization, heat transfer characteristics and applications. Renew. Sustain. Energy Rev.. 2016;64:163-173.
[Google Scholar]
Sheremet M.A., Pop I., Rahman M.M., . Three-dimensional natural convection in a porous enclosure filled with a nanofluid using Buongiorno’s mathematical model. Int. J. Heat Mass Transfer. 2015;82:396-405.
[Google Scholar]
Shukla K.N., Koller T.M., Rausch M.H., Fröba A.P., . Effective thermal conductivity of nanofluids – a new model taking into consideration Brownian motion. Int. J. Heat Mass Transf.. 2016;99:532-540.
[Google Scholar]
Singh R., Sanchez O., Ghosh S., Kadimcherla N., Sen S., Balasubramanian G., . Viscosity of magnetite-toluene nanofluids: dependence on temperature and nanoparticle concentration. Phys. Lett. Sect. A Gen. At. Solid State Phys.. 2015;379(40-41):2641-2644.
[Google Scholar]
Sundar L.S., Singh M.K., Sousa A.C.M., . Enhanced heat transfer and friction factor of MWCNT-Fe₃O₄/water hybrid nanofluids. Int. Commun. Heat Mass Transfer. 2014;52:73-83.
[Google Scholar]
Sundar L.S., Hortiguela M.J., Singh M.K., Sousa A.C.M., . Thermal conductivity and viscosity of water based nanodiamond (ND) nanofluids: an experimental study. Int. Commun. Heat Mass Transfer. 2016;76:245-255.
[Google Scholar]
Syam Sundar L., Venkata Ramana E., Singh M.K., Sousa A.C.M., . Thermal conductivity and viscosity of stabilized ethylene glycol and water mixture Al2O3 nanofluids for heat transfer applications: An experimental study. Int. Commun. Heat Mass Transfer. 2014;56:86-95.
[Google Scholar]
Toghraie D., Alempour S.M., Afrand M., . Experimental determination of viscosity of water based magnetite nanofluid for application in heating and cooling systems. J. Magn. Magn. Mater.. 2016;417:243-248.
[Google Scholar]
Tso C.Y., Fu S.C., Chao C.Y.H., . A semi-Analytical model for the thermal conductivity of nanofluids and determination of the nanolayer thickness. Int. J. Heat Mass Transfer. 2014;70:202-214.
[Google Scholar]
Wang X., Xu X., Choi S.U.S., . Thermal conductivity of nanoparticle – fluid mixture. J. Thermophys. Heat Transfer. 1999;13(4):474-480.
[Google Scholar]
Wang B.X., Zhou L.P., Peng X.F., . A fractal model for predicting the effective thermal conductivity of liquid with suspension of nanoparticles. Int. J. Heat Mass Transfer. 2003;46(14):2665-2672.
[Google Scholar]
Yang Y., Zhang Z.G., Grulke E.A., Anderson W.B., Wu G., . Heat transfer properties of nanoparticle-in-fluid dispersions (nanofluids) in laminar flow. Int. J. Heat Mass Transfer. 2005;48(6):1107-1116.
[Google Scholar]
Yang J.-C., Li F., Zhou W.-W., He Y., Jiang B.-C., . Experimental investigation on the thermal conductivity and shear viscosity of viscoelastic-fluid-based nanofluids. Int. J. Heat Mass Transfer. 2012;55(11–12):3160-3166.
[Google Scholar]
Yu C.-J., Richter A., Datta A., Durbin M., Dutta P., . Molecular layering in a liquid on a solid substrate: an X-ray reflectivity study. Phys. B Condens. Matter. 2000;283(1–3):27-31.
[Google Scholar]
Zhai Y.L., Xia G.D., Liu X.F., Li Y.F., . Heat transfer enhancement of Al₂O₃-H₂O nanofluids flowing through a micro heat sink with complex structure. Int. Commun. Heat Mass Transfer. 2015;66:158-166.
[Google Scholar]
Żyła G., Fal J., . Experimental studies on viscosity, thermal and electrical conductivity of aluminum nitride–ethylene glycol (AlN–EG) nanofluids. Thermochim. Acta. 2016;637:11-16.
[Google Scholar]

Show Sections

[1] Alawi O.A., Sidik N.A.C., . The effect of temperature and particles concentration on the determination of thermo and physical properties of SWCNT-nanorefrigerant. Int. Commun. Heat Mass Transfer. 2015;67:8-13.
[Google Scholar]

[2] Angayarkanni S.A., Philip J., . Review on thermal properties of nanofluids: recent developments. Adv. Colloid Interface Sci.. 2015;225:146-176.
[Google Scholar]

[3] Avsec J., Oblak M., . The calculation of thermal conductivity, viscosity and thermodynamic properties for nanofluids on the basis of statistical nanomechanics. Int. J. Heat Mass Transfer. 2007;50(21–22):4331-4341.
[Google Scholar]

[4] Baratpour M., Karimipour A., Afrand M., Wongwises S., . Effects of temperature and concentration on the viscosity of nanofluids made of single-wall carbon nanotubes in ethylene glycol. Int. Commun. Heat Mass Transfer. 2016;74:108-113.
[Google Scholar]

[5] Batchelor G.K., . The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech.. 1977;83(1):97.
[Google Scholar]

[6] Botha S.S., Ndungu P., Bladergroen B.J., . Physicochemical properties of oil-based nanofluids containing hybrid structures of silver nanoparticles supported on silica. Ind. Eng. Chem. Res.. 2011;50(6):3071-3077.
[Google Scholar]

[7] Brinkman H.C., . The viscosity of concentrated suspensions and solutions. J. Chem. Phys.. 1952;20(4):571-581.
[Google Scholar]

[8] Chen L., Xie H., Li Y., Yu W., . Nanofluids containing carbon nanotubes treated by mechanochemical reaction. Thermochim. Acta. 2008;477(1–2):21-24.
[Google Scholar]

[9] Chen L.F., Cheng M., Yang D.J., Yang L., . Enhanced thermal conductivity of nanofluid by synergistic effect of multi-walled carbon nanotubes and Fe₂O₃ nanoparticles. Appl. Mech. Mater.. 2014;548:118-123.
[Google Scholar]

[10] Chevalier J., Tillement O., Ayela F., . Rheological properties of nanofluids flowing through microchannels. Appl. Phys. Lett.. 2007;91(23):1-4.
[Google Scholar]

[11] Yu W., Choi S.U.S., . The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated maxwell model. J. Nanopart. Res.. 2003;5:167.
[Google Scholar]

[12] Choi S.U.S., Eastman J.A., . Enhancing Thermal Conductivity of Fluids With Nanoparticles. Mater. Sci.. 1995;231:99-105.
[Google Scholar]

[13] Colangelo G., Favale E., Miglietta P., Milanese M., de Risi A., . Thermal conductivity, viscosity and stability of Al₂O₃-diathermic oil nanofluids for solar energy systems. Energy. 2016;95:124-136.
[Google Scholar]

[14] Dalkilic A.S., Çebi A., Celen A., Yildiz O., Acikgoz O., Jumpholkul C., Bayrak M., Surana K., Wongwises S., . Prediction of graphite nanofluids’ dynamic viscosity by means of artificial neural networks. Int. Commun. Heat Mass Transfer. 2016;73:33-42.
[Google Scholar]

[15] Duangthongsuk W., Wongwises S., . An experimental study on the heat transfer performance and pressure drop of TiO₂-water nanofluids flowing under a turbulent flow regime. Int. J. Heat Mass Transfer. 2010;53(1–3):334-344.
[Google Scholar]

[16] Einstein A., . Eine neue Bestimmung der Molekul-dimensionen. Ann. d. Phys.. 1906;19:289-306.
[Google Scholar]

[17] Esfe M.H., Yan W., Akbari M., Karimipour A., Hassani M., . Evaluation of thermal conductivity of COOH-functionalized MWCNTs/water via temperature and solid volume fraction by using experimental data and ANN methods. J. Therm. Anal. Calorim.. 2015;121(3):1273-1278.
[Google Scholar]

[18] Garg J., Poudel B., Chiesa M., Gordon J.B., Ma J.J., Wang J.B., Ren Z.F., Kang Y.T., Ohtani H., Nanda J., McKinley G.H., Chen G., . Enhanced thermal conductivity and viscosity of copper nanoparticles in ethylene glycol nanofluid. J. Appl. Phys.. 2008;103(7)
[Google Scholar]

[19] Ghanbarpour M., Nikkam N., Khodabandeh R., Toprak M.S., . Thermal performance of inclined screen mesh heat pipes using silver nanofluids. Int. Commun. Heat Mass Transfer. 2015;67:14-20.
[Google Scholar]

[20] Halelfadl, S., Estell, P., Aladag, B., Doner, N., Mar, T., Halelfadl, S., Estell, P., Aladag, B., Doner, N., Mar, T., 2013. Viscosity of carbon nanotubes water based nanofluids: Influence of concentration and temperature to cite this version.

[21] He Y., Jin Y., Chen H., Ding Y., Cang D., Lu H., . Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int. J. Heat Mass Transfer. 2007;50(11–12):2272-2281.
[Google Scholar]

[22] Hemmat Esfe M., Saedodin S., Mahian O., Wongwises S., . Efficiency of ferromagnetic nanoparticles suspended in ethylene glycol for applications in energy devices: effects of particle size, temperature, and concentration. Int. Commun. Heat Mass Transfer. 2014;58:138-146.
[Google Scholar]

[23] İlhan B., Kurt M., Ertürk H., . Experimental investigation of heat transfer enhancement and viscosity change of hBN nanofluids. Exp. Therm. Fluid Sci.. 2016;77:272-283.
[Google Scholar]

[24] Jang S.P., Choi S.U.S., . Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett.. 2004;84(21):4316-4318.
[Google Scholar]

[25] Kasaeian A., Eshghi A.T., Sameti M., . A review on the applications of nanofluids in solar energy systems. Renew. Sustain. Energy Rev.. 2015;43:584-598.
[Google Scholar]

[26] Koo J., Kleinstreuer C., . Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transfer. 2005;48(13):2652-2661.
[Google Scholar]

[27] Krieger I.M., Dougherty T.J., . A mechanism for non-newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol.. 1959;3(1):137-152.
[Google Scholar]

[28] Lee G.J., Kim C.K., Lee M.K., Rhee C.K., Kim S., Kim C., . Thermal conductivity enhancement of ZnO nanofluid using a one-step physical method. Thermochim. Acta. 2012;542:24-27.
[Google Scholar]

[29] Leong K.C., Yang C., Murshed S.M.S., . A model for the thermal conductivity of nanofluids – the effect of interfacial layer. J. Nanoparticle Res.. 2006;8(2):245-254.
[Google Scholar]

[30] Li X., Zou C., . International Journal of Heat and Mass Transfer Thermo-physical properties of water and ethylene glycol mixture based SiC nanofluids: an experimental investigation. Int. J. Heat Mass Transf.. 2016;101:412-417.
[Google Scholar]

[31] Lu W.Q., Fan Q.M., . Study for the particle’s scale effect on some thermophysical properties of nanofluids by a simplified molecular dynamics method. Eng. Anal. Bound. Elem.. 2008;32(4):282-289.
[Google Scholar]

[32] Mahbubul I.M., Saidur R., Amalina M.A., . Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transfer. 2012;55(4):874-885.
[Google Scholar]

[33] Mahian O., Kianifar A., Kalogirou S.A., Pop I., Wongwises S., . A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transfer. 2013;57(2):582-594.
[Google Scholar]

[34] Mar T., Halelfadl S., Van Vaerenbergh S., Estell?? P., . Unexpected sharp peak in thermal conductivity of carbon nanotubes water-based nanofluids. Int. Commun. Heat Mass Transfer. 2015;66:80-83.
[Google Scholar]

[35] Masoumi N., Sohrabi N., Behzadmehr A., . A new model for calculating the effective viscosity of nanofluids. J. Phys. D Appl. Phys.. 2009;42(5):55501.
[Google Scholar]

[36] Mena J.B., Ubices De Moraes A.A., Benito Y.R., Ribatski G., Parise J.A.R., . Extrapolation of Al₂O₃-water nanofluid viscosity for temperatures and volume concentrations beyond the range of validity of existing correlations. Appl. Therm. Eng.. 2013;51(1–2):1092-1097.
[Google Scholar]

[37] Mori Y., Ototake N., . On the viscosity of suspensions. Chem. Eng.. 1956;20(9):488-494.
[Google Scholar]

[38] Mukherjee S., Paria S., . Preparation and stability of nanofluids-a review. IOSR J. Mech. Civ. Eng.. 2013;9(2):63-69.
[Google Scholar]

[39] Munkhbayar B., Tanshen M.R., Jeoun J., Chung H., Jeong H., . Surfactant-free dispersion of silver nanoparticles into MWCNT-aqueous nanofluids prepared by one-step technique and their thermal characteristics. Ceram. Int.. 2013;39(6):6415-6425.
[Google Scholar]

[40] Murshed S.M.S., Estellé P., . A state of the art review on viscosity of nanofluids. Renew. Sustain. Energy Rev.. 2017;76(March):1134-1152.
[Google Scholar]

[41] Murshed S.M.S., Leong K.C., Yang C., . Thermophysical and electrokinetic properties of nanofluids – a critical review. Appl. Therm. Eng.. 2008;28(17–18):2109-2125.
[Google Scholar]

[42] Murshed S.M.S., Leong K.C., Yang C., . A combined model for the effective thermal conductivity of nanofluids. Appl. Therm. Eng.. 2009;29(11–12):2477-2483.
[Google Scholar]

[43] Nabeel Rashin M., Hemalatha J., . Viscosity studies on novel copper oxide-coconut oil nanofluid. Exp. Therm. Fluid Sci.. 2013;48:67-72.
[Google Scholar]

[44] Nabeel Rashin M., Hemalatha J., . Synthesis and viscosity studies of novel ecofriendly ZnO-coconut oil nanofluid. Exp. Therm. Fluid Sci.. 2013;51:312-318.
[Google Scholar]

[45] Nguyen C.T., Desgranges F., Galanis N., Roy G., Mar?? T., Boucher S., Angue Mintsa H., . Viscosity data for Al₂O₃-water nanofluid-hysteresis: is heat transfer enhancement using nanofluids reliable? Int. J. Therm. Sci.. 2008;47(2):103-111.
[Google Scholar]

[46] Nine M.J., Munkhbayar B., Rahman M.S., Chung H., Jeong H., . Highly productive synthesis process of well dispersed Cu2O and Cu/Cu2O nanoparticles and its thermal characterization. Mater. Chem. Phys.. 2013;141(2–3):636-642.
[Google Scholar]

[47] Nkurikiyimfura I., Wang Y., Pan Z., . Heat transfer enhancement by magnetic nanofluids – a review. Renew. Sustain. Energy Rev.. 2013;21:548-561.
[Google Scholar]

[48] Pastoriza-Gallego M.J., Lugo L., Legido J.L., Piñeiro M.M., . Thermal conductivity and viscosity measurements of ethylene glycol-based Al₂O₃ nanofluids. Nanoscale Res. Lett.. 2011;6(1):221.
[Google Scholar]

[49] Pastoriza-Gallego M.J., Casanova C., Legido J.L., Piñeiro M.M., . CuO in water nanofluid: Influence of particle size and polydispersity on volumetric behaviour and viscosity. Fluid Phase Equilib.. 2011;300(1–2):188-196.
[Google Scholar]

[50] Phillpot, S., Eastman, J.A., 2002. Mechanisms of heat flow in suspensions of nano-sized particles (nano fluids), 45, 2002, 855–863.

[51] Phuoc T.X., Massoudi M., . Experimental observations of the effects of shear rates and particle concentration on the viscosity of Fe2O3-deionized water nanofluids. Int. J. Therm. Sci.. 2009;48(7):1294-1301.
[Google Scholar]

[52] Prasher R., Bhattacharya P., Phelan P.E., . Thermal conductivity of nanoscale colloidal solutions (nanofluids) Phys. Rev. Lett.. 2005;94(2):3-6.
[Google Scholar]

[53] Prasher R., Bhattacharya P., Phelan P.E., . Brownian-motion-based convective-conductive model for the effective thermal conductivity of nanofluids. J. Heat Transfer. 2006;128(6):588.
[Google Scholar]

[54] Prasher R., Song D., Wang J., Phelan P., . Measurements of nanofluid viscosity and its implications for thermal applications. Appl. Phys. Lett.. 2006;89(13):67-70.
[Google Scholar]

[55] Raja M., Vijayan R., Dineshkumar P., Venkatesan M., . Review on nanofluids characterization, heat transfer characteristics and applications. Renew. Sustain. Energy Rev.. 2016;64:163-173.
[Google Scholar]

[56] Sheremet M.A., Pop I., Rahman M.M., . Three-dimensional natural convection in a porous enclosure filled with a nanofluid using Buongiorno’s mathematical model. Int. J. Heat Mass Transfer. 2015;82:396-405.
[Google Scholar]

[57] Shukla K.N., Koller T.M., Rausch M.H., Fröba A.P., . Effective thermal conductivity of nanofluids – a new model taking into consideration Brownian motion. Int. J. Heat Mass Transf.. 2016;99:532-540.
[Google Scholar]

[58] Singh R., Sanchez O., Ghosh S., Kadimcherla N., Sen S., Balasubramanian G., . Viscosity of magnetite-toluene nanofluids: dependence on temperature and nanoparticle concentration. Phys. Lett. Sect. A Gen. At. Solid State Phys.. 2015;379(40-41):2641-2644.
[Google Scholar]

[59] Sundar L.S., Singh M.K., Sousa A.C.M., . Enhanced heat transfer and friction factor of MWCNT-Fe₃O₄/water hybrid nanofluids. Int. Commun. Heat Mass Transfer. 2014;52:73-83.
[Google Scholar]

[60] Sundar L.S., Hortiguela M.J., Singh M.K., Sousa A.C.M., . Thermal conductivity and viscosity of water based nanodiamond (ND) nanofluids: an experimental study. Int. Commun. Heat Mass Transfer. 2016;76:245-255.
[Google Scholar]

[61] Syam Sundar L., Venkata Ramana E., Singh M.K., Sousa A.C.M., . Thermal conductivity and viscosity of stabilized ethylene glycol and water mixture Al2O3 nanofluids for heat transfer applications: An experimental study. Int. Commun. Heat Mass Transfer. 2014;56:86-95.
[Google Scholar]

[62] Toghraie D., Alempour S.M., Afrand M., . Experimental determination of viscosity of water based magnetite nanofluid for application in heating and cooling systems. J. Magn. Magn. Mater.. 2016;417:243-248.
[Google Scholar]

[63] Tso C.Y., Fu S.C., Chao C.Y.H., . A semi-Analytical model for the thermal conductivity of nanofluids and determination of the nanolayer thickness. Int. J. Heat Mass Transfer. 2014;70:202-214.
[Google Scholar]

[64] Wang X., Xu X., Choi S.U.S., . Thermal conductivity of nanoparticle – fluid mixture. J. Thermophys. Heat Transfer. 1999;13(4):474-480.
[Google Scholar]

[65] Wang B.X., Zhou L.P., Peng X.F., . A fractal model for predicting the effective thermal conductivity of liquid with suspension of nanoparticles. Int. J. Heat Mass Transfer. 2003;46(14):2665-2672.
[Google Scholar]

[66] Yang Y., Zhang Z.G., Grulke E.A., Anderson W.B., Wu G., . Heat transfer properties of nanoparticle-in-fluid dispersions (nanofluids) in laminar flow. Int. J. Heat Mass Transfer. 2005;48(6):1107-1116.
[Google Scholar]

[67] Yang J.-C., Li F., Zhou W.-W., He Y., Jiang B.-C., . Experimental investigation on the thermal conductivity and shear viscosity of viscoelastic-fluid-based nanofluids. Int. J. Heat Mass Transfer. 2012;55(11–12):3160-3166.
[Google Scholar]

[68] Yu C.-J., Richter A., Datta A., Durbin M., Dutta P., . Molecular layering in a liquid on a solid substrate: an X-ray reflectivity study. Phys. B Condens. Matter. 2000;283(1–3):27-31.
[Google Scholar]

[69] Zhai Y.L., Xia G.D., Liu X.F., Li Y.F., . Heat transfer enhancement of Al₂O₃-H₂O nanofluids flowing through a micro heat sink with complex structure. Int. Commun. Heat Mass Transfer. 2015;66:158-166.
[Google Scholar]

[70] Żyła G., Fal J., . Experimental studies on viscosity, thermal and electrical conductivity of aluminum nitride–ethylene glycol (AlN–EG) nanofluids. Thermochim. Acta. 2016;637:11-16.
[Google Scholar]

Predicting the effective viscosity of nanofluids based on the rheology of suspensions of solid particles

Abstract

Abstract

Nomenclature

Greek symbols

Subscripts

Abbreviation

1 Introduction

2 Theoretical models

2.1 Einstein model

2.2 Brinkman model

2.3 Batchelor model

2.4 Graham model

2.5 Wang et al. model

2.6 Avsec and Oblak model

2.7 Masoumi et al. model

3 Methodology

3.1 Experimental database

3.2 Factors consider in the new correlation

4 Description of the new correlation

4.1 Development of the model

4.2 The new correlation

5 Results and discussion

5.1 Statically analysis

5.2 Present model comparison with existing theoretical models

5.3 Effective parameters on the effective viscosity of nanofluid

5.3.1 Effect of particle size

5.3.2 Effect of temperature

5.3.3 Effect of volume concentration

5.3.4 Effect of nanoparticle material

5.3.5 Effect of particle shape

5.4 Comparison of dynamic and static parts

5.5 Particle size in micrometer

5.6 Non-Newtonian nanofluid

5.7 Viscosity and nanofluid stability

5.8 Hybrid nanofluids

6 Future works

7 Conclusions

Acknowledgment

Conflict of interest

References