Translate this page into:
Exponentiated generalized exponential Dagum distribution
⁎Corresponding author. sulemanstat@gmail.com (Suleman Nasiru), snasiru@uds.edu.gh (Suleman Nasiru),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this study, the exponentiated generalized exponential Dagum distribution has been proposed and studied. This family of distribution consists of a number of sub-models such as the exponentiated generalized Dagum distribution, Dagum distribution, Fisk distribution, Burr III distribution and exponentiated generalized exponential Burr III distribution among others. Statistical properties of the new family were also derived. Maximum likelihood estimators of the parameters of the distribution were developed and simulation studies performed to assess the properties of the estimators. Applications of the model was demonstrated to show its usefulness.
Keywords
Dagum
Quantile
Moment
Entropy
Reliability measure
Order statistics
1 Introduction
Identifying an appropriate distribution for modeling data sets is very important in statistical analysis. Knowing the appropriate distribution a particular data sets follow helps in making sound inference about the data. Because of this, barrage of techniques have been developed for modifying existing statistical distributions to make them more flexible in modeling data sets that arise in different fields of study. The Dagum distribution (Dagum, 1977) just like other existing statistical distributions has received much attention recently due to its usefulness in modeling of size distribution of personal income and reliability analysis among others. For an extensive review on the genesis and on empirical applications of the Dagum see (Kleiber and Kotz, 2003; Kleiber, 2008).
With the goal of increasing the flexibility of the Dagum distribution in modeling lifetime data, different modifications of the distribution have been proposed in literature recently and includes: Dagum-Poisson distribution (Oluyede et al., 2016), Mc-Dagum distribution (Oluyede and Rajasooriya, 2013), gamma-Dagum distribution (Oluyede et al., 2014), transmuted Dagum distribution (Elbatal and Aryal, 2015), exponentiated Kumaraswamy-Dagum distribution (Huang and Oluyede, 2014), extended Dagum distribution (Silva et al., 2015), beta-Dagum distribution (Domma and Condino, 2013), weighted Dagum distribution (Oluyede and Ye, 2014) and log-Dagum distribution (Domma and Perri, 2009).
In addition, other authors have studied the properties and methods of estimation of the parameters of the Dagum distribution. Shahzad and Asghar (2013) employed the TL-moments to estimate the parameters of the Dagum distribution. Dey et al. (2017) studied the properties and different methods of estimating the parameters of the Dagum distribution. Domma et al. (2011) estimated the Dagum distribution with censored sample using maximum likelihood estimation. In another study, Al-Zahrani (2016) proposed a reliability test plan to determine the termination time of the experiment for a given sample size, producer risk and termination number when the quantity of interest follows the Dagum distribution.
Thus, in this study a new extension of the Dagum distribution called the exponentiated generalized exponential Dagum distribution with tractable cumulative distribution function is proposed with the basic motivation of modeling lifetime data with both monotonic and non-monotonic failure rates, control skewness, kurtosis and tail variations. The rest of the paper is organized as follows: in Section 2, the cumulative distribution function, probability density function, survival function and hazard function of the new distribution were defined. In Section 3, some sub-models of the new distribution were presented. In Section 4, statistical properties of the new distribution were discussed. In Section 5, the parameters of the new distribution were estimated using maximum likelihood estimation and Monte Carlo simulation performed to assess the stability of the parameters. In Section 6, the applications of the new model was demonstrated using two data sets. Finally, the concluding remarks of the study was given in Section 7.
2 New model
Let T be a random variable with probability density function (PDF)
and let X be a continuous random variable with cumulative distribution function (CDF)
. Then the CDF of the exponentiated generalized exponential (EGE)-X family of distribution is defined as
For positive integers and c, a physical interpretation of the EGE-X family of distribution CDF is given as follows. Eq. (1) represents the CDF of the lifetime of a series-parallel system consisting of independent components with the CDF corresponding to the Lehman type II distribution. Given that a system is formed by independent component series subsystems and that each of the subsystems is made up of c independent parallel components. Suppose , for and , represents the lifetime of the component in the subsystem and X is the lifetime of the entire system. Then, we have and X has the CDF defined in Eq. (1).
Suppose
is the CDF of type I Dagum distribution, then the CDF of the exponentiated generalized exponential-Dagum distribution (EGEDD) is given by
The PDF of the EGEDD can be expressed in terms of the density function of the Dagum distribution as
For a real non-integer
, a series expansion for
, for
is
Applying the series expansion in Eq. (5) twice and the fact that
, implies that
Substituting Eq. (6) into Eq. (3) yields
Applying the series expansion again to gives us the expansion of the density as □
Eq. (4) revealed that the PDF of the EGEDD can be written as a linear combination of the Dagum distribution with different shape parameters. The expansion of the PDF is important in providing the mathematical properties of the EGEDD. The triple infinite series in Eq. (4) is convergent for all
and
. This can easily be verified using symbolic computational softwares such as MATHEMATICA, MAPLE and MATLAB. Fig. 1 displays different shapes of the PDF of the EGEDD for different parameter values. The survival function of this distribution is
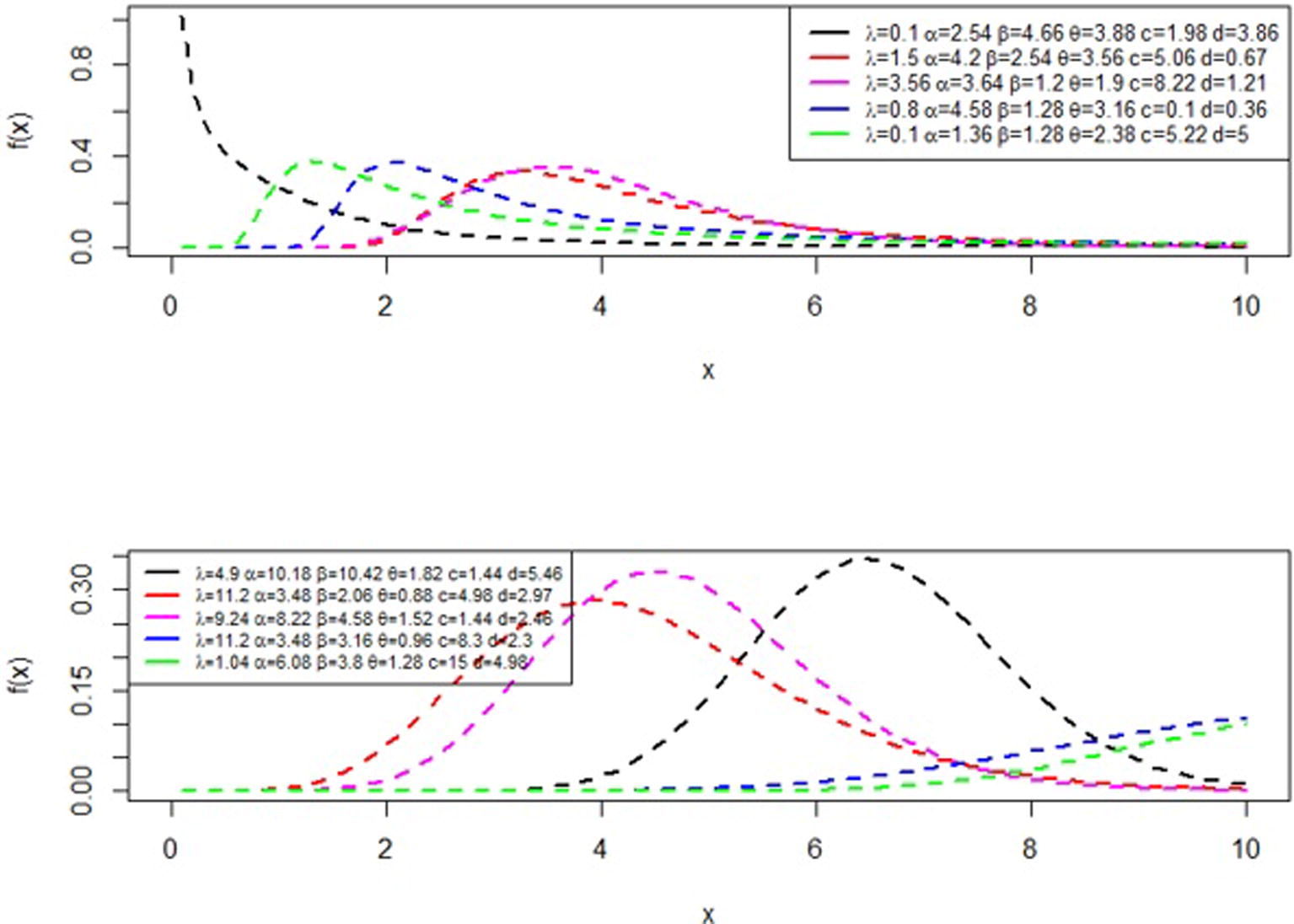
EGEDD density function.
The plots of the hazard function display various attractive shapes such as monotonically decreasing, monotonically increasing, upside down bathtub, bathtub and bathtub followed by upside down bathtub shapes for different combination of the values of the parameters. These features make the EGEDD suitable for modeling monotonic and non-monotonic failure rates that are more likely to be encountered in real life situation. Fig. 2 displays the various shapes of the hazard function.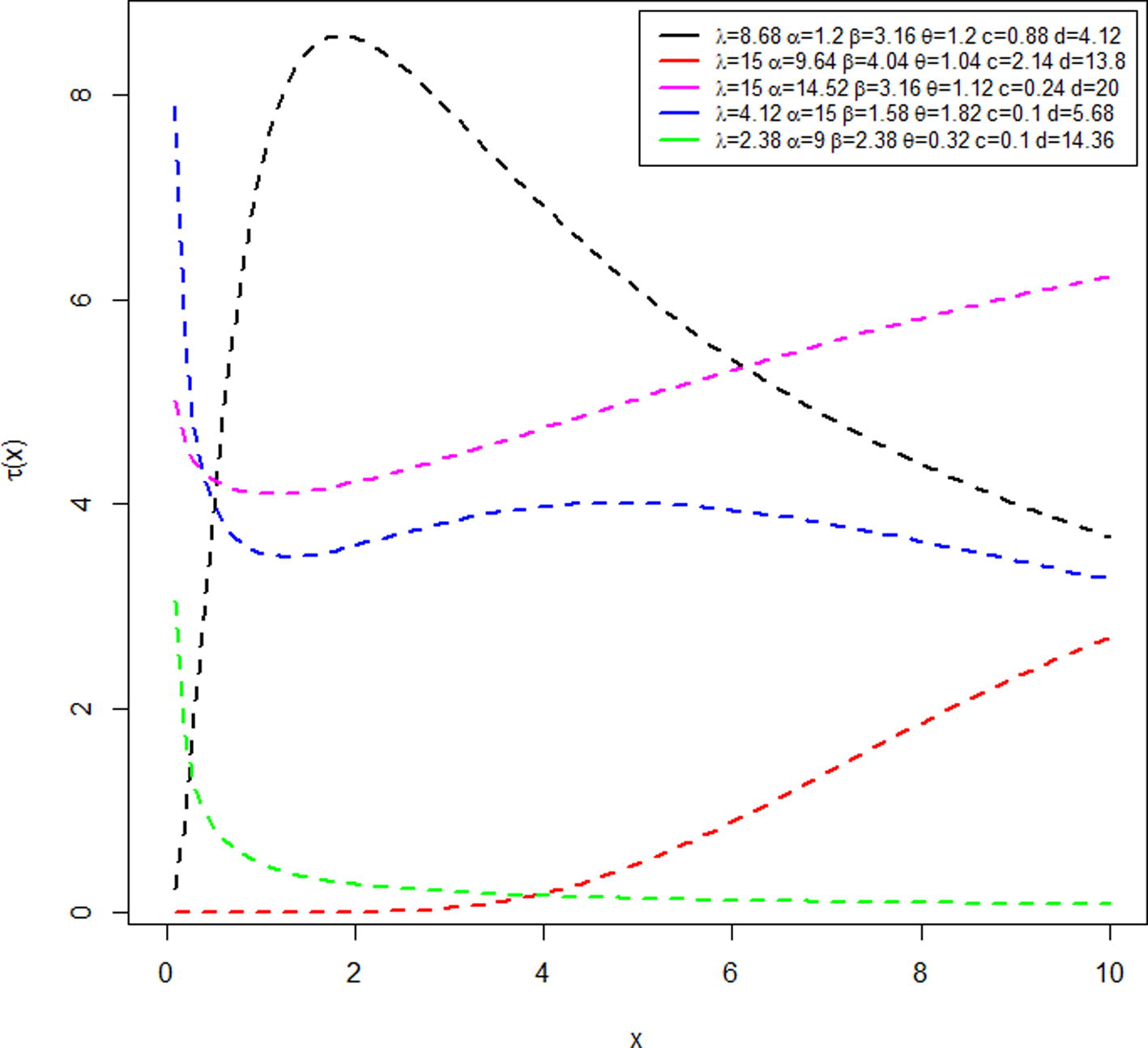
Plots of the EGEDD hazard function.
3 Sub-models
The EGEDD consists of a number of important sub-models that are widely used in lifetime modeling. These include: exponentiated generalized Dagum distribution (EGDD), Dagum distribution (DD), exponentiated generalized exponential Burr III distribution (EGEBD), Burr III distribution, exponentiated generalized Burr III distribution (EGBD), exponentiated generalized exponential Fisk distribution (EGEFD), exponentiated generalized Fisk distribution (EGFD) and Fisk distribution (FD). Table 1 displays a list of models that can be derived from the EGEDD.
Distribution
c
d
EGDD
1
c
d
DD
1
1
1
EGEBD
1
c
d
BD
1
1
1
1
EGBD
1
1
c
d
EGEFD
1
c
d
EGFD
1
1
c
d
FD
1
1
1
1
4 Statistical properties
In this section, various statistical properties of the EGEDD such as the quantile, moment, reliability measure, entropy and order statistics were derived.
4.1 Quantile function
The distribution of a random variable can be described using its quantile function. The quantile function is useful in computing the median, kurtosis and skewness of the distribution of a random variable.
The quantile function of the EGEDD for
is given by
By definition, the quantile function returns the value x such that
Thus
Letting in Eq. (10) and solving for using inverse transformation yields □
When and , we obtain the first quartile, the median and the third quartile of the EGEDD respectively.
4.2 Moment
It is imperative to derive the moments when a new distribution is proposed. They play a significant role in statistical analysis, particularly in applications. Moments are used in computing measures of central tendency, dispersion and shapes among others.
The
non-central moment of the EGEDD is given by
By definition □
The triple infinite series in Eq. (11) is convergent for all and .
4.3 Entropy
Entropy plays a vital role in science, engineering and probability theory, and has been used in various situations as a measure of variation of uncertainty of a random variable (Rényi, 1961). The Rényi entropy of a random X having the EGEDD is given by the following proposition.
If
, then the Rényi entropy is given by
The Rényi entropy (Rényi, 1961) is defined as
Using the same approach for expanding the density, Thus
Letting , when and when . Also, and . Hence where and .
The Rényi entropy tends to Shannon entropy as . It can easily be verified from standard calculus that the triple infinite series in Eq. (12) is convergent for all and .
4.4 Reliability
The estimation of reliability is vital in stress-strength models. If is the strength of a component and is the stress, the component fails when . Then the estimate of the reliability of the component R is .
If
and
, then the estimation of reliability R is given by
By definition □
The triple infinite series in Eq. (13) is convergent for all and .
4.5 Order statistics
Let
be a random sample from the EGEDD and
are order statistics obtained from the sample. Then the PDF,
, of the
order statistic
is given by
where
and
are the CDF and PDF of the EGEDD respectively, and
is the beta function. Since
for
, using the binomial series expansion of
, which is given by
we have
Therefore, substituting the CDF and PDF of the EGEDD into Eq. (14) yields
5 Parameter estimation
In this section, the maximum likelihood estimators of the unknown parameters of the EGEDD are derived and their finite sample properties assessed. Let
be a random sample of size n from the EGEDD. Let
, then the log-likelihood function is given by
Taking the first partial derivatives of the log-likelihood function in Eq. (16) with respect to the parameters
and d, we obtain the score functions as
The estimates for the parameters and d are obtained by equating the score functions to zero and solving the system of non-linear equations numerically. In order to construct confidence intervals for the parameters, the observed information matrix is used since the expected information matrix is complicated. The observed information matrix is given by where . The explicit expression for the elements of the observed information matrix are available upon request. When the usual regularity conditions are fulfilled and that the parameters are within the interior of the parameter space, but not on the boundary, converges in distribution to , where is the expected information matrix. The asymptotic behavior is still valid when is replaced by the observed information matrix evaluated at . The asymptotic multivariate normal distribution can be used to construct an approximate two-sided confidence intervals for the model parameters, where is the significance level.
5.1 Monte Carlo simulation
In this sub-section, a simulation study is carried out to examine the average bias (AB) and root mean square error (RMSE) of the maximum likelihood estimators of the parameters of the EGEDD. The experiment was conduct through various simulations for different sample sizes and different parameter values. The quantile function given in Eq. (9) was used to generate random samples from the EGEDD. The simulation experiment was repeated for
times each with sample sizes
and parameter values
and
. The AB and the RMSE of the parameters were computed using the following relations:
and
where
. Table 2 presents the AB and RMSE values of the parameters
and d for different sample sizes. From the results, it can be seen that as the sample size increases, the RMSE decay towards zero. In addition, the AB decreases as the sample size increases. Hence, the maximum likelihood estimates and their asymptotic properties can be used for constructing confidence intervals even for reasonably small sample size.
I
II
Parameter
n
AB
RMSE
AB
RMSE
25
13.724
58.702
17.105
98.897
50
0.681
12.444
2.634
32.134
75
0.268
0.980
1.124
27.832
100
0.204
0.891
0.286
1.249
200
0.105
0.365
0.187
0.507
25
105.848
532.196
40.717
211.657
50
3.892
59.077
7.484
96.125
75
0.806
7.613
1.728
45.595
100
0.195
2.625
0.332
3.204
200
-0.031
1.268
0.097
0.354
25
0.763
2.226
0.030
1.703
50
1.039
2.960
0.198
1.989
75
0.891
2.571
0.258
2.138
100
0.759
2.205
0.259
1.727
200
0.382
1.089
0.031
1.175
25
-0.041
0.263
0.133
0.247
50
-0.090
0.221
0.059
0.158
75
-0.107
0.209
0.033
0.122
100
-0.109
0.197
0.017
0.110
200
-0.095
0.158
0.008
0.082
c
25
9.384
41.310
6.311
32.040
50
0.499
5.113
1.481
21.073
75
0.254
0.904
0.270
2.625
100
0.207
0.716
0.222
0.658
200
0.106
0.323
0.143
0.299
d
25
3.668
0.676
1.950
0.376
50
0.233
0.062
0.518
0.084
75
0.155
0.204
0.395
0.064
100
0.114
0.011
0.471
0.053
200
0.074
0.008
0.299
0.044
6 Applications
In this section, the application of the EGEDD is provided by fitting the distribution to two real data sets. The goodness-of-fit of the EGEDD is compared with that of its sub-models, the exponentiated Kumaraswamy Dagum (EKD) distribution and the Mc-Dagum (McD) distribution using Kolmogorov-Smirnov (K-S) statistic and Cramér-von (W∗) misses distance values, as well as Akaike information criterion (AIC), corrected Akaike information criterion (AICc) and Bayesian information criterion (BIC). The maximum likelihood estimates of the fitted model parameters were computed by maximizing the log-likelihood function via the subroutine mle2 using the bbmle package in R (Bolker, 2014). This was done using a wide range of initial values. The process often leads to more than one maximum, thus in such situation, the maximum likelihood estimates corresponding to the largest maxima is chosen. In few cases were no maximum is identified for the selected initial values, new sets of initial values are employed in order to get a maximum. The PDF of EKD distribution is given by
6.1 Yarn data
The data in Table 3 represents the time to failure of a 100 cm polyster/viscose yarn subjected to
strain level in textile experiment in order to assess the tensile fatigue characteristics of the yarn. The data set can be found in Quesenberry and Kent (1982) and Pal and Tiensuwan (2014).
86
146
251
653
98
249
400
292
131
169
175
176
76
264
15
364
195
262
88
264
157
220
42
321
180
198
38
20
61
121
282
224
149
180
325
250
196
90
229
166
38
337
65
151
341
40
40
135
597
246
211
180
93
315
353
571
124
279
81
186
497
182
423
185
229
400
338
290
398
71
246
185
188
568
55
55
61
244
20
289
393
396
203
829
239
236
286
194
277
143
198
264
105
203
124
137
135
350
193
188
The maximum likelihood estimates of the parameters of the fitted models with their corresponding standard errors in brackets are given in Table 4. All the parameters of the EGEDD are significant at the
significance level. The EGEDD provides a better fit to the yarn data than its sub-models, the McD distribution and the EKD distribution. From Table 5, the EGEDD has the highest log-likelihood and the smallest K-S, W∗, AIC, AICc, and BIC values compared to the other models. Although the EGEDD provides the best fit to the data, the McD distribution, EGEBD and EGEFD are alternatively good models for the data since their measures of fit values are close to that of the EGEDD.
Model
EGEDD
0.026
75.310
0.017
3.513
45.692
0.090
(0.007)
(0.007)
(0.005)
(0.631)
(0.036)
(0.011)
EGDD
1.992
10.480
4.733
75.487
0.223
(0.251)
(13.022)
(0.587)
(27.669)
(0.032)
DD
19.749
11.599
1.126
(10.814)
(5.008)
(0.069)
EGEBD
35.463
35.965
4.859
15.667
0.070
(0.271)
(0.120)
(0.666)
(2.714)
(0.011)
EGBD
24.801
4.196
73.9120
0.258
(15.068)
(1.808)
(22.832)
(0.112)
EGEFD
20.662
34.477
5.217
16.438
0.65
(2.365)
(0.278)
(0.578)
(2.708)
(0.009)
EGFD
10.537
5.239
21.341
0.140
(1.115)
(0.429)
(4.089)
(0.015)
McD
0.027
0.600
98.780
0.333
25.042
46.276
EKD
46.109
39.413
5.188
0.203
31.169
(1.295)
(5.006)
(0.961)
(0.040)
(11.023)
Model
AIC
AICc
BIC
K-S
W∗
EGEDD
−628.170
1268.336
1269.553
1283.967
0.124
0.249
EGDD
−653.070
1316.137
1317.040
1329.163
0.172
0.948
DD
−649.260
1304.517
1304.938
1312.333
0.164
0.821
EGEBD
−630.870
1271.745
1272.648
1284.771
0.136
0.340
EGBD
−653.030
1314.056
1314.694
1324.447
0.174
0.969
EGEFD
−630.760
1271.523
1272.426
1284.549
0.139
0.339
EGFD
−666.880
1341.757
1342.395
1352.177
0.236
0.760
McD
−628.200
1268.399
1269.616
1284.030
0.128
0.285
EKD
−653.960
1317.913
1318.816
1330.938
0.178
0.985
In order to make a complete statistical inference about a model, it is imperative to reduce the number of parameters of the model and examine how that affects the ability of the reduce model to fit the data. The likelihood ratio test (LRT) is therefore performed to compare the EGEDD with its sub-models. The LRT statistic and their corresponding P-values in Table 6 revealed that the EGEDD provides a good fit than its sub-models.
Model
Hypotheses
LRT
P-values
EGDD
vs
is false
49.801
DD
vs
is false
42.181
EGEBD
vs
is false
5.409
0.020
EGBD
vs
is false
49.721
EGEFD
vs
is false
5.187
0.023
EGFD
vs
is false
77.421
The asymptotic variance-covariance matrix for the estimated parameters of the EGEDD for the yarn data is given by
Thus, the approximate confidence interval for the parameters and d of the EGEDD are and respectively.
6.2 Appliances data
The appliances data was obtained from (Lawless, 1982). The data set consists of failure times for 36 appliances subjected to an automatic life test. The data set are given in Table 7.
11
35
49
170
329
381
708
958
1062
1167
1594
1925
1990
2223
2327
2400
2451
2471
2551
2565
2568
2694
2702
2761
2831
3034
3059
3112
3214
3478
3504
4329
6367
6976
7846
13403
Table 8 provides the maximum likelihood estimates of the parameters with their corresponding standard errors in brackets for the models fitted to the appliances data. From Table 8, all the parameters of the EGED are significant at the
significance level.
Model
EGEDD
0.001
27.198
4.560
2.838
20.866
0.070
(0.001)
(0.847)
(0.123)
(0.010)
(0.003)
EGDD
7.977
0.404
3.570
15.862
0.130
(0.651)
(0.044)
(0.391)
(5.196)
(0.021)
DD
0.018
1495.519
0.509
(0.0062)
(0.056)
EGEBD
25.705
14.152
3.412
8.332
0.047
(0.514)
(0.110)
(0.247)
(1.934)
(0.009)
EGBD
9.504
3.392
11.226
0.129
(3.205)
(0.388)
(3.440)
(0.022)
EGEFD
13.048
27.555
3.561
9.084
0.047
(1.817)
(0.071)
(0.392)
(2.186)
(0.009)
EGFD
8.4843
3.429
16.533
0.143
(1.550)
(0.711)
(5.833)
(0.034)
McD
1.427
3.455
1.275
10.505
0.064
500.556
(0.092)
(0.212)
(6.875)
(56.906)
(0.012)
(6.796)
EKD
5.562
12.683
3.716
0.128
11.609
(1.517)
(2.158)
(0.755)
(0.029)
(3.922)
From Table 9, it is clear that the EGEDD provides a better fit to the appliances data than the other models. It has the highest log-likelihood and the smallest K-S, W∗, AIC, AICc and BIC values. Alternatively, the EGEBD and EGEFD are good models since their goodness-of-fit measures are close to that of the EGEDD.
Model
AIC
AICc
BIC
K-S
W∗
EGEDD
−328.870
669.740
670.957
679.241
0.253
0.569
EGDD
−340.910
691.818
692.721
699.736
0.264
0.882
DD
−339.610
685.225
685.646
689.976
0.257
0.858
EGEBD
−330.910
671.823
672.726
679.741
0.272
0.634
EGBD
−341.520
691.037
691.675
697.371
0.268
0.881
EGEFD
−330.730
671.460
672.363
679.377
0.269
0.625
EGFD
−341.030
690.054
690.692
696.388
0.269
0.907
McD
−356.480
724.955
728.950
734.456
0.347
0.986
EKD
−341.650
693.295
694.198
701.213
0.269
0.925
The LRT was performed in order to compare the EGEDD with its sub-models. From Table 10, the LRT revealed that the EGEDD provides a better fit to the appliances data than its sub-models. Although the LRT favored the EGEFD at the
level of significance, the EGEDD was better than it at the
level of significance.
Model
Hypotheses
LRT
P-values
EGDD
vs
is false
24.078
DD
vs
is false
21.486
EGEBD
vs
is false
4.084
0.043
EGBD
vs
is false
25.297
EGEFD
vs
is false
3.720
0.054
EGFD
vs
is false
24.315
The asymptotic variance-covariance matrix for the estimated parameters of the EGEDD for the appliances data is given by
Thus, the approximate confidence interval for the parameters and d of the EGEDD are and respectively.
7 Conclusion
This study proposed and presented results on the statistical properties of the EGEDD. The EGEDD contains a number of sub-models with potential applications to a wide area of probability and statistics. Statistical properties such as the quantile function, moment, entropy, reliability and order statistic were derived. The estimation of the parameters of the model was approached using maximum likelihood estimation and the applications of the EGEDD was also demonstrated to show its usefulness.
Addendum
During the review process, one of the reviewers referred us to a work done by Rezaei et al. (2017), we found out that our proposed CDF for the EGE-X family of distribution possess exactly analogous form with the CDF of their generalized exponentiated class of distribution. However, we conducted our research without any prior knowledge of their work. The content of that paper, is however different from ours.
Competing interests
The authors declare that there is no conflict of interest regarding the publications of this article.
Acknowledgment
The first author wishes to thank the African Union for supporting his research at the Pan African University, Institute for Basic Sciences, Technology and Innovation. The authors wish to thank the Editor-in-chief and the anonymous reviewers for their valuable comments and suggestions that have greatly improved the content of this manuscript.
References
- Reliability test plan based on Dagum distribution. Int. J. Adv. Stat. Prob.. 2016;4(1):75-78.
- [Google Scholar]
- Bolker, B., 2014. Tools for general maximum likelihood estimation. r development core team.
- New model of personal income distribution specification and estimation. Econ. Appl.. 1977;30(3):413-437.
- [Google Scholar]
- Dagum distribution: properties and different methods of estimation. Int. J. Stat. Prob.. 2017;6(2):74-92.
- [Google Scholar]
- The beta-Dagum distribution: definition and properties. Commun. Stat.-Theory Methods. 2013;42(22):4070-4090.
- [Google Scholar]
- Maximum likelihood estimation in Dagum distribution with censored sample. J. Appl. Stat.. 2011;38(12):2971-2985.
- [Google Scholar]
- Some developments on the log-Dagum distribution. Stat. Methods Appl.. 2009;18:205-209.
- [Google Scholar]
- Exponentiated Kumaraswamy-Dagum distribution with applications to income and lifetime data. J. Stat. Distrib. Appl.. 2014;1(8):1-20.
- [Google Scholar]
- A guide to the Dagum distribution. In: Duangkamon C., ed. Modeling Income Distributions and Lorenz Curves Series: Economics Studies in Inequality, Social Exclusion and Well-being. New York: Springer; 2008. vol. 5
- [Google Scholar]
- Statistical Size Distribution in Economics and Actuarial Sciences. John Wiley and Sons; 2003.
- Statistical Models and Methods for Lifetime Data. New York: Wiley; 1982.
- A new generalized Dagum distribution with applications to income and lifetime data. J. Stat. Econ. Methods. 2014;3(2):125-151.
- [Google Scholar]
- The Dagum-Poisson distribution: model, properties and application. Electron. J. Appl. Stat. Anal.. 2016;9(1):169-197.
- [Google Scholar]
- The Mc-Dagum distribution and its statistical properties with applications. Asian J. Math. Appl.. 2013;44:1-16.
- [Google Scholar]
- The beta transmuted exponentiated Weibull geometric distribution. Austrian J. Stat.. 2014;43(2):133-149.
- [Google Scholar]
- Selecting among probability distributions used in reliability. Technometrics. 1982;24(1):59-65.
- [Google Scholar]
- Rényi, A., 1961. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability. University of California Press, Berkeley, CA, pp. 547–561.
- A new exponentiated class of distributions: properties and applications. Commun. Stat.-Theory Methods. 2017;46:6054-6073.
- [Google Scholar]
- Comparing TL-moments, L-moments and conventional moments of Dagum distribution by simulated data. Revista Colombiana de Estadistica. 2013;36(1):79-93.
- [Google Scholar]
- The extended Dagum distribution:properties and applications. J. Data Sci.. 2015;13:53-72.
- [Google Scholar]
Appendix A
Appendix
R Algorithm
### EGEDD PDF
EGEDD_PDF<-function(x,alpha,lambda,beta,theta,c,d){
A<-(1+alpha*(x∧(-theta)))∧(-beta-1)
B<-1-(1+alpha*(x∧(-theta)))∧(-beta)
fxn<-lambda*alpha*beta*theta*c*d*(x∧(-theta-1))*A*(B∧(d-1))*
((1-(B∧d))∧(c-1))*((1-(1-(B∧d))∧c)∧(lambda-1))
return(fxn)
}
### EGEDD CDF
EGEDD_CDF<-function(x,alpha, lambda, beta,theta,c,d){
fxn<-1-(1-(1-(1-(1+alpha*(x∧(-theta)))∧(-beta))∧d)∧c)∧lambda
return(fxn)
}
### EGEDD survival function
EGEDD_Surv<-function(x,alpha,lambda,beta,theta,c,d){
fxn<-(1-(1-(1-(1+alpha*(x∧(-theta)))∧(-beta))∧d)∧c)∧lambda
return(fxn)
}
### EGEDD Hazard function
EGEDD_Hazard<-function(x,alpha,lambda,beta,theta,c,d){
PDF<-EGEDD_PDF(x,alpha,lambda,beta,theta,c,d)
Survival<-EGEDD_Surv(x,alpha,lambda,beta,theta,c,d)
hazard<-PDF/Survival
return(hazard)
}
### EGEDD Quantile function
Quantile<-function(alpha,lambda,beta,theta,c,d,u){
A<-(1-u)∧(1/lambda)
B<-(1-A)∧(1/c)
C<-(1-B)∧(1/d)
D<-(1-C)∧(-1/beta)
result<-((1/alpha)*(D-1))∧(-1/theta)
return(result)
}
### EGEDD Moment
EGEDD_Moment<-function(alpha,lambda,beta,theta,c,d){
func<-function(x,alpha,lambda,beta,theta,c,d,r){
(x∧r)*(EGEDD_PDF(x,alpha,lambda,beta,theta,c,d))}
results<-integrate(func,lower=0,upper=Inf,subdivisions=10000,
alpha=alpha,lambda=lambda,beta=beta,theta=theta,c=c,d=d,r=r)
return(results$value)
}
### Negative Log-likelihood function of EGEDD
EGEDD_LL<-function(alpha,lambda,beta,theta,c,d){
A<-(1+alpha*(x∧(-theta)))∧(-beta-1)
B<-1-(1+alpha*(x∧(-theta)))∧(-beta)
fxn<- -sum(log(lambda*alpha*beta*theta*c*d*(x∧(-theta-1))*A*(B∧(d-1))*
((1-(B∧d))∧(c-1))*((1-(1-(B∧d))∧c)∧(lambda-1))))
return(fxn)
}
### Fitting EGEDD to Real Data Set
library(bbmle)
fit<-mle2(EGEDD_LL, start=list alpha=alpha,lambda=lambda,beta=beta,
theta=theta,c=c,d=d),method=‘‘BFGS",data=list(x))
summary(fit)
### Computing the variance-covariance matrix
vcov(fit)







