Translate this page into:
Numerical solution of thin plates problem via differential quadrature method using G-spline
⁎Corresponding author. uhm@sc.nahrainuniv.edu.iq (Osama H. Mohammed)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this article the numerical solution of thin plates problem is introduced by using the differential quadrature method together with Chebyshev Gauss Lobatto sampling points for modeling the vibration of a square thin plate.
The explicit formula of the weighting coefficients for approximation of derivatives is utilized with the aid of the G-spline interpolation function.
A numerical example is presented and the results that have been obtained are compared with the existing methods in order to illustrate the validity and accuracy of the proposed approach.
Keywords
Differential quadrature method
Hermite-Birkhoff problem (HB-problem)
G-spline interpolation
Chebyshev Gauss Lobatto points
1 Introduction
Bellman and Casti was proposed a numerical method which is so called differential quadrature (DQ) for evaluating the derivatives of sufficiently smooth function, (Bellman and Casti, 1971). Their basic idea came from the well-known approach Gauss Quadrature for calculating the integral numerically.
Evaluating the derivatives of different orders of a sufficiently smooth function can be considered as an extension which is give rise to DQ (Bellman and Casti, 1971; Jalaal et al., 2011), where the derivatives of a smooth function are approximated with weighting sum of function values at a group of so called sampling points or nodes (Zong and Zhang, 2009).
Bellman and his co-authors presented two methods for calculating the weighting coefficients which is the key procedure in the DQ applications (Shu, 2000).
Differential Quadrature (DQ) aroused many authors and because of that, its applications rapidly developed, (Quan and Chang, 1989; Shu and Richards, 1992; Shu and Xue, 1997; Shu and Wu, 2007; Korkmaz and Dag, 2008; Jiwari et al., 2012; Pekmen and Tezer-Sezgin, 2012; Ragb et al., 2014; Jiwari, 2015; Eftekhari, 2015; Shamani et al., 2015; Ghasemi et al., 2016; Mittal and Dahiyah, 2016, 2017; Ghasemi, 2017; Thoudam, 2017; Shamani and Aghdam, 2017a,b; Shamani and Aghdam, 2018).
A comprehensive review of the differential quadrature method has been given by Bert and Malik (1996). This paper employs function approximation theory using G-spline interpolation to formulate DQ.
Nearly 71 years ago, I.J. Schoenberg (1968) introduced the subject of “spline function” since that time splines may be considered as an important tool in different branches of mathematics such as approximation theory, numerical analysis, numerical treatment of ordinary, integral, partial differential equations, statistics, etc. There are several types of splines appeared in literature given by Deboor (1978), Powell (1981) and Stephen (2002).
Among these types of spline the so called G-spline interpolation which is necessary to the work of this paper, was initially presented by Schoenberg (1968). Schoenberg used the term “G-spline” instead of generalized splines because the natural spline term “generalized spline” describes an extension of another type of spline.
The G-spline is used to interpolate the HB-data (problem), the data in this problem are the values of the function and its derivatives but without Hermite’s condition that the only consecutives be used at each node. Further, Schoenberg (1968) define G-spline as smooth piecewise polynomials, where the smoothness is governed by the incidence matrix, and then he proved that G-splines, satisfies the ”minimum norm property”, which is used for the optimality of the G-spline function, that is defined mathematically by the following inequality:
2 The G-spline interpolation function:
I.J. Schoenberg (1968) proposed a tool in order to specify the HB-problem or the interpolatory condition:
and let
be the maximum order of the derivatives to be specified at the nodes. Define an incidence matrix E, by:
Let
be prescribed real numbers for each
, then the HB-problem is to find
,such that:
The G-spline interpolant of order mto f can be given in terms of the fundamental G-spline functions
, which is described in detail in Schoenberg (1968) by:
2.1 Approximation of linear functional with the sense of G-spline formula
Let I = [a, b] be a finite interval containing the node points and let us consider a linear functional:
of the form:
Schoenberg (1968) states two procedures to determine one of them is Sard procedure, which can be summarized by the following theorem:
2.1.1 Theorem (Schoenberg, 1968)
If and the HB-problem (4) is m-poised, then Sard’s best approximation (8) to of order m is obtained by operating with on both sides of the G-spline interpolation formula (6) of order m.
In other words, the coefficients are given by:
, where are the fundamental functions of (6).
Details can be found in Schoenberg (1968) for the generation of these fundamentals G-splines.
3 The G-spline interpolation-based differential quadrature method
Suppose that the function is sufficiently smooth on the interval , and consider an m-poised HB- problem:
, on the N distinct nodes:
.
Based on differential Quadrature, we have
3.1 Computation of the weighting coefficients for the first and second order derivatives using G-spline interpolation formula
To find the weights
and
,we need to consider an m-poised HB-problem to approximate the function. Our purpose is to construct a polynomial of x, which is of the form
4 Analysis of differential quadrature of thin plates
In this section, the implementation of the G-spline interpolation-based DQM will be illustrated for thin plates problem.
4.1 The controlling equations and boundary conditions
The non-dimensional controlling equations for the deflection, free vibration and buckling for a plate may be written as Shu (2000):
Plate deflection
There are three basic boundary conditions, for free vibration analysis, these boundary conditions are:
Simply supported edge (SS)
4.2 Numerical discretization of the problem
The domain of computation for a rectangular plate is
and for a numerical calculation, the mesh generation will be given as:
Eqs. (29)–(31) can be put in matrix form and the solution of these matrix forms can be calculated using standard solvers such as QR-algorithm.
4.3 Direct substitution of boundary conditions into discrete controlling equation
The derivatives that appeared in the boundary conditions must also discretize by the DQM and as follows:
Obviously, Eq. (32) can be easily substituted into Eq. (30). However, Eqs. (33)–(36) cannot be directly substituted into Eq. (30).
Using the direct approach given in Shu (2000), Eqs. (33) and (34) can be coupled to give two solutions
and
, where
and
represent the minimum partial order derivatives of Wwith respect to X at
and
respectively, which are located at the grid points shown by the symbol
in Fig. 1
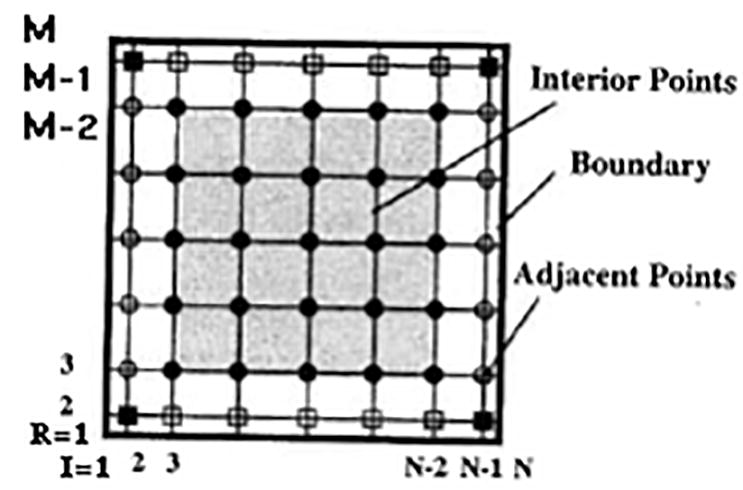
Description of the points for a rectangular plate.
In a similar way, Eqs. (35) and (36) can be coupled to give the solutions
and
where
and
represent the minimum partial order derivatives of W with respect to Y at
and
respectively, which are located at the net points shown by the symbol
in Fig. 1,
For the points near the four corners shown by the symbol
in Fig. 1, the four Eqs. (33)–(36) have to be coupled in order to give the following four solutions:
Eq. (45) gives a system of algebraic equations with unknowns.
5 The free vibration analysis of square plates via G-spline based differential quadrature method
In this section the free vibration analysis of square plates as given in Eq. (30) with will be solved numerically using the proposed approach given in section four. Two different sets of HB- problems have been considered in order to find the solution of such problems as follows:
Case1:
To construct the approximate solution via G-spline-based differential quadrature method an m-poised HB-problem must be chosen.
In this case we shall take a 5-poised HB- problem given for X and Y respectively by the sets
with the node points given by Eqs. (27) and (28) taking
and
. First,apply the G-spline interpolation-based DQM for the simply supported simply supported simply supported simply supported (SS-SS-SS-SS) boundary conditions, and secondly for the clamped clamped clamped clamped (C-C-C-C) boundary conditions. The natural low of frequency of the (SS-SS-SS-SS) and (C-C-C-C) boundary conditions will be given in Table 1.
Boundary conditions
(DQM), M = N = 6
(Shu, 2000), M = N = 6
SS-SS-SS-SS
19.0665
19.0970
C-C-C-C
36.4037
36.4441
The fundamental G-spline functions and are given in Appendix A.
Case 2:
In this case we shall consider another 5-poised HB sets for X and Y respectively given by:
with the node points given by Eqs. (27) and (28) with
and
, first, apply the G-spline interpolation-based DQM for the (SS-SS-SS-SS) boundary conditions and (C-C-C-C) boundary conditions. The natural low frequency for (SS-SS-SS-SS) and (C-C-C-C) boundary conditions will be given in Table 2.
Boundary conditions
(DQM), M = N = 6
(Shu, 2000), M = N = 6
SS-SS-SS-SS
19.1797
19.0970
C-C-C-C
36.9222
36.4441
The fundamental G-spline functions and are given in Appendix B.
6 Conclusions
It is clear that the G-spline-based differential quadrature can be considered as a generalization to the usual differential quadrature method. Also, from Tables 1 and 2 one can conclude that G-spline based differential quadrature gave accurate results, although a small number of node points have been introduced.
Acknowledgements
Authors are very grateful to the reviewers for carefully reading the paper and for their comments and suggestions which have improved the paper.
References
- Differential quadrature and longterm integration. J. Math. Anal. Appl.. 1971;34:235-238.
- [Google Scholar]
- Differential quadrature method in computational mechanics: a review. Appl. Mech. Rev.. 1996;49:1-28.
- [Google Scholar]
- A Practical Guide to Splines. New York Inc: Springer-Verlag; 1978.
- A note on mathematical treatment of the Dirac-delta function in the differential quadrature bending and forced vibration analysis of beams and rectangular plates subjected to concentrated loads. Appl. Math. Model.. 2015;39(20):6223-6242.
- [Google Scholar]
- An efficient approach to study the pulsatile blood flow in femoral and coronary arteries by differential Quadrature Method. Phys. A. 2016;443:406-414.
- [Google Scholar]
- High order approximations using spline-based differential quadrature method: implementation to the multi-dimensional PDEs. Appl. Math. Model. 2017
- [CrossRef] [Google Scholar]
- Numerical simulation of electric field in complex geometries for different electrode arrangements using meshless local MQ-DQ method. J. Electrostat. 2011:1-8. URL:www.elsevier.com/locate/elstat
- [Google Scholar]
- Numerical simulation of two-dimensional sine-Gordon solitons by differential quadrature method. Comput. Phys. Commun.. 2012;183:600-616.
- [Google Scholar]
- Lagrange interpolation and modified cubic B-spline differential quadrature methods for solving hyperbolic partial differential equations with Dirichelet and Neumann boundary conditions. Comput. Phys. Commun. 2015
- [CrossRef] [Google Scholar]
- A differential quadrature algorithm for simulations of nonlinear Schrödinger equation. Comput. Math. Appl.. 2008;56:2222-2234. URL:www.elsevier.com/locate/camwa
- [Google Scholar]
- A study of quintic B-spline based differential quadrature method for a class of semi-linear Fisher-Kolmogorov equations. Alexandria Eng. J.. 2016;55:2893-2899.
- [Google Scholar]
- Numerical simulation of three-dimensional telegraphic equation using cubic B-spline differential quadrature method. Appl. Math. Comput.. 2017;313:442-452.
- [Google Scholar]
- Differential quadrature solution of nonlinear Klein-Gordon and sine-Gordon equations. Comput. Phys. Commun.. 2012;183(8):1702-1713.
- [Google Scholar]
- Approximation Theory and Methods. Cambridge University Press; 1981.
- Quan, J.R., Chang C.T., 1989. New insights in solving distributed system equations by the quadrature methods. II. Numerical Experiment, 13,9. pp. 1017–1024.
- Analysis of composite plates using moving least squares differential quadrature method. Appl. Math. Comput.. 2014;238:225-236.
- [Google Scholar]
- Differential Quadrature and Its Application in Engineering. Springer-Verlag, London Limited; 2000.
- Application of generalized differential quadrature to solve two dimensional incompressible Navier Stokes equations. Int. J. Numer. Methods Fluids. 1992;15:791-798.
- [Google Scholar]
- Explicit computation of weighting coefficients in the harmonic differential quadrature. J. Sound Vib.. 1997;204(3):549-555.
- [Google Scholar]
- Integrated radial basis functions-based differential quadrature method and its performance. Int. J. Numer. Methods Fluids. 2007;53:969-984.
- [Google Scholar]
- On the free vibration characteristics of postbuckled third-order shear deformable FGM nanobeams including surface effects. Compos. Struct.. 2015;121:377-385.
- [Google Scholar]
- Nonlinear vibrations of pre- and post-buckled lipid supramolecular micro/nano-tubules via nonlocal strain gradient elasticity theory. J. Biomech.. 2017;65:49-60.
- [Google Scholar]
- Size-dependent nonlinear bending of micro/nano-beams made of nanoporous biomaterials including a refined truncated cube cell. Phys. Lett. A. 2017;381:3818-3830.
- [Google Scholar]
- Nonlocal strain gradient shell model for axial buckling and postbuckling analysis of magneto-electro-elastic composite nanoshells. Compos. Part B: Eng. 2018:258-274.
- [Google Scholar]
- On the Ahlberg-Nilson extension of spline interpolation: the G-spline and their optimal properties. J. Math. Anal. Appl.. 1968;21:207-231.
- [Google Scholar]
- Stephen, W., 2002. An introduction to the mathematics and construction of splines. Addix software consultancy limited. Veraion 1.6.
- Numerical solutions of coupled Klein Gordon Zakharov equations by quintic B-spline differential quadrature method. Appl. Math. Comput.. 2017;307:50-61.
- [Google Scholar]
- Advanced Differential Quadrature Methods. Taylor & Francis Group LLC; 2009.
Appendix A
where
Appendix B







