Translate this page into:
Generalizing the meaning of derivatives and integrals of any order differential equations by fuzzy-order derivatives and fuzzy-order integrals
⁎Corresponding author. israr_ahmad.niz@cas.edu.om (Israr Ahmad),
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
This paper develops the correlation between fuzzy numbers and order of differential equations and overcomes the limitation in the existence of fractional order in the formulation of equation. In the view of fractional calculus, a new logic called fuzzy order by generalizing the meaning of derivatives and integrals of any order as fuzzy-order derivatives and fuzzy-order integral. We discuss , where is derivative of order α and α may be a triangular fuzzy number or trapezoidal fuzzy number, and propose to rewrite , when and (where N is the set of natural numbers) and rewrite Riemann-Liouville integral, Riemann-Liouville derivative and Caputo fractional derivatives with respect to this new logic of fuzzy order. The proposed approach also covers multi cases, where the order is either integer or fractional. At the end, three numerical examples are presented to demonstrate the application of new logic, when the order of derivatives and integrals are given as triangular fuzzy numbers. These include time fractional heat equation represented as a time fuzzy-order heat equation and the time-fractional diffusion wave equation represented as a time-fuzzy-order diffusion wave equation.
Keywords
Fractional calculus
Fuzzy numbers
Riemann-Liouville fuzzy definitions
Caputo fuzzy definitions
1 Introduction
In this modern evolving world especially in the field of applied sciences and engineering, many continuous changes are observed and such changes require a thorough understanding of the nature and characteristics of the situation where undeniably certainty as well uncertainty prevail. Handling the issue of uncertainty in our daily lives is not just a matter of choosing a method or providing an answer to a question, but it is closely linked to the accuracy of the question itself and the consequences brought about by the question. These consequences could be the performance of a device or a machine, or it might be the efficiency of the daily instrument that surrounds us, be it natural or man-made. The consequences might be interrelated such as the evolution of global climate change and health consequence in pollution issues where there is a need of some form of appropriate questions to be raised so as to bring about mathematical formulas to explain them.
Questions are often raised as the results of suspicious knowledge or ignorance. An example of great importance was the incident of a falling apple which raised the question that inspired Newton to learn and reveal the concept of gravity and achieve a breakthrough through the discovery of the laws of gravity in 1966 (Ahmad, 2015; Riggs et al., 2015). The question regarding the falling apple has led to many other discoveries and concepts which in turn has played the role of eliminating doubts on further logical questions.
In 1695, an important question was raised by Leibniz in his letter to L'Hospital:
“Can the meaning of derivatives with integer order be generalized to derivatives with non-integer orders?“
L'Hospital was said to be somewhat curious about the question and replied by another simple question to Leibniz:
“What if the order will be ?”
Leibniz in a letter dated September 30, 1695, replied as follows:
“It will lead to a paradox, from which one day useful consequences will be drawn.”
It is well known that this famous question by Leibniz has opened doors to numerous types of research in new areas in the field of differential equations (Selvam et al., 2015; Bernardis et al., 2016; Patil et al., 2015; Area et al., 2016; Yunquan and Chunfang, 2015). Although he himself did not really provide the answer to his own question, after 300 years, this particular question and the subsequent research work, which have led to a tremendous amount of applications in numerous areas such as science, engineering, astronomical science and in the interpretation of natural phenomena, have coined a new science which is known as the science of fractional differential equations (Li, 2015; Miller and Ross, 1993; Machado et al., 2014). The most popular definitions in relation to the question by Leibniz were formulated by Riemann, Liouville and Caputo where the definitions have been used in many theoretical and application studies.
Fractional differential equation can be defined as a differential equation which has non-integer order, and the following general formula can be considered:
Fuzzy set theory was pioneered by Zadeh in 1965 (Zadeh, 1965). Zadeh stated that uncertainty and probability terms that have been earlier introduced in mathematics in theory as well as in applications are inadequate since the probability theory was limited (Zadeh, 1965). In light of this limitation and also the motivating question of how to explain uncertainty, Zadeh explored new concepts (Zadeh, 1966) with applicable rules of possibilities. These new concepts opened many paths to a new breakthrough in the field of scientific research, and thus providing answers to many ambiguous issues. He was questioning on how to mathematically define classes of objects where he himself has succeeded in providing the answer to the question. This new finding has been known as the fuzzy set theory. Goguen (Jalab and Ibrahim, 2015) began to relate and expanded Zadeh’s findings to a bigger scope. Zadeh then continued to prove his previous work through a new study in the field of probability measures, while Chang (1968) made a study on fuzzy topological spaces. Among other applications, fuzzy set theory has also been used in decision-making (Chang and Zadeh, 1972). The fuzzy set theory became the language of redefining concepts through practical concepts and rules.
In relation of fuzzy set theory to the field of differential equations, the actual extension of fuzzy logic in differential equations was observed in the study of Chang and Zadeh in 1972 (Chang and Zadeh, 1972). In 1982, Dubois and Prade (1982) wrote about the fuzzy sets related to many applications such as differential equations and used the phrase ‘fuzzy differential equation’. Furthermore, the authors (Dubois and Prade, 1982) introduced new applications in the fuzzy logic field specifically, in the integration of fuzzy mappings. Kaleva (1987) and Wang and Wu (1987) made applications of fuzzy in differential equations. Kaleva further worked on Cauchy problem for fuzzy differential equations (Kaleva, 1990). Kloeden (1991) wrote remarks on Peano-like theorems of fuzzy differential equations; Buckley and Qu (1991) solved the first-order fuzzy differential equations. The expansion of the fuzzy concept in numerical methods for solving differential equation has been studied (Friedman et al., 1999). Solution methods include Taylor methods (Abbasbandy and Viranloo, 2002), by Runge-Kutta method (Abbasbandy et al., 2004), predictor–corrector method (Allahviranloo et al., 2007), Nystrom method (Khastan and Ivaz, 2009), differential transformation method (Allahviranloo and Salahshour, 2011) and Laplace transforms (De Oliveira and Machado, 2013).
It is clear that the field of fuzzy differential equation has been expanding day by day. However, these studies were focused on the concept of fuzzy only within the scope of the initial values or the boundary values and such formulation may not represent the entire problem at hand. The current practice assumes the existence of certainty in the order of the equation. The concept of fuzzy was not taken into consideration in the order of the differential equation. Thus, the whole formulation is limiting and may not represent the entire problem at hand.
Therefore, we propose to raise a new question by restating the question posed by Leibniz in 1695 as follows:
“Can the meaning of derivatives and integrals of any order be generalized to fuzzy-order derivatives and fuzzy-order integrals?”
To be more specific, we propose to raise the following subsequent question which is parallel to L’Hospital reply to Leibniz:
“What if the order will be fuzzy number?”
We propose to view fractional calculus with a new logic which is a new order called fuzzy order. The proposition is to generalize the meaning of derivatives and integrals of any order as Fuzzy-order Derivatives and Fuzzy-order Integrals.
The rest of the paper is organized as follows. Section 2 includes some basic definitions in fractional calculus, followed by some main definitions in fuzzy set theory in Section 3. Section 4 presents equations with respect to the fuzzy order and provide new definition of differential calculus related to the new order. To employ the new logic, three numerical examples are given in Section 5. The paper concludes in Section 6.
2 Riemann-Liouville and Caputo definitions in fractional calculus
Fractional definitions, which have been originally formulated by Riemann and Caputo are given as follows.
(Salgado and Aguirre, 2016; Almeida, 2017; Momani and Odibat, 2007; Salahshour et al., 2012) (Riemann-Liouville integral)
The left and the right fractional integrals for Riemann-Liouville are defined as:
and
(Salgado and Aguirre, 2016; Almeida, 2017; Momani and Odibat, 2007; Salahshour et al., 2012) (Riemann-Liouville derivative)
The left and the right fractional derivatives for Riemann-Liouvilleare defined as:
and
(Salgado and Aguirre, 2016; Almeida, 2017; Momani and Odibat, 2007; Salahshour et al., 2012; Zhang, 2014) (Caputo fractional derivatives)
The left and the right Caputo fractional derivatives are defined as:
and
3 Some important definitions in fuzzy theory
(Dubois and Prade, 1980). The Triangular fuzzy numbers
are defined as follows:
where
, and its r-cut is defined as follows:
(Dubois and Prade, 1980). The Trapezoidal fuzzy numbers
are defined as follows:
If .
4 The new concept of fuzzy order
In this section, we discuss differential equations with respect to fuzzy order and provide new definition of differential calculus related to the new order.
4.1 Fuzzy-order differential equation
By the logic of the question posed by Leibniz, rephrasing the Eq. (1) by redefining
as a fuzzy number as follows:
By Definition 4 and Eq. (8), the new form of Eq. (12) yields:
4.2 Fuzzy-order definitions
When we defined
as
, then Eq. (2) is converted to the following form:
Using the r-cut definition in Eqs. (8) and (9), Eq. (12) is converted to the following form:
By similar logic in Eqs. (12)–(15), we can rewrite the definitions in Eqs. (2)–(7) as follows:
The left Riemann-Liouville fuzzy-order integral
is given by:
where is the left terminal point of the interval .
The right Riemann-Liouville fuzzy-order integral
is given by:
where is the right terminal point of the interval
The definition of the left and right Riemann-Liouville fuzzy-order derivatives are as follows.
The left Riemann-Liouville fuzzy-order derivative
is given by:
where is the left terminal point of the interval
The right Riemann-Liouville fuzzy-order derivative
can given by:
The definition of left and right fuzzy-order derivatives in the Caputo sense are as follows.
The left Caputo fuzzy-order derivative is given by:
where
5 Numerical examples
In this section, three numerical examples are provided to validate the proposed logic and new definitions.
The time fractional heat equation (Koch and Brady, 1988) is given by:
Using the new proposed logic, when
is defined as a
where
, the equation with this fuzzy order is able to cover all situations in diffusion theory. In this example, we have shown that the meaning of derivatives of any order can be generalized to fuzzy-order derivatives. Therefore, we can reformulate Eq. (22) by Eq. (8) as:
Clearly, Eq. (24) gives different heat conduction property when
, where this new formulation gives different ranges for heat conduction property between subdiffusion and superdiffusion. The proposed fuzzy order is more suitable to describe the order of the fractional differential equation in this example. Using the new logic, we can observe the two diffusion situations for all
. This can be illustrated by the new formula of Eq. (22) as follows:
It is clear that the time fractional heat equation can be represented as a time fuzzy-order heat equation.
For the equations in diffusion wave between subdiffusion and ballistic diffusion, such as time-fractional diffusion wave equation (Ott et al., 1990; Metzler and Klafter, 2000), where the time-fractional diffusion wave equation is obtained from the classical wave equation, which continues to the diffusion equation when and to the wave equation when .
In typical diffusion is 1, while other phenomena are called anomalous, where for and , the phenomena are called superdiffusion, subdiffusion and ballistic diffusion, respectively.
By Definition 4, we can use the new logic by positioning the order given by fuzzy triangular numbers that leads to cover cases of subdiffusion (weak diffusion) and normal diffusion for the first and second order differential equations, respectively as well as the cases of superdiffusion (strong diffusion) and ballistic diffusion for first level and second level for fractional differential equations, respectively. Hence, the time-fractional diffusion wave equation can be represented by the Time-fuzzy-order diffusion wave equation.
By new logic presented in this paper, let us assumed the following equation:
From Eqs. (8) and (9), we can rewrite Eq. (26) as the follow:
Now, by using the methods in Albzeirat et al. (2017, 2018), we can solve Eq. (27) when and Figs. 1 and 2 illustrate the approximate solution of Eq. (26) when with different value of .
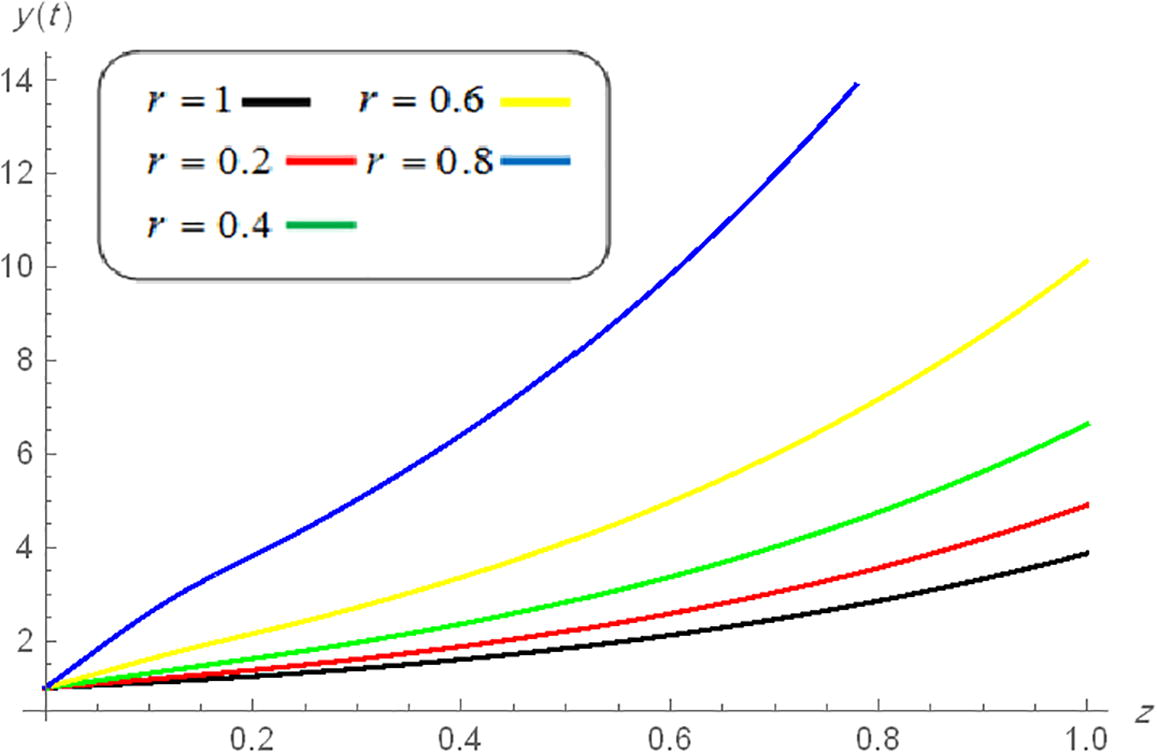
- Approximate solution of
when
with different values of r.
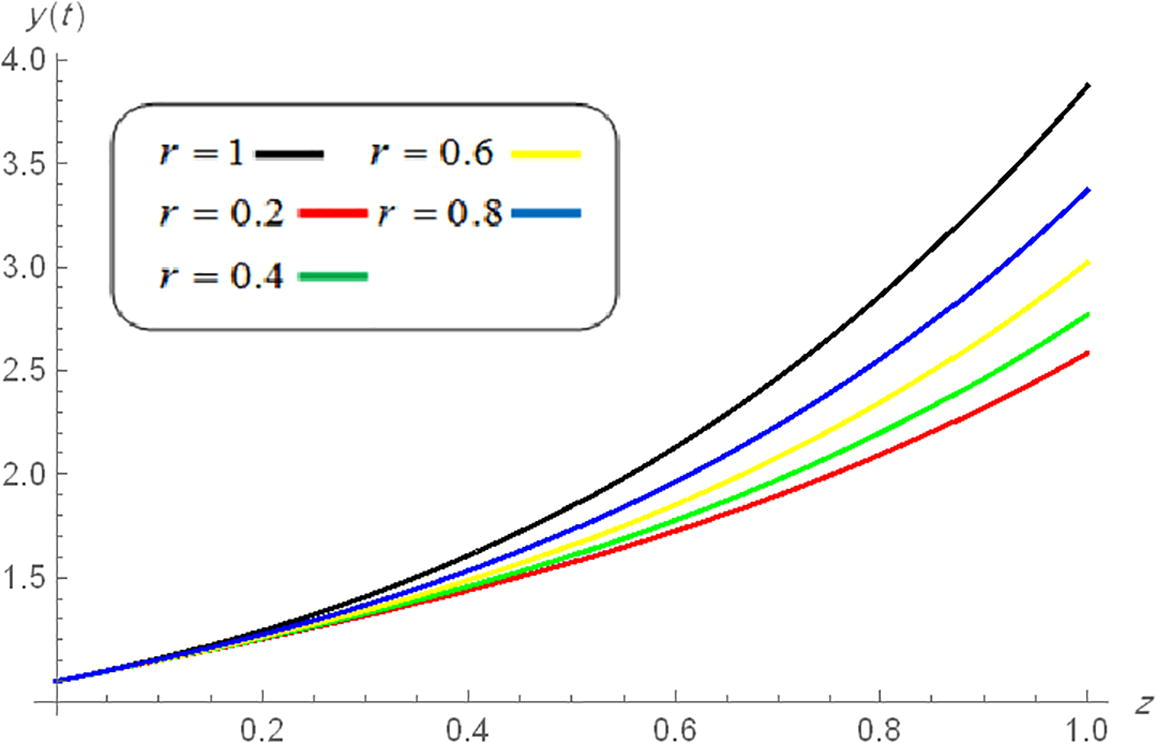
- Approximate solution of
when
with different values of r.
6 Conclusion
This paper rephrased a renowned question by Liebnizin 1695 with respect to the proposed new logic called fuzzy-order and extended the fuzzy logic in order of differential equations. New fuzzy-order definitions have been introduced through the reformulation of the main definitions of fractional derivatives and integrals for Riemann-Liouville and Caputo. This work generalized the meaning of derivatives and integrals of any order to fuzzy-order derivatives and fuzzy-order integrals. The proposed new logic is employed for the generalization of time fractional heat equation and time fractional diffusion wave equation to time fuzzy-order heat equation and time-fuzzy-order diffusion wave equation, respectively as examples. It is noticeable that the actual application of this new logic presented here is still in early stages and could be investigated further in the future.
References
- Numerical solutions of fuzzy differential equations by Taylor method. Comput. Meth. Appl. Math.. 2002;2(2):113-124.
- [Google Scholar]
- Numerical methods for fuzzy differential inclusions. Comput. Meth. Appl. Math.. 2004;48(10):1633-1641.
- [Google Scholar]
- Fractional calculus and fractional differential equations in nonreflexive Banach spaces. Comm. Non. Sci. Num. Sim.. 2015;20(1):59-73.
- [Google Scholar]
- People’s History of Science: miners, midwives and low mechanics. Afr. J. Sci. Tech. Innova. Devel.. 2015;7(2):161-162.
- [Google Scholar]
- Numerical solution of second-order fuzzy differential equation of integer and fractional order by using reproducing kernel hilbert space method tools. Far East J. Math. Sci.. 2017;101(6):1327.
- [Google Scholar]
- New implementation of reproducing kernel Hilbert space method for solving a fuzzy integro-differential equation of integer and fractional orders. J. King Saud Univ. Sci.. 2018;30(3):352-358.
- [Google Scholar]
- Euler method for solving the hybrid fuzzy differential equation. Soft Comp.. 2011;15(7):1247-1253.
- [Google Scholar]
- Numerical solution of fuzzy differential equations by predictor–corrector method. Infor. Sci.. 2007;177(7):1633-1647.
- [Google Scholar]
- Caputo fractional derivative of a function with respect to another function. Comm. Non. Sci. Num. Simul.. 2017;44:460-481.
- [Google Scholar]
- Identities involving some new special polynomials arising from the applications of fractional calculus. Appl. Math.. 2015;9(5):1-6.
- [Google Scholar]
- A note on the fractional logistic equation. Phys. A, Statis. Mech. Apps.. 2016;444:182-187.
- [Google Scholar]
- Maximum principles, extension problem and inversion for nonlocal one-sided equations. J. Diff. Equs.. 2016;260(7):6333-6362.
- [Google Scholar]
- Fractional calculus: a mathematical tool from the past for present engineers [the past and present] Ind. Elec. Mag.. 2007;1(2):35-40.
- [Google Scholar]
- P. Cornetti and Sapora, Nonlocal elasticity: an approach based on fractional calculus. Meccanica. 2014;49(11):2551-2569.
- [Google Scholar]
- On fuzzy mapping and control. Systems, Man, and Cybernetics. IEEE Trans. On.. 1972;1:30-34.
- [Google Scholar]
- A review of definitions for fractional derivatives and integral. Math. Prob. Eng. 2013 Article ID 238459, 6 pages
- [Google Scholar]
- Towards fuzzy differential calculus part 2: integration on fuzzy intervals. Fuzz. Sets. Sys.. 1982;8(2):105-116.
- [Google Scholar]
- Towards fuzzy differential calculus part 1: Integration of fuzzy mappings. Fuzz. Sets. Sys.. 1982;8(1):1-17.
- [Google Scholar]
- Fourier, J., Theorieanalytic de la chaleur, par M. Fourier. Chez Firmin Didot, père et fils, (1822).
- Numerical Solutions of Fuzzy Differential and Integral Equations. Fuzz. Sets. Sys.. 1999;106:35-48.
- [Google Scholar]
- The Cauchy problem for fuzzy differential equations. Fuzz. Sets. Sys.. 1990;35(3):389-396.
- [Google Scholar]
- Numerical solution of fuzzy differential equations by Nyström method. Chaos, Solit. Frac.. 2009;41(2):859-868.
- [Google Scholar]
- Remarks on Peano-like theorems for fuzzy differential equations. Fuzz. Sets. Sys.. 1991;44(1):161-163.
- [Google Scholar]
- Anomalous diffusion in heterogeneous porous media. Phy. Fluid.. 1988;31(5):965-973.
- [Google Scholar]
- Letter from Hanover, Germany, September 30, 1695, to GA L’Hospital. J Leibnizen Mathematische Schriften.. 1849;2:301-302.
- [Google Scholar]
- Several results of fractional derivatives in D’ (R+) Fract. Calc. App. Anal.. 2015;18(1):192-207.
- [Google Scholar]
- On the development of fractional calculus during the last fifty years. Scie.. 2014;98(1):577-582.
- [Google Scholar]
- The random walk's guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep.. 2000;339(1):1-77.
- [Google Scholar]
- An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: John Wiley & Sons; 1993.
- Numerical approach to differential equations of fractional order. J. Comp. App. Math.. 2007;207(1):96-110.
- [Google Scholar]
- Anomalous diffusion in living polymers: A genuine Levy flight. Phy. Rev. Lett.. 1990;65(17):2201.
- [Google Scholar]
- Patil, D.S., Patil, M.D., Vyawahare, V.A., The design of fractional-order controller for fractional-order systems using Bode's ideal loop transfer function method. In: Proc. Int. Conf. on Industrial Instrumentation and Control, (Pune, India, 2015) 490-495.
- Leave her out of it: Person presentation of strategies is harmful to transfer. Cong. Sci. 2015
- [Google Scholar]
- Solving fuzzy fractional differential equations by fuzzy Laplace transforms. Non. Sci. Num. Simul.. 2012;17(3):1372-1381.
- [Google Scholar]
- A hybrid algorithm for Caputo fractional differential equations. Comm. Non. Sci. Num. Simul.. 2016;33:133-140.
- [Google Scholar]
- Dynamics in a fractional order prey-predator interactions. Mathe, Model. Appl. Comp.. 2015;6(1):1-6.
- [Google Scholar]
- Wang, Y., Wu, S., Fuzzy differential equations. Proc. 2nd IFSA Conf. (Tokyo, Japan, 1987) 20–25.
- Colloquium: Fractional calculus view of complexity: a tutorial. Rev. Mod. Phys.. 2014;86(4):11-69.
- [Google Scholar]
- Mittag-Leffler stability of fractional-order Lorenz and Lorenz-family systems. Non. Dyn.. 2015;83(3):1237-1246.
- [Google Scholar]
- High performance computing for solving fractional differential equations with applications. Fract. Calc. App. Anal.. 2014;17(3)
- [Google Scholar]
- Zhou, Y., The Basic Theory of Fractional Differential Equations, (World Scientific, first Ed. Singapore, 2014).







