Translate this page into:
Soliton solutions of (3 + 1)-dimensional Korteweg-de Vries Benjamin–Bona–Mahony, Kadomtsev–Petviashvili Benjamin–Bona–Mahony and modified Korteweg de Vries–Zakharov–Kuznetsov equations and their applications in water waves
⁎Corresponding author at: Mathematics Department, Faculty of Science, Taibah University, Al-Ula, Saudi Arabia. Aly742001@yahoo.com (A.R. Seadawy)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this article, the analytical solution of (3 + 1)-dimensional Korteweg-de Vries Benjamin–Bona–Mahony equation, Kadomtsev–Petviashvili Benjamin–Bona–Mahony equation and modified Korteweg-de Vries–Zakharov–Kuznetsov equation have been extracted. These results hold numerous traveling wave solutions that are of key importance in elucidating some physical circumstance. The technique can also be functional to other sorts of nonlinear evolution equations in contemporary areas of research.
Keywords
Korteweg-de Vries Benjamin–Bona–Mahony equation
Kadomtsev–Petviashvili Benjamin–Bona–Mahony equation
Modified Korteweg-de Vries–Zakharov–Kuznetsov equation
1 Introduction
The propagation of nonlinear wave is one of the key phenomenon of nature and a growing interest has been drawn to the study of nonlinear waves in the dynamical system. The nonlinear equations have plenty of applications in sciences and engineering like electrochemistry, electromagnetic theory, fluid dynamics, acoustics, cosmology, astrophysics and plasma physics etc., see for references (Eslami, 2015, 2016a,b; Helal and Seadawy, 2009; Helal and Seadawy, 2011; Seadawy, 2015).
In the last few eras great improvement have been made in the progress of methods for finding the exact solutions of nonlinear equations but the advancement achieved is inadequate. Taking into account the merits and demerits of analytic methods, it is observed that there is no single outstanding preferable method which can be applied to any kind of nonlinear problems to obtain exact solutions. Consequently, it is apprehended that all of these methods are problem dependent, viz. some approaches work well with certain problems but not the others. Therefore, it is rather substantial to relate some established techniques in the literature to nonlinear partial differential equations, for details see also (Zabusky, 1967; Zhu, 1996; Seadawy, 2012; Seadawy and Sayed, 2013; Johnson, 1997).
The dynamics of shallow water waves is an important area of research in oceanography. There are several models that describe this kind of dynamics. A few of them are the Korteweg-de Vries (KdV) equation (Gardner et al., 1967), Korteweg-de Vries Burgers (KdV-B) equation (Zhibin and Mingliang, 1993), modified KdV (mKdV) equation (Ito, 1980), modified Korteweg-de Vries Zakharov-Kuznetsov (mKdv-ZK) equation, Boussinesq equation (Wang, 1995), Perergrine equation (Triki et al., 2010), Kawahara equation (Wazwaz, 2007a,b), Benjamin–Bona–Mahoney equation (Seadawy and Sayed, 2014), coupled Boussinesq equation (Mohapatra and Soares, 2015) and many others. Another model that is also considered and studied at times is the Gardner equation (GE) it is a combination of KdV and mKdV equation (Li and Wang, 2007). Therefore, occasionally, GE is referred to as the KdVmKdV equation, Kadomtsev–Petviashvili (KP) equation (Yong et al., 2003) and Gardner-Kadomtsev–Petviashvili (G-KP) equation (Yan et al., 2012).
Numerous dominant approaches have been offered, such as, Cole-Hopf transformation, Painleve method, Backlund transformation, sine–cosine method, Darboux transformation, Hirota method, Lie group analysis, homogeneous balance method (HBM), similarity reduced method, tanh method and so on, for details see also (Ma, 2011; Gai et al., 2012; Dutykha and Pelinovsky, 2014; Seadawy, 2014, 2016a,b, 2017; Seadawy and El-Rashidy, 2016).
The Korteweg-de Vries equation within the scope of the local fractional derivative formulation was investigated. The exact traveling wave solutions of non-differentiable type with the generalized functions defined on Cantor sets were analyzed (Yang et al., 2016). A family of local fractional two-dimensional Burgers-type equations was investigated. The local fractional Riccati differential equation method was proposed here for the first time. The travelling wave transformation of the non-differentiable type was presented. The non-differentiable exact travelling wave solutions for the problems were obtained (Yang et al., 2017).
Recently, there has been a growing interest in finding exact analytical solutions to nonlinear wave equations by using appropriate techniques. The investigation of exact traveling wave solutions for nonlinear partial differential equations (NPDEs) plays an important role in studying nonlinear physical phenomena (Xu and Li, 2005). These exact solutions can help better understand the mechanism of the complicated physical phenomena and dynamical processes modeled by nonlinear evolution equations (El-Wakil et al., 2006). Meanwhile, many powerful methods have been established and developed to construct exact solutions of NPDEs, leading to one of the most exciting advances in nonlinear science and theoretical physics. In fact, many kinds of exact soliton solutions have been obtained by using the inverse scattering method (Ablowitz and Clarkson, 1991), Hirota’s bilinear method (Hirota, 1971), the homogeneous balance method (Hu, 2005), variational method (Helal and Seadawy, 2009; Seadawy, 2011), algebraic method (Hu, 2005), sine–cosine method (Wazwaz, 2007a,b), the Jacobi elliptic function method, the F-expansion method, the expansion method, the tanh and extended tanh method, conferred traveling wave solutions, including periodic traveling wave solutions, and rational solutions, the exact traveling wave solutions and their bifurcations obtained the solutions by using the new generalized transformation in HBM and so on (Kutluay et al., 2010; Abazari, 2010; Liu et al., 2001; Zhou et al., 2003).
The analytical solution of (3 + 1)-dimensional Korteweg-de Vries Benjamin–Bona–Mahony (KdV-BBM), Kadomtsev–Petviashvili Benjamin–Bona–Mahony (KP-BBM) and modified Kortewegde Vries–Zakharov–Kuznetsov (mKdv-ZK) equations are considered, the governing equations are as follows:
This article has been devised as follows: in Section 2, the auxiliary equation method is introduced, while in Section 3, the solutions of three nonlinear PDEs have been presented. In last Section 4, the conclusions have been drawn.
2 The description of the auxiliary equation method
We will briefly present the main steps of the AEM that will be applied to the non-linear equations (1.1)–(1.3), as in the following steps:
-
Step 1.
Let us have a general form of nonlinear PDE
(2.4)where F is a polynomial function with respect to the indicated variables. -
Step 2.
-
Step 3.
The main idea of the auxiliary equation method based on expanding the traveling wave solution of Eqs. (2.6) as a finite series
(2.7)satisfies
(2.8)(2.9)where are constants. -
Step 4.
-
Step 5.
Substituting (2.7)–(2.9) in (2.4) and collecting the coefficients of , then setting coefficients equal zero, we will obtain a set of over-determined equations for and . By solving the system, we may determine these parameters.
-
Step 6.
Substituting and obtained in step 5 into (2.7), to obtain the solution of Eq. 1.1,1.2.1.3.
3 Applications of the method
3.1 (3 + 1)-D KdV- BMM equation
Consider the transformation
Substituting (2.7), (2.8) and (3.13) in (3.12) and collecting the coefficients of , Mathematica 10.4 is used to carry out symbolic computations.
-
Case I.(3.14)where(3.15)
The parameters become
(3.16)(3.17)(3.18)(3.19)so the solution of (1.1) will be(3.20) -
Case II.(3.21)
The parameters
become
3.2 (3 + 1)-D KP-BBM equation
Consider the transformation
Substituting (2.7), (2.8) and (3.31) in (3.30) and collecting the coefficients of , Mathematica 10.4 is used to carry out symbolic computations.
-
Case I.(3.32)where(3.33)
The parameters become
(3.34)(3.35)(3.36)(3.37)so the solution of (1.2) will be(3.38) -
Case II.(3.39)
The parameters
become
3.3 (3 + 1)-D mKdv-ZK equation
Consider the transformation
Substituting (2.7), (2.8) and (3.49) in (3.48) and collecting the coefficients of , Mathematica 10.4 is used to carry out symbolic computations.
-
Case I.(3.50)where(3.51)
The parameters become
(3.52)(3.53)(3.54)(3.55)so the solution of (1.3) will be(3.56) -
Case II.(3.57)
The parameters
become
4 Conclusion
In this article, the analytical solutions to (3 + 1)-dimensional Korteweg-de Vries Benjamin–Bona–Mahony equation, Kadomtsev–Petviashvili Benjamin–Bona–Mahony equation and modified Kortewegde Vries–Zakharov–Kuznetsov equations have been extracted with the help of the auxiliary equation method. These results are very auspicious for further investigation and stances on a strong basis for the solution of NPDEs (see Figs. 1–3).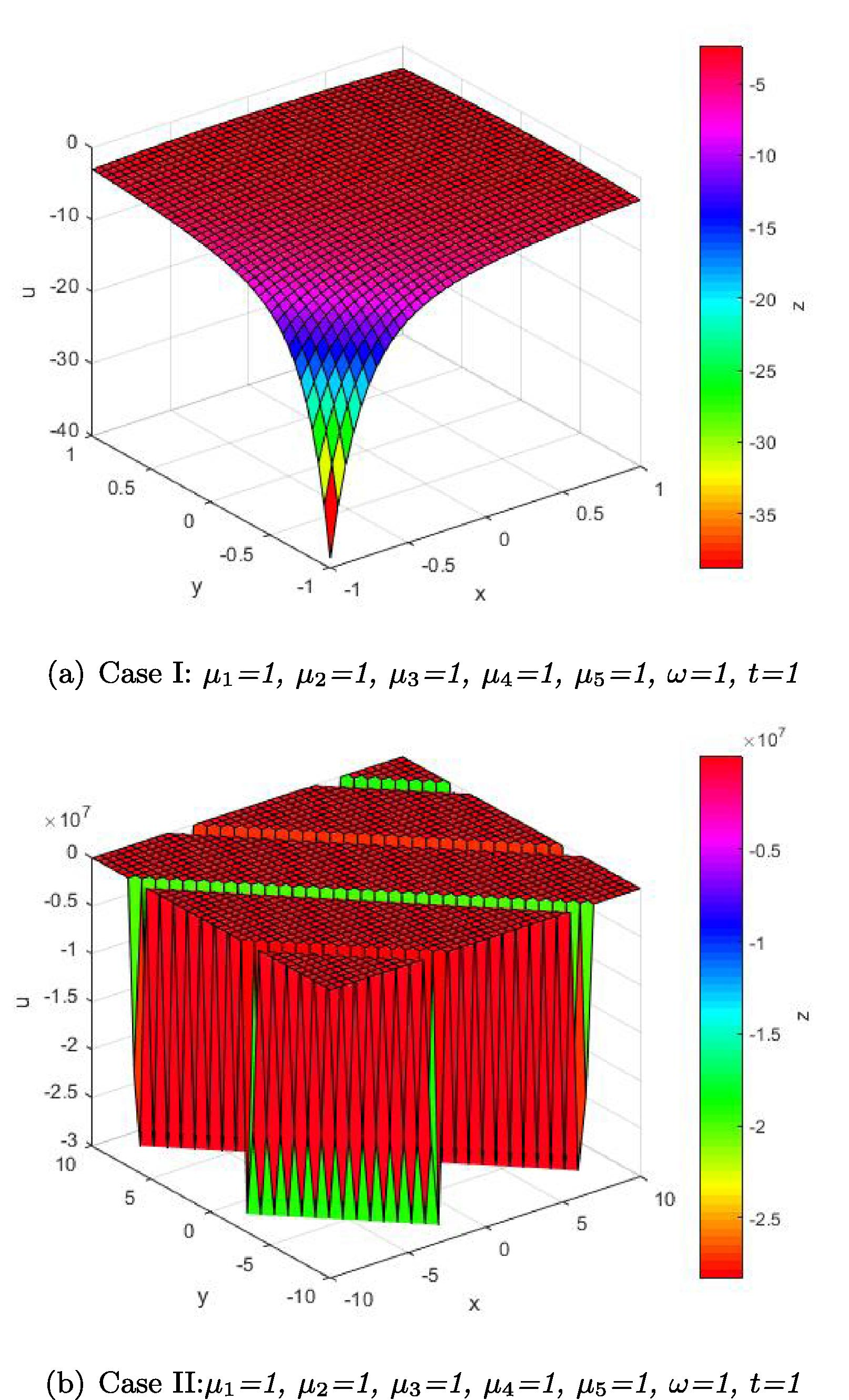
(3 + 1)-D KdV-BBM equation.
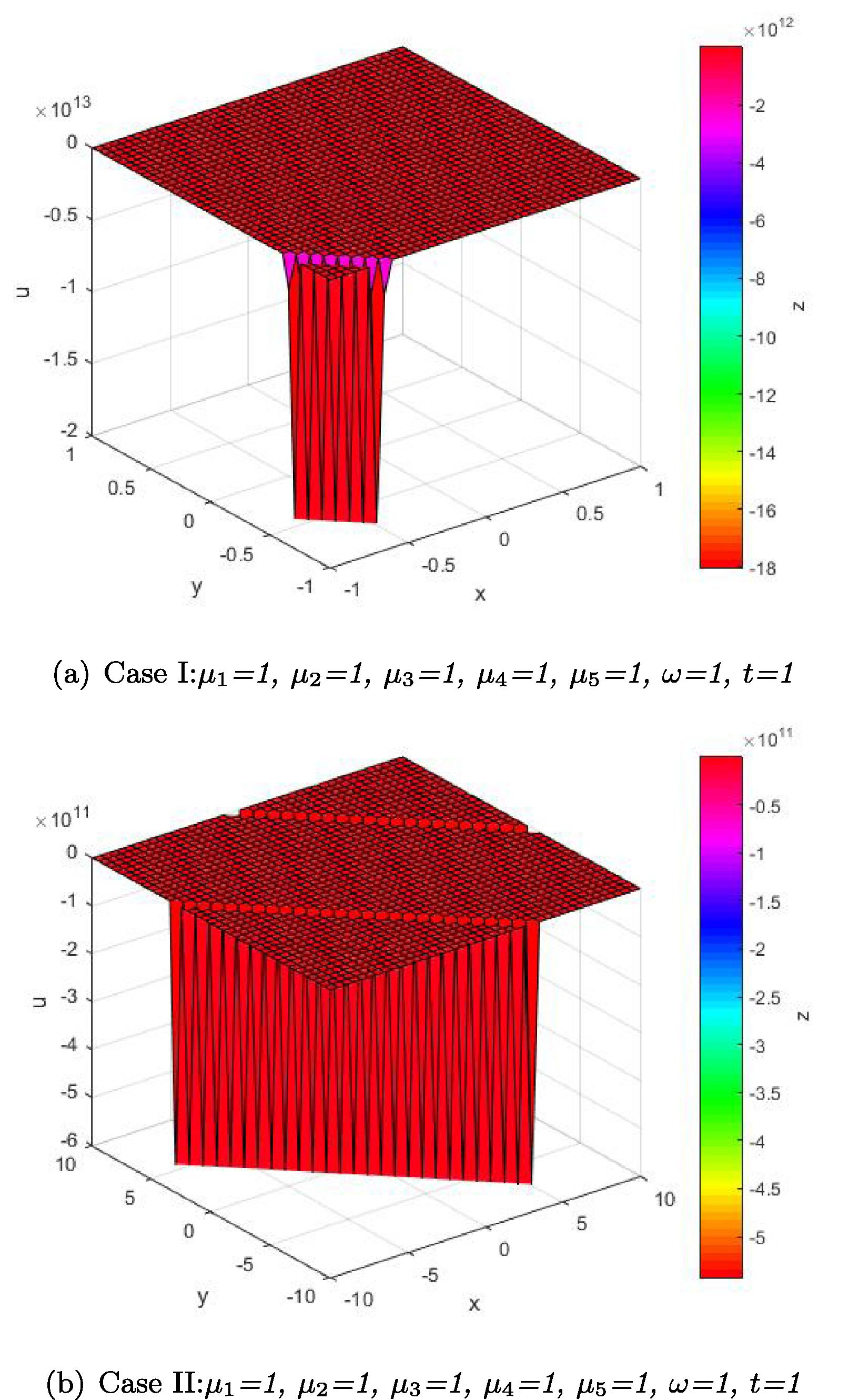
(3 + 1)-D KP-BBM equation.
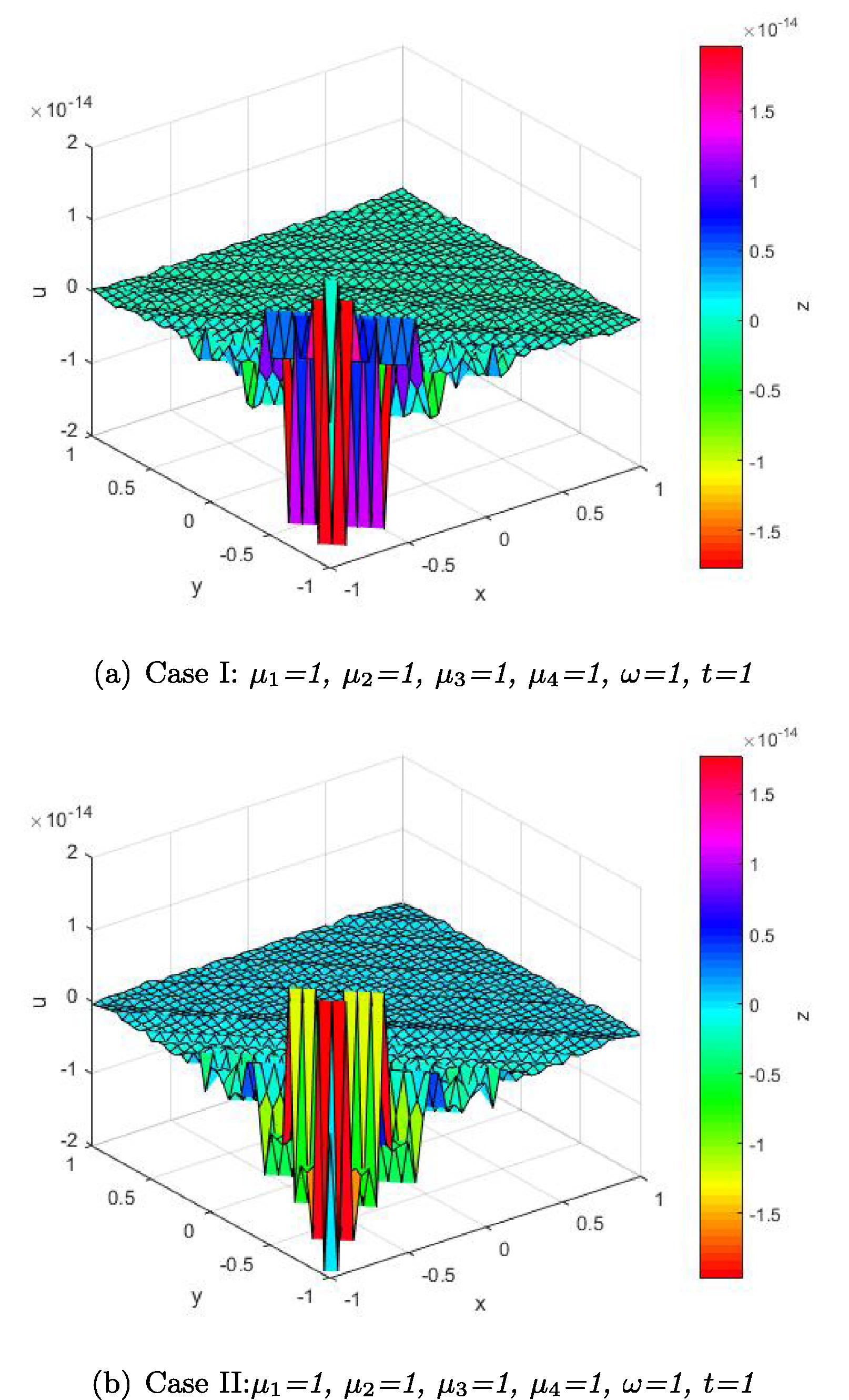
(3 + 1)-D KdV-ZK equation.
References
- Application of -expansion method to travelling wave solutions of three nonlinear evolution equation. Comput. Fluids. 2010;39:1957-1963.
- [Google Scholar]
- Soliton, Nonlinear Evolution Equations and Inverse Scattering. USA: Cambridge University Press; 1991.
- Numerical simulation of a solitonic gas in KdV and KdV-BBM equations. Phys. Lett. A. 2014;378:3102-3110.
- [Google Scholar]
- New solitons and periodic wave solutions for nonlinear evolution equations. Phys. Lett. A. 2006;353:40-47.
- [Google Scholar]
- Solitary wave solutions for perturbed nonlinear Schrodinger’s equation with Kerr law nonlinearity under the DAM. Optik-Int. J. Light Electron. Opt.. 2015;126(13):1312-1317.
- [Google Scholar]
- Exact traveling wave solutions to the fractional coupled nonlinear Schrodinger equations. Appl. Math. Comput.. 2016;285:141-148.
- [Google Scholar]
- Soliton-like solutions for the coupled Schrodinger-Boussinesq equation. Optik-Int. J. Light Electron. Opt.. 2016;126(23):3987-3991.
- [Google Scholar]
- Soliton Interactions for the Generalized (3 + 1)-dimensional Boussinesq equation. Int. J. Mod. Phys. B. 2012;26(7):1250062.
- [Google Scholar]
- Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett.. 1967;19:1095-1097.
- [Google Scholar]
- Variational method for the derivative nonlinear Schrödinger equation with computational applications. Physica Scripta. 2009;80:350-360.
- [Google Scholar]
- Exact soliton solutions of a D-dimensional nonlinear Schrodinger equation with damping and diffusive terms. Zeitschrift fur Angewandte Mathematik und Physik. 2011;62:839-847.
- [Google Scholar]
- Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett.. 1971;27:1192-1194.
- [Google Scholar]
- An algebraic method exactly solving two high-dimensional nonlinear evolution equations. Chaos Solit. Fract.. 2005;23:391-398.
- [Google Scholar]
- An extension of nonlinear evolution equation of the K-dV(mK-dV) type to higher order. J. Phys. Soc. Jpn.. 1980;49:771-778.
- [Google Scholar]
- A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge: Cambridge University Press; 1997.
- The -expansion method for some nonlinear evolution equations. Appl. Math. Comput.. 2010;217:384-391.
- [Google Scholar]
- A sub-ODE method for finding exact sollutions of a generalized KdV-mKdV equation with high-order nonlinear terms. Phys. Lett. A. 2007;361:115-118.
- [Google Scholar]
- Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A. 2001;289:69-74.
- [Google Scholar]
- Comment on the (3 + 1) dimensional Kadomtsev–Petviashvili equations. Commun Nonlinear Sci Numer Simulat. 2011;16:2663-2666.
- [Google Scholar]
- Comparing solutions of the coupled Boussinesq equations in shallow water. London: Maritime Technology and Engineering, Francis Group; 2015.
- New exact solutions for the KdV equation with higher order nonlinearity by using the variational method. Comp. Math. Appl.. 2011;62:3741-3755.
- [Google Scholar]
- The solutions of the Boussinesq and generalized fifth-order KdV equations by using the direct algebraic method. Appl. Math. Sci.. 2012;6(82):4081-4090.
- [Google Scholar]
- Stability analysis for Zakharov–Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma. Comput. Math. Appl.. 2014;67:172-180.
- [Google Scholar]
- Approximation solutions of derivative nonlinear Schrodinger equation with computational applications by variational method. Eur. Phys. J. Plus. 2015;130(182):1-10.
- [Google Scholar]
- Stability analysis solutions for nonlinear three-dimensional modified Korteweg-de Vries–Zakharov–Kuznetsov equation in a magnetized electron-positron plasma. Physica A: Stat. Mech. Appl.. 2016;455:44-51.
- [Google Scholar]
- Three-dimensional nonlinear modified Zakharov–Kuznetsov equation of ion-acoustic waves in a magnetized plasma. Comput. Math. Appl.. 2016;71:201-2012.
- [Google Scholar]
- Travelling wave solutions of a weakly nonlinear two-dimensional higher order Kadomtsev–Petviashvili dynamical equation for dispersive shallow water waves. Eur. Phys. J. Plus. 2017;132:29.
- [Google Scholar]
- Rayleigh–Taylor instability of the cylindrical flow with mass and heat transfer. Pramana-J. Phys.. 2016;87:20.
- [Google Scholar]
- Travelling wave solution of two-dimensional nonlinear KdV-Burgers equation. Appl. Math. Sci.. 2013;7:3367-3377.
- [Google Scholar]
- Traveling wave solutions of the Benjamin–Bona–Mahony water wave equations. Abstract Appl. Anal.. 2014;2014(926838):1-7.
- [Google Scholar]
- Solitary wave solutions for a generalized KdV-mKdV equation with variable coefficients. Math. Comput. Simul.. 2010;80:1867-1873.
- [Google Scholar]
- Solitary wave solutions for variant Boussinesq equations. Phys. Lett. A. 1995;199:169-172.
- [Google Scholar]
- Analytic study for fifth-order KdV-type equations with arbitrary power nonlinearities. Commun. Nonlin. Sci. Numer. Simul.. 2007;12:904-909.
- [Google Scholar]
- New solitary wave solutions to the modified Kawahara equation. Phys. Lett. A. 2007;360:588-592.
- [Google Scholar]
- Exact travelling wave solutions of the Whitham–Broer–Kaup and Broer–Kaup–Kupershmidt equations. Chaos Solit. Fract.. 2005;24:549-556.
- [Google Scholar]
- The exact traveling wave solutions and their bifurcations in the Gardner and Gardner-KP Equations. Int. J. Bifurcation Chaos. 2012;22(5):1250126.
- [Google Scholar]
- On exact traveling-wave solutions for local fractional Korteweg-de Vries equation. Chaos. 2016;26(8):084312.
- [Google Scholar]
- Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comp. Math. Appl.. 2017;73(2):203-210.
- [Google Scholar]
- New explicit solitary wave solutions for (2 + 1)-dimensional Boussinesq equation and (3 + 1)-dimensional KP equation. Phys. Lett. A. 2003;307:107-113.
- [Google Scholar]
- A synergetic approach to problems of nonlinear dispersive wave propagation and interaction. In: Nonlinear Partial Differential Equations. New York: Academic Press; 1967.
- [Google Scholar]
- Travelling wave solutions to the two-dimensional Kdv-Burgers equation. J. Phys. A: Math. Gen.. 1993;26:6027-6031.
- [Google Scholar]
- Periodic wave solutions to a coupled KdV equations with variable coefficients. Phys. Lett. A. 2003;308:31-36.
- [Google Scholar]
- Exact solutions for a two-dimensional KdV-Burgers-type equation. Chin. J. Phys.. 1996;34:1101-1105.
- [Google Scholar]







