Extra two new piezoelectromagnetic SH-SAWs with dramatic dependence on small electromagnetic constant

A.A. Zakharenko

doi:10.1016/j.jksus.2017.05.005

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original article

30 (

); 544-548

doi:

10.1016/j.jksus.2017.05.005

Extra two new piezoelectromagnetic SH-SAWs with dramatic dependence on small electromagnetic constant

A.A. Zakharenko

International Institute of Zakharenko Waves (IIZWs), 660014, ul. Chaikovskogo, 20-304 Krasnoyarsk, Russia

Received: 2017-3-21, Accepted: 2017-5-5, Published: 2017-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

It is expected that this theoretical report finalizes the research regarding to the shear-horizontal surface acoustic wave (SH-SAW) propagation along the suitable surface of the transversely isotropic (6 mm) piezoelectromagnetics. This report examines extra two new SH-SAWs, the existence of which dramatically depends on the small electromagnetic constant that is responsible for the magnetoelectric effect. This study also provides some comparison with the previously obtained theoretical results and the phenomenon called the Goldstone excitation. The obtained results can be useful for educational purposes, creation of novel technical devices based on the magnetoelectric effect that can find applications in spintronics, further theoretical treatments of the SH-wave propagation in plates, nondestructive testing and evaluation of apt surfaces and plates, etc.

Keywords

Transversely isotropic magnetoelectroelastics

Magnetoelectric effect

New shear-horizontal surface acoustic waves

Goldstone excitation

Show Related Articles from PubMed

1 Introduction

Acoustic phonons are collective oscillations in a periodic, elastic arrangement of atoms or molecules in condensed matter. Under action of external exciters, these long wavelength oscillations can result in coupled behavior of groups of atoms that can cause a wave motion propagating far from an excitation spot. It is well-known that in solids, the caused wave motion can be organized in different ways, namely it can possess the in-plane or anti-plane polarization (Auld, 1990; Dieulesaint and Royer, 1980). This theoretical report has an interest in discovery and study of extra new shear-horizontal surface acoustic waves (SH-SAWs) having the anti-plane polarization. This type of polarization can exist only in solids. The studied solids must have the transversely isotropic symmetry of class 6 mm and possess both the piezoelectric (PE) and piezomagnetic (PM) effects resulting in appearance of the additional effect called the magnetoelectric (ME) effect. Such ME materials are called the piezoelectromagnetics (PEMs), also known as the magnetoelectroelastics (MEEs). The PEM materials are typically composites of PE materials and magnetic materials. The linear ME effect is the phenomenon of inducing magnetic (electric) polarization by applying an external electric (magnetic) field. Recent review (Hu et al., 2016) summarizes the most recent progresses in the basic principles and possible applications of the interface-based ME effect in multiferroic heterostructures, and presents perspectives on some key issues that require further investigations concerning realizations of their practical device applications.

There is single book (Zakharenko, 2010) regarding to the existence of the SH-SAWs in the transversely isotropic PEMs that was published as a PhD thesis carried out for the International Institute of Zakharenko Waves (IIZWs). Zakharenko (2010) has discovered seven new PEM SH-SAWs. Also, book (Zakharenko, 2010) and theoretical work (Wei et al., 2009) have confirmed the propagation possibility of the other three PEM SH-SAWs discovered by Melkumyan (2007). They are called the surface Bleustein-Gulyaev-Melkumyan (BGM) wave, the piezoelectric exchange surface Melkumyan (PEESM) wave, and the piezomagnetic exchange surface Melkumyan (PMESM) wave. The first surface Melkumyan wave is called the BGM wave to have an analogy with the well-known surface Bleustein-Gulyaev wave (Bleustein, 1968; Gulyaev, 1969) discovered to the end of the 1960s that can propagate in a pure PEs or a pure PMs. The BGM wave and the rest two, PEESM and PMESM, were also studied in papers (Zakharenko, 2011) and (Zakharenko, 2012), respectively. The fifth new SH-SAW discovered in book (Zakharenko, 2010) and studied in paper (Zakharenko, 2012) can exist only in the case when the ME effect is taken into account, namely in the case of nonzero electromagnetic constant α ≠ 0. In general, for real known ME materials, the value of α is very small but nonzero. The fifth new SH-SAW relates to the third coupling mechanism responsible for the ME effect such as (εµ − α²) of the three ones of the coefficient of the magnetoelectromechanical coupling (CMEMC), where ε and µ are the electric and magnetic constants of the PEM solid, respectively. There are also the eighth and tenth new PEM SH-SAWs (Zakharenko, 2013a, 2015a,b ) relevant to (εµ − α²) that have more dramatic dependence on the constant α because the small value of α must be big enough to allow the propagation of the eighth and tenth new PEM SH-SAWs. For these new SH-waves, the values of α smaller than the threshold value α_th must lead to the dissipation case when the wave velocity is imaginary. This short theoretical report provides extra new PEM SH-SAWs belonging to the CMEMC coupling mechanism (εµ − α²) revealing the dissipation at α < α_th.

The following section refers the reader to the short theoretical description leading to the existence of the extra two new PEM SH-SAWs. The third section compares the obtained results with the other existing results and the phenomenon called the Goldstone excitation, respectively. It is also necessary to mention that in comparison with the conventional piezoelectrics, the PEM materials are preferable for excitation of the SH-SAWs with the noncontact EMAT method (Thompson, 1990; Hirao and Ogi, 2003; Ribichini et al., 2010 ). Also, the reader can find some reviews (Zakharenko, 2013b; Pullar, 2012; Srinivasan, 2010; Özgür et al., 2009; Fiebig, 2005; Kimura, 2012 ) on PEM SH-SAWs, smart PEM materials and their applications that can play their useful role for development of spintronics – the modern electronics free of charges, i.e. a technology utilizing the electron spin. The spin can either be “up” or “down”, and this property could be used to store and process information in spintronic devices. Switching spins from up to down can be done using very little energy. Thus, spintronic circuits can be smaller and more efficient than conventional electronic circuits relying on just switching charge. The reader can find some bridges between the low-power spintronics and ME devices in recent work (Fusil et al., 2014). Ceramic materials based on bismuth ferrite (Jartych et al., 2016) represent an example of perspective ME materials. Review (Kimura, 2012) discusses that ME crystals such as ME hexaferrites can be perspective to the ME composite materials.

2 Two new PEM SH-SAWs

Let’s treat a bulk hexagonal (6 mm class) PEMs and study the wave propagation in such transversely isotropic ME medium utilizing the rectangular coordinate system {x₁, x₂, x₃}. Review (Gulyaev, 1998) provides the proper propagation direction in the solid when pure SH-wave (Auld, 1990; Dieulesaint and Royer, 1980; Lardat et al., 1971 ) coupled with both the electrical (φ) and magnetic (ψ) potentials can be studied: the propagation direction is along the x₁-axis and perpendicular to both the 6-fold symmetry axis managed along the x₂-axis and the x₃-axis aligned along the normal to the free surface of the ME solid when the x₃-axis negative values are managed towards the solid depth. The coordinate beginning is situated at the interface between the solid and a vacuum. For the treated problem, it is natural to apply the quasi-static approximation because the acoustic wave speed is five orders slower than the electromagnetic wave speed. As a result of the used propagation direction (Auld, 1990; Dieulesaint and Royer, 1980; Zakharenko, 2010; Wei et al., 2009; Melkumyan, 2007; Bleustein, 1968; Gulyaev, 1969; Lardat et al., 1971 ), it is possible to separately consider the differential form of the coupled equations of motion for the pure SH-wave possessing the third mechanical displacement U = U₂ directed along the x₂-axis and coupled with both the electrical and magnetic potentials. Besides the mass density ρ there are the following thermodynamically defined material parameters for the PEM solid: the electromagnetic constant α, elastic stiffness constant C, piezomagnetic coefficient h, piezoelectric constant e, magnetic permeability coefficient μ, dielectric permittivity coefficient ε. So, the set of the partial differential equations of the second order (the differential form of the coupled equations of motion) can be written for this case as follows:

(1)

\{\begin{matrix} C \nabla^{2} U + e \nabla^{2} ϕ + h \nabla^{2} ψ = ρ \partial^{2} U / \partial t^{2} \\ e \nabla^{2} U - ε \nabla^{2} ϕ - α \nabla^{2} ψ = 0 \\ h \nabla^{2} U - α \nabla^{2} ϕ - μ \nabla^{2} ψ = 0 \end{matrix}

where t is time and

\nabla^{2} = \partial^{2} / \partial x_{1}^{2} + \partial^{2} / \partial x_{3}^{2}

is the two-dimensional differentiation operator called the Laplacian.It is blatant that the solution of set (1) can be written in the plane wave form of

U_{I} = U_{I}^{0} \exp [j (k_{1} x_{1} + k_{2} x_{2} + k_{3} x_{3} - ω t)]

, where the index I is equal to 2, 4, 5; U₄ = φ and U₅ = ψ. The parameters U⁰, φ⁰, and ψ⁰ are the unknown coefficients called the eigenvector components that must be determined. Also, j and ω are the imaginary unity and angular frequency, respectively. {k₁,k₂,k₃} = k{n₁,n₂,n₃} are the wavevector components, where k is the wavenumber in the propagation direction because the directional cosines are n₁ = 1, n₂ = 0, n₃ ≡ n₃. The last represents the eigenvalue. Substituting the plane wave solutions into set (1), the tensor form of the coupled equations of motion known as the Green-Christoffel equation can be obtained and composed in the form of the following equations’ set:

(2)

(\begin{matrix} {GL}_{22} - C {(V_{ph} / V_{t 4})}^{2} & {GL}_{24} & {GL}_{25} \\ {GL}_{42} & {GL}_{44} & {GL}_{45} \\ {GL}_{52} & {GL}_{54} & {GL}_{55} \end{matrix}) (\begin{matrix} U^{0} \\ ϕ^{0} \\ ψ^{0} \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})

where V_ph = ω/k stands for the phase velocity, V_t₄ = (C/ρ)^1/2 denotes the purely mechanical bulk acoustic wave (BAW) with the shear-horizontal (SH) polarization. In set (2), the Green-Christoffel tensor components are:

{GL}_{22} = C (1 + n_{3}^{2})

{GL}_{24} = {GL}_{42} = e (1 + n_{3}^{2})

{GL}_{25} = {GL}_{52} = h (1 + n_{3}^{2})

{GL}_{44} = - ε (1 + n_{3}^{2})

{GL}_{55} = - μ (1 + n_{3}^{2})

{GL}_{54} = {GL}_{45} = - α (1 + n_{3}^{2})

. An expansion of the determinant of the coefficient matrix in expression (2) leads to a sixth order polynomial in one indeterminate n₃. Thus, the found six suitable eigenvalues n₃ representing the polynomial roots read:

n_{3}^{(1, 2)} = n_{3}^{(3, 4)} = \pm j

and

n_{3}^{(5, 6)} = \pm j \sqrt{1 - {(V_{ph} / V_{tem})}^{2}}

. Here

V_{tem} = \sqrt{C / ρ} {(1 + K_{em}^{2})}^{1 / 2}

represents the velocity of the SH-BAW coupled with both the electrical and magnetic potentials via the following coefficient of the magnetoelectromechanical coupling (CMEMC):

K_{em}^{2} = ({eM}_{2} - {hM}_{1}) / {CM}_{3}

. Also,

M_{1} = e α - h ε

M_{2} = e μ - h α

, and

M_{3} = ε μ - α^{2}

are the three CMEMC coupling mechanisms discussed in paper (Zakharenko, 2013c).

It is also necessary to state that for the used coordinate system described at the beginning of this section, the three apt eigenvalues of six must have a negative sign because the amplitudes of the solutions U, φ, and ψ defined after equations’ set (1) must damp towards the PEM solid depth. Paper (Zakharenko, 2014a) discusses that two suitable sets of the eigenvector components U⁰, φ⁰, and ψ⁰ can be found. The first one reads:

(3)

(\begin{matrix} U^{0 (1)} \\ ϕ^{0 (1)} \\ ψ^{0 (1)} \end{matrix}) = (\begin{matrix} U^{0 (3)} \\ ϕ^{0 (3)} \\ ψ^{0 (3)} \end{matrix}) = (\begin{matrix} 0 \\ α \\ - ε \end{matrix}), (\begin{matrix} U^{0 (5)} \\ ϕ^{0 (5)} \\ ψ^{0 (5)} \end{matrix}) = (\begin{matrix} M_{1} / {CK}_{em}^{2} \\ α - eh / {CK}_{em}^{2} \\ - ε + e^{2} / {CK}_{em}^{2} \end{matrix})

Using the following equality

e ϕ^{0 (1)} + h ψ^{0 (1)} = e ϕ^{0 (5)} + h ψ^{0 (5)} = M_{1}

, it is possible to state that the corresponding eigenvector components are coupled via the first coupling mechanism M₁ of the CMEMC.

The second set of the eigenvector components can be introduced as follows:

(4)

(\begin{matrix} U^{0 (1)} \\ ϕ^{0 (1)} \\ ψ^{0 (1)} \end{matrix}) = (\begin{matrix} U^{0 (3)} \\ ϕ^{0 (3)} \\ ψ^{0 (3)} \end{matrix}) = (\begin{matrix} 0 \\ μ \\ - α \end{matrix}), (\begin{matrix} U^{0 (5)} \\ ϕ^{0 (5)} \\ ψ^{0 (5)} \end{matrix}) = (\begin{matrix} M_{2} / {CK}_{em}^{2} \\ μ - h^{2} / {CK}_{em}^{2} \\ - α + eh / {CK}_{em}^{2} \end{matrix})

Here there is already the coupling of the corresponding eigenvector components through the second coupling mechanism M₂ of the CMEMC:

e ϕ^{0 (1)} + h ψ^{0 (1)} = e ϕ^{0 (5)} + h ψ^{0 (5)} = M_{2}

.The found eigenvalues and the corresponding eigenvector components are now used for composition of the complete mechanical displacement (

U_{2}^{Σ} = U^{Σ}

), complete electrical potential (

U_{4}^{Σ} = ϕ^{Σ}

), and complete magnetic potential (

U_{5}^{Σ} = ψ^{Σ}

). They therefore read:

U_{I}^{Σ} = \sum_{p = 1, 3, 5} F^{(p)} U_{I}^{0 (p)} \exp [j k (x_{1} + n_{3}^{(p)} x_{3} - V_{ph} t)]

, where the index I is equal to 2, 4, 5. It is obvious that the studied case represents a three-partial SH-wave because p = 1, 3, 5. Let’s further use F₁, F₂, and F₃ instead of the weight factors F⁽¹⁾, F⁽³⁾, and F⁽⁵⁾, respectively. Let’s also to further employ F = F₁ + F₂ because there are two identical eigenvalues defined in the context after expression (2) that actually give two identical eigenvectors. Using F and F₃, the studied three-partial case can represent a hidden two-partial SH-wave.

Exploiting the complete parameters in different mechanical, electrical, and magnetic boundary conditions at the interface between the PEM solid and a vacuum, various determinants of the boundary conditions can be composed. Possible boundary conditions for the treated case of the wave propagation along the free surface of the PEM solid were perfectly described by Al’shits et al. (1992). In this study, the used mechanical boundary condition at the interface is for the normal component of the stress tensor: σ₃₂ = 0. The electrical boundary conditions at the interface are the continuity of the electrical potential φ and the continuity of the normal component of the electrical displacement D₃, namely φ = φ^f and D₃ = D^f, where the superscript “f” belongs to the free space. Besides, the used magnetic ones are continuity of the magnetic potential ψ and the continuity of the normal component of the magnetic displacement B₃: ψ = ψ^f and B₃ = B^f. It is unnecessary to write down all the explicit forms for the five boundary conditions resulting in a set of three homogeneous equations for the determination of the suitable propagation velocity of a new SH-SAW. To be familiar with the complete procedure, the reader can find book (Zakharenko, 2010) and open access papers (Zakharenko, 2013a, 2015a). It is now possible to give some vacuum parameters: the dielectric permittivity constant ε₀ = 8.854187817 × 10^–12 [F/m] and the magnetic permeability constant μ₀ = 12.5663706144 × 10^–7 [H/m]. These vacuum constants will present below in the final results for the propagation velocity of the SH-wave and are crucial for the wave existence. Indeed, Laplace’s equations such as Δφ^f = 0 and Δψ^f = 0 must be written for the potentials in a vacuum and they must exponentially vanish in a vacuum far from the free surface of the PEM medium. Utilizing the vacuum constants, let’s consider additional two new cases unrecorded in book (Zakharenko, 2010) and papers (Zakharenko, 2013a, 2015a,b ).The treated two new cases (i) and (ii) below pertain to the third coupling mechanism of the CMEMC such as $ε μ - α^{2}$ that is actually responsible for the ME effect. Taking into account the aforementioned vacuum parameters, the third coupling mechanism can be rewritten in the form of $[(ε + ε_{0}) (μ + μ_{0}) - α^{2}]$ instead.

(i) Using first eigenvectors (3) for the aforementioned five boundary conditions (σ₃₂ = 0, φ = φ^f, D₃ = D^f, ψ = ψ^f, B₃ = B^f) it is possible to construct corresponding five homogeneous equations with the weight factors F₁, F₂, F₃, F_E and F_M. It is usual to find function F_E(F₁, F₂, F₃) from one suitable equation and the function F_M(F₁, F₂, F₃) from the other one and to substitute them into the rest equations in order to exclude the vacuum weight factors F_E and F_M. So, one naturally deals now with three homogeneous equations in three unknowns F₁, F₂, and F₃. Finally, it is possible to compose three consistent equations when the first one represents a sum of the rest two. Using F = F₁ + F₂, they read:

(5)

\{\begin{matrix} (ε μ + ε_{0} μ + ε μ_{0} + ε_{0} μ_{0} - α^{2}) [F + F_{3} b (1 + K_{em}^{2}) / K_{em}^{2}] = 0 \\ ε_{0} (μ + μ_{0}) [F + F_{3} (K_{em}^{2} - K_{α}^{2}) / K_{em}^{2}] = 0 \\ F [ε (μ + μ_{0}) - α^{2}] + F_{3} ε μ_{0} (K_{em}^{2} - K_{e}^{2}) / K_{em}^{2} = 0 \end{matrix}

where

b^{2} = 1 - {(V_{ph} / V_{tem})}^{2}

; the nondimensional parameter

K_{e}^{2} = e^{2} / C ε

is called the coefficient of the electromechanical coupling (CEMC) and

K_{α}^{2} = eh / C α

is also the nondimensional coefficient combining the terms with the electromagnetic constant α in the CMEMC.

To obtain the first new result, it is indispensable in set (5) to successively subtract the second and third equations form the first. As a result, the explicit form for the calculation of the velocity of the fourteenth new SH-SAW is given by the following expression:

(6)

V_{new 14} = V_{tem} {[1 - {(\frac{\frac{μ_{0}}{μ} (K_{em}^{2} - K_{e}^{2}) + \frac{ε_{0}}{ε} (1 + \frac{μ_{0}}{μ}) (K_{em}^{2} - K_{α}^{2})}{(1 + K_{em}^{2}) (1 + \frac{ε_{0}}{ε} + \frac{μ_{0}}{μ} + \frac{ε_{0} μ_{0} - α^{2}}{ε μ})})}^{2}]}^{1 / 2}

If one would like to consider only dependence on ε₀, i.e. µ₀ = 0 in expression (6), the velocity V_new₁₄ reduces to the following form:

(7)

V_{new 14} (μ_{0} = 0) = V_{tem} {[1 - {(\frac{ε_{0} μ}{(ε + ε_{0}) μ - α^{2}} \frac{K_{em}^{2} - K_{α}^{2}}{1 + K_{em}^{2}})}^{2}]}^{1 / 2}

(ii) Exploiting second eigenvectors (4) for the same boundary conditions, three consistent equations can be also constructed when the first equation represents a sum of the other two. The equations read:

(8)

\{\begin{matrix} (ε μ + ε_{0} μ + ε μ_{0} + ε_{0} μ_{0} - α^{2}) [F + F_{3} b (1 + K_{em}^{2}) / K_{em}^{2}] = 0 \\ F [(ε + ε_{0}) μ - α^{2}] + F_{3} ε_{0} μ (K_{em}^{2} - K_{m}^{2}) / K_{em}^{2} = 0 \\ (ε + ε_{0}) μ_{0} [F + F_{3} (K_{em}^{2} - K_{α}^{2}) / K_{em}^{2}] = 0 \end{matrix}

In (8), the nondimensional characteristic

K_{m}^{2} = h^{2} / C μ

is called the coefficient of the magnetomechanical coupling (CMMC). A successive subtraction of the second and third equations from the first in set (8) leads to the second new result. Indeed, the velocity of the fifteenth new SH-SAW can be calculated with the following formula:

(9)

V_{new 15} = V_{tem} {[1 - {(\frac{\frac{ε_{0}}{ε} (K_{em}^{2} - K_{m}^{2}) + \frac{μ_{0}}{μ} (1 + \frac{ε_{0}}{ε}) (K_{em}^{2} - K_{α}^{2})}{(1 + K_{em}^{2}) (1 + \frac{ε_{0}}{ε} + \frac{μ_{0}}{μ} + \frac{ε_{0} μ_{0} - α^{2}}{ε μ})})}^{2}]}^{1 / 2}

In the case of ε₀ = 0, it reduces to the following form:

(10)

V_{new 15} (ε_{0} = 0) = V_{tem} {[1 - {(\frac{ε μ_{0}}{ε (μ + μ_{0}) - α^{2}} \frac{K_{em}^{2} - K_{α}^{2}}{1 + K_{em}^{2}})}^{2}]}^{1 / 2}

It is now essential to stress the peculiarity existing in final results (6) and (9). It is clearly seen in expressions (6) and (9) that they depend on the coefficient

K_{α}^{2} = eh / C α

. This coefficient approaches an infinity when α = 0. If

K_{α}^{2}

is large enough, i.e. the electromagnetic constant α is small enough, the propagating new SH-SAWs cannot exist due to the dissipation, i.e. the velocities V_new₁₄ in (6) and V_new₁₅ in (9) become imaginary. This means that there can exist a dramatic dependence on small values of α. In general, the value of α is small for real PEM solids. It is expected that these new SH-SAWs can propagate only in selective PEM solids with the strong enough ME effect. However, this peculiarity vanishes when ε₀ = 0 in expression (6) and µ₀ = 0 in expression (9). Therefore, the corresponding vacuum parameters are crucial for the existence of the peculiarity. The following section compares the obtained new results with the previously found wave phenomena.

3 Comparison with previous results and the phenomenon called the Goldstone excitation

First of all, it is natural to compare the obtained 14th and 15th new SH-SAWs in this report with the 8th and 10th new SH-SAWs discovered in papers (Zakharenko, 2013a) and (Zakharenko, 2015a), respectively. These all mentioned four new SH-SAWs allow some dissipation at small enough values of the electromagnetic constant α. This phenomenon was briefly discussed to the end of the previous section. This phenomenon of dissipation can exist for the 14th and 10th new SH-SAWs only if the vacuum electric constant ε₀ is taken into account. Moreover, the dependence of the 10th new SH-SAW on ε₀ is vital because ε₀ = 0 cancels the SH-BAW instability, i.e. V_new₁₀(ε₀ = 0) = V_tem, see formula (60) in paper Zakharenko, 2015a. Also, V_new₁₄(ε₀ = 0) in formula (6) written in the previous section does not reduce to V_tem. It is now possible to compare 15th and 8th new SH-SAWs. The phenomenon of dissipation exists for these new waves only if the vacuum magnetic constant µ₀ is taken into account. Analogically, µ₀ = 0 actually annuls the SH-BAW instability, i.e. V_new₈(µ₀ = 0) = V_tem, see formula (73) in paper Zakharenko (2013a). However, it is allowable for the 15th new SH-SAW existence: V_new₁₅(µ₀ = 0) ≠ V_tem.

Fig. 1 shows the dependencies of the velocities of the nondispersive 8th, 10th, 14th, and 15th new SH-SAWs on the small values of the electromagnetic constant α. The material parameters for the PEM composite materials BaTiO₃–CoFe₂O₄ and PZT-5H–Terfenol-D were borrowed from papers (Zakharenko, 2011, 2014b, 2015b ). The first and second solids are relatively weak and significantly stronger PEMs, respectively, that provides a contrast for comparison. It is clearly seen in the figure that the dissipation phenomenon corresponding to imaginary velocity appears at significantly smaller values of the constant α for the weaker PEM BaTiO₃–CoFe₂O₄. The reader can readily evaluate the threshold values of (α²/εµ)_th from the figure. Also, it is natural that at small values of the α, the normalized velocities of the 8th and 15th new SH-SAWs only slightly differ from each other and this difference is larger for the stronger PEM PZT-5H–Terfenol-D. It worth mentioning that for this pair of the new SH-SAWs, the vacuum parameter µ₀ is crucial for the existence of the dissipation phenomenon. For PZT-5H–Terfenol-D, the normalized velocities of the 8th and 15th new SH-SAWs are equal to zero at α²/εµ = 0.86 and 1.0, respectively. Concerning the 10th and 14th new SH-SAWs’ normalized velocities at small values of α²/εµ, they look like they coincide for both the studied composites. For this pair of new SH-SAWs, the vacuum parameter ε₀ is vital for the existence of the dissipation phenomenon. However, for α²/εµ → 1, the 10th and 14th new SH-SAWs’ normalized velocities approach 1 and 0, respectively. With the found characteristics of the 14th and 15th new SH-SAWs, it is also necessary to perform a further theoretical study on dispersive wave propagation in plates similar to research (Zakharenko, 2015c), in which the speeds of the corresponding new dispersive waves approach the nondispersive 8th new SH-SAW speed at large values of the plate thickness. It is expected that new disposition relations can be more complicated than those obtained in paper (Zakharenko, 2015c). The two-dimensional structures (plates) can be suitable for further miniaturization of some technical devices including ones with a high level of integration. It is also natural to use the dissipation phenomenon around the threshold values of (α²/εµ)_th for constitution of various smart technical devices such as switches, delay lines, computer logics, etc.Next, it is possible to compare the obtained theoretical results (6) and (9) with those theoretically obtained in 2007 papers (Wang et al., 2007; Liu et al., 2007). The authors of references (Wang et al., 2007; Liu et al., 2007) have used the same coupled equations of motion (1) for the PEM SH-wave propagation coupled with both the electrical and magnetic potentials. Their final results for the PEM SH-wave propagation velocities also depend on both the vacuum parameters ε₀ and µ₀ but different from each other, see formula (27) introduced in review (Zakharenko, 2013b) in the convenient form for comparison. This is similar to results (6) and (9) obtained in this short report. Review (Zakharenko, 2013b) has also stated that their results are incorrect, even fake, because they have mixed different eigenvectors (3) and (4). So, their incorrect results for the propagation velocities do not allow any dissipation at some small values of the electromagnetic constant α because there is no dependence on the coefficient $K_{α}^{2}$ . Instead of that, they have even introduced their results in very complicated forms unsuitable for any comparison.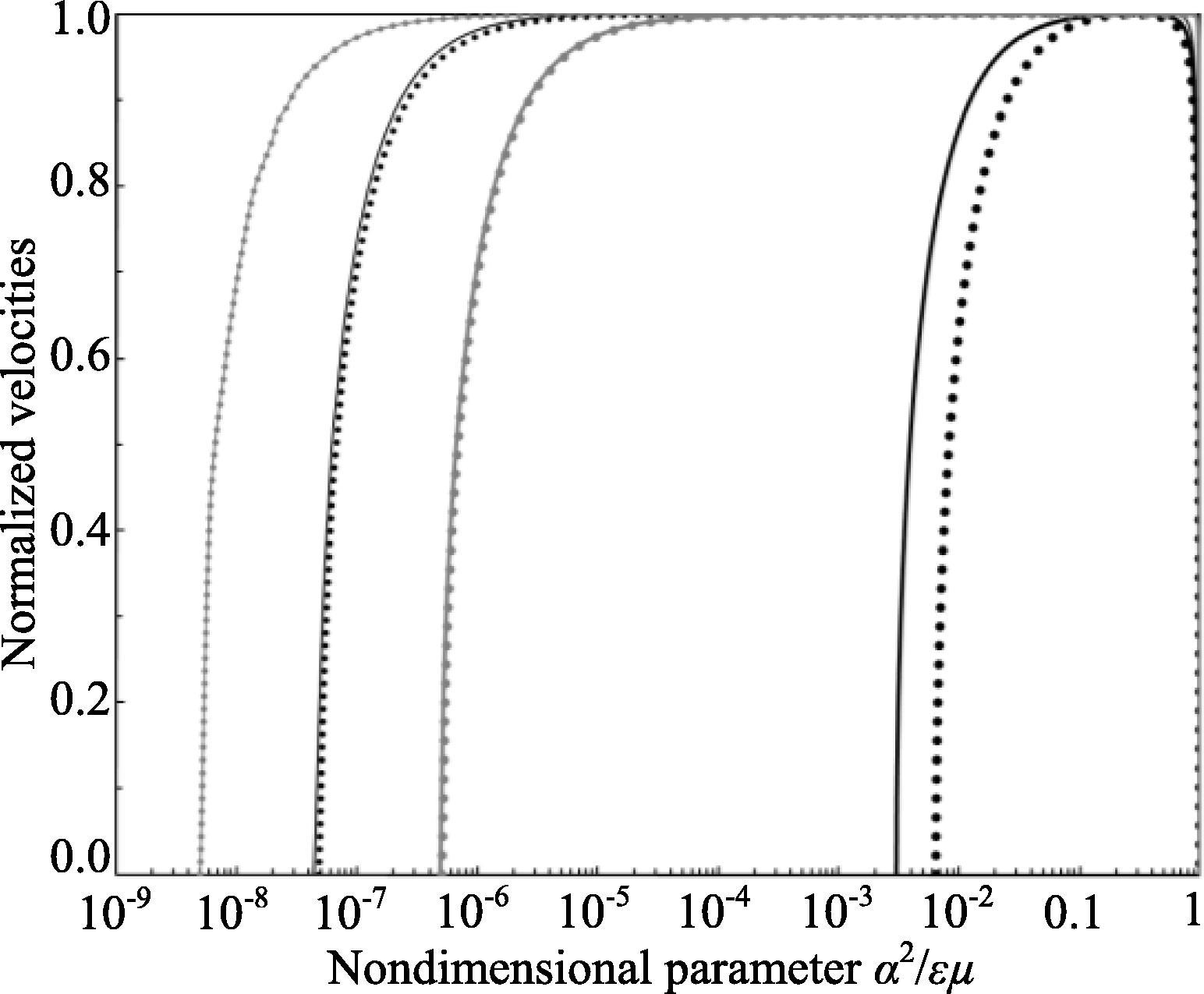

The normalized velocities Vnew8 (big dots), Vnew10 (smaller dots), Vnew14 (thin solid lines), and Vnew15 (thick solid lines) versus α2/εµ: for BaTiO3–CoFe2O4 (grey) and PZT-5H–Terfenol-D (black).

The author has to state that the final part of this section is written for further discussions and is based on some interesting comments of one of the first readers (referees, namely Professor Dr. V.G. Shavrov) of my previous work (Zakharenko, 2013a, 2015a,b ). It concerns the theory developed in the 1960s (Wagner, 1966; Goldstone, 1961; Nambu, 1960 ), namely the Goldstone excitation phenomenon pertaining to quantum nongap long-wavelength elementary excitations. These excitations can be associated with some longitudinal phonons in crystals, phonons in the superfluid helium-II and superconductors, magnons in magnetic systems. Following the Shavrov comments and using the condition of thermodynamic stability α² < εµ (Özgür et al., 2009; Fiebig, 2005), the threshold of the Goldstone excitation is defined by

(11)

\frac{ε μ eh}{C ε μ + μ e^{2} + ε h^{2}} > α or \frac{K_{α}^{2}}{1 + K_{e}^{2} + K_{m}^{2}} > 1

It is clearly seen in inequality (11) that the fraction numerator depends on the electromagnetic constant α because the coefficient

K_{α}^{2} = eh / C α

defined after Eq. (5) depends on the α. Concerning the fraction denominator in inequality (11), it does not depend on the α because

K_{em}^{2} (α = 0) = K_{e}^{2} + K_{m}^{2}

. It is also possible to discuss that the α can have a negative sign and therefore, it is possible to deal with the absolute values to compare the left and right sides in inequality (11). If the reader would also like to associate one of the four new SH-SAWs discussed in this section with the Goldstone excitation, the author has to state that Goldstone excitation threshold (11) and therefore, their theory leading to the threshold is incorrect because this theory does not take into account any vacuum parameters, ε₀ or µ₀. Indeed, the dissipation phenomenon discussed in the context above can exist for the four new SH-SAWs at small enough values of the electromagnetic constant α only if the corresponding vacuum constants are taken into account and therefore does not relate to the Goldstone excitation phenomenon. Also, it is necessary to mention that there are three different branches of the acoustic excitations in solids and they can relate to the possible three bulk acoustic waves (BAWs). So, the discovered different new SH-SAWs caused by different mechanisms, for instance, by the ME effect, represent an instability of the same SH-BAW under action of various mechanical, electrical, and magnetic boundary conditions and relate to the same SH-BAW branch but not to some additional branches.

4 Conclusion

This short theoretical report has examined extra two new SH-SAWs, the propagation of which in the transversely isotropic PEM solids can dramatically depend on the magnetoelectric effect characterized by the electromagnetic constant α. It was discussed that taking into account the corresponding vacuum parameter in the new SH-SAW velocity expression allows the existence of the dissipation phenomenon at small values of α. So, some comparison with the previously obtained theoretical results and the phenomenon called the Goldstone excitation was performed. The theoretically obtained new results can be handy for educational purposes and even creation of suitable technical devices based on the ME effect for spintronics. Also, it is recommended that further theoretical researches of the SH-wave propagation in plates must be carried out that can be called for nondestructive testing and evaluation of apt surfaces and plates, etc. It is possible that some gravitational phenomena can be applied as an addiction to the electromagnetic properties or instead of them. These gravitational phenomena were discussed in recently developed theory (Zakharenko, 2016).

Acknowledgements

The author would like to thank to RAS Academician Yury Vasilievich Gulyaev and Professor Dr. Vladimir Grigorievich Shavrov for their useful notes for some my previous work that resulted in the appearance of this further theoretical work concerning the existence of extra two new PEM-SH-SAWs.

References

Al’shits V.I., Darinskii A.N., Lothe J., . On the existence of surface waves in half-infinite anisotropic elastic media with piezoelectric and piezomagnetic properties. Wave Motion. 1992;16(3):265-283.
[Google Scholar]
Auld B.A., . Acoustic Fields and Waves in Solids, Volumes I and II (set of two volumes) (second ed.). Krieger Publishing Company; 1990. 878 pages
Bleustein J.L., . A new surface wave in piezoelectric materials. Appl. Phys. Lett.. 1968;13(12):412-413.
[Google Scholar]
Dieulesaint E., Royer D., . Elastic Waves in Solids: Applications to Signal Processing/translated. In: Bastin A., Motz M., eds. Chichester [English]. New York: J. Wiley; 1980. 511 pages
[Google Scholar]
Fiebig M., . Revival of the magnetoelectric effect. J. Phys. D Appl. Phys.. 2005;38(8):R123-R152.
[Google Scholar]
Fusil S., Garcia V., Barthélémy A., Bibes M., . Magnetoelectric devices for spintronics. Annu. Rev. Mater. Res.. 2014;44(1):91-116.
[CrossRef] [Google Scholar]
Goldstone J., . Field theories with “superconductor” solutions. Nuovo Cimento. 1961;19(1):154-164.
[Google Scholar]
Gulyaev Yu.V., . Electroacoustic surface waves in solids. Sov. Phys. J. Exp. Theor. Phys. Lett.. 1969;9(1):37-38.
[Google Scholar]
Gulyaev Yu.V., . Review of shear surface acoustic waves in solids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998;45(4):935-938.
[Google Scholar]
Hirao M., Ogi H., . EMATs for Science and Industry: Non-contacting Ultrasonic Measurements, Boston. MA: Kluwer Academic; 2003.
Hu J.-M., Chen L.-Q., Nan C.-W., . Multiferroic heterostructures integrating ferroelectric and magnetic materials. Adv. Mater.. 2016;28(1):15-39.
[Google Scholar]
Jartych E., Pikula T., Kowal K., Dzik J., Guzdek P., Czekaj D., . Magnetoelectric effect in ceramics based on bismuth ferrite. Nanoscale Res. Lett.. 2016;11:234. 8 pages
[CrossRef] [Google Scholar]
Kimura T., . Magnetoelectric hexaferrites. Ann. Rev. Condens. Matter Phys.. 2012;3(1):93-110.
[Google Scholar]
Lardat C., Maerfeld C., Tournois P., . Theory and performance of acoustical dispersive surface wave delay lines. Proc. IEEE. 1971;59(3):355-364.
[Google Scholar]
Liu J.-X., Fang D.-N., Liu X.-L., . A shear horizontal surface wave in magnetoelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007;54(7):1287-1289.
[Google Scholar]
Melkumyan A., . Twelve shear surface waves guided by clamped/free boundaries in magneto-electro-elastic materials. Int. J. Solids Struct.. 2007;44(10):3594-3599.
[Google Scholar]
Nambu Yo., . Quasi-particles and gauge invariance in the theory of superconductivity. Phys. Rev.. 1960;117(3):648-663.
[Google Scholar]
Özgür Ü., Alivov Ya., Morkoç H., . Microwave ferrites, part 2: passive components and electrical tuning. J. Mater. Sci.: Mater. Electron.. 2009;20(10):911-952.
[Google Scholar]
Pullar R.C., . Hexagonal ferrites: a review of the synthesis, properties and applications of hexaferrite ceramics. Prog. Mater Sci.. 2012;57(7):1191-1334.
[Google Scholar]
Ribichini R., Cegla F., Nagy P.B., Cawley P., . Quantitative modeling of the transduction of electromagnetic acoustic transducers operating on ferromagnetic media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010;57(12):2808-2817.
[Google Scholar]
Srinivasan G., . Magnetoelectric composites. Annu. Rev. Mater. Res.. 2010;40(1):153-178.
[Google Scholar]
Thompson R.B., . Physical principles of measurements with EMAT transducers. In: Mason W.P., Thurston R.N., eds. Physical Acoustics. Vol vol. 19. New York, NY: Academic Press; 1990. p. :157-200.
[Google Scholar]
Wagner H., . Long-wavelength excitations and the Goldstone theorem in many-particle systems with “broken symmetries”. Z. Phys.. 1966;195(3):273-299.
[Google Scholar]
Wang B.L., Mai Y.-W., Niraula O.P., . A horizontal shear surface wave in magnetoelectroelastic materials. Philos. Mag. Lett.. 2007;87(1):53-58.
[Google Scholar]
Wei W.-Y., Liu J.-X., Fang D.-N., . Existence of shear horizontal surface waves in a magneto-electro-elastic material. Chin. Phys. Lett.. 2009;26(10):104301. 3 pages
[Google Scholar]
Zakharenko A.A., . Propagation of Seven New SH-SAWs in Piezoelectromagnetics of Class 6 mm. Saarbruecken – Krasnoyarsk, LAP LAMBERT Academic Publishing GmbH Co. KG; 2010. 84 pages, 2010, ISBN: 978-3-8433-6403-4
Zakharenko A.A., . Analytical investigation of surface wave characteristics of piezoelectromagnetics of class 6 mm. ISRN Appl. Math. 2011 Article ID 408529, 8 pages
[CrossRef] [Google Scholar]
Zakharenko A.A., . On wave characteristics of piezoelectromagnetics. Pramana – J. Phys. (Indian Academy of Science). 2012;79(2):275-285.
[Google Scholar]
Zakharenko A.A., . New nondispersive SH-SAWs guided by the surface of piezoelectromagnetics. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2013;7(3):2557-2570.
[Google Scholar]
Zakharenko A.A., . Piezoelectromagnetic SH-SAWs: a review. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2013;7(1):2227-2240.
[Google Scholar]
Zakharenko A.A., . Peculiarities study of acoustic waves' propagation in piezoelectromagnetic (composite) materials. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2013;7(2):2459-2461.
[Google Scholar]
Zakharenko A.A., . Some problems of finding of eigenvalues and eigenvectors for SH-wave propagation in transversely isotropic piezoelectromagnetics. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2014;8(1):2783-2787.
[Google Scholar]
Zakharenko A.A., . Investigation of SH-wave fundamental modes in piezoelectromagnetic plate: Electrically closed and magnetically closed boundary conditions. Open J. Acoust. (Scientific Research Publishing, California, USA). 2014;4(2):90-97.
[Google Scholar]
Zakharenko A.A., . A study of new nondispersive SH-SAWs in magnetoelectroelastic medium of symmetry class 6 mm. Open J. Acoust. (Scientific Research Publishing, Los Angeles, California, USA). 2015;5(3):95-111.
[Google Scholar]
Zakharenko A.A., . Dramatic influence of the magnetoelectric effect on the existence of the new SH-SAWs propagating in magnetoelectroelastic composites. Open J. Acoust. (Scientific Research Publishing, Los Angeles, California, USA). 2015;5(3):73-87.
[CrossRef] [Google Scholar]
Zakharenko A.A., . On new dispersive SH-waves propagating in piezoelectromagnetic plates. Open J. Acoust. (Scientific Research Publishing, Los Angeles, California, USA). 2015;5(3):122-137.
[Google Scholar]
Zakharenko A.A., . On piezogravitocogravitoelectromagnetic shear-horizontal acoustic waves. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2016;10(3):4011-4028.
[Google Scholar]

Introduction

Two new PEM SH-SAWs

Comparison with previous results and the phenomenon called the Goldstone excitation

Conclusion

Fulltext Views
5

PDF downloads
1

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Al’shits V.I., Darinskii A.N., Lothe J., . On the existence of surface waves in half-infinite anisotropic elastic media with piezoelectric and piezomagnetic properties. Wave Motion. 1992;16(3):265-283.
[Google Scholar]

[2] Auld B.A., . Acoustic Fields and Waves in Solids, Volumes I and II (set of two volumes) (second ed.). Krieger Publishing Company; 1990. 878 pages

[3] Bleustein J.L., . A new surface wave in piezoelectric materials. Appl. Phys. Lett.. 1968;13(12):412-413.
[Google Scholar]

[4] Dieulesaint E., Royer D., . Elastic Waves in Solids: Applications to Signal Processing/translated. In: Bastin A., Motz M., eds. Chichester [English]. New York: J. Wiley; 1980. 511 pages
[Google Scholar]

[5] Fiebig M., . Revival of the magnetoelectric effect. J. Phys. D Appl. Phys.. 2005;38(8):R123-R152.
[Google Scholar]

[6] Fusil S., Garcia V., Barthélémy A., Bibes M., . Magnetoelectric devices for spintronics. Annu. Rev. Mater. Res.. 2014;44(1):91-116.
[CrossRef] [Google Scholar]

[7] Goldstone J., . Field theories with “superconductor” solutions. Nuovo Cimento. 1961;19(1):154-164.
[Google Scholar]

[8] Gulyaev Yu.V., . Electroacoustic surface waves in solids. Sov. Phys. J. Exp. Theor. Phys. Lett.. 1969;9(1):37-38.
[Google Scholar]

[9] Gulyaev Yu.V., . Review of shear surface acoustic waves in solids. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998;45(4):935-938.
[Google Scholar]

[10] Hirao M., Ogi H., . EMATs for Science and Industry: Non-contacting Ultrasonic Measurements, Boston. MA: Kluwer Academic; 2003.

[11] Hu J.-M., Chen L.-Q., Nan C.-W., . Multiferroic heterostructures integrating ferroelectric and magnetic materials. Adv. Mater.. 2016;28(1):15-39.
[Google Scholar]

[12] Jartych E., Pikula T., Kowal K., Dzik J., Guzdek P., Czekaj D., . Magnetoelectric effect in ceramics based on bismuth ferrite. Nanoscale Res. Lett.. 2016;11:234. 8 pages
[CrossRef] [Google Scholar]

[13] Kimura T., . Magnetoelectric hexaferrites. Ann. Rev. Condens. Matter Phys.. 2012;3(1):93-110.
[Google Scholar]

[14] Lardat C., Maerfeld C., Tournois P., . Theory and performance of acoustical dispersive surface wave delay lines. Proc. IEEE. 1971;59(3):355-364.
[Google Scholar]

[15] Liu J.-X., Fang D.-N., Liu X.-L., . A shear horizontal surface wave in magnetoelectric materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007;54(7):1287-1289.
[Google Scholar]

[16] Melkumyan A., . Twelve shear surface waves guided by clamped/free boundaries in magneto-electro-elastic materials. Int. J. Solids Struct.. 2007;44(10):3594-3599.
[Google Scholar]

[17] Nambu Yo., . Quasi-particles and gauge invariance in the theory of superconductivity. Phys. Rev.. 1960;117(3):648-663.
[Google Scholar]

[18] Özgür Ü., Alivov Ya., Morkoç H., . Microwave ferrites, part 2: passive components and electrical tuning. J. Mater. Sci.: Mater. Electron.. 2009;20(10):911-952.
[Google Scholar]

[19] Pullar R.C., . Hexagonal ferrites: a review of the synthesis, properties and applications of hexaferrite ceramics. Prog. Mater Sci.. 2012;57(7):1191-1334.
[Google Scholar]

[20] Ribichini R., Cegla F., Nagy P.B., Cawley P., . Quantitative modeling of the transduction of electromagnetic acoustic transducers operating on ferromagnetic media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2010;57(12):2808-2817.
[Google Scholar]

[21] Srinivasan G., . Magnetoelectric composites. Annu. Rev. Mater. Res.. 2010;40(1):153-178.
[Google Scholar]

[22] Thompson R.B., . Physical principles of measurements with EMAT transducers. In: Mason W.P., Thurston R.N., eds. Physical Acoustics. Vol vol. 19. New York, NY: Academic Press; 1990. p. :157-200.
[Google Scholar]

[23] Wagner H., . Long-wavelength excitations and the Goldstone theorem in many-particle systems with “broken symmetries”. Z. Phys.. 1966;195(3):273-299.
[Google Scholar]

[24] Wang B.L., Mai Y.-W., Niraula O.P., . A horizontal shear surface wave in magnetoelectroelastic materials. Philos. Mag. Lett.. 2007;87(1):53-58.
[Google Scholar]

[25] Wei W.-Y., Liu J.-X., Fang D.-N., . Existence of shear horizontal surface waves in a magneto-electro-elastic material. Chin. Phys. Lett.. 2009;26(10):104301. 3 pages
[Google Scholar]

[26] Zakharenko A.A., . Propagation of Seven New SH-SAWs in Piezoelectromagnetics of Class 6 mm. Saarbruecken – Krasnoyarsk, LAP LAMBERT Academic Publishing GmbH Co. KG; 2010. 84 pages, 2010, ISBN: 978-3-8433-6403-4

[27] Zakharenko A.A., . Analytical investigation of surface wave characteristics of piezoelectromagnetics of class 6 mm. ISRN Appl. Math. 2011 Article ID 408529, 8 pages
[CrossRef] [Google Scholar]

[28] Zakharenko A.A., . On wave characteristics of piezoelectromagnetics. Pramana – J. Phys. (Indian Academy of Science). 2012;79(2):275-285.
[Google Scholar]

[29] Zakharenko A.A., . New nondispersive SH-SAWs guided by the surface of piezoelectromagnetics. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2013;7(3):2557-2570.
[Google Scholar]

[30] Zakharenko A.A., . Piezoelectromagnetic SH-SAWs: a review. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2013;7(1):2227-2240.
[Google Scholar]

[31] Zakharenko A.A., . Peculiarities study of acoustic waves' propagation in piezoelectromagnetic (composite) materials. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2013;7(2):2459-2461.
[Google Scholar]

[32] Zakharenko A.A., . Some problems of finding of eigenvalues and eigenvectors for SH-wave propagation in transversely isotropic piezoelectromagnetics. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2014;8(1):2783-2787.
[Google Scholar]

[33] Zakharenko A.A., . Investigation of SH-wave fundamental modes in piezoelectromagnetic plate: Electrically closed and magnetically closed boundary conditions. Open J. Acoust. (Scientific Research Publishing, California, USA). 2014;4(2):90-97.
[Google Scholar]

[34] Zakharenko A.A., . A study of new nondispersive SH-SAWs in magnetoelectroelastic medium of symmetry class 6 mm. Open J. Acoust. (Scientific Research Publishing, Los Angeles, California, USA). 2015;5(3):95-111.
[Google Scholar]

[35] Zakharenko A.A., . Dramatic influence of the magnetoelectric effect on the existence of the new SH-SAWs propagating in magnetoelectroelastic composites. Open J. Acoust. (Scientific Research Publishing, Los Angeles, California, USA). 2015;5(3):73-87.
[CrossRef] [Google Scholar]

[36] Zakharenko A.A., . On new dispersive SH-waves propagating in piezoelectromagnetic plates. Open J. Acoust. (Scientific Research Publishing, Los Angeles, California, USA). 2015;5(3):122-137.
[Google Scholar]

[37] Zakharenko A.A., . On piezogravitocogravitoelectromagnetic shear-horizontal acoustic waves. Can. J. Pure Appl. Sci. (SENRA Academic Publishers, Burnaby, British Columbia, Canada). 2016;10(3):4011-4028.
[Google Scholar]