On s-weakly gw-closed sets in w-spaces

Won Keun Min

doi:10.1016/j.jksus.2017.05.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

30 (

); 479-482

doi:

10.1016/j.jksus.2017.05.004

On s-weakly gw-closed sets in w-spaces

Won Keun Min

Department of Mathematics, Kangwon National University, Chuncheon, 24341 Republic of Korea

Received: 2017-2-8, Accepted: 2017-5-3, Published: 2017-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

The purpose of this note is to introduce the notion of s-weakly gw-closed set in w-spaces and to study its some basic properties. In particular, the relationships among wg-closed sets, w-semi-closed sets and s-weakly g-closed sets are investigated.

Keywords

gw-closed

Weakly gw-closed

s-weakly gw-closed

Show Related Articles from PubMed

1 Introduction

In (Siwiec, 1974), the author introduced the notions of weak neighborhoods and weak base in a topological space. We introduced the weak neighborhood systems defined by using the notion of weak neighborhoods in (Min, 2008). The weak neighborhood system induces a weak neighborhood space which is independent of neighborhood spaces (Kent and Min, 2002) and general topological spaces (Csázár, 2002). The notions of weak structure and w-space were investigated in (Kim and Min, 2015). In fact, the set of all g-closed subsets (Levine, 1970) in a topological space is a kind of weak structure. We introduced the notion of gw-closed set in (Min and Kim, 2016a) and some its basic properties. In (Min, 2017), we introduced and studied the notion of weakly gw-closed sets for the sake of extending the notion of gw-closed sets in w-spaces. The purpose of this note is to extend the notion of gw-closed sets in w-spaces in a different way than the notion of weakly gw-closed sets. So, we introduce the new notion of s-weakly gw-closed sets in weak spaces, and investigate its properties. In particular, the relationships among weakly wg-closed sets, w-semi-closed sets and s-weakly g-closed sets are investigated.

2 Preliminaries

Let S be a subset of a topological space X. The closure (resp., interior) of S will be denoted by clS (resp., intS). A subset S of X is called a pre-open (Mashhour et al., 1982) (resp., $α$ -open (Njastad, 1964), semi-open (Levine, 1963)) set if $S \subset int (cl (S))$ (resp., $S \subset int (cl (int (S))), S \subset cl (int (S)))$ . The complement of a pre-open (resp., $α$ -open, semi-open) set is called a pre-closed (resp., $α$ -closed, semi-closed) set. The family of all pre-open (resp., $α$ -open, semi-open) sets in X will be denoted by $PO (X)$ (resp., $α (X), SO (X)$ ). The $δ$ -interior of a subset A of X is the union of all regular open sets of X contained in A and it is denoted by $δ - int (A)$ (Velicko, 1968). A subset A is called $δ - open$ if $A = δ - int (A)$ . The complement of a $δ - openset$ is called $δ - closed$ . The $δ - closure$ of a set A in a space $(X, τ)$ is defined by ${x \in X : A \cap int (cl (B)) \neq, B \in τ and x \in B}$ and it is denoted by $δ - cl (A)$ . A subset A of a space $(X, δ)$ is said $a - open$ (Ekici, 2008) if $A \subseteq int (cl (δ - int (A)))$ and $a - closed$ if $A \subseteq cl (int (δ - cl (A)))$ . And A is said $ω^{*}$ -open (Ekici and Jafari, 2010) if for every $x \in V$ , there exists an open subset $U \subseteq X$ containing x such that $U - δ - int (A)$ is countable. The family of all a-open (resp., $ω^{*}$ -open) sets in X will be denoted by $aO (X)$ (resp., $ω^{*} O (X)$ ).

A subset A of a topological space $(X, τ)$ is said to be:

g-closed (Levine, 1970) if $cl (A) \subseteq U$ whenever $A \subseteq U$ and U is open in X;
gp-closed (Noiri et al., 1998) if $pcl (A) \subseteq U$ whenever $A \subseteq U$ and U is open in X;
gs-closed (Arya and Nori, 1990) if $scl (A) \subseteq U$ whenever $A \subseteq U$ and U is open in X;
$g α$ -closed (Maki et al., 1994) if $τ^{α} cl (A) \subseteq U$ whenever $A \subseteq U$ and U is $α$ -open in X where $τ^{α} = α (X)$ ;

And the complement of a g-closed (resp., gp-closed, gs-closed, $g α$ -closed) set is called a g-open (resp., gp-open, gs-open, $g α$ -open) set. The family of all g-open (resp., gp-open sets, gs-open, $g α$ -open) sets in X will be denoted by $GO (X)$ (resp., $GPO (X), GSO (X), G α O (X)$ ).

Let X be a nonempty set. A subfamily $w_{X}$ of the power set $P (X)$ is called a weak structure (Kim and Min, 2015) on X if it satisfies the following:

$\emptyset \in w_{X}$ and $X \in w_{X}$ .
For $U_{1}, U_{2} \in w_{X}, U_{1} \cap U_{2} \in w_{X}$ .

Then the pair $(X, w_{X})$ is called a w-space on X. Then $V \in w_{X}$ is called a w-open set and the complement of a w-open set is a w-closed set.

Then the family $τ, α (X), GO (X), aO (X), ω^{*} O (X)$ and $g α O (X)$ are all weak structures on X. But $PO (X), SO (X), GPO (X)$ and $GSO (X)$ are not weak structures on X.

Let $(X, w_{X})$ be a w-space. For a subset A of X, the w-closure of A and the w-interior (Kim and Min, 2015) of A are defined as follows:

$wC (A) = \cap {F : A \subseteq F, X - F \in w_{X}}$ .
$wI (A) = \cup {U : U \subseteq A, U \in w_{X}}$ .

Theorem 2.1

[Kim and Min, 2015] Let $(X, w_{X})$ be a w-space and $A \subseteq X$ .

$x \in wI (A)$ if and only if there exists an element $U \in W (x)$ such that $U \subseteq A$ .
$x \in wC (A)$ if and only if $A \cap V \neq \emptyset$ for all $V \in W (x)$ .
If $A \subseteq B$ , then $wI (A) \subseteq wI (B); wC (A) \subseteq wC (B)$ .
$wC (X - A) = X - wI (A); wI (X - A) = X - wC (A)$ .
If A is w-closed (resp., w-open), then $wC (A) = A$ (resp., $wI (A) = A$ ).

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then A is called a generalized w-closed set (simply, gw-closed set) (Min and Kim, 2016a) if $wC (A) \subseteq U$ , whenever $A \subseteq U$ and U is w-open. If the $w_{X}$ -structure is a topology, the generalized w-closed set is exactly a generalized closed set in sense of Levine in (Levine, 1970). Obviously, every w-closed set is generalized w-closed, but in general, the converse is not true.

And A is called a weakly generalized w-closed set (simply, weakly gw-closed set) (Min, 2017) if $wC (wI (A)) \subseteq U$ whenever $A \subseteq U$ and U is w-open. Obviously, every gw-closed set is weakly gw-closed. In (Min, 2017), we showed that every w-pre-closed set (Min and Kim, 2016b) is weakly gw-closed.

3 Main results

Now, we introduce an extended notion of gw-closed sets in w-spaces as the following:

Definition 3.1

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then A is said to be s-weakly generalized w-closed (simply, s-weakly gw-closed) if $wI (wC (A)) \subseteq U$ whenever $A \subseteq U$ and U is w-open.

Obviously, the next theorem is obtained:

Theorem 3.2

Every gw-closed set is s-weakly g-closed.

Remark 3.3

In general, the converse of the above theorem is not true. Furthermore, there is no any relation between s-weakly gw-closed sets and weakly gw-closed sets as shown in the examples below:

Example 3.4

Let $X = {a, b, c}$ and $w = {\emptyset, {a}, {b}, X}$ be a weak structure in X. For a w-open set $A = {b}$ , note that $wI (A) = A, wC (A) = {b, c}$ and $wI (wC (A)) = wI ({b, c}) = A$ . So A is s-weakly gw-closed but not gw-closed. And since $wC (wI (A)) = {b, c}, A$ is also not weakly gw-closed.

Example 3.5

For $X = {a, b, c, d}$ , let $w = {\emptyset, {d}, {a, b}, {a, b, c}, X}$ be a structure in X. Consider $A = {a}$ . Then since $wI (A) = \emptyset$ , obviously A is weakly gw-closed. For a w-open set $U = {a, b}$ with $A \subseteq U, wI (wC (A)) = wI ({a, b, c}) = {a, b, c} \subseteq U$ . So A is not s-weakly gw-closed.

In general, the intersection as well as the union of two s-weakly gw-closed sets is not s-weakly gw-closed as shown in the next examples:

Example 3.6

For $X = {a, b, c, d}$ , let $w = {\emptyset, {a}, {b}, {c}, {a, c}, {a, c, d}, X}$ be a weak structure in X.

Let us consider $A = {a}$ and $B = {c}$ . Note that $wI (wC (A)) = wI ({a, d}) = A, wI (wC (B)) = wI ({c, d}) = B$ and $wI (wC (A \cup B)) = wI ({a, c, d}) = {a, c, d}$ . Then we know that A and B are all s-weakly gw-closed sets but the union $A \cup B$ is not s-weakly gw-closed.
Consider two s-weakly gw-closed sets $A = {a, b, c}$ and $B = {a, c, d}$ . Then $A \cap B = {a, c}$ is not s-weakly gw-closed in the above (1).

Theorem 3.7

Let $(X, w_{X})$ be a w-space. Then every w-semi-closed set is s-weakly gw-closed.

Proof

Let A be a w-semi-closed set and U be a w-open set containing A. Since $wI (wC (A)) \subseteq A$ , obviously it satisfies $wI (wC (A)) \subseteq U$ . It implies that A is s-weakly gw-closed. □

Remark 3.8

In (2) of Example 3.6, the s-weakly gw-closed set $A = {a, b, c}$ is not w-semi-closed. So, the converse of the above theorem is not always true.

From the above theorems and examples, the following relations are obtained: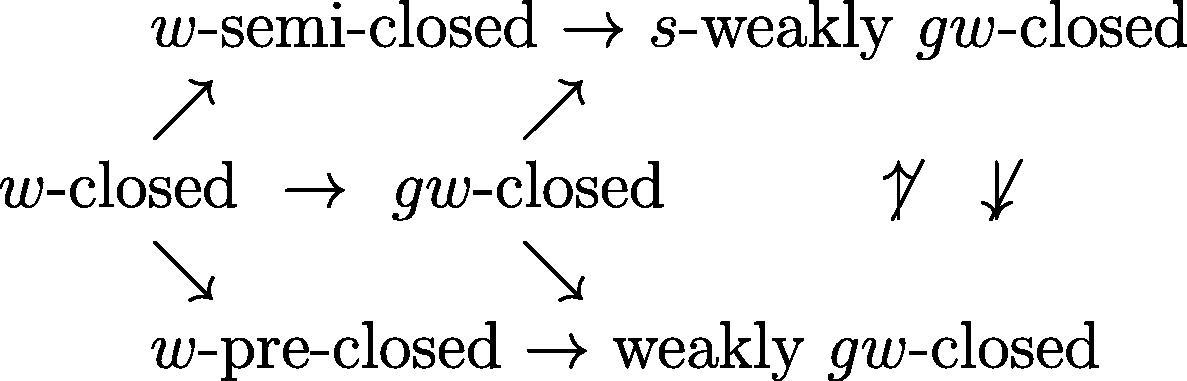

Let X be a nonempty set. Then a family $m (\subseteq P (X))$ of subsets of X is called a minimal structure (Maki, 1996) if $\emptyset, X \in m$ .

Theorem 3.9

Let $(X, w_{X})$ be a w-space. Then the family of all s-weakly gw-closed sets is a minimal structure in X.

Lemma 3.10

[Kim and Min, 2015] Let $(X, w_{τ})$ be a w-space and $A, B \subseteq X$ . Then the following things hold:

(1) $wI (A) \cap wI (B) = wI (A \cap B)$ .
(2) $wC (A) \cup wC (B) = wC (A \cup B)$ .

Let X be a w-space and $A \subseteq X$ . Then A is said to be w-semi-open (resp., w-semi-closed) (Min and Kim, 2016c) if $A \subseteq wC (wI (A))$ (resp., $wI (wC (A)) \subseteq A$ ).

Lemma 3.11

Let $(X, w_{X})$ be a w-space. Then for $A \subseteq X, A \cup wI (wC (A))$ is w-semi-closed.

Proof

From Lemma 3.10 and Theorem 2.1, $wI (wC (A \cup wI (wC (A)))) = wI (wC (A) \cup wC (wI (wC (A)))) = wI (wC (A)) \subseteq A \cup wI (wC (A))$ .

So, $A \cup wI (wC (A))$ is w-semi-closed. □

Lemma 3.12

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . If F is any w-semi-closed set such that $A \subseteq F$ , then $A \cup wI (wC (A)) \subseteq F$ .

Proof

Let F be a w-semi-closed set with $A \subseteq F$ . Then $wI (wC (A)) \subseteq wI (wC (F)) \subseteq F$ , and so $A \cup wI (wC (A)) \subseteq F$ . □

Let $(X, w_{X})$ be a w-space. For $A \subseteq X$ , the w-semi-closure (Min and Kim, 2016c) of A, denoted by $wsC (A)$ , is defined as:

$wsC (A) = \cap {F \subseteq X : A \subseteq F, F is w - semi - closed in X}$ .

Theorem 3.13

Let $(X, w_{X})$ be a w-space. Then for $A \subseteq X, wsC (A) = A \cup wI (wC (A))$ .

Proof

It is obtained from Lemma 3.11 and Lemma 3.12. □

Finally, we have the following theorem:

Theorem 3.14

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then A is s-weakly wg-closed if and only if $wsC (A) \subseteq U$ whenever $A \subseteq U$ and U is w-open.

Proof

Let A be an s-weakly gw-closed subset of X and let U be any w-open set such that $A \subseteq U$ . Then $wI (wC (A)) \subseteq U$ and $A \cup wI (wC (A)) \subseteq U$ . So, by Theorem 3.13, $wsC (A) \subseteq U$ .

For $A \subseteq X$ , suppose that $wsC (A) \subseteq U$ whenever $A \subseteq U$ and U is w-open. Let U be any w-open set with $A \subseteq U$ . Then from hypothesis and Theorem 3.13, $wI (wC (A)) \subseteq A \cup wI (wC (A)) = wsC (A) \subseteq U$ . Hence, A is s-weakly gw-closed. □

Recall that: Let X be a topological space and $A \subseteq X$ . Then A is call a gs-closed set (Arya and Nori, 1990) if $scl (A) \subseteq U$ whenever $A \subseteq U$ and U is open.

Theorem 3.15

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . If $w_{X}$ is a topology, then the following thing hold: A is gs-closed if and only if $int (cl (A)) \subseteq U$ whenever $A \subseteq U$ and U is open.

Proof

From $scl (A) = A \cap int (cl (A))$ , $scl (A) \subseteq U$ whenever $A \subseteq U$ and U is open if and only if $int (cl (A)) \subseteq U$ whenever $A \subseteq U$ and U is open. So, this theorem is obtained. □

Theorem 3.16

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-closed set, then $wI (wC (A)) - A$ contains no any non-empty w-closed set.

Proof

For an s-weakly gw-closed set A, let F be a w-closed subset such that $F \subseteq wI (wC (A)) - A$ . Then $A \subseteq X - F$ and $X - F$ is w-open. Since A is s-weakly gw-closed, $wI (wC (A)) \subseteq X - F$ . From the facts, $F \subseteq X - wI (wC (A))$ and $F \subseteq wI (wC (A)) - A$ , and so $F = \emptyset$ . □

In general, the converse in Theorem 3.16 is not true as shown in the next example.

Example 3.17

Let $X = {a, b, c, d}$ and a weak structure $w = {\emptyset, {a}, {b},$ ${a, c}, {a, b, c}, X}$ in X. For $A = {a}, wI (wC (A)) = int ({a, c, d}) = {a, c}$ and $wI (wC (A)) - A = {c}$ . So, we know that there is no any nonempty w-closed set contained in $wI (wC (A)) - A$ . But A is not s-weakly gw-closed.

Corollary 3.18

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-closed set, then $wsC (A) - A$ contains no any non-empty w-closed set.

Proof

Since $wI (wC (A)) - A = (A \cup wI (wC (A))) - A = wsC (A) - A$ , by Theorem 3.16, the statement is satisfied. □

Theorem 3.19

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-closed set and $A \subseteq B \subseteq wsC (A)$ , then B is s-weakly gw-closed.

Proof

Let U be any w-open set such that $B \subseteq U$ . By hypothesis, obviously $wsC (B) = wsC (A)$ . Since A is s-weakly gw-closed and $A \subseteq U, wsC (B) = wsC (A) \subseteq U$ . So B is s-weakly gw-closed. □

Corollary 3.20

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-closed set and $A \subseteq B \subseteq wI (wC (A))$ , then B is s-weakly gw-closed.

Proof

From $A \subseteq B \subseteq wI (wC (A)), A \subseteq B \subseteq A \cup wI (wC (A)) = wsC (A)$ . By Theorem 3.19, the corollary is obtained. □

From now on, we introduce the notion of s-weakly gw-open sets and study its basic properties.

Definition 3.21

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then A is called an s-weakly generalized open set (simply, s-weakly gw-open set) if $X - A$ is s-weakly gw-closed.

Theorem 3.22

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then A is s-weakly gw-open if and only if $F \subseteq wC (wI (A))$ whenever $F \subseteq A$ and F is w-closed.

Proof

Obvious. □

From Theorem 3.13, the following is easily obtained:

Theorem 3.23

Let $(X, w_{X})$ be a w-space. Then for $A \subseteq X$ , $wsI (A) = A \cap wC (wI (A))$ .

Theorem 3.24

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then A is s-weakly gw-open if and only if $F \subseteq wsI (A)$ whenever $F \subseteq A$ and F is w-closed.

Proof

For an s-weakly gw-open subset A of X, let F be a w-closed set such that $F \subseteq A$ . Then $F \subseteq wC (wI (A))$ . Since $F \subseteq A \cap wC (wI (A))$ , by Theorem 3.23, $F \subseteq wsI (A)$ .

For $A \subseteq X$ , suppose that $F \subseteq wsI (A)$ whenever $F \subseteq A$ and F is w-closed. If F is any w-closed set and $F \subseteq A$ , then by hypothesis and Theorem 3.23, $F \subseteq wsI (A) = A \cap wC (wI (A))$ , and so $F \subseteq wC (wI (A))$ . Hence, A is s-weakly gw-open. □

Theorem 3.25

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then if A is s-weakly gw-open, then $U = X$ , whenever $wC (wI (A)) \cup (X - A) \subseteq U$ and U is w-open.

Proof

Let U be any w-open set and $wC (wI (A)) \cup (X - A) \subseteq U$ . Then $X - U \subseteq (X - wC (wI (A))) \cap A = wI (wC (X - A)) \cap A = wI (wC (X - A)) - (X - A)$ . Since $X - A$ is s-weakly gw-closed, by Theorem 3.16, the w-closed set $X - U$ must be empty. Hence, $U = X$ . □

Corollary 3.26

Let $(X, w_{X})$ be a w-space and $A \subseteq X$ . Then if A is s-weakly gw-open, then $U = X$ , whenever $wsI (A) \cup (X - A) \subseteq U$ and U is w-open.

Proof

Since $wsI (A) \cup (X - A) = (A \cap wC (wI (A))) \cup (X - A)$ , by the above theorem, it is obtained. □

Theorem 3.27

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-open set and $wC (wI (A)) \subseteq B \subseteq A$ , then B is s-weakly gw-open.

Proof

It is similar to the proof of Theorem 3.19 and Corollary 3.20. □

Theorem 3.28

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-closed set, then $wI (wC (A)) - A$ is s-weakly gw-open.

Proof

If A is an s-weakly gw-closed set, then by Theorem 3.12, $\emptyset$ is the only one w-closed subset of $wI (wC (A)) - A$ . So, $\emptyset \subseteq wC (wI (wI (wC (A)) - A))$ . Hence, $wI (wC (A)) - A$ is s-weakly gw-open. □

Corollary 3.29

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-closed set, then $wsC (A) - A$ is s-weakly gw-open.

Proof

From $wsC (A) - A = (A \cup wI (wC (A))) - A = wI (wC (A)) - A$ , it is obtained. □

Theorem 3.30

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-open set, then $wC (wI (A)) \cup (X - A)$ is s-weakly gw-closed.

Proof

If A is an s-weakly gw-open set, then by Theorem 3.25, X is the only one w-open set containing $wC (wI (A)) \cup (X - A)$ . So, obviously, $wC (wI (A)) \cup (X - A)$ is s-weakly gw-closed. □

Corollary 3.31

Let $(X, w_{X})$ be a w-space. Then if A is an s-weakly gw-open set, then $wsI (A) \cup (X - A)$ is s-weakly gw-closed.

Proof

It follows from $wsI (A) \cup (X - A) = (A \cap wC (wI (A))) \cup (X - A) = wC (wI (A)) \cup (X - A)$ and Theorem 3.30. □

Acknowledgments

The author is thankful to the referee for his/her useful suggestions.

References

Arya S.P., Nori T., . Characterizations of s-normal spaces. Indian J. Pure Appl. Math.. 1990;21:717-719.
[Google Scholar]
Csázár Á., . Generalized topology, generalized continuity. Acta Math. Hung.. 2002;96(4):351-357.
[Google Scholar]
Ekici E., . On a-open sets, $A^{*}$ -sets and decompositions of continuity and super-continuity. Ann. Univ. Sci. Budapest. 2008;51:39-51.
[Google Scholar]
Ekici E., Jafari S., . On a new topology and decompositions of continuity. Int. J. Math. Game Theory Algebra. 2010;19(1/2):129-141.
[Google Scholar]
Kent D.C., Min W.K., . Neighborhood spaces. Int. J. Math. Math. Sci.. 2002;32(7):387-399.
[Google Scholar]
Kim Y.K., Min W.K., . On weak structures and w-spaces. Far East J. Math. Sci.. 2015;97(5):549-561.
[Google Scholar]
Levine N., . Semi-open sets and semi-continuity in topological spaces. Am. Math. Mon.. 1963;70:36-41.
[Google Scholar]
Levine N., . Generalized closed sets in topology. Rend. Cir. Mat. Palermo. 1970;19:89-96.
[Google Scholar]
Maki H., Devi R., Balachandran K., . Associated topologies of generalized $α$ -closed sets and $α$ -generalized closed sets. Mem. Fac. Sci. Kochi Univ. Ser. A. Math.. 1994;15:51-63.
[Google Scholar]
Maki H., . On generalizing semi-open and preopen sets, Report for Meeting on Topological Spaces Theory and its Applications, August 1996. Yatsushiro College of Technology; 1996. 13-18
Mashhour A.S., Abd El-Monsef M.E., El-Deeb S.N., . On precontinuous and weak precontinuous mappings. Proc. Math. Phys. Soc. Egypt. 1982;53:47-53.
[Google Scholar]
Min W.K., . On weak neighborhood systems and spaces. Acta Math. Hung.. 2008;121(3):283-292.
[Google Scholar]
Min W.K., Kim Y.K., . On generalized w-closed sets in w-spaces. Int. J. Pure Appl. Math.. 2016;110(2):327-335.
[Google Scholar]
Min W.K., Kim Y.K., . w-preopen sets and W-precontinuity in weak spaces. Int. J. Math. Anal.. 2016;10(21):1009-1017.
[Google Scholar]
Min W.K., Kim Y.K., . w-semiopen sets and W-semicontinuity in weak spaces. Int. J. Pure Appl. Math.. 2016;110(1):49-56.
[Google Scholar]
Min W.K., . On weakly gw-closed sets in w-spaces. Int. J. Pure Appl. Math.. 2017;112:437-442.
[Google Scholar]
Noiri T., Maki H., Umehara J., . Generalized preclosed functions. Mem. Fac. Sci. Kochi Univ. Ser. A. 1998;19:13-20.
[Google Scholar]
Njastad O., . On some classes of nearly open sets. Pac. J. Math.. 1964;15(3):961-970.
[Google Scholar]
Siwiec F., . On defining a space by a weak base. Pac. J. Math.. 1974;52(1):351-357.
[Google Scholar]
Velicko N.V., . H-closed topological spaces. Am. Math. Soc. Trans.. 1968;78(2):103-118.
[Google Scholar]

Introduction

Preliminaries

Main results

Fulltext Views
4

PDF downloads
1

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Arya S.P., Nori T., . Characterizations of s-normal spaces. Indian J. Pure Appl. Math.. 1990;21:717-719.
[Google Scholar]

[2] Csázár Á., . Generalized topology, generalized continuity. Acta Math. Hung.. 2002;96(4):351-357.
[Google Scholar]

[3] Ekici E., . On a-open sets, $A^{*}$ -sets and decompositions of continuity and super-continuity. Ann. Univ. Sci. Budapest. 2008;51:39-51.
[Google Scholar]

[4] Ekici E., Jafari S., . On a new topology and decompositions of continuity. Int. J. Math. Game Theory Algebra. 2010;19(1/2):129-141.
[Google Scholar]

[5] Kent D.C., Min W.K., . Neighborhood spaces. Int. J. Math. Math. Sci.. 2002;32(7):387-399.
[Google Scholar]

[6] Kim Y.K., Min W.K., . On weak structures and w-spaces. Far East J. Math. Sci.. 2015;97(5):549-561.
[Google Scholar]

[7] Levine N., . Semi-open sets and semi-continuity in topological spaces. Am. Math. Mon.. 1963;70:36-41.
[Google Scholar]

[8] Levine N., . Generalized closed sets in topology. Rend. Cir. Mat. Palermo. 1970;19:89-96.
[Google Scholar]

[9] Maki H., Devi R., Balachandran K., . Associated topologies of generalized $α$ -closed sets and $α$ -generalized closed sets. Mem. Fac. Sci. Kochi Univ. Ser. A. Math.. 1994;15:51-63.
[Google Scholar]

[10] Maki H., . On generalizing semi-open and preopen sets, Report for Meeting on Topological Spaces Theory and its Applications, August 1996. Yatsushiro College of Technology; 1996. 13-18

[11] Mashhour A.S., Abd El-Monsef M.E., El-Deeb S.N., . On precontinuous and weak precontinuous mappings. Proc. Math. Phys. Soc. Egypt. 1982;53:47-53.
[Google Scholar]

[12] Min W.K., . On weak neighborhood systems and spaces. Acta Math. Hung.. 2008;121(3):283-292.
[Google Scholar]

[13] Min W.K., Kim Y.K., . On generalized w-closed sets in w-spaces. Int. J. Pure Appl. Math.. 2016;110(2):327-335.
[Google Scholar]

[14] Min W.K., Kim Y.K., . w-preopen sets and W-precontinuity in weak spaces. Int. J. Math. Anal.. 2016;10(21):1009-1017.
[Google Scholar]

[15] Min W.K., Kim Y.K., . w-semiopen sets and W-semicontinuity in weak spaces. Int. J. Pure Appl. Math.. 2016;110(1):49-56.
[Google Scholar]

[16] Min W.K., . On weakly gw-closed sets in w-spaces. Int. J. Pure Appl. Math.. 2017;112:437-442.
[Google Scholar]

[17] Noiri T., Maki H., Umehara J., . Generalized preclosed functions. Mem. Fac. Sci. Kochi Univ. Ser. A. 1998;19:13-20.
[Google Scholar]

[18] Njastad O., . On some classes of nearly open sets. Pac. J. Math.. 1964;15(3):961-970.
[Google Scholar]

[19] Siwiec F., . On defining a space by a weak base. Pac. J. Math.. 1974;52(1):351-357.
[Google Scholar]

[20] Velicko N.V., . H-closed topological spaces. Am. Math. Soc. Trans.. 1968;78(2):103-118.
[Google Scholar]