The integrated model of the Kolmogorov–Smirnov distribution-free statistic approach to process control and maintenance

1 Introduction

Since the first control chart was provided in 1924 by Dr. Shewhart, the concept of the control chart has been considered in many models from past to present, and currently the quality control is widely used in various industry areas. One popular application on control chart used in manufacturing is economic design of control charts. Montgomery (2009) stated that the economic design of control charts refers to the control charts that have been designed with respect to statistical criteria only. This usually involves selecting sample size and control limits such that the average run length (ARL) of the chart to detect a particular shift in the quality characteristic and the ARL of the procedure when the process is in control are equal to specified values. Practically, frequency of sampling is considered from factors including production rate, expected frequency of shifts to an out-of-control state, and possible consequences of such process shifts in determination of sampling interval. In many cases, statistical criteria and practical experience have been used in setting up general guidelines for the design of control charts. One thing that should be noted in designing a control chart is the choice of control chart parameter can cause economic consequences. For this reason, an economic viewpoint such as costs of sampling and testing, costs associated with investigating out-of-control signals and possibly correcting assignable causes, and costs of allowing nonconforming units to reach a consumer should be taken into account in the design of a control chart.

In recent years, considerable research has been devoted to economic models of control charts. Duncan (1956) used optimum methodology to establish design parameters including subgroup size (n), sampling interval (h), and control-limit width (±L standard deviations) for minimizing the loss cost, where the cost items include a sampling and testing cost, an increasing cost from out-of-control process, false alarm cost, and searching and repairing cost. Pongpullponsak et al. (2009) studied a chart in conjunction with an age replacement preventive maintenance policy. From the report, they also introduced an economic model established using the Shewhart method and determined the efficiency of the control chart when the data were in skewed distributions. Saniga (1977) proposed a joint economic design of and R control charts based on two assignable causes in production process. In this model, one assignable cause results in a shift of the process mean whereas the other one results in a shift of the process variance. Yu et al. (2010) studied the possibility in economic statistical design of control charts by considering only one assignable cause. In fact, multiple assignable causes such as machine problem, material deviation, human errors, etc. can occur during the production process so for this research, establishment of an economic-statistical model of control chart will be extended from consideration of single, in the original research, to multiple assignable causes for a real application. Zhou and Zhu (2008) established an economic statistical design of control chart from integrating the concepts between Statistical Process Control (SPC) and Maintenance Management (MM), which are in science and business practice, respectively. The integrated model was then used to find the optimal values of policy variables (n, h, L, k) that minimize hourly cost, subsequently optimal product quality, little downtime, and cost reduction can be achieved by controlling variances in the process. The effects of cost parameters on the solution of the design were investigated using a numerical experiment.

Generally, the process in construction of control chart includes gathering the sampling properties of monitoring statistic, determining the chart’s behavior, and comparing its performance with other existing charts. In most cases, the data are treated as normality but in some occasions, the underlying population distribution or the necessary sampling properties could not be ruled out. Some researchers have proposed reasonable alternative as a solution. For instance, Yang et al. (2011) introduced a nonparametric approach, namely a nonparametric EWMA sing control chart for dealing with such situations. The Kolmogorov–Smirnov (KS) control chart is another good example. The knowledge of sampling distribution is useful for nonparametric statistics inference because the exact sampling distributions are considerably easier to calculate compared with that for distribution-free statistic $(D_n)$ , or Kolmogorov–Smirnov one-sample statistic (Gibbons, 1971). Pongpullponsak and Jayathavaj (2014) considered distribution-free statistics when the population from which selected samples are not normally distributed or normality cannot be met was used. Additionally, there are several nonparametric tests that have been further applied in case of nominal or ordinal data. Bakir (2012) introduced a modified version of the two – sample Kolmogorov–Smirnov test statistic where the difference of the reference and test empirical distribution function are maximized only over the training sample values. Khrueasom and Pongpullponsak (2014) developed the distribution-free or unknown distribution quality control chart based on the KS.

This research is aimed to find the optimal values of four variables (n, h, L, k) that minimize the cost of integrated system approach to process control and maintenance model on the basis of the distribution-free/KS – control chart.

2 Materials and methods

2.2

2.2 Problem statement and assumptions

Fig. 1 shows the framework in development of integrated model. The process starts with an in-control state with a process failure mechanism that is distribution-free or follows an unknown distribution. The best-known test is the KS, the cumulative distribution function (cdf) of the sample, called the empirical distribution function (edf), may be considered, and an estimate of the population and $D_n$ can be written as follows:

(1)

$$D_n={\displaystyle \underset{x}{\sup }}\left|S_n(x)-F_X\left(x\right)\right|$$

Close

Figure 1

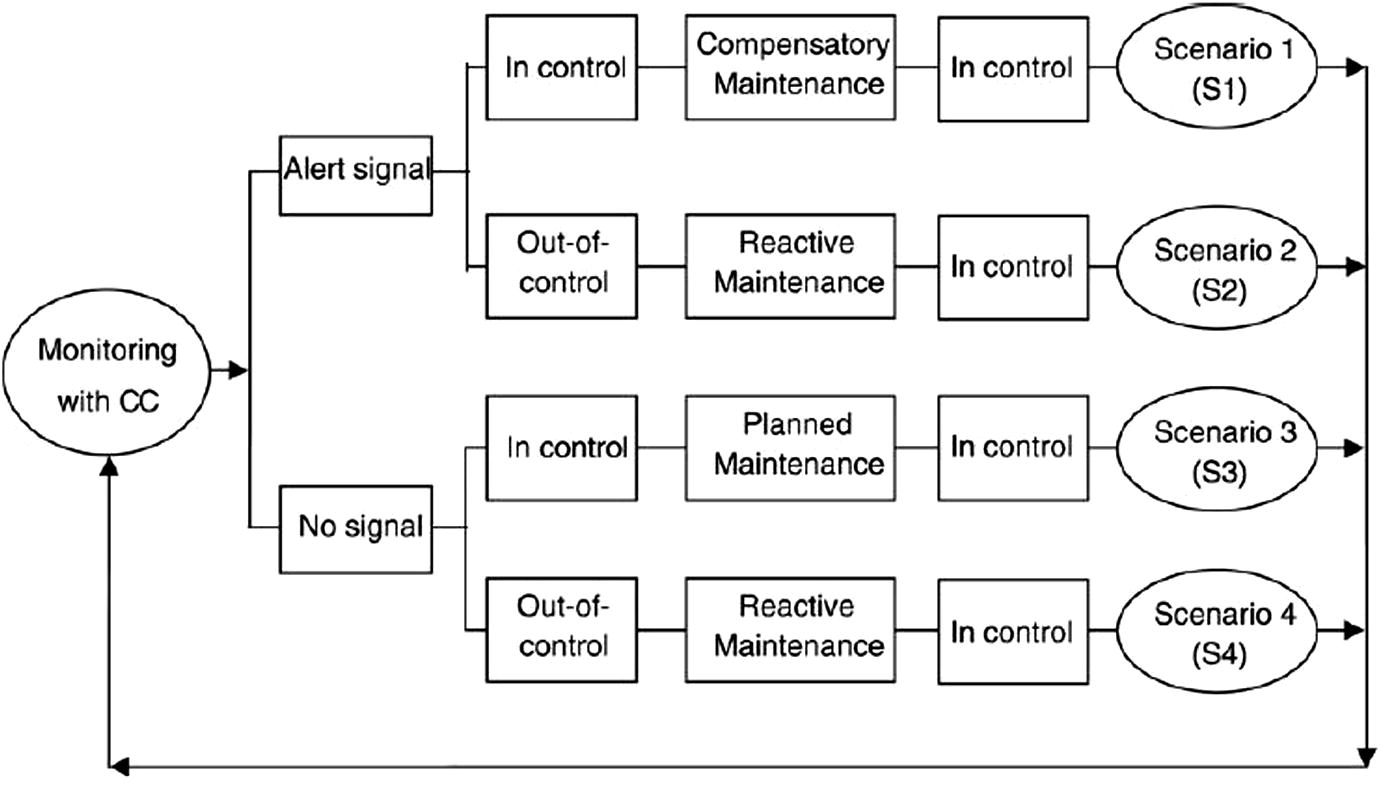
Four monitoring – maintenance scenarios of the integrated mode.

Export to PPT

For the random variable S_n(x), which is the edf of a random sample X₁, X₂, X_n, a distribution F_X can be derived from “Nonparametric statistical Inference” by Gibbons (1971),

(2)

$$P\left[S_n\left(x\right)=\frac{i}{n}\right]=\left(\begin{array}{c}\hfill n\hfill \\ \hfill i\hfill \end{array}\right){\left[F_X\right]}^i{\left[1-F_X\right]}^{n-i}\text{,}i=0\text{,}1\text{,}...\text{,}n$$

Define the indicator random variables as below;

(3)

$${\delta }_i\left(t\right)=\left\{\begin{array}{cc}\hfill 1\hfill & \hfill \text{if}{X}_i⩽t\hfill \\ \hfill 0\hfill & \hfill \text{otherwise}\hfill \end{array}\right.$$

The ${\delta }_1(t)\text{,}{\delta }_2(t)\text{,}\dots {\delta }_n(t)$ constitutes a set of n independent random variables from the Bernoulli distribution with parameter $\theta$ , where $\theta =P\left[{\delta }_i(t)=1\right]=P(X_i⩽t)=F_X(t)$ . Therefore, we obtain

(4)

$$S_n\left(x\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\delta }_i\left(x\right)$$

The random variables ${\mathit{nS}}_n(x)$ is the sum of n independent Bernoulli random distribution, which follows the binomial distribution with parameter $\theta =F_X(x)$ .

From Eqs. (2)–(4), we consider a sequence of t independent Bernoulli trials, where the probability of the event is λ and the probability of the non-event is 1 − λ. If we consider the event to be the elimination of the player, then its absence over n trials can be described as their survival. The probability of this survival throughout t trials will be given by the binomial mass function B (x; t, λ) when x = 0 (Pollock, 2007), which is

(5)

$$B(0\text{,}t\text{,}\lambda )$$

Likewise, in the case of the non-occurrence of eliminating event over a continuous finite period of time the model of survival or elimination can be converted through Bernoulli trials into similar model in which the events are distributed randomly in time. To achieve this, a Poisson’s process in continuous time should be depicted as a limiting case of a binomial process. It can be carried out by taking, as the departure point, the special case of the binomial given under Eq. (5) and considering that of each trial representing a single unit of time. Subsequently, the probability of the occurrence of the eliminating event within a single period can be denoted by λ. Also, it is assumed that the probability of the occurrence of two such events within the same interval is vanishingly small or zero.

Then

(6)

$$B(0\text{;}t\text{,}\lambda )={\left[{\left(1-\frac{\lambda }{n}\right)}^n\right]}^t\approx {\left(1-\lambda \right)}^t\text{,}$$ where the approximation is obtained by taking the first two terms of the binomial expansion.

(7)

$${\left(1-\frac{\lambda }{n}\right)}^n=\left(1-\lambda \right)+\frac{\left(n-1\right)}{2n}{\lambda }^2-\frac{\left(n-1\right)\left(n-2\right)}{n^{2}3!}{\lambda }^3+\dots$$

In the limit, when the number of subdivisions increases indefinitely, we have

(8)

$${\displaystyle \underset{n\to \infty }{\lim }}{\left(1-\frac{\lambda }{n}\right)}^n=e^{-\lambda }$$

At this point, the probability of survival in the period 0, t can be described by

(9)

$$S(t)=e^{-\lambda t}$$ which is the continuous-time analog of Eq. (5). The probability of being eliminated during the period [0, t] or a cdf is written as

(10)

$$1-S\left(t\right)=F\left(t\right)={\int }_0^{t}f\left(s\right)\mathit{ds}=1-e^{-\lambda t}$$

Next, the corresponding density function, defined over the set of times at which elimination might occur, or a probability density function is

(11)

$$f(t)=\lambda e^{-\lambda t}$$ which is a cumulative function F(t) in respect of t. This exponential waiting time function is used to describe a duration distribution.

3 Results and analysis

In this research, the numerical example and sensitivity analyses are conducted to study the effect of model parameters in the solution of economic design of the KS chart. Using the genetic algorithms (GA) with MATLAB, 7.6.0 (R2009a) software The Math WorksTM, 2009, the solution procedure is carried out to obtain the optimal values of $(n^{\ast }\text{,}{h}^{\ast }\text{,}{L}^{\ast }\text{,}{k}^{\ast })$ which will be subsequently used to minimize in Eq. (45).

The GA is the stochastic and optimization search technique of natural selection and natural genetics. The GA solves problems used the approach to the process of Darwinian evolution. In recent years, many research have been devoted to the GA solves problems of economic-statistical, engineering, mathematics, production processes, etc. Current, GA models were introduced and investigated by Holland (1975). The solution procedures of GA (e.g., Charongrattanasakul and Pongpullponsak, 2011; Chou et al., 2006, 2008; Lin et al., 2009, 2012; Chen and Yeh, 2009; Franco et al., 2012), in this the research are briefly described below.

Step 1. Initial Population: The procedure starts at randomly generating 100 solutions that reach the constraint condition of individual test parameter. Meanwhile, the constraint condition represented for individual test parameter is set as below, $$1⩽n⩽25\text{,}0.1⩽h⩽5\text{,}2⩽L⩽2.5\text{,}20⩽k⩽40$$

Step 2. Evaluation: This step, is evaluated through the fitness function. Each solution used the expected cost per hour E [H] in Eq. (45).

Step 3. Selection: The selected function chooses parents (survivors) for the next generation based on their scaled values of the fitness scaling function. The four individual solutions are selected randomly and the best is chosen (For the first generation the chromosome with the lowest cost is selected to replace the highest cost chromosome).

Step 4. Crossover: In this step by step 3, generate new chromosomes for the next generation and a pair of parents (survivors) are selected randomly as shown in this example, parents (survivors) used for crossover operations to produce new chromosomes (or children) for the next generation. This research used crossover rate 0.8 as below, $$D_1=0.8R+0.2M\text{,}{D}_2=0.2R+0.8M$$ where $D_1$ is the first new chromosome, $D_2$ is the second new chromosome, and R and M are the parent (survivors) chromosomes. If 30 parents (survivors) are randomly selected, then there are 60 children that will be produced. Thus, the population size increases to 90 (i.e., 30 parents (survivors) + 60 children) in this step.

Step 5. Mutation: Mutation function is the small change of genes in chromosomes in the population, suppose that the mutation rate is 0.1, which is also determined by $D_2$ orthogonal array experiment.

In this example, we have 90 solutions and we can randomly select 9 chromosomes $\left(\text{i}.e.\text{,}90\times 0.1=9\right)$ to mutate some parameters (or genes) in this step.

Step 6. Stopping criteria: Repeat Step 2 to Step 5 until the stopping criteria is found. In this example, we use ‘‘50 generations or greater than” as our stopping criteria.

The initial values of the necessary parameters are given in Tables 1 and 2, where eight independent parameters which will be tested in the sensitivity analysis and their corresponding level planning are illustrated. Accordingly, the effect of model parameters on the solution of economic design of the KS chart can be investigated by conducting numerical example and sensitivity analysis. For the sensitivity determination, L₁₆ orthogonal-array experimental design shown in Table 3 is used in the test.

After calculation, the best value parameters by L₁₆ orthogonal array are obtained as shown in Table 4. From Table 5, the optimal values of the policy variables that minimize $E[H]$ are found to be $n^{\ast }=1.006\text{,}{h}^{\ast }=0.133\text{,}{L}^{\ast }=2.001\text{,}{k}^{\ast }=20.000$ and the corresponding hourly cost is $E[H]=102.569$ .

Table 6 illustrates the output of the nonparametric linear regression applied in order to fit the regression line according to Brown and Mood (1951) where Wilcoxon Matched–Pair Test (Corder and Foreman, 2009) is used in hypothesis testing at 0.05 significance levels by the statistical software SPSS 15.0. It is noticed that the sign of the coefficient parameter of constant is often estimated by assuming that the hourly cost E [H] is positive, which is consistent with the principle of nonparametric statistical hypothesis testing.

Using nonparametric linear regression test, the numerical results of the optimal values of the policy variables which minimize $E[H]$ are found to be $n^{\ast }=1.026\text{,}{h}^{\ast }=0.209\text{,}{L}^{\ast }=2.114\text{,}{k}^{\ast }=20.011$ and the corresponding hourly cost is $E[H]=102.569$ (Table 7). In Table 8, the comparison between four policies of the integrated model (KS) and other models shows that the model proposed in this study has a better economic behavior when it is distribution-free.

Finally, from Table 9, it can be seen that the performance for ARL of KS control chart, equals to 430.96, is greater than that of the control chart with the general model which is 370.

4 Conclusion

This research proposes the method used in searching the appropriate products for the Kolmogorov–Smirnov KS control chart that is distribution-free. This control chart is suitable for detection of small changes. In some occasions, small changes in the process can lead to incredible damage. For this reason, those factories who produce non-restricted goods using appropriate control charts would reduce or eliminate unnecessary cost. Conclusively, these four control charts shown in Table 8 are suitable for using in various types of factories and products; however, selection of appropriate control chart is recommended in order to reduce unnecessary cost.

The numerical results, when sample size $n⩾20$ is used, are summarized in Table 8. According to the optimal values of the policy variables that minimize E [H], this provides evidence that when it is distribution-free the integrated KS model will have a better economic behavior than those previously reported models (Charongrattanasakul and Pongpullponsak, 2009, 2011). Besides, the results show that the performance for ARL of KS (Table 9), equals to 430.96, is greater than that of the ARL obtained from the general model which is equal to 370. However, the proposed model may have some defective in which investigating any weak point and improving for better performance would be an interesting issue for further study.

5 Future work

For future work, it is of interest to develop integrated economic model and control chart for nonparametric multivariate which is distribution-free or follows an unknown distribution.