Lateral mass flux and thermal radiation on natural convection heat and mass transfer from a vertical flat plate in porous media considering Soret/Dufour effects

1 Introduction

Coupled convection heat and mass transfer due to buoyancy in saturated porous media has many important applications in energy-related engineering problem, for example, the migration of moisture in fibrous insulation, the spreading of chemical pollutants in saturated soil, and the underground disposal of nuclear wastes. Nield and Bejan (1992) recently presented a comprehensive account of the available information in the field.

Regarding pure heat transfer with lateral mass flux, Cheng (1977) studied the effect of lateral mass flux with prescribed temperature and velocity as power law on the vertical surface. Govindarajulu and Malarvizhi (1987) presented a note on the solution of the free convection boundary layer flow over a vertical flat plate with the effect of lateral mass flux in a saturated porous medium. Brouwers (1994) studied the heat transfer process between a saturated porous medium and a permeable wall with fluid injection or withdrawal. Magyari and Keller (2000) investigated the extension of the problem to include the influence of lateral mass flux.

Postelnicu et al. (2000) presented the free convection boundary-layer over a vertical permeable flat plate in a porous medium with internal heat generation.

In a study of coupled heat and mass transfer, Bejan and Khair (1985) used Darcy’s law to study the vertical natural convective flows driven by temperature and concentration gradients. Lai and Kulacki (1991) studied the coupled heat and mass transfer along a vertical surface in a saturated porous medium. An integral procedure is derived to solve the problem along the lines of Nakayama and Hossain (1995). Yih (1999) examined coupled heat and mass transfer by free convection over a truncated cone in porous media under variable wall temperature and concentration (VWT/VWC) and variable heat flux and variable mass flux (VHF/VMF). Cheng (2000) used an integral method to study how natural convection transfers heat and mass from truncated cones in porous media with variable wall temperature and concentration. Makinde (2012) studied the heat and mass transfer by MHD mixed convection stagnation point flow toward a vertical plate embedded in a highly porous medium with radiation and internal heat generation.

A well-known phenomenon of coupled heat and mass transfer is the thermal energy flux resulting from concentration gradients which is referred to as the Dufour (diffusion-thermal) effect. Similarly, the Soret (thermo-diffusion) effect is the contribution of the temperature gradient to mass flux. The Dufour and Soret effects are considered second order phenomena since they are of a smaller order of magnitude compared to the effects described by Fourier and Fick, but their importance may increase in geosciences and chemical engineering. Coupled heat and mass transfer processes by natural convection from vertical surfaces in porous media considering Soret and Dufour effects was reported by Postelnicu (2004). Partha et al. (2006) examined the Soret and Dufour effects in a non-Darcy porous medium. Lakshmi Narayana and Murthy (2008) considered both the Soret and Dufour effects on a free convection boundary layer of a horizontal flat plate in a Darcy porous medium. Cheng (2009) reported the Soret and Dufour effects on natural convection heat and mass transfer from a vertical cone in a porous medium with uniform wall temperature and concentration (UWT/UWC). The Soret and Dufour effects on heat and mass transfer by natural convection from a vertical truncated cone in a fluid-saturated porous medium with variable wall temperature and concentration were studied by Cheng (2010). Makinde (2011) studied the mixed convection flow with Soret and Dufour effects past a vertical plate embedded in a porous medium. Makinde et al. (2012) used a numerical method to study of chemically-reacting hydromagnetic boundary layer flow with Soret/Dufour effects and a convective surface boundary condition.

As the difference between the surface temperature and the ambient temperature increases, the effects of radiation increase. The radiation effect on convection flow is a problem in many important applications, e.g., space technology and processes involving high temperatures such as the geothermal engineering, the sensible heat storage bed, the nuclear reactor cooling system and the underground nuclear wastes disposal. A free convection flow through a porous medium in the presence of radiation was considered by Raptis (1998). Badruddin et al. (2006) studied free convection and radiation in a vertical wall embedded in a porous medium under variable wall temperature. Tai and Char (2010) investigated the Soret and Dufour effects on free convection flow of non-Newtonian fluids through a porous medium with thermal radiation. Olanrewaju and Makinde (2011) discussed the effects of thermal diffusion and diffusion thermo on chemically reacting MHD boundary layer flow of heat and mass transfer past a moving vertical plate with suction/injection.

The present work investigated the heat and mass transfer by natural convection flow over a vertical flat plate under uniform wall temperature and uniform wall concentration (UWT/UWC) embedded in porous media considering the Soret and Dufour effects with lateral mass flux and thermal radiation.

2 Analysis

The considered problem is the Soret/Dufour effects on combined heat and mass free convection flow over a vertical flat plate embedded in a saturated porous medium with lateral mass flux and thermal radiation and where the boundary condition of uniform wall temperature $T_w$ and uniform wall concentration $C_w$ (UWT/UWC), respectively. The surface variable blowing/suction velocity is $V_w(x)$ . Fig. 1 shows the flow model and physical coordinate system. The origin of the coordinate system is the leading edge of the vertical flat plate, where x and y are Cartesian coordinates for the distance along and normal to, respectively, the vertical flat plate surface.

Close

Figure 1

Flow model and the physical coordinate system.

Export to PPT

All fluid properties are assumed to be constant except for the density variation in the buoyancy term. For the Boussinesq and Rosseland diffusion approximations (2010) in the boundary layer, the governing equations and the boundary conditions based on the Darcy law can be written as follows:

The stream function $\psi$ is defined by,

Therefore, the continuity equation is automatically satisfied.

Next consider the governing Eqs. (2) and (3). Cross-differentiation $[\partial u/\partial y-\partial v/\partial x]\text{,}$ eliminates the pressure terms in Eqs. (2) and (3). Further, using the boundary layer approximation $(\partial /\partial x\ll \partial /\partial y)$ ,

The second and third terms on the right-hand side of the energy Eq. (4) represents the Dufour effect and the heat absorbed per unit volume, and the last term of concentration Eq. (5) denotes the Soret effect. Note that, in Eq. (6), the Rosseland diffusion approximation is used to describe the radiative heat flux (2010). Further assume that the temperature differences within the flow are sufficiently small so that T⁴ in Eq. (6) can be expanded in Taylor series about $T_{\infty }$ , and discard higher-order terms in the usual manner. Thus,

The following dimensionless variables are invoked:

Substituting Eqs. (12) and (13) into Eqs. (11), (4)–(6) and (8)–(9) obtains

The boundary conditions are defined as follows:

Eq. (14) can be obtained by integrating Eq. (11) once and with the aid of Eq. (9.1-3).

For the new variables, the Darcian velocities in the x- and y-directions are also respectively obtained by,

By inserting Eq. (8.1) into Eq. (20), the lateral mass flux parameter $f_w$ (see Cheng (1977) and Chamkha et al. (2014)) is as follows:

For blowing, $V_w(x)$  > 0; hence, $f_w$  < 0. For suction, however, $V_w(x)$  < 0; hence, $f_w$  > 0.

Besides, the buoyancy ratio N, the Lewis number Le, the Dufour parameter $D$ , the Soret parameter $S$ , and the thermal radiation parameter $R_d$ are respectively defined as follows:

The results for heat and mass transfer rates have practical applications. The heat and mass transfer rates are expressed in terms of the local Nusselt number ${\mathit{Nu}}_x$ and the local Sherwood number ${\mathit{Sh}}_x$ respectively, which are respectively defined as follows:

By applying Eqs. (6), (12) and (13), the local Nusselt number ${\mathit{Nu}}_x$ and the local Sherwood number ${\mathit{Sh}}_x$ in terms of ${\mathit{Ra}}_x^{1/2}$ are respectively obtained by,

3 Numerical method

Eqs. (14)–(18) are integrating by combining the implicit finite difference approximation with the modified Keller box method of Cebeci and Bradshaw (1984). First, the partial differential converted into a system of five first-order equations. These first-order equations are then expressed in finite difference forms and solved along with their boundary conditions by applying an iterative scheme. This approach improves the convergence rate and the computation time.

Computations were performed with a personal computer with the first step size $\mathrm{\Delta }{\eta }_l=0.01$ . The variable grid parameter is chosen 1.01 and the value of ${\eta }_{\infty }=20$ . When the errors in computing the $|{\theta }_w^{\prime }|$ and $|{\phi }_w^{\prime }|$ in the next procedure become less than ${10}^{-5}$ , the iterative procedure is stopped, and the final temperature and concentration distributions are obtained.

4 Results and discussion

The accuracy of this method was verified by comparing the results with those of Cheng (1977), Govindarajulu and Malarvizhi (1987), Postelnicu et al. (2000), Chamkha et al. (2014), Bejan and Khair (1985), Nakayama et al. (1995), Yih (1999), Postelnicu (2004) and Tai and Char (2010). Table 1 compares the values $-{\theta }^{\prime }(0)$ for various values of f_w with N = D = S = R_d = 0. Table 2 compares $-{\theta }^{\prime }(0)$ and $-{\phi }^{\prime }(0)$ for various values of N and Le with f_w = R_d = D = S = 0. Table 3 compares $-{\theta }^{\prime }(0)$ and $-{\phi }^{\prime }(0)$ for various values of N, D and S with f_w = R_d = 0, Le = 1. Table 4 compares ${\mathit{Nu}}_x/{\mathit{Ra}}_x^{1/2}$ and ${\mathit{Sh}}_x/{\mathit{Ra}}_x^{1/2}$ for various values of D and S with f_w = 0, N = 0.5, R_d = 1.25 and Le = 4. All values in Tables 1–4 show excellent agreement. Table 5 lists the values of ${\mathit{Nu}}_x/{\mathit{Ra}}_x^{1/2}$ and ${\mathit{Sh}}_x/{\mathit{Ra}}_x^{1/2}$ for various values of N, Le, D, S, f_w, and R_d.

The numerical results are graphically presented for N = 1, Le = 2 with the Soret parameter S ranging from 0 to 0.2, the Dufour parameter D ranging from 0 to 0.2, the thermal radiation parameter R_d ranging from 0 to 1, and the lateral mass flux parameter $f_w$ ranging from $-1$ to 1.

The dimensionless temperature and concentration profiles for three values of the lateral mass flux parameter f_w ( $f_w=-1\text{,}$ 0 and 1) are shown in Fig. 2. These two figures show the dimensionless temperature profile $\theta$ and the dimensionless concentration profile $\phi$ decrease monotonically from the surface of the vertical plate to the ambient. Both the thermal boundary layer thickness ${\delta }_T$ and the concentration boundary layer thickness ${\delta }_C$ decrease for the case of suction ( $f_w$  > 0). However, this trend is reversed in the case of blowing ( $f_w$  < 0).

Close

Figure 2

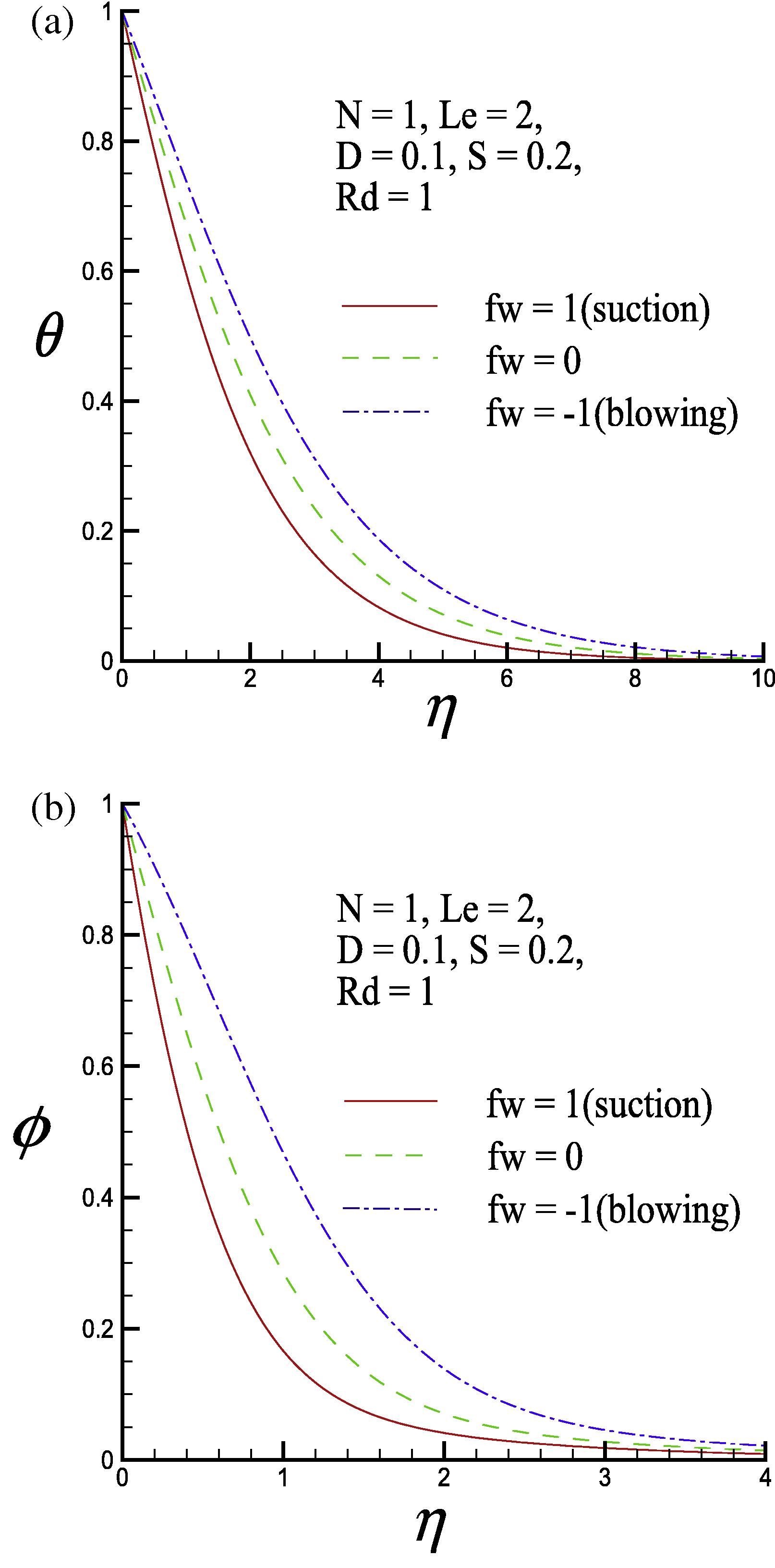
(a) Dimensionless temperature profile and (b) dimensionless concentration profile for three values of the lateral mass flux parameter f_w.

Export to PPT

The dimensionless temperature and concentration profiles for three values of the Dufour parameter D (D = 0, 0.1 and 0.2) are shown in Fig. 3. Fig. 3(a) shows that increasing the Dufour parameter tends to decrease the dimensionless surface temperature gradient $-{\theta }^{\prime }(0)$ , which decreases the heat transfer rate at the wall. Moreover, Fig. 3(b) shows that, as the Dufour parameter increases, the dimensionless surface concentration gradient $-{\phi }^{\prime }(0)$ increases, which increases the mass transfer rate at the wall.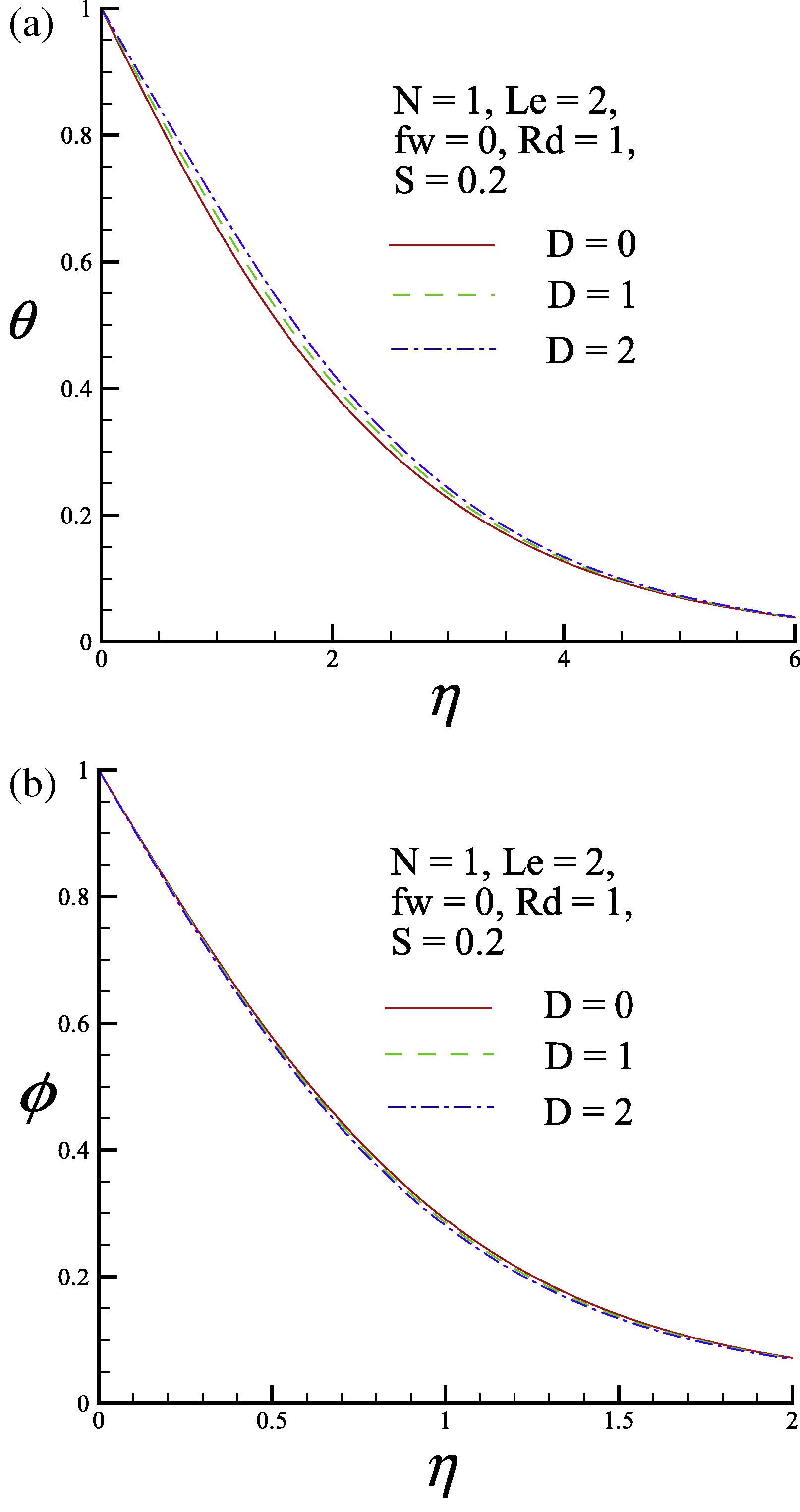

Close

Figure 3

(a) Dimensionless temperature profile and (b) dimensionless concentration profile for three values of the Dufour parameter D.

Export to PPT

The dimensionless temperature and concentration profiles for three values of the Soret parameter S (S = 0, 0.1 and 0.2) are presented in Fig. 4. In Fig. 4(a), the dimensionless surface temperature gradient increases as the Soret parameter S increases. However, Fig. 4(b) shows that increasing the Soret parameter S reduces the dimensionless surface concentration gradient.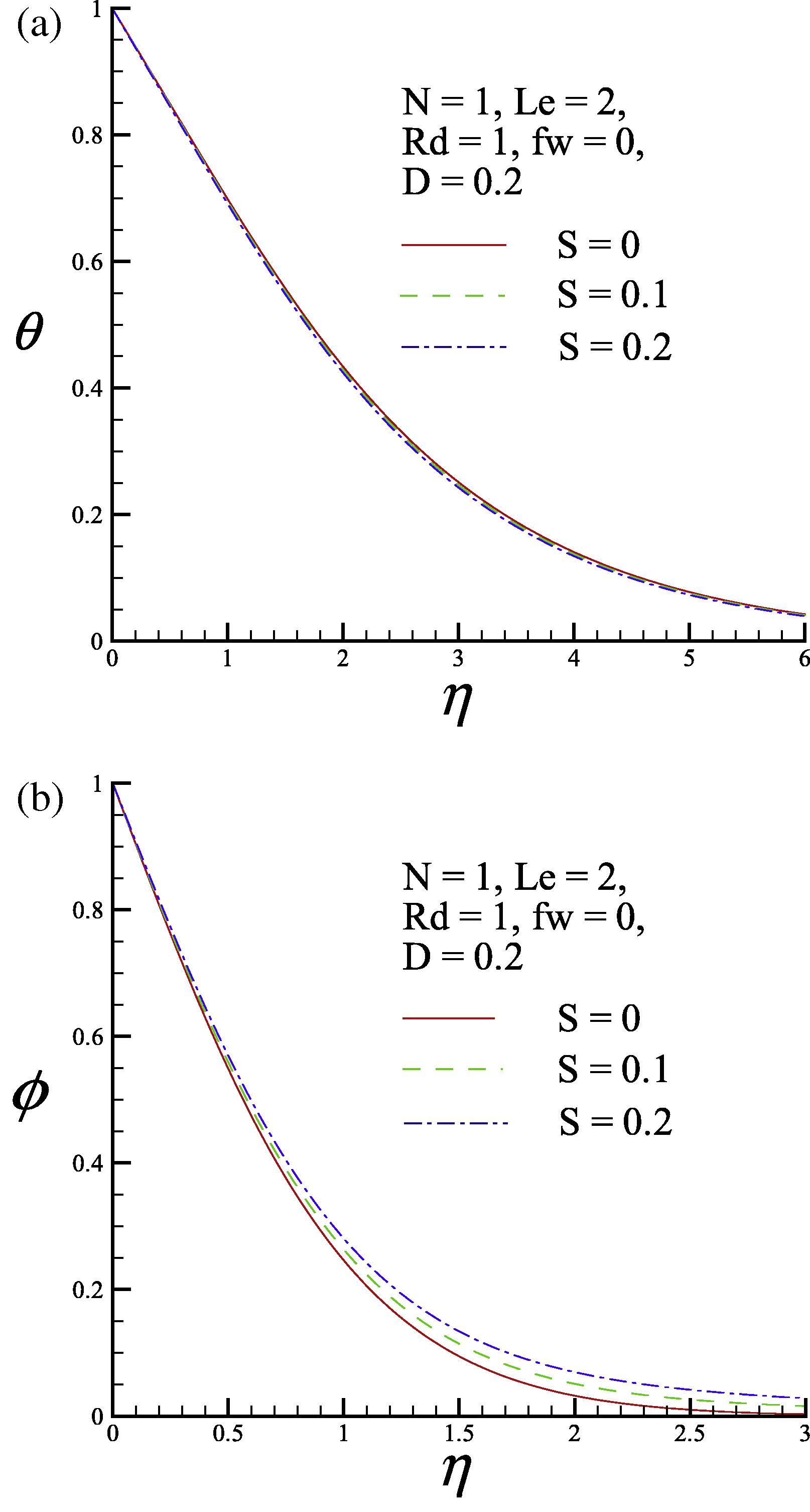

Close

Figure 4

(a) Dimensionless temperature profile and (b) dimensionless concentration profile for three values of the Soret parameter S.

Export to PPT

The dimensionless temperature and concentration profiles for three values of the thermal radiation parameter R_d (R_d = 0, 1 and 5) are illustrated in Fig. 5. Fig. 5(a) shows that, when $R_d$ increases, the dimensionless temperature profiles become large, but the dimensionless surface temperature gradients become small. As the value of $R_d$ increases, the radiation absorption in the boundary layer increases, which increases the sizes of the dimensionless temperature profiles. However, Fig. 5(b) shows that increasing the thermal radiation parameter R_d, increases the dimensionless surface concentration gradient $-{\phi }^{\prime }(0)$ , but decreases the dimensionless concentration profiles $\phi$ .

Close

Figure 5

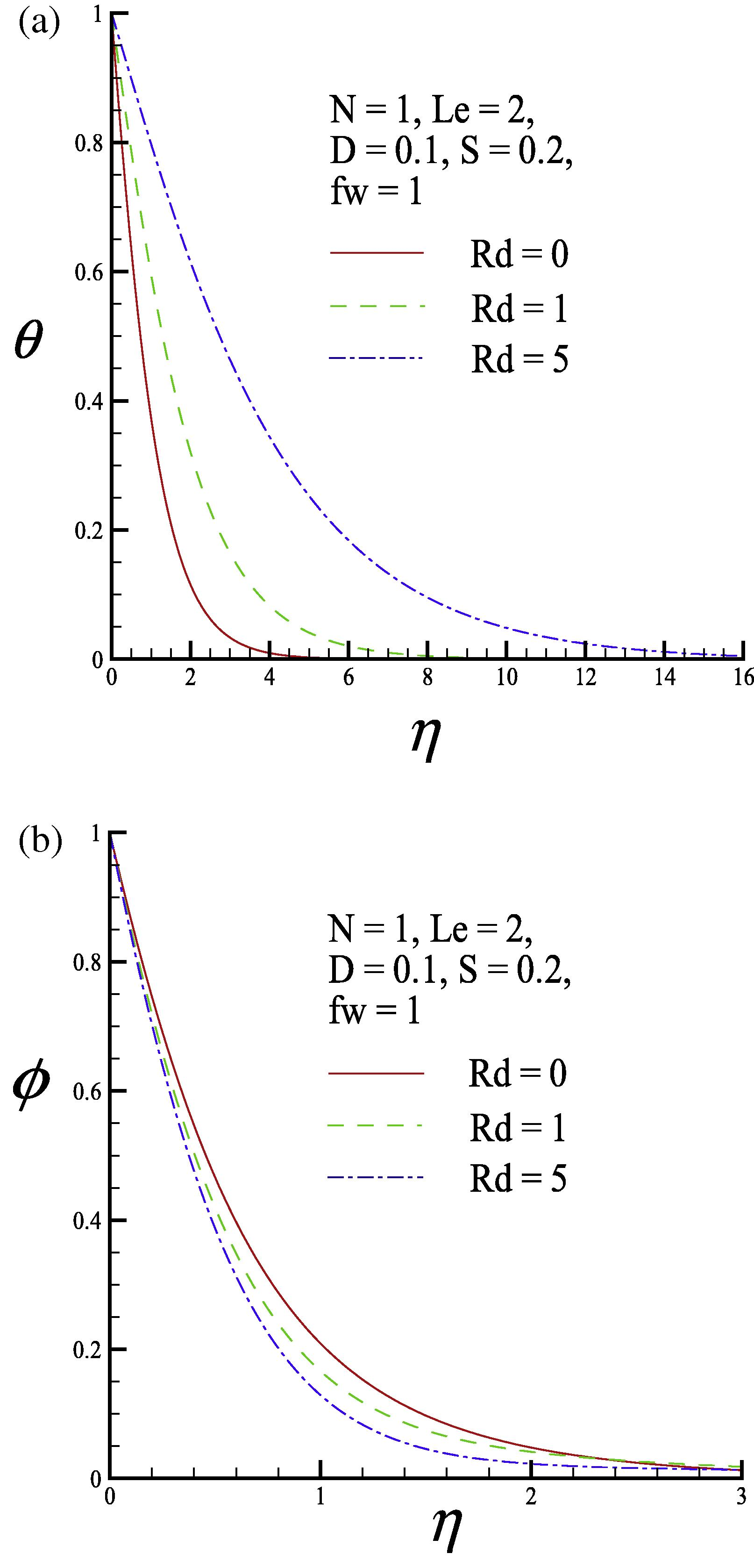
(a) Dimensionless temperature profile and (b) dimensionless concentration profiles for three values of the thermal radiation parameter R_d.

Export to PPT

The local Nusselt number Nu_x/Ra_x^1/2 and the local Sherwood number Sh_x/Ra_x^1/2 as functions of the lateral mass flux parameter f_w for three values of the Dufour parameter (D = 0, 0.1 and 0.2) are depicted in Fig. 6. Generally, suction increases both the local Nusselt number and the local Sherwood number, i.e., f_w > 0 because, as Fig. 2 shows, suction decreases both the thermal and concentration boundary thicknesses ${\delta }_T$ and ${\delta }_C$ , respectively. This trend is reversed in the case of blowing. Besides, for the fixed f_w, increasing the Dufour parameter tends to decrease the local Nusselt number while it tends to increase the local Sherwood number. This occurs because increasing the Dufour parameter D decreases the dimensionless surface temperature gradient but increases the dimensionless surface concentration gradient, as illustrated in Fig. 3.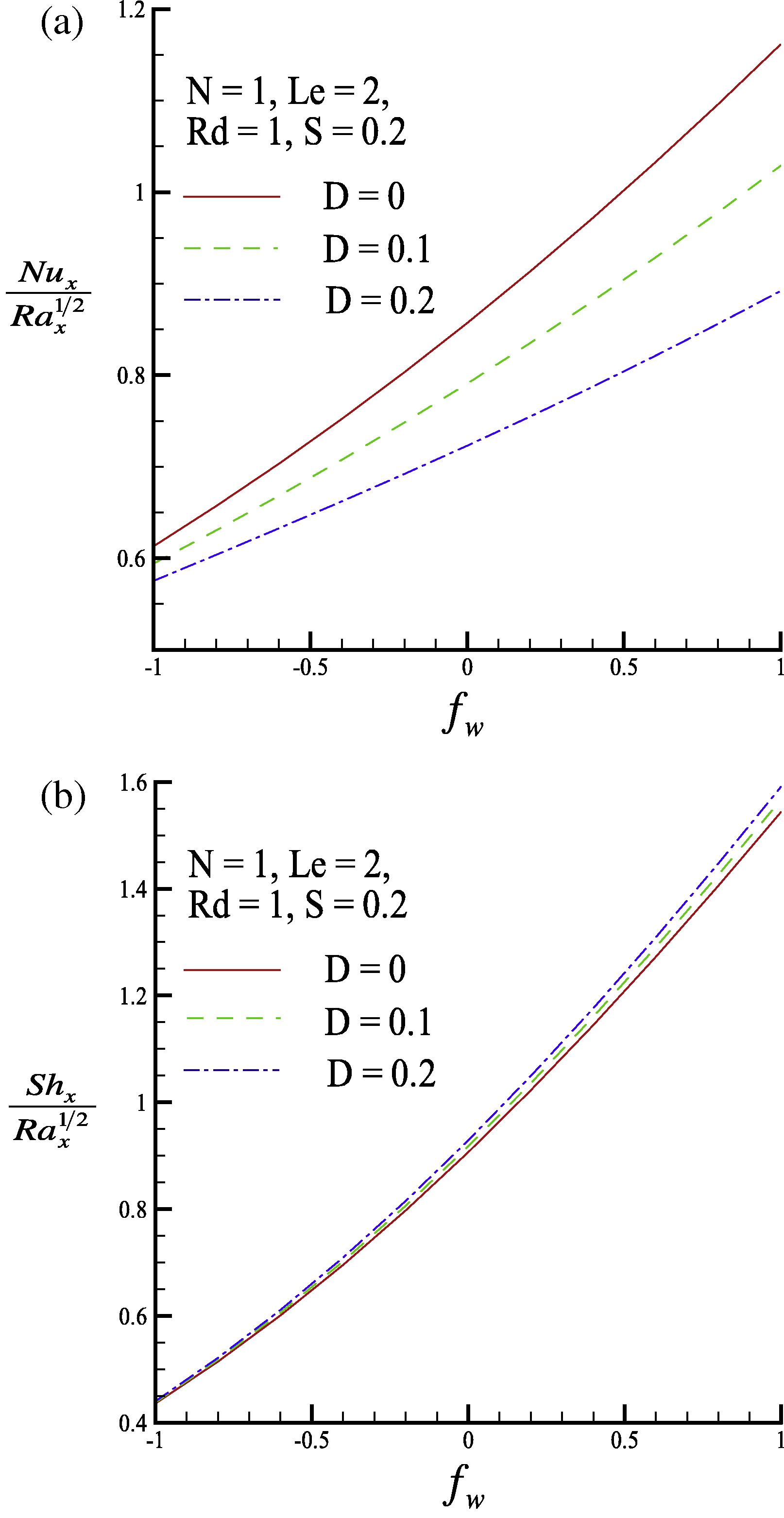

Close

Figure 6

(a) Local Nusselt number and (b) local Sherwood number for three values of the Dufour parameter D.

Export to PPT

The local Nusselt number Nu_x/Ra_x^1/2 and the local Sherwood number Sh_x/Ra_x^1/2 as functions of the lateral mass flux parameter f_w for three values of the Soret parameter S (S = 0, 0.1 and 0.2) are shown in Fig. 7. Enhancing the Soret parameter tends to increase the local Nusselt number but tends to decrease the local Sherwood number. This occurs because, as Fig. 4 shows, increasing the Soret parameter S increases the dimensionless surface temperature gradient but decreases the dimensionless surface concentration gradient.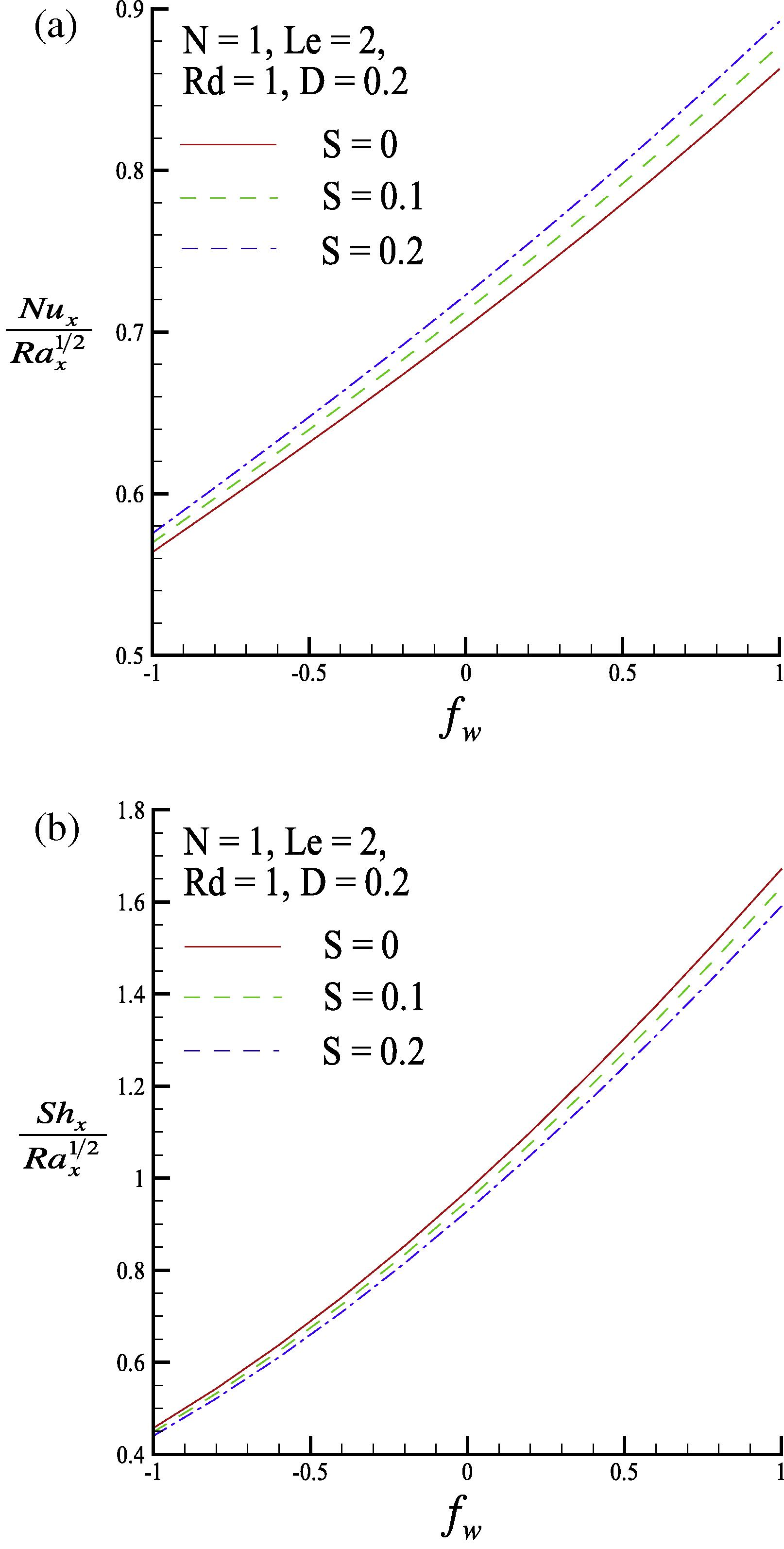

Close

Figure 7

(a) Local Nusselt number and (b) local Sherwood number for three values of the Soret parameter S.

Export to PPT

The variation in the local Nusselt number Nu_x/Ra_x^1/2 and the local Sherwood number Sh_x/Ra_x^1/2 for three values of the thermal radiation coefficient R_d (R_d = 0, 1 and 5) are shown in Fig. 8, respectively. In the pure free convection heat transfer, the Nusselt number is only proportional to the dimensionless surface temperature gradient $-{\theta }^{\prime }(0)$ . In the case of large $R_d$ (pronounced radiation effect), Fig. 5(a) shows that, even if the value of $-{\theta }^{\prime }(0)$ is low, the Nusselt number is still large. Eq. (28) shows that this occurs because the Nusselt number is more sensitive to $R_d$ than to $-{\theta }^{\prime }(0)$ .

Close

Figure 8

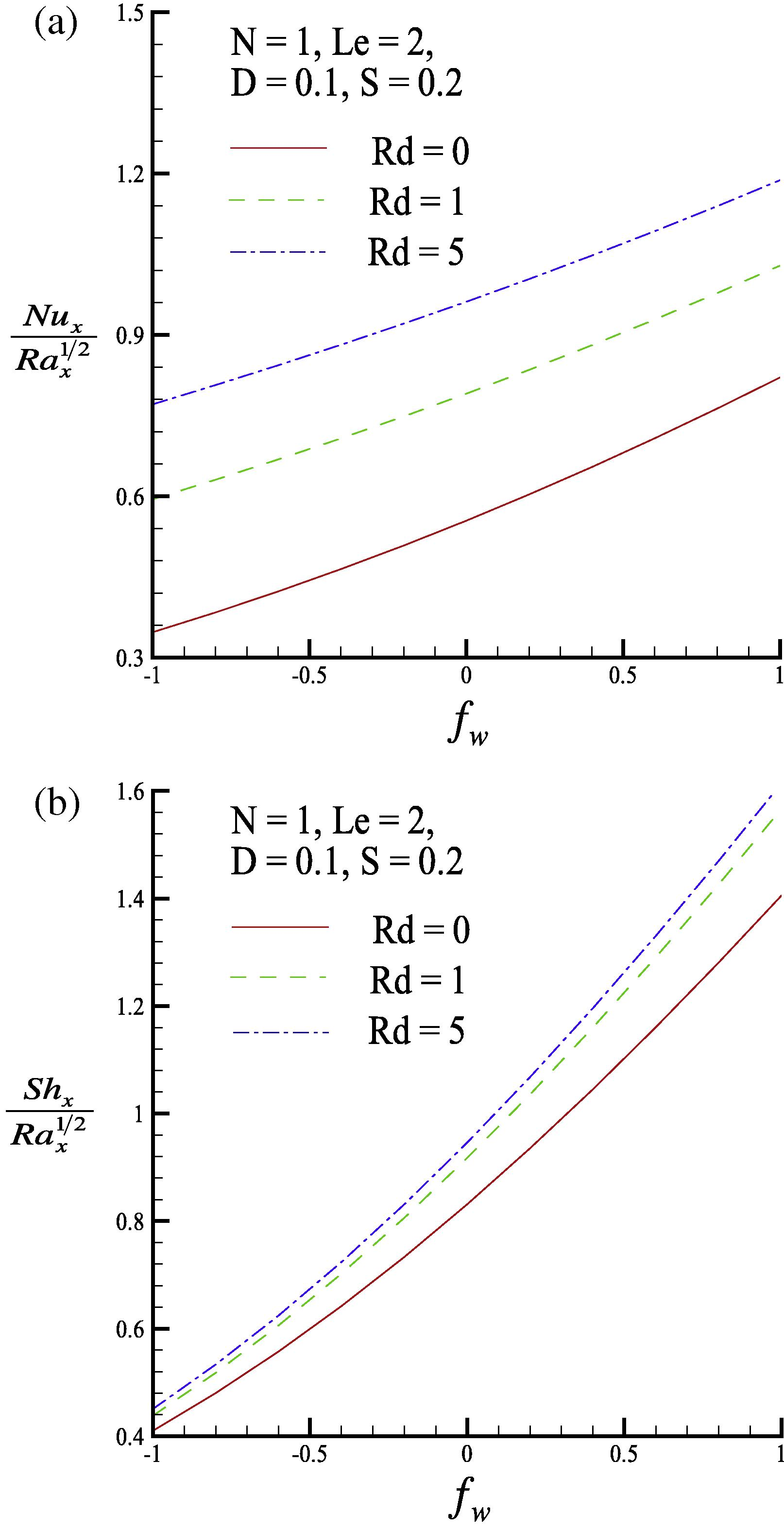
(a) Local Nusselt number and (b) local Sherwood number for two values of the thermal radiation parameter R_d.

Export to PPT

5 Conclusions

A two-dimensional laminar boundary layer analysis is presented to study the Soret/Dufour effects on coupled heat and mass transfer by free convection over a vertical permeable plate in porous media with thermal radiation. After the coordinate transformation, the transformed similar governing equation is solved by Keller box method (KBM). Comparisons with previously published works show excellent agreement. Numerical solutions are obtained for different values of the thermal radiation parameter R_d, the lateral mass flux parameter f_w, the Dufour parameter D, the Soret parameter S, the buoyancy ratio N, and the Lewis number Le. The calculations show that, when the thermal radiation R_d, the buoyancy ratio N and the lateral mass flux parameter f_w increase, both the local Nusselt number and the local Sherwood number increase. The local Nusselt number decreases as the Lewis number Le and the Dufour parameter D increase. In contrast, the local Sherwood number increases when Le and D increase. Finally, enhancing the Soret parameter S increases the local Nusselt number and decreases the local Sherwood number.