Analytical study of the non orthogonal stagnation point flow of a micro polar fluid

M. Ali. Abbas; Naeem Faraz; Yan-Qin Bai; Yasir Khan

doi:10.1016/j.jksus.2015.05.004

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Review Article

29 (

); 126-132

doi:

10.1016/j.jksus.2015.05.004

Analytical study of the non orthogonal stagnation point flow of a micro polar fluid

M. Ali. Abbas^{^a}, Naeem Faraz^{^a,^b,⁎}, Yan-Qin Bai^{^a}, Yasir Khan^{^c}

a Department of Mathematics Shanghai University, Shanghai 200444, China

b Center of International Program (C.I.P.), Donghua University, 1882 Yan’an Xilu Road, Shanghai 200051, China

c Department of Mathematics, Zhejiang University, Hangzhou 310027, China

⁎Corresponding author at: Department of Mathematics Shanghai University, Shanghai 200444, China.

Received: 2015-3-24, Accepted: 2015-5-15, Published: 2015-01-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

In this paper we consider the steady two dimensional flow of micro polar fluids on a flat plate. The flow under discussion is the modified Hiemenz flow for a micro polar fluid which occurs in the hjkns + skms boundary layer near an orthogonal stagnation point. The full governing equation reduced to a modified Hiemenz flow. The solution to the boundary value problem is governed by two non dimensional parameters, the material parameter K and the ratio of the micro rotation to skin friction parameter n. The obtained nonlinear coupled ordinary differential equations are solved by using the Homotopy perturbation method. Comparison between numerical and analytical solutions of the problem is shown in tables form for different values of the governing parameters K and n. Effects of the material parameter K on the velocity profile and microrotation profiles for different cases of n are discussed graphically as well as numerically. Velocity profile decreases as the material parameter K increases and the microrotation profile increases as the material parameter K increases for different cases of n.

Keywords

Micro polar fluid

Hiemenz flow

Homotopy perturbation method (HPM)

Show Related Articles from PubMed

1 Introduction

The behavior of the flow near a stagnation-point is a fundamental topic in fluid dynamics, and it has attracted the attention of many researchers during the past several decades because of its wide industrial and technical applications, such as heat exchangers placed in a low-velocity environment, cooling of nuclear reactors during emergency shutdown, solar central receivers exposed to wind currents, cooling of electronic devices by fans, and many hydrodynamic processes. Hiemenz (1911) and Homann (1936) initiated the study of two dimensional and axisymmetric three dimensional stagnation point flows, respectively. Eckert (1942) extended Hiemenz’s work by including the energy equation and obtained an exact similarity solution for the thermal field. Later, the problem of stagnation point flow was extended numerically by Schlichting and Bussmann (1943) and analytically by Ariel (1994) to include the effect of suction. Further, Mabood et al. (2015) worked on heat and mass transfer by Magnetohydrodynamics (MHD) stagnation point flow toward a permeable stretching surface. Rosali et al. (2014) analyzed the unsteady boundary layer flow toward a mixed convection stagnation point flow on a heated vertical surface. Borrelli et al. (2015) has discussed the influence of a non uniform external magnetic field on the steady three dimensional stagnation point flow of a micropolar fluid.

In fluid mechanics we study the behavior of particles at every point within the domain under various physical conditions. To describe the physical phenomena in fluid mechanics we use mathematical models for different types of fluids such as Newtonian fluids (Picchi et al., 2014; Fzal and Kim, 2014; Villone et al., 2014; Hatami and Domairry, 2014 ) and non Newtonian fluids (Hatami and Ganji, 2014a,b; Liu et al., 2013 ). There are many special cases of non-Newtonian fluids such as nano fluids (Domairry and Hatami, 2014; Hatami et al., 2014; Ahmadi et al., 2014; Shaikhoeslam et al., 2014 ), micropolar fluid (Srinivasacharya and Upendar, 2014; Hatami and Ganji, 2014c; Pažanin, 2013 ).

Models of micropolar fluids were first pioneered by Eringen (1966) and explained the characters of certain real fluid flows. The attractiveness and power of the model of micropolar fluids come from the fact that it is both a significant and a simple generalization of the classical Navier Stokes model. Recently many researchers worked on different models of micropolar fluids. Faltas and Saad (2014) obtained a solution of Stokes axisymmetrical flow problems of viscous fluid moving perpendicular to an impermeable bounding surface for cylindrical and spherical cases. Borrelli et al. (2015) examined the effects of the magnetic field and the temperature on the steady mixed convection of a micropolar fluid. Similarly, Mohanty et al. (2015) investigated heat and mass transfer effects of micropolar fluid over stretching sheet numerically. Shaikhoeslam et al. (2014) has studied the flow of micropolar fluid and heat transfer in a permeable channel.

Micropolar fluid problems can be studied in different applications like Liquid crystals, animal blood, colloidal fluids, flow of low concentration suspensions etc. Some researchers worked on the two main applications. Oahimire and Olajuwa (2014) solved heat and mass transfer effects on an unsteady flow of a chemically reacting micropolar fluid through porous medium. Abd Alla et al. (2013) studied effects of rotation and magnetic field of a micropolar fluid through a porous medium. Abdalla et al. obtained closed form solution under the consideration of long wavelength and low renold number. Another important application is Lubrication theory. Prakash and Sinha (1975) considered a steady laminar flow of a incompressible micropolar fluid of Lubrication theory. Bayada and Łkaszewic (1996) derived an analog of the classical renold equation of the theory of lubrication and discussed its particular forms depending on the assumption imposed on the viscosities and the data.

Lok and Pop (2007) analyzes the steady two dimensional stagnation-point flow of a micropolar fluid impinging on a flat rigid wall obliquely. This flow appears when a jet of viscous fluids impinge on a rigid wall obliquely. In many cases, the jet may be oblique to the impinged surface due to surface contouring or physical constraints on the nozzle (Wang, 1985). In particular, we investigate the behavior of the micropolar fluid and velocity profile of the fluid particle near the wall for various values of the micropolar parameter and rate of particle rotation to the skin friction at the plate.

To deal with such kind of problems, we needed a strong analytical tool. Interest in analytical techniques for studying nonlinear problems increased dramatically over the past two decades. Analytical methods have significant advantages over numerical methods in providing analytic, verifiable, rapidly convergent approximations. Therefore, many methods have been used to deal with highly nonlinear problems such as the homotopy perturbation transform method (Khan and Muhammad, 2014; Khan and Wu, 2011), differential transform method (Masayebidorchen et al., 2014; Hatami et al., 2014; Shaikholeslam et al., 2015; Domairy and Shaikholeslam, 2012 ), optimal homotopy analysis method (Shaikholeslam and Ganji, 2014; Shaikholeslam et al., 2012), least square method (Sheikholeslami et al., 2013; Hatami et al., 2014), Hamiltonian approach (Nianga and Recho, 2014; Reinhardt and Heffner, 2012; Lan, 2011 ), homotopy analysis method (Sheikholeslami et al., 2012, 2014), variational iteration method (Biazar et al., 2010; Faraz, 2011; Faraz et al., 2011 ), and decomposition method (Sheikhoeslami et al., 2013; Sheikholeslami et al., 2012; Shakeri Aski et al., 2014; Guo-cheng, 2011 ). One of the semi-exact methods is the homotopy perturbation method (HPM) (Sheikholeslami and Ganji, 2013; Shaikholeslami et al., 2011; Sheikholeslami et al., 2012, 2013; Jun Yang et al., 2014 ). He (2007, 2003, 2004a,b) developed and formulated HPM by merging the standard homotopy and perturbation. He’s HPM is proved to be compatible with the versatile nature of physical problems and has been applied to a wide class of functional equations (Brzdęk et al., 2014; Galleas and Lamers, 2014). In general the solutions produced by the HPM are as accurate as the solutions given by the other methods like the tanh method (Shukri and Al-Khaled, 2010; Bekir and Cevikel, 2009), the transformed rational function method (Nasiri Soloklo and Maghfoori Farsangi, 2013) and linear superposition principle (Stiver and Mackay, 1995).

The aim of present study is to improve the results given by Lok for non orthogonal stagnation point flow of a micro polar fluid. Particularly, we investigated and analyzed the velocity profile and microrotation profile of fluid particles. Microrotation of the particles is represented as a vector quantity that is transported and dispersed inside the fluid. It also has influence over the fluid velocity presenting a two way coupled non linear system.

2 Formulation of the problem

We consider two dimensional steady flow of a micropolar fluid near a non-orthogonal stagnation point at a fixed flat plate coinciding with the plane y > 0, the flow being confined to y > 0. Cartesian coordinates (x, y) fixed in space are taken, the x-axis being along the plate and the y-axis normal to it, respectively. Under these assumptions the steady two dimensional flow of a micropolar fluid is described by the following equations:

(1)

\frac{\partial \bar{u}}{\partial \bar{x}} + \frac{\partial \bar{v}}{\partial \bar{y}} = 0

(2)

\bar{u} \frac{\partial \bar{u}}{\partial \bar{x}} + \bar{v} \frac{\partial \bar{v}}{\partial \bar{y}} = - \frac{1}{ρ} \frac{\partial \bar{p}}{\partial \bar{x}} + (\frac{μ + κ}{ρ}) {\bar{\nabla}}^{2} \bar{u} + \frac{κ}{ρ} \frac{\partial \bar{N}}{\partial \bar{y}}

(3)

\bar{u} \frac{\partial \bar{v}}{\partial \bar{x}} + \bar{v} \frac{\partial \bar{v}}{\partial \bar{y}} = - \frac{1}{ρ} \frac{\partial \bar{p}}{\partial \bar{y}} + (\frac{μ + κ}{ρ}) {\bar{\nabla}}^{2} \bar{v} - \frac{κ}{ρ} \frac{\partial \bar{N}}{\partial \bar{x}}

(4)

ρ ζ (\bar{u} \frac{\partial \bar{N}}{\partial \bar{x}} + \bar{v} \frac{\partial \bar{N}}{\partial \bar{y}}) = γ {\bar{\nabla}}^{2} N - κ (2 N + \frac{\partial \bar{u}}{\partial \bar{y}} - \frac{\partial \bar{v}}{\partial \bar{x}})

where

\bar{u}

and

\bar{v}

are the velocity components along the

\bar{x}

and

\bar{y}

-axes, respectively.

\bar{N}

is the component of the microrotation vector normal to the

\bar{x} \bar{y}

plane, ρ is the density, μ is the absolute viscosity, k is the vortex viscosity, γ is the spin-gradient viscosity, ζ is the micro inertia density and

{\bar{\nabla}}^{2}

is the Laplacian in Cartesian coordinates

(\bar{x}, \bar{y}) .

It is assumed that all physical quantities are constant. We eliminate the pressure from Eqs. (2) and (3) and introducing the non dimensional variables.

x = \frac{\bar{x}}{λ}, y = \frac{\bar{y}}{λ}, u = \frac{λ}{ν} \bar{u}, u = \frac{λ}{ν} \bar{v}

N = \frac{\bar{N}}{a}, p = \frac{\bar{p}}{ρ a^{2} λ^{2}}

By eliminating pressure, Eqs. (2)–(4) can be written in the non dimensional form as,

(5)

\frac{\partial Φ}{\partial x} \frac{\partial}{\partial y} (\nabla^{2} Φ) - \frac{\partial Φ}{\partial y} \frac{\partial}{\partial x} (\nabla^{2} Φ) + (1 + K) \nabla^{4} Φ + K \nabla^{2} N = 0

(6)

\frac{\partial Φ}{\partial y} \frac{\partial N}{\partial x} - \frac{\partial Φ}{\partial x} \frac{\partial N}{\partial y} = + (1 + \frac{K}{2}) \nabla^{2} N - K (2 N + \nabla^{2} Φ) = 0

where Φ is the non dimensional stream function which is defined by the usual way as

u = \frac{\partial Φ}{\partial y}

and

v = - \frac{\partial Φ}{\partial x}

with u and v being the non dimensional velocity components along x-axis and y-axis. Using non dimensional variables the skin friction can be shown as,

(7)

C_{f} = [(1 + K) (\frac{\partial^{2} Φ}{\partial y^{2}} - \frac{\partial^{2} Φ}{\partial x^{2}}) + KN]

where K is the material parameter defined as

K = \frac{κ}{μ}

In the case of orthogonal flow the boundary condition of Eqs. (5) and (6) can be written as

(8)

\begin{matrix} Φ = \frac{\partial Φ}{\partial y} = 0, N = - n \nabla^{2} Φ on y = 0 \\ Φ \approx xy N \to 0 as y \to \infty \end{matrix}

where n is the constant such that

0 ⩽ n ⩽ 1

. It should be mentioned that the case n = 0, called strong concentration by Guram and Smith (1980), indicating N = 0 near the wall, represents concentrated particle flows in which the microelements close to the wall surface are unable to rotate. The case n = 1/2 indicates the vanishing of anti-symmetrical part of the stress tensor and denotes weak concentration. The

n = 0

as suggested by Peddieson (1972), is used for the modeling of turbulent boundary layer flows. The solution of Eqs. (5) and (6) subject to the boundary condition (8) can be sought in the form

(9)

Φ (x, y) = xf (y) N (x, y) = xg (y),

By using Eqs. (9), (5) and (6), we get the following set of ordinary differential equations:

For case n = 0:

(10)

\begin{matrix} (1 + K) f^{‴} + {ff}^{″} + 1 - f^{' 2} + {Kg}^{'} = 0 \\ (1 + \frac{K}{2}) g^{″} + {fg}^{'} - f^{'} g - K (2 g + f^{″}) = 0 \\ f (0) = f^{'} (0) = 0, g (0) = 0 \\ f^{'} (\infty) = 1, g (\infty) = 0 \end{matrix}

For case n = 1/2:

(11)

\begin{matrix} (1 + \frac{K}{2}) f^{‴} + {ff}^{″} + 1 - f^{' 2} = 0 \\ f (0) = f^{'} (0) = 0, f^{'} (\infty) = 1 \end{matrix}

where prime denotes differentiation with respect to y. The skin friction becomes:

(12)

C_{f} = [(1 + (1 - n) K)] {xf}^{″} (0)

In the case of the Oblique flow, it can be assumed that the stream function from the wall has the form

(13)

Φ (x, y) = xy + α y^{2}, y \to \infty

where

α

is a constant and the microrotation N → constant as y → 1. Expression (14) suggests that Eqs. (5) and (6) have the solution of the form

(14)

Φ (x, y) = xF (x) + G (y), N (x, y) = xH (y) + T (y)

The boundary conditions take the form:

(15)

\begin{matrix} F (0) = F^{'} (0) = 0, G (0) = G^{'} (0) = 0 \\ H (0) = - {nF}^{″} (0), T (0) = - {nG}^{″} (0) \end{matrix}

substituting (14) in (5) and (6) and we get the following equations:

(16)

(1 + K) F^{‴} + {FF}^{″} + 1 - F^{' 2} + {KH}^{'} = 0

(17)

(1 + K) G^{‴} + {FG}^{″} - F^{'} G^{'} + {KT}^{'} = 2 α A

(18)

(1 + \frac{K}{2}) H^{″} + {FH}^{'} - F^{'} H - K (2 H + F^{″}) = 0

(19)

(1 + \frac{K}{2}) T^{″} + {FT}^{'} - G^{'} H - K (2 T + G^{″}) = 0

subject to the boundary conditions

F (0) = F^{'} (0) = 0, G (0) = G^{'} (0) = 0

(20)

H (0) = - {nF}^{″} (0), T (0) = - {nG}^{″} (0)

F^{'} (\infty) = 1, G^{″} (\infty) = 2 α, H (\infty) = 0, T (\infty) = - α

We can see that Eqs. (16) and (18) subject to the boundary condition are identical with those of Eq. (10), by introducing new variables as: $G (y) = 2 α h (y), T (y) = 2 α t (y)$

Eqs. (17) and (19) can be written as, $(1 + K) h^{″} + {Fh}^{'} - F^{'} h + {Kt}^{'} = A$ $(1 + \frac{K}{2}) t^{″} + {Ft}^{'} - Hh - K (2 t + h^{'}) = 0$

(21)

h (0) = 0, t (0) = - {nh}^{'} (0)

h^{'} (\infty) = 1, t (\infty) = - \frac{1}{2}

where A can calculated from the following equation:

(22)

f (y) \approx y + A

Values for $F^{″} (0)$ and h′(0) can be calculated for some values of parameters K and n. It is worth to mention that $F^{″} (0) = f^{″} (0)$ because solution of Eqs. (16) and (18) subject to the boundary condition (20) is identical with the solution of (10).

In the view of HPM (Sheikholeslami et al., 2012, 2013), Eq. (10) can be expressed as, $(1 - p) L_{1} (f - f_{o}) + p [(1 + K) f^{‴} + {ff}^{″} + 1 - f^{' 2} + Kg] = 0$

(23)

(1 - p) (1 + \frac{K}{2}) L_{2} (g - g_{o}) + p [(1 + \frac{K}{2}) g^{″} + {fg}^{'} - f^{'} g - K (2 g + f^{″})] = 0

Assuming L₁ f = 0, and L₂ g = 0, the following expansions for f and g can be introduced into the Eq. (23) as,

(24)

\begin{matrix} f = f_{0} + {pf}_{1} + p^{2} f_{2} + \cdot \cdot \cdot \\ g = g_{0} + {pg}_{1} + p^{2} g_{2} + \cdot \cdot \cdot \end{matrix}

After some simplifications and rearrangements based on the powers of p-terms, the following equations can be obtained,

(25)

\begin{matrix} p^{(0)} : L_{1} f_{0} = 0 and L_{2} g_{0} = 0 \\ f_{0} (0) = f_{0}^{/} (0) = 0, g_{0} (0) = 0 \\ f_{0}^{/} (\infty) = 1, g_{0} (\infty) = 0 \end{matrix}

where

L_{1}

and L₂ can be defined as,

(26)

L_{1} = \frac{\partial^{3}}{\partial y^{3}} + \frac{\partial^{2}}{\partial y^{2}} and L_{2} = \frac{\partial^{2}}{\partial y^{2}} - 1

Initial guesses can be obtained by solving Eq. (25) as,

(27)

f_{0} (y) = y + e^{- y} - 1, g_{0} (y) = e^{- y} - e^{- 2 y}

Higher order terms can be determined as,

(28)

\begin{matrix} (1 - p) L_{1} (f - f_{o}) + p [(1 + K) f^{‴} + {ff}^{″} + 1 - f^{' 2} + Kg] = 0 \\ (1 - p) (1 + \frac{K}{2}) L_{2} (g - g_{o}) + p [(1 + \frac{K}{2}) g^{″} + {fg}^{'} - f^{'} g - K (2 g + f^{″})] = 0 \\ p^{(1)} : L_{1} f_{1} + [(1 + K) f_{0}^{'''} + f_{0} f_{0}^{/ /} + 1 - f_{0}^{/ 2} + {Kg}_{0}] = 0 \\ f (0) = f^{'} (0) = 0, f^{'} (\infty) = 1 \end{matrix}

(29)

\begin{matrix} p^{(1)} : L_{2} g_{1} + [(1 + \frac{K}{2}) g_{0}^{/ /} + f_{0} g_{0}^{/} - f_{0}^{/} g_{0} - K (2 g_{0} + f_{0}^{/ /})] = 0 \\ g (0) = 0, g (\infty) = 0 \\ p^{(j)} : L_{1} f_{j} - L_{1} f_{j - 1} + [(1 + K) f_{j - 1}^{/ / /} + \sum_{k = 0}^{j - 1} f_{k} f_{j - 1 - k}^{/ /} + 1 - \sum_{k = 0}^{j - 1} f_{k}^{/} f_{j - 1 - k}^{/} + {Kg}_{j - 1}] = 0 \\ f (0) = f^{'} (0) = 0, f^{'} (\infty) = 1 \end{matrix}

(30)

\begin{matrix} p^{(j)} : L_{2} g_{j} - L_{2} g_{j - 1} + [(1 + \frac{K}{2}) g_{j - 1}^{/ /} + \sum_{k = 0}^{j - 1} f_{k} g_{j - 1 - k}^{/} - \sum_{k = 0}^{j - 1} f_{k}^{/} g_{j - 1 - k} - K (2 g_{j - 1} + f_{j - 1}^{/ /})] \\ g (0) = 0, g (\infty) = 0 \\ ⋮ \end{matrix}

Similarly for Eq. (21) we define the initial guess as

(31)

h_{0} (y) = y + e^{- y} - 1, t_{0} (y) = - \frac{1}{2} + \frac{e^{- y}}{2}

We can obtain the higher order term for Eq. (21) as we obtained in Eq. (9)…

Graphical behavior of the physical parameters has been calculated for the 10th order approximation.

3 Results and discussion

In this study we have examined the two dimensional stagnation point flow of a micropolar fluid. The obtained nonlinear coupled ordinary differential equations are solved by using Homotopy perturbation method. Effects of the material parameter K on the velocity profile and microrotation profile for different cases of n are investigated and obtained results compared with the Kaller Box method (Lok and Pop, 2007).

Tables 1 and 2 shows the comparison of $f^{″} (0)$ , h′(0) for some values of K and n between HPM and Kaller Box. Values for g(0) and t(0) are not calculated as we calculate them from $f^{″} (0), h^{'} (0)$ . They result from the boundary condition (10) and (21) where g(0) = − ${nf}^{″} (0)$ n, t(0) = − nh′(0). It is noticed from the table that the effect of increasing values of material parameter K results in a decrease in values of reduced skin friction $f^{″} (0)$ and also the values are greater for n = 1/2 than for n = 0. This indicates that the micropolar fluid displays a reduction in drag as compared to Newtonian fluids.

Table 1 Comparison of the velocity profile between HPM and KB (Lok and Pop, 2007) for different values of K and n.

K	HPM	HPM	KB (Lok and Pop, 2007)	KB Lok and Pop, 2007
	$f^{″} (0)$ n = 0	$f^{″} (0)$ n = 1/2	$f^{″} (0)$ n = 0	$f^{″} (0)$ n = 1/2
0.0	1.221927	1.223627	1.232627	1.232627
0.5	0.932657	1.082486	0.992657	1.102486
1.0	0.821085	1.016423	0.841085	1.006423
1.5	0.706835000	0.922764	0.736835	0.931764
2.0	0.620349	0.869584	0.660479	0.871584
2.5	0.84321	0.869584	0.601906	0.821736
3.0	0.504374	0.735566	0.555374	0.779566

Table 2 Comparison of the velocity profile between HPM and KB for different values of K and n.

K	HPM	HPM	KB	KB
	$h^{'} (0)$ n = 0	$h^{'} (0)$ n = 1/2	$h^{'} (0)$ n = 0	$h^{'} (0)$ n = 1/2
0.0	1.406592	1.386592	1.406592	1.406592
0.5	1.305981	1.376579	1.305981	1.406579
1.0	1.230837	1.366572	1.230837	1.406572
1.5	1.174002	1.386569	1.174002	1.406569
2.0	1.129859	1.396566	1.129859	1.406566
2.5	1.0948	1.4165	1.094646	1.406563
3.0	1.065887	1.376561	1.065887	1.406561

In order to provide physical insights into the flow problems, Figs. 1–4 are plotted for the velocity profile and the microrotation profile. The material parameter K is the ratio of vortex viscosity to absolute viscosity. If this parameter is small then it can be said that the viscous effect is confined in a very thin layer near the wall and the thickness of this layer is proportional to $κ = \frac{κ}{μ}$ and inversely proportional to f′(0). Therefore it can be analyzed from Figs. 1 and 2 that as the values of K increase, values of f′(0) near the wall are decreasing. Consequently, the velocity gradient at the wall decreases as K increases. This describes very well the trend of the values of obtained in Table 1. For case n = 1/2 (Fig. 3), the microrotation decreases continuously from its maximum value at the wall to zero far from the wall. On the other hand, the microrotation increases in function with parameter K. It can be seen from Fig. 4 that the microrotation increases as K increases for the case when n = 0. The peak value of microrotation occurs near the wall then decreases monotonically to zero as y increases. Finally, it is observed that Figs. 1–4 that, as expected, the velocity and microrotation boundary layer thicknesses increases as the material parameter K increases.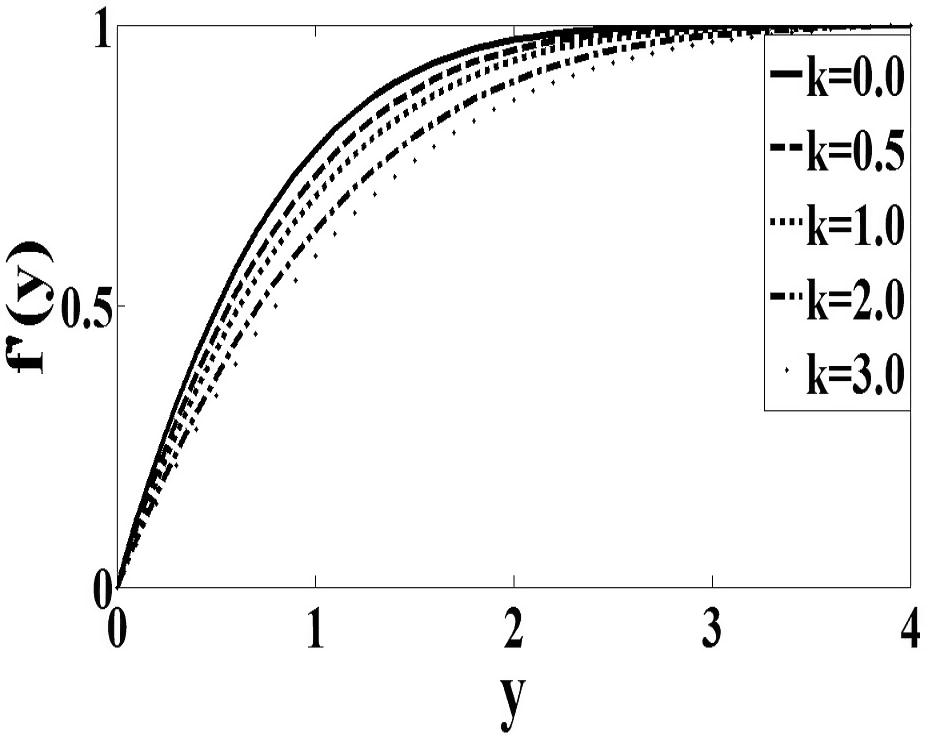

Figure 1

Velocity profile for the case n = 0.5.

Figure 2

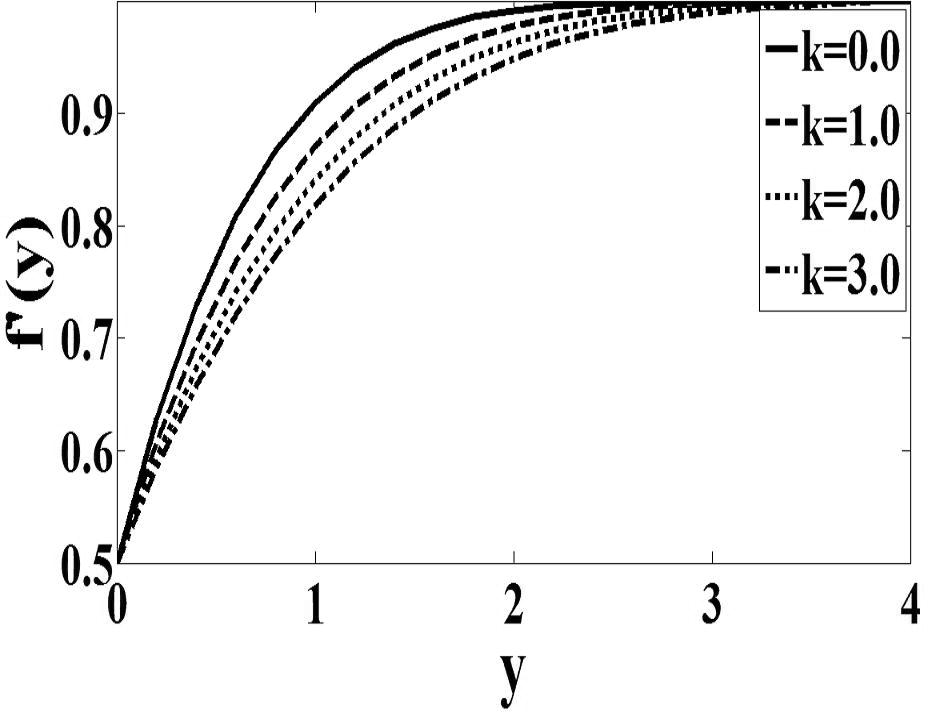
Velocity profile for the case n = 0.

Figure 3

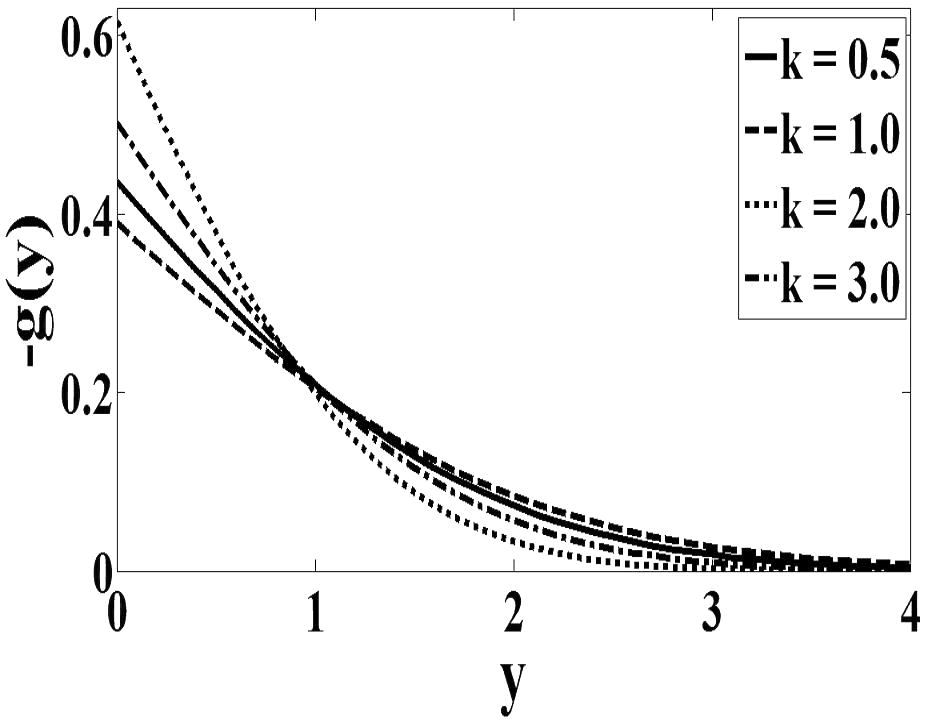
Micro rotation profile for case n = 0.5.

Figure 4

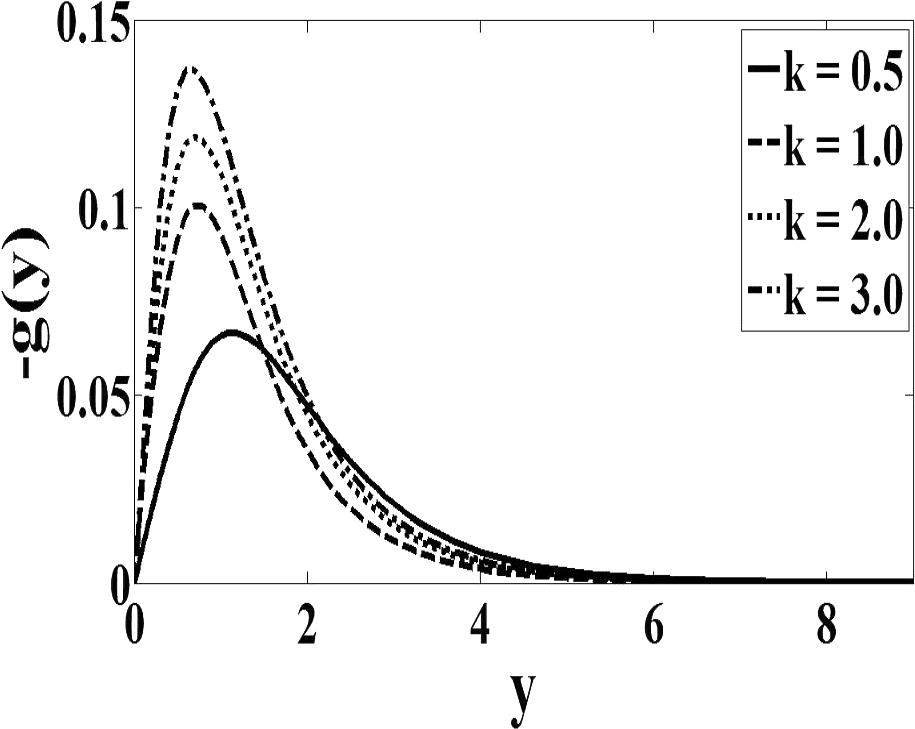
Micro rotation profile for case

n = 0

4 Conclusion

The series solution of steady two dimensional non orthogonal stagnation point flow of the micropolar fluid is studied and the main points of the study are listed below.

The velocity profile strongly decreases as the material parameter increases at strong concentrations, which clearly shows that the viscous effects are confined in a very thin layer near the wall.
For the weak concentration the velocity profile decreases as material parameter increases and remains uniform throughout the domain.
The microrotation velocity decreases continuously from its maximum value at the wall to zero far from the wall for the weak concentration case.
The microrotation velocity profile has a parabolic distribution in the case of strong concentration. It increases strongly near the wall then decreases continuously to zero as y increases.

References

Abd Alla A.M., Abo-Dahab S.M., Al-Simery R.D., . Effect of rotation on peristaltic flow of a micropolar fluid through a porous medium with an external magnetic field. J. Magn. Magn. Mater.. 2013;348:33-43.
[Google Scholar]
Ahmadi A.R., Zahmetkhash A., Hatami H., Ganji D.D., . A comprehensive analysis of flow and heat transfer for a nano fluid over an unsteady stretching sheet. Powder Technol.. 2014;258:125-133.
[Google Scholar]
Ariel P.D., . Stagnation point flow with suction: an approximate solution. J. Appl. Mech.. 1994;61:976-978.
[Google Scholar]
Bayada Guy, Łkaszewic Grzegorz, . On micropolar fluids in the theory of lubrication. Rigorous derivation of an analogue of the reynolds equation. Int. J. Eng. Sci.. 1996;34:1477-1490.
[Google Scholar]
Bekir A., Cevikel A.C., . Solitary wave solution of two nonlinear physical models by tanh-coth method. Commun. Non linear Sci.. 2009;14:1804-1809.
[Google Scholar]
Biazar J., Gholamin P., Hosseini K., . Variational iteration method for solving Fokker-Planck equation. J. Franklin. Inst.. 2010;347:1137-1147.
[Google Scholar]
Borrelli A., Giantesio G., Patria M.C., . Megnetoconvection of a micropolar fluid in a vertical channel. Int. J. Heat Mass Transf.. 2015;80:614-625.
[Google Scholar]
Borrelli A., Giantesio G., Patria M.C., . An exact solution of 3D MHD stagnation point flow of a micropolar fluid. Commun. Nonlinear Sci. Numer. Simul.. 2015;20:121-135.
[Google Scholar]
Brzdęk J., Popa D., Xu B., . Remarks on stability and non stability of the linear functional equation of the first order. Appl. Math. Comput.. 2014;238:14-148.
[Google Scholar]
Domairry G., Hatami M., . Squeezing Cu-water nano fluid flow analysis between parallel plates by DTM-Pade Method. J. Mol. Liquid. 2014;193:37-44.
[Google Scholar]
Domairy D., Shaikholeslam M., . Natural convection flow of a non-Newtonian nanofluid between two vertical flat plates. J. Nanoeng. Nanosyst.. 2012;225:115-122.
[Google Scholar]
Eckert, E.R.G., 1942. VDI Forschungsheft, Berlin. pp. 416–418.
Eringen A.C., . Theory of micropolar fluids. J. Math. Mech.. 1966;16:1-18.
[Google Scholar]
Faltas M.S., Saad E.I., . Slow motion of spherical droplet in a micropolar fluid flow perpendicular to a planer solid surface. Eur. J. Mech.. 2014;48:266-276.
[Google Scholar]
Faraz N., . Study of the effects of the Reynolds number on circular porous slider via variational iteration algorithm-II. Comput. Math. Appl.. 2011;61:1991-1994.
[Google Scholar]
Faraz N., Khan Y., Yildirim A., . Analytical approach to two-dimensional viscous flow with a shrinking sheet via variational iteration algorithm-II. J. King Saud Univ.. 2011;23:77-81.
[Google Scholar]
Fzal A., Kim K.Y., . Flow and mixing analysis of Newtonian fluid in straight and serpentine microchannels. Chem. Eng. Sci.. 2014;116:263-274.
[Google Scholar]
Galleas W., Lamers J., . Reflection algebra and functional equation. Nucl. Phys. B. 2014;886:1003-1028.
[Google Scholar]
Guo-cheng Wu, . Adomian decomposition method for non smooth initial value problems. Math. Comput. Model.. 2011;54:2104-2108.
[Google Scholar]
Guram G.S., Smith C., . Stagnation flows of micropolar fluid with strong and weak strong and weak interactions. Comput. Math. Appl.. 1980;6:213-233.
[Google Scholar]
Hatami M., Domairry G., . Transient vertically motion of a soluble particle in a Newtonian fluid media. J. Powder Technol.. 2014;253:481-485.
[Google Scholar]
Hatami H., Ganji D.D., . Thermal behavior of longitudinal Convective radiative porous fins with different section shapes and ceramics materials. J. Ceramics Int.. 2014;40:6765-6775.
[Google Scholar]
Hatami M., Ganji D.D., . Natural convection of sodium alginate Non-Newtonian nano fluid flow between two vertical flat plates by analytical and numerical methods. Case Studies Thermal Eng.. 2014;2:14-22.
[Google Scholar]
Hatami H., Ganji D.D., . Investigation of refrigeration efficiency for fully wet circular porous fins with variable sections by combined heat and mass transfer analysis. Int. J. Refrig.. 2014;40:140-151.
[Google Scholar]
Hatami M., Shaikhoeslam M., Hossani M., Ganji D.D., . Analytical investigation of MHD nano fluid flow in a non parallel walls. J. Mol. Liq.. 2014;194:251-259.
[Google Scholar]
Hatami M., Shaikholeslam M., Ganji D.D., . High accuracy analysis for motion of a spherical particle in plane Couette fluid flow by multi-step differential transformation method. Powder Technol.. 2014;260:59-67.
[Google Scholar]
Hatami M., Shaikholeslam M., Ganji D.D., . Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Powder Technol.. 2014;253:769-779.
[Google Scholar]
He Ji-Huan, . Homotopy perturbation method: a new nonlinear analytical technique. Appl. Math. Comput.. 2003;135:73-79.
[Google Scholar]
He Ji-Huan, . The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput.. 2004;151:287-292.
[Google Scholar]
He Ji-Huan, . Comparison of homotopy perturbation method and homotopy analysis method. Appl. Maths. Comput.. 2004;156:527-539.
[Google Scholar]
He Ji-Huan, . A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Nonlinear Mech.. 2007;35:37-43.
[Google Scholar]
Hiemenz K., . Grenzschicht an einem in den gleichf¨ormigen gl¨ussigkeitsstrom einge-tauchten geraden kreiszylinder. Dinglers Polytechnisches J.. 1911;326:321-410.
[Google Scholar]
Homann F., . Der einfluss grosser zahigkeit bei der str¨omung um den zylinder und um die kugel. Z. Angew. Math. Mech.. 1936;16:153-165.
[Google Scholar]
JunYang X., Srivastava H.M., Carlo Cattani, . Local fractional homotopy perturbation method for solving fractal partial differential equation arising in mathematical physics. Romanian Rep. Phys.. 2014;67
[Google Scholar]
Khan Y., Muhammad U., . Modified homotopy perturbation transform method. Int. J. Nonlinear Sci. Numer. Simul.. 2014;15:19-25.
[Google Scholar]
Khan Y., Wu Qingbiao, . Homotopy perturbation transform method for non linear equation using He’s polynomials. Comp. Math. Appl.. 2011;61:25-28.
[Google Scholar]
Lan Xu., . A Hamiltonian approach for a plasma physics problem. Comp. Math. Appl.. 2011;61:1909-1911.
[Google Scholar]
Liu J., Zhu C., Fu T., Ma Y., Li H., . Numerical simulation of the interaction between three equal interval parallel bubbles rising in non Newtonian fluid. Chem. Eng. Sci.. 2013;93:55-66.
[Google Scholar]
Lok Y.Y., Pop I., . Non orthogonal stagnation point flow of a micropolar fluid. Int. J. Eng. Sci.. 2007;45:173-184.
[Google Scholar]
Mabood F., Khan W.A., Ismail A.I.Md., . MHD stagnation point flow and heat transfer impinging on stretching sheet with chemical reaction and transpiration. J. Chem. Eng.. 2015;273:430-437.
[Google Scholar]
Masayebidorchen S., Sheikholeslam M., Hatami M., Ganji D.D., . Analysis of turbulent MHD Couette nanofluid flow and heat transfer using hybrid DTM-FDM. Particuology 2014
[CrossRef] [Google Scholar]
Mohanty B., Mishra S.R., Pattanayak H.B., . Numerical investigation on heat and mass transfer of micropolar fluid through a porous medium. J. Alexanderia Eng.. 2015;54(2):223-232.
[Google Scholar]
Nasiri Soloklo H., Maghfoori Farsangi M., . Chebyshev rational functions approximation for model order reduction using harmony search. Scientia Iranica. 2013;20:771-777.
[Google Scholar]
Nianga J.M., Recho N., . Hamiltonian approach to piezoelectric fracture. Procedia. Mater. Sci.. 2014;3:318-324.
[Google Scholar]
Oahimire J.I., Olajuwa B.I., . Effect of Hall current and thermal radiation on heat and mass transfer of a chemically reacting MHD flow micropolar fluid through a porous medium. J. King Saud Univ. Eng. Sci.. 2014;2:112-121.
[Google Scholar]
Pažanin, . Modeling of solute dispersion in a circular pipe filled with micropolar fluid. Math. Comput. Modell.. 2013;57:2366-2373.
[Google Scholar]
Peddieson J., . An application of the micropolar fluid model to the calculation of turbulent shear flow. Int. J. Eng. Sci.. 1972;10:23-32.
[Google Scholar]
Picchi D., Correra S., Poesio P., . Flow pattern transition, pressure gradient, hold up predictions in Newtonian power law fluid stratified flow. Int. J. Multiphase Flow. 2014;63:105-115.
[Google Scholar]
Prakash J., Sinha Prawal, . Lubrication theory for micropolar fluids and its application to a journal bearing. Int. J. Eng. Sci.. 1975;13:217-232.
[Google Scholar]
Reinhardt H., Heffner J., . The effective potential of the confinement order parameter in the Hamiltonian approach. Phys. Lett. B. 2012;718:672-677.
[Google Scholar]
Rosali H., Ishak A., Nazar R., . The effect of unsteadiness on mixed convection boundary layer stagnation point flow over a vertical flat surface embedded in a porous medium. Int. J. Heat Mass Transf.. 2014;77:147-156.
[Google Scholar]
Schlichting H., Bussmann K., . Exakte l¨osungen fur die laminare reibungsschicht mit absaugung und ausblasen. Schriftenr. Dtsch. Akad. der Luftfahrtforschung Ser. B. 1943;7:25-69.
[Google Scholar]
Shaikhoeslam M., Hatami M., Ganji D.D., . Nano fluid and heat transfer in an asymmetric porous channel with expanding or contracting wall. J. Mol. Liq.. 2014;195:230-239.
[Google Scholar]
Shaikhoeslam M., Hatami M., Ganji D.D., . Micropolar fluid and heat transfer in a permeable channel using analytical method. J. Mol. Liq.. 2014;194:30-36.
[Google Scholar]
Shaikholeslam M., Ganji D.D., . Magnetohydrodynamic flow in a permeable channel filled with nanofluid. Sci. Iranica B. 2014;21(1):203-212.
[Google Scholar]
Shaikholeslam M., Ashorynejad H.R., Ganji D.D., Hashim I., Raza H., . Investigation of the laminar viscous flow in a semi-porous channel in the presence of uniform magnetic field using optimal homotopy asymptotic method. Sains Malaysiana. 2012;41(10):1177-1229.
[Google Scholar]
Shaikholeslam M., Ganji D.D., Ashorynejad H.R., Reddy Gorla R.S., Khani Mustafa, . Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput. Meth. Appl. Mech. Eng.. 2015;283:651-663.
[Google Scholar]
Shaikholeslami M., Ashorynejad H.R., Ganji D.D., Kolahdooz A., . Investigation of Rotating MHD Viscous Flow and Heat Transfer Between Stretching Porous Surface Using Analytical Methods. Hindawi Publishing Corporation Mathematical Problem in Engineering; 2011.
Shakeri Aski F., Jalal Nasirkhani Seyed, Mohammadian E., Asgari A., . Application of Adomian decomposition method for micropolar flow in a porous channel. Propulsion Power Res.. 2014;3:15-21.
[Google Scholar]
Sheikhoeslami M., Ganji D.D., Ashorynejad H.R., . Investigation of squeezing unsteady nano fluid flow using ADM. Power Technol.. 2013;239:259-265.
[Google Scholar]
Sheikholeslami M., Ganji D.D., . Heat transfer of CU water nano fluid flow between parallel plates. Powder Technol.. 2013;235:873-879.
[Google Scholar]
Sheikholeslami M., Ashorynejad H.R., Ganji D.D., Hashim I., . Flow and Heat Transfer of CU Water Nano Fluid between a Stretching Sheet and a Porous Surface in a Rotating System. Hindawi Publishing Corporation Journal of Applied Mathematics; 2012.
Sheikholeslami M., Ganji D.D., Ashorynejad H.R., Rokni H.B., . Analytical Investigation of Jeffery-Hamel flow with high magnetic field and nano particle by ADM. Appl. Math. Eng. Ed.. 2012;33(1):1553-1564.
[Google Scholar]
Sheikholeslami M., Ashorynejad H.R., Ganji D.D., Yildirim A., . Homotopy perturbation method for three dimensional problems of condensation film on inclined rotating disk. Scientia Iranica. 2012;19:437-442.
[Google Scholar]
Sheikholeslami M., Hatami M., Ganji D.D., . Analytical investigation of MHD nanofluid flow in a Semi-Porous Channel. Powder Technol.. 2013;246:327-336.
[Google Scholar]
Sheikholeslami M., Ganji D.D., Rokni H.B., . Nano fluid of semi porous channel in the presence of uniform Magnetic field. IJE Trans.. 2013;26:653-662.
[Google Scholar]
Sheikholeslami M., Ellahi R., Ashorynejad H.R., Domairry G., Hayat T., . Effects of heat transfer in flow of nano fluid over a permeable stretching wall in a porous medium. J. Comput. Theor. Nano Sci.. 2014;11:1-11.
[Google Scholar]
Shukri S., Al-Khaled K., . The extended tanh method for solving system of nonlinear wave equation. Appl. Math. Comput.. 2010;217:1997-2006.
[Google Scholar]
Srinivasacharya D., Upendar M., . Effect of double stratification on MHD free convection in a micropolar fluid. J. Egypt. Math. Soc.. 2014;18
[Google Scholar]
Stiver W., Mackay D., . Linear superposition in modeling contaminant behavior in aquatic systems. Water Res.. 1995;29:329-335.
[Google Scholar]
Villone M.M., Greco F., Hulsen M.A., Maffettone P.L., . Simulation of an elastic particle in Newtonian and Viscoelastic fluids subjected to confined shear flow. J. Non-Newtonian Fluid Mech.. 2014;210:47-55.
[Google Scholar]
Wang C.Y., . The unsteady oblique stagnation point flow through a nozzle. Phys. Fluids. 1985;28:2046.
[Google Scholar]

Introduction

Formulation of the problem

Results and discussion

Conclusion

Fulltext Views
7

PDF downloads
17

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Abd Alla A.M., Abo-Dahab S.M., Al-Simery R.D., . Effect of rotation on peristaltic flow of a micropolar fluid through a porous medium with an external magnetic field. J. Magn. Magn. Mater.. 2013;348:33-43.
[Google Scholar]

[2] Ahmadi A.R., Zahmetkhash A., Hatami H., Ganji D.D., . A comprehensive analysis of flow and heat transfer for a nano fluid over an unsteady stretching sheet. Powder Technol.. 2014;258:125-133.
[Google Scholar]

[3] Ariel P.D., . Stagnation point flow with suction: an approximate solution. J. Appl. Mech.. 1994;61:976-978.
[Google Scholar]

[4] Bayada Guy, Łkaszewic Grzegorz, . On micropolar fluids in the theory of lubrication. Rigorous derivation of an analogue of the reynolds equation. Int. J. Eng. Sci.. 1996;34:1477-1490.
[Google Scholar]

[5] Bekir A., Cevikel A.C., . Solitary wave solution of two nonlinear physical models by tanh-coth method. Commun. Non linear Sci.. 2009;14:1804-1809.
[Google Scholar]

[6] Biazar J., Gholamin P., Hosseini K., . Variational iteration method for solving Fokker-Planck equation. J. Franklin. Inst.. 2010;347:1137-1147.
[Google Scholar]

[7] Borrelli A., Giantesio G., Patria M.C., . Megnetoconvection of a micropolar fluid in a vertical channel. Int. J. Heat Mass Transf.. 2015;80:614-625.
[Google Scholar]

[8] Borrelli A., Giantesio G., Patria M.C., . An exact solution of 3D MHD stagnation point flow of a micropolar fluid. Commun. Nonlinear Sci. Numer. Simul.. 2015;20:121-135.
[Google Scholar]

[9] Brzdęk J., Popa D., Xu B., . Remarks on stability and non stability of the linear functional equation of the first order. Appl. Math. Comput.. 2014;238:14-148.
[Google Scholar]

[10] Domairry G., Hatami M., . Squeezing Cu-water nano fluid flow analysis between parallel plates by DTM-Pade Method. J. Mol. Liquid. 2014;193:37-44.
[Google Scholar]

[11] Domairy D., Shaikholeslam M., . Natural convection flow of a non-Newtonian nanofluid between two vertical flat plates. J. Nanoeng. Nanosyst.. 2012;225:115-122.
[Google Scholar]

[12] Eckert, E.R.G., 1942. VDI Forschungsheft, Berlin. pp. 416–418.

[13] Eringen A.C., . Theory of micropolar fluids. J. Math. Mech.. 1966;16:1-18.
[Google Scholar]

[14] Faltas M.S., Saad E.I., . Slow motion of spherical droplet in a micropolar fluid flow perpendicular to a planer solid surface. Eur. J. Mech.. 2014;48:266-276.
[Google Scholar]

[15] Faraz N., . Study of the effects of the Reynolds number on circular porous slider via variational iteration algorithm-II. Comput. Math. Appl.. 2011;61:1991-1994.
[Google Scholar]

[16] Faraz N., Khan Y., Yildirim A., . Analytical approach to two-dimensional viscous flow with a shrinking sheet via variational iteration algorithm-II. J. King Saud Univ.. 2011;23:77-81.
[Google Scholar]

[17] Fzal A., Kim K.Y., . Flow and mixing analysis of Newtonian fluid in straight and serpentine microchannels. Chem. Eng. Sci.. 2014;116:263-274.
[Google Scholar]

[18] Galleas W., Lamers J., . Reflection algebra and functional equation. Nucl. Phys. B. 2014;886:1003-1028.
[Google Scholar]

[19] Guo-cheng Wu, . Adomian decomposition method for non smooth initial value problems. Math. Comput. Model.. 2011;54:2104-2108.
[Google Scholar]

[20] Guram G.S., Smith C., . Stagnation flows of micropolar fluid with strong and weak strong and weak interactions. Comput. Math. Appl.. 1980;6:213-233.
[Google Scholar]

[21] Hatami M., Domairry G., . Transient vertically motion of a soluble particle in a Newtonian fluid media. J. Powder Technol.. 2014;253:481-485.
[Google Scholar]

[22] Hatami H., Ganji D.D., . Thermal behavior of longitudinal Convective radiative porous fins with different section shapes and ceramics materials. J. Ceramics Int.. 2014;40:6765-6775.
[Google Scholar]

[23] Hatami M., Ganji D.D., . Natural convection of sodium alginate Non-Newtonian nano fluid flow between two vertical flat plates by analytical and numerical methods. Case Studies Thermal Eng.. 2014;2:14-22.
[Google Scholar]

[24] Hatami H., Ganji D.D., . Investigation of refrigeration efficiency for fully wet circular porous fins with variable sections by combined heat and mass transfer analysis. Int. J. Refrig.. 2014;40:140-151.
[Google Scholar]

[25] Hatami M., Shaikhoeslam M., Hossani M., Ganji D.D., . Analytical investigation of MHD nano fluid flow in a non parallel walls. J. Mol. Liq.. 2014;194:251-259.
[Google Scholar]

[26] Hatami M., Shaikholeslam M., Ganji D.D., . High accuracy analysis for motion of a spherical particle in plane Couette fluid flow by multi-step differential transformation method. Powder Technol.. 2014;260:59-67.
[Google Scholar]

[27] Hatami M., Shaikholeslam M., Ganji D.D., . Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Powder Technol.. 2014;253:769-779.
[Google Scholar]

[28] He Ji-Huan, . Homotopy perturbation method: a new nonlinear analytical technique. Appl. Math. Comput.. 2003;135:73-79.
[Google Scholar]

[29] He Ji-Huan, . The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl. Math. Comput.. 2004;151:287-292.
[Google Scholar]

[30] He Ji-Huan, . Comparison of homotopy perturbation method and homotopy analysis method. Appl. Maths. Comput.. 2004;156:527-539.
[Google Scholar]

[31] He Ji-Huan, . A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Nonlinear Mech.. 2007;35:37-43.
[Google Scholar]

[32] Hiemenz K., . Grenzschicht an einem in den gleichf¨ormigen gl¨ussigkeitsstrom einge-tauchten geraden kreiszylinder. Dinglers Polytechnisches J.. 1911;326:321-410.
[Google Scholar]

[33] Homann F., . Der einfluss grosser zahigkeit bei der str¨omung um den zylinder und um die kugel. Z. Angew. Math. Mech.. 1936;16:153-165.
[Google Scholar]

[34] JunYang X., Srivastava H.M., Carlo Cattani, . Local fractional homotopy perturbation method for solving fractal partial differential equation arising in mathematical physics. Romanian Rep. Phys.. 2014;67
[Google Scholar]

[35] Khan Y., Muhammad U., . Modified homotopy perturbation transform method. Int. J. Nonlinear Sci. Numer. Simul.. 2014;15:19-25.
[Google Scholar]

[36] Khan Y., Wu Qingbiao, . Homotopy perturbation transform method for non linear equation using He’s polynomials. Comp. Math. Appl.. 2011;61:25-28.
[Google Scholar]

[37] Lan Xu., . A Hamiltonian approach for a plasma physics problem. Comp. Math. Appl.. 2011;61:1909-1911.
[Google Scholar]

[38] Liu J., Zhu C., Fu T., Ma Y., Li H., . Numerical simulation of the interaction between three equal interval parallel bubbles rising in non Newtonian fluid. Chem. Eng. Sci.. 2013;93:55-66.
[Google Scholar]

[39] Lok Y.Y., Pop I., . Non orthogonal stagnation point flow of a micropolar fluid. Int. J. Eng. Sci.. 2007;45:173-184.
[Google Scholar]

[40] Mabood F., Khan W.A., Ismail A.I.Md., . MHD stagnation point flow and heat transfer impinging on stretching sheet with chemical reaction and transpiration. J. Chem. Eng.. 2015;273:430-437.
[Google Scholar]

[41] Masayebidorchen S., Sheikholeslam M., Hatami M., Ganji D.D., . Analysis of turbulent MHD Couette nanofluid flow and heat transfer using hybrid DTM-FDM. Particuology 2014
[CrossRef] [Google Scholar]

[42] Mohanty B., Mishra S.R., Pattanayak H.B., . Numerical investigation on heat and mass transfer of micropolar fluid through a porous medium. J. Alexanderia Eng.. 2015;54(2):223-232.
[Google Scholar]

[43] Nasiri Soloklo H., Maghfoori Farsangi M., . Chebyshev rational functions approximation for model order reduction using harmony search. Scientia Iranica. 2013;20:771-777.
[Google Scholar]

[44] Nianga J.M., Recho N., . Hamiltonian approach to piezoelectric fracture. Procedia. Mater. Sci.. 2014;3:318-324.
[Google Scholar]

[45] Oahimire J.I., Olajuwa B.I., . Effect of Hall current and thermal radiation on heat and mass transfer of a chemically reacting MHD flow micropolar fluid through a porous medium. J. King Saud Univ. Eng. Sci.. 2014;2:112-121.
[Google Scholar]

[46] Pažanin, . Modeling of solute dispersion in a circular pipe filled with micropolar fluid. Math. Comput. Modell.. 2013;57:2366-2373.
[Google Scholar]

[47] Peddieson J., . An application of the micropolar fluid model to the calculation of turbulent shear flow. Int. J. Eng. Sci.. 1972;10:23-32.
[Google Scholar]

[48] Picchi D., Correra S., Poesio P., . Flow pattern transition, pressure gradient, hold up predictions in Newtonian power law fluid stratified flow. Int. J. Multiphase Flow. 2014;63:105-115.
[Google Scholar]

[49] Prakash J., Sinha Prawal, . Lubrication theory for micropolar fluids and its application to a journal bearing. Int. J. Eng. Sci.. 1975;13:217-232.
[Google Scholar]

[50] Reinhardt H., Heffner J., . The effective potential of the confinement order parameter in the Hamiltonian approach. Phys. Lett. B. 2012;718:672-677.
[Google Scholar]

[51] Rosali H., Ishak A., Nazar R., . The effect of unsteadiness on mixed convection boundary layer stagnation point flow over a vertical flat surface embedded in a porous medium. Int. J. Heat Mass Transf.. 2014;77:147-156.
[Google Scholar]

[52] Schlichting H., Bussmann K., . Exakte l¨osungen fur die laminare reibungsschicht mit absaugung und ausblasen. Schriftenr. Dtsch. Akad. der Luftfahrtforschung Ser. B. 1943;7:25-69.
[Google Scholar]

[53] Shaikhoeslam M., Hatami M., Ganji D.D., . Nano fluid and heat transfer in an asymmetric porous channel with expanding or contracting wall. J. Mol. Liq.. 2014;195:230-239.
[Google Scholar]

[54] Shaikhoeslam M., Hatami M., Ganji D.D., . Micropolar fluid and heat transfer in a permeable channel using analytical method. J. Mol. Liq.. 2014;194:30-36.
[Google Scholar]

[55] Shaikholeslam M., Ganji D.D., . Magnetohydrodynamic flow in a permeable channel filled with nanofluid. Sci. Iranica B. 2014;21(1):203-212.
[Google Scholar]

[56] Shaikholeslam M., Ashorynejad H.R., Ganji D.D., Hashim I., Raza H., . Investigation of the laminar viscous flow in a semi-porous channel in the presence of uniform magnetic field using optimal homotopy asymptotic method. Sains Malaysiana. 2012;41(10):1177-1229.
[Google Scholar]

[57] Shaikholeslam M., Ganji D.D., Ashorynejad H.R., Reddy Gorla R.S., Khani Mustafa, . Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput. Meth. Appl. Mech. Eng.. 2015;283:651-663.
[Google Scholar]

[58] Shaikholeslami M., Ashorynejad H.R., Ganji D.D., Kolahdooz A., . Investigation of Rotating MHD Viscous Flow and Heat Transfer Between Stretching Porous Surface Using Analytical Methods. Hindawi Publishing Corporation Mathematical Problem in Engineering; 2011.

[59] Shakeri Aski F., Jalal Nasirkhani Seyed, Mohammadian E., Asgari A., . Application of Adomian decomposition method for micropolar flow in a porous channel. Propulsion Power Res.. 2014;3:15-21.
[Google Scholar]

[60] Sheikhoeslami M., Ganji D.D., Ashorynejad H.R., . Investigation of squeezing unsteady nano fluid flow using ADM. Power Technol.. 2013;239:259-265.
[Google Scholar]

[61] Sheikholeslami M., Ganji D.D., . Heat transfer of CU water nano fluid flow between parallel plates. Powder Technol.. 2013;235:873-879.
[Google Scholar]

[62] Sheikholeslami M., Ashorynejad H.R., Ganji D.D., Hashim I., . Flow and Heat Transfer of CU Water Nano Fluid between a Stretching Sheet and a Porous Surface in a Rotating System. Hindawi Publishing Corporation Journal of Applied Mathematics; 2012.

[63] Sheikholeslami M., Ganji D.D., Ashorynejad H.R., Rokni H.B., . Analytical Investigation of Jeffery-Hamel flow with high magnetic field and nano particle by ADM. Appl. Math. Eng. Ed.. 2012;33(1):1553-1564.
[Google Scholar]

[64] Sheikholeslami M., Ashorynejad H.R., Ganji D.D., Yildirim A., . Homotopy perturbation method for three dimensional problems of condensation film on inclined rotating disk. Scientia Iranica. 2012;19:437-442.
[Google Scholar]

[65] Sheikholeslami M., Hatami M., Ganji D.D., . Analytical investigation of MHD nanofluid flow in a Semi-Porous Channel. Powder Technol.. 2013;246:327-336.
[Google Scholar]

[66] Sheikholeslami M., Ganji D.D., Rokni H.B., . Nano fluid of semi porous channel in the presence of uniform Magnetic field. IJE Trans.. 2013;26:653-662.
[Google Scholar]

[67] Sheikholeslami M., Ellahi R., Ashorynejad H.R., Domairry G., Hayat T., . Effects of heat transfer in flow of nano fluid over a permeable stretching wall in a porous medium. J. Comput. Theor. Nano Sci.. 2014;11:1-11.
[Google Scholar]

[68] Shukri S., Al-Khaled K., . The extended tanh method for solving system of nonlinear wave equation. Appl. Math. Comput.. 2010;217:1997-2006.
[Google Scholar]

[69] Srinivasacharya D., Upendar M., . Effect of double stratification on MHD free convection in a micropolar fluid. J. Egypt. Math. Soc.. 2014;18
[Google Scholar]

[70] Stiver W., Mackay D., . Linear superposition in modeling contaminant behavior in aquatic systems. Water Res.. 1995;29:329-335.
[Google Scholar]

[71] Villone M.M., Greco F., Hulsen M.A., Maffettone P.L., . Simulation of an elastic particle in Newtonian and Viscoelastic fluids subjected to confined shear flow. J. Non-Newtonian Fluid Mech.. 2014;210:47-55.
[Google Scholar]

[72] Wang C.Y., . The unsteady oblique stagnation point flow through a nozzle. Phys. Fluids. 1985;28:2046.
[Google Scholar]