Translate this page into:
Steady nanofluid flow between parallel plates considering thermophoresis and Brownian effects
⁎Corresponding author. Houman.Babazadehrokni@du.edu (Houman B. Rokni)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this article, heat and mass transfer behavior of steady nanofluid flow between parallel plates in the presence of uniform magnetic field is studied. The important effect of Brownian motion and thermophoresis has been included in the model of nanofluid. The governing equations are solved via the Differential Transformation Method. The validity of this method was verified by comparison of previous work which is done for viscous fluid. The analysis is carried out for different parameters namely: viscosity parameter, Magnetic parameter, thermophoretic parameter and Brownian parameter. Results reveal that skin friction coefficient enhances with rise of viscosity and Magnetic parameters. Also it can be found that Nusselt number augments with an increase of viscosity parameters but it decreases with augment of Magnetic parameter, thermophoretic parameter and Brownian parameter.
Keywords
Nanofluid
Brownian
MHD
Thermophoresis
Differential Transformation Method
Nomenclature
- C
-
nanofluid concentration
- Cf
-
skin friction coefficients
- Cp
-
specific heat at constant pressure
- h
-
distance between the plates
- k
-
thermal conductivity
- Nu
-
Nusselt number
- p∗
-
modified fluid pressure
- Pr
-
Prandtl number
- R
-
viscosity parameter
-
velocity components along x, y, z axes respectively
- uw(x)
-
velocity of the stretching surface
- α
-
thermal diffusivity
- ϕ
-
dimensionless concentration
- η
-
dimensionless variable
- μ
-
dynamic viscosity
- υ
-
kinematic viscosity
- θ
-
dimensionless temperature
- ρ
-
fluid density
- σ
-
electrical conductivity
- τw
-
skin friction or shear stress along the stretching surface
Greek symbols
1 Introduction
Because of increment in energy price, heat transfer (HT) management is important in energy systems. Recently, nanofluid technology is planned and studied by some researchers experimentally or numerically in order to enhance HT process. The nanofluid can be applied to engineering problems, such as heat exchangers, cooling of electronic equipment and chemical processes. In most of the studies, it is assumed that nanofluid treats as the common pure fluid. Abu-Nada et al. (2008) investigated the enhancement of natural convection in horizontal concentric annuli field. They concluded that as Rayleigh number decreases, the thermal conductivity effects of nanoparticles cause more HT enhancement. Jou and Tzeng (2006) numerically studied the natural convection enhancements of nanofluid within a two-dimensional enclosure. They analyzed HT performance using Khana-fer’s model for various parameters, such as volume fraction, aspect ratio of the enclosure, and Grashof number. Results showed that increasing the buoyancy parameter and volume fraction of nanofluid causes an increase in the average HT coefficient. Rashidi et al. (2013) modeled the application of the second law of thermodynamics to an electrically conducting incompressible nanofluid fluid flowing over a porous rotating disk.
Malvandi and Ganji (2014a) studied the laminar flow and convective HT of alumina/water nanofluid inside a circular microchannel in the presence of a uniform magnetic field. For smaller nanoparticles, more uniform volume fraction is observed and abnormal variations in the HT rate are vanished. MHD effect on natural convection HT in an inclined L-shape enclosure filled with nanofluid was studied by Sheikholeslami et al. (2014). They found that enhancement in HT has reverse relationship with Hartmann number and Rayleigh number. They concluded that using magnetic rotating disk affects HT rate in renewable energy systems and industrial thermal management. Recently several authors investigated nanofluid flow and HT enhancement applications (Cortell, 2014; Mabood et al., 2014; Garoosi et al., 2015a,b,c; Ashorynejad et al., 2013a,b Hatami and Ganji, 2014a,b; Hatami et al., 2014a–c; Domairry et al., 2012; Sheikholeslami et al., 2013a; Sheikholeslami and Ganji, 2013; Sheikholeslami et al., 2013b–e; Kefayati, 2013a,b; Kefayati, 2013c; Sheikholeslami et al., 2012a–c; Shehzad et al., 2012; Shehzad et al., 2013a,b; Shehzad et al., 2014a,b; Sheikholeslami et al., 2014a; Sheikholeslami et al., 2014b–f; Sheikholeslami Kandelousi, 2014a,b; Sheikholeslami and Ganji, 2015a; Sheikholeslami et al., 2015a–c; Sheikholeslami and Rashidi, 2015; Ellahi, 2013; Ellahi et al., 2012, 2013, 2015; Raptis, 1998; Rashidi et al., 2015; Akbar et al., 2014a,b; Umavathi and Mohite, 2014: Zeeshan et al., 2014). In all the above articles, it is assumed that there are no slip velocities between nanoparticles and fluid molecules and assumed that the nanoparticle concentration is uniform. Nield and Kuznetsov (2009) studied the natural convection in a horizontal layer of a porous medium saturated by a nanofluid. Khan and Pop (2010) investigated boundary-layer flow of a nanofluid past a stretching sheet as a first paper in that field. Their model used for the nanofluid incorporates the effects of Brownian motion and thermophoresis. They have taken into account the Prandtl number, Lewis number, Thermophores number, and Brownian motion number. The investigation of heat and mass transfer unsteady squeezing viscous flow between two parallel plates in motion normal to their own surfaces independent of each other and arbitrary with respect to time has been regarded as one of the most important research topics due to its wide spectrum of scientific and engineering applications such as hydrodynamical equipment, lubrication system, polymer processing, chemical processing tool, materials damage due to freezing, food processing and cooling towers. Mahmood et al. (2007) investigated the HT characteristics in the squeezed flow over a porous surface. Differential Transformation Method is one of the semi-exact methods which do not have the limitation of the perturbation method. Against the traditional higher-order Taylor series procedure, this method applies a polynomial solution that is computationally expensive for higher orders. DTM is a substitute method and its main advantage is applying the nonlinear differential equations without discretization and linearization. This method was introduced by Zhou (1986), by applying the DTM method to different problems in electrical applications. Many researchers investigated Multi-step DTM in different applications, for example Hatami and his colleagues (2014d) studied spherical particles motion in plane Couette fluid flow (Yang and Baleanu, 2013; Cattani et al., 2015 El-Zahar, 2013; Sheikholeslami and Ganji, 2015b: Rashidi, 2009).
The main purpose of this study is to investigate the problem of unsteady nanofluid flow between parallel plates using the Differential Transformation Method. The influence of the radiation parameter, squeeze number, Hartmann number, Brownian motion parameter and thermophoretic parameter on temperature and concentration profiles is investigated.
2 Governing equations
Consider the steady nanofluid flow between two horizontal parallel plates when the fluid and the plates rotate together around the y-axis which is normal to the plates with an angular velocity. A Cartesian coordinate system is considered as followed: the x-axis is along the plate, the y-axis is perpendicular to it (see Fig. 1). The plates are located at
and
. The lower plate is being stretched by two equal and opposite forces so that the position of the point (0, 0, 0) remains unchanged. A uniform magnetic flux with density B0 is acting along y-axis about which the system is rotating. The governing equations in a rotating frame of reference are:
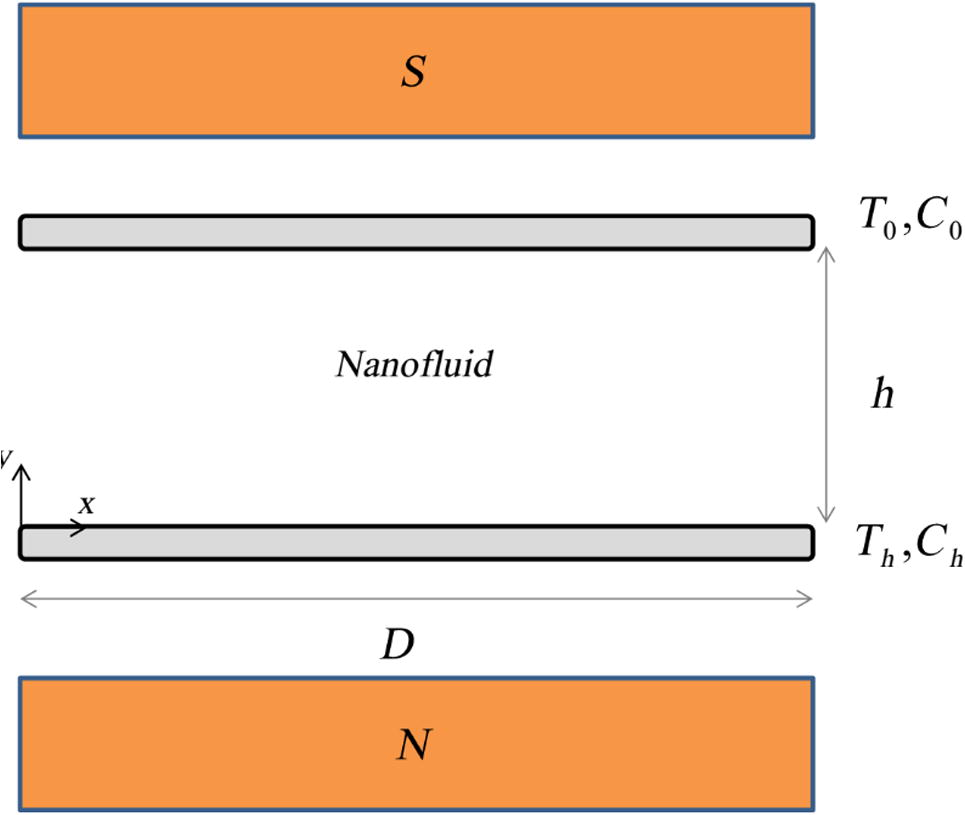
Geometry of problem.
Here u and v are the velocities in the x and y directions respectively. And T, C, ρf, μ, k, cP, and DB are temperature, concentration, base fluid’s density, dynamic viscosity, thermal conductivity, specific heat of nanofluid, and diffusion coefficient of the diffusing species. Also p∗ is the modified fluid pressure. The relevant boundary conditions are:
The following non-dimensional variables are introduced:
Therefore, the governing equations and boundary conditions for this case in non-dimensional form are given by:
With these boundary conditions:
The non-dimensional quantities are defined through in which R is the viscosity parameter, M is the Magnetic parameter, Pr is the Prandtl number, Sc is the Schmidt number, Nb is the Brownian motion parameter and Nt is the thermophoretic parameter.
Skin friction coefficient Cf along the stretching wall and Nusselt number Nu along the stretching wall are defined as
3 Differential Transform Method (DTM)
3.1 Basic of DTM
Basic definitions and operations of differential transformation are introduced as follows. Differential transformation of the function f(η) is defined as follows:
In (14), f(η) is the original function and F(k) is the transformed function which is called the T-function (it is also called the spectrum of the f(η) at η = η0, in the k domain). The differential inverse transformation of F(k) is defined as:
Eq. (16) implies that the concept of the differential transformation is derived from Taylor’s series expansion, but the method does not evaluate the derivatives symbolically. However, relative derivatives are calculated by an iterative procedure that is described by the transformed equations of the original functions. From the definitions of (14) and (15), it is easily proven that the transformed functions comply with the basic mathematical operations shown below. In real applications, the function f(η) in (16) is expressed by a finite series and can be written as:
Eq. (16) implies that is negligibly small, where N is series size.
Theorems to be used in the transformation procedure, which can be evaluated from (14) and (15), are given below (Table 1).
Original function
Transformed function
f(η) = αg(η) ± βh(η)
F[k] = αG[k] ± βH[k]
f(η) = g(η)h(η)
f(τ) = sin (ϖη + α)
f(τ) = cos (ϖη + α)
F(η) = (1 + η)m
f(η) = ηm
3.2 Solution with Differential Transformation Method
Now Differential Transformation Method has been applied into governing equations (Eqs. 8–10). Taking the differential transforms of Eqs. 8–10 with respect to χ and considering H = 1 gives:
Substituting Eqs. 23–25 into the main Eq. (18), closed form of the solutions can be obtained:
By substituting the boundary condition from Eq. (11) into Eqs. 26–28 in point η = 1 it can be obtained the values of a1, a2, a3, a4. By substituting obtained a1, a2, a3, a4 into Eqs. 26–28, it can be obtained the expression of F(η), Θ(η) and Φ(η).
4 Results and discussion
In this study, DTM is applied to simulate nanofluid flow and heat transfer in the presence of magnetic field. The influences of the viscosity parameter, Magnetic parameter, thermophoretic parameter and Brownian parameter on flow, heat and mass transfer characteristics have been investigated. In order to verify the correctness of the present DTM code, we have compared the results for the temperature profiles with those reported by Mehmood and Ali (2008) when ϕ = 0 (regular or Newtonian fluid) and also with those of Vajravelu and Kumar (2004) when Kr = 0 (non-rotational fluid). This comparison shows a good agreement (Fig. 2).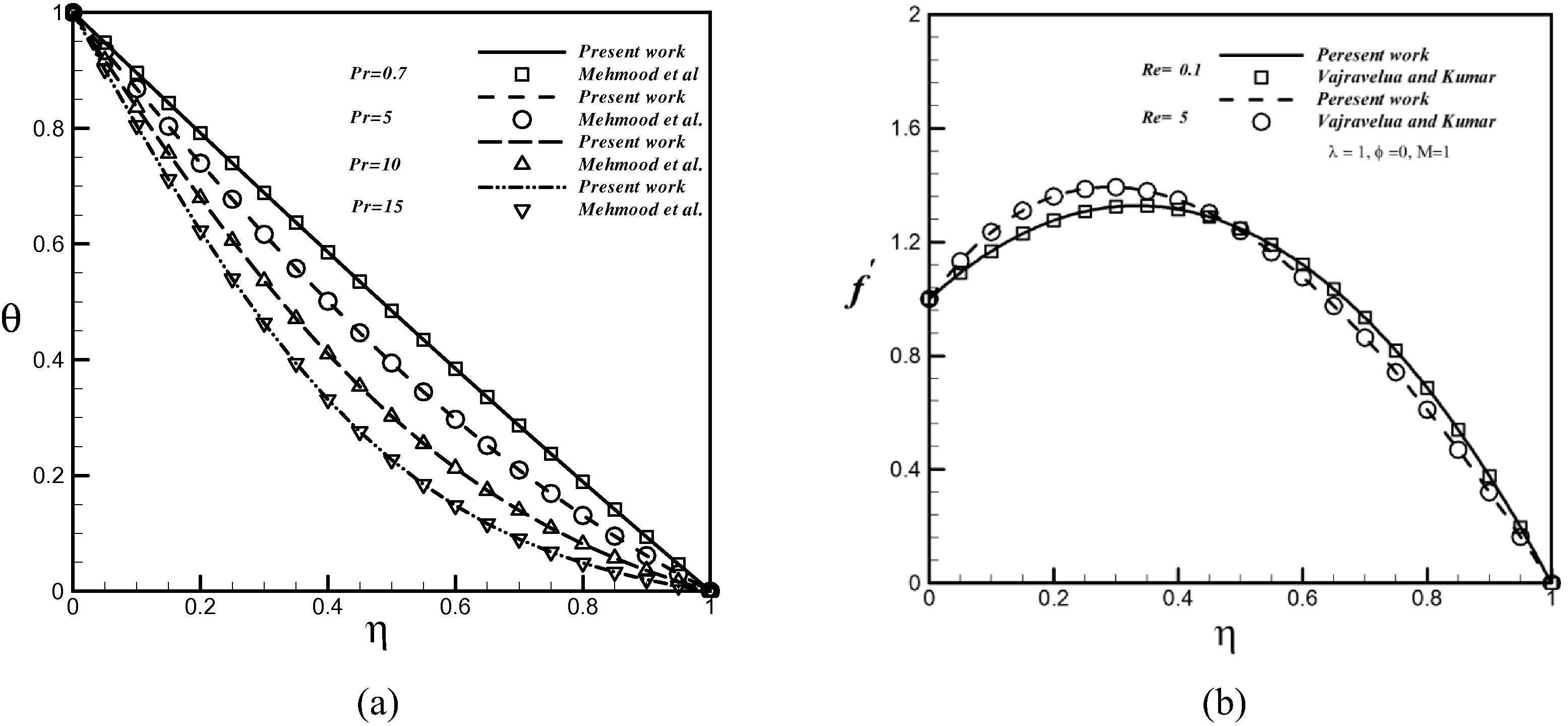
Comparison of (a) the temperature profiles between the present work and Mehmood and Ali (2008) when
and Kr = 0.5; (b) velocity profile between the present work and (Vajravelu and Kumar (2004)) when
and
.
Figs. 3 and 4 show the effect of viscosity and Magnetic parameters on velocity, temperature and concentration profiles. Effects of viscosity and Magnetic parameters on skin friction coefficient and Nusselt number are shown in Fig. 5. As viscosity parameter increases velocity decreases especially at middle point. Effect of Magnetic parameter on velocity profile is similar to that of viscosity parameter. So, skin friction coefficient is an increasing function of viscosity and Magnetic parameters. Thermal boundary layer thickness decreases with an increase of viscosity parameter but an opposite trend is observed for concentration boundary layer thickness. Increasing Magnetic parameter leads to augment in thermal boundary layer thickness. As shown in Fig. 5, Nusselt number increases with the rise of viscosity parameter while it reduces with the rise of Magnetic parameter. Fig. 6 shows the effect of Eckert number on temperature profile and Nusselt number. Temperature increases with an increase of viscous dissipation. So Nusselt number decreases with an increase of Eckert number.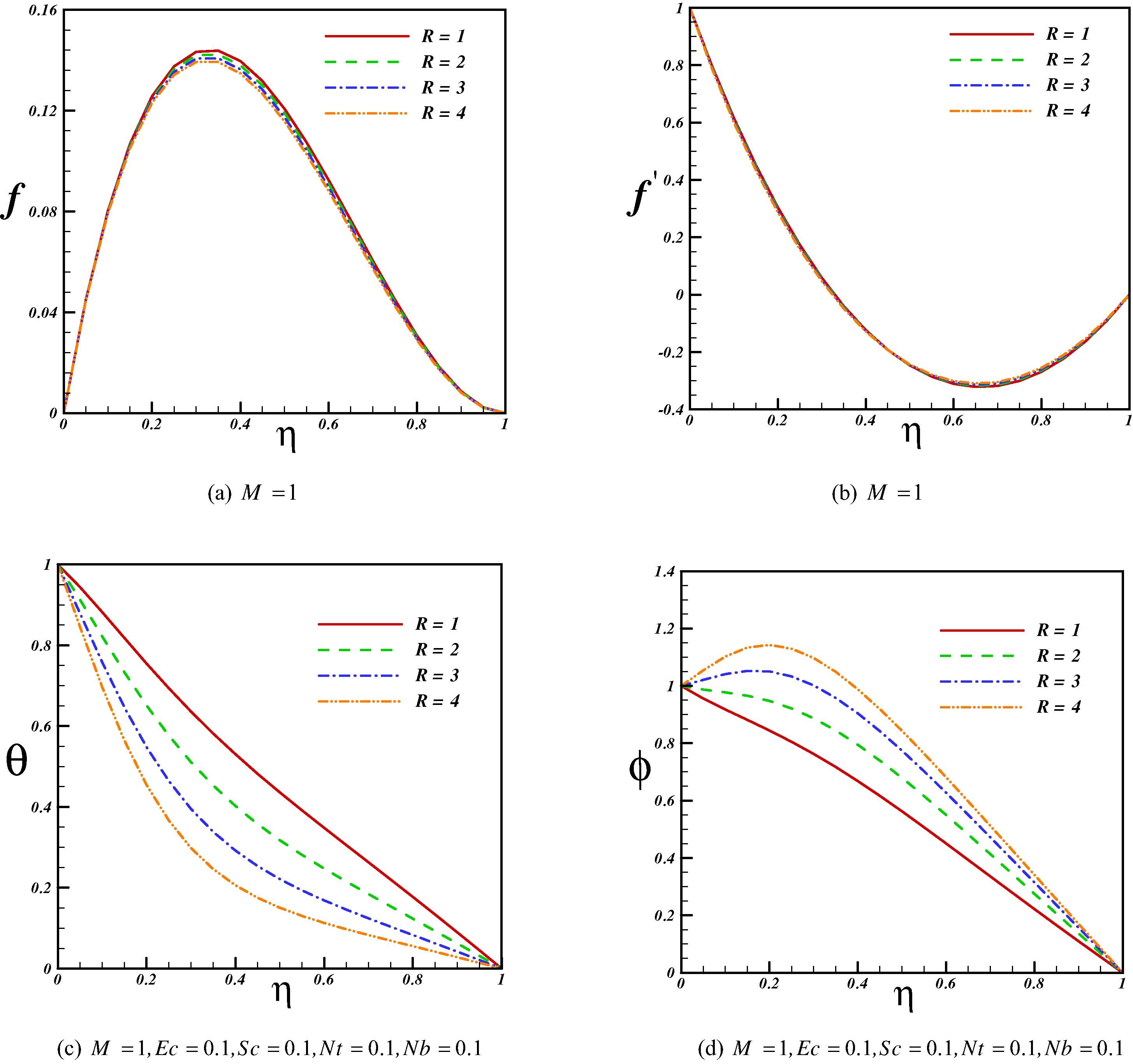
Effect of viscosity parameter on velocity, temperature and concentration profiles when Pr = 10.
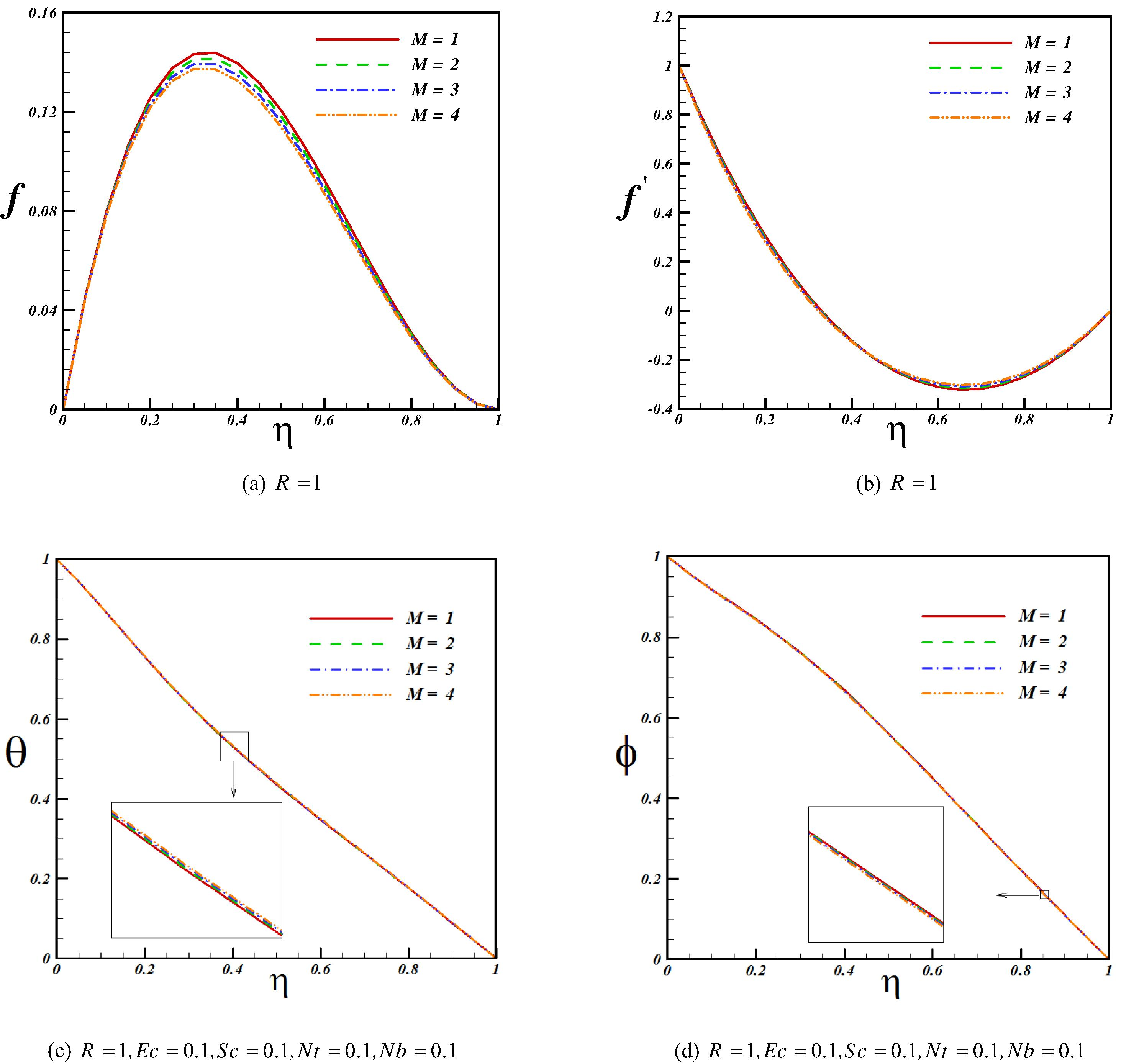
Effect of Magnetic parameter on velocity, temperature and concentration profiles when Pr = 10.
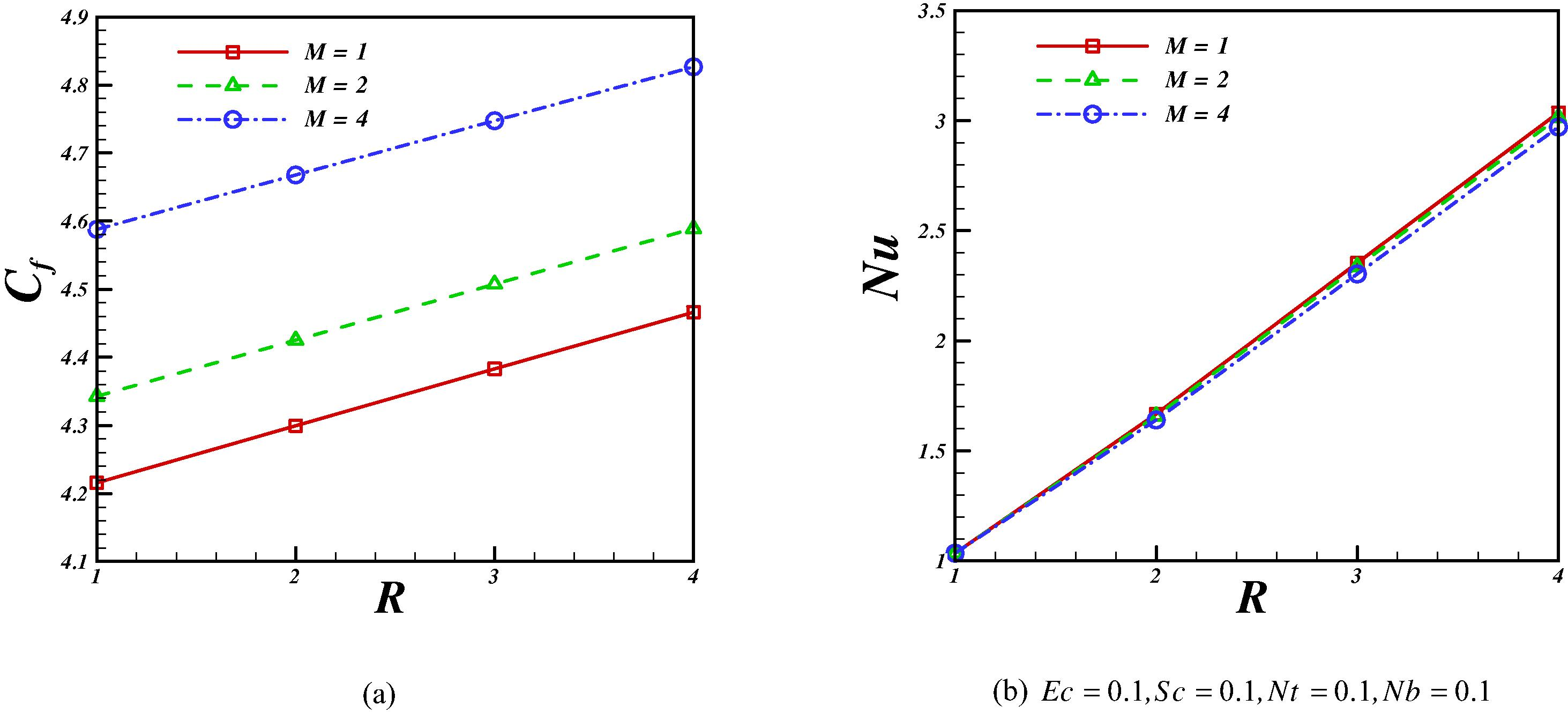
Effects of viscosity and Magnetic parameters on skin friction coefficient and Nusselt number when Pr = 10.
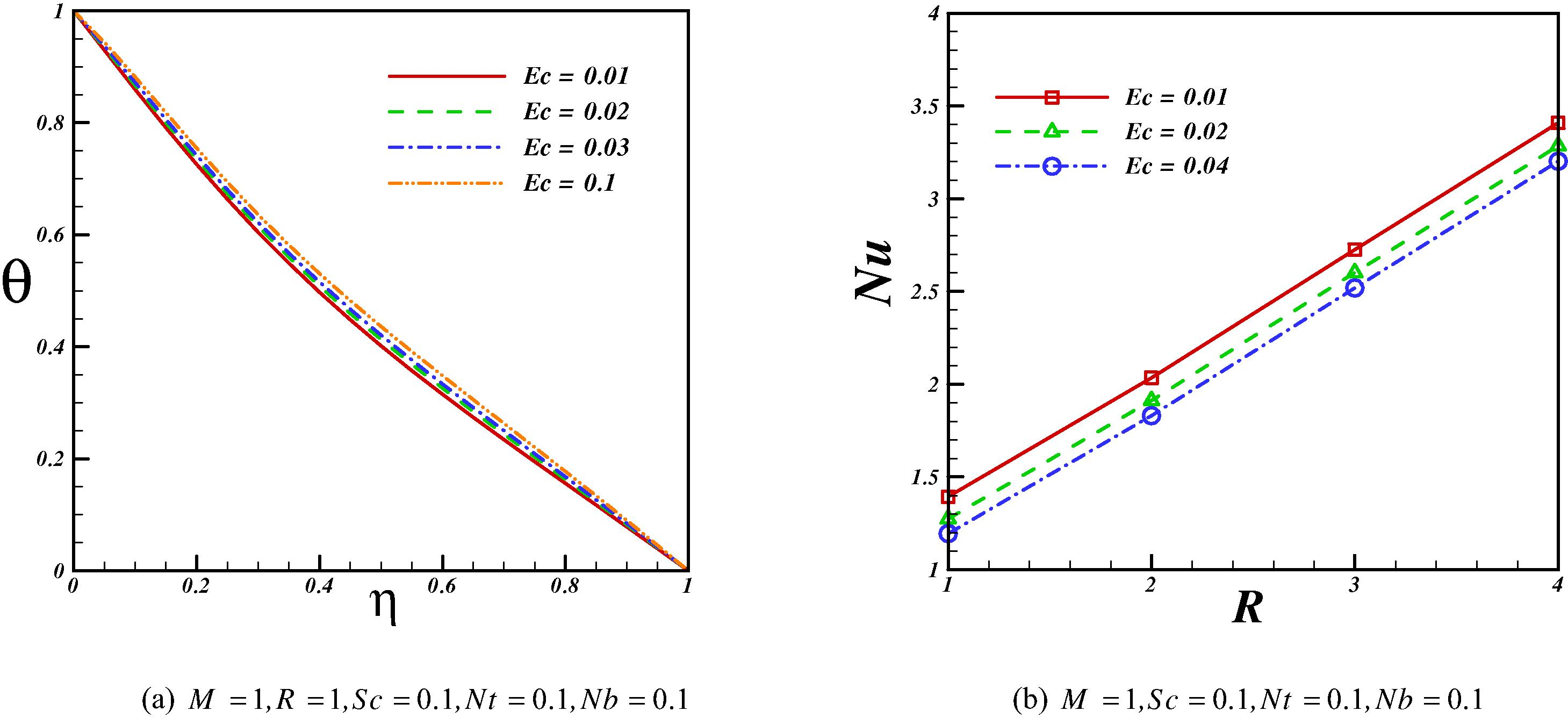
Effect of Eckert number on temperature profile and Nusselt number when Pr = 10.
Effects of thermophoretic and Brownian parameter on temperature profile and Nusselt number are depicted in Figs. 7 and 8. These parameters have a similar effect on temperature profile. It means that temperature increases with augment of these parameters and in turn Nusselt number has reverse relationship with thermophoretic and Brownian parameter. Fig. 9 depicts the effects of Brownian and thermophoretic parameters on concentration profile. As Brownian motion increases concentration of nanofluid decreases while opposite trend is observed for thermophoretic parameter.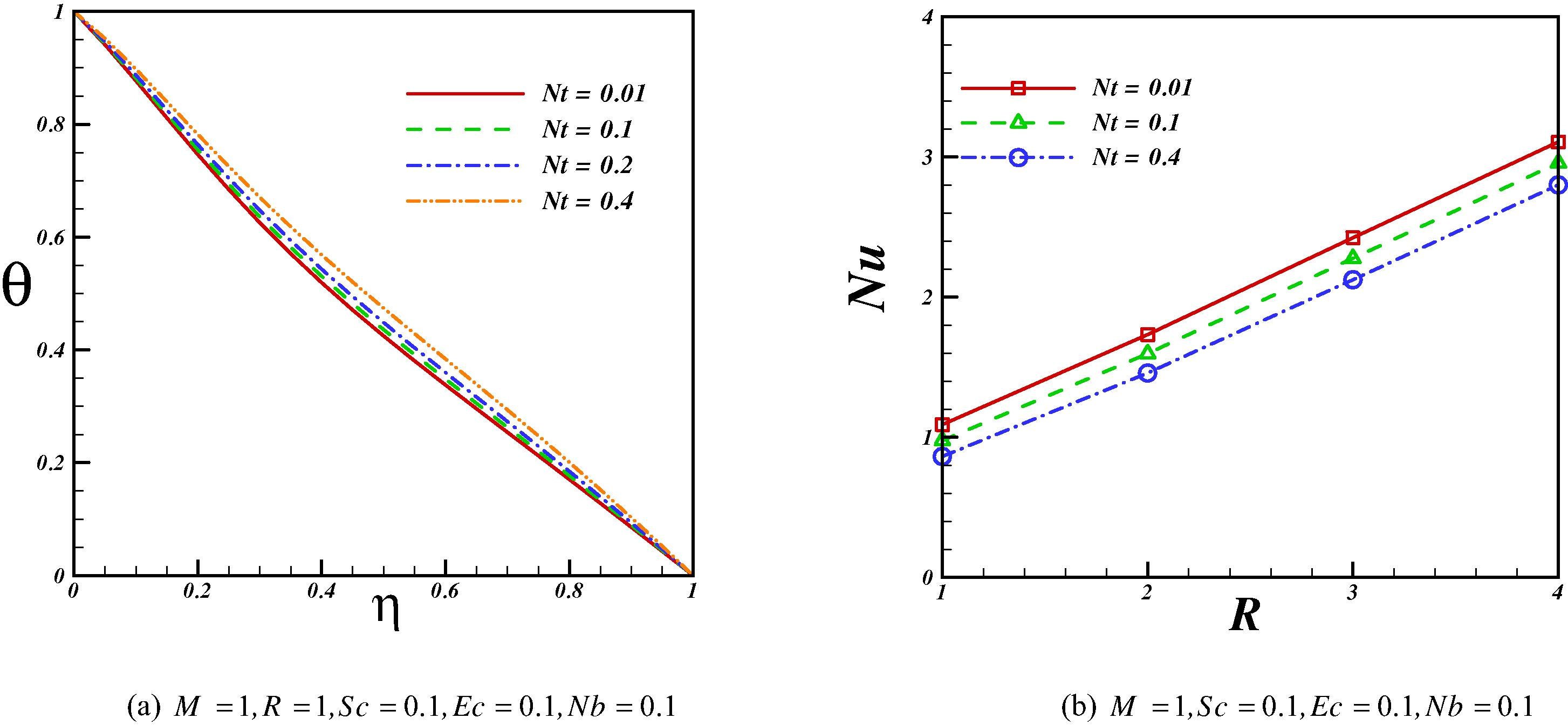
Effect of thermophoretic parameter on temperature profile and Nusselt number when Pr = 10.
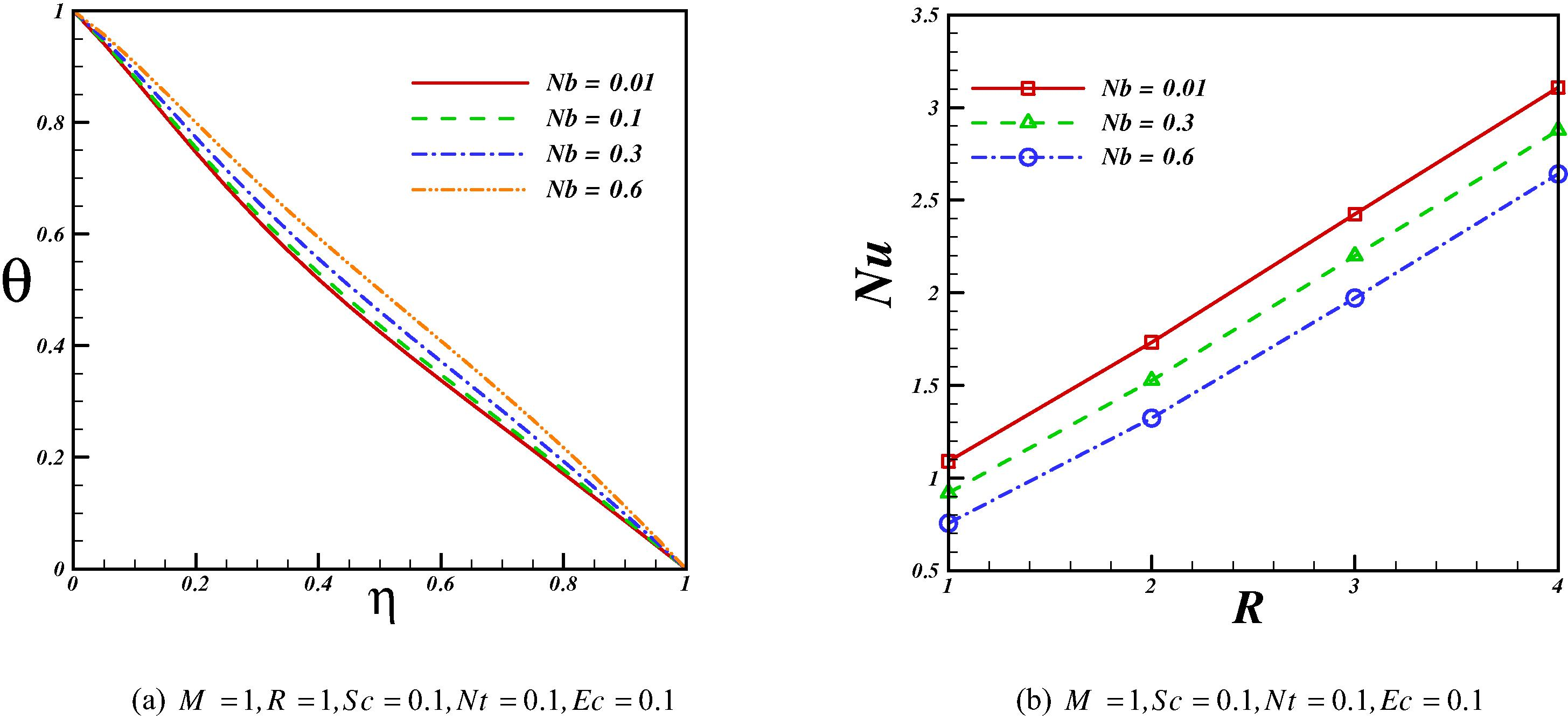
Effect of Brownian parameter on temperature profile and Nusselt number when Pr = 10.
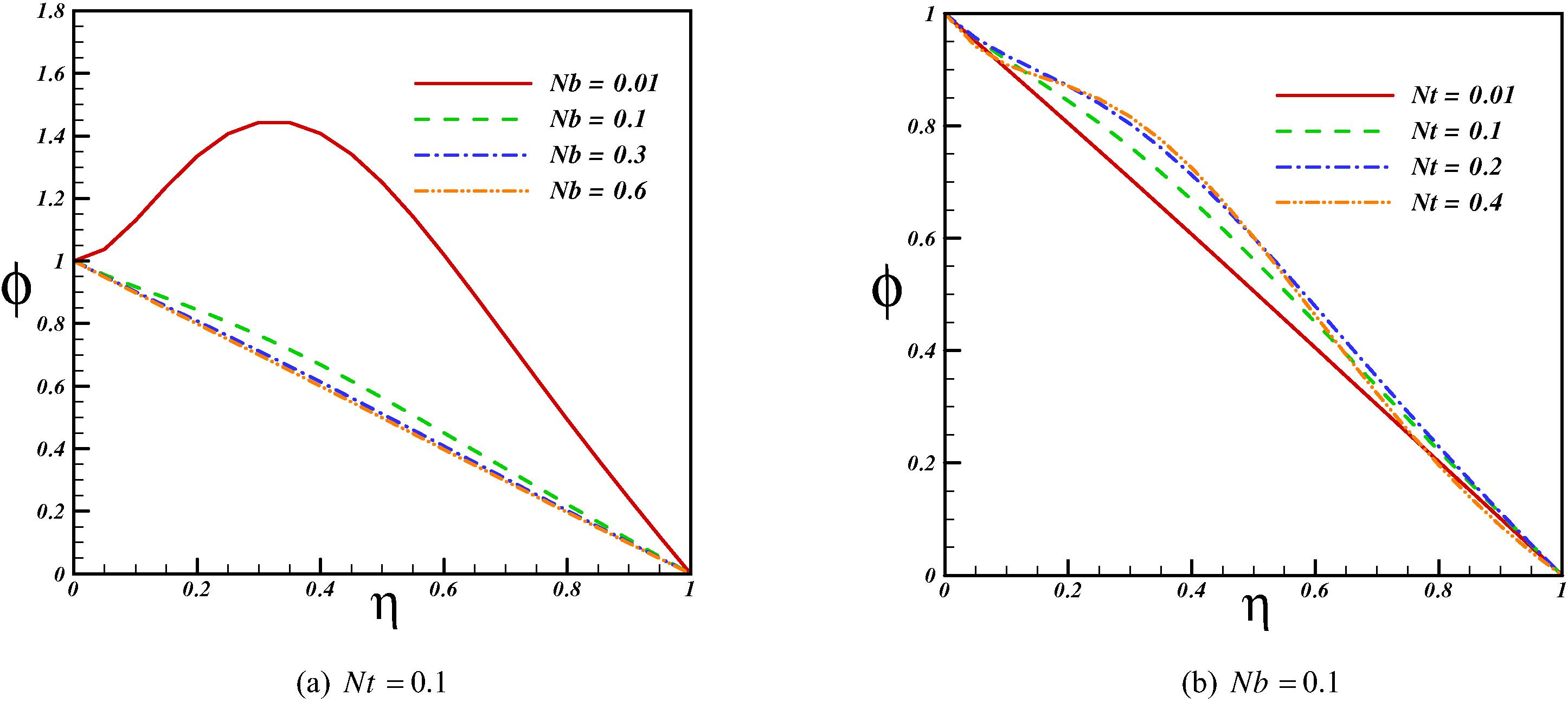
Effects of Brownian and thermophoretic parameters on concentration profile when M = 1, R = 1, Sc = 0.1, Ec = 0.1, Pr = 10.
5 Conclusion
MHD nanofluid flow, heat and mass transfer between two horizontal parallel plates are investigated to count in the effects of Brownian motion and thermophoresis in the nanofluid model. Differential Transformation Method is used to solve the governing equations. The effects of thermophoretic parameter, Magnetic parameter, Brownian parameter, and viscosity parameter on profiles of concentration, velocity, and temperature are examined. Results show that skin friction increases with an increase of viscosity and Magnetic parameters. Also it can be found that Nusselt number increases with increase of viscosity parameter while it decreases with an increase of Magnetic parameter, thermophoretic parameter and Brownian parameter.
References
- Natural convection heat transfer enhancement in horizontal concentric annuli using nanofluids. Int. Commun. Heat Mass Transfer. 2008;35:657-665.
- [Google Scholar]
- Influence of heat generation and heat flux in peristalsis with interaction of nanoparticles. Eur. Phys. J. Plus. 2014;129:185-195.
- [Google Scholar]
- Nanofluid flow in tapering stenosed arteries with permeable walls. Int. J. Therm. Sci.. 2014;85:54-61.
- [Google Scholar]
- Nanofluid flow and heat transfer due to a stretching cylinder in the presence of magnetic field. Heat Mass Transfer. 2013;49:427-436.
- [Google Scholar]
- Magnetic field effects on natural convection flow of a nanofluid in a horizontal cylindrical annulus using Lattice Boltzmann method. Int. J. Therm. Sci.. 2013;64:240-250.
- [Google Scholar]
- Fractional Dynamics. Emerging science publishers; 2015.
- Fluid flow and radiative nonlinear heat transfer over a stretching sheet. J. King Saud Univ. Sci.. 2014;26:161-167.
- [Google Scholar]
- Natural convection flow of a non-Newtonian nanofluid between two vertical flat plates. Proc. IMechE Part N: J. Nanoeng. Nanosyst.. 2012;225(3):115-122. ©IMechE
- [CrossRef] [Google Scholar]
- The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: analytical solutions. Appl. Math. Model.. 2013;37(3):1451-1457.
- [Google Scholar]
- Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method. Math. Comput. Model.. 2012;55:1876-1891.
- [Google Scholar]
- Non Newtonian nanofluids flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media. 2013;16(3):205-216.
- [Google Scholar]
- Shape effects of nanosize particles in Cu-H20 nanofluid on entropy generation. Int. J. Heat Mass Transfer. 2015;81:449-456.
- [Google Scholar]
- Approximate analytical solutions of singularly perturbed fourth order boundary value problems using differential transform method. J. King Saud Univ. Sci. 2013:257-265.
- [Google Scholar]
- Two phase simulation of natural convection and mixed convection of the nanofluid in a square cavity. Powder Technol.. 2015;275:239-256.
- [Google Scholar]
- Two-phase mixture modeling of mixed convection of nanofluids in a square cavity with internal and external heating. Powder Technol.. 2015;275:304-321.
- [Google Scholar]
- Numerical simulation of natural convection of the nanofluid in heat exchangers using a Buongiorno model. Appl. Math. Comput.. 2015;254:183-203.
- [Google Scholar]
- Motion of a spherical particle in a fluid forced vortex by DQM and DTM. Particuology. 2014;16:206-212.
- [Google Scholar]
- Motion of a spherical particle on a rotating parabola using Lagrangian and high accuracy multi-step differential transformation method. Powder Technol.. 2014;258:94-98.
- [Google Scholar]
- Analytical investigation of MHD nanofluid flow in non-parallel walls. J. Mol. Liq.. 2014;194:251-259.
- [Google Scholar]
- Nanofluid flow and heat transfer in an asymmetric porous channel with expanding or contracting wall. J. Mol. Liq.. 2014;195:230-239.
- [Google Scholar]
- Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Powder Technol.. 2014;253:769-779.
- [Google Scholar]
- High accuracy analysis for motion of a spherical particle in plane Couette fluid flow by multi-step differential transformation method. Powder Technol.. 2014;260:59-67.
- [Google Scholar]
- Numerical research of nature convective heat transfer enhancement filled with nanofluids in rectangular enclosures. Int. Commun. Heat Mass Transfer. 2006;33:727-736.
- [Google Scholar]
- Lattice Boltzmann simulation of natural convection in a nanouid-filled inclined square cavity at presence of magnetic field. Sci. Iran.. 2013;20:1517-1527.
- [Google Scholar]
- Lattice Boltzmann simulation of natural convection in nanofluid-filled 2D long enclosures at presence of magnetic source. Theoret. Comput. Fluid Dyn.. 2013;27:865-883.
- [Google Scholar]
- Lattice Boltzmann simulation of MHD natural convection in a nanofluid-filled cavity with sinusoidal temperature distribution. Powder Technol.. 2013;243:171-183.
- [Google Scholar]
- Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transfer. 2010;53:2477-2483.
- [Google Scholar]
- MHD flow over exponential radiating stretching sheet using homotopy analysis method. J. King Saud Univ. Eng. Sci. 2014
- [CrossRef] [Google Scholar]
- Squeezed flow and heat transfer over a porous surface for viscous fluid. Heat Mass Transfer. 2007;44:165-173.
- [Google Scholar]
- Brownian motion and thermophoresis effects on slip flow of alumina/water nanofluid inside a circular microchannel in the presence of a magnetic field. Int. J. Therm. Sci.. 2014;84:196-206.
- [Google Scholar]
- Analytic solution of three-dimensional viscous flow and heat transfer over a stretching flat surface by homotopy analysis method. ASME J Heat Transfer. 2008;130:21701-21707.
- [Google Scholar]
- Thermal instability in a porous medium layer saturated by a nanofluid. Int. J. Heat Mass Transfer. 2009;52:5796-5801.
- [Google Scholar]
- Radiation and free convection flow through a porous medium. Int. Commun. Heat Mass Transfer. 1998;25:289-295.
- [Google Scholar]
- The modified differential transform method for solving MHD boundary-layer equations. Comput. Phys. Commun.. 2009;180:2210-2217.
- [Google Scholar]
- Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transfer. 2013;62:515-525.
- [Google Scholar]
- Study of stream wise transverse magnetic fluid flow with heat transfer around a porous obstacle. J. Magn. Magn. Mater.. 2015;378:128-137.
- [Google Scholar]
- Three-dimensional flow of Jeffery fluid with convective surface boundary conditions. Int. J. Heat Mass Transfer. 2012;55:3971-3976.
- [Google Scholar]
- Effects of mass transfer on MHD flow of Casson fluid with chemical reaction and suction. Braz. J. Chem. Eng.. 2013;30:187-195.
- [Google Scholar]
- Combined effects of thermal stratification and thermal radiation in mixed convection flow of thixotropic fluid. Eur. Phys. J. Plus 2013:128-137.
- [Google Scholar]
- Thermophoresis particle deposition in mixed convection three-dimensional radiative flow of an Oldroyd-B fluid. J. Taiwan Inst. Chem. Eng.. 2014;45:787-794.
- [Google Scholar]
- MHD mixed convection flow of thixotropic fluid with thermal radiation. Heat Transfer Res.. 2014;45:659-676.
- [Google Scholar]
- Heat transfer of Cu–water nanofluid flow between parallel plates. Powder Technol.. 2013;235:873-879.
- [Google Scholar]
- Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann method. Phys. A. 2015;417:273-286.
- [Google Scholar]
- Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput. Methods Appl. Mech. Eng.. 2015;283:651-663.
- [Google Scholar]
- Effect of space dependent magnetic field on free convection of Fe3O4–water nanofluid. J. Taiwan Inst. Chem. Eng. 2015
- [CrossRef] [Google Scholar]
- Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid. Int. Commun. Heat Mass Transfer. 2012;39:978-986.
- [Google Scholar]
- Flow and heat transfer of Cu–water nanofluid between a stretching sheet and a porous surface in a rotating system. J. Appl. Math. 2012:19. Hindawi Publishing Corporation, Article ID 421320
- [CrossRef] [Google Scholar]
- Analytical investigation of Jeffery–Hamel flow with high magnetic field and nano particle by adomian decomposition method. Appl. Math. Mech. Eng. Ed.. 2012;33(1):1553-1564.
- [Google Scholar]
- Two phase simulation of nanofluid flow and heat transfer using heatline analysis. Int. Commun. Heat Mass Transfer. 2013;47:73-81.
- [Google Scholar]
- Numerical investigation of MHD effects on Al2O3–water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy. 2013;60:501-510.
- [Google Scholar]
- Free convection of nanofluid filled enclosure using lattice Boltzmann method (LBM) Appl. Math. Mech. Eng. Ed.. 2013;34(7):1-15.
- [Google Scholar]
- Natural convection in a nanofluid filled concentric annulus between an outer square cylinder and an inner elliptic cylinder. Sci. Iran. Trans. B: Mech. Eng.. 2013;20(4):1241-1253.
- [Google Scholar]
- Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol.. 2013;239:259-265.
- [Google Scholar]
- Magnetic field effect on nanofluid flow and heat transfer using KKL model. J. Taiwan Inst. Chem. Eng.. 2014;45:795-807.
- [Google Scholar]
- Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Int. J. Heat Mass Transfer. 2014;79:212-222.
- [Google Scholar]
- Effect of magnetic field on Cu–water nanofluid heat transfer using GMDH-type neural network. Neural Comput. Appl.. 2014;25:171-178.
- [Google Scholar]
- A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder. Int. J. Numer. Methods Heat Fluid Flow. 2014;24(8):1906-1927.
- [Google Scholar]
- Effects of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium. Comput. Theor. Nanosci.. 2014;11(2):486-496.
- [Google Scholar]
- Simulation of CuO–water nanofluid flow and convective heat transfer considering Lorentz forces. J. Magn. Magn. Mater.. 2014;369:69-80.
- [Google Scholar]
- Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3–water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder. Int. J. Heat Mass Transfer. 2015;80:16-25.
- [Google Scholar]
- Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation. J. Taiwan Inst. Chem. Eng.. 2015;47:6-17.
- [Google Scholar]
- Effect of thermal radiation on nanofluid flow and heat transfer using two phase model. J. Magn. Magn. Mater.. 2015;374:36-43.
- [Google Scholar]
- Effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition. Eur. Phys. J. Plus 2014:129-248.
- [Google Scholar]
- KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel. Phys. Lett. A. 2014;378(45):3331-3339.
- [Google Scholar]
- Convective transport in a porous medium layer saturated with a Maxwell nanofluid. J. King Saud Univ. Eng. Sci. 2014
- [CrossRef] [Google Scholar]
- Analytic and numerical solutions of coupled nonlinear system arising in three-dimensional rotating flow. Int. J. Non Linear Mech.. 2004;39:13-24.
- [Google Scholar]
- Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci.. 2013;17:625-628.
- [Google Scholar]
- Magnetohydrodynamic flow of water/ethylene glycol based nanofluids with natural convection through porous medium. Eur. Phys. J. Plus. 2014;129:261-271.
- [Google Scholar]
- Differential Transformation and its Applications for Electrical Circuits. Wuhan, China: Huazhong Univ. Press; 1986.







