Translate this page into:
Quasi-periodic non-stationary solutions of 3D Euler equations for incompressible flow
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
A novel derivation of non-stationary solutions of 3D Euler equations for incompressible inviscid flow is considered here. Such a solution is the product of 2 separated parts: one consisting of the spatial component and the other being related to the time dependent part.
Spatial part of a solution could be determined if we substitute such a solution to the equations of motion (equation of momentum) with the requirement of scale-similarity in regard to the proper component of spatial velocity. So, the time-dependent part of equations of momentum should depend on the time-parameter only.
The main result, which should be outlined, is that the governing (time-dependent) ODE-system consists of 2 Riccati-type equations in regard to each other, which has no solution in general case. But we obtain conditions when each component of time-dependent part is proved to be determined by the proper elliptical integral in regard to the time-parameter t, which is a generalization of the class of inverse periodic functions.
Keywords
Euler equations
Riccati equations
Non-stationary solutions
1 Introduction: the Euler system of equations
In accordance with (Landau and Lifshitz, 1987; Ladyzhenskaya, 1969; Lighthill, 1986), the Euler system of equations for incompressible flow of inviscid fluid should be presented in the Cartesian coordinates as below (under the proper initial conditions):
2 The originating system of PDE for Euler equations
Using the identity (u · ∇)u = (1/2)∇(u2) − u × (∇ × u), we could present the Euler equations in the case of incompressible flow of inviscid fluid u = {u1, u2, u3} as below (Saffman, 1995; Milne-Thomson, 1950):
3 Conditions for the space-part of exact solution
Let us search for solutions {u, p} of the system (2.1) in a form below:
Besides, there exists the proper restriction from continuity equation (1.1) as below (∂u/∂x ≠ 0):
The system of equations (3.2) should be transformed under conditions (3.1) as below:
4 The space-part of exact solution
As for the structure of space part of exact solution (3.1), the system of equations (3.5)–(3.7) could be solved by the proper analytical way as below:
Eq. (3.5) yields:
Eq. (3.6) yields:
So, the space part of the solution should be presented as below:
Thus, if we choose for simplicity the proper constants as:
5 Time-dependent part of exact solution
As for the structure of time-dependent part of exact solution (3.1) with space part (4.6), it could be obtained from system of Eq. (3.4) which should be transformed as below:
Along with the invariant from the continuity equation (besides, a9 · b3 + b9 · b6 + c9 · a3 = 0):
a system of Eq. (5.1) immediately yields the invariant for function P(t) as below:
So, analyzing the system (5.1), we finally should obtain the system of 2 ordinary differential equations of the 1-st order for any 2 of 3 functions U(t), V(t), W(t) (the last 3-rd function could be obtained by expressing it from the continuity equation above).
These governing ODE-equations form together a system of 2 Riccati-type equations in regard to each other, which is the system of 2 ordinary differential equations of the 1-st kind with the right parts, consisting of polynomials of the 2-nd extent in regard to the functions U(t), V(t), W(t).
Riccati type of equations has no analytical solution in general case (Kamke, 1971). We should note also that modern methods exist for obtaining the solution of Riccati equations with a good approximation (Bender and Orszag, 1999; Rosu et al., 2012; Christianto and Smarandache, 2008). But if we choose proper constants for the system (5.1):
The left side of expression (5.7) could be transformed to the proper elliptical integral (Lawden, 1989) in regard to function U(t):
6 Discussion
In fluid mechanics, a lot of authors have been executing their researches to obtain the analytical solutions of Euler and Navier–Stokes equations (Drazin and Riley, 2006), even for 3D case of compressible gas flow (Ershkov and Schennikov, 2001). But there is an essential deficiency of non-stationary solutions indeed.
Our presentation (3.1) of the non-stationary solutions of 3D Euler equations (1.1) and (1.2) for incompressible flow is considered here. The spatial part of such a solution is determined by equalities (4.4), under the given initial conditions; but the time-dependent part is determined by Eqs. (5.1)–(5.3).
Besides, the real example of exact solution is obtained. The spatial part of such a solution is presented by the equalities (4.5) and (4.6), but the time-dependent part is presented by equalities (5.2)–(5.4) and (5.8).
Also, we should especially note that the components of flow velocity (4.6) of the solution (3.1) will be uniformly increasing when (x, y, z) → ∞. So, such a solution should be defined within the limited domain of the meanings of variables (x, y, z), it should be given by the initial conditions.
The explicit solutions for U(t) can easily be obtained from Eqs. (5.7) and (5.6), therefore, the explicit form of the special solutions (3.1) should be provided: where: here we should choose a3 = {|b3| − b3 · |b3| − b3 · |b3| · (b6)2} ≠ 0, →b3 · (1 + (b6)2) ≠ 1, but the key function U(t) should be given as below (b8 = b3 · b6):
For example, if we choose c3 = b6 (C ≠ 0) it should simplify the expression for U(t):
and, if we additionally choose c2 = 2b3, b3 = 2/C (C ≠ 0), b6 = 1, we should obtain (see Figs. 1–5):
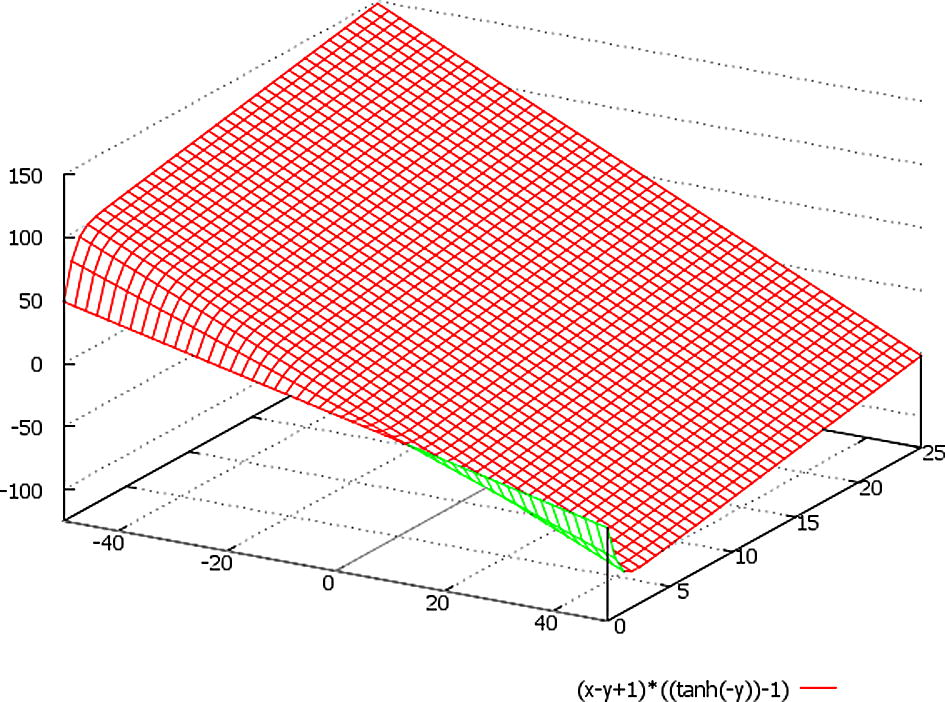
A schematic plot of the function ∼ (x − y + 1) * {tanh(−t) − 1}, here we designate: x ∈ (−50, 50), t = y ∈ (0, 25).
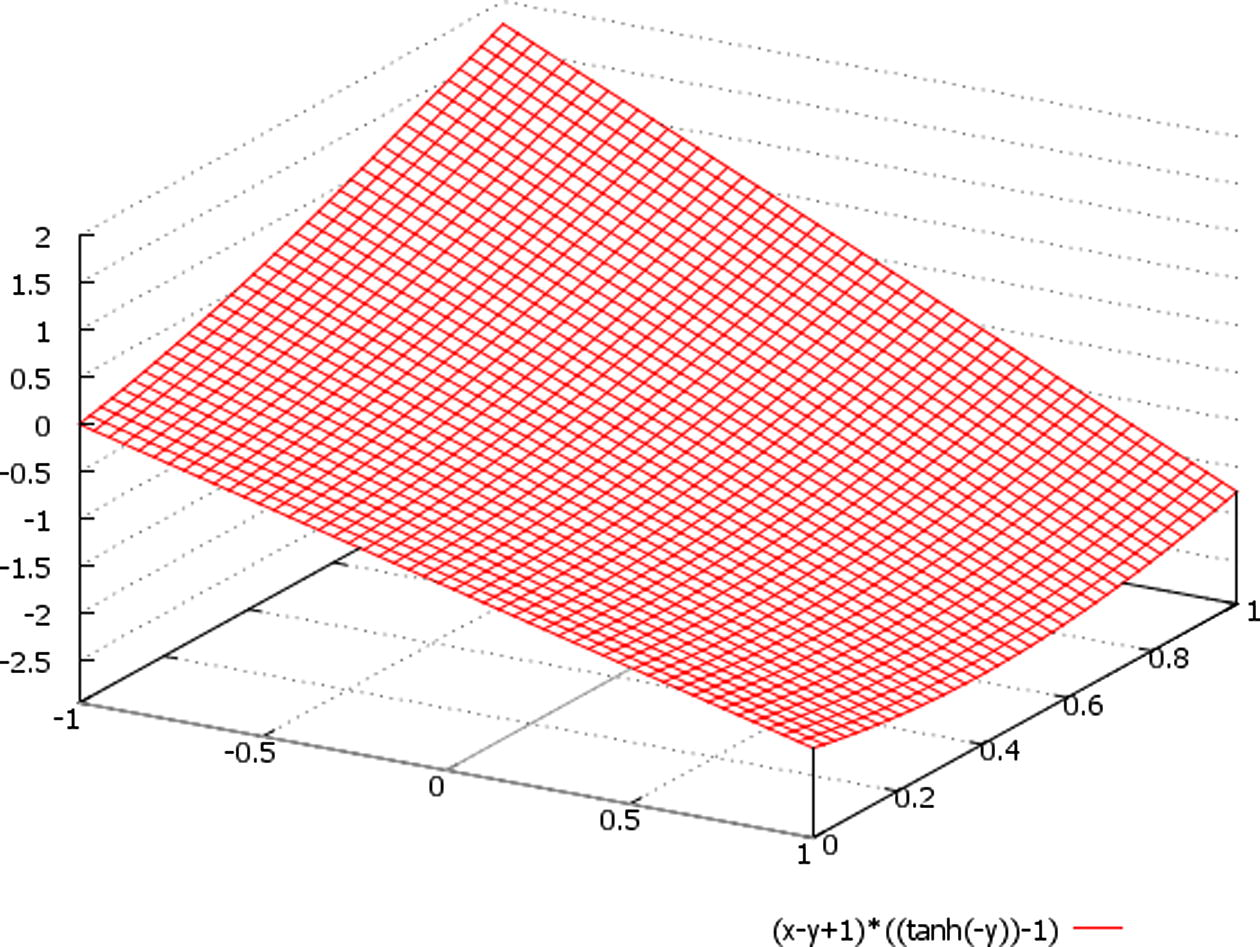
A schematic plot of the function ∼ (x − y + 1) * {tanh(−t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
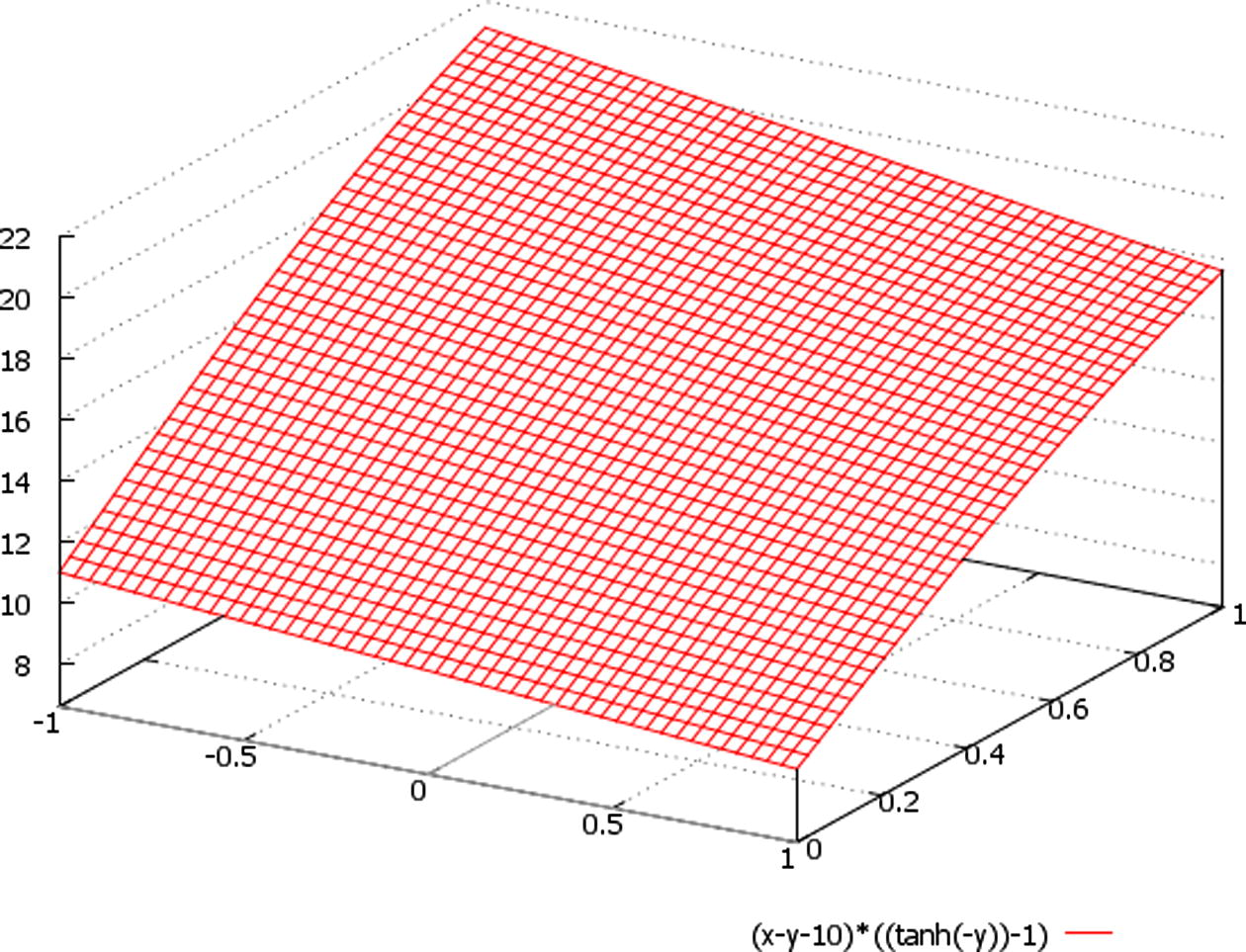
A schematic plot of the function ∼ (x − y − 10) * {tanh(−t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
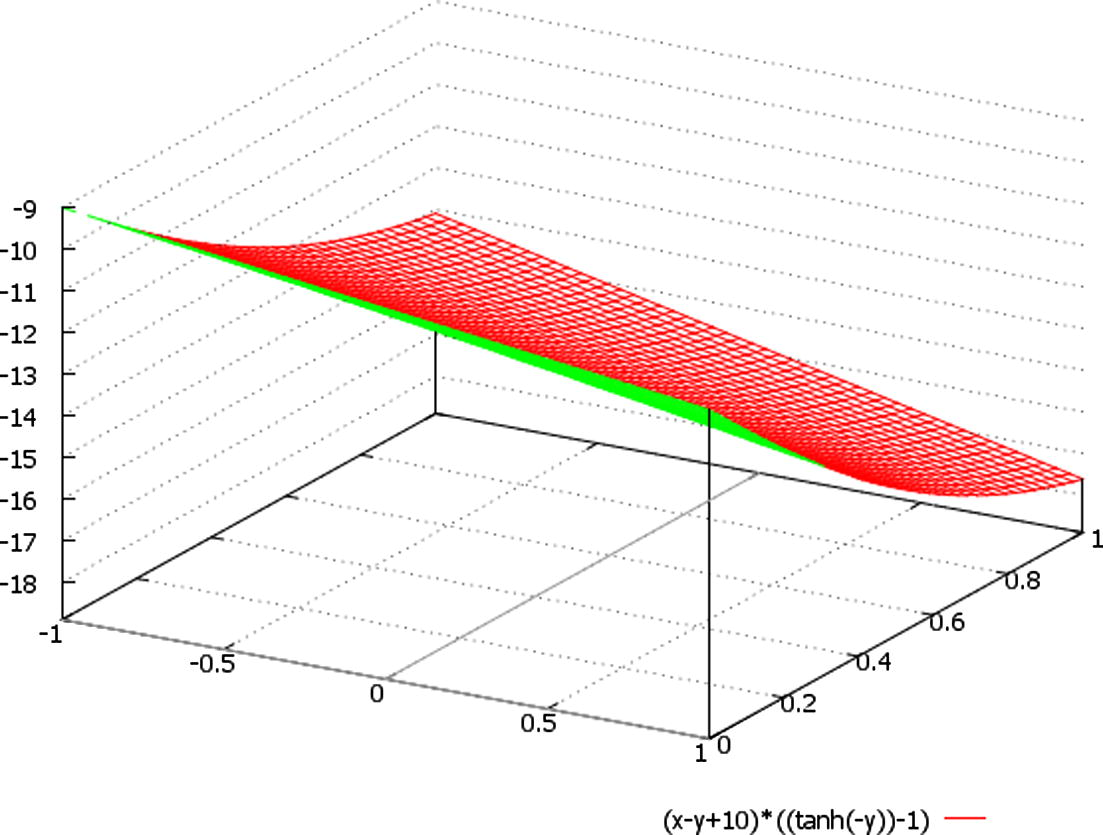
A schematic plot of the function ∼ (x − y + 10) * {tanh(−t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
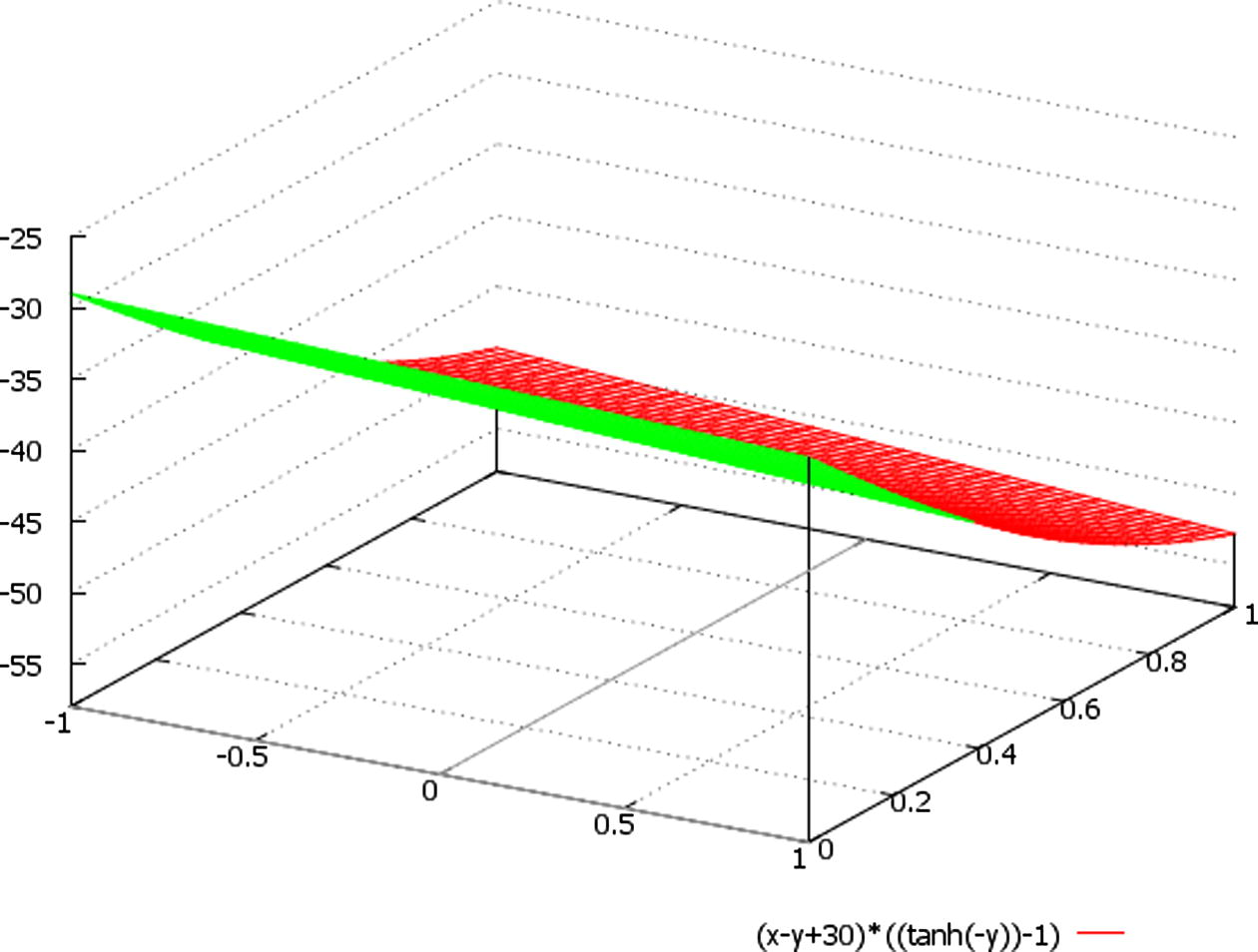
A schematic plot of the function ∼ (x − y + 30) * {tanh(−t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
We assume at Figs. 1–5 that in the expressions (x − y − 10), (x − y + 1), (x − y + 10), (x − y + 30) set of meanings {−10, 1, 10, 30} is varying according to the varying of the range of variable z; besides, the factor {tanh(−t) − 1} could be schematically presented (for imagination of the plots of solutions) by the changing of parameter t to variable y, for example.
At Figs. 6–8 we schematically imagined solutions for the case Δ > 0.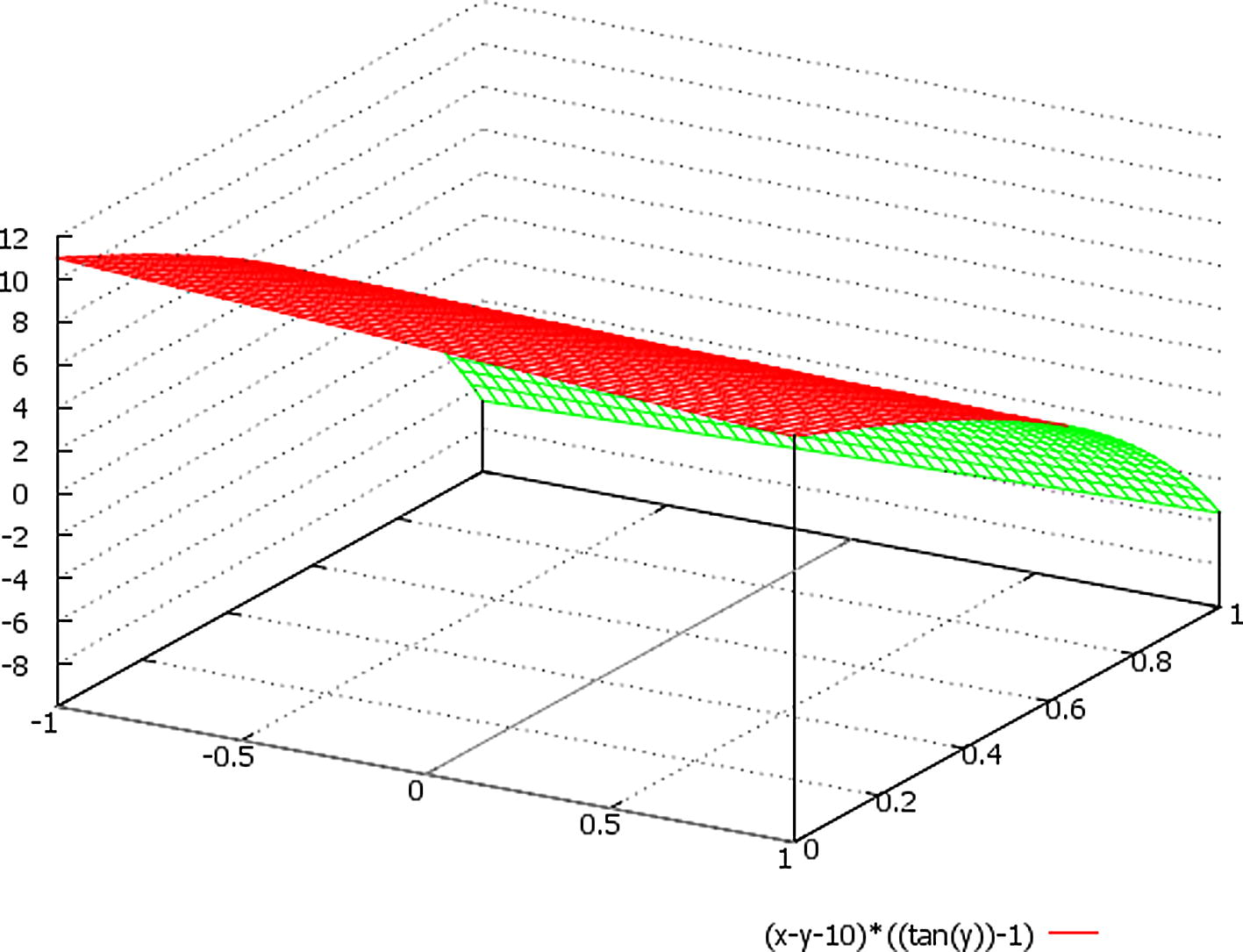
A schematic plot of the function ∼ (x − y − 10) * {tan(t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
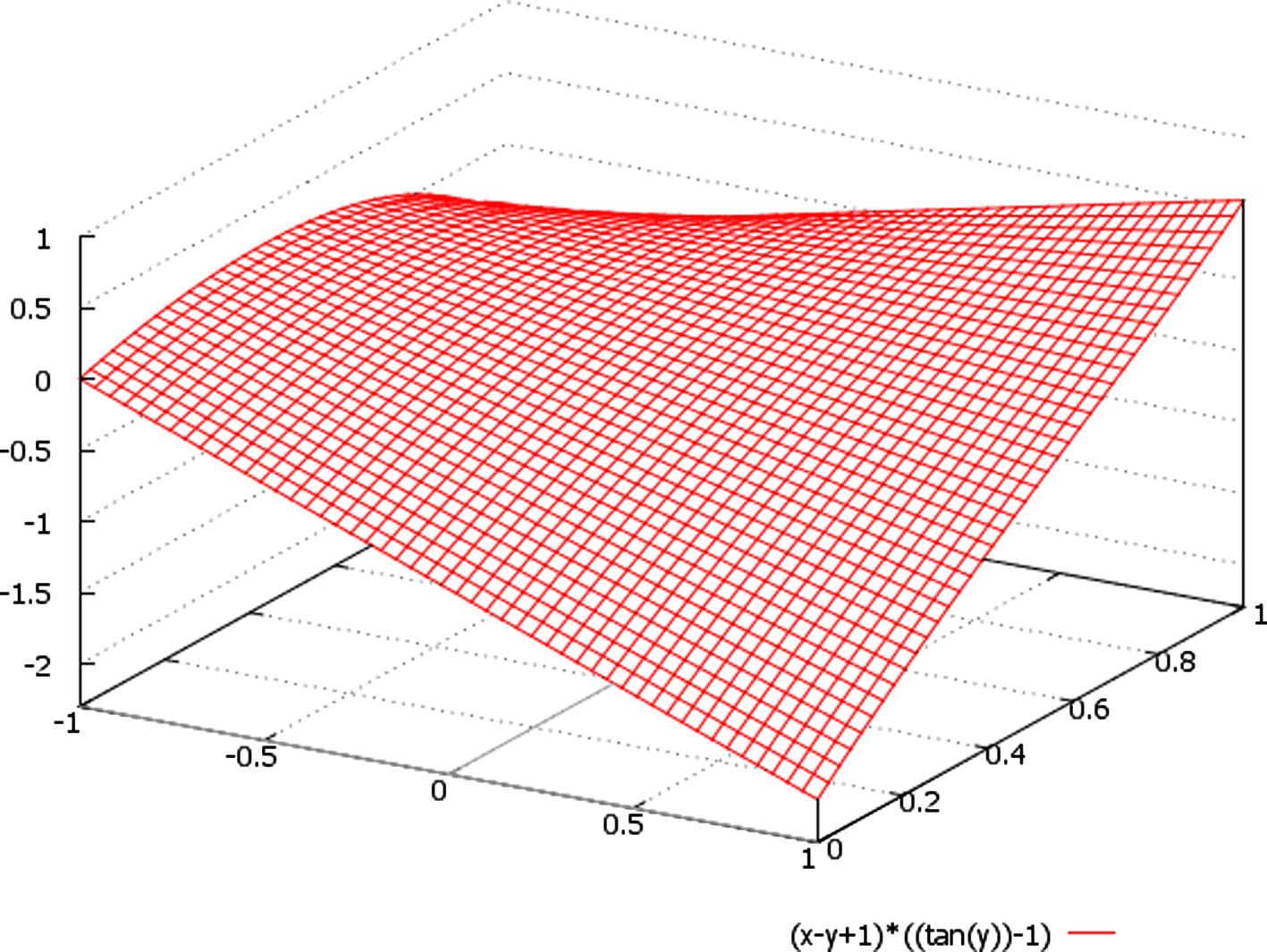
A schematic plot of the function ∼ (x − y + 1) * {tan(t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
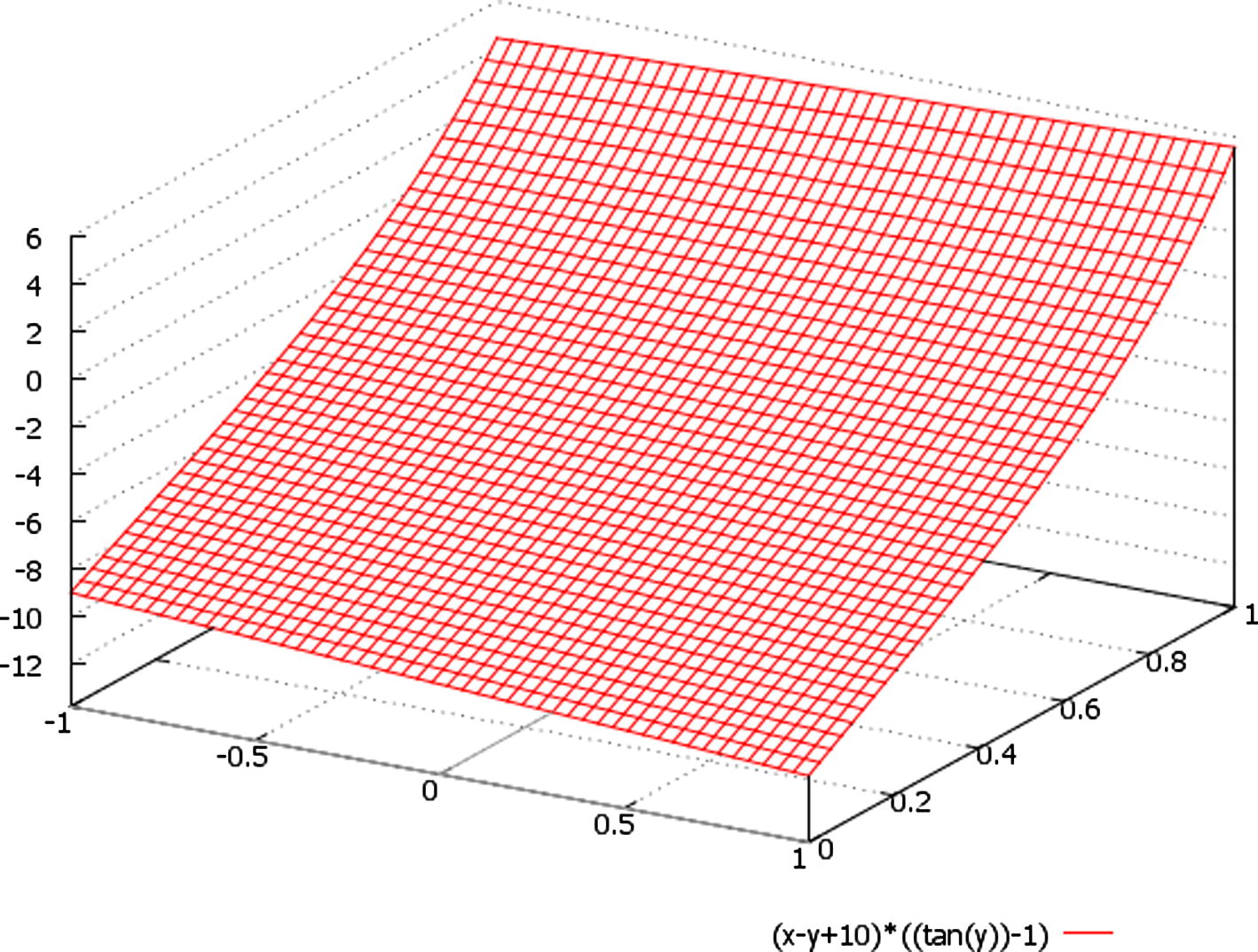
A schematic plot of the function ∼ (x − y + 10) * {tan(t) − 1}, here we designate: x ∈ (−1, 1), t = y ∈ (0, 1).
Also, we should note that since some solutions are unbounded (see for instance Eq. (5.8) for Δ > 0), such a solution should be defined within the limited range of the meanings of time-parameter t (it should be given by the initial conditions).
Besides, we should additionally note that the only periodic (and unbounded) solutions are the ones given by U(t) for Δ > 0 (Figs. 6–8), since the hyperbolic tangent is a non periodic but bounded function in this case (Figs. 1–5).
7 Conclusion
A new presentation of non-stationary solutions of 3D Euler equations for incompressible inviscid flow is considered here. Such a solution is the product of 2 separated parts: - spatial and the time-dependent parts.
Spatial part of a solution could be determined if we substitute such a solution to the equations of motion (equation of momentum) under the demand of scale-similarity in regard to the proper component of spatial velocity. So, the time-dependent part of equations of momentum should depend on the time-parameter only.
The main result, which should be outlined, is that the governing (time-dependent) ODE-system consists of 2 Riccati-type equations in regard to each other, which has no solution in general case. But we obtain conditions when each component of time-dependent part is proved to be determined by the proper elliptical integral in regard to the time-parameter t, which is a generalization of the class of inverse periodic functions. Thus, by the proper obtaining of re-inverse dependence of a solution from time-parameter we could present the expression for each component of motion as a set of periodic cycles.
Acknowledgements
I am thankful to unknown esteemed Reviewers for valuable advices in preparing of this manuscript. Especially I appreciate Dr. Rizwan Irshad for his kind help and assistance during navigating in submission process of my articles to JKSUS.
References
- An exact mapping from Navier–Stokes equation to Schrodinger equation. Prog. Phys.. 2008;1:38-39.
- [Google Scholar]
- Lawden D., 1989. Elliptic Functions and Applications. Springer-Verlag. See also: <http://mathworld.wolfram.com/EllipticIntegral.html>.
- The Navier–Stokes Equations: A Classification of Flows and Exact Solutions. Cambridge: Cambridge University Press; 2006.
- Self-similar solutions to the complete system of Navier–Stokes equations for axially symmetric swirling viscous compressible gas flow. Comput. Math. Math. Phys. J.. 2001;41(7):1117-1124.
- [Google Scholar]
- Hand-book for Ordinary Differential Eq. Moscow: Science; 1971.
- The Mathematical Theory of viscous Incompressible Flow (2nd ed.). New York: Gordon and Breach; 1969.
- Landau, L.D., Lifshitz, E.M., 1987. Fluid mechanics, Course of Theoretical Physics 6 (2nd revised ed.), Pergamon Press, ISBN 0-08-033932-8.
- Lighthill, M.J., 1986. An Informal Introduction to Theoretical Fluid Mechanics. Oxford University Press, ISBN 0-19-853630-5.
- Bender, Carl M., Orszag, Steven A., 1999. Advanced Mathematical Methods for Scientists and Engineers. Origin published by McGraw Hill, 1978, XIV. pp. 20–22.
- Milne-Thomson, L.M., 1950. Theoretical Hydrodynamics. Macmillan.
- Traveling kinks in cubic nonlinear Ginzburg–Landau equations. Phys. Rev. E. 2012;85:037102.
- [Google Scholar]
- Vortex Dynamics. Cambridge University Press; 1995.







