Ab initio study of opto electric properties of the molecules pyrimethamine and sulfadoxine

S. Nouemo; W.E. Geh; F. Tchoffo; J.M.B. Ndjaka; S. Domngang

doi:10.1016/j.jksus.2015.03.002

View/Download PDF

Buy Reprints

PDF

Translate this page into:

Original Article

27 (

); 349-355

doi:

10.1016/j.jksus.2015.03.002

Ab initio study of opto electric properties of the molecules pyrimethamine and sulfadoxine

S. Nouemo^{^a,⁎}, W.E. Geh^{^b}, F. Tchoffo^{^a}, J.M.B. Ndjaka^{^a}, S. Domngang^{^a}

a University of Yaounde I, Faculty of Science, Department of Physics, P.O. Box: 812, Yaounde, Cameroon

b University of Dschang, Institute of Technology Fotso Victor, Department of General and Sciences Studies, P.O. Box: 134, Bandjoun, Cameroon

⁎Corresponding author. nouem_s@yahoo.com (S. Nouemo)

Received: 2014-11-30, Accepted: 2015-3-7, Published: 2015-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

The optical and electrical properties of the molecules pyrimethamine and sulfadoxine in gas phase and in different mediums (water and ethanol) were calculated using density-functional theory at the B3LYP level and the Restricted Hartree–Fock (RHF) level by employing 6-311++G^∗∗ basis set. The dipole moment, polarization density, the electric susceptibility, the refractive index, the dielectric constant and the magnitude of the displacement vector of these molecules have been calculated. Small values of polarization density, dielectric constant, magnitude of the displacement vector, high values of electric susceptibility, refractive index and small HOMO–LUMO energy gaps of these molecules show that, these molecules have very good opto electronic applications.

Keywords

Organic compound

Ab initio calculations

Optical properties

Electrical properties

Dielectric properties

Show Related Articles from PubMed

1 Introduction

Over the last twenty years, π-conjugated oligomers and polymers have received increasing interest, owing to their versatile functions that are requested for their breakthrough in many interdisciplinary fields like bio-imaging or plastic electronics. Much research has lately been directed toward the understanding of the microscopic origin of the non linearity (or linearity) of opto electric molecular properties (Kurt et al., 1994).

A basic goal in this research has been to relate the appearance of strong non linearity (or linearity) to opto electronic and geometric structures, with the ultimate goal to design conducting devices through the use of molecular modeling and computations. Semi empirical as well as ab initio calculations of non linear (or linear) electric properties have mostly focused on hyperpolarizability from which we can determine directly the opto electric properties of organic and polymeric materials that are regarded as holding potential for developments of charge storage, analytical sensors, electroluminescent devices, optical data processing and integrated optics (Garay, 2000).

For example, nowadays, it is clear that sensor sensitivities and specificity can be increased by using redox polymers (Ivaska, 1991) ; or that the parameters characterizing the relative strength of nonlinear optical (NLO) effects are typically 50 or 100 times greater in organic molecular systems than in inorganic dielectric insulators and semiconductors (Nalwa and Miyata, 1997). Several methodologies including semi empirical, ab initio, and density functional theory (DFT) have been employed for the calculation of NLO properties of the organic molecules in recent years (Sagdinca and Esmeb, 2010).

The molecular systems that have been accessed by quantum methods fall largely into three categories: small systems, such as neon isoelectronic hydrides, for which extensive computational tests on electron correlation, basis sets, role of frequency dependence, and vibrational dependence have been accomplished (Sekino and Bartlett, 1993). Oligomer sequences, in particular polyenes and polynes (Michael et al., 1993) in which the length dependence and convergence to the polymer value of the hyperpolarizability is of interest; and special donor–acceptor compounds, in particular disubstituted benzenes (Agren et al., 1993) in which the charge transfer character of the HOMO–LUMO excitations implies large polarizabilities and hyperpolarizabilities. An electronic system with a larger HOMO–LUMO gap should be less reactive than one having a smaller gap (Ciğdem et al., 2010).

Most calculations to date have been carried out at zero frequency with single configuration wave functions. Recently, calculations have appeared, that address both the frequency dispersion and the role of electron correlation (Sim et al., 1993).

The electronic (hyper) polarizabilities are commonly predicted by means of ab initio and/or density functional theory (DFT) computations (Andrea, 2013a,b). However, as well-known in literature, for an accurate determination of the electronic (hyper) polarizabilities, the choice of the functional is critical, especially in the choice of π-conjugate compounds (Champagne et al., 1998). In fact, the conventional DFT methods tend to systematically overestimate the electronic (hyper) polarizabilities obtained by high level correlated ab initio levels (Andrea, 2013a,b). On the other hand, the long range corrected DFT methods incorporating nonlocal effects (Sekino et al., 2007) describe adequately the diffuse regions of the charge distributions, giving much more satisfactory performances for the prediction of the response electric properties. Since the great bulk of measurements are conducted for solvated or solid species and since evidence has been given of strong induction of the hyperpolarizability by the medium, the current theoretical incitement is intended to investigate such effects. Mostly, solvent effects have been modeled by so-called local field factors, and such factors have also been used in deriving various quantities, such as hyperpolarizability, from experimental measurements in solutions. Local field factors relate the total hyperpolarizability (first, second, or higher order) with corresponding macroscopic susceptibilities simulating the change of the effective field experienced by a molecule when immersed in a liquid (Kurt et al., 1994). Hyperpolarizability of solvated molecules has been estimated by scaling the gas phase value by the local field factors. Some investigations, see, e.g., Ref. (Stahelin et al., 1992) have unraveled the rather severe limitations of this procedure and called for more realistic models to model the effect of a surrounding medium. The polarizability of an atom or molecule describes the response of the electron cloud to an external field (Junmei et al., 2007). The atomic or molecular energy shift ΔW due to an external electric field E is proportional to E² for external fields which are weak compared to the internal electric fields between the nucleus and electron cloud (William, 2012; Bonin and Kadar, 1994).

The electric dipole polarizability α is the constant of proportionality defined by ΔW = −αE²/2. The induced electric dipole moment is αE. Hyperpolarizabilities, coefficients of higher powers of E, are less often required (Bonin and Kadar, 1994). Technically, the polarizability is a tensor quantity but for spherically symmetric charge distributions, it is reduced to a scalar number (Bonin and Kadar, 1994). In many cases, an average polarizability is usually adequate in calculations. Frequency-dependent or dynamic polarizabilities are needed for electric fields which vary in time, except for frequencies which are much lower than electron orbital frequencies (Bonin and Kresin, 1997). Polarizability of atoms and molecules in excited states is found to be larger than that at ground states and may be positive or negative. Molecular polarizabilities are very slightly temperature dependent since the size of the molecule depends on its vibrational state (Gould and Miller, 2005).

In the present work we have used the Gaussian 03W suit to calculate the hyperpolarizability, dipole moment, polarization density, electric susceptibility, index of refraction, dielectric constant and the magnitude of the displacement vector of the molecules pyrimethamine and sulfadoxine in gas and solvent medium (water and ethanol). This work is a continuation of an ongoing research that we began since in 2009.

2 Methodology

The opto electric properties of the molecules pyrimethamine and sulfadoxine both in gas phase and in different solvent mediums were fully optimized by using Windows version of Gaussian 03 (Frisch et al., 2004) suit of quantum chemical program. The calculations were performed using ab initio quantum mechanical calculations at the Restricted Hartree–Fock (RHF) level of theory with the double polarized triple zeta split valence 6-311++G^∗∗ basis set. The calculations were further carried out using density functional theory which is a cost effective method for inclusion of electron correlations with the three-parameter density functional generally known as Becke3LYP (B3LYP), which includes Becke’s gradient exchange corrections (Becke, 1988) the Lee, Yang and Parr correlation functional (Lee et al., 1988) and the Vosko, Wilk and Nusair correlation functional (Vosko et al., 1980) with a 6-311++G^∗∗ basis set.

Since the gas phase results are inadequate for describing the behavior of these molecules in solutions, therefore the effect of solvating the molecules in bulk water and ethanol was investigated. For this purpose, the simplest Onsager reaction field model of the self-consistent reaction field (SCRF) theory (Miertus et al., 1981) was used with the 6-311++G^∗∗ basis set.

In other to have the calculated properties of the above molecules, we convert a.u to SI unit using conversion factors: 1 a.u of α = 1.648778 × 10⁻⁴¹ C² m² J⁻²; 1a.u of β = 3.206361 × 10⁻⁵³ C³ m³ J⁻² (Andrea, 2013a,b) and 1debye = 627.51 Kcal mol⁻¹ (Frisch et al., 2004).

3 Results and discussion

3.1

3.1 Opto electric properties of pyrimethamine

Some molecular properties of the molecule pyrimethamine obtained at RHF and B3LYP methods both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set are shown in Table 1. From Table 1, one can observe that the calculated value of the dipole moment, the average polarizability and the first molecular hyperpolarizability at RHF/6-311++G^∗∗ level are constant in gas, water and ethanol, the corresponding values obtained at the DFT/B3LYP//6-311++G^∗∗ level change when we move from RHF/6-311++G^∗∗ to DFT/B3LYP//6-311++G^∗∗ level and as we move from gas to water, from gas to ethanol and from water to ethanol. In fact, the dipole moment (μ) (Debye) value decreases by 0.1745 (−0.13%) and 0.0026 (−0.19%) respectively when we move from gas to water and from gas to ethanol where it increases by 0.1719 (+14.71%) when we move from water to ethanol; the 〈α〉 (a.u) value decreases by 0.2475 (−0.14%); and the β_mol (u.a) remains constant at the RHF/6-311++G^∗∗ and changes as we move from RHF/6-311++G^∗∗ to DFT/B3LYP//6-311++G^∗∗ level. At the DFT/B3LYP//6-311++G^∗∗ level of theory, its value changes as we move from gas to water, from gas to ethanol and from water to ethanol. In fact, its value increases by 653.665 (63.80%) when we move from gas to water and decreases by 8.804 (−2.37%) when we move from gas to ethanol and 662.469 (−64.66%) when we move from water to ethanol. The change in μ, 〈α〉 and β_mol values for the molecule pyrimethamine as we move from RHF/6-311++G^∗∗ level to DFT/B3LYP//6-311++G^∗∗ level is due to the effect of electron correlation. Theoretical determination of hyperpolarizability of a molecule is quite useful both in understanding the relationship between the molecular structure and non-linear optical properties (Hamit et al., 2009). Molecules with large hyperpolarizability value have the potential to produce second order optical effects much larger than those obtainable with inorganic materials and hyperpolarizability is a measure of the nonlinear optical activity of a molecule (Hamit, 2013; Ejuh and Ndjaka, 2013).

Table 1 Some molecular properties of the molecule pyrimethamine obtained at RHF and B3LYP methods both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set: μ is a dipole moment, 〈α〉 is the average of the polarizability, and β_mol is the first molecular hyperpolarizability (Ejuh and Ndjaka, 2013; Ejuh et al., 2011).

RHF				B3LYP
Properties of the molecule	Gas	Water	Ethanol	Gas	Water	Ethanol
μ (Debye)	1.1780	1.1780	1.1780	1.3425	1.1680	1.3399
〈α〉 (u.a)	184.546	184.546	184.546	216.366	216.119	216.382
β_mol (u.a)	173.322	173.319	173.319	370.854	1024.519	362.050

Table 2 shows the opto electric properties of the molecule pyrimethamine obtained both at RHF and B3LYP level of theory gas phase and in solvated phase by employing 6-311++G^∗∗ basis set. P is the polarization density, E is the average electric field, χ is electric susceptibility, η is the index of refraction, ε is the dielectric constant of the molecule and D the magnitude of the displacement vector. These results show that the value of each property obtained at the RHF level of calculations does not depend on the medium. At the B3LYP level of theory, the value of the average electric field and the polarization density change considerably when we move from gas to water, from gas to ethanol and from water to ethanol; these values also change when we move from RHF/6-311++G^∗∗ level to B3LYP/6-311++G^∗∗ level. The value of the electric susceptibility, the refractive index, the dielectric constant and the magnitude of the displacement vector remain practically constant when we move from gas to ethanol, but change drastically when we move from gas to water or from water to ethanol. These values also change when we move from RHF/6-311++G^∗∗ to B3LYP/6-311++G^∗∗ level. The high value of the refractive index of the molecule pyrimethamine is due to its high average polarizability. There are no corresponding experimental data in the existing literature, neither are there any other ab initio and DFT calculations on the opto electric properties for the molecule pyrimethamine.

Table 2 Opto electric properties of pyrimethamine molecule obtained at RHF and B3LYP methods both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set where P is the polarization density, E is the average electric field, χ is electric susceptibility η is the index of refraction, ε is the dielectric constant of the molecule, and D the magnitude of the displacement vector.

RHF				B3LYP
Properties of the molecule	Gas	Water	Ethanol	Gas	Water	Ethanol
E.10⁸ (V m⁻¹)	0.0129098	0.0129099	0.0129099	0.0147127	3.370514	3.866568
P.10⁻²	3.3993714	3.3993714	3.3993714	3.8740714	3.370512	3.866565
χ.10³	2.9752932	2.9752932	2.9752932	2.9752944	1.789701	2.975293
ε.10⁻⁸	2.6340194	2.6340194	2.6340194	2.6340203	1.5847703	2.6340195
η	54.555414	54.555414	54.555414	54.555422	42.316675	54.555414
D.10⁻²	3.4005137	3.4005137	3.4005137	3.8753734	3.3723973	3.8678679

3.2

3.2 Opto electric properties of sulfadoxine

Some molecular properties of the molecule sulfadoxine obtained at RHF and B3LYP level both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set are shown in Table 3. From these results, one can observe that the calculated value of the dipole moment, the average polarization density and the first molecular hyperpolarizability at RHF/6-311++G^∗∗ level are constant in gas, water and ethanol but their corresponding values obtained at the DFT/B3LYP//6-311++G^∗∗ level vary slightly as we move from gas to water but remain constant as we move from water to ethanol. In fact, the μ, 〈α〉 and β_mol values decrease by 0.2011 Debye (−4.88%), 7.319 (u.a) (−3.41%), and 1956.654 (u.a) respectively as we move from gas to water or ethanol. The change in μ, 〈α〉 and β_mol for the molecule sulfadoxine as we move from RHF/6-311++G^∗∗ level to DFT/B3LYP//6-311++G^∗∗ level is due to the effect of electron correlation.

Table 3 Some molecular properties of the molecule Sulfadoxine obtained at RHF and B3LYP methods both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set: μ is a dipole moment, 〈α〉 is the average of the polarizability, β_mol is the first molecular hyperpolarizability of the molecule (Ejuh and Ndjaka, 2013; Ejuh et al., 2011).

Properties of the molecule	RHF			B3LYP
Properties of the molecule	Gas	Water	Ethanol	Gas	Water	Ethanol
μ (Debye)	4.5681	4.5681	4.5681	4.1149	3.9138	3.9138
〈α〉 (u.a)	205.391	205.391	205.391	214.461	207.142	207.142
β_mol (u.a)	2386.567	2386.567	2386.567	3183.648	1226.994	1226.994

Table 4 shows the opto electric properties of sulfadoxine molecule obtained at RHF and B3LYP level both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set. The results in Table 4 show that the values of the electric susceptibility, the refractive index, the dielectric constant of the molecule obtained from RHF and B3LYP calculations do change as we move from gas phase to solvated phase where as the polarization density, the average electric field, the magnitude of the displacement vector change. The polarization density, the average electric field, the magnitude of the displacement vector change considerably as their values decrease by 0.412 (4.88%), 0.0022 V/m (−4%), and 0.412 (4.88%) respectively as we move from gas to water or ethanol. These values remain constant as we move from water to ethanol. There are no corresponding experimental data in the existing literature, neither are there any other ab initio and DFT calculations on the opto electric properties of this molecule. The high value of the refractive index of the molecule sulfadoxine is due to its high average polarizability. Equally, there are no corresponding experimental data in the existing literature, neither are there any other ab initio and DFT calculations on the opto electric properties for the molecule sulfadoxine.

Table 4 Opto electric properties of sulfadoxine obtained at RHF and B3LYP methods both in gas phase and in solvated phase by employing 6-311++G^∗∗ basis set where P is the polarization density, E is the average electric field, χ is electric susceptibility η is the index of refraction, ε is the dielectric constant of the molecule, and D the magnitude of the displacement vector.

Properties of the molecule	RHF			B3LYP
Properties of the molecule	Gas	Water	Ethanol	Gas	Water	Ethanol
E.10⁸ (V m⁻¹)	0.0500628	0.0500628	0.0500628	0.04509616	0.0428922	0.0428922
P.10⁻²	9.3455056	9.3455056	9.3455056	8.4259245	8.0141397	8.0141397
χ.10³	2.1093255	2.1093255	2.1093255	2.111226	2.111226	2.111226
ε.10⁻⁸	1.867638	1.867638	1.867638	1.86932	1.869319	1.869319
η	45.938279	45.938279	45.938279	45.9589599	45.958958	45.958958
D.10⁻²	9.3499355	9.3499355	9.3499355	8.4299153	8.0179355	8.0179355

3.3

3.3 HOMO and LUMO energy gap and diagram

Many organic molecules, containing conjugated pi electrons are characterized by large values of molecular first hyperpolarizabilities. The interaction of two atomic (or) molecule orbital produces two new orbitals. One of the new orbitals is higher in energy than the original one (the anti bonding orbital) and one is lower (the lower orbital). HOMO and LUMO energy are characterized by their ability to accept electrons (Vijayakumar et al., 2008). When we are dealing with interacting molecular orbitals, the two that interact are generally the highest energy occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of the compound (Arulmozhi et al., 2011; Arunagiri et al., 2011, 2013 ). These orbitals are a pair of orbitals in the compound, which allows them to interact more strongly. These orbitals are sometimes called the frontier orbitals, because they lie at the outermost boundaries of the electrons of compound (Arunagiri et al., 2011, 2013). The HOMO–LUMO molecular orbital shown below are obtained using RHF/6-311++G^∗∗ and B3LYP/6-311++G^∗∗ level. The HOMO–LUMO energy gap value of the molecule pyrimethamine at the RHF/6-311++G^∗∗ level is −0.133 a.u both in gas phase and in solvated phase; and at the B3LYP/6-311++G^∗∗ level is -0.133 a.u in gas phase and −0.134 a.u in solvated phase (Figs. 3.1 and 3.2).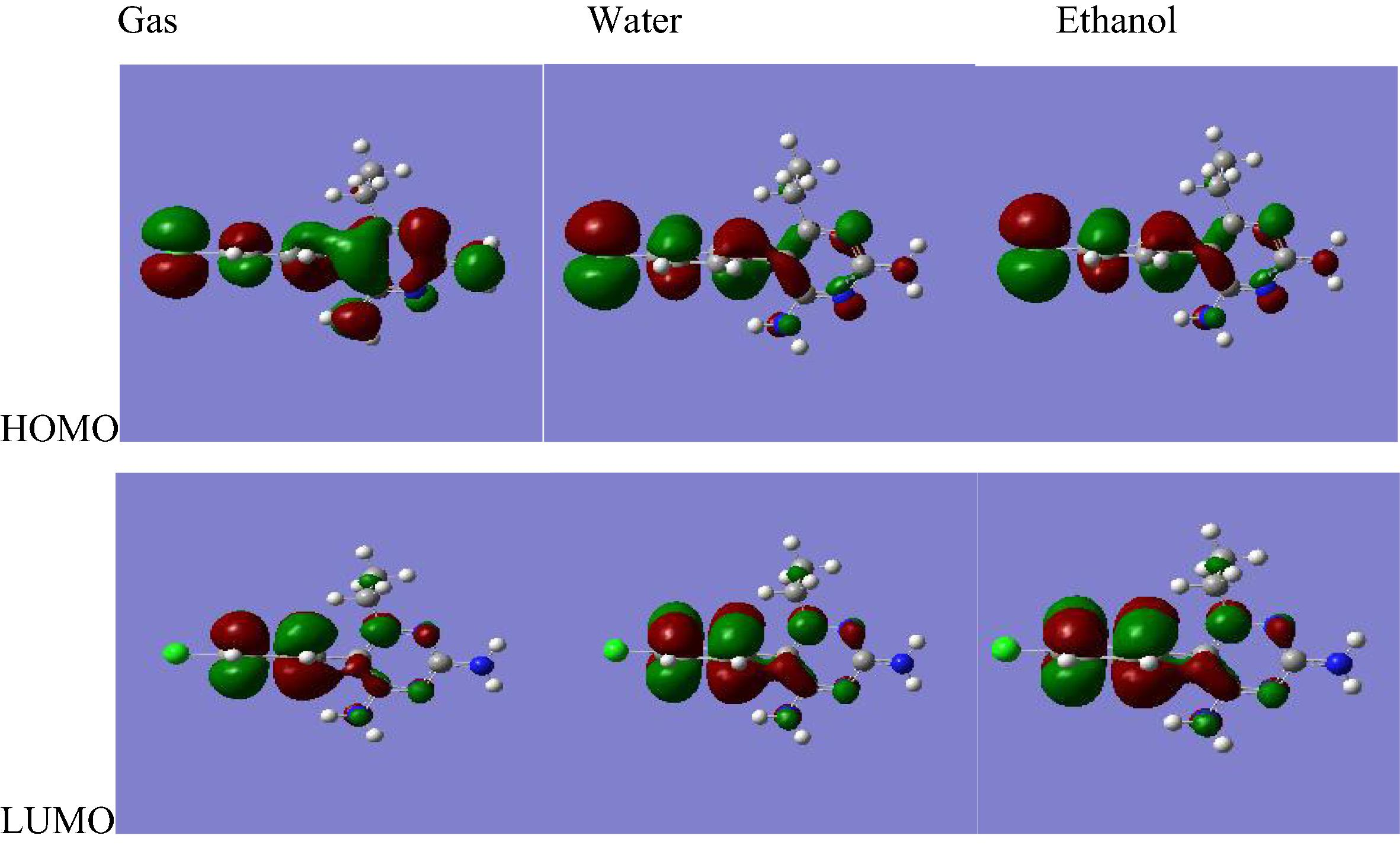

RHF/6-311++G∗∗ HOMO and LUMO molecular orbitals for pyrimethamine.

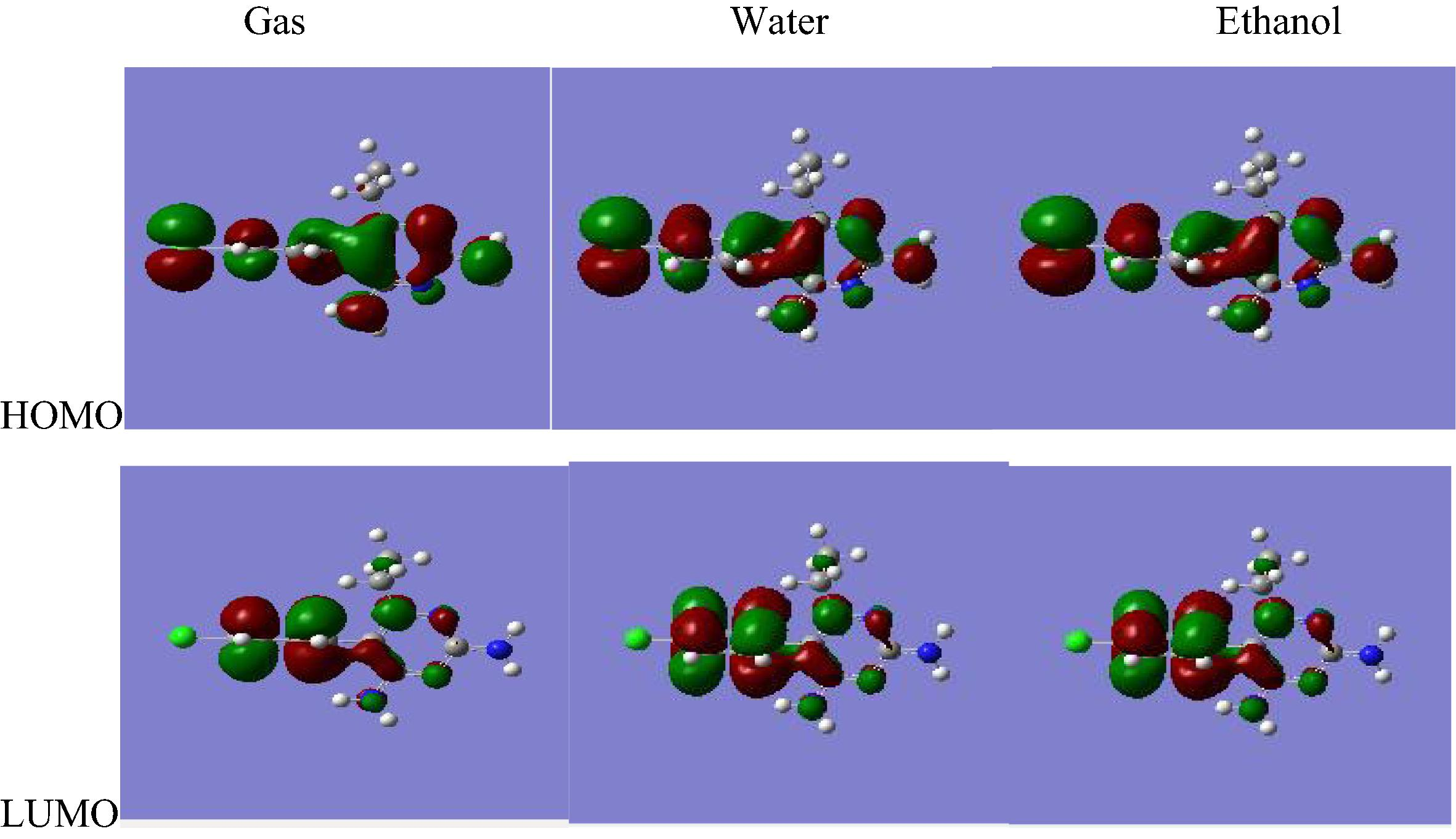
B3LYP/6-311++G∗∗ HOMO and LUMO molecular orbitals for pyrimethamine.

For the molecule sulfadoxine, the HOMO–LUMO gap value at the RHF/6-311++G^∗∗ level is −0.120 a.u both in gas phase and in solvated phase; and at the B3LYP/6-311++G^∗∗ level is −0.110 a.u in gas phase and −0.120 a.u in solvated phase (Figs. 3.3 and 3.4).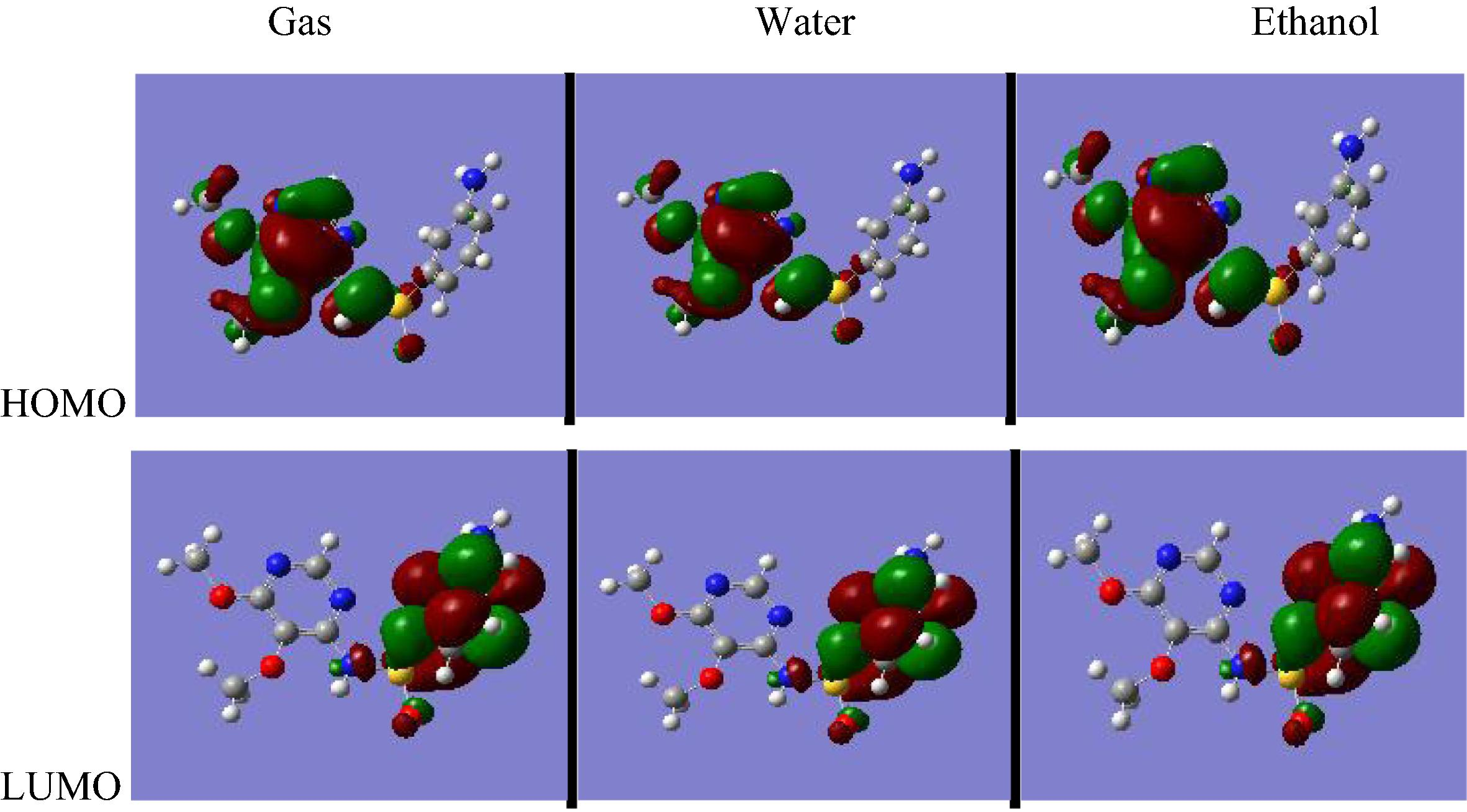

RHF/6-311++G∗∗ HOMO and LUMO molecular orbitals for sulfadoxine.

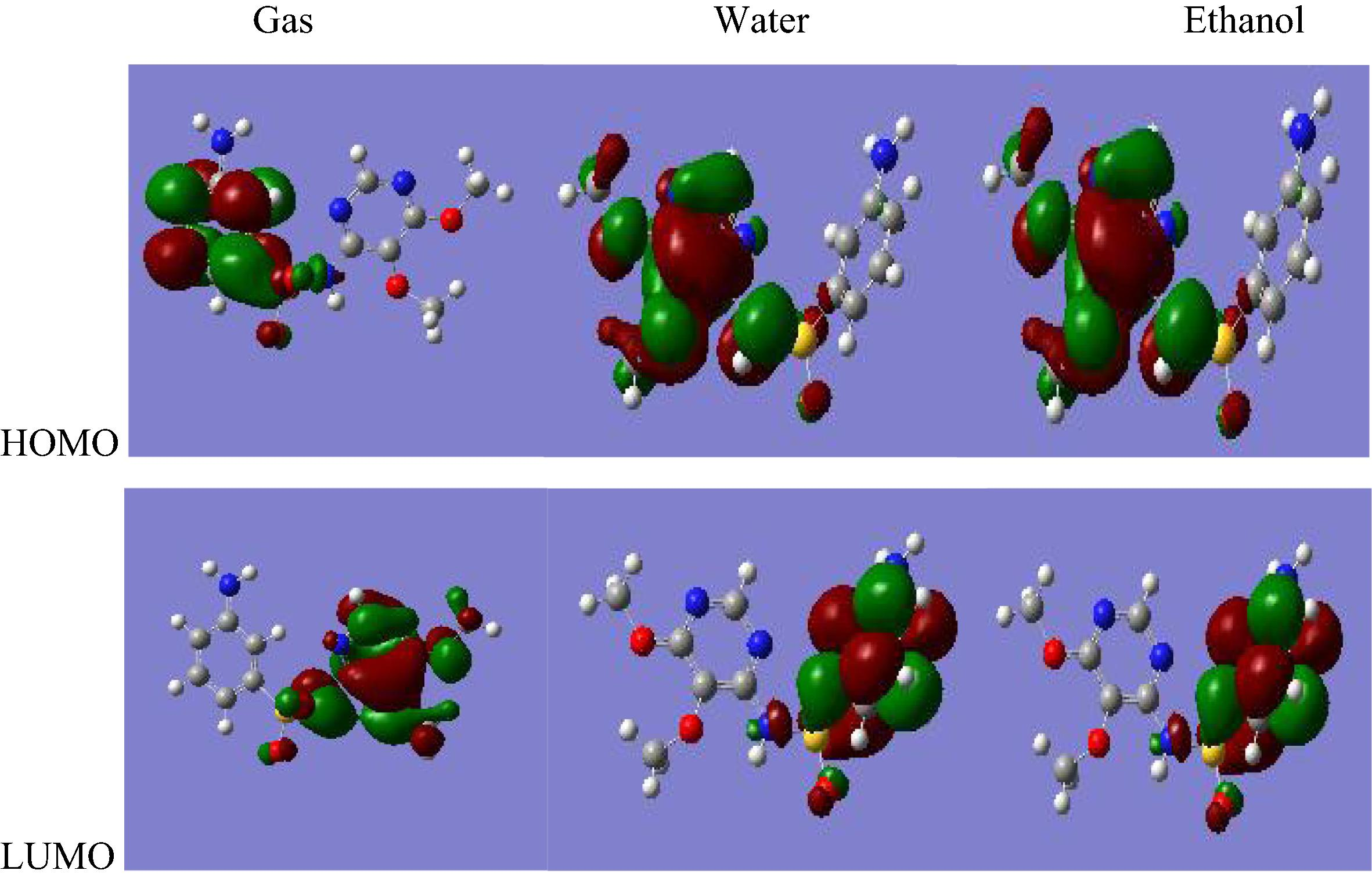
B3LYP/6-311++G∗∗ HOMO and LUMO molecular orbitals for sulfadoxine.

4 Conclusion

From the results obtained, we observed that the solvated phase does not have any effect on the opto electric properties of the molecules pyrimethamine and sulfadoxine at RHF/6-311++G^∗∗ level of theory. At the B3LYP/6-311++G^∗∗ level, in the solvated phase, there is some effect on the dipole moment, average polarizability, first molecular hyperpolarizability, polarization density, average electric field and on the magnitude of the displacement vector for sulfadoxine whereas there is no effect on the electric susceptibility, the dielectric constant and the refractive index of the molecule sulfadoxine.

The phenyl moiety being an acceptor due to the strong electron-withdrawing capability of the pyrimidine ring in both pyrimethamine and sulfadoxine molecules, and the ease with which structural modification can be performed on these molecules, we can conclude that these molecules have opto electronics applications.

Due to the small values of the polarization density, the dielectric constant, magnitude of the displacement vector and HOMO–LUMO energy gaps of the molecules pyrimethamine and sulfadoxine; and the high values of the electric susceptibility and refractive index we can again conclude that these molecules have very good opto electronic applications.

Due to the fact that there are no corresponding experimental data in the existing literature, neither are there any other ab initio and DFT calculations on the opto electric properties of these molecules, we are optimistic that these results will serve as a benchmark for other studies.

References

Agren H., Valtras O., Koch H., Jorgensen P., Helgaker T., . Direct atomic orbital based self-consistent-field calculations of nonlinear molecular properties. Application to the frequency dependent hyperpolarizability of paranitroaniline. J. Chem. Phys.. 1993;98:6417-6423.
[Google Scholar]
Andrea A., . Static and dynamic electronic (hyper) polarizabilities of dimethylnaphthalene isomers: characterization of spatial contributions by density analysis. Sci. World J. 2013 Art. ID 832682
[Google Scholar]
Andrea A., . Second harmonic generation, electrooptical pockels effect, and static first-order hyperpolarizabilities of 2,2-bithiophene conformers: an HF, MP2, and DFT theoretical investigation. Hind. Publ. Corp. Adv. Phys. Chem. 2013:8. 394697
[Google Scholar]
Arulmozhi S., Victor A.R.M., Madhavan J., . HOMO, LUMO analysis and first order hyperpolarizability of 2-amino-5-chloro benzophenone using computational methods. Chem. Sin.. 2011;2:158-163.
[Google Scholar]
Arunagiri C., Arivazhagan M., Subashini A., . Vibrational spectroscopic (FT-IR and FT-Raman), first-order hyperpolarizability, HOMO, LUMO, NBO, Mulliken charges and structure determination of 2-bromo-4-chlorotoluene.Spect. Acta Part A: Mol. Biomol. Spectrosc.. 2011;79:1747-1756.
[Google Scholar]
Arunagiri C., Subashini A., Saranya M., Thomas M.P., . Molecular structure, optimized geometry, HOMO–LUMO energy and Mulliken charges of a new schiff base 2-(naphtalen-2-yliminomethyl) phenol by ab initio and density functional theory calculations. Ind. J. Appl. Res. 2013:3. 2249-555
[Google Scholar]
Becke A.D., . Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098-3100.
[Google Scholar]
Bonin K.D., Kadar K.M.A., . Linear electric-dipolepolarizabilities. Int. J. Mod. Phys. B. 1994;8:3313.
[Google Scholar]
Bonin, K.D., Kresin, V.V., 1997. Electric dipolepolarizabilities of atoms, molecules, and clusters. W. Sci., Singapore.
Champagne B., Perete E.A., Van G.S.J.A., . Assessment of conventional density functional schemes for computing the polarizabilities and hyperpolarizabilities of conjugated oligomers: an ab initio investigation of polyacetylene chains. J. Chem. Phys.. 1998;109:10489-10498.
[Google Scholar]
Ciğdem Y., Hanife S., Nezihe C., Ibrahim Y., Alaaddin C., . Experimental and ab initio computational studies on dimethyl-(4-{4-[(3-methyl-3-phenyl-cyclobutyl)-thiazol-2-yl]-hydrazonomethyl}-amine. Bull. Korean Chem. Soc.. 2010;31 123553
[Google Scholar]
Ejuh G.W., Ndjaka J.M., . Linear and non linear optical effects of pyrimethamine and sulfadoxine: ab-initio and density functional study. Afr. Rev. Phys.. 2013;8(62)
[Google Scholar]
Ejuh G.W., Ndjaka J.M., Singh A.N., . Study of the structures and physico-chemical properties of the molecules pyrimethamine and sulfadoxine by ab initio and DFT methods. Can. J. Pure Appl. Sci.. 2011;5:5. 1591-1532
[Google Scholar]
Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R.J., . Gaussian 03, Revision C.02. Wallingford CTX: Gaussian Inc.; 2004.
Garay R.O., . Synthesis of polymers with electro-optical properties. Molecules. 2000;5:304.
[Google Scholar]
Gould H., Miller T.M., . Adv. At. Mol. Opt. Phys.. 2005;51:243.
Hamit A., . A review on nonlinear optical properties of donor-acceptor derivatives of naphthalene and azanaphthalene. Rev. Adv. Mater. Sci.. 2013;34:7987.
[Google Scholar]
Hamit A., Champane B., Spassova M., . Theoretical investigation on the polarizability and second hyperpolarizability of polysilole. Chem. Phys. Lett.. 2009;471:111-115.
[Google Scholar]
Ivaska A., . Electroanalysis. 1991;3:247.
Junmei W., Xiang Q.X., Tingjun H., Xiaojie X., . Fast approaches for molecular polarizability calculations. J. Phys. Chem. A 2007
[Google Scholar]
Kurt V.Mikkelsen, Yi L., Hans Å., Poul J., . Solvent induced polarizabilities and hyperpolarizabilities of paranitroaniline studied by reaction field linear response theory. J. Chem. Phys.. 1994;100:8240.
[CrossRef] [Google Scholar]
Lee C., Yang W., Parr R.G., . Development of the Colle-Salvetti correlation-energy formula into a functional of electron density. Phys. Rev. B. 1988;37:735.
[Google Scholar]
Michael Jaszunski., Poul J., Henrick K., Hans A., Trygve H., . Frequency dependent hyperpolarizabilities of polyynes. J. Chem. Phys. 1993;98(9):1.
[Google Scholar]
Miertus S., Scrocco E., Tomasi J., . Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys.. 1981;55:117-129.
[Google Scholar]
Nalwa H.S., Miyata S., eds. Nonlinear Optics of Organics Molecules and Polymers. CRC Press Inc.; 1997. p. :611.
Seda G.Sagdinca, Asli Esmeb, . Theoretical and vibrational studies of 4,5-diphenyl-2-2 Oxazole propionic acid (oxaprozin) Spectrochim. Acta A Mol. Biomol. Spectrosc. 2010:1386-1425. doi:10.1016
[Google Scholar]
Sekino H., Bartlett R.J., . Molecular hyperpolarizabilities. J. Chem. Phys.. 1993;98:3022-3037.
[Google Scholar]
Sekino H., Maeda Y., Kamiya M., Hirao K., . Polarizability and second hyperpolarizability evaluation of long molecules by the density functional theory with long-range correction. J. Chem. Phys.. 2007;126:014107.
[Google Scholar]
Sim F., Chin S., Dupuis M., Rice J.E., . Electron correlation effects in hyperpolarizabilities of p-nitroaniline. J. Phys. Chem.. 1993;97(6):1158-1163.
[Google Scholar]
Stahelin M., Burland D.M., Rice J.E., . Solvent dependence of the second order hyperpolarizability in p-nitroaniline. Chem. Phys. Lett.. 1992;191:245.
[Google Scholar]
Vijayakumar T., Hubert J.I., Reghunadhan N.C.P., Jayakumar V.S., . Efficient-electrons delocalization in prospective push–pull non linear optical chromophore 4-[N,N-dimethylamino]-40-nitrostilbene (DANS): a vibrational spectroscopic study. Chem. Phys.. 2008;343:83.
[Google Scholar]
Vosko S.H., Wilk L., Nusair M., . Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis can. J. Phys.. 1980;58:1200.
[Google Scholar]
William, M. Haynes, 2012. Science CRC Handbook of Chemistry and Physics, 93rd ed.

Introduction

Methodology

Results and discussion

Opto electric properties of pyrimethamine
Opto electric properties of sulfadoxine
HOMO and LUMO energy gap and diagram

Conclusion

Fulltext Views
5

PDF downloads
4

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Agren H., Valtras O., Koch H., Jorgensen P., Helgaker T., . Direct atomic orbital based self-consistent-field calculations of nonlinear molecular properties. Application to the frequency dependent hyperpolarizability of paranitroaniline. J. Chem. Phys.. 1993;98:6417-6423.
[Google Scholar]

[2] Andrea A., . Static and dynamic electronic (hyper) polarizabilities of dimethylnaphthalene isomers: characterization of spatial contributions by density analysis. Sci. World J. 2013 Art. ID 832682
[Google Scholar]

[3] Andrea A., . Second harmonic generation, electrooptical pockels effect, and static first-order hyperpolarizabilities of 2,2-bithiophene conformers: an HF, MP2, and DFT theoretical investigation. Hind. Publ. Corp. Adv. Phys. Chem. 2013:8. 394697
[Google Scholar]

[4] Arulmozhi S., Victor A.R.M., Madhavan J., . HOMO, LUMO analysis and first order hyperpolarizability of 2-amino-5-chloro benzophenone using computational methods. Chem. Sin.. 2011;2:158-163.
[Google Scholar]

[5] Arunagiri C., Arivazhagan M., Subashini A., . Vibrational spectroscopic (FT-IR and FT-Raman), first-order hyperpolarizability, HOMO, LUMO, NBO, Mulliken charges and structure determination of 2-bromo-4-chlorotoluene.Spect. Acta Part A: Mol. Biomol. Spectrosc.. 2011;79:1747-1756.
[Google Scholar]

[6] Arunagiri C., Subashini A., Saranya M., Thomas M.P., . Molecular structure, optimized geometry, HOMO–LUMO energy and Mulliken charges of a new schiff base 2-(naphtalen-2-yliminomethyl) phenol by ab initio and density functional theory calculations. Ind. J. Appl. Res. 2013:3. 2249-555
[Google Scholar]

[7] Becke A.D., . Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098-3100.
[Google Scholar]

[8] Bonin K.D., Kadar K.M.A., . Linear electric-dipolepolarizabilities. Int. J. Mod. Phys. B. 1994;8:3313.
[Google Scholar]

[9] Bonin, K.D., Kresin, V.V., 1997. Electric dipolepolarizabilities of atoms, molecules, and clusters. W. Sci., Singapore.

[10] Champagne B., Perete E.A., Van G.S.J.A., . Assessment of conventional density functional schemes for computing the polarizabilities and hyperpolarizabilities of conjugated oligomers: an ab initio investigation of polyacetylene chains. J. Chem. Phys.. 1998;109:10489-10498.
[Google Scholar]

[11] Ciğdem Y., Hanife S., Nezihe C., Ibrahim Y., Alaaddin C., . Experimental and ab initio computational studies on dimethyl-(4-{4-[(3-methyl-3-phenyl-cyclobutyl)-thiazol-2-yl]-hydrazonomethyl}-amine. Bull. Korean Chem. Soc.. 2010;31 123553
[Google Scholar]

[12] Ejuh G.W., Ndjaka J.M., . Linear and non linear optical effects of pyrimethamine and sulfadoxine: ab-initio and density functional study. Afr. Rev. Phys.. 2013;8(62)
[Google Scholar]

[13] Ejuh G.W., Ndjaka J.M., Singh A.N., . Study of the structures and physico-chemical properties of the molecules pyrimethamine and sulfadoxine by ab initio and DFT methods. Can. J. Pure Appl. Sci.. 2011;5:5. 1591-1532
[Google Scholar]

[14] Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R.J., . Gaussian 03, Revision C.02. Wallingford CTX: Gaussian Inc.; 2004.

[15] Garay R.O., . Synthesis of polymers with electro-optical properties. Molecules. 2000;5:304.
[Google Scholar]

[16] Gould H., Miller T.M., . Adv. At. Mol. Opt. Phys.. 2005;51:243.

[17] Hamit A., . A review on nonlinear optical properties of donor-acceptor derivatives of naphthalene and azanaphthalene. Rev. Adv. Mater. Sci.. 2013;34:7987.
[Google Scholar]

[18] Hamit A., Champane B., Spassova M., . Theoretical investigation on the polarizability and second hyperpolarizability of polysilole. Chem. Phys. Lett.. 2009;471:111-115.
[Google Scholar]

[19] Ivaska A., . Electroanalysis. 1991;3:247.

[20] Junmei W., Xiang Q.X., Tingjun H., Xiaojie X., . Fast approaches for molecular polarizability calculations. J. Phys. Chem. A 2007
[Google Scholar]

[21] Kurt V.Mikkelsen, Yi L., Hans Å., Poul J., . Solvent induced polarizabilities and hyperpolarizabilities of paranitroaniline studied by reaction field linear response theory. J. Chem. Phys.. 1994;100:8240.
[CrossRef] [Google Scholar]

[22] Lee C., Yang W., Parr R.G., . Development of the Colle-Salvetti correlation-energy formula into a functional of electron density. Phys. Rev. B. 1988;37:735.
[Google Scholar]

[23] Michael Jaszunski., Poul J., Henrick K., Hans A., Trygve H., . Frequency dependent hyperpolarizabilities of polyynes. J. Chem. Phys. 1993;98(9):1.
[Google Scholar]

[24] Miertus S., Scrocco E., Tomasi J., . Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys.. 1981;55:117-129.
[Google Scholar]

[25] Nalwa H.S., Miyata S., eds. Nonlinear Optics of Organics Molecules and Polymers. CRC Press Inc.; 1997. p. :611.

[26] Seda G.Sagdinca, Asli Esmeb, . Theoretical and vibrational studies of 4,5-diphenyl-2-2 Oxazole propionic acid (oxaprozin) Spectrochim. Acta A Mol. Biomol. Spectrosc. 2010:1386-1425. doi:10.1016
[Google Scholar]

[27] Sekino H., Bartlett R.J., . Molecular hyperpolarizabilities. J. Chem. Phys.. 1993;98:3022-3037.
[Google Scholar]

[28] Sekino H., Maeda Y., Kamiya M., Hirao K., . Polarizability and second hyperpolarizability evaluation of long molecules by the density functional theory with long-range correction. J. Chem. Phys.. 2007;126:014107.
[Google Scholar]

[29] Sim F., Chin S., Dupuis M., Rice J.E., . Electron correlation effects in hyperpolarizabilities of p-nitroaniline. J. Phys. Chem.. 1993;97(6):1158-1163.
[Google Scholar]

[30] Stahelin M., Burland D.M., Rice J.E., . Solvent dependence of the second order hyperpolarizability in p-nitroaniline. Chem. Phys. Lett.. 1992;191:245.
[Google Scholar]

[31] Vijayakumar T., Hubert J.I., Reghunadhan N.C.P., Jayakumar V.S., . Efficient-electrons delocalization in prospective push–pull non linear optical chromophore 4-[N,N-dimethylamino]-40-nitrostilbene (DANS): a vibrational spectroscopic study. Chem. Phys.. 2008;343:83.
[Google Scholar]

[32] Vosko S.H., Wilk L., Nusair M., . Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis can. J. Phys.. 1980;58:1200.
[Google Scholar]

[33] William, M. Haynes, 2012. Science CRC Handbook of Chemistry and Physics, 93rd ed.