Unsteady viscous flow over a shrinking cylinder

1 Introduction

The study of fluid flow over a stretching cylinder has attracted the interest of many researchers. It should be mentioned that the boundary layer flow due to a stretching or shrinking surface is a relevant type of flow appearing in many industrial and engineering processes. There are several applications in the engineering processes, for example in polymer and metallurgy industries such as manufacture and extraction of polymer and rubber sheets, melt-spinning, hot rolling, paper production, wire drawing and glass-fiber production, etc. In these situations, the quality of the final product depends to a great extent on the rate of cooling in process and the process of stretching/shrinking (Bachok et al., 2012). Another example of flow toward a shrinking sheet is a rising, shrinking balloon (Wang, 2008). Wang (1988) investigated the steady flow of an incompressible viscous fluid outside a stretching hollow cylinder in an ambient fluid at rest. This problem was then extended by Ishak et al. (2008a) by including the suction and injection effects. It was reported that injection reduces the skin friction as well as the heat transfer rate at the surface while suction acts in the opposite manner.

Wang and Ng (2011) obtained similarity solution for flow due to a stretching cylinder with partial slip condition at the surface. They found that the slip effect significantly decreases the magnitude of the fluid velocity and the shear stress. Later, Wang (2012) solved the problem of a natural convection on a vertical stretching cylinder. The result obtained is an exact similarity solution of the Navier–Stokes equations. In a subsequent paper, Ishak et al. (2008b) have solved numerically the problem of magnetohydrodynamic flow and heat transfer over a stretching cylinder. They observed that the heat transfer rate at the surface decreases with increasing values of the magnetic parameter, while the magnitude of the skin friction coefficient increases as the magnetic parameter and the Reynolds number increase.

Recently, Fang et al. (2011) studied the unsteady viscous flow over an expanding stretching cylinder which provides an exact similarity solution to the Navier–Stokes equations. They indicated that the reversal flows exist due to the expansion of the cylinder and the flow field is strongly affected by Reynolds number and the unsteadiness parameter. Later, Fang et al. (2012) reported the numerical solution of the unsteady viscous flow on the outside of an expanding or contracting cylinder. The solution is an exact solution to the unsteady Navier–Stokes equations.

Compared to a stretching cylinder as mentioned above, there is a limited contribution to the problem of an unsteady viscous flow over a shrinking cylinder. The problem of the steady stagnation point flow of a viscous and incompressible fluid over a permeable shrinking circular cylinder was solved numerically by Lok and Pop (2011). They found that up to three solutions exist for a certain range of the shrinking parameter. It is worth mentioning that the flow over a shrinking sheet was considered by Bhattacharyya et al. (2011), Fang et al. (2010), Faraz et al. (2011), Ishak et al. (2010), Lok et al. (2011), Miklavčič and Wang (2006), and Wang (2008), among others. It seems that Miklavčič and Wang (2006) were the first to investigate the flow over a shrinking surface. For this flow configuration, the fluid is stretched toward a slot and the flow is quite different from the stretching case. It has been shown by these authors that mass suction is required generally to maintain the flow over the shrinking sheet. For this new type of shrinking flow, it is essentially a backward flow as discussed by Goldstein (1965). For a backward flow configuration, the fluid loses any memory of the perturbation introduced by the leading edge, say the slot. Therefore, the flow induced by a shrinking surface shows quite distinct physical phenomena from the forward stretching surface.

It is worth mentioning that the unsteady nature of a wide range of fluid flows is of practical importance and has received considerable attention in the past several years. In many applications, the ideal flow environment around the device is nominally steady, but undesirable unsteady effects arise either due to self-induction of the body, or due to fluctuations or non-uniformities in the surrounding fluid. On the other hand, some devices are required to execute time-dependent motion in order to perform their basic functions (McCroskey, 1977). The study of unsteady boundary layers owes its importance to the fact that all boundary layers, which occur in practice are, in a sense, unsteady. Unsteady viscous flows have been studied rather extensively and all the characteristic features of unsteady effects are now more or less familiar to fluid mechanicists. Stewartson (1960), Stuart (1964), Riley (1975,1990), McCroskey (1977), Telionis (1981) and Wang (1989) have concisely reviewed the main ideas and important contributions on the topic. An improved understanding of unsteady fluid flows and the application of this knowledge to new design techniques should provide substantial improvements in performance, reliability, and costs of many fluid dynamic devices.

The aim of the present paper is to investigate the behavior of the unsteady viscous flow over a shrinking cylinder which has not been considered before. The effects of suction and the unsteadiness parameters on the flow field are also investigated. The governing partial differential equations are first reduced to nonlinear ordinary differential equations, before being solved numerically using a shooting method for some values of the governing parameters.

2 Mathematical formulation

Consider the flow of an unsteady, laminar, viscous and incompressible fluid past a permeable infinite cylinder in shrinking motion as shown in Fig. 1. The diameter of the cylinder is assumed as a function of time with unsteady radius $a(t)=a_0\sqrt{1-\beta t}$ . Let u and w be the velocity components in the r and z directions, respectively.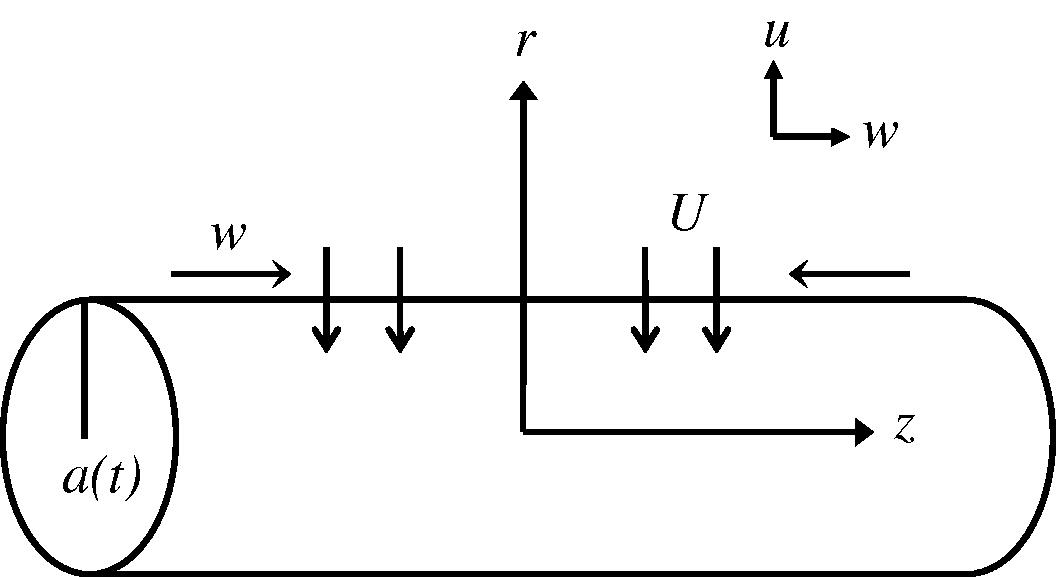

Close

Figure 1

The physical model and coordinate system.

Export to PPT

For incompressible fluids without body force and based on the axisymmetric flow assumptions, and there is no azimuthal velocity component, the unsteady Navier–Stokes equations governing the flow are (Fang et al., 2011,2012😉

Using the similarity variables (Fang et al., 2012)

3 Numerical method

Numerical solutions to the ordinary differential Eq. (6) subject to the boundary conditions (7) were obtained using a shooting method with the shootlib function in Maple software. This method is described in detail in the book by Jaluria and Torrance (2003) and effectively used by several authors in solving boundary layer flows and heat transfer problem (see Fang et al. (2011, 2012), Rohni et al. (2012) and Wan Zaimi and Ishak (2012)). In the shooting method, dual solutions are obtained by setting different initial values for the values of $f^{″}(1)$ where all the velocity profiles satisfy the infinity boundary conditions (7) asymptotically but with different shapes.

In the present study, for one particular value of suction parameter γ and the unsteadiness parameter S, two different velocity profiles were found when considering two different initial guesses of $f^{″}(1)$ . As a result, two different shapes of variations for the skin friction coefficient $f^{″}(1)$ were obtained as shown in Fig. 2 while two different shapes of velocity profiles were presented in Figs. 3 and 4.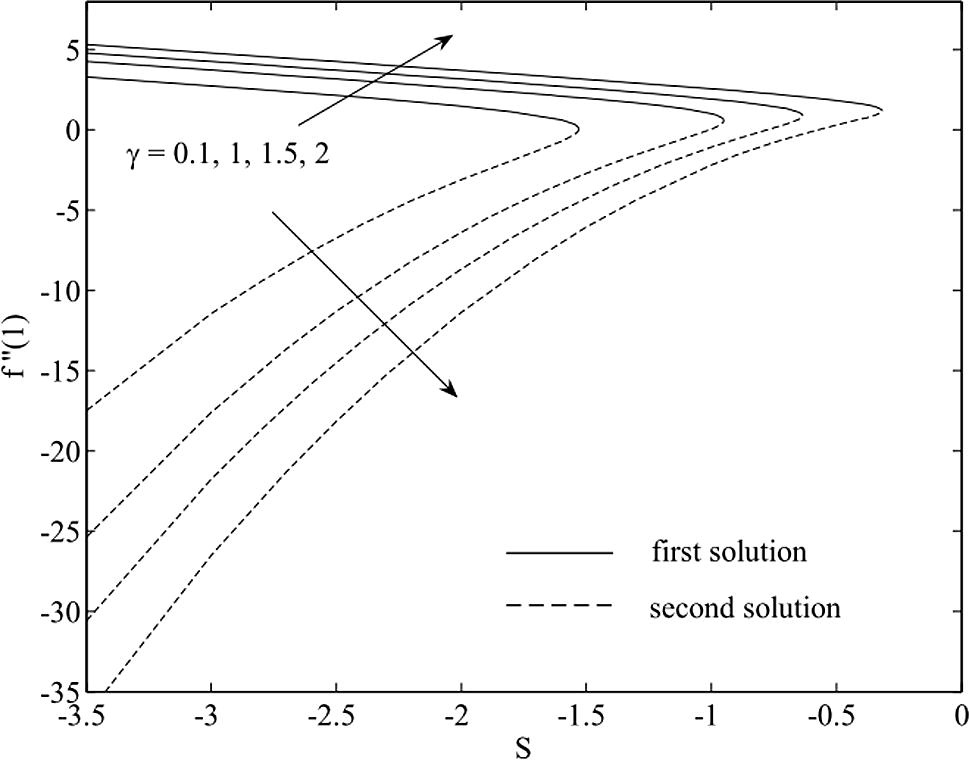

Close

Figure 2

Variation of the skin friction coefficient with S for different values of γ.

Export to PPT

Close

Figure 3

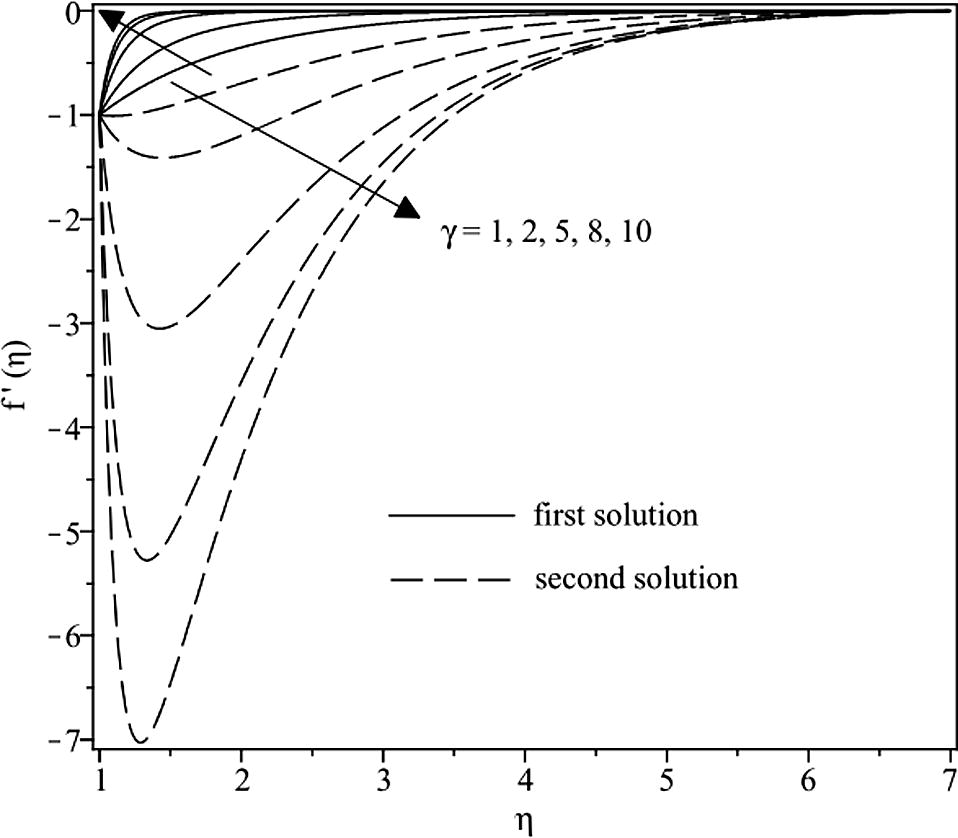
Velocity profiles for different values of γ when S = −1.

Export to PPT

Close

Figure 4

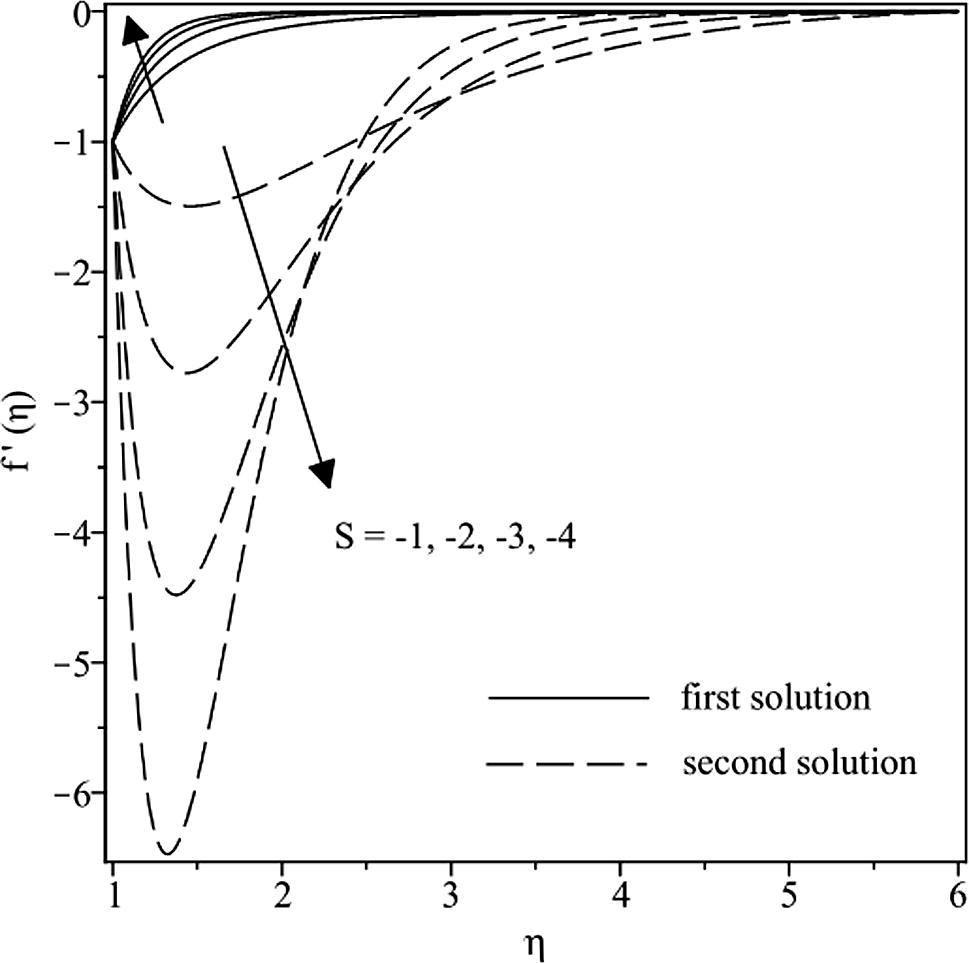
Velocity profiles for different values of S when γ = 2.

Export to PPT

In this method we have to choose a suitable finite value of η_∞ (where η_∞ corresponds to η → ∞). We run our computations with the value η_∞ = 8, which is sufficient to achieve the far field boundary conditions asymptotically for all values of the parameters considered.

4 Results and discussion

Eq. (6) subjected to the boundary conditions (7) was solved numerically for some values of suction parameter γ and the unsteadiness parameter S. The results obtained are used to carry out a parametric study showing influences of the governing parameters γ and S on the skin friction coefficient as well as the velocity profiles. Table 1 shows the comparison values of $f^{″}(1)$ with those of Fang et al. (2011) for the case of a stretching cylinder by setting f′(1) = 1 in the boundary conditions (7) and Re = 1 in Eq. (5) of the paper by Fang et al. (2011). The present results were also compared with those obtained by Fang et al. (2012) by setting f′(1) = 0 in boundary conditions (7), for unsteady viscous flow of an expanding or contracting cylinder as presented in Table 2. The comparisons are found to be in good agreement, thus give confidence to the results for the shrinking case to be reported subsequently.

Fig. 2 shows the variation of the reduced skin friction or surface shear stress coefficient $f^{″}(1)$ as a function of the unsteadiness parameter S for some values of suction parameter γ. This figure shows the existence of dual solutions, upper and lower branch solutions, of the similarity Eq. (6) for a particular value of S and of γ. In the following discussion, we classify the upper and lower branch solutions as how they appear in Fig. 2, i.e. the upper branch solution has a higher value of $f^{″}(1)$ than the lower branch solution. Dual solutions are found to exist for negative values of S. The duality nature of the solution is consistent with the results reported by Fang et al. (2009) for the problem of viscous flow over an unsteady shrinking sheet with mass transfer. It is seen from Fig. 2 that the magnitude of $f^{″}(1)$ increases as the parameter γ increases. The opposite trend is observed for the variation of S, i.e. increasing S is to decrease the magnitude of the reduced skin friction coefficient $f^{″}(1)$ . The increasing value of $f^{″}(1)$ with increasing γ is due to the suction effect which increases the reduced skin friction or the surface shear stress coefficient. Fig. 2 shows that the effect of suction is to widen the range of S for which the solution exists. Moreover, the solution exists up to the critical values of S, say S_c. There is one solution at S = S_c, two solutions for S < S_c and no solution when S > S_c. These critical values of S_c for different values of γ are presented in Table 3, while the values of $f^{″}(1)$ for some values of S and γ are shown in Table 4. In Table 4, the values in parentheses represent the second solutions.

In order to further understand the effects of the mass suction and the unsteadiness parameters on the flow over the shrinking cylinder, two examples of the velocity profiles f′(η) are illustrated. Fig. 3 presents the velocity profiles for some values of γ with a fixed value of S. It is seen that the fluid velocity inside the boundary layer increases as the parameter γ increases. This observation occurs because suction effect produces an increase in the skin friction coefficient. For the first solution, the boundary layer thickness decreases as γ increases. This is because the velocity penetration into the fluid becomes shorter as the mass suction parameter increases. The opposite trend is observed for the second solution, where the velocity penetrates deeper with the increase of mass suction parameter. This finding is in accordance with the results reported by Fang et al. (2009). Both first and second solutions satisfy the far field boundary conditions asymptotically. From Fig. 3, one can see that the velocity profiles for the first solution have positive velocity gradients, and those of the second solution have negative velocity gradients at the surface which are consistent with the results presented in Fig. 2. The variation of the reduced skin friction coefficient is significantly influenced by the effect of suction at the boundary which increases/decreases the boundary layer thickness.

Fig. 4 depicts the velocity profiles f′(η) for some values of S with a fixed value of γ. This figure shows the existence of two different velocity profiles. It is found that the velocity boundary layer thickness decreases as S decreases which implies the increase in the velocity gradient, in consequence of increases in the values of $|f^{″}(1)|$ . It is evident from this figure that the velocity gradient shows positive gradient for the first solution, and satisfies the far field boundary condition (7). In contrast, for the second solution, negative velocity gradient near the surface is initially shown and the velocity increases steadily with positive velocity gradient to reach the far field boundary condition (7) asymptotically. It is also found that the velocity of the fluid is damped faster as the magnitude of the unsteadiness parameter increases for the second solution. These observations are again consistent with the results reported by Fang et al. (2009). It is worth highlighting at this end that, the stability analysis of multiple solutions for some viscous and porous media problems has been done in several studies (Merkin, 1985; Weidman et al., 2006; Paullet and Weidman (2007); Harris et al., 2009; and Postelnicu and Pop, 2011), and it was shown in those papers that only the first (upper branch) solution is stable and physically realizable in practice, while the second (lower branch) solution is not. We will, however, not repeat this analysis here.

5 Conclusion

The problem of unsteady viscous flow over a permeable shrinking cylinder was solved numerically using the shooting method. The effect of suction and unsteadiness parameters on the flow velocity and the skin friction coefficient have been analyzed and presented graphically. Some conclusions can be drawn from this study:

• The present problem admits dual solutions.

• The magnitude of the skin friction coefficient increases as the suction parameter increases.

• The magnitude of the skin friction coefficient decreases with the increasing of the unsteadiness parameter.

• The flow velocity and the skin friction coefficient are clearly influenced by the suction and the unsteadiness parameters.