Reliable analysis for delay differential equations arising in mathematical biology

Ahmet Yıldırım; Hüseyin Koçak; Serap Tutkun

doi:10.1016/j.jksus.2011.08.005

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

24 (

); 359-365

doi:

10.1016/j.jksus.2011.08.005

Reliable analysis for delay differential equations arising in mathematical biology

Ahmet Yıldırım^a, Hüseyin Koçak^b,*, Serap Tutkun^a

a Ege University, Department of Mathematics, 35100 Bornova, İzmir, Turkey

b Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK

*Corresponding author. Tel.: +44 905687895. hkocak.ege@gmail.com (Hüseyin Koçak)

Received: 2011-7-27, Accepted: 2011-8-20, Published: 2011-10-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Available online 27 August 2011

Peer review under responsibility of King Saud University.

Abstract

In this study, delay differential equations are investigated using the variational iteration method. Delay differential equations (DDEs) have a wide range of application in science and engineering. They arise when the rate of change of a time-dependent process in its mathematical modeling is not only determined by its present state but also by a certain past state. Recent studies in such diverse fields as biology, economy, control and electrodynamics have shown that DDEs play an important role in explaining many different phenomena. The procedure of present method is based on the search for a solution in the form of a series with easily computed components. Some numerical illustrations are given. These results reveal that the proposed method is very effective and simple to perform.

Keywords

Variational iteration method

Delay differential equations

Applications in mathematical biology and engineering

Show Related Articles from PubMed

1 Introduction

Analytical methods commonly used to solve nonlinear equations are very restricted and numerical techniques involving discretization of the variables on the other hand gives rise to rounding off errors. Recently introduced variational iteration method by He (2007, 1997a,b, 1998a,b, 1999, 2000), which gives rapidly convergent successive approximations of the exact solution if such a solution exists, has proven successful in deriving analytical solutions of linear and nonlinear differential equations. This method is preferable over numerical methods as it is free from rounding off errors and neither requires large computer power/memory. He (2007, 1997a,b, 1998a,b, 1999, 2000) has applied this method for obtaining analytical solutions of autonomous ordinary differential equation, nonlinear partial differential equations with variable coefficients and integro-differential equations. The variational iteration method was successfully applied to linear and nonlinear problems by researchers (Öziş and Yıldırım, 2007; Yıldırım and Öziş, 2008; Yıldırım, 2008a,b; Momani et al., 2006; Momani and Abuasad, 2006; Tatari and Dehghan, 2007a,b; Wang and He, 2007; Wazwaz, 2007a,b; Xu et al., 2007; Abdou and Soliman, 2005a,b; Abdou, 2007 ).

In the mathematical description of a physical process, one generally assumes that the behavior of the process considered depends only on the present state, an assumption which is verified for a large class of dynamical systems. However, there exist situations where this assumption is not satisfied and the use of a “classical” model in systems analysis and their design may lead to poor performance. In such cases, it is better to consider that the system's behavior includes also information on the former state. These systems are called time-delay systems. Many of the processes, both natural and artificial, in biology, medicine, chemistry, physics, engineering, economics etc involve time delays. In fact, time delays occur so often, in almost every situation, that to ignore them is to ignore reality. A simple example in nature is that of reforestation (Kuang, 1993). A cut forest, after replanting, will take at least 20 years before reaching any kind of maturity. For certain species of trees (redwoods for example) it would be much longer. Hence, any mathematical model of forest harvesting and regeneration clearly must have time delays built into it.

So, while in many applications it is assumed that the system under consideration is governed by a principle of causality, that is, the future state of the system is independent of the past and is determined solely by the present, one should keep in mind that this is only a first approximation to the true situation. A more realistic model must include some of the past history of the system.

1.1

1.1 Applications of delay differential equations

In this section, in order to show the great importance of DDEs, we present some applications of them.

1.1.1

1.1.1 A delayed epidemic model

Mathematical biologist A.J. Lotka investigated, in a series of papers from 1912 on, a differential equation model of malaria epidemics due toRoss (1911). In particular, he examined the effect of incubation delays. The equations are for the human population $\dot{h} t = bgm t - u [p - h t - u] / p - M + rh t,$ and for the mosquito population $\dot{m} t = bfh t - v [q - m t - u] / p - N + sm t .$ Here, u = 0.5 month in humans and v = 0.6 months in mosquitos, p and q are the total human and mosquito populations, treated as constant quantities, which is a standard practice in simple epidemiological models. The functions h(t) and m(t) stand for human and mosquito populations carrying the malaria organism (the infected or diseased population), respectively. A fixed proportion of each of these populations is assumed to be infective, with the infective populations being fh and gm, respectively. The quantities M and N are death rates, while r and s are recovery rates. It is assumed that each mosquito bites b people in unit time, and that each person receives a bites in unit time (Kuang, 1993). The delay is from the time of a bite to the time at which the human or mosquito is infective.

1.1.2

1.1.2 Delay models in physiology: Dynamic diseases

There are many acute physiological diseases where the initial symptoms are manifested by an alteration or irregularity in a control system that is normally periodic, or by the onset of an oscillation in a nonoscillatory process. Such physiological diseases have been termed dynamical diseases by Glass and Mackey (1979), who have made a systematic study of several important and interesting physiological models with time delays. The following are three examples of these models: $\begin{matrix} \dot{x} t = λ - \frac{α V_{m} x {tx}^{N} t - τ}{θ^{n} + x^{n} t - τ}, \\ \dot{p} t = \frac{β_{0} θ^{n}}{θ^{n} + p^{n} t - τ} - γ p t, \\ \dot{p} t = \frac{β_{0} θ^{n} p t - τ}{θ^{n} + p^{n} t - τ} - γ p t . \end{matrix}$ Here, λ, α, V_m, n, τ, θ, β₀ and γ are positive constants. The first equation is used to study a “dynamic disease” involving respiratory disorders, where x(t) denotes the arterial CO₂ concentration of a mammal, λ is the CO₂ production rate, V_m denotes the maximum “ventilation” rate of CO₂, and τ is the time between oxygenation of blood in the lungs and simulation of chemoreceptors in the brainstem. The second and third equations are proposed as models of hematopoiesis (blood cell production). In these two equations, p(t) denotes the density of mature cells in blood circulation, and τ is the time delay between the production of immature cells in the bone marrow and their maturation for release in the circulating bloodstream (Kuang, 1993).

1.1.3

1.1.3 Chemical industry

Consider a first order, exothermic, irreversible reaction: A ↦ B. Since, in practice, the conversion from A to B is not complete, one classical technique uses a recycle stream (which increases overall conversion, reduces costs of the reaction, etc.). In order to recycle, the output must be separated from the input and must flow through some length of pipe. This process does not take place “instantaneously”; it requires some “transport” time from the output to the input, and thus one may consider a system model involving a transport delay. Suppose now that the unreacted A has a recycle flow rate (1 − λ)q and τ is the transport delay. Then the material and energy balances are described by a dynamical system including delayed states of the form $\begin{matrix} \frac{d A t}{d t} = \frac{q}{V} [λ A_{0} + 1 - λ A t - τ - A t] - K_{0} e^{- \frac{Q}{T}} A t, \\ \frac{d T t}{d t} = \frac{1}{V} [λ T_{0} + 1 - λ T t - τ - T t] \frac{Δ H}{C_{ρ}} - K_{0} e^{- \frac{Q}{T}} A t \\ - \frac{1}{{VC}_{ρ}} U T t - T_{w}, \end{matrix}$ where A(t) is the concentration of the component A, T(t) is the temperature and λ is the recycle coefficient, which satisfies the condition λ ∈ [0, 1]. The limits 0 and 1 correspond to no recycle stream and to a complete recycle, respectively (Dugard and Verriest, 1997). In the last 50 years, much researches have been focused on the analysis and numerical solutions of delay differential equations. Recently Shakeri and Dehghan (2008) used homotopy perturbation method successfully for solving delay differential equations.

In this work we focus on the delay differential equation of the following form which contains a large class of the DDEs:

(1.1)

u^{(m)} (t) = \sum_{j = 0}^{J} \sum_{k = 0}^{m - 1} μ_{jk} (t) u^{(k)} (α_{jk} t + β_{jk}) + g (u) + f (t),

with the initial conditions

\sum_{k = 0}^{m - 1} c_{ik} u^{k} (0) = λ_{i}, i = 0, 1, \dots, m - 1,

where

g (u) = bu + \sum_{i = 1}^{l} d_{i} u^{γ_{i}}

d_{i} \in R

γ_{i} \in N

γ_{i} > 1

l \in N

0 ⩽ α_{jk} ⩽ 1

β_{jk} \in R

and .^(m) in u^(m) is considered as the mth derivative of the function u. In order to solve this equation, we use the variational iteration method.

This paper is organized as follows: In Section 2, we describe the variational iteration method briefly and apply this technique to Eq. (1.1). To show the efficiency of this method, we give some examples and numerical results in Section 3. A conclusion is drawn in Section 4.

2 He's variational iteration method

To clarify the basic ideas of He's variational iteration method, we consider the following nonlinear differential equation:

(2.1)

L (u) + N (u) - f (t) = 0, t \in Ω

where L is linear operator, N is a nonlinear operator and f(t) is a known analytical function.

According to the variational iteration method, we can construct a correction functional as follows:

(2.2)

u_{n + 1} (t) = u_{n} (t) + \int_{0}^{t} λ (s) (L (u_{n} (s)) + N ({\tilde{u}}_{n} (s)) - f (s)) d s,

where λ is a general Lagrange multiplier, which can be identified optimally via the variational theory (He, 2007), the subscript n denotes the nth approximation, and

{\tilde{u}}_{n}

is considered as a restricted variation, i.e.,

δ {\tilde{u}}_{n} = 0

It is obvious now that the main steps of the variational iteration method require first the determination of the Lagrangian multiplier λ that will be identified optimally. Having determined the Lagrangian multiplier, the successive approximations u_n+1, n ⩾ 0, of the solution u will be readily obtained upon using any selective function u₀. Consequently, the solution

(2.3)

u = \lim_{n \to \infty} u_{n} .

In order to solve Eq. (1.1) by means of variational iteration method, according to (2.2), we can construct a correction functional such that

(2.4)

u_{n + 1} (t) = u_{n} (t) + \int_{0}^{t} λ (s) (u_{n}^{(m)} (s) - \sum_{j = 0}^{J} \sum_{k = 0}^{m - 1} μ_{jk} (s) {\tilde{u}}_{n}^{(k)} (α_{jk} s + β_{jk}) - g ({\tilde{u}}_{n}) - f (s)) d s,

where

δ {\tilde{u}}_{n}

is considered as restricted variation. Making the correction functional, Eq. (2.4), stationary, noticing that

δ {\tilde{u}}_{n} = 0

\begin{matrix} δ u_{n + 1} (t) = δ u_{n} (t) + δ \int_{0}^{t} λ (s) (u_{n}^{(m)} (s) - \sum_{j = 0}^{J} \sum_{k = 0}^{m - 1} μ_{jk} (s) \\ \times {\tilde{u}}_{n}^{(k)} (α_{jk} s + β_{jk}) - g ({\tilde{u}}_{n}) - f (s)) d s, \\ δ u_{n + 1} (t) = δ u_{n} (t) + δ \int_{0}^{t} λ (s) u_{n}^{(m)} (s) d s, \end{matrix}

Lagrange multiplier can be easily identified as (He, 2007):

(2.5)

λ (s) = (- 1)^{m} \frac{1}{(m - 1)!} (s - t)^{(m - 1)} .

As a result, we obtain the following iteration formula of Eq. (1.1):

(2.6)

u_{n + 1} (t) = u_{n} (t) + (- 1)^{m} \int_{0}^{t} \frac{1}{(m - 1)!} (s - t)^{(m - 1)} (u_{n}^{(m)} (s) - \sum_{j = 0}^{J} \sum_{k = 0}^{m - 1} μ_{jk} (s) u_{n}^{(k)} (α_{jk} s + β_{jk}) - g (u_{n}) - f (s)) d s,

Then starting with an initial approximation u₀ and using above iteration formula, we can obtain u_n for n = 1, 2 , … which is the nth approximation of the exact solution. In the next section, we will implement the above method to obtain numerical results of given examples.

3 Test problems

In this section, we present some examples with known analytical solution in order to show the efficiency and high accuracy of the method described for solving Eq. (1.1).

Example 3.1

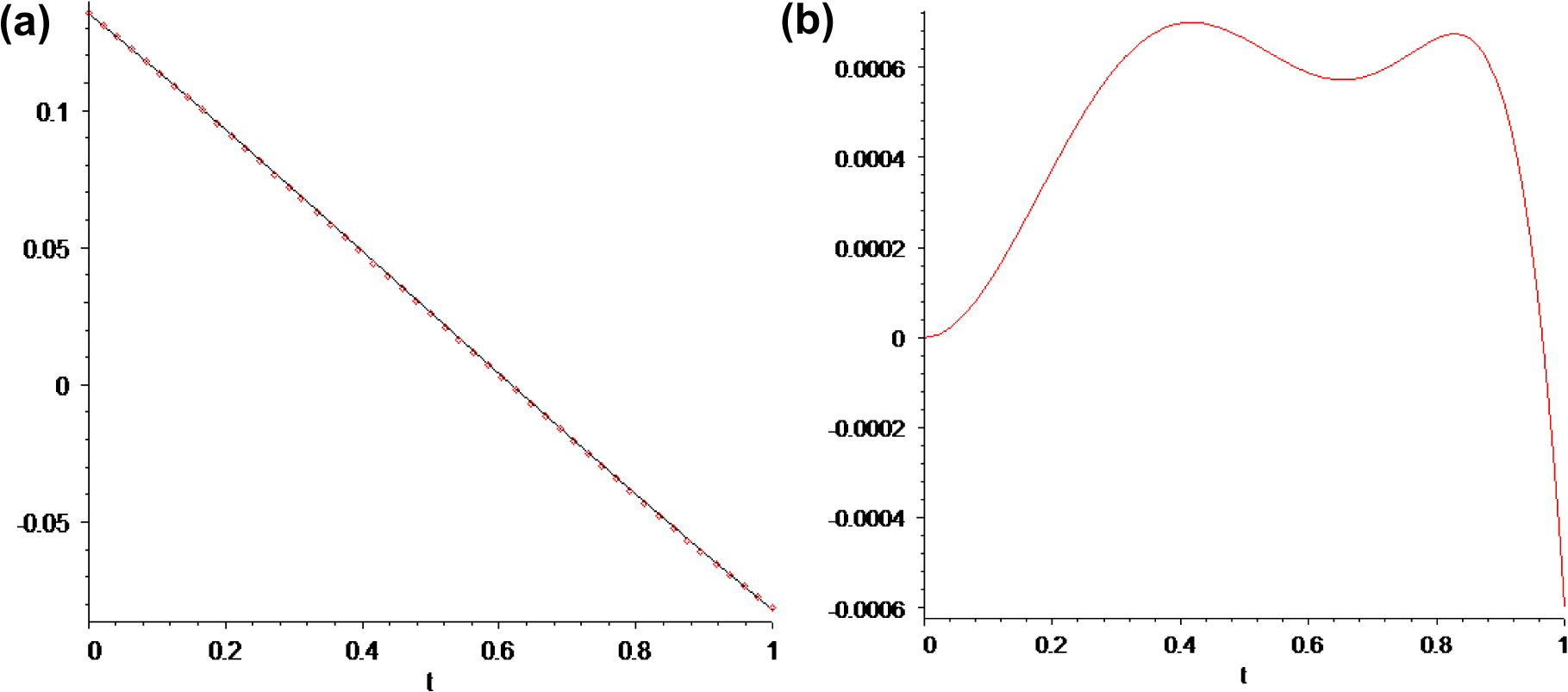
We first consider Eq. (1.1) with m = 1, J = 2 and the following nonzero coefficients μ_jk, α_jk and β_jk (Shakeri and Dehghan, 2008): $\begin{matrix} μ_{00} (t) = - 2 t, μ_{10} (t) = - t^{2}, μ_{20} (t) = 2 \sin (t), \\ α_{00} = 1, α_{10} = 1, α_{20} = \frac{1}{2}, β_{00} = - \frac{1}{2}, g (u) = u^{3} and \\ f (t) = e^{- \frac{t}{2} - 2} (- t^{4} - t^{3} + \frac{3}{2} t^{2} - \frac{3}{2} t - \frac{3}{2}) + 2 {te}^{- \frac{t}{2} - \frac{7}{4}} (- t^{2} + \frac{5}{4}) \\ - e^{- \frac{3 t}{8} - 6} {(- \frac{1}{16} t^{2} - \frac{1}{4} t + 1)}^{3} - 2 \sin (t) e^{- \frac{t}{4} - 2} (- \frac{1}{4} t^{2} - \frac{1}{2} t + 1), \end{matrix}$ with the initial condition u(0) = e⁻². The simple form of the equation which results from the above coefficients is as follows:

(3.1)

u^{(1)} (t) = - 2 tu (t - \frac{1}{2}) - t^{2} u (t) + 2 \sin (t) u (\frac{t}{2}) + u^{3} (\frac{t}{4}) + f (t) .

The exact solution of this problem is

(3.2)

u (t) = 1 - t - t^{2} e^{- \frac{t}{2} - 2} .

In order to solve this equation by means of the variational iteration method, according to (2.6), we have

(3.3)

u_{n + 1} (t) = u_{n} (t) - \int_{0}^{t} (u_{n}^{(1)} (s) + 2 {su}_{n} (s - \frac{1}{2}) + s^{2} u_{n} (s) - 2 \sin (s) u_{n} (\frac{s}{2}) - u_{n}^{3} (\frac{s}{4}) - f (s)) d s .

Beginning with initial approximation u₀(t) = u(0) = e⁻², by the iteration formula (3.3), we obtain the following successive approximations

u_{0} (t) = e^{- 2},

u_{1} (t) = u_{0} (t) - \int_{0}^{t} (u_{0}^{(1)} (s) + 2 {su}_{0} (s - \frac{1}{2}) + s^{2} u_{0} (s) - 2 \sin (s) u_{0} (\frac{s}{2}) - u_{0}^{3} (\frac{s}{4}) - f (s)) d s, = - 182 e^{- \frac{7}{4}} + (t + \frac{40}{27}) e^{- 6} + (- t^{2} - \frac{t^{3}}{3} - 2 \cos t - \frac{4166798}{4913}) e^{- 2} + (- \frac{t^{2}}{6} - \frac{14}{9} t - \frac{40}{27}) e^{- \frac{3}{8} t - 6} + (182 + 91 t + 24 t^{2} + 4 t^{3}) e^{- \frac{t}{2} - \frac{7}{4}} + \dots

and so on, nth approximation can be calculated using (3.3). Getting n = 2, we obtain the second-order approximation, u₂(t). The second-order approximation solution, exact solution (3.2) and error between the second-order approximation solution and exact solution, u_exact(t) − u₂(t) are plotted in Fig. 1.

In the same manner, we obtained the higher-order approximation solution of Eq. (3.1) with high accuracy by using the iteration formula (3.3) and Maple.

Example 3.2

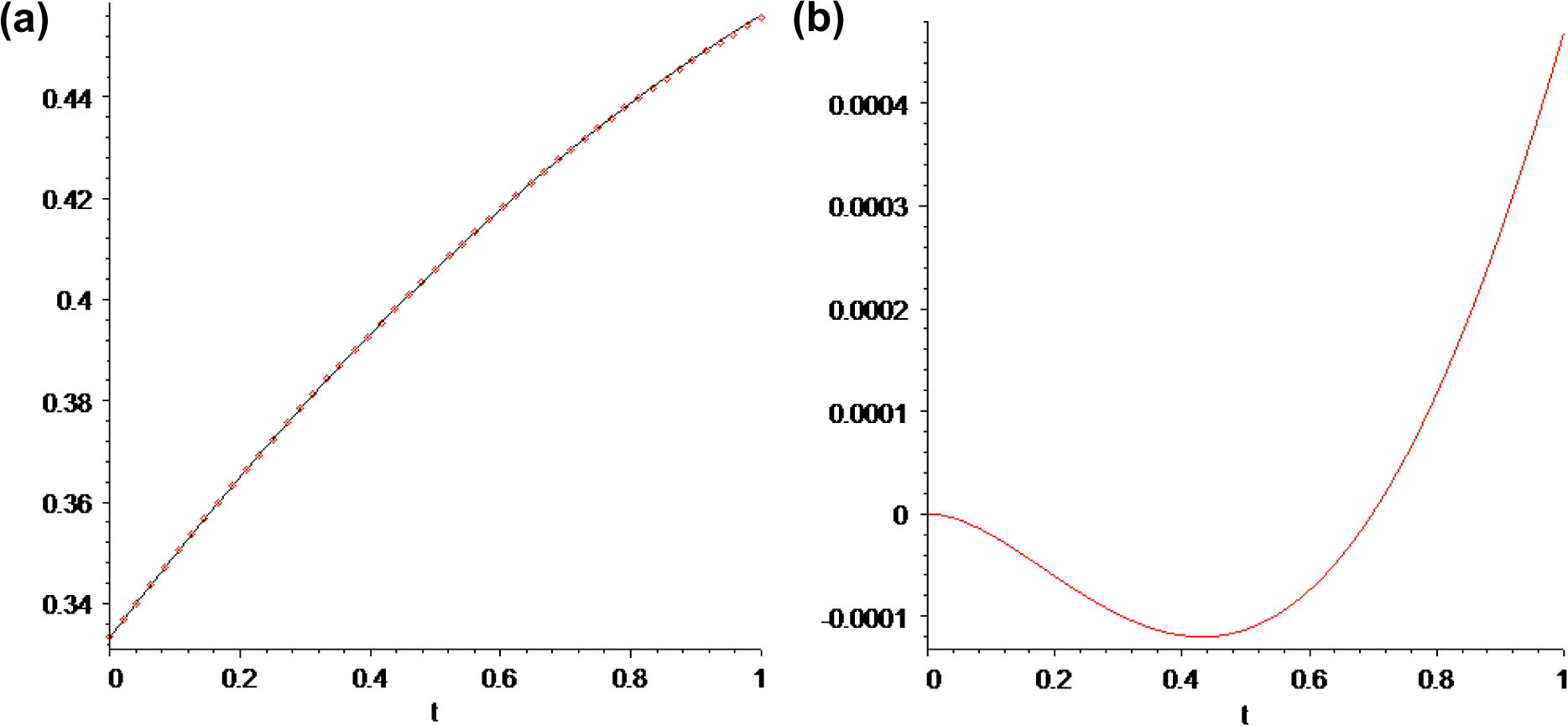
We next consider Eq. (1.1) with m = 2, J = 1 and the following nonzero coefficients μ_jk, α_jk and β_jk (Shakeri and Dehghan, 2008): $\begin{matrix} μ_{00} (t) = t - 1, μ_{01} (t) = e^{- t}, μ_{10} (t) = - 2, \\ α_{00} = 1, α_{01} = 1, α_{10} = \frac{1}{3}, β_{01} = - \frac{1}{5}, g (u) = u^{2} \end{matrix}$ and $f (t) = - \frac{1}{4} \sin^{2} (\frac{t}{3}) - \frac{1}{3} \sin (\frac{t}{3}) \cos (\frac{t}{2}) - \frac{1}{9} \cos^{2} (\frac{t}{2}) + (- \frac{1}{2} \sin (\frac{t}{3}) - \frac{1}{3} \cos (\frac{t}{2})) t + \frac{1}{4} \cos (\frac{t}{2}) - e^{- t} (\frac{1}{6} \cos (\frac{t}{3} - \frac{1}{15}) - \frac{1}{6} \cos (\frac{t}{2} - \frac{1}{10})) + \sin (\frac{t}{9}) + \frac{2}{3} \cos (\frac{t}{6}) + \frac{4}{9} \sin (\frac{t}{3})$ and the nonzero coefficients c_ik and λ_i in the initial conditions are given as $\begin{matrix} c_{00} = 3, c_{01} = 6, c_{10} = - 2, c_{11} = 1, \\ λ_{0} = 2, λ_{1} = - \frac{1}{2} . \end{matrix}$ The above coefficients result in the following problem:

(3.4)

u^{(2)} (t) = e^{- t} u^{(1)} (t - \frac{1}{5}) + (t - 1) u (t) - 2 u (\frac{t}{3}) + u^{2} (t) + f (t),

with initial conditions

(3.5)

\{\begin{matrix} 3 u (0) + 6 u^{(1)} (0) = 2, \\ - 2 u (0) + u^{(1)} (0) = - \frac{1}{2} . \end{matrix}

The exact solution of this problem is

(3.6)

u (t) = \frac{1}{2} \sin (\frac{t}{3}) + \frac{1}{3} \cos (\frac{t}{2}) .

To solve this equation using the variational iteration method, according to (2.6), we have

(3.7)

u_{n + 1} (t) = u_{n} (t) + \int_{0}^{t} (s - t) (u_{n}^{(2)} (s) - e^{- s} u_{n}^{(1)} (s - \frac{1}{5}) - (s - 1) u_{n} (s) + 2 u_{n} (\frac{s}{3}) - u_{n}^{2} (s) - f (s)) d s .

We start with initial approximation u₀(t) = a + bt. Now we find the coefficients a and b such that u₀(t) satisfies the initial conditions (3.5). Then we have the following system

\{\begin{matrix} 3 a + 6 b = 2, \\ - 2 a + b = - \frac{1}{2}, \end{matrix}

which yields

a = \frac{1}{3}, b = \frac{1}{6},

and therefore

u_{0} (t) = \frac{1}{3} + \frac{1}{6} t

Beginning with above initial approximation, by the iteration formula (3.7), we obtain the following successive approximations $u_{0} (t) = \frac{1}{3} + \frac{1}{6} t,$ $u_{1} (t) = u_{0} (t) + \int_{0}^{t} (s - t) (u_{0}^{(2)} (s) - e^{- s} u_{0}^{(1)} (s - \frac{1}{5}) - (s - 1) u_{0} (s) + 2 u_{0} (\frac{s}{3}) - u_{0}^{2} (s) - f (s)) d s = - \frac{463}{288} + \frac{64}{5} t - \frac{77}{144} t^{2} + \frac{1}{36} t^{3} + \frac{7}{432} t^{4} + e^{- t} (\frac{1}{6} + \frac{8}{75} \cos (\frac{t}{2} - \frac{1}{10}) + \frac{2}{25} \sin (\frac{t}{2} - \frac{1}{10}) + \frac{9}{100} \sin (\frac{t}{3} - \frac{1}{15}) - \frac{3}{25} \cos (\frac{t}{3} - \frac{1}{15})) + \dots$ and so on, nth approximation can be calculated using (3.7). Getting n = 2, we obtain the second-order approximation, u₂(t). The second-order approximation solution, exact solution (3.6) and error between the second-order approximation solution and exact solution, u_exact(t) − u₂(t) are plotted in Fig. 2.

In the same manner, we obtained the higher-order approximation solution of Eq. (3.4) with high accuracy by using the iteration formula (3.7) and Maple.

Example 3.3

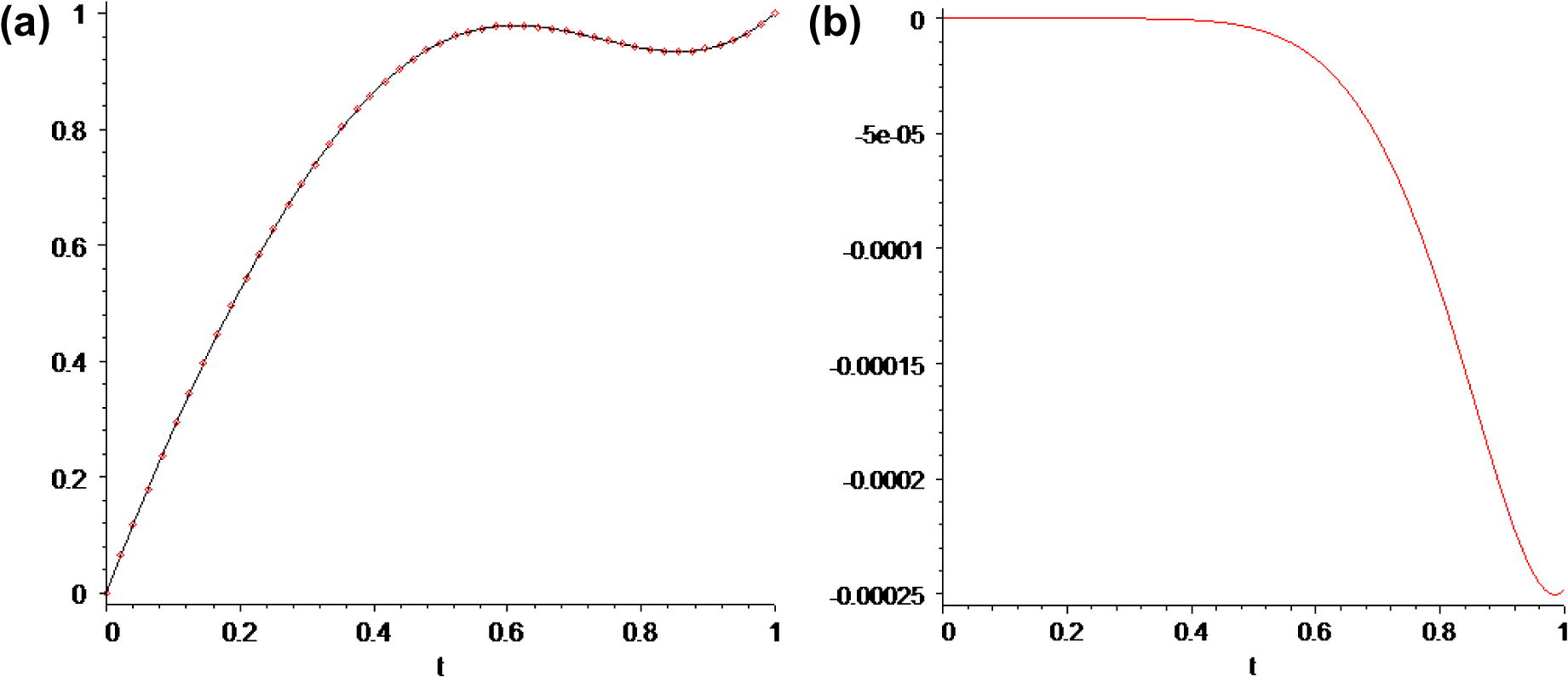
We now consider Eq. (1.1) with m = 3, J = 1 and the following nonzero coefficients μ_jk, α_jk and β_jk (Shakeri and Dehghan, 2008): $\begin{matrix} μ_{01} (t) = 3 e^{t - 1}, μ_{11} (t) = - 2, μ_{02} (t) = \frac{t}{3}, \\ α_{01} = \frac{1}{3}, α_{11} = \frac{1}{2}, α_{02} = 1, \end{matrix}$ and $f (t) = - e^{t - 1} (- \frac{8}{2187} t^{7} + \frac{2}{27} t^{5} + \frac{5}{81} t^{4} - \frac{16}{27} t^{3} + \frac{1}{3} t^{2} - \frac{4}{3} t + 3) + \frac{893}{48} t^{7} - \frac{5847}{16} t^{5} - \frac{305}{48} t^{4} + 374 t^{3} + \frac{235}{4} t^{2} - \frac{290}{3} t + 9,$ and the nonzero coefficients c_ik and λ_i in the initial conditions are given as $\begin{matrix} c_{00} = 1, c_{01} = - 1, c_{02} = - 2, c_{11} = 1, c_{12} = - 1, c_{21} = 2, c_{22} = 3, \\ λ_{0} = 5, λ_{1} = 7, λ_{2} = - 6 . \end{matrix}$ These coefficients result in the following problem:

(3.8)

u^{(3)} (t) = \frac{t}{3} u^{(2)} (t) + 3 e^{t - 1} u^{(1)} (\frac{t}{3}) - 2 u^{(1)} (\frac{t}{2}) + f (t),

with initial conditions

(3.9)

\{\begin{matrix} u (0) - u^{(1)} (0) - 2 u^{(2)} (0) = 5, \\ u^{(1)} (0) - u^{(2)} (0) = 7, \\ 2 u^{(1)} (0) + 3 u^{(2)} (0) = - 6 . \end{matrix}

The exact solution of this problem is

(3.10)

u (t) = 3 t - 2 t^{2} + t^{3} - 4 t^{4} + t^{5} + 3 t^{6} - t^{8} .

To solve this equation using the variational iteration method, according to (2.6), we have

(3.11)

u_{n + 1} (t) = u_{n} (t) - \int_{0}^{t} \frac{1}{2} (s - t)^{2} (u_{n}^{(3)} (s) - \frac{s}{3} u_{n}^{(2)} (s) - 3 e^{s - 1} u_{n}^{(1)} (\frac{s}{3}) + 2 u_{n}^{(1)} (\frac{s}{2}) - f (s)) d s .

We start with initial approximation u₀(t) = a + bt + ct². By the same manipulation as in the previous example, we find the coefficients a, b and c such that u₀(t) satisfies the initial conditions (3.9). In this manner, we will get

a = 0, b = 3, c = - 2,

and therefore u₀(t) = 3t − 2t².

Beginning with above initial approximation, by the iteration formula (3.11), we obtain the following successive approximations $\begin{matrix} u_{0} (t) = 3 t - 2 t^{2}, \\ u_{1} (t) = u_{0} (t) - \int_{0}^{t} \frac{1}{2} (s - t)^{2} (u_{0}^{(3)} (s) - \frac{s}{3} u_{0}^{(2)} (s) - 3 e^{s - 1} u_{0}^{(1)} (\frac{s}{3}) + 2 u_{0}^{(1)} (\frac{s}{2}) - f (s)) d s . \\ = 3 t - 2 t^{2} + t^{3} - 4 t^{4} + \frac{47}{48} t^{5} + \frac{187}{60} t^{6} - \frac{61}{2016} t^{7} - \frac{1949}{1792} t^{8} + \frac{893}{34560} t^{10} \\ + \frac{14548}{27} e^{- 1} - \frac{14548}{27} e^{t - 1} + \dots \end{matrix}$ and so on, nth approximation can be calculated using (3.11). Getting n = 2, we obtain the second-order approximation, u₂(t). The second-order approximation solution, exact solution (3.10) and error between the second-order approximation solution and exact solution, u_exact(t) − u₂(t) are plotted in Fig. 3.

In the same manner, we obtained the higher-order approximation solution of Eq. (3.8) with high accuracy by using the iteration formula (3.11) and Maple.

The results show that the variational iteration method produces highly accurate approximations with only a few iterations.

(a) Line: exact solution (3.2) of Eq. (3.1), point: second-order approximation solution u2(t), (b) error between the second-order approximation solution and exact solution, uexact(t)–u2(t).

(a) Line: exact solution (3.6) of Eq. (3.4), point: second-order approximation solution u2(t), (b) error between the second-order approximation solution and exact solution, uexact(t)–u2(t).

(a) Line: exact solution (3.10) of Eq.(3.8), point: second-order approximation solution u2(t), (b) error between the second-order approximation solution and exact solution, uexact(t)–u2(t).

4 Conclusion

Our study deals with the numerical solution of delay differential equations using variational iteration method. This technique was tested on some examples and was seen to produce satisfactory results. The reliability of the method and the reduction in the size of computational domain give this method a wider applicability. Furthermore this technique, in contrast to the traditional perturbation methods, does not require a small parameter in the system and the approximations obtained by the proposed method are uniformly valid not only for small parameters, but also for very large parameters.

References

Abdou M.A., . On the variational iteration method. Phys. Lett. A. 2007;366:61-68.
[Google Scholar]
Abdou M.A., Soliman A.A., . Variational iteration method for solving Burger's and coupled Burger's equations. J. Comput. Appl. Math.. 2005;181(2):245-251.
[Google Scholar]
Abdou M.A., Soliman A.A., . New applications of variational iteration method. Physica D. 2005;211:1-8.
[Google Scholar]
Dugard L., Verriest E.I., . Stability and control of time-delay systems. In: Lecture Notes in Control and Information Sciences. Vol vol. 228. Springer; 1997.
[Google Scholar]
Glass L., Mackey C., . A simple model for phase locking of biological oscillators. J. Math. Bio.. 1979;7:339-352.
[Google Scholar]
He J.H., . A new approach to nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simulat.. 1997;2(4):230-235.
[Google Scholar]
He J.H., . Variational iteration method for delay differential equations. Commun. Nonlinear Sci. Numer. Simulat.. 1997;2(4):235-236.
[Google Scholar]
He J.H., . Approximate solution of nonlinear differential equations with convolution product non-linearities. Comput. Methods Appl. Mech. Eng.. 1998;167:69-73.
[Google Scholar]
He J.H., . Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng.. 1998;167:57-68.
[Google Scholar]
He J.H., . Variational iteration method – a kind of non-linear analytical technique: some examples. Int. J. Nonlinear Mech.. 1999;34:699-708.
[Google Scholar]
He J.H., . Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput.. 2000;114:115-123.
[Google Scholar]
He J.H., . Variational iteration method – some recent results and new interpretations. J. Comput. Appl. Math.. 2007;207:3-17.
[Google Scholar]
Kuang Y., . Delay Differential Equations with Applications in Population Dynamics. New York: Academic press, Inc; 1993.
Momani S., Abuasad S., . Application of He's variational iteration method to Helmholtz equation. Chaos, Solitons & Fractals. 2006;27(5):1119-1123.
[Google Scholar]
Momani S., Abuasad S., Odibat Z., . Variational iteration method for solving nonlinear boundary value problems. Appl. Math. Comput.. 2006;183:1351-1358.
[Google Scholar]
Öziş T., Yıldırım A., . A study of nonlinear oscillators with u^1/3 force by He's variational iteration method. J. Sound Vib.. 2007;306:372-376.
[Google Scholar]
Ross R., . The Prevention of Malaria. London: Murray; 1911.
Shakeri F., Dehghan M., . Solution of delay differential equations via a homotopy perturbation method. Math. Comput. Modell.. 2008;48:486-498.
[Google Scholar]
Tatari M., Dehghan M., . On the convergence of He's variational iteration method. J. Comput. Appl. Math.. 2007;207:121-128.
[Google Scholar]
Tatari M., Dehghan M., . Solution of problems in calculus of variations via He's variational iteration method. Phys. Lett. A. 2007;362:401-406.
[Google Scholar]
Wang S.Q., He J.H., . Variational iteration method for solving integro-differential equations. Phys. Lett. A. 2007;367:188-191.
[Google Scholar]
Wazwaz A.M., . A comparison between the variational iteration method and Adomian decomposition method. J. Comput. Appl. Math.. 2007;207:129-136.
[Google Scholar]
Wazwaz A.M., . The variational iteration method for exact solutions of Laplace equation. Phys. Lett. A. 2007;363:260-262.
[Google Scholar]
Xu L., He Ji-Huan, Wazwaz Abdul-Majid, . Variational iteration method – reality, potential, and challenges. J. Comput. Appl. Math.. 2007;207:1-2.
[Google Scholar]
Yıldırım A., . Applying He's variational iteration method for solving differential-difference equation. Math. Prob. Eng. 2008 2008:Article ID 869614
[Google Scholar]
Yıldırım A., . Variational iteration method for modified Camassa–Holm and Degasperis–Procesi equations. Commun. Numer. Meth. Eng. 2008
[CrossRef] [Google Scholar]
Yıldırım A., Öziş T., . Solutions of singular IVPs of Lane–Emden type by the variational iteration method. Nonlinear Anal. Ser. A: Theory Method. Appl. 2008
[CrossRef] [Google Scholar]