Kinetics and vaporization of anil in nitrogen atmosphere – Non-isothermal condition

G. Manikandan; J. Jayabharathi; G. Rajarajan; V. Thanikachalam

doi:10.1016/j.jksus.2011.04.002

View/Download PDF

Buy Reprints

PDF

Translate this page into:

ORIGINAL ARTICLE

24 (

); 265-270

doi:

10.1016/j.jksus.2011.04.002

Kinetics and vaporization of anil in nitrogen atmosphere – Non-isothermal condition

G. Manikandan, J. Jayabharathi, G. Rajarajan, V. Thanikachalam^*

Department of Chemistry, Annamalai University, Annamalainagar 608 002, India

*Corresponding author. Tel.: +91 4144 239523; mobile: +91 9488476098 pvta1998@yahoo.co.in (V. Thanikachalam)

Received: 2010-12-13, Accepted: 2011-4-25, Published: 2011-07-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Available online 29 April 2011

Abstract

The thermal vaporization kinetics of Schiff’s base was studied by thermogravimetry (TG) and differential thermal analysis (DTA) techniques using non-isothermal conditions. The kinetic parameters were calculated under model-free (Friedman’s, Kissinger–Akahira–Sunose (KAS) and Flynn–Wall–Ozawa (FWO) methods) and model-fitting (Coats–Redfern, CR) methods. The results of the Friedman’s isoconversional analysis of the TG data suggest that the investigated vaporization process follows a single-step reaction. Based on the obtained results, the mass loss is caused mainly by vaporizations and not by decomposition. The most probable kinetic model for vaporization of the compound is P2 (power law).

Keywords

Schiff’s base

Thermogravimetric analysis

Kinetic parameters

Non-isothermal

Isoconversional

Show Related Articles from PubMed

1 Introduction

Schiff bases are nitrogen donor ligands $(– CH⚌ \ddot{N} –)$ that form complexes by donating an electron pair to a metal atom in the formation of coordination compounds. Schiff bases have found wide applications in the field of coordination chemistry (Sallam, 2006), biological processes (Snatos et al., 2005), several enzymes (Clarkson and Basolo, 1973), microcalorimetry (Li-Xia et al., 2006), cytotoxic (Tarafder et al., 2002), insulin mimetic agents (McNeill et al., 1992), anticonvulsant (Panchagnula et al., 2004), antiproliterative (Vicini et al., 2003), antifungal activities (Pignatello et al., 1974), transport of oxygen in mammalian and other respiratory systems (Singh et al., 2010). Few Schiff’s bases are prepared, characterized and determined the kinetic parameters of chitosan with salicylaldehyde (Guinesi and Cavalheiro, 2006), trans 1,2-cyclohexadiamine with salicylaldehyde (Aranha et al., 2007) and 4-aminoantipyridine with 2-aminophenol (Mohamed et al., 2009). Literature data show that no work has been reported on thermal decomposition of anil at different heating rates (10, 15 and 20 K min⁻¹) under non-isothermal condition in nitrogen atmosphere.

2 Experimental

2.1

2.1 Preparation of anil

Anil was prepared by refluxing equimolar quantities of benzaldehyde and aniline in alcohol for about 1–2 h. The resulting solution was cooled and poured into cold water. The precipitated anil was filtered off, washed with cold ethanol and dried. It was recrystallized from alcohol. The purity of anil was checked by melting point and FT-IR spectrum (m.p. 53 °C, lit. 54 °C), microanalysis; Found %C: 86.10, %H: 6.02, %N: 7.68; Calculated %C: 86.18, %H: 6.07, %N: 7.73.

2.2

2.2 Measurements

Elemental analysis was performed on a Carlo Analyzer at Central Drug Research Institute (CDRI), Lucknow, India. FT-IR spectrum was recorded in a KBr-pellet on an Avatar-330 spectrometer (with resolution 2 cm⁻¹). The simultaneous TGA and DTA curves were obtained with the thermal analysis system model Perkin Elmer TAC 7/DX Thermal Analysis Controller TAC-7. The TG and DTA analyses of anil were carried out under static nitrogen atmosphere (100 mL min⁻¹), in an alumina crucible with sample mass around 10 mg with heating rates of 10, 15 and 20 K min⁻¹ from 308 to 973 K. The kinetic parameters E_a and ln A were calculated using Microsoft® Excel 2007® Software. The sample temperature, which is controlled by a thermocouple, did not exhibit any systematic deviation from the preset linear temperature program.

3 Theoretical background

3.1

3.1 Model fitting method

The integral method (Horowitz and Metzger, 1963) of Coats and Redfern (1964) has been most successfully used for studying the kinetics of dehydration and vaporization of different solid substances (Wendlandt, 1974). The kinetic parameters can be derived from modified Coats and Redfern Eq. (1),

(1)

\ln [\frac{g (α)}{T^{2}}] = \ln (\frac{AR}{β E_{a}}) (1 - \frac{2 RT}{E_{a}}) - \frac{E_{a}}{RT}

where g(α) is an integral form of the conversion function, the expression of which depends on the kinetic model of the occurring reaction. If the correct g(α) function is used, a plot of ln [g(α)/T²] against l/T should give a straight line from which the values of the activation energy, E_a and the pre-exponential factor, A can be calculated.

3.2

3.2 Model free methods

Friedman’s method (Friedman, 1963) is a differential method and was one of the first isoconversional methods. The non-isothermal rate law Eq. (2)

(2)

β \frac{d α}{dT} = {Ae}^{\frac{- E_{a}}{RT}} f (α)

gives

(3)

\ln [β \frac{d α}{dT}] = \ln [A_{α} f (α)] - \frac{E_{a, α}}{{RT}_{α}}

A plot of ln (β dα/dT) versus 1/T at each α gives E_a from the slope of the plot.

In the present study to evaluate the values of the activation energies of thermal vaporization of solid materials, Flynn–Wall–Ozawa equation (Flynn and Wall, 1966; Ozawa, 1965) (Eq. (4))

(4)

\ln β = \ln \frac{0.0048 {AE}_{a}}{g (α) R} - 1.0516 \frac{E_{a}}{RT}

and Kissinger–Akahira–Sunose (KAS) equation (Kissinger, 1957; Akahira and Sunose, 1971) (Eq. (5)) were used.

(5)

\ln (\frac{β}{T^{2}}) = \ln \frac{{AE}_{a}}{g (α) R} - \frac{E_{a}}{RT}

The plots of ln (β dα/dT) versus 1/T (Eq. (3)), ln β versus 1/T (Eq. (4)) and ln (β/T²) versus 1/T (Eq. (5)) have been shown to give the values of apparent activation energies for the vaporization of anil at different α values. According to these equations, the reaction mechanism and shape of g(α) function do not affect the values of the activation energies of the vaporization stage.

3.3

3.3 Thermodynamic parameters

The kinetic parameters, energy of activation and pre-exponential factors are obtained from Kissinger single point (Kissinger, 1957) kinetic method using the Eq. (6).

(6)

\ln (β / T_{m}^{2}) = - E_{a} / {RT}_{m} + \ln (AR / E_{a})

where T_m is temperature that corresponds to the maximum of dα/dT. This ‘model-free’ kinetic method can be applied with a reasonable approximation without being limited to n-order kinetics (Malek, 1989), providing a single E_a value for each reaction step.

Based on the values of activation energy and pre-exponential factors for the vaporization stage, the values of ΔS^≠, ΔH^≠ and ΔG^≠ for the formation of activated complex from the reactants were calculated (Cordes, 1968).

4 Results and discussion

4.1

4.1 TG and DTA curves of vaporization of anil

The TG and DTA curves of vaporization of anil obtained at three heating rates (10, 15 and 20 K min⁻¹) are shown in Fig. 1. The weight loss observed in TG curves on heating the anil from room temperature to 350 °C is associated with the peak of curves. The weight loss is due to complete vaporization of the anil and curves are asymmetric figures and move to high temperature with increase in heating rates (Fig. 1).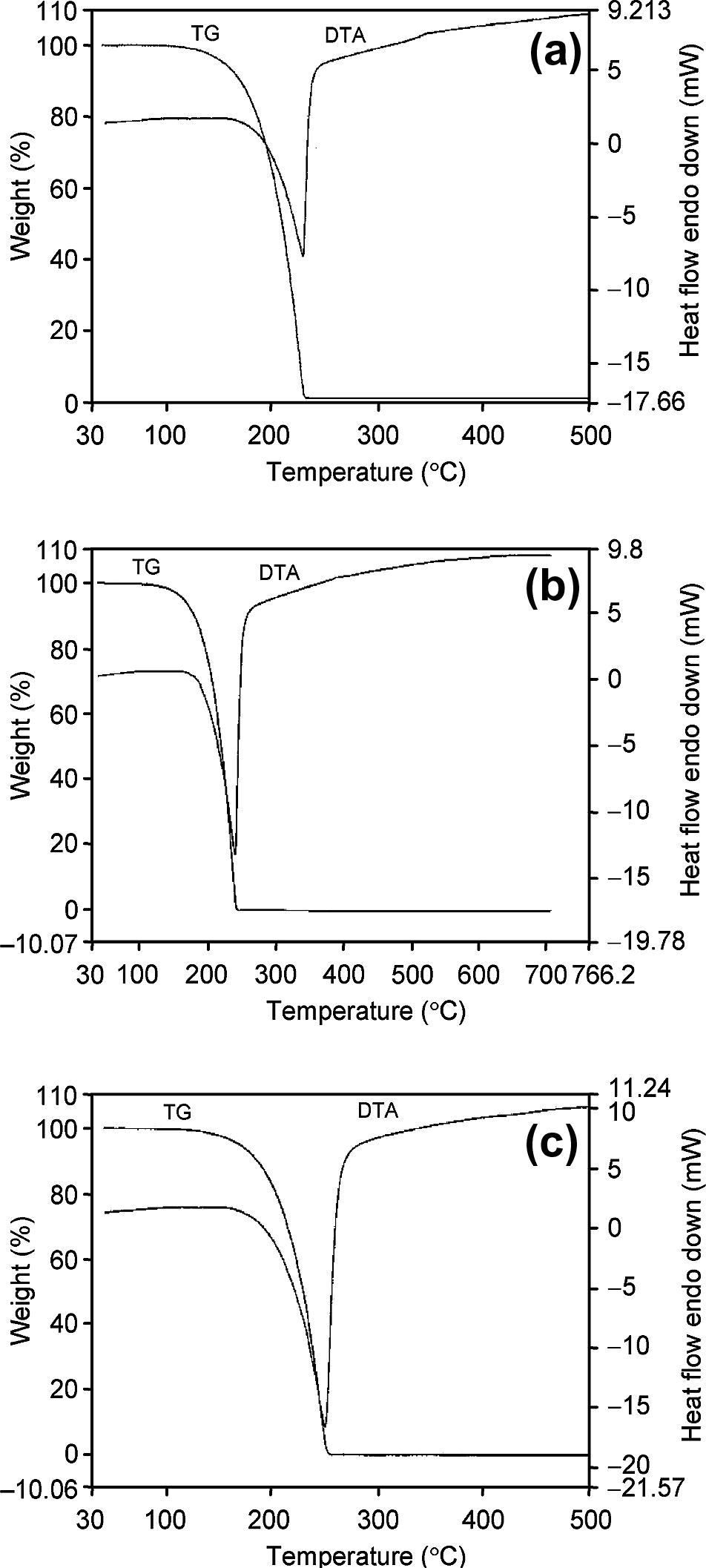

TG and DTA curves of anil at (a) 10 K min−1, (b) 15 K min−1, and (c) 20 K min−1 heating rates in nitrogen atmosphere.

4.2

4.2 Model-free analysis

The non-isothermal vaporization kinetics of anil was first analyzed by model-free methods viz., Friedman, Kissinger–Akahira–Sunose and Flynn–Wall–Ozawa. The data show that the variation of apparent activation energy E_a, as a function of extent of conversion α, for vaporization of anil. E_a value increases slightly in the conversion range of 0.20 ⩽ α ⩽ 0.90. It was pointed out (Vyazovkin and Linert, 1995) that when E_a changes with α, the Friedman and KAS isoconversional methods lead to close value of E_a. The applied isoconversional method does not suggest a direct way for evaluating either the pre-exponential factor (A) or the analytical form of the reaction model (f(α)), for the investigated vaporization process of anil. In addition, the obtained data reveal that the dependence of the apparent activation energy (E_a) on the extent of conversion (α) helps not only to disclose the complexity of vaporization process, but also to identify its sublimation or evaporation mechanism. Similar type of effect is observed in the study of dichloroglyoxime (Pourmortazavi et al., 2007). The value of activation energy E_a changes slightly with α which suggests that the vaporization stage is a single step (Sbirrazzuoli et al., 2005). The average values of E_a energy of vaporization are 26.92 ± 1.90 kJ mol⁻¹ (0.20 ⩽ α ⩽ 0.90, Friedman method). From Fig. 2 it is evident that the values of activation energies obtained by the Friedman method is little lower than the values of activation energies obtained by FWO method and closer to KAS method. Regardless of the calculation procedure used, the activation energy remains practically constant in the 0.20 ⩽ α ⩽ 0.90 range, with average values of E_a = 26.92 ± 1.90, 26.43 ± 0.40 and 33.09 ± 0.59 kJ mol⁻¹ calculated by using the Friedman, KAS and FWO methods, respectively. The observed energy of activation error varied from 1% to 5%, in our case KAS method shows least when compared with Friedman method.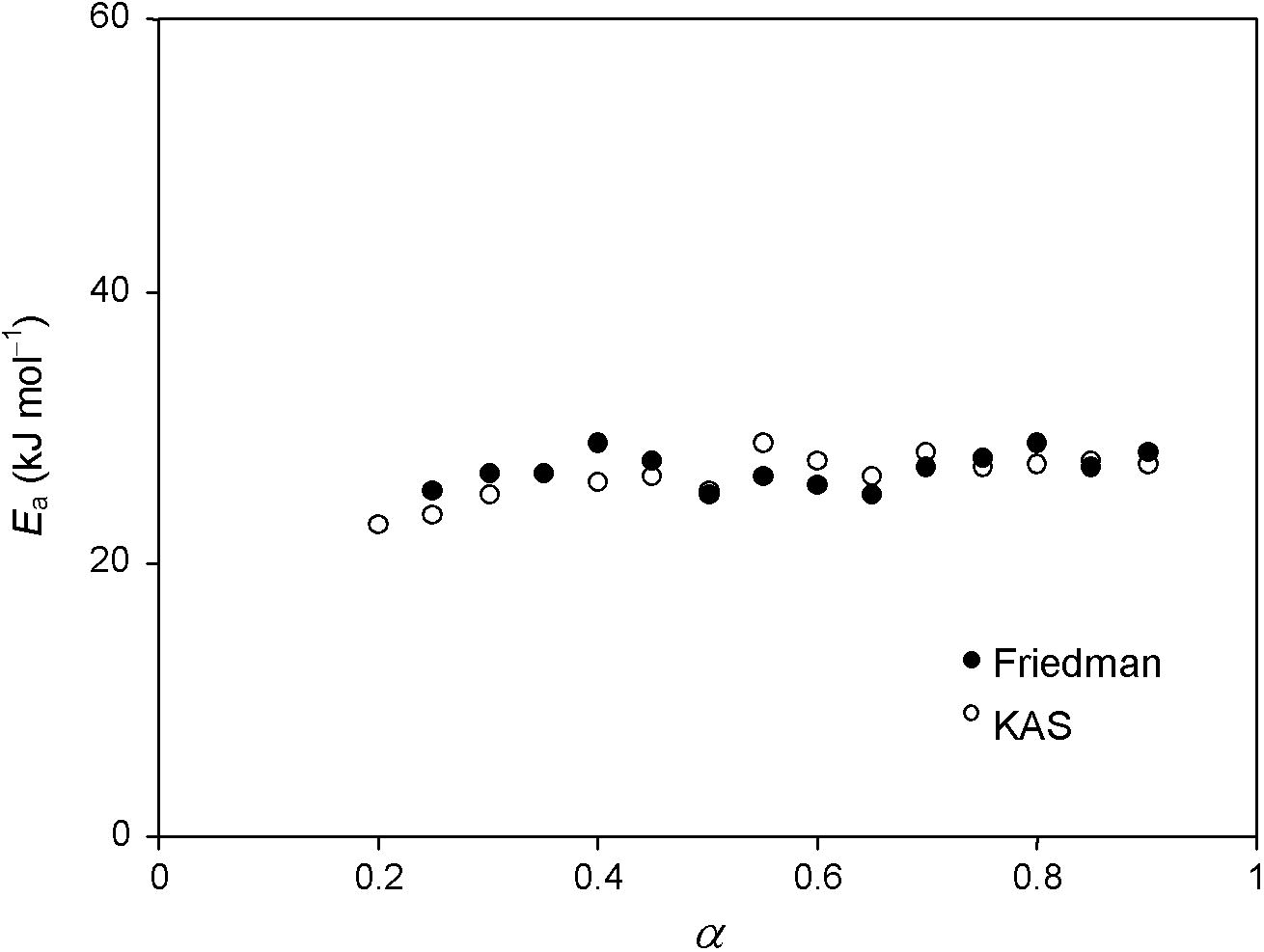

Ea versus α plot for the vaporization of anil under non-isothermal condition.

4.3

4.3 Model-fitting analysis

After model-free analysis is performed, model-fitting can be done in the conversion region where apparent activation energy is approximately constant where a single model may fit. The non-isothermal kinetic data of anil at 0.20 ⩽ α ⩽ 0.90 where model-free analysis indicates approximately constant activation energy, were then fitted to each of the 15 models listed in Table 1. As shown in Table 1, for the applied method (Coats–Redfern), Arrhenius parameters (E_a, ln A) for vaporization or decomposition process, exhibit strong dependence on the reaction model chosen. The values of E_a (mean average values are calculated by Friedman method) for anil coincidence with values are calculated by Coats–Redfern method (E_a and ln A). Based on the kinetic data, it is concluded that the vaporization occurred in a single mechanism (i.e., P2) which is also confirmed by invariant kinetic parameters method.

Table 1 Apparent activation parameters by Coats–Redfern method for each heating rate for anil.

Kinetic model	β = 10 K min⁻¹			β = 15 K min⁻¹			β = 20 K min⁻¹
Kinetic model	E_a (kJ mol⁻¹)	ln A (A s⁻¹)	−r	E_a (kJ mol⁻¹)	ln A (A s⁻¹)	−r	E_a (kJ mol⁻¹)	ln A (A s⁻¹)	−r
P2	28.15	4.74	0.999	32.07	5.75	0.999	32.66	5.89	0.999
P3	16.13	1.30	0.999	18.60	2.13	0.999	18.61	2.31	0.999
P4	10.15	−0.59	0.999	11.91	0.16	0.999	12.07	0.35	0.999
F1	85.34	20.12	0.996	97.75	22.47	0.994	99.59	22.43	0.994
F2	111.78	27.41	0.985	130.98	31.13	0.976	133.39	30.99	0.975
F3	143.09	35.96	0.972	171.18	41.51	0.954	174.27	41.23	0.952
D1	146.55	42.13	1.000	164.24	44.99	0.999	167.62	44.89	0.999
D2	148.64	34.91	0.999	167.57	37.97	0.999	170.91	37.78	0.999
D3	163.38	37.41	0.998	185.28	41.03	0.998	188.91	40.78	0.998
D4	169.13	38.65	0.999	193.40	42.73	0.999	197.20	42.46	0.999
A2	38.75	7.88	0.995	44.74	9.28	0.994	45.54	9.39	0.993
A3	22.91	3.47	0.994	26.73	4.55	0.992	27.17	4.71	0.992
A4	15.45	1.24	0.993	18.24	2.19	0.991	18.51	2.36	0.990
R2	74.10	16.29	0.999	84.11	18.18	0.999	85.73	18.19	0.999
R3	70.78	15.63	0.999	80.16	17.41	0.999	81.71	17.43	0.999

4.4

4.4 Invariant kinetic parameters (IKP) method

Criado and Morales (1976) reported that almost any α = α(T) or (dα/dt) (T) experimental curve may be correctly described by several conversion functions. The use of an integral or differential model-fitting method leads to different values of the activation parameters. Although obtained with high accuracy, the values change with different heating rates and among conversion functions.

Lesnikovich and Levchik (1983) suggested that correlating these values by the apparent compensation effect, ln A = a_β + b_βE_a, one obtains the compensation effect parameters, a_β and b_β, which strongly depend on the heating rates (β) as well as on the considered set of conversion functions. The straight lines ln A versus E_a for three constant heating rates should intersect at a point (isoparametric point (Lesnikovich and Levchik, 1985)) which corresponds to the true values of the activation energy and pre-exponential factor. These were named as invariant kinetic parameters. To establish the best combination (r → 1), a better resolution is determining the invariant kinetic parameters and the closest values to the mean isoconversional activation energies (Budrugeac and Segal, 2007; Vyazovkin and Lesnikovich, 1988). For (all kinetics models) AKM – {P4; F1; F2; F3; D1; D2; D3; D4; R2; R3} has the highest correlation coefficient (r = 0.999) and is a true straight line (Table 2). For these six groups, the invariant activation energy is 26.93 kJ mol⁻¹, which is equal to 26.92 ± 1.90 kJ mol⁻¹ obtained by Friedman method and invariant E_inv = 26.93 ± 0.3 kJ mol⁻¹ and ln A_inv = 4.48 A s⁻¹. Depending on the chosen group of kinetic models, the compensation effect parameters are obtained with different accuracies, their values and derived invariant activation parameters varying substantially.

Table 2 IKP for several combinations of kinetic models for anil.

Kinetic model	E_inv (kJ mol⁻¹)	ln A_inv (A s⁻¹)	−r
AKM	32.71	5.95	1.000
AKM – {D1; D2; D3; D4}	30.15	5.11	0.999
AKM – {F3; D1; D2; D3; D4}	30.74	5.28	0.999
AKM – {P4; F1; F2; F3; D1; D2; D3; D4; R2; R3}	26.93	4.48	0.999
AKM – {P3; P4; D1; D2; D3; D4; R3}	30.24	5.26	0.999
AKM – {P3; P4; F3; D1; D2; D3; D4; R3}	30.96	5.48	0.999

By using Dollimore method (Dollimore et al., 1992), most reliable kinetic model was developed from recreated DTG curves (Fig. S1). The extent of activation energy and pre-exponential factor are calculated from the Arrhenius plot. Table S1 shows the E_a and A values obtained from lines drawn through various ranges of α in order to illustrate the disadvantages of extracting these parameters directly from Arrhenius plot.

Carrying out the vaporization of anil under a dynamic flowing atmosphere of nitrogen, and using a heating rate of 10 K min⁻¹ gave α_max equal to 0.62 and half-width of 59 °C. Referring to Table S2, the data show two possible mechanisms having a α_max range comparable to the experimentally determined value. Thus the P2 equation is possible with magnitude of the half-width making the power law mechanism most suitable. Table S2 shows the reconstructed α_max and half-width values as function of the kinetically related Arrhenius parameters obtained for the vaporization of anil, using the P2 mechanism.

The most probable kinetic model for vaporization process of anil is therefore P2 model. By introducing the derived reaction model g(α) = (α)^1/2, the following Eq. (7) is obtained:

(7)

{(α)}^{1 / 2} = \frac{{AE}_{a}}{R β} p (x)

The plot of (α)^1/2 against (E_a/Rβ)p(x) at the different heating rates is constructed in Fig. 3. By using the above equation, the A value was determined from the slope of the fitted line shown in Fig. 3. For power law model (P2) and E_a = 26.92 ± 0.34 kJ mol⁻¹, the pre-exponential (frequency) factor was found to be A = 1.21 × 10² s⁻¹ (ln A = 4.80). The obtained value of ln A is in good agreement with average value of Friedman isoconversional intercept (ln [Af(α)] = 5.14).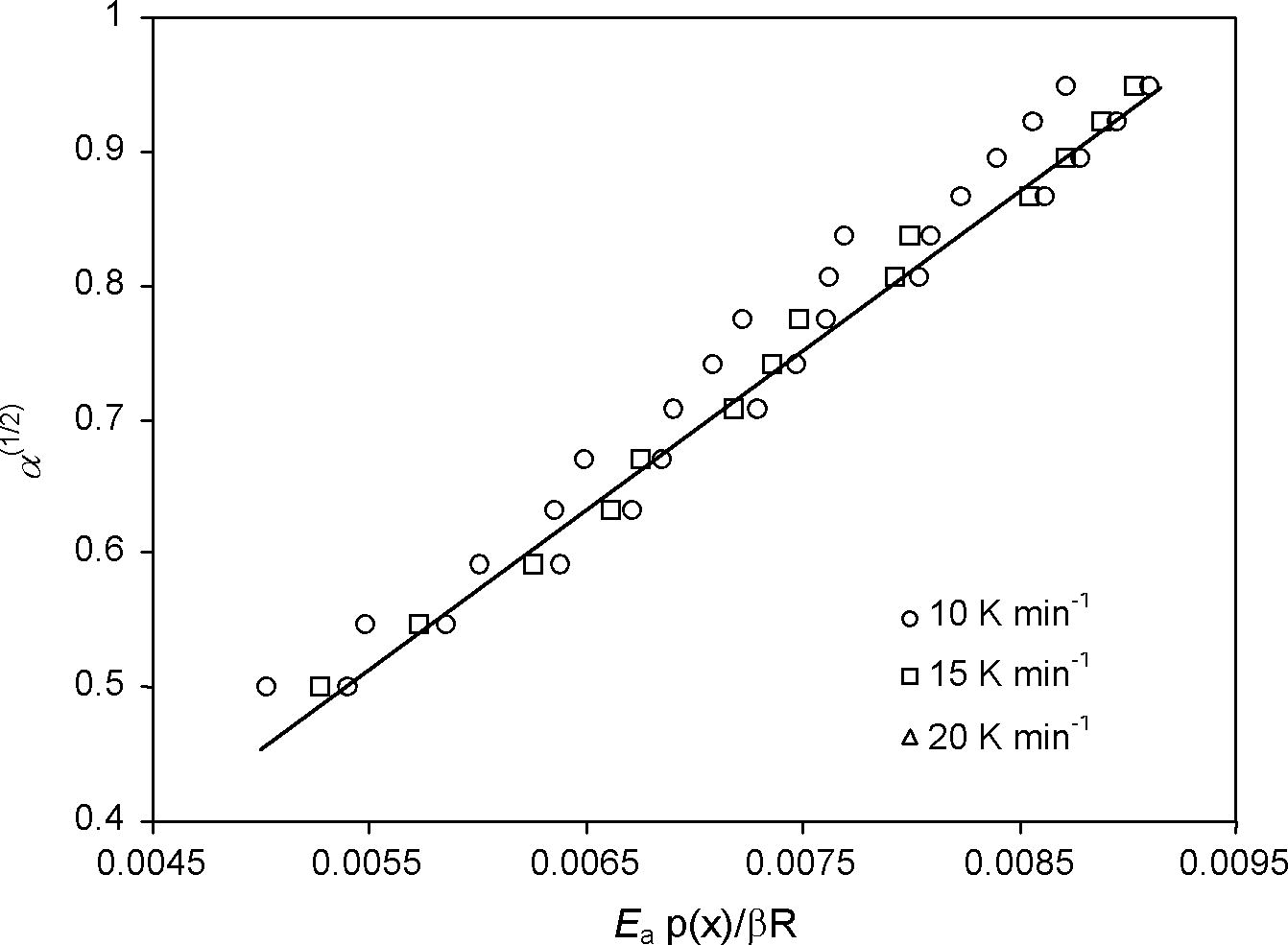

Determination of A value by plotting α(1/2) against Ea p(x)/β R for the vaporization process of anil at the different heating rates (β).

For the non-isothermal decomposition of anil, model P2 is the best for all three heating rates. Model P2 gives raise to an activation energy that varies in the range of 28.15–32.66 kJ mol⁻¹. Fitting of the reaction-order model followed by statistical analysis resulted in the following confidence limits −1.0 ⩽ n < 0.6, 26.92 ⩽ E_a ⩽ 50 kJ mol⁻¹ and 4.8 ⩽ log A/min⁻¹ ⩽ 8. The kinetic triplet corresponding to the minimum (r = −0.999) is n = 0.33, E_a = 26.92 kJ mol⁻¹ and ln |A| min⁻¹ = 4.8. According to the statistical test (Vyazovkin and Wight, 1999) this kinetic triplet is equivalent to the triplet corresponding to model P2.

4.5

4.5 Thermodynamic parameters

From the DTA curves, the peak temperatures for anil are 503.04, 514.09 and 522.49 K and used to evaluate single point kinetic parameters (Kissinger, 1957).

The energy of activation for anil is less. Free energy of activation (ΔG^#) is more positive, which indicates that vaporization of anil is non spontaneous in nature. The lower value of energy of activation, shows that anil is thermally less stable. The positive values of ΔH^≠ and ΔG^≠ for anil show that they are connected with absorption of heat and they are non-spontaneous processes (Criado et al., 2005). The obtained E_a value is coincided with invariant kinetic parameter.

Based on the obtained results, the kinetic description of mass loss can be accomplished through one mechanism (P2). The low values of apparent activation energy attributed to phase transformation may occur. So the loss in this stage should be caused mainly by vaporizations and not by decomposition. It is confirmed by TG and DTA curves.

5 Conclusion

The studied compound is vaporized in a single stage with absorption of heat. The model for the vaporization mechanism is P2. The thermal stability of anil is less and the energy of activation also less. Free energy is positive which indicates that the vaporization is non-spontaneous process.

Acknowledgments

The authors thank Prof. L.D. Prabhakar, Chemistry Wing (DDE), Annamalai University, Annamalainagar, India, for his fruitful suggestions and The Head, Indian Institute of Technology, RISC, Chennai for TGA-DTA studies.

References

Akahira T., Sunose T., . Joint convention of four electrical institutes. Res. Report CHIBA Inst. Technol.. 1971;16:22-31.
[Google Scholar]
Aranha P.E., Souza J.M., Romera S., Ramos L.A., Santos M.P., Dockal E.R., Cavalheiro E.T.G., . Thermal behaviour of vanadyl complexes with Schiff bases derived from trans-N,N-bis(salicylidene)-1,2-cyclohexadiamine(t-salcn) Thermochim. Acta. 2007;453:9-13.
[Google Scholar]
Budrugeac C.P., Segal E., . Applicability of the Kissinger equation in thermal analysis revisited. J. Therm. Anal. Calorim.. 2007;88:703-707.
[Google Scholar]
Clarkson S.G., Basolo F., . Reaction of some cobalt nitrosyl complexes with oxygen. Inorg. Chem.. 1973;12:1528-1534.
[Google Scholar]
Coats A.W., Redfern J.P., . Kinetic parameters for thermogravimetric data. Nature (London). 1964;201:68-69.
[Google Scholar]
Cordes H.F., . Preexponential factors for solid-state thermal decomposition. J. Phys. Chem.. 1968;72:2185-2189.
[Google Scholar]
Criado J.M., Morales J., . Defects of thermogravimetric analysis for discerning between first-order reactions and those taking place through the Avrami-Erofeev’s mechanism. Thermochim. Acta. 1976;16:382-387.
[Google Scholar]
Criado J.M., Perez-Maqueda L.A., Sanchez-Jimenez P.E., . Dependence of the preexponential factor on temperature errors in the activation energies calculated by assuming that A is constant. J. Therm. Anal. Calorim.. 2005;82:671-675.
[Google Scholar]
Dollimore D., Evans T.A., Lee Y.F., Wilburn F.W., . Correlation between the shape of a TG/DTG curve and the form of the kinetic mechanism which is applying. Thermochim. Acta. 1992;198:249-257.
[Google Scholar]
Flynn J.H., Wall L.A., . General treatment of the thermogravimetric of polymers. J. Res. Natl. Bur. Stand. A. 1966;70:487-523.
[Google Scholar]
Friedman H.L., . Kinetics of thermal degradation of char-foaming plastics from thermogravimetry-application to a phenolic resin. Polym. Sci. C. 1963;6:183-195.
[Google Scholar]
Guinesi L.S., Cavalheiro E.T.G., . Influence of the degree of substitution in biopolymeric Schiff bases on the kinetic of thermal decomposition by non-isothermal procedure. Thermochim. Acta. 2006;449:1-7.
[Google Scholar]
Horowitz H.H., Metzger G., . A new analysis of thermogravimetric traces. Anal. Chem.. 1963;35:1464-1468.
[Google Scholar]
Kissinger H.E., . Reaction kinetics in differential thermal analysis. Anal. Chem.. 1957;29:1702-1706.
[Google Scholar]
Lesnikovich A.I., Levchik S.V., . A method of finding invariant values of kinetic parameters. J. Therm. Anal. Calorim.. 1983;27:89-93.
[Google Scholar]
Lesnikovich A.I., Levchik S.V., . Isoparametric kinetic relations for chemical transformations in condensed substances (analytical survey). I. Theoretical fundamentals. J. Therm. Anal. Calorim.. 1985;30:237-262.
[Google Scholar]
Li-Xia Z., Yi L., Li-Hua C., Yan-Jun H., Jun Y., Pei-Zhi H., . Inhibitory of some novel Schiff base derivatives on Staphylococcus aureus by microcalorimetry. Thermochim. Acta. 2006;440:51-56.
[Google Scholar]
Malek J., . A computer program for kinetic analysis of non-isothermal thermoanalytical data. Thermochim. Acta. 1989;136:337-346.
[Google Scholar]
McNeill J.H., Yuen V.G., Hoveyda H.R., Orvig C., . Bis(maltolato)oxovanadium(IV) is a potent insulin mimic. J. Med. Chem.. 1992;35:1489-1491.
[Google Scholar]
Mohamed G.G., Omar M.M., Ibrahim A.A., . Biological activity studies on metal complexes of novel tridentate Schiff base ligand. Spectroscopic and thermal characterization. Eur. J. Med. Chem.. 2009;44:4801-4812.
[Google Scholar]
Ozawa T., . A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn.. 1965;38:1881-1886.
[Google Scholar]
Panchagnula R., Sharma P., Kandavilli S., Varma M.V.S., . RP-HPLC method and its validation for the determination of naloxone from a novel transdermal formulation. IL Farmaco. 2004;59:839-842.
[Google Scholar]
Pignatello R., Panico A., Mazzone P., Pinizzotto M.R., Garozzo A., Fumeri P.M., . Schiff bases of N-hydroxy-N′-aminoguanidines as antiviral, antibacterial and anticancer agents. Eur. J. Med. Chem.. 1974;29:781-785.
[Google Scholar]
Pourmortazavi S.M., Kohsari I., Teimouri M.B., Haji Mirsadeghi S.S., . Thermal behaviour kinetic study of dihydroglyoxime and dichloroglyoxime. Mater. Lett.. 2007;61:4670-4673.
[Google Scholar]
Sallam S.A., . Binuclear copper(II), nickel(II) and cobalt(II) complexes with N₂O₂ chromophores of glycylglycine Schiff-bases of acetyl acetone, benzoylacetone and thenoyltrifluoroacetone. Transit. Met. Chem.. 2006;31:46-55.
[Google Scholar]
Sbirrazzuoli N., Vecchio S., Catalani A., . Isoconversional kinetic study of alachlor and metolachlor vaporization by thermal analysis. Int. J. Chem. Kinet.. 2005;37:74-80.
[Google Scholar]
Singh B.K., Prakash A., Rajouir H.K., Bhojak N., Adhikari D., . Spectroscopic characterization and biological activity of Zn(II), Cd(II), Sn(II) and Pb(II) complexes with Schiff base derived from pyrrole-2-carboxaldehyde and 2-amino phenol. Spectrochim. Acta A. 2010;76:376-383.
[Google Scholar]
Snatos J.E., Dockal E.R., Cavalheiro E.T.G., . Thermal behaviour of Schiff bases from chitosan. J. Therm. Anal. Calorim.. 2005;79:243-248.
[Google Scholar]
Tarafder M.T.H., Kasbollah A., Saravanan N., Crouse K.A., Ali A.M., Tin OoK., . S-Methyldithiocarbazate and its Schiff bases: evaluation of bondings and biological properties. J. Biochem. Mol. Biol. Biophys.. 2002;6:85-91.
[Google Scholar]
Vicini P., Geronikaki A., Incerti M., Busonera B., Poni G., Cabras C.A., Colla P.L., . Synthesis and biological evaluation of benzo[d]isothiazole, benzothiazole and thiazole Schiff bases. Bioorg. Med. Chem.. 2003;11:4785-4789.
[Google Scholar]
Vyazovkin S.V., Lesnikovich A.I., . Estimation of the pre-exponential factor in the isoconversional calculation of effective kinetic parameters. Thermochim. Acta. 1988;128:297-300.
[Google Scholar]
Vyazovkin S., Linert W., . False isokinetic relationships found in the nonisothermal decomposition of solids. Chem. Phys.. 1995;193:109-118.
[Google Scholar]
Vyazovkin S., Wight C.A., . Model-free and model-fitting approaches to kinetic analysis of isothermal and non-isothermal data. Thermochim. Acta 1999:53-68.
[Google Scholar]
Wendlandt W.W., . Thermal Methods of Analysis. New York: John Wiley and Sons Inc.; 1974.