Translate this page into:
The Nyström method for hybrid fuzzy differential equation IVPs
*Corresponding author. Tel.: +98 5251253 omidsfard@gmail.com (Omid Solaymani Fard)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Available online 21 July 2010
Peer-review under responsibility of King Saud University.
Abstract
In this paper, the Nyström method is developed to approximate the solutions for hybrid fuzzy differential equation initial value problems (IVPs) using the Seikkala derivative. A proof of convergence of this method is also discussed in detail. The accuracy and efficiency of the proposed method are demonstrated by applying it to two different numerical experiments.
Keywords
Hybrid systems
Fuzzy differential equations
Fuzzy interpolation
Fuzzy polynomials
Seikkala derivative
Nyström method
1 Introduction
Fuzzy differential equation (FDE) models play a prominent role in a range of application areas, including papulation models (Guo and Li, 2003; Guo et al., 2003), civil engineering (Oberguggenberger and Pittschmann, 1999), particle systems (El Naschie, 2004a,b, 2005), medicine (Abbod et al., 2001; Barro and Marn, 2002; Helgason and Jobe, 1998; Nieto and Torres, 2003), bioinformatics and computational biology (Bandyopadhyay, 2005; Casasnovas and Rossell, 2005; Chang and Halgamuge, 2002). Particularly, the use of hybrid fuzzy differential equations (HFDEs) is a natural way to model control systems with embedded uncertainty (containing fuzzy valued functions) that are capable of controlling complex systems which have discrete event dynamics as well as continuous time dynamics.
In recent years, many works have been performed by several authors in numerical solutions of fuzzy differential equations (Fard, 2009a,b; Fard et al., 2009, 2010; Fard and Kamyad, 2010; Friedman et al., 1999; Hullermeier, 1999). Furthermore, there are some numerical techniques to solve hybrid fuzzy differential equations, for example, Pederson and Sambandham (2007, 2008) have investigated the numerical solution of HFDEs by using the Euler and Runge–Kutta methods, respectively, and Prakash and Kalaiselvi (2009) have studied the predictor–corrector method for hybrid fuzzy differential equations.
In this study, we develop numerical methods for hybrid fuzzy differential equations by an application of the Nyström method (Khastan and Ivaz, 2009). This paper is organized as follows: in Section 2, we provide some background on ordinary differential equations, fuzzy numbers and fuzzy differential equations. Section 3 contains a brief review of the hybrid fuzzy differential equation IVPs. In Sections 4 and 5, the Nyström method for hybrid fuzzy differential equations, a convergence theorem are discussed. Finally in Section 6, we present two numerical examples based on examples in Pederson and Sambandham (2007, 2008) to illustrate the theory.
2 Preliminaries
2.1 Notations and definitions
[Khastan and Ivaz (2009)] Consider the initial value problem
When , the method is known as explicit, since Eq. (2) gives explicit in terms of previously determined values. Also, when , the method is known as implicit, since occurs on both sides of Eq. (2) and is specified only implicitly.
A especial case of multistep method is Nyström's methods (Henrici, 1962). Here, we set
(Henrici, 1962) Associated with the difference equation the following, called the characteristic polynomial of the method is
If for each and all roots with absolute value 1 are simple roots, then the difference method is side to satisfy the root condition.
A multistep method of the form (2) is stable if and only if satisfies the root condition.
See Isaacson and Keller (1966). □
A fuzzy number u is a fuzzy subset of the real line with a normal, convex and upper semicontinuous membership function of bounded support. The family of fuzzy numbers will be denoted by E. An arbitrary fuzzy number is represented by an ordered pair of functions that, satisfies the following requirements:
-
–
is a bounded left continuous nondecreasing function over , with respect to any .
-
–
is a bounded left continuous nonincreasing function over , with respect to any .
-
–
.
Then, the -level set is a closed bounded interval, denoted
A triangular fuzzy number is a fuzzy set u in E that is characterized by an ordered triple with such that and .
The
-level set of a triangular fuzzy number u is given by
Definition 2.6 Dubois and Prade, 2000
Let two nonempty bounded subsets of . The Hausdorff distance between A and B is
The supremum metric D on E is as follows:
With the supremum metric, the space is a complete metric space.
Definition 2.7 Dubois and Prade, 2000
A fuzzy set-valued mapping is continuous at if for every there exists a such that , for all with .
Definition 2.8 Dubois and Prade, 2000
A mapping is Hukuhara differentiable at if for some , the Hukuhara differences and exist in E, for all and if there exists an such that and
The fuzzy set is called the Hukuhara derivative of F at .
Definition 2.9 Dubois and Prade, 2000
The fuzzy integral is defined by provided the Lebesgue integrals on the right exist.
Remar 2.10 Kaleva, 1987
If is Hukuhara differentiable and its Hukuhara derivative is integrable over then for all values of where .
Definition 2.11 Seikkala, 1987
Let I be a real interval. A mapping is called a fuzzy process, and its -level set is denoted by
The Seikkala derivative of a fuzzy process y is defined by provided the is equation defines a fuzzy number .
Remar 2.12 Seikkala, 1987
If is Seikkala differentiable and its Seikkala derivative is integrable over , then for all values of where .
2.2 Interpolation of fuzzy number
The problem of interpolation for fuzzy sets is as follows:
Suppose that at various time instant t information is presented as fuzzy set. The aim is to approximate the function , for all t in the domain of f. Let be distinct points in R and let be fuzzy sets in E. A fuzzy polynomial interpolation of the data is a fuzzy-value continuous function satisfying:
-
.
-
If the data is crisp, then the interpolation f is a crisp polynomial.
The interpolation polynomial can be written level setwise as when the data presents as triangular fuzzy numbers, values of the interpolation polynomial are also triangular fuzzy numbers. Then has a particular simple form that is well suited to computation.
Let be the observed data and suppose that each of is a element of E. Then for each , , where .
See Kaleva (1994). □
3 The hybrid fuzzy differential system
Consider the hybrid fuzzy differential system
Here, we assume that the existence and uniqueness of solution of the hybrid system hold on each to be specific the system would look like:
By the solution of (5) we mean the following function:
We note that the solutions of (5) are piecewise differentiable in each interval for for a fixed and .
4 Nyström methods
In this section, for a hybrid fuzzy differential equation (5), we develop the Nyström method via an application of the Nyström method for fuzzy differential equations in (Khastan and Ivaz, 2009) when f and in Eq. (5) can obtained via the Zadeh extension principle form and . We assume that the existence and uniqueness of solutions of Eq. (5) hold for each .
For a fixed r, we replace each interval by a set of discrete equally spaced grid points, (including the endpoints) at which the exact solution is approximated by some .
Fix
. The fuzzy initial value problem
Let fuzzy initial values be
, i.e.,
, which are triangular fuzzy numbers are shown by
also
By fuzzy interpolation, we have:
Regarding to the sign of
in the integrating interval
we have from Eq. (7)
The sign of depends on q that is even or odd. We suppose q is even. Also for the q is odd, we can proceed similarly.
For , by definition of , we can write: and for :
Thus, for
, we have:
From (4) to (7) it follows that:
where
According to Eq. (11), if (12), (13), (15), (16) are situated in (18) and (13), (14), (16) and (17) in (19), we obtain
If we define
and
, thus from (4) we have
Therefore, Nyström method is obtained as follows:
Worthy of note is the especial case
. Here
and (22) becomes
This is the so-called Midpoint rule.
5 Convergence
By Theorem 5.2 in Kaleva (1987), we may replace (5) by an equivalent system:
For a fixed r, to integrate the system in (25) in
, we replace each interval by a set of
discrete equally spaced grid points (including the end points) at which the exact solution
is approximated by some
. For the chosen grid points on
at
,
, let
.
and
may be denoted respectively by
and
. For example, the Midpoint rule approximations
and
, Eq. (23), can be written as:
However, (26) we will use and if . Then (26) represents an approximation of , for each of the intervals .
For a prefixed k and , the proof of convergence of the approximations in (22), i.e. is a application of Theorem 4.2. in Khastan and Ivaz (2009) and Lemma 5.1 below. The convergence is pointwise in r for a fixed k.
In the following, we show the convergence of the Midpoint rule, i.e., the Nyström method with . For the other values of q, the proof can be done similarly.
Suppose
,
,
, and
are fixed. Let
be the Midpoint approximation with
to the fuzzy IVP:
Fix
,
,
, and
. Let
be the Nyström approximation with
to the fuzzy IVP (27). Suppose
denotes the result of (26) from some
. By (26), for each
,
Let
. Since
and
are continuous, there exists a
such that
and
imply
Let
. If
and
then by (28) and (29) with
and (2) and (31) we have
Continue inductively for each
as follows. Since
and
are continuous, there exists a
such that
and
imply
Let
. If
and
then by (28) and (29) with
and (34) and (35) we have
Then, for we see and imply
For we see and imply
Continue decreasing to to see and imply
But it was already shown in (32) and (33) that and imply
This proves the lemma with . □
Consider the systems (24) and (26). For a fixed
and
Fix and Choose . For each we will find a such that implies where the values are allowable by regular partition of the ’s. By Theorem 4.2. in Khastan and Ivaz (2009), there exists a such that if then
We may assume
. Then
. By Lemma 5.1 there exists a
such that
Therefore if
and (40) holds then
By Theorem 4.2. in Khastan and Ivaz (2009), there exists a such that if then
We may assume
. Then
. By Lemma 5.1 there exists a
such that
Therefore if
and (43) holds then
Continue inductively for each to find a such that if then
We may assume each
. Then each
. By Lemma 5.1 there exists a
such that
Therefore if and (46) holds then
In particular, there exists a such that if and (46) holds with then
By Theorem 4.2. in Khastan and Ivaz (2009), we may choose
such that
implies
Suppose for each that . Since (48) is the same as (46) with we obtain (47) with . Since (47) with implies (46) with , we obtain (47) with . Continue inductively to obtain (40) and (41), proving (38) and (39). □
6 Numerical illustration
To give a clear overview of our study and to illustrate the above discussed technique, we consider the following examples.
Consider the following hybrid fuzzy IVP,
For the which define as if and if . The hybrid fuzzy initial value problem (49) is equivalent to the following system of fuzzy initial value problems:
In (49),
is a continuous function of
and
. Therefore by Example 6.1 of Kaleva (1987), for each
the fuzzy IVP
For , the exact solution of (49) satisfies
For , the exact solution of (49) satisfies
The comparison between the exact and numerical solutions on is shown in Fig. 1.
Consider the following hybrid fuzzy IVP,
The hybrid fuzzy initial value problem (53) is equivalent to the following system:
For [0, 1], the exact solution of Eq. (53) satisfies
For [1, 2], the exact solution of Eq. (53) satisfies,
The comparison between the exact and numerical solutions on is shown in Fig. 2.
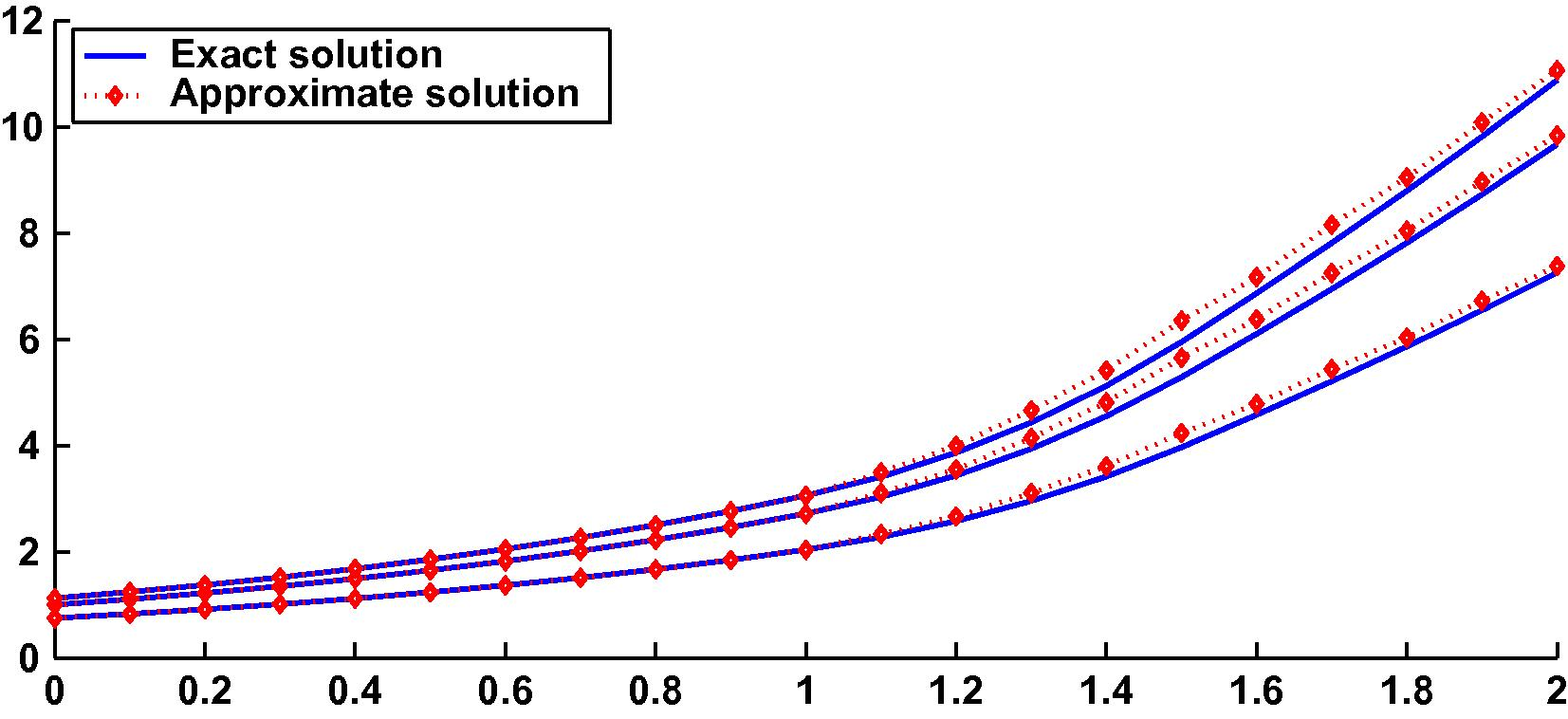
- The results of Example 6.1.
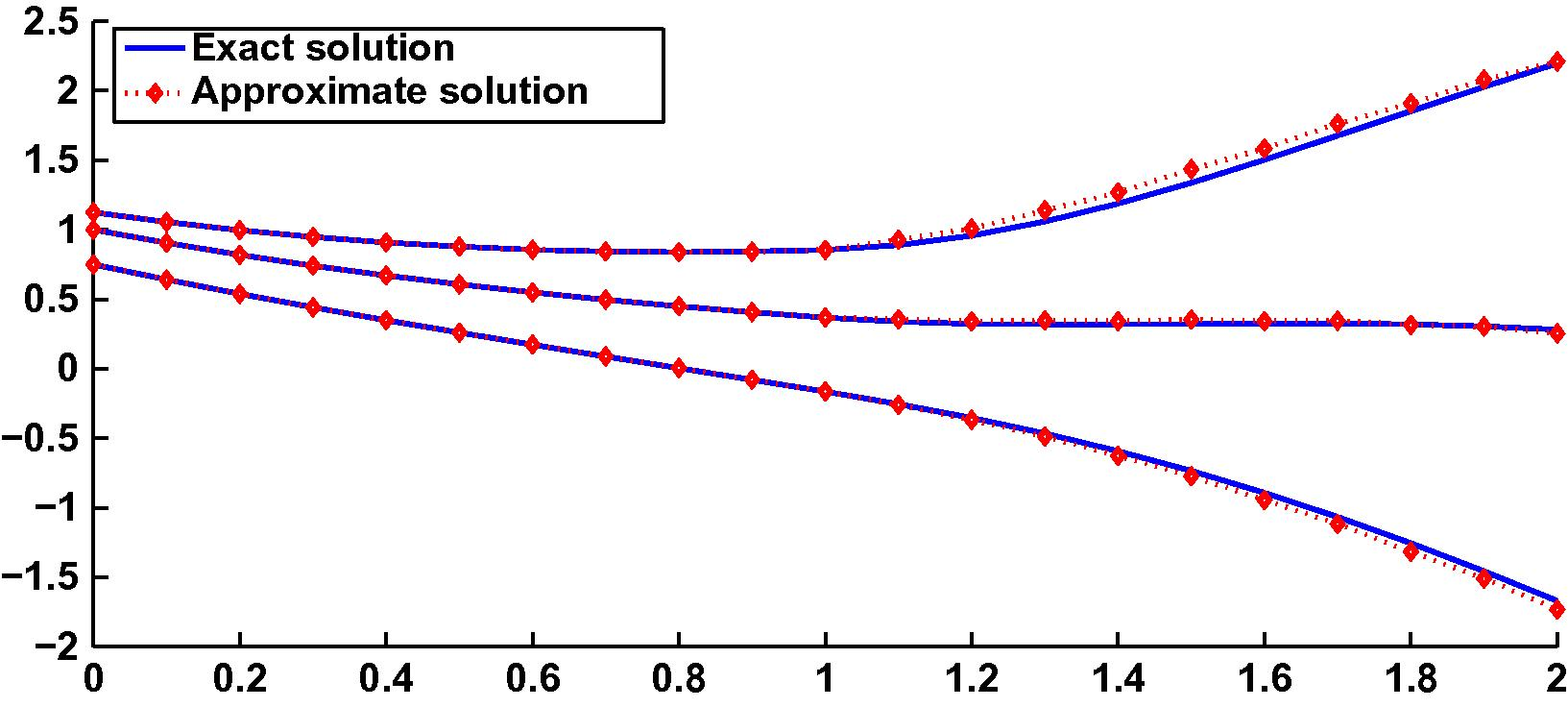
- The results of Example 6.2.
References
- Survey of utilisation of fuzzy technology in medicine and healthcare. Fuzzy Set Syst.. 2001;120:331-349.
- [Google Scholar]
- An efficient technique for superfamily classification of amino acid sequences: feature extraction, fuzzy clustering and prototype selection. Fuzzy Set Syst.. 2005;152:5-16.
- [Google Scholar]
- Fuzzy Logic in Medicine. Heidelberg: Physica-Verlag; 2002.
- Protein motif extraction with neuro-fuzzy optimization. Bioinformatics. 2002;18:1084-1090.
- [Google Scholar]
- Fundamentals of Fuzzy Sets. USA: Kluwer Academic Publishers; 2000.
- A review of E-infinite theory and the mass spectrum of high energy particle physics. Chaos Solitons Fract.. 2004;19:209-236.
- [Google Scholar]
- The concepts of E-infinite: an elementary introduction to the Cantorian-fractal theory of quantum physics. Chaos Solitons Fract.. 2004;22:495511.
- [Google Scholar]
- On a fuzzy Khler manifold which is consistent with the two slit experiment. Int. J. Nonlinear Sci. Numer. Simulat.. 2005;6:95-98.
- [Google Scholar]
- An iterative scheme for the solution of generalized system of linear fuzzy differential equations. World Appl. Sci. J.. 2009;7:1597-1604.
- [Google Scholar]
- A note on iterative method for solving fuzzy initial value problems. J. Adv. Res. Sci. Comput.. 2009;1:22-33.
- [Google Scholar]
- Approximate-analytical approach to nonlinear FDEs under generalized differentiability. J. Adv. Res. Dyn. Control Syst.. 2010;2:56-74.
- [Google Scholar]
- Fard, O.S., Kamyad, A.V., 2010. Modified k-step method for solving fuzzy initial value problems. Iran. J. Fuzzy Syst.
- Numerical solution of fuzzy differential and integral equations. Fuzzy Sets Syst.. 1999;106:35-48.
- [Google Scholar]
- Impulsive functional differential inclusions and fuzzy population models. Fuzzy Sets Syst.. 2003;138:601-615.
- [Google Scholar]
- The oscillation of delay differential inclusions and fuzzy biodynamics models. Math. Comput. Model.. 2003;37:651-658.
- [Google Scholar]
- The fuzzy cube and causal efficacy: representation of concomitant mechanisms in stroke. Neural Networks. 1998;11:549-555.
- [Google Scholar]
- Discrete Variable Methods in Ordinary Differential Equations. John Wiley and Sons; 1962.
- Numerical methods for fuzzy initial value problems. Int. J. Uncertainty Fuzziness Knowledge-Based Syst.. 1999;7:439-461.
- [Google Scholar]
- Analysis of Numerical Methods. New York: Wiley; 1966.
- Numerical solution of fuzzy differential equations by Nyström method. Chaos, Solutions Fract.. 2009;41:859-868.
- [Google Scholar]
- Midpoints for fuzzy sets and their application in medicine. Artif. Intell. Med.. 2003;27:81-101.
- [Google Scholar]
- The Runge–Kutta method for hybrid fuzzy differential equations. Nonlinear Anal. Hybrid Syst.. 2008;2:626-634.
- [Google Scholar]
- Numerical solution of hybrid fuzzy differential equations by predictor–corrector method. Int. J. Comp. Math.. 2009;86(1):121-134.
- [Google Scholar]







