Application of particle swarm optimization to transportation network design problem

1 Introduction

In transportation planning and development, transportation network design problem (TNDP) is an important subject in which certain objective(s) is(are) minimized through choosing among a given set of projects under resource constraints. Objectives are (usually) related to user benefits (or costs), and constraints are related to various resources which bring about such benefits at the cost of the operator of the network. However, solving such a problem requires too much time. For an n-project case, considering an accept/reject decision for each project, there are 2ⁿ alternative networks which are to be compared. Assuming that half of the networks may be rejected on accounts of resource constraints, and considering 1 min cpu time for evaluating the value of the objective function for each alternative network, the computation time would be 2ⁿ⁻¹ minutes. For n = 20, for instance, one needs over 1 year computation time to reach the optimum network.

Various approaches have been taken to solve TNDP. Steenbrink (1974a), Wong (1984), and Magnanti and Wong (1984) surveyed some earlier algorithms of solving this problem. A branch and bound algorithm was presented by LeBlanc (1975) to solve TNDP. Since this algorithm does not perform well in large scale problems, the need for trade-off between the solution accuracy and speed of attaining it was felt early in the development of such solution algorithms.

There have been several methods to trade-off accuracy with speed. These are as follows: (a) using system equilibrium flows instead of user equilibrium (UE) ones (Sheffi, 1985) in the network loading (Steenbrink, 1974b; Dantzig et al., 1979; Chen and Sul Alfa, 1991); (b) assuming constant link cost functions (Boyce et al., 1973; Holmberg and Hellstrand, 1998); (c) relaxation of the integer constraints on decision variables (Steenbrink, 1974b; Abdulaal and LeBlanc, 1979; Dantzig et al., 1979); (d) decomposition of the problem (Steenbrink, 1974b; Dantzig et al., 1979; Hoang, 1982; Solanki et al., 1998); (e) aggregation of the network by link and node abstraction or extraction (Haghani and Daskin, 1983); (f) using an intrinsic approach by defining a surrogate problem which lacks the complexity of the original one (Yang and Bell, 1998); (g) heuristic procedures (Poorzahedy and Turnquist, 1982; Chen and Sul Alfa, 1991); (h) meta-heuristic (evolutionary) procedures, such as genetic algorithm (GA) (Yin, 2000), simulated annealing (SA) (Lee and Yang, 1994), GA, SA, and Tabu search (TS) (Cantarella et al., 2002), ant colony optimization (ACO) (Poorzahedy and Abulghasemi, 2005); (i) hybrid meta-heuristics, such as hybridized ACO (HACO) with GA, SA, and TS (Poorzahedy and Rouhani, 2007).

In this paper, an application of a modern evolutionary method, namely particle swarm optimization (PSO), to solve the TNDP is presented. The results are compared with those of the ACO and HACO existing on the same problem network in the last reference. The reminder of the paper is organized as follows. The next section is devoted to define the TNDP mathematically. In the two subsequent sections, the PSO is described in detail, and then adapted to the TNDP. Computational results are reported in the final section.

2 The TNDP

Let G = (V, A) be a graph representing a transportation network with node set V and arc set A, and define P ⊆ {(r, s) ɛ V × V : r ≠ s} as the set of origin–destination (OD) pairs. Each arc corresponds to a pair (i, j) of the nodes, where i is the tail and j is the head node of the arc. For each OD pair (r, s) ɛ P, there is a nonnegative flow rate (travel demand) from r to s, denoted by d_rs. In order to simplify the presentation, suppose that G is strongly connected, that is each node j can be reached from every other node i by following a directed path in G, and let K_rs be the non-empty set of paths from the origin r to the destination s.

Define $\overline{A}(\overline{A}\ne A)$ as the set of project arcs, and let the decision vector be $y=(y_a){\hspace{0.17em}}_{a\in \overline{A}}$ with y_a being the binary project decision variable, taking values 0 or 1 depending on rejection or acceptance of any project $a\in \overline{A}$ . For a given vector y, define the decision network G(y) = (V, A(y)) with $A(y)=A\cup \{a\in \overline{A}:y_a=1\}$ as the set of arcs followed by decision y, and for each (r, s) ɛ P denote by K_rs(y) the set of paths joining r to s in G(y). For each path k ɛ K_rs(y), let f_k be the flow of path k from origin r to destination s. Moreover, let δ_ak equals 1 if arc a ɛ A(y) lies on path k, and 0 otherwise.

Assume further that each arc $a\in A\cup \overline{A}$ has a nondecreasing and continuously differentiable travel time function t_a(x_a): [0, ∞) → [0, ∞) with x_a being the flow rate assigned to arc a. Then, letting c_a be the construction cost of project arc $a\in \overline{A}$ , and considering the total construction cost being limited to the level of budget B, the TNDP can be illustrated with the upper level problem, ULP: $$\begin{array}{cc}[\mathrm{ULP}]\hfill & \underset{y}{\mathrm{Min}}T(y)=\sum _{a\in A(y)}{x}_a{t}_a(x_a)\hfill \\ \hfill & \text{s}.\text{t}.\sum _{a\in \overline{A}}{c}_a{y}_a⩽B\hfill \\ \hfill & y_a=0\text{or}1\forall a\in \overline{A}\hfill \\ \hfill & x(y)\text{is a solution of}[\mathrm{LLP}(y)]\hfill \end{array}$$ where x(y) = (x_a)_aɛA(y) is the user equilibrium flow in the decision network G(y), given as the solution of the lower level (traffic assignment) problem, LLP(y), for given y: $$\begin{array}{cc}[\mathrm{LLP}(y)]\hfill & \mathrm{Min}\sum _{a\in A(y)}{\int }_{\circ }^{x_a}{t}_a(w)\mathit{dw}\hfill \\ \hfill & \text{s}.\text{t}.\sum _{k\in K_{\mathit{rs}}(y)}{f}_k=d_{\mathit{rs}}\forall (r\text{,}s)\in P\hfill \\ \hfill & f_k⩾0\forall k\in K_{\mathit{rs}}(y)\text{,}\forall (r\text{,}s)\in P\hfill \\ \hfill & x_a=\sum _{(r\text{,}s)\in P}\sum _{k\in K_{\mathit{rs}}(y)}{f}_k{\delta }_{\mathit{ak}}\forall a\in A(y)\hfill \end{array}$$ This is a well-known bilevel programming problem, where the [ULP] seeks a decision vector y for minimizing the total travel time T(y) of the (assigned) traveler, and the [LLP(y)] is the traffic assignment model which estimates the traveler flows, given the decision y.

3 The PSO

Particle swarm optimization, also called PSO, is a population based stochastic optimization technique developed by Kennedy and Eberhart (1995) and Eberhart and Kennedy (1995). PSO mimics the behaviour of flocks of birds, swarms of insects or schools of fish, in which individuals are called particles and the population is called a swarm. In a problem space, each particle is given a position and a velocity. Once a particle finds a good direction to food, other particles are notified and will be able to speed toward that, immediately. The particles roam in the space, convey good positions to each other, and adjust their own positions and velocities based on these good positions (Abraham et al., 2006).

PSO is analogous to evolutionary algorithms, like GA, in a sense that it starts with randomly generated solutions, and evolves the solution until a desirable one is found. However, unlike GA, the evolutionary process in PSO only evolves the positions of the particles, rather than creating new particles (Shi and Eberhart, 1998a). The main strength of PSO is its fast convergence, which compares favourably with many meta-heuristics like GA and SA (Abraham et al., 2006). Moreover, it may be easily implemented, and requires few parameter settings and computational memory (You, 2008).

PSO has been successfully applied to many areas. Voss and Feng (2002), Jiang et al. (2007), Yisu et al. (2008) and You (2008) report some of this applications. This paper describes an application of such method in solving the TNDP.

4 Adapting the PSO to the TNDP

Employing the PSO for solving TNDP needs some modifications to the algorithm given in the previous section. First, the PSO is basically developed for continuous optimization problems. This is while the TNDP is formulated as a combinatorial optimization problem in terms of variables y denoted as $|\overline{A}|$ -bit binary strings. To adapt the algorithm for this combinatorial nature, one may provide some mapping from the one-dimensional real-valued space to the $|\overline{A}|$ -dimensional binary space. This is done here by transforming each real number p_i to its nearest integer in $[0\text{,}{2}^{|\overline{A}|}-1]$ , and then transforming the resulting integer into the base-2 number system as an $|\overline{A}|$ -bit binary code. To facilitate the presentation, the latter transformation is illustrated by the function $y(p_i):[0\text{,}{2}^{|\overline{A}|}-1]\subset Z\to \{0\text{,}1\}{\hspace{0.17em}}^{|\overline{A}|}$ .

The canonical PSO must also be adapted for the budget constraint embedded in the [ULP]. In this regard, one may apply a very simple modification that is assigning an adequately large fitness value (say M) to any infeasible solution p_i, i.e. f(p_i) = M.

The following is a formal statement of the proposed PSO algorithm:

• Step 1.

  Initialization.

  • Select the particle swarm size n, the parameters c₁ and c₂, the initial and final values of the inertia weight w, and the maximum velocity v_max.

  • For i = 1 to n do: initialize (randomly or partially randomly) the decision variable p_i in [ $0\text{,}{2}^{|\overline{A}|}-1$ ] so that ${\sum }_{a\in \overline{A}}{c}_a{y}_a(p_i)⩽B$ ; set $p_i^{\ast }=p_i$ ; initialize ${\nu }_i$ randomly in [ $-{\nu }_{\max }\text{,}{\nu }_{\max }$ ].

  • Set $p_g^{\ast }=\arg \min (f(p_1)\text{,}\dots \text{,}f(p_n))$ . Set the iteration counter t = 0.

• Step 2.

  Updating each particle’s position and velocity.

  • For i = 1 to n do: generate random numbers r₁ and r₂ in [0, 1]; update $v_i\leftarrow {\mathit{wv}}_i+c_1{r}_1(p_i^{\ast }-p_i)+c_2{r}_2(p_g^{\ast }-p_i)$ ; clamp in v_i between the range [−v_max, v_max] as v_i = sign(v_i) min(|v_i|, v_max); update p_i ← p_i + v_i; clamp p_i to the range [ $0\text{,}{2}^{|\overline{A}|}-1$ ].

• Step 3.

  Calculating each particle’s fitness value.

  • For i = 1 to n do: set y = y(p_i); if ${\sum }_{a\in \overline{A}}{c}_a{y}_a>B$ then set f(p_i) = M; else, solve the user equilibrium problem [LLP(y)] to compute T(y), and set f(p_i) = T(y).

• Step 4.

  Updating local bests and global best.

  • For i = 1 to n do: update $p_i^{\ast }\leftarrow \arg \min (f(p_i^{\ast })\text{,}f(p_i))$ .

  • Update $p_g^{\ast }\leftarrow \arg \min (f(p_g^{\ast })\text{,}f(p_1)\text{,}\dots \text{,}f(p_n))$ .

• Step 5.

  End criterion.

  • Set t = t + 1. If end criterion is not met, go to Step 2. Otherwise, $y=y(p_g^{\ast })$ is the best solution found so far with the objective function value $T(y)=f(p_g^{\ast })$ . Collect the necessary information, and stop. □

5 Numerical example

In order to demonstrate the capability of the PSO algorithm in solving the TNDP, it will be applied on the network of Sioux Falls. This network has 24 nodes and 76 arcs, as shown in Fig. 1. The parameters of the travel time function $t_a(x_a)={\alpha }_a+{\beta }_a{x}_a^4$ for each arc a = (i, j), and the OD (origin/destination) demands are basically those given in Poorzahedy and Turnquist (1982), and LeBlanc (1975), and are given in Tables 1 and 2, respectively.

Close

Figure 1

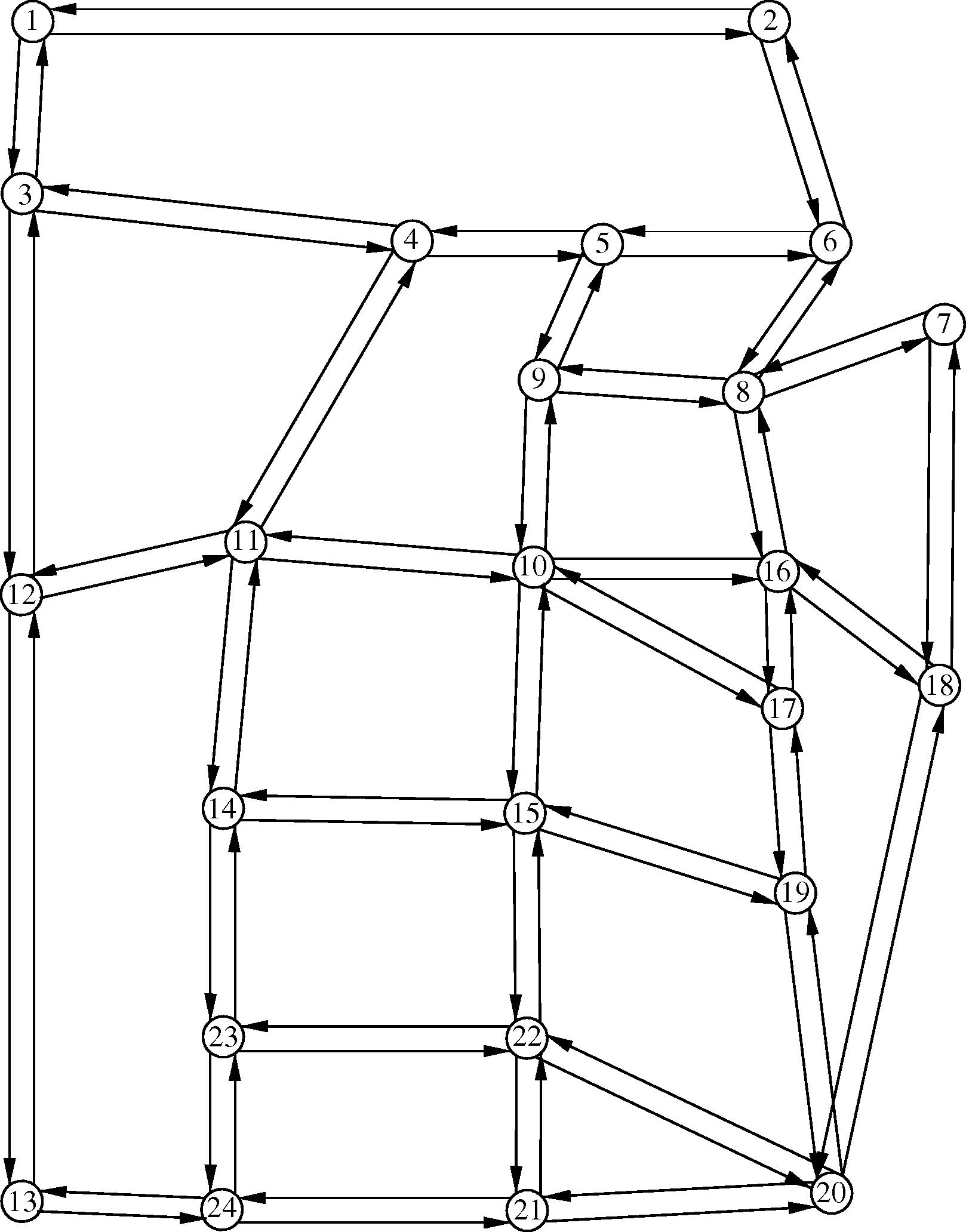
The Sioux Falls network.

Export to PPT

There are 10 pairs of project arcs $(|\overline{A}|=10)$ , of which 5 projects are improvement on existing arcs, and 5 are new arcs. The parameters of the travel time functions and the construction costs (in units of money) of the projects 1–10 are given in Table 3 (Poorzahedy and Abulghasemi, 2005). Considering 10 projects, there are 2¹⁰ (=1024) alternative networks. A complete enumeration was used to compute the optimal solution of the TNDP for any given budget level for checking purposes (Poorzahedy and Abulghasemi, 2005; Poorzahedy and Rouhani, 2007). The PSO network design algorithm was implemented in a program in MATLAB on a Laptop with Intel Core 2 due 2 GHz processor. In all experiments, the PSO parameters are set as shown in Table 4.

5.2

5.2 Comparison of PSO with ACO and HACO

In this section, the performance of the PSO in solving the TNDP is compared with those of the ACO and the best HACO algorithms presented by Poorzahedy and Rouhani (2007) for the test network of Sioux Falls. The PSO parameter values used here are as before, and the ACO and HACO results are those given in Poorzahedy and Rouhani (2007). To make the results comparable, the initial solutions of the PSO are made by the same way as described in this reference.

Three measures of performance are considered in Table 6. These are average NTAPS, average of OFVs for all particles, as in Poorzahedy and Rouhani (2007), and frequency of finding the optimal solution. These measures are for 50 runs of each algorithm, and they are given for each of 8 iterations of the algorithms, and in total, for B/C = 0.625. This B/C value is a middle value which requires higher efforts and is exposed to higher errors. As may be seen in this table, except for iteration 5 of the HACO, all algorithms experience decreasing NTAPS as iteration number increases. Moreover, it may be seen that the PSO is comparable with HACO regarding total NTAPS. Fig. 2 demonstrates the performance of these three algorithms in the space of effort-accuracy, where the effort is measured by the average NTAPS, and accuracy is measured by the average OFV for all particles. Fig. 2 is based on 50 runs for each algorithm, and it is given for each of 8 iterations of them for B/C = 0.625, as in Table 6. According to Fig. 2, the HACO has the least average effort (24.2) and the highest accuracy (64,445), while those of ACO has been the most and lowest ones (25.1 and 64,814, respectively), showing that the HACO is more effective than ACO in solving the problem. In comparison with HACO, the accuracy of PSO (64,452) at a comparable effort (24.3) seems a remarkable performance. This is particularly so, if one notes that the PSO algorithm used here is based on the canonical PSO, which points to the fact that it has the chance of performing better if it is modified and calibrated to suit the problem better.

Table 6 Performance of PSO, ACO and HACO algorithms (in 50 runs, B/C = 0.625).

Iteration No.	Average NTAPS			Average OFVa			Frequency of finding the optimal solution
	PSO	ACO	HACO	PSO	ACO	HACO	PSO	ACO	HACO
1	10.0	8.6	8.7	65,134	65,134	65,095	12	9	12
2	5.8	5.3	3.9	64,878	64,903	64,595	6	12	12
3	1.5	3.4	2.0	64,637	64,758	64,330	6	7	2
4	1.7	2.1	0.7	64,528	64,663	64,197	2	4	1
5	1.1	2.2	8.4	64,853	64,750	65,631	18	4	20
6	1.6	1.6	0.2	63,654	64,693	63,851	2	4	0
7	1.3	1.2	0.2	63,934	64,794	63,937	1	1	1
8	2.0	0.8	0.1	63,914	64,821	63,924	1	0	0
All	24.3	25.1	24.2	64,452	64,814	64,445	48	41	48

a For all particles.

Close

Figure 2

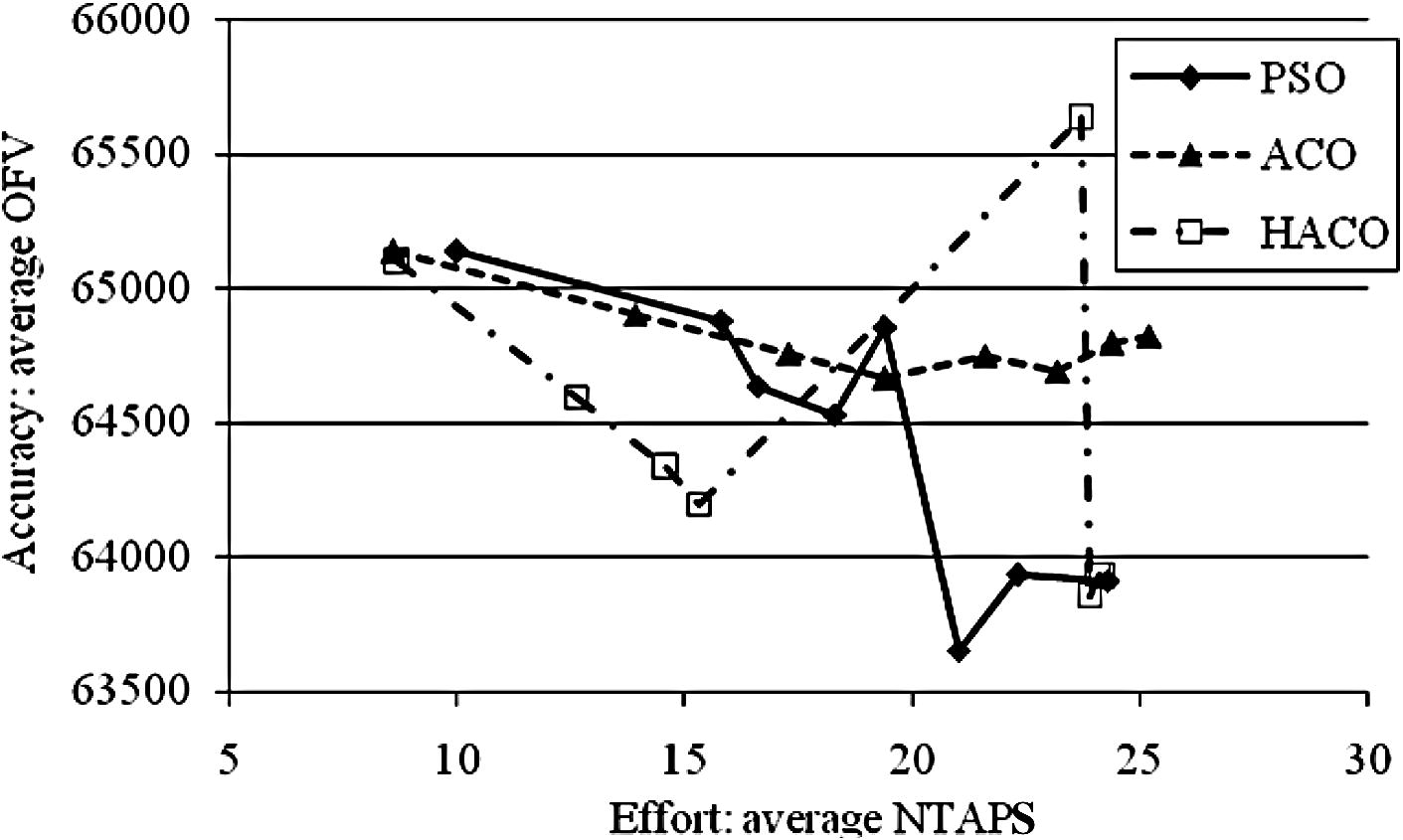
Comparison of PSO, ACO and HACO regarding objective function value and computation effort (in 50 runs, B/C = 0.625).

Export to PPT

Fig. 3 depicts another type of the effort-accuracy diagram with the accuracy being measured by the odds (probability) of finding the optimal solution (in 50 runs for B/C = 0.625, as in Table 6), and the effort being measured as before. The figure shows that HACO and PSO have the best accuracy levels (0.96) at comparable effort levels (24.2 and 24.3, respectively). The accuracy of 0.96 seems a very high performance for the PSO, when compares it to that of ACO (0.82) which has been gained at a somewhat higher effort level (25.1).

Close

Figure 3

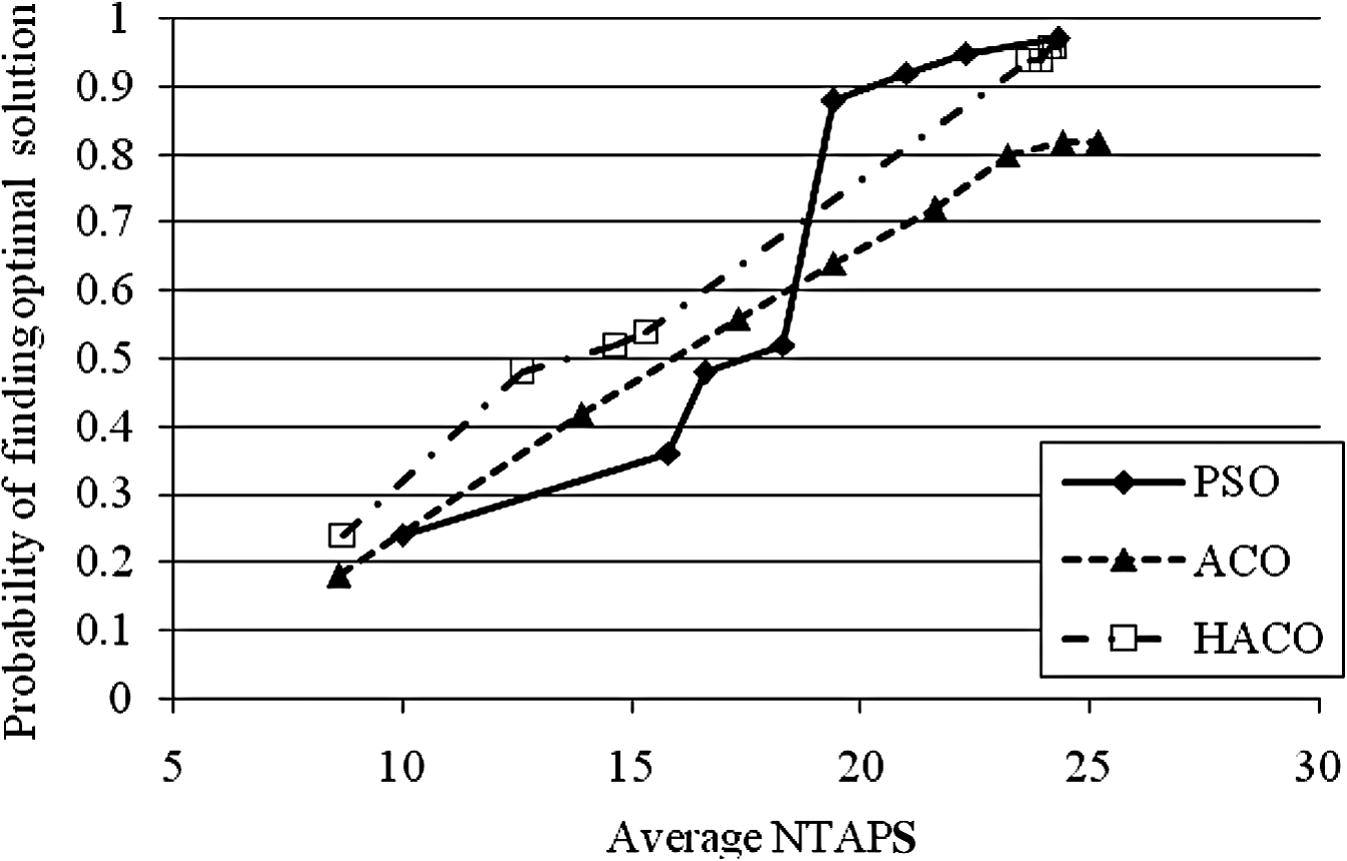
Comparison of PSO, ACO and HACO algorithms in probability of finding the optimal solution (in 50 runs, B/C = 0.625).

Export to PPT

Table 7 summarizes the results of Table 5 for B/C = 0.625, and compares them with the respective ones for B/C = 0.45 (another mid-value B/C with less difficulty in finding the optimal solution than B/C = 0.625). As may be seen in this table, both ACO and HACO algorithms happen to find the optimal solutions in all 50 runs for B/C = 0.45, while PSO does this in 48 out of 50. In this case, however, PSO has done this with much lower effort than others (20.8 as compared with 25.9 and 29.4, the average efforts of ACO and HACO, respectively). It is worth pointing out that the number of feasible alternative networks for B/Cs of 0.45 and 0.625 are 398 and 761, in that order. Table 7 illustrates that the average NTAPS for the algorithm PSO for B/Cs of 0.45 and 0.625 are 20.8 and 24.3, respectively, which are 5.2% and 3.2% of the total feasible networks at the respective budget levels.

Table 7 Performance of PSO, ACO and HACO algorithms for two medium budget levels.

Algorithm	B/C	Average NTAPSa	Frequency of finding the optimal solutiona	Average of solution OFVsa
PSO	0.45	20.8	48	66,672
ACO	0.45	25.9	50	66,650
HACO	0.45	29.4	50	66,650
PSO	0.625	24.3	48	61,472
ACO	0.625	25.1	41	61,532
HACO	0.625	24.2	48	61,469

a In 50 runs.

6 Summary and conclusions

In this paper, the meta-heuristic of particle swarm optimization was employed to solve a well-known combinatorial bilevel programming model, namely the transportation network design problem. Various kinds of approaches have been proposed to solve this problem. Following two recent attempts in the solution of this problem by ant colony optimization, ACO (Poorzahedy and Abulghasemi, 2005) and hybrid ant colony optimization, HACO (Poorzahedy and Rouhani, 2007), this paper attempted to show the power of the recent meta-heuristic search, the particle swarm optimization, and compared it to ACO and HACO. The experiments presented in this paper on the network of Sioux Falls showed that the particle swarm algorithm outperforms ACO in that it needs noticeably less effort to find comparable solutions (in the values of the objective function), and have a comparable performance to HACO in that it gives similar solutions at comparable effort. These are promising results which encourage more experiments in this area to explore the capability of this new algorithm further in solving the TNDP, and similar combinatorial problems.