Solving two-dimensional integral equations

1 Introduction

Homotopy analysis method (HAM), first proposed by Liao (1992). HAM properly overcomes restrictions of perturbation techniques because it does not need any small or large parameters to be contained in the problem. Liao, in his book (Liao, 2003a), proves that this method is a generalization of some previously used techniques such as d-expansion method, artificial small parameter method and ADM. This method has proven to be very effective and result in considerable saving in computation time (Liao, 1995, 2003b,c, 2004; Liao and Chwang, 1998; Sami et al., 2008; Abbasbandy, 2007).

2 Analysis of the method

Consider the following linear integral equation of two-dimensional $$u(x\text{,}y)=f(x\text{,}y)+{\int }_c^y{\int }_a^{b}k(x\text{,}y\text{,}s\text{,}t)u(s\text{,}t)\mathit{dsdt}\text{.}$$

To illustrate the homotopy analysis method, we consider

Thus, as p increases from 0 to 1, the solution $\phi (r\text{,}t\text{;}p)$ varies from the initial guesses $u_0(r\text{,}t)$ to the solution $u(r\text{,}t)$ . Expanding $\phi (r\text{,}t\text{;}p)\text{,}$ in Taylor series with respect to p, we have

If the auxiliary linear operator, the initial guess, the auxiliary parameter $\hslash$ , and the auxiliary function are so properly chosen, the series (4) converges at p = 1, then we have

Define the vector ${\overrightarrow{u}}_n=\{u_0=f\text{,}{u}_1\text{,}\dots u_n\}$ . Differentiating Eq. (2) m times with respect to the embedding parameter p and then setting $p=0$ and finally dividing them by $m!$ , we obtain the mth-order deformation equation

Applying $L^{-1}$ on both side of Eq. (7), we get

In this way, it is easily to obtain $u_m$ form $m⩾1$ , at Mth-order, we have

When $M\to \infty$ we get an accurate approximation of the original Eq. (1). For the convergence of the above method we refer the reader to Liao (2003a).

3 Numerical example

To solve the Eq. (12) by means of homotopy analysis method we choose

We now define a nonlinear operator as $$N[u(x\text{,}y)]=\phi (x\text{,}y\text{;}p)-f(x\text{,}y)-{\int }_{-1}^y{\int }_{-1}^1\phi (x\text{,}y\text{;}p)\mathit{dsdt}\text{.}$$

Using above definition, with assumption $H(x\text{,}t)=1$ . We construct the zeroth-order deformation equation $$(1-p)L(\phi (x\text{,}t\text{;}p)-u_0(x\text{,}t))=p\hslash N(\phi (x\text{,}t\text{;}p))\text{,}$$ obviously, when p = 0 and 1, $$\phi (x\text{,}t\text{;}0)=u_0(x\text{,}t)\text{,}\phi (x\text{,}t\text{;}0)=u(x\text{,}t)\text{.}$$

Thus, we obtain the mth-order deformation equations

Now, the solution of the mth-order order deformation Eq. (14)

Finally, we have $$u(x\text{,}t)=u_0(x\text{,}t)+\sum _{m=1}^{\infty }{u}_m(x\text{,}t)\text{.}$$

From Eqs. (13) and (15) and subject to initial condition $$u_m(x\text{,}0)=0\text{,}m⩾1\text{.}$$

We obtain $$\begin{array}{cc}\hfill & u_0(x\text{,}y)=x^2-\frac{13}{15}\mathit{xy}-\frac{2}{15}{\mathit{xy}}^4\text{,}\hfill \\ \hfill & u_1(x\text{,}y)=-\hslash \frac{2}{15}\mathit{xy}(y^3+1)\text{,}\hfill \\ \hfill & u_2(x\text{,}y)=0\text{.}\hfill \end{array}$$

And by repeating this approach, we obtain $$u_3(x\text{,}t)=u_4(x\text{,}t)=\cdots =0\text{.}$$

When $\hslash =-1$ we have $$u(x\text{,}t)=\sum _{i=0}^{\infty }{u}_i(x\text{,}t)=x^2-\frac{13}{15}\mathit{xy}-\frac{2}{15}{\mathit{xy}}^4+\frac{2}{15}\mathit{xy}(y^3+1)+0+0+\cdots \text{,}$$ $$u(x\text{,}y)=x^2+\mathit{xy}\text{,}$$ which is an exact solution.

To solve Eq. (16) by means of homotopy analysis method, we have

We now define a nonlinear operator as $$N[u(x\text{,}y)]=\phi (x\text{,}y\text{;}p)-f(x\text{,}y)-{\int }_0^y{\int }_{-1}^1{x}^2{e}^{-s}u(s\text{,}t)\mathit{dsdt}\text{.}$$

Using above definition, with assumption $H(x\text{,}t)=1\text{.}$ We construct the zeroth-order deformation equations $$(1-p)L(\phi (x\text{,}t\text{;}p)-u_0(x\text{,}t))=p\hslash N(\phi (x\text{,}t\text{;}p))\text{,}$$ obviously, when p = 0 and 1, $$\phi (x\text{,}t\text{;}0)=u_0(x\text{,}t)\text{,}\phi (x\text{,}t\text{;}0)=u(x\text{,}t)\text{.}$$

Thus, we obtain the mth-order deformation equations

Now, the solution of the mth-order order deformation Eq. (16)

Finally, we have $$u(x\text{,}t)=u_0(x\text{,}t)+\sum _{m=1}^{\infty }{u}_m(x\text{,}t)\text{.}$$

From Eqs. (17) and (18) and subject to initial condition $$u_m(x\text{,}0)=0\text{,}m⩾1\text{.}$$

We obtain $$\begin{array}{cc}\hfill & u_0(x\text{,}y)=y^2{e}^x-\frac{2}{3}{x}^2{y}^3\text{,}\hfill \\ \hfill & u_1(x\text{,}y)=\hslash \frac{1}{6}{y}^4{x}^{2}e-\hslash \frac{5}{6}{y}^4{x}^2{e}^{-1}-\hslash \frac{2}{3}{x}^2{y}^3\text{,}\hfill \\ \hfill & ⋮\hfill \end{array}$$

When $\hslash =-1\text{,}$ we have $$u=\sum _{i=0}^{\infty }{u}_i=y^2{e}^x-\frac{2}{3}{x}^2{y}^3-\frac{1}{6}{y}^4{x}^{2}e+\frac{5}{6}{y}^4{x}^2{e}^{-1}+\frac{2}{3}{x}^2{y}^3+\frac{1}{3}{y}^5{x}^2-\frac{5}{6}{y}^5{x}^2{e}^{-2}-\frac{1}{30}{y}^5{x}^2{e}^2-\frac{5}{6}{y}^4{x}^2{e}^{-1}+\frac{1}{6}{y}^4{x}^{2}e+\cdots \text{.}$$

The exact solution and HAM results are shown in Figs. 1 and 2, respectively.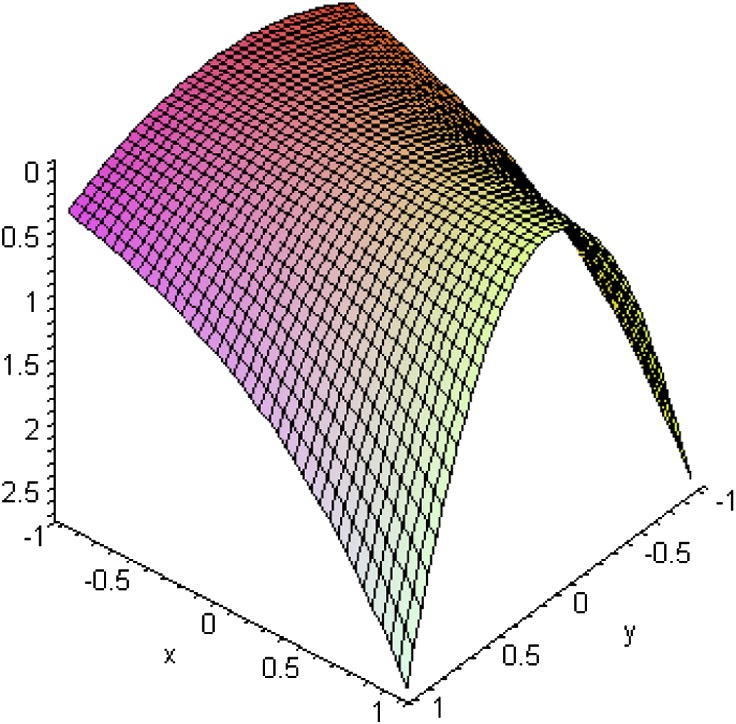

Close

Figure 1

HAM solution for Example 2.

Export to PPT

Close

Figure 2

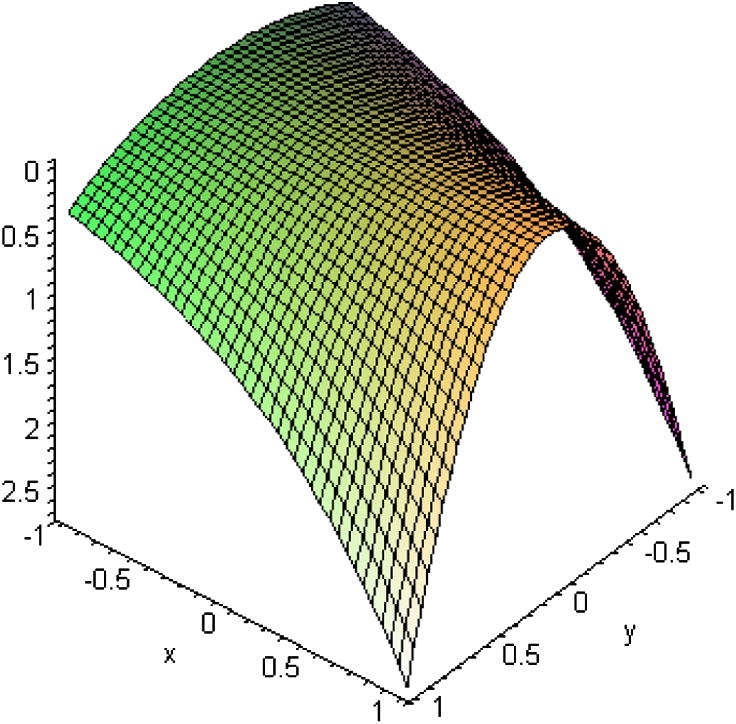
Exact solution for Example 2.

Export to PPT

4 Conclusion

In this work we applied homotopy analysis method for solving integral equations of two-dimensional. The approximate solutions obtained by the homotopy analysis method are compared with exact solutions. It can be concluded that the homotopy analysis method is very powerful and efficient technique in finding exact solutions for wide classes of problems. In our work, we use the MAPLE 11 package to carry the computations.