Analytical approach to two-dimensional viscous flow with a shrinking sheet via variational iteration algorithm-II

1 Introduction

This paper presents a reliable comparison between two recently developed, popular iteration methods, the variational iteration algorithm-II (VIM-II) developed by He et al. (2009) and the Adomian decomposition method (ADM) introduced by Adomian (1988). The use of both methods is common in the literature. The most extensive work carried out on the variational iteration algorithm (VIM) generally is that of He (2000, 2004, 2007, 2008) and He and Lee (2009). Although many researchers have compared the VIM with the ADM, to the best of the authors’ knowledge, no comparison of the VIM-II and the ADM has appeared in the literature thus far. The objectives of this paper are threefold: first, to introduce the advantages of the VIM-II, which primarily lie in its ability to avoid the unnecessary calculations of other iteration methods, namely, the VIM and ADM; second, to illustrate through this comparison that, unlike the widely used ADM, the VIM-II does not require the calculation of Adomian polynomials (Adomian, 1988) for the nonlinear terms that appear in differential equations, as a solution can be obtained without the incorporation of these polynomials; and third, to apply the VIM-II to a fluid mechanics problem, namely, a viscous flow for a shrinking sheet (Fang et al., 2009). An analytical approach is followed to find the numerical value of f″(0), which Wazwaz (2007) has calculated to solve the Blasius equation. This goal is achieved by employing the reliable VIM-II developed by He (2007) and the ADM (Adomian, 1988). For numerical approximation, the resulting series is best manipulated by Padé approximants (Baker, 1975).

2 Padé approximants

Padé approximants constitute the best approximation of a function by a rational function of a given order. Developed by Henri Padé, Padé approximants often provide better approximation of a function than does truncating its Taylor Series, and they may still work in cases in which the Taylor series does not converge. For these reasons, Padé approximants are used extensively in computer calculations, and it is now well known that these approximants have the advantage of being able to manipulate polynomial approximation into the rational functions of polynomials. Through such manipulation, we can gain more information about the mathematical behavior of the solution. In addition, power series are not useful for large values of a variable, say η → ∞, which can be attributed to the possibility of the radius of convergence not being sufficiently large to contain the boundaries of the domain. To provide an effective tool that can handle boundary value problems on an infinite or semi-infinite domain, it is therefore essential to combine the series solution, which is obtained by the iteration method or any other series solution method, with the Padé approximants.

3 Formulation

In this paper, we consider the two basic equations of fluid mechanics in Cartesian coordinates. The continuity equation and momentum equations for viscous flow are

The boundary conditions applicable to the present flow are

For shrinking phenomena, a > 0, a is a shrinking constant, and W is the suction velocity. m = 1 when the sheet shrinks in the x-direction alone, and m = 2 when it shrinks axisymmetrically. We introduce the following similarity transformations.

4 Methods

4.2

4.2 Adomian decomposition method

A detailed description of the ADM is given in Adomian (1988). Here, we provide only the basic steps as a reminder. Writing Eq. (8) in operator form, we have

(18)

$$\mathit{Lf}(\eta )+\mathit{Rf}(\eta )+\mathit{Nf}(\eta )=0\text{,}$$ where L is the linear operator, i.e., $\mathit{Lf}=\frac{d^{3}f}{d{\eta }^3}$ , which is the highest order derivative; R = 0; and

(19)

$$\mathit{Nf}={\left(\frac{\mathit{df}}{d\eta }\right)}^2-\mathit{mf}\frac{d^{2}f}{{\mathit{df}}^2}\text{.}$$ The linear operator is also the inverse operator, i.e.,

(20)

$$L^{-1}(·)={\int }_0^{\eta }{\int }_0^{\eta }{\int }_0^{\eta }(·)d\eta d\eta d\eta \text{.}$$ The ADM defines the unknown function, f(η), by an infinite series:

(21)

$$f(\eta )=\sum _{\eta =0}^{\infty }{f}_n(\eta )\text{,}$$ where the components f_n(η) are usually determined recurrently. The nonlinear operator, G(f), can be decomposed into infinite polynomials given by

(22)

$$G(f)=\underset{n=0}{\overset{\infty }{m}}{A}_n\text{,}$$ where A_n are the so-called Adomian polynomials of f₀, f₁, f₂,…,f_n defined by

(23)

$$A_n=\frac{1}{n!}\frac{d^n}{d{\lambda }^n}{\left[G\left(\sum _{i=0}^n{\lambda }^i{f}_i\right)\right]}_{\lambda =0}\text{,}n=0\text{,}1\text{,}2\text{,}...\text{,}$$ or, equivalently,

(24)

$$\begin{array}{cc}\hfill & A_0=G(f_0)\text{,}\hfill \\ \hfill & A_1=f_1{G}^{\prime }(f_0)\text{,}\hfill \\ \hfill & A_2=f_2{G}^{\prime }(f_0)+\frac{1}{2}{f}_1^2{G}^{″}(f_0)\text{,}\hfill \\ \hfill & A_3=f_3{G}^{\prime }(f_0)+f_1{f}_2{G}^{″}(f_0)+\frac{1}{3}{f}_1^3{G}^{‴}(f_0)\text{,}\hfill \\ \hfill & A_4=f_4{G}^{\prime }(f_0)+\left(f_1{f}_3+\frac{1}{2}{f}_2^2\right)G^{″}(f_0)\hfill \\ \hfill & +\frac{1}{2}{f}_1^2{f}_2{G}^{‴}(f_0)+\frac{1}{24}{f}_1^4{G}^{\mathit{iv}}(f_0)\text{.}\hfill \\ \hfill & ⋮\hfill \end{array}$$ It is now well known that these polynomials can be generated for all classes of nonlinearity according to specific algorithms.

Write the general algorithm of Eq. (8) with the initial approximation mentioned in Eq. (14)

(25)

$$f_{n+1}(\eta )={\int }_0^{\eta }{\int }_0^{\eta }{\int }_0^{\eta }\left(\sum _{n=0}^{\infty }{A}_n-2\sum _{n=0}^{\infty }{B}_n\right)d\eta d\eta d\eta n=0\text{,}1\text{,}2\text{,}\dots$$ where

(26)

$$\begin{array}{cc}\hfill & A_0=(f_0^{\prime }){\text{,}}^2\hfill \\ \hfill & A_1=2f_0^{\prime }{f}_1^{\prime }\text{,}\hfill \\ \hfill & A_2=2f_0^{\prime }{f}_2^{\prime }+f_1^{\prime }{f}_1^{\prime }\text{,}\hfill \\ \hfill & A_2=2f_0^{\prime }{f}_3^{\prime }+f_1^{\prime }{f}_2^{\prime }\text{.}\hfill \\ \hfill & ⋮\hfill \end{array}$$ Similarly,

(27)

$$\begin{array}{cc}\hfill & B_0=f_0{f}_0^{″}\text{,}\hfill \\ \hfill & B_1=f_0{f}_1^{″}+f_1{f}_0^{″}\text{,}\hfill \\ \hfill & B_2=f_0{f}_2^{″}+f_1{f}_2^{″}+f_2{f}_1^{″}\text{,}\hfill \\ \hfill & B_3=f_0{f}_3^{″}+f_1{f}_2^{″}+f_2{f}_1^{″}+f_3{f}_0^{″}\text{.}\hfill \\ \hfill & ⋮\hfill \end{array}$$ After successive iterations, we obtain the following results

(28)

$$f_0=2-\eta +\frac{\alpha {\eta }^2}{2}\text{,}$$

(29)

$$f_1=\frac{{\eta }^3}{6}-\frac{2\alpha {\eta }^3}{3}\text{,}$$

(30)

$$f_2=-\frac{{\eta }^4}{6}+\frac{2\alpha {\eta }^4}{3}+\frac{{\eta }^5}{60}-\frac{\alpha {\eta }^5}{15}+\frac{\alpha {\eta }^6}{360}-\frac{{\alpha }^2{\eta }^6}{90}\text{,}$$

(31)

$$f_3=\frac{2{\eta }^5}{15}-\frac{8\alpha {\eta }^5}{15}-\frac{{\eta }^6}{30}+\frac{2\alpha {\eta }^6}{15}+\frac{{\eta }^7}{504}-\frac{\alpha {\eta }^7}{315}-\frac{2{\alpha }^2{\eta }^7}{105}-\frac{\alpha {\eta }^8}{5040}+\frac{{\alpha }^2{\eta }^8}{1260}-\frac{{\alpha }^2{\eta }^9}{9072}+\frac{{\alpha }^3{\eta }^9}{2268\text{,}}$$

(32)

$$\begin{array}{cc}\hfill & f_4=-\frac{4{\eta }^6}{45}+\frac{16\alpha {\eta }^6}{45}+\frac{4{\eta }^7}{105}-\frac{16\alpha {\eta }^7}{105}-\frac{{\eta }^8}{360}-\frac{\alpha {\eta }^8}{126}\hfill \\ \hfill & +\frac{8{\alpha }^2{\eta }^8}{105}-\frac{{\eta }^9}{90720}+\frac{37\alpha {\eta }^9}{11340}-\frac{73{\alpha }^2{\eta }^9}{5670}\hfill \\ \hfill & -\frac{47\alpha {\eta }^{10}}{30400}+\frac{37{\alpha }^2{\eta }^{10}}{56700}-\frac{{\alpha }^3{\eta }^{10}}{8100}-\frac{{\alpha }^2{\eta }^{11}}{178200}\hfill \\ \hfill & +\frac{{\alpha }^3{\eta }^{11}}{44550}+\frac{{\alpha }^3{\eta }^{12}}{213840}-\frac{{\alpha }^4{\eta }^{12}}{53460}\text{,}\hfill \\ \hfill & ⋮\hfill \end{array}$$ and so on. In this manner, the remainder of the terms in the decomposition series (21) can be calculated.

The series solution is given by

(33)

$$f=f_0+f_1+f_2+f_3+f_4+\dots \text{,}$$ Substituting Eqs. (27)–(32) into Eq. (33), we obtain the following series solution

(34)

$$f(\eta )=2-\eta +\frac{\alpha {\eta }^2}{2}+\frac{{\eta }^3}{6}-\frac{2\alpha {\eta }^3}{3}-\frac{{\eta }^4}{6}+\frac{2\alpha {\eta }^4}{3}+\frac{3{\eta }^5}{20}-\frac{3\alpha {\eta }^5}{5}-\frac{11{\eta }^6}{90}+\frac{59\alpha {\eta }^6}{120}-\frac{{\alpha }^2{\eta }^6}{90}+\frac{101{\eta }^7}{2520}-\frac{7\alpha {\eta }^7}{45}-\frac{2{\alpha }^2{\eta }^7}{105}-\frac{{\eta }^8}{360}-\frac{41\alpha {\eta }^8}{5040}+\frac{97{\alpha }^2{\eta }^8}{1260}-\frac{{\eta }^9}{90720}+\frac{37\alpha {\eta }^9}{11340}-\frac{589{\alpha }^2{\eta }^9}{45360}+\frac{{\alpha }^3{\eta }^9}{2268}-\frac{47\alpha {\eta }^{10}}{302400}+\frac{37{\alpha }^2{\eta }^{10}}{56700}-\frac{{\alpha }^3{\eta }^{10}}{8100}-\frac{{\alpha }^2{\eta }^{11}}{178200}+\frac{{\alpha }^3{\eta }^{11}}{44550}+\frac{{\alpha }^3{\eta }^{12}}{213840}-\frac{{\alpha }^4{\eta }^{12}}{53460}+\dots$$ Software packages such as Mathematica or Maple can be used to solve the polynomial f′(η) to calculate the value of α with the help of boundary condition f′(η) → 0 for η → ∞. By using the table above, we can choose the value of α = f′(η) → 0 = 0.249243 for both solutions, which is an average value of [5/5] Padé approximation (Table 1).

Table 1 The numerical values for f″(0) = α using Padé approximation.

Padé approximation	f″(0) = α for ADM	f″(0) = α for AVIM
[1/1]	0.292893	0.224748
[2/2]	Complex number	Complex number
[3/3]	Complex number	0.294748
[4/4]	0.247723	0.308086
[5/5]	0.24893	0.249556

The result of VIM and ADM solutions are depicted in Figs. 1 and 2. Fig. 3 compares the two solutions.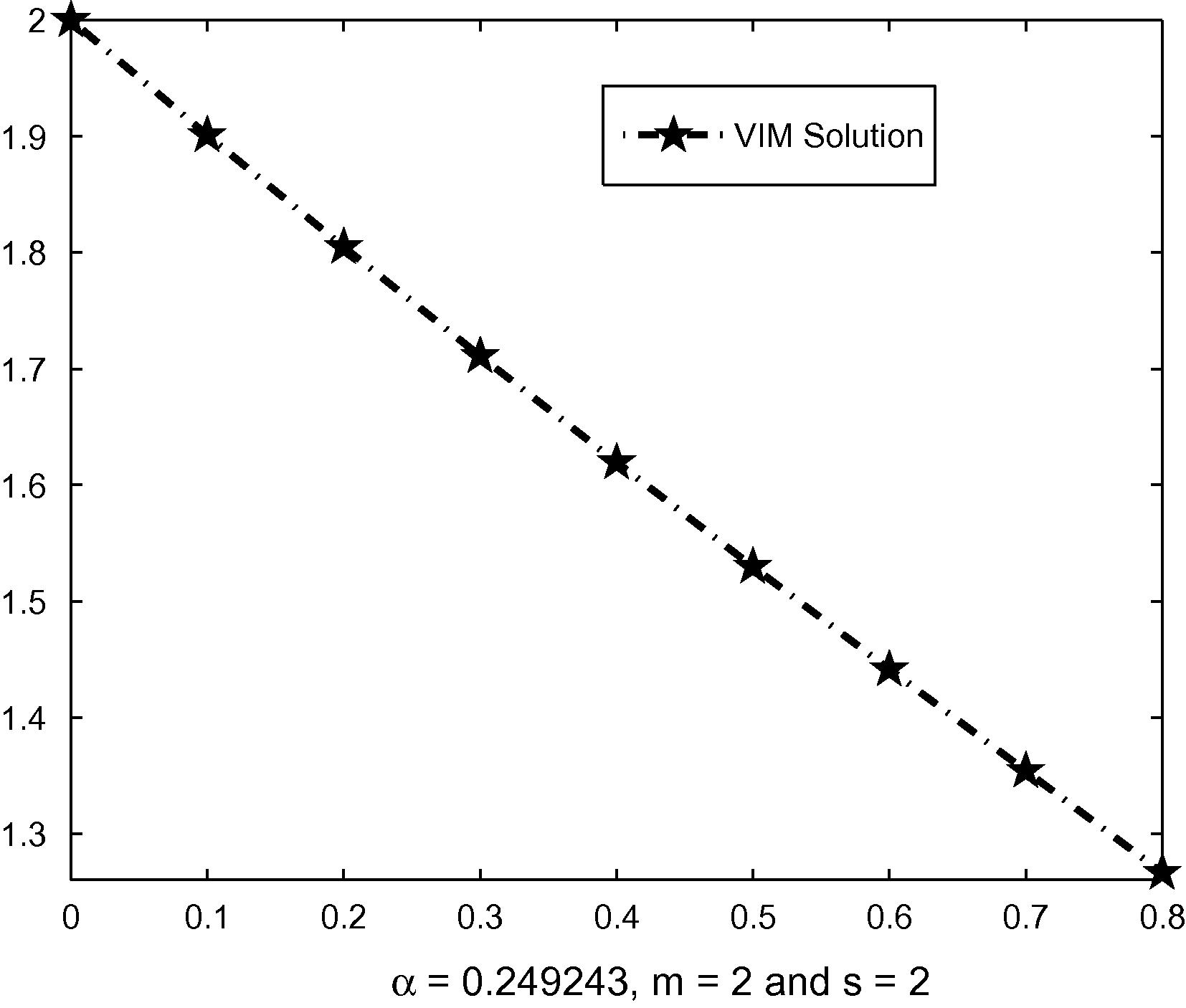

Close

Figure 1

Graphical presentation of VIM solution.

Export to PPT

Close

Figure 2

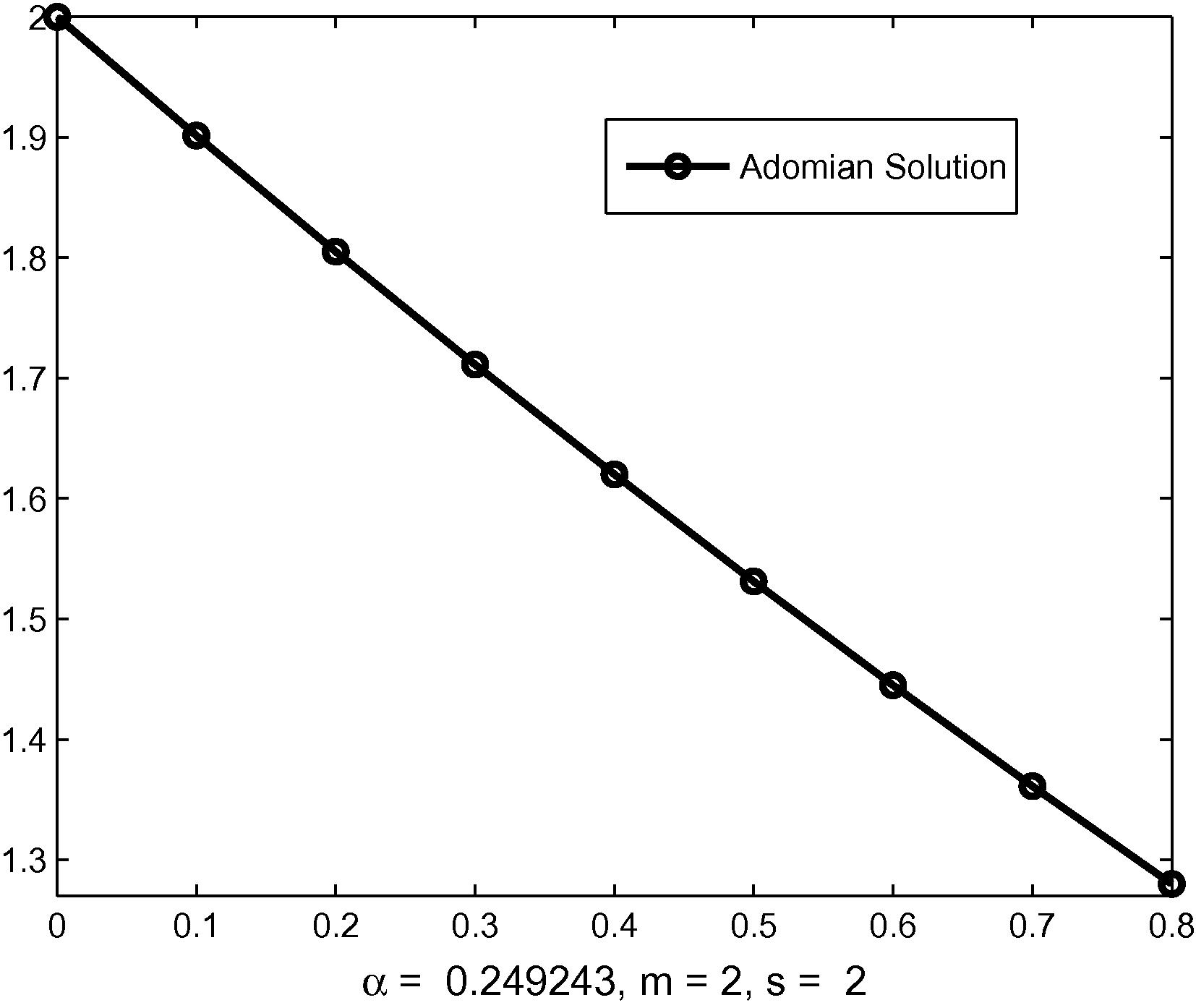
Graphical presentation of Adomian solution.

Export to PPT

Close

Figure 3

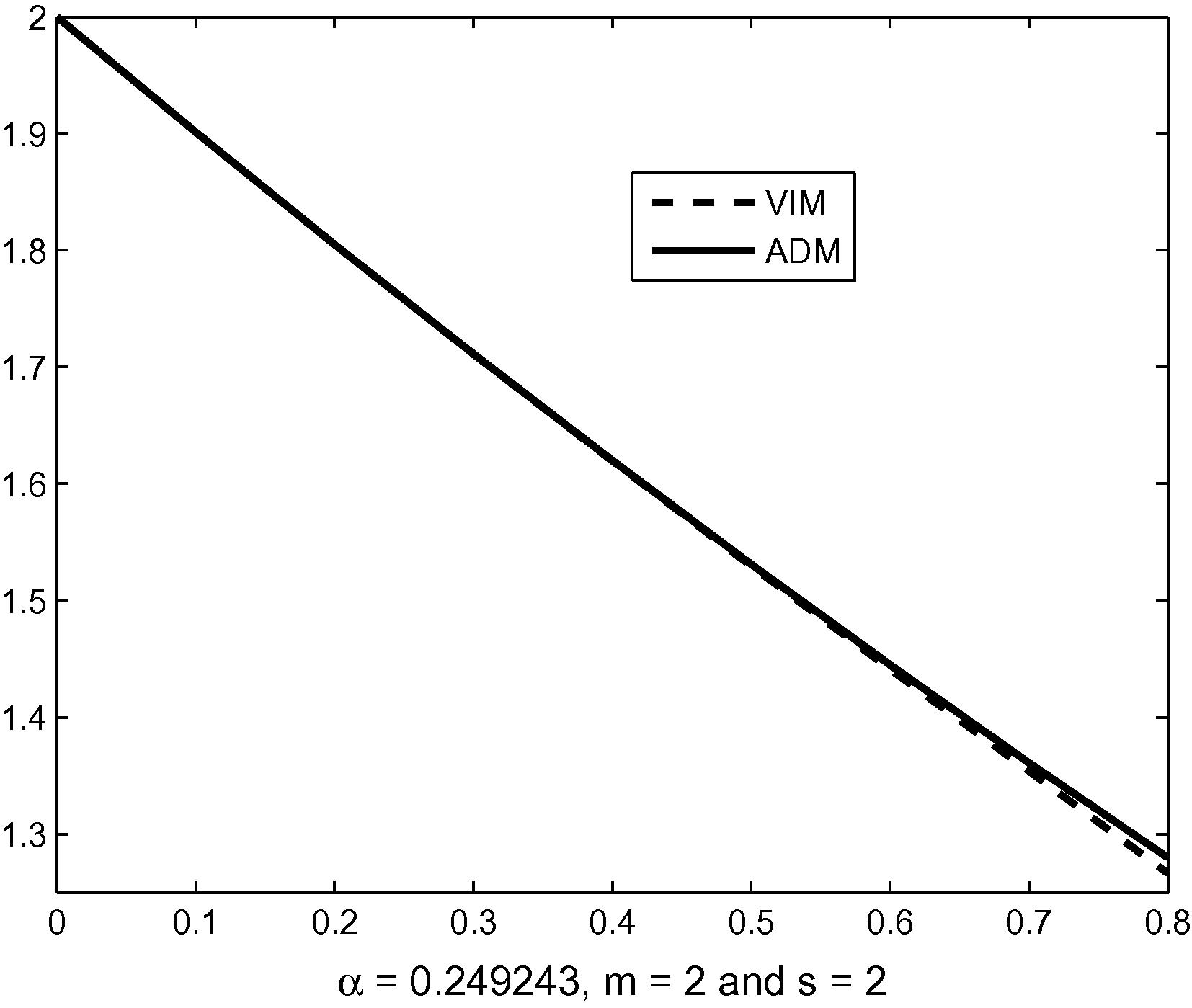
Comparison of the VIM solution and the Adomian solution.

Export to PPT

5 Conclusion

This paper presents a variational iteration method, the VIM-II, that can be employed to solve nonlinear differential equations. The method is applied here in a direct manner without the use of linearization, transformation, discretization, perturbation, or restrictive assumptions. The proposed algorithm’s ability to solve nonlinear problems without the use of Adomian polynomials is evidence of its clear advantage over the decomposition method. This study has considered only an axisymmetrically shrinking sheet by taking m = 2.