Translate this page into:
Numerical solution of the linear two-dimensional Fredholm integral equations of the second kind via two-dimensional triangular orthogonal functions
*Corresponding author. Tel./fax: +98 851 3339944 f.mirzaee@malayeru.ac.ir (Farshid Mirzaee) mirzaee@mail.iust.ac.ir (Farshid Mirzaee)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Abstract
In this paper, we will give some results for developing the two-dimensional triangular orthogonal functions (2D-TFs) for numerical solution of the linear two-dimensional Fredholm integral equations of the second kind. The product of 2D-TFs and some formulas for calculating definite integral of them are derived and utilized to reduce the solution of two-dimensional Fredholm integral equation to the solution of algebraic equations. Also a theorem is proved for convergence analysis. Numerical examples are presented and results are compared with analytical solution to demonstrate the validity and applicability the method.
Keywords
Linear two-dimensional Fredholm integral equations of the second kind
Triangular orthogonal functions
Two-dimensional triangular orthogonal functions
Orthogonal functions
1 Introduction
Many problems in engineering and mechanics can be transformed into two-dimensional Fredholm integral equations of the second kind. For example, it is usually required to solve Fredholm integral equations in the calculation of plasma physics (Farengo et al., 1983). There are many works on developing and analyzing numerical methods for solving Fredholm integral equations of the second kind (see Alipanah and Esmaeili, 2009; Alpert et al., 1993; Anselon, 1971; Atkinson, 1976, 1997; Baker, 1977; Delves and Mohamed, 1985). The subject of the presented paper is applying the 2D-TFs method for solving two-dimensional linear Fredholm integral equations. For this purpose we consider the two-dimensional Fredholm integral equations of the form
2 Review of two-dimensional block pulse functions (2D-BPFs)
As shown in Maleknejad et al. (2010), a set of 2D-BPFs
is defined in the region of
and
as:
According to (2), the interval and are, respectively, divided into and subintervals.
One of the important properties of the 2D-BPFs is the disjointness of them,
The orthogonality of 2D-BPFs is derived immediately from
3 Two-dimensional triangular orthogonal functions
We usually call the triangular orthogonal functions containing one variable as one-dimensional (1D) triangular orthogonal functions (1D-TFs) and those containing two variables as two-dimensional (2D) triangular orthogonal functions (2D-TFs). 1D-TFs have been widely used for solving different problems (Babolian et al., 2008; Deb et al., 2006). A complete detail for 1D-TFs is given in Babolian et al. (2008, 2006). These discussions can also be extended to the 2D-TFs.
3.1 Definition
In the following, we have dissected a 2D-BPFs into two 2D-TFs as shown in Fig. 1. Thus, we have
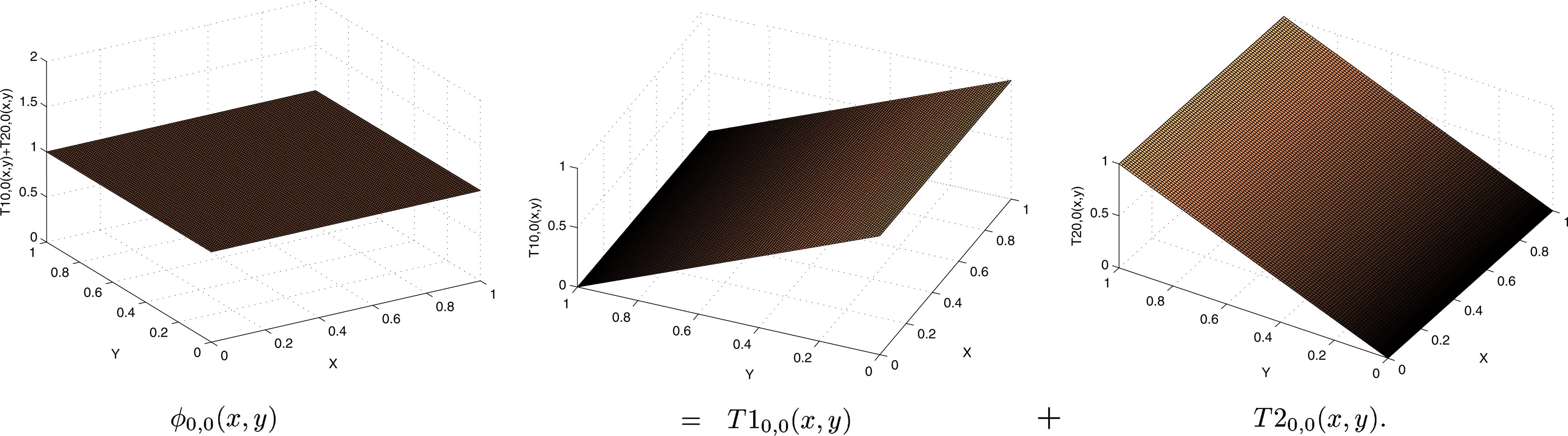
Dissection of
into two 2D-TFs.
3.2 Vector forms
We can generate two vectors of orthogonal 2D-TFs, namely
and
, such that
We now show that Eq. (17) holds. For it
3.3 2D-TFs expansion
We can approximate the function
by 2D-TFs as follows:
thus
Preference (Maleknejad et al., 2010)
It is apparent from (6) and (27) that unlike 2D-BPFs the representation by 2D-TFs does not need any integration to evaluate the coefficients, there by reducing a lot of computational efforts.
3.3.1 Expanding four variables function by 2D-TFs
We can expand
by 2D-TFs vectors, with
and
components, respectively. For convenience, consider
For obtaining desired results, we first fix the independent variables t, s. Then, expand
by 2D-TFs with respect to independent variables x, y as follows:
Now each of
for
can be expanded by 2D-TFs with respect to independent variables t, s. Hence, the expansion of
can be written as
which in equation above
3.4 Other properties
Other properties that we will need are
4 Two-dimensional Fredholm integral equation of the second kind
In this section, we present a 2D-TFs method for solving Eq. (1). Changing the variables
and
Eq. (1) can be written as
Let us expand
and
by 2D-TFs (LH2D-TF and RH2D-TF) as follows:
5 Convergence analysis
Assume the Banach space of all continuous functions on with norm .
Let . We denote the error 2D-TFS by where and show the approximate and exact solutions of the two-dimensional linear Fredholm integral equation, respectively. If we note to Eq. (27), we will see the coefficients 's and 's are not optimal. By using the optimal coefficients, the representational errors can be reduced.
The solution of the two-dimensional linear Fredholm integral equation by using 2D-TFs approximation converges if
Let where
We get and choose , by increasing m, it implies as . □
6 Numerical illustration
In this section, we present one example and their numerical results to show the high accuracy of the solution obtained by 2D-TFs.
Consider the two-dimensional linear Fredholm integral equation
| Nodes (x, y) | 2D-TFs method with m = 32 | Error of 2D-TFs method with m = 32 | Exact solution |
|---|---|---|---|
| (0, 0) | 1.0000e−000 | 0 | 1.0000e−000 |
| (0.1, 0.1) | 7.020e−001 | −7.5800e−003 | 6.9444e−001 |
| (0.2, 0.2) | 5.1974e−001 | −9.5400e−003 | 5.1020e−001 |
| (0.3, 0.3) | 4.0022e−001 | −9.6000e−003 | 3.9062e−001 |
| (0.4, 0.4) | 3.1767e−001 | −9.0300e−003 | 3.0864e−001 |
| (0.5, 0.5) | 2.5030e−001 | −3.0000e−004 | 2.5000e−001 |
| (0.6, 0.6) | 2.0704e−001 | −4.3000e−004 | 2.0661e−001 |
| (0.7, 0.7) | 1.7585e−001 | −2.2400e−003 | 1.7361e−001 |
| (0.8, 0.8) | 1.5055e−001 | −2.6200e−003 | 1.4793e−001 |
| (0.9, 0.9) | 1.3036e−001 | −2.8100e−003 | 1.2755e−001 |
7 Conclusion
Two-dimensional Fredholm integral equations are usually difficult to solve analytically. In many cases, it is required to obtain the approximate solutions, for this purpose the presented method can be proposed. We have investigated the application of orthogonal functions by 2D-TFs for solving the linear two-dimensional Fredholm integral equations. This technique is very simple and involves less computation. Also we can expand this method to higher dimensional problems and other classes of integral equations such as nonlinear two-dimensional Fredholm integral equations, linear and nonlinear two-dimensional Volterra integral equations.
References
- Alipanah, A., Esmaeili, S., 2009. Numerical solution of the two-dimensional Fredholm integral equations using Gaussian radial basis function. J. Comput. Appl. Math., in press.
- Wavelets for the fast solution of second-kind integral equations. SIAM J. Sci. Comput.. 1993;14:159-184.
- [Google Scholar]
- Collectively Compact Operator Approximation Theory. Englewood Cliffs, NJ: Prentice-Hall; 1971.
- A Survey of Numerical Methods for the Solution of Fredholm Integral Equations of the Second Kind. Philadelphia, PA: SIAM; 1976.
- The Numerical Solution of Integral Equations of the Second Kind. Cambridge: Cambridge University Press; 1997.
- Using triangular orthogonal functions for solving Fredholm integral equations of the second kind. Appl. Math. Comput.. 2008;201:452-456.
- [Google Scholar]
- The Numerical Treatment of Integral Equations. Oxford: Clarendon Press; 1977.
- A new set of orthogonal functions and its application to the analysis of dynamic systems. J. Franklin Inst.. 2006;343:1-26.
- [Google Scholar]
- Computational Method for Integral Equations. New York: Cambridge University Press; 1985.
- An electromagnetic integral equation: application to microtearing modes. Phys. Fluids. 1983;26:3515-3523.
- [Google Scholar]
- Application of 2D-BPFs to nonlinear integral equations. Commun. Nonlinear Sci. Numer. Simulat.. 2010;15:527-532.
- [Google Scholar]







