Applications of new integral transform for linear and nonlinear fractional partial differential equations

This study aims to obtain the approximate resolution of the fractional partial differential equation through the help of unprecedented new integral transform (NIT) called Elzaki Decomposition Method (EDM), applied to the new integral transform for fractional partial differential equations (PDEs). The technique converges to the right solution, fractional partial differential equations. Some examples were illustrated to confirm the accuracy of the method.

Keywords

Fractional partial differential equation

New integral transform method (NIT)

Adomian decomposition method (ADM)

Show Related Articles from PubMed

1 Introduction

Many of phenomena emerging from many scientific displaces such as plasma physics, solid state physics, mathematical biology, fluid dynamics and chemical kinetic are technicality partial differential equation (Miller and Ross, 1993; Podlubny, 1999; Mahdy et al., 2015 ).

The new integral transform was proposed by tarig Elzaki to enable solving ordinary and partial differential equation in time domain. Several mathematical tools can be used to solve differential equation like Fourier, Laplace and Sumudu transform (Elzaki, 2011; Mohamed and Elzaki, 2014). For a broad spectrum of functional equations, (ADM) is used with success (Adomian, 1994). This method relies on infinite series to represent a solution and it is often the case where the series converges to the accurate solution. In (Bulut and Evans, 2002); (ADM) is applied to dissolve differential equation. (El-Tawil et al., 2004) solved the differential equation and then obtained results that were compared to the results obtained by using standard (ADM). In this dissertation, we applied (NIT) method to obtained accurate analytical and approximate solutions to equation of fractional order.

The paper is structured as follows: in Section 2, the foundations of the fractional calculus are presented. In Section 3, the methodology of the study, we used (NIT) algorithm for PDEs. Section 4 contains the efficiency and strength of the method with illustrative examples showing it. Stopping points are offered in Section 5.

2 Fundamental concepts of fractional theory

In this segment, we remark the subject requisite definitions and attributes of the fractional calculus theory and ELzaki Transform.

Definition (1)

A function $h (τ), τ > 0,$ is told to be in the space $C_{η}, η \in R,$ if the yonder be a real number $σ > η$ such that $h (τ) = τ^{σ} h_{1} (τ),$ where $h_{1} (τ) \in C [0, \infty),$ clearly $C_{η} \subset C_{v} i f v ⩽ η .$

Definition (2)

let’s Riemann-Liouville fractional integral operator of order $υ ⩾ 0,$ then $h (τ) \in C_{η}, η ⩾ - 1,$ is known as, accordingly (Miller and Ross, 1993; Podlubny, 1999; Mahdy et al., 2015 );

(2.1)

J^{υ} h (τ) = \frac{1}{Γ (υ)} \int_{0}^{τ} {(τ - ξ)}^{υ - 1} h (ξ) d ξ υ, τ, ξ > 0,

Definition (3)

Caputo fractional derivative of the left sided, $h,$ $h \in C_{- 1}^{n}, n \in N \cup \{0\},$ is known as, accordingly

(2.2)

D^{υ} h (τ) = \frac{\partial^{υ} h (τ)}{\partial τ^{υ}} = J^{r - υ} [\frac{\partial^{r} h (τ)}{\partial τ^{r}}], r - 1 < υ ⩽ r, r \in N .

we hold properties of the operator (Miller and Ross, 1993; Podlubny, 1999; Mahdy et al., 2015; Elzaki, 2011; Mohamed and Elzaki, 2014; Adomian, 1994; Bulut and Evans, 2002; El-Tawil et al., 2004; Arife and Yildirim, 2011; He, 1997; He, 1997; He, 1998; He, 1998; He, 1999; Wazwaz, 2007 );

(2.3)

\begin{matrix} 1 . J^{υ} J^{σ} h (τ) = J^{υ + σ} h (τ), υ, σ ⩾ 0 . \\ 2 . J^{υ} t^{γ} = \frac{Γ (γ + 1)}{Γ (υ + γ + 1)} τ^{υ + γ}, υ > 0, γ > - 1, τ > 0 . \\ 3 . J^{υ} (D_{*}^{υ} h (τ)) = h (τ) - \sum_{γ = 0}^{r - 1} h^{(k)} (0^{+}) \frac{τ^{k}}{γ!}, τ > 0, r - 1 < υ ⩽ r . \end{matrix}

Definition (4)

the new integral transform (NIT) is known as, accordingly (Elzaki, 2011; Mohamed and Elzaki, 2014); $A = \{|h (τ)| < N e^{\frac{τ}{k_{j}}}, i f τ \in {(- 1)}^{i} \times [0, \infty)\}$

Before the next formulation,

(2.4)

E [h (τ)] = ρ \int_{0}^{\infty} h (τ) e^{\frac{- τ}{ρ}} d τ = H (ρ) r ⩾ 0, k_{1} ⩽ ρ ⩽ K_{2} .

Definition (5)

If $r - 1 < σ ⩽ r, r \in N,$ then the new integral transform (NIT) of the fractional derivative $D_{*}^{σ} h (ξ, τ)$ is,

(2.5)

E [D_{*}^{σ} h (ξ, τ)]] = \frac{H (ξ, ρ)}{ρ^{σ}} - \sum_{k = 0}^{r - 1} ρ^{2 - σ + k} h^{(k)} (ξ, 0), r - 1 < σ ⩽ r,

where $H (ξ, ρ)$ be the (NIT) $h (ξ, τ)$ (Mohamed and Elzaki, 2014).

3 The new integral decomposition (NIT)

The purpose of this subdivision is to talk about the use of The (NIT) algorithm for linear and nonlinear fractional partial differential equation. We take the universal form of inhomogeneous linear and Non-linear Partial Fractional differential equations of the frame.

(3.1)

D_{τ}^{σ} ψ (ξ, τ) + M ψ (ξ, τ) + Y ψ (ξ, τ) = g (ξ, τ), ξ, τ ⩾ 0, r - 1 < σ ⩽ r .

where

D_{τ}^{σ} = \frac{\partial^{σ}}{\partial τ^{σ}}

is the order fractional derivative differential equation, where

M

is the linear term operator,

Y

is a nonlinear part of the equation above, and

g

is the exporter function. The Eq. (3.1) is correlating with the initial and boundary conditions, as, accordingly

(3.2)

ψ (ξ, 0) = R (ξ), ψ_{τ} (ξ, 0) = F (ξ), 0 < σ ⩽ 1, 1 < σ ⩽ 2 .

Applying the (NIT) to both parties of Eq. (3.1), and referring to the linearity of the (NIT), the result is: $E (D_{τ}^{σ} ψ (ξ, τ)) + E (M ψ (ξ, τ)) + E (Y ψ (ξ, τ)) = E (g (ξ, τ)), σ > 0 .$

Applying the (NIT) property, we will get: $\frac{ψ (ξ, ρ)}{ρ^{σ}} - \sum_{k = 0}^{r - 1} ρ^{2 - σ + k} h^{(k)} (ξ, 0) = E (g (ξ, τ)) - E ((M ψ (ξ, τ)) + (Y ψ (ξ, τ))), σ > 0 .$

Suppose $w = \sum_{k = 0}^{r - 1} ρ^{2 - σ + k} h^{(k)} (ξ, 0),$ to will get

(3.4)

ψ (ξ, ρ) = ρ^{σ} E (g (ξ, τ)) + ρ^{σ} (w) - ρ^{σ} E ((M ψ (ξ, τ)) + (Y ψ (ξ, τ))), σ > 0 .

The criterion of the new integral decomposition method defines the solution $ψ (ξ, τ)$ in sequences

(3.5)

ψ (ξ, τ) = \sum_{r = 0}^{\infty} ψ_{r} (ξ, τ),

The Non-linear Formula is Decomposition as, accordingly:

(3.6)

Y ψ (ξ, τ) = \sum_{n = 0}^{\infty} A_{n},

For the nonlinear, function $Y ψ (ξ, τ)$ the first Adomian polynomials (Adomian, 1994), to will get:

(3.7)

E (\sum_{r = 0}^{\infty} ψ_{r} (ξ, τ)) = ρ^{σ} E (g (ξ, τ)) + ρ^{σ} (w) - ρ^{σ} E (M (\sum_{r = 0}^{\infty} ψ_{r} (ξ, τ)) + (Y \sum_{n = 0}^{\infty} A_{n} (ψ))), σ > 0 .

Finally, by using the two parties of the equation, we get the repeated algorithm as the following

(3.8)

E (ψ_{0} (ξ, τ)) = ρ^{σ} E (g (ξ, τ)) + ρ^{σ} (w)

(3.9)

E (ψ_{1} (ξ, τ)) = - ρ^{σ} (E (M ψ_{0} (ξ, τ) - A_{0} (ψ))) .

(3.10)

E (ψ_{2} (ξ, τ)) = - ρ^{σ} (E (M ψ_{1} (ξ, τ) - A_{1} (ψ))) .

As accordingly, we conclude that the repeating relation is specified by:

(3.11)

E (ψ_{r + 1} (ξ, τ)) = - ρ^{σ} (E (M ψ_{r} (ξ, τ) - A_{r} (ψ))) . r ⩾ 1 .

Applying the inverse (NIT) Eqs. (3.8)–(3.11), to obtain:

(3.12)

ψ_{0} (ξ, τ) = Z (τ)

(3.13)

ψ_{r + 1} (ξ, τ) = - E^{- 1} (ρ^{σ} (E (M ψ_{r} (ξ, τ) - A_{r} (ψ)))), r ⩾ 1 .

In which $Z (τ)$ is the function that comes from the origin term and the specific initial condition. Now first applying The (NIT) of the terms on the right hand side of Eq. (3.13) then applying inverse Elzaki transform we get the value of $u_{1}, u_{2}, . . . u_{n} . . .$ .

4 Illustrative examples

In this segment, we use the fractional new integral transform decomposition method for solving Time- Fractional PDEs in a pipe.

Example 1

Consider the following one-dimensional linear inhomogeneous fractional wave equation (Adomian, 1994).

(4.1)

D^{σ} ψ_{τ} (ξ, τ) + ψ_{ξ} (ξ, τ) = \frac{τ^{1 - σ}}{Γ (2 - σ)} sin ξ + τ cos ξ, ξ, τ ⩾ 0, 0 < τ ⩽ 1 .

Subject to the initial condition:

(4.2)

ψ (ξ, 0) = 0 .

Applying the (NIT) to both parties Eq. (4.1), to get:

(4.3)

ψ (ξ, ρ) = ρ^{2} ψ (ξ, 0) + ρ^{σ} E [\frac{τ^{1 - σ}}{Γ (2 - σ)} sin ξ + τ cos ξ] - ρ^{σ} E [ψ_{ζ} (ξ, τ)] .

Using given initial condition Eq. (4.3), become

(4.4)

ψ (ξ, ρ) = ρ^{σ} E [\frac{τ^{1 - σ}}{Γ (2 - σ)} sin ξ + τ cos ξ] - ρ^{σ} E [ψ_{ζ} (ξ, τ)] .

For the nonlinear, function $Y ψ (ξ, τ),$ the first Adomian polynomials (Adomian, 1994), to obtain:

(4.5)

\sum_{r = 0}^{\infty} ψ_{r} (ξ, ρ) = ρ^{σ} E [\frac{τ^{1 - σ}}{Γ (2 - σ)} sin ξ + τ cos ξ] - ρ^{σ} E [\sum_{r = 0}^{\infty} ψ_{r ζ} (ξ, τ)] .

Finally, by using the two parties of the Eq. (4.5), we get the repeated algorithm as the following

(4.6)

ψ_{0} (ξ, ρ) = ρ^{σ} E [\frac{τ^{1 - σ}}{Γ (2 - σ)} sin ξ + τ cos ξ],

(4.7)

ψ_{r + 1} (ξ, ρ) = - ρ^{σ} E [ψ_{r ζ} (ξ, τ)] .

Applying the inverse (NIT) Eqs. (4.6) and (4.7), to obtain: $ψ_{0} (ξ, τ) = E^{- 1} [ρ^{σ} E [\frac{τ^{1 - σ}}{Γ (2 - σ)} sin ξ + τ cos ξ]],$

(4.8)

ψ_{r + 1} (ξ, τ) = - E [ρ^{σ} E [ψ_{r ζ} (ξ, τ)]] .

Consequently,

(4.9)

ψ_{0} (ξ, τ) = τ sin ξ + \frac{τ^{σ + 1}}{(σ + 1)!} cos ξ,

(4.10)

ψ_{1} (ξ, τ) = - \frac{τ^{σ + 1}}{(σ + 1)!} cos ξ + \frac{τ^{2 σ + 1}}{(2 σ + 1)!} sin ξ,

(4.11)

ψ_{2} (ξ, τ) = - \frac{τ^{2 σ + 1}}{(2 σ + 1)!} sin ξ - \frac{t^{3 σ + 1}}{(3 σ + 1)!} cos ξ,

By excluding the noise terms and holding the part that contains the non-noise terms, we get the accurate solution of the Eq. (4.1). Starting by $ψ_{0}$ , and repeating the process twice, we obtain the accurate solution $ψ (ξ, τ) = τ sin ξ$ .

Example 2

Consider the following one-dimensional linear inhomogeneous fractional Burgers equation (Odibat and Momani, 2009);

(4.12)

D_{τ}^{σ} ψ (ξ, τ) = ψ_{ξ ξ} (ξ, τ) - ψ_{ξ} (ξ, τ) + \frac{2 τ^{2 - σ}}{Γ (3 - σ)} + 2 ξ - 2, ξ, τ ⩾ 0, 0 < σ ⩽ 1 .

Subject to the initial condition:

(4.13)

ψ (ξ, 0) = ξ^{2} .

Applying the (NIT) to both parties Eq. (4.12), to get:

(4.14)

ψ (ξ, ρ) = ρ^{2} ψ (ξ, 0) + ρ^{σ} E [\frac{t^{2 - σ}}{Γ (3 - σ)} + 2 ξ - 2] - ρ^{σ} E [ψ_{ξ} (ξ, ρ) - ψ_{ξ ξ} (ξ, ρ)]

Using given initial condition Eq. (5.14) become,

(4.15)

ψ (ξ, ρ) = ρ^{2} ξ^{2} + ρ^{σ} E [\frac{t^{2 - σ}}{Γ (3 - σ)} + 2 ξ - 2] - ρ^{σ} E [ψ_{ξ} (ξ, ρ) - ψ_{ξ ξ} (ξ, ρ)] .

The nonlinear function $Y ψ (ξ, τ),$ the first Adomian polynomials (Adomian, 1994), to obtain;

(4.16)

\sum_{r = 0}^{\infty} ψ_{r} (ξ, τ) = ξ^{2} ρ^{2} + ρ^{σ} E [\frac{t^{2 - σ}}{Γ (3 - σ)} + 2 ξ - 2] - ρ^{σ} E [\sum_{r = 0}^{\infty} ψ_{r ξ} (ξ, ρ) - \sum_{r = 0}^{\infty} ψ_{r ξ ξ} (ξ, ρ)] .

Finally, by using the two parties of the Eq. (4.16), we get the repeated algorithm as the following:

(4.17)

ψ_{0} (ξ, ρ) = ρ^{2} ξ^{2} + ρ^{σ} E [\frac{t^{2 - σ}}{Γ (3 - σ)} + 2 ξ - 2],

(4.18)

ψ_{r + 1} (ξ, ρ) = - ρ^{σ} E [\sum_{r = 0}^{\infty} ψ_{r ξ} (ξ, ρ) - \sum_{r = 0}^{\infty} ψ_{r ξ ξ} (ξ, ρ)] .

Applying the inverse (NIT) Eqs. (4.17) and (4.18), to obtain: $ψ_{0} (ξ, τ) = E^{- 1} [ρ^{2} ξ^{2} + ρ^{σ} E [\frac{t^{2 - σ}}{Γ (3 - σ)} + 2 ξ - 2]],$ $ψ_{r + 1} (ξ, τ) = - E^{- 1} [ρ^{σ} E [\sum_{r = 0}^{\infty} ψ_{r ξ} (ξ, ρ) - \sum_{r = 0}^{\infty} ψ_{r ξ ξ} (ξ, ρ)]] .$

Consequently,

(4.19)

ψ_{0} (ξ, τ) = ξ^{2} + τ^{2} + (2 ξ - 2) \frac{τ^{σ}}{σ!},

(4.20)

ψ_{1} (ξ, τ) = (2 ξ - 2) \frac{τ^{σ}}{σ!} - 2 \frac{τ^{2 σ}}{2 σ!},

(4.21)

ψ_{2} (ξ, τ) = 2 \frac{τ^{2 σ}}{2 σ!},

(4.22)

ψ_{3} (ξ, τ) = 0 .

Canceled noise terms of $ψ_{0}$ satisfy Eq. (4.12), we find that the exact solution is given by $ψ (ξ, τ) = ξ^{2} + τ^{2} .$

Example 3

Consider the following nonlinear Time- Fraction KdV equation (Wazwaz, 2007)

(4.23)

D^{σ} ψ_{τ} (ξ, τ) - 3 ψ_{ξ}^{2} (ξ, τ) + ψ_{ξ ξ ξ} (ξ, τ) = 0, ξ, τ ⩾ 0, 0 < σ ⩽ 1 .

Subject to the initial condition:

(4.24)

ψ (ξ, 0) = 6 ξ .

Applying the (NIT) to both parties Eq. (4.23), we will get:

(4.25)

ψ (ξ, τ) = ρ^{σ} ψ (ξ, 0) - ρ^{σ} E [3 ψ_{ξ}^{2} (ξ, τ) + ψ_{ξ ξ ξ} (ξ, τ)] .

Using the given initial condition, Eq. (4.25) become,

(4.26)

ψ (ξ, τ) = 6 ξ ρ^{σ} - ρ^{σ} E [3 ψ_{ξ}^{2} (ξ, τ) + ψ_{ξ ξ ξ} (ξ, τ)] .

the nonlinear function

Y ψ (ξ, τ),

the first Adomian polynomials (Adomian, 1994), to get,

(4.27)

\sum_{r = 0}^{\infty} ψ_{r} (ξ, ρ) = 6 ξ ρ^{σ} - ρ^{σ} E [\sum_{r = 0}^{\infty} A_{r} + \sum_{r = 0}^{\infty} ψ_{ξ ξ ξ} (ξ, τ)] .

The first few components of $A_{r}$ polynomials are given by: $\begin{matrix} A_{0} = ψ_{0 ξ}^{2}, \\ A_{1} = {(2 ψ_{0} ψ_{1})}_{ξ}, \\ A_{2} = {(2 ψ_{0} ψ_{2} + ψ_{1}^{2})}_{ξ}, \end{matrix}$

Finally, by using the two parties of the Eq. (4.27), we get the repeated algorithm as the following:

(4.28)

ψ_{0} (ξ, ρ) = 6 ξ ρ^{2},

(4.29)

ψ_{r + 1} (ξ, ρ) = - ρ^{σ} E [\sum_{r = 0}^{\infty} A_{r} + ψ_{r ξ ξ ξ} (ξ, τ)]

Applying the inverse (NIT) for Eqs. (4.28) and (4.29), to obtain: $ψ_{0} (ξ, τ) = 6 ξ,$ $ψ_{r + 1} (ξ, τ) = - E^{- 1} [ρ^{σ} E [\sum_{r = 0}^{\infty} A_{r} + ψ_{r ξ ξ ξ} (ξ, τ)]] .$

Consequently,

(4.30)

\begin{matrix} ψ_{0} (ξ, τ) = 6 ξ, \\ ψ_{1} (ξ, τ) = 6 ξ \frac{36}{σ!} τ^{σ}, \\ ψ_{2} (ξ, τ) = 2 (6 ξ) \frac{{(36)}^{2}}{2 σ!} τ^{2 σ}, \\ ψ_{3} (ξ, τ) = (6 ξ) {(36)}^{3} [\frac{4}{2 σ!} + \frac{1}{{(σ!)}^{2}}] \frac{2 σ!}{3 σ!} τ^{3 σ}, \end{matrix}

The other components of the EDM competence are determined in an identical format, then approximate solution of (4.23) in sequence, $ψ (ξ, τ) = 6 ξ [1 + \frac{36}{σ!} τ^{σ} + 2 \frac{{(36)}^{2}}{2 σ!} τ^{2 σ} + {(36)}^{3} [\frac{4}{2 σ!} + \frac{1}{{(σ!)}^{2}}] \frac{2 σ!}{3 σ!} τ^{3 σ} + \dots]$

And when $σ = 1,$ we obtain the exact solution of the nonlinear KdV Equation (Wazwaz, 2007) (see Table 1 and Fig. 1).

Example 4

Consider the following nonlinear Time- Fraction differential equation (Wazwaz, 2007);

(4.31)

D^{σ} ψ_{τ} (ξ, τ) - 2 \frac{ξ^{2}}{τ} ψ (ξ, τ) ψ_{ξ} (ξ, τ) = 0, ξ, τ ⩾ 0, 1 < σ ⩽ 2 .

Subject to initial condition:

(4.32)

ψ (ξ, 0) = 0, ψ_{ξ} (ξ,) = ξ .

Applying the (NIT) to both parties Eq. (4.31), we will get:

(4.33)

ψ (ξ, ρ) = ρ^{2} ψ (ξ, 0) + ρ ψ_{ξ} (ξ, 0) + ρ^{σ} E [2 \frac{ξ^{2}}{τ} ψ (ξ, τ) ψ_{ξ} (ξ, τ)],

Using given initial condition Eq. (4.33) become,

(4.34)

ψ (ξ, ρ) = ρ ξ + ρ^{σ} E [2 \frac{ξ^{2}}{τ} ψ (ξ, τ) ψ_{ξ} (ξ, τ)],

The Nonlinear function $Y ψ (ξ, τ),$ the first Adomian polynomials (Adomian, 1994), to will get

(4.35)

\sum_{r = 0}^{\infty} ψ_{r} (ξ, ρ) = ρ ξ + ρ^{σ} E [2 \frac{ξ^{2}}{τ} \sum_{r = 0}^{\infty} A_{r}],

The first few components of $A_{n} (x, t)$ polynomials are given by:

(4.36)

\begin{matrix} A_{0} = ψ_{0} ψ_{0 ξ}, \\ A_{1} = ψ_{0} ψ_{1 ξ} + ψ_{1} ψ_{0 ξ}, \\ A_{2} = ψ_{0} ψ_{02} + ψ_{2} ψ_{0 ξ} + ψ_{1} ψ_{1 ξ}, \end{matrix}

Finally, by using the two parties of the Eq. (4.35), we get the repeated algorithm as the following

(4.37)

ψ_{0} (ξ, ρ) = ρ ξ,

(4.38)

ψ_{r + 1} (ξ, ρ) = ρ^{σ} E [2 \frac{ξ^{2}}{τ} \sum_{r = 0}^{\infty} A_{r}] .

Applying the inverse (NIT) Eqs. (4.37) and (4.38), to obtain:

(4.39)

ψ_{0} (ξ, τ) = ξ τ,

(4.40)

ψ_{r + 1} (ξ, ζ) = E^{- 1} [ρ^{σ} E [2 \frac{ξ^{2}}{τ} \sum_{r = 0}^{\infty} A_{r}]] .

Consequently,

(4.41)

\begin{matrix} ψ_{0} (ξ, τ) = ξ τ, \\ ψ_{1} (ξ, τ) = \frac{2 ξ^{3}}{(σ + 1)!} τ^{σ + 1}, \\ ψ_{2} (ξ, τ) = \frac{16 ξ^{5}}{(2 σ + 1)!} τ^{2 σ + 1}, \\ ψ_{3} (ξ, τ) = [\frac{32 \times 6}{(σ + 1)!} + \frac{24}{{((σ + 1)!)}^{2}}] \frac{(2 σ + 1)! ξ^{7}}{(3 σ + 1)!} τ^{3 σ + 1}, \end{matrix}

(4.42)

ψ (ξ, τ) = ξ τ + \frac{2 ξ^{3}}{(σ + 1)!} τ^{σ + 1} + \frac{16 ξ^{5}}{(2 σ + 1)!} τ^{2 σ + 1} + [\frac{32 \times 6}{(σ + 1)!} + \frac{24}{{((σ + 1)!)}^{2}}] \frac{(2 σ + 1)! ξ^{7}}{(3 σ + 1)!} τ^{3 σ + 1}

When $σ = 2,$ Eq. (4.42) becomes:

(4.43)

ψ (ξ, τ) = ξ τ + \frac{1}{3} {(ξ τ)}^{3} + \frac{2}{15} {(ξ τ)}^{5} + \frac{17}{315} {(ξ τ)}^{7} + \dots .

On the side, we catch sight of that the development of the function $ψ (ξ, τ) = tan (ξ τ),$ according to the Taylor series in the vicinity of $τ = 0,$ is will get:

(4.44)

ψ (ξ, τ) = ξ τ + \frac{1}{3} {(ξ τ)}^{3} + \frac{2}{15} {(ξ τ)}^{5} + \frac{17}{315} {(ξ τ)}^{7} + 0 {(\frac{τ}{ξ})}^{8} .

Therefore, we conclude that: $ψ (ξ, τ) = tan (ξ τ),$ that is the accurate solution of Eq. (4.31) in the status $σ = 2$ (see Table 2 and Fig. 2).

Table 1 Results of four term approximate solution of Example (3). Where (EADM) Elzaki Adomian Decomposition Method.

$τ$	$ζ$	$σ = 0.94$	$σ = 0.96$	$σ = 0.98$	$σ = 1$	$exact$
$τ$	$ζ$	$EADM$				$exact$
0.01	0 0.1000	0	0	0	0	0
	0.2000	1.0237	0.9935	0.9658	0.9404	0.9375
	0.3000	2.0474	1.9871	1.9317	1.8808	1.8750
	0.4000	3.0711	2.9806	2.8975	2.8212	2.8125
	0.5000	4.0949	3.9742	3.8634	3.7617	3.7500
	0.6000	5.1186	4.9677	4.8292	4.7021	4.6875
	0.7000	6.1423	5.9612	5.7951	5.6425	5.6250
	0.8000	7.1660	6.9548	6.7609	6.5829	6.5625
	0.9000	8.1897	7.9483	7.7268	7.5233	7.5000
	1.0000	9.2134	8.9419	8.6926	8.4637	8.4375
		10.2372	9.9354	9.6585	9.4042	9.3750

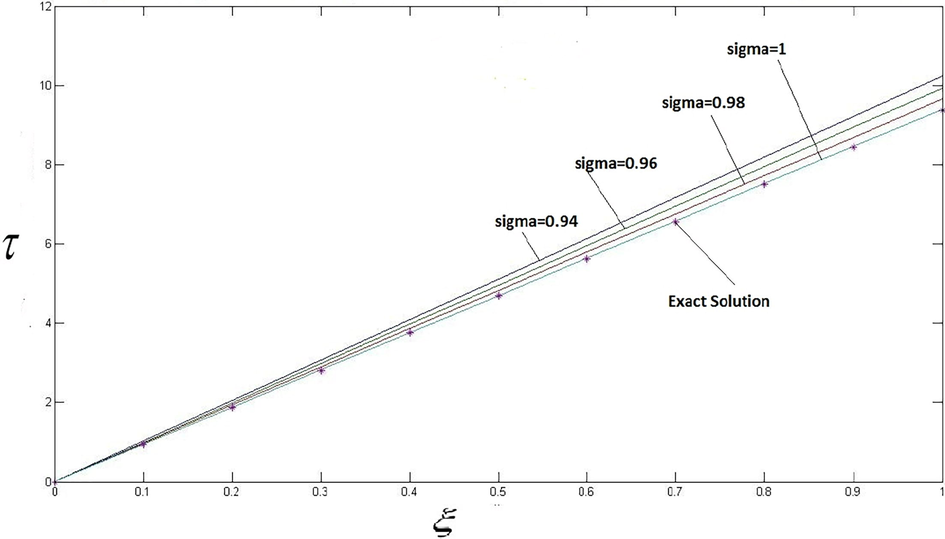
The plot of solution of Example 4.3, when τ = 1.01 and ξ = 0 : 1 .

Table 2 Results of four term approximate solution of Example (4). Where (EADM) Elzaki Adomian Decomposition Method.

$τ$	$ς$	$σ = 1.94$	$σ = 1.96$	$σ = 1.98$	$σ = 2$	$exact$
$τ$	$ς$	$EADM$				$exact$
1.1	0	0	0	0	0	0
	0.1000	0.1105	0.1105	0.1105	0.1104	0.1104
	0.2000	0.2239	0.2238	0.2237	0.2236	0.2236
	0.3000	0.3435	0.3432	0.3429	0.3425	0.3425
	0.4000	0.4735	0.4726	0.4718	0.4709	0.4708
	0.5000	0.6197	0.6176	0.6156	0.6137	0.6131
	0.6000	0.7906	0.7862	0.7820	0.7781	0.7761
	0.7000	0.9993	0.9906	0.9824	0.9745	0.9697
	0.8000	1.2659	1.2493	1.2337	1.2190	1.2097
	0.9000	1.6208	1.5902	1.5616	1.5348	1.5237
	1.0000	2.1086	2.0540	2.0033	1.9560	1.9648

The plot of solution of Example 4.4 when, τ = 1.1 and ξ = 0 : 1 .

5 Conclusions

New transform decomposition method has been utilized to apply to find an exact solution of Fractional Partial Differential Equations, with constant coefficients. Definitions and theorems are introduced, and special formulas of Mittage -Leffler function are observed with their proofs, it is concluded that the new decomposition transform is a potent, effective and reliable instrument to determine the resolution of fractional partial differential equations.

References

Adomian G., . Solving Frontier Problems of Physics: The Decomposition Method. Dordrecht: Kluwer Academic Publishers; 1994.
Arife A.S., Yildirim A., . New modified variational iteration transform method (MVITM) for solving eighth-order boundary value problems in one step. World Appl. Sci. J.. 2011;13(10):2186-2190.
[Google Scholar]
Bulut H., Evans D.J., . On the solution of the Riccati equation by the decomposition method. Int. J. Comput. Math.. 2002;79:103-109.
[Google Scholar]
Elzaki Tarig M., . The new integral transform “ELzaki Transform”. Global J. Pure Appl. Math.. 2011;7(1):57-64. ISSN 0973–1768
[Google Scholar]
El-Tawil M.A., Bahnasawi A.A., Abdel-Naby A., . Solving Riccati differential equation using Adomian’s decomposition method. Appl. Math. Comput.. 2004;157:503-514.
[Google Scholar]
He J.H., . Variational iteration method for delay differential equations. Commun. Nonlinear Sci. Numer. Simul.. 1997;2(4):235-236.
[Google Scholar]
He J.H., . Semi-inverse method of establishing generalized principles for fluid mechanics with emphasis on turbo machineryaero dynamics. Int. J. Turbo Jet-Engines. 1997;14(1):23-28.
[Google Scholar]
He J.H., . approximate solution of nonlinear differential equations with convolution product nonlinearities. Comput. Meth. Appl. Mech. Eng.. 1998;167:69-73.
[Google Scholar]
He J.H., . approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Meth. Appl. Mech. Eng.. 1998;167:57-68.
[Google Scholar]
He J.H., . Variational iteration method – a kind of non-linear analytical technique: some examples. Int. J. Nonlinear Mech.. 1999;34:699-708.
[Google Scholar]
Mahdy Amr M.S., Mohamed Adel S., Mtawa Ahmad A.H., . Implementation of the homotopy perturbation sumudu transform method for solving klein-gordon equation. Appl. Math.. 2015;6:617-628.
[Google Scholar]
Miller K.S., Ross B., . An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: John Wiley and Sons; 1993.
Mohamed Mohamed Z., Elzaki Tarig M., . Solutions of fractional ordinary differential equations by using Elzaki transform. Appl. Math.. 2014;9(1):27-33. ISSN 0973–4554
[Google Scholar]
Odibat Zaid, Momani Shaher, . The variational iteration method: An efficient scheme for handling fractional partial differential equations in fluid mechanics. Comput. Math. Appl.. 2009;58:2199-2208.
[Google Scholar]
Podlubny I., . Fractional Differential Equations. San Diego, CA: Academic Press; 1999.
Wazwaz A., . The variational iteration method for rational solutions for KdV, K(2,2), Burgers, and cubic Boussinesqequations. J. Comput. Appl. Math. 2007;207:18-23.
[Google Scholar]