A Riccati-type solution of 3D Euler equations for incompressible flow

1 Introduction the Euler system of equations

The Euler system of equations for incompressible flow of inviscid fluid is known to be one of the old famous problems in classical fluid mechanics, besides we should especially note that a lot of great scientists have been trying to solve such a problem during last 265 years.

In accordance with (Landau and Lifshitz, 1987; Ladyzhenskaya, 1969; Lighthill, 1986), the Euler system of equations for incompressible flow of inviscid fluid should be presented in the Cartesian coordinates as below (under the proper initial or boundary conditions):

2 The originating system of PDE for Euler Eqs

Using the identity (u·∇)u = (1/2)∇(u²) − u×(∇ × u), we could present Eqs. (1)–(2) in case of incompressible flow u = {u₁, u₂, u₃} as below (Saffman, 1995; Milne-Thomson, 1950):

1. Steady inviscid flow (the solution does not depend on time);

2. Irrotational flow (the fluid particles don't spin, i.e., the curl of velocity is zero).

3 Presentation of the time-dependent part of solution

The second of the equations of system (3) with the additional demand (5) is proved to have the analytical way to present its solution (Ershkov, 2015, 2016, 2017) in a form below (in regard to the time-parameter t):

It is clear that for the correct solving of system (3) with additional demand (5) we should obtain from Eqs. (4), (6) the three additional equations below (which should determine the spatial part of the curl field w):

Thus, let us search for the exact solution in a form (11); in this case, expressions for the components of the curl field (8) should be presented as below: $$\left\{w_1\text{,}{w}_2\text{,}{w}_3\right\}=\left\{\frac{\partial (\mathrm{\sigma }(x\text{,}y\text{,}t))}{\partial y}+\frac{\partial (\mathrm{\lambda }(x\text{,}z\text{,}t))}{\partial z}\text{,}-\frac{\partial (\sqrt{({\mathrm{\gamma }}^2(x\text{,}y\text{,}z)-{\mathrm{\sigma }}^2(x\text{,}y\text{,}t)-{\mathrm{\lambda }}^2(x\text{,}z\text{,}t))})}{\partial z}-\frac{\partial (\mathrm{\sigma }(x\text{,}y\text{,}t))}{\partial x}\text{,}-\frac{\partial (\mathrm{\lambda }(x\text{,}z\text{,}t))}{\partial x}+\frac{\partial (\sqrt{({\mathrm{\gamma }}^2(x\text{,}y\text{,}z)-{\mathrm{\sigma }}^2(x\text{,}y\text{,}t)-{\mathrm{\lambda }}^2(x\text{,}z\text{,}t))})}{\partial y}\right\}$$ which, taking into account expressions (10)–(11), should be transformed to the form below (γ² > σ²):

Obviously, system of Eqs. (14) is the system of two non-linear ordinary differential equations of the 1-st order for two functions A(t), σ(t) (which could be solved by numerical methods only).

But nevertheless, the solution of system (14) exists, that’s why solution of the system of Eqs. (3) should exist also (for the presented, previously chosen form of the solution (5) + (6)). Approximate solutions of (14) are presented in the next section.

4 Final presentation of the solution

Let us present the non-stationary exact solution {p, u} of the Euler Eqs. (3) in its final form, which should conserve the Bernoulli-function (B = const) (5) to be invariant for the aforementioned system:

Let us especially note that function γ(x,y,z) along with the functions {u₁, u₂, u₃} are proved to satisfy to the continuity Eq. (1) for such an expressions.

System of Eqs. (14) could be transformed as below (let us note again that we consider variables {x,y,z} as variable parameters):

or, it can be transformed properly

Let us schematically imagine at Figs. 1–3 the appropriate components of velocity field {u₁, u₂, u₃}, according to the formulae (15), which correspond to the approximate solutions (20) for functions A(t), σ(t) via derivation (18)–(19): $$u_1=-\sqrt{{\mathrm{\gamma }}^2(y\text{,}z)-{(\exp (-(t-t_0))+D·\mathrm{\gamma }(y\text{,}z))}^2}$$ $$\begin{array}{c}{u}_2=-\cos (A(t)·x)·\mathrm{\sigma }(t)\text{,}\Rightarrow \hfill \\ \Rightarrow u_2=\mathit{cos}(A(t)·x)·(\mathit{exp}(-(t-t_0))+D·\mathrm{\gamma }(y\text{,}z))\text{,}\hfill \\ A(t)=\frac{\mathit{exp}(-t_0)}{D·\mathrm{\gamma }(y\text{,}z)}·\left(\frac{\mathit{exp}(-t)}{(D·\mathrm{\gamma }(y\text{,}z)·\mathit{exp}(-t_0)+\mathit{exp}(-t))}-\frac{\mathrm{\gamma }(y\text{,}z)}{x}\right)\hfill \end{array}$$ $$\begin{array}{c}{u}_3\equiv \mathrm{\sigma }(x\text{,}t)=\sin (A(t)·x)·\mathrm{\sigma }(t)\text{,}\Rightarrow \hfill \\ \Rightarrow u_3=-\sin (A(t)·x)·(\exp (-(t-t_0))+D·\mathrm{\gamma }(y\text{,}z))\text{,}\hfill \\ A(t)=\frac{\exp (-t_0)}{D·\mathrm{\gamma }(y\text{,}z)}·\left(\frac{\exp (-t)}{(D·\mathrm{\gamma }(y\text{,}z)·\exp (-t_0)+\exp (-t))}-\frac{\mathrm{\gamma }(y\text{,}z)}{x}\right)\hfill \end{array}$$

Close

Fig. 1

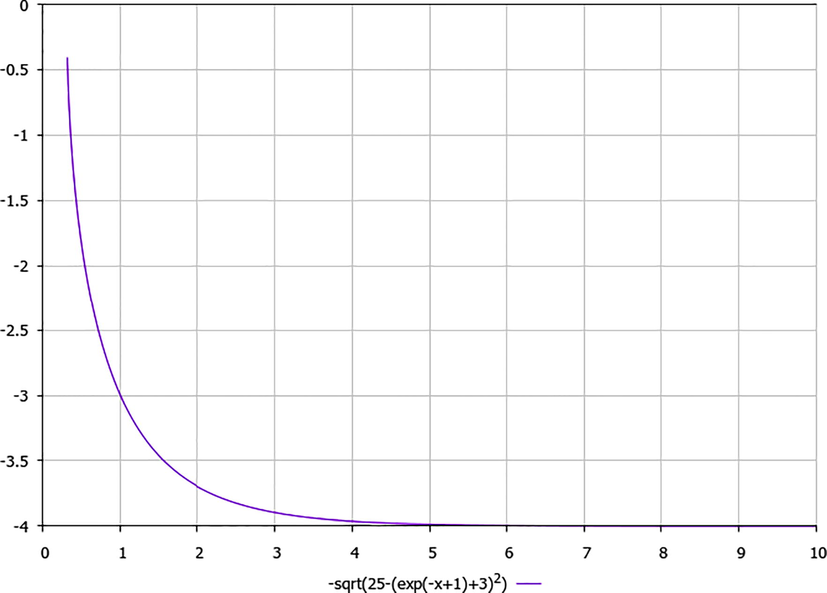
A schematic plot of the component u₁ (t) of velocity field (15), depending on time t (for simplicity, B = 1).

Export to PPT

Close

Fig. 2

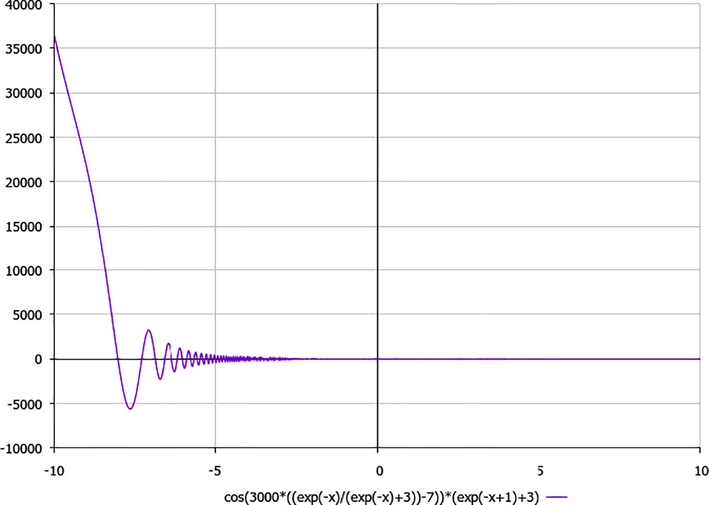
A schematic plot of the component u₂ (t) of velocity field (15), depending on time t (for simplicity, B = 1).

Export to PPT

Close

Fig. 3

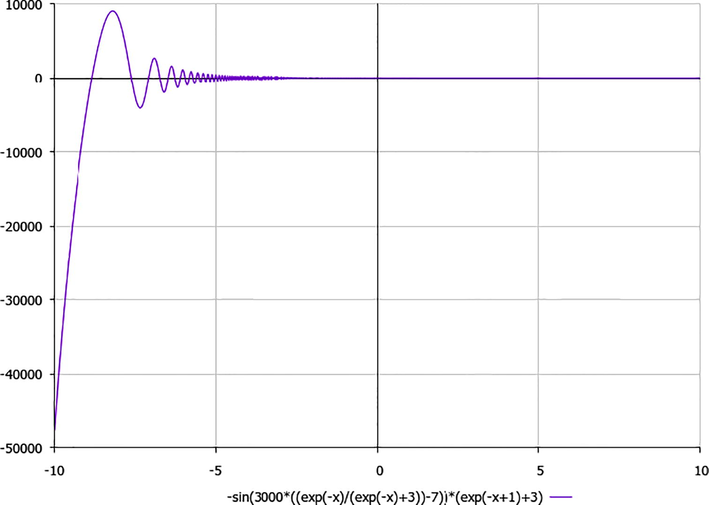
A schematic plot of the component u₃ (t) of velocity field (15), depending on time t (for simplicity, B = 1).

Export to PPT

5 Discussion and conclusion

Meanwhile, the intriguing fact is that Riccati-type seems to be the specific feature for a lot of the solutions in fluid mechanics and magneto-hydrodynamics (Christianto and Smarandache, 2008; Gibbon et al., 2006). We should mention very interesting results of article (Gibbon, 2002), where author discusses the presentation of components of the time-dependent solution for 3D Euler equation, which are supposed to be associated with complex Riccati equation via quaternionic formulation.

We should also mention the paper (Wilchynski, 2009), in which author provides an example of the Riccati equation without periodic solutions which appears in the Euler vorticity dynamics.

All in all, Euler and Navier-Stokes equations have already been investigated in many researches including their numerical and analytical solutions (Drazin and Riley, 2006). However essential deficiency exists in the studies of non-stationary solutions of even the Euler equations for ideal, inviscid flow.

In this derivation, we explore the case of non-stationary flows of the Euler equations for incompressible fluids, which should conserve the Bernoulli-function for the flow.

The aforementioned approach quite differs from that which was used previously in investigation of Euler equations (Ershkov, 2015) by one of the authors. Indeed, an exuberant assumption was made in (Ershkov, 2015), such as separating of variables for the presenting of each components of the solution (including the pressure field). As for the relevance of such the purely mathematical assumption, it seems not to be physically reasonable if we will compare it with the approach for obtaining of our new solution with constant Bernoulli-function which should be invariant inside the limited domain of the flow.

To obtain new solution, we use previously suggested ansatz for solving of the system of Navier-Stokes equations (which is proved to have the analytical way to present its solution in case of conserving the Bernoulli-function for this type of the flows). Conditions for the existence of exact solution of the aforementioned type are proposed. The restrictions at choosing of the form of 3D solution for the given constant Bernoulli-function B are emphasized: for example, the pressure field should be calculated from the given constant Bernoulli-function B, if all the components of velocity field are obtained.

Besides, we should especially note that in our case of solution, we need some boundary conditions that preserve the aforementioned solution inside of the limited domain: indeed, the pressure field should strongly depend on the spatial part of the initial conditions for the components of velocity field (according to the Bernoulli invariant).

Also we should note that since the fluid is incompressible for the development above, there is a strong link between boundary conditions and the solution inside.

The uniqueness of the presented solutions is not considered. In this respect we confine ourselves to mention the paper (Galdi and Rionero, 1979), in which all the difficulties concerning the uniqueness in unbounded domain are remarked (which should be the same for analytical solutions in inviscid fluids if the kinematic viscosity tends to zero).

The last but not least, we have found an elegant way to simplify the presented solution up to the analytical presentation of the approximate solution. Also it has to be specified that the solutions that are constructed can be considered as a class of perturbation of a solutions, absorbed exponentially as t going to infinity ∞ by the null solution.