On Skolem odd and even difference mean graphs

Gee-Choon Lau; P. Jeyanthi; D. Ramya; R. Kalaiyarasi

doi:10.1016/j.jksus.2017.09.018

View/Download PDF

Buy Reprints

PDF

Translate this page into:

30 (

); 286-291

doi:

10.1016/j.jksus.2017.09.018

On Skolem odd and even difference mean graphs

Gee-Choon Lau^{^a,⁎}, P. Jeyanthi^{^d}, D. Ramya^{^c}, R. Kalaiyarasi^{^b}

a Faculty of Computer & Mathematical Sciences, Universiti Teknologi MARA Johor, 85000 Segamat, Malaysia

b Department of Mathematics, Dr. SivanthiAditanar College of Engineering, Tiruchendur 628 215, India

c Department of Mathematics, Government Arts College for Women, Ramanathapuram, India

d Research Centre, Department of Mathematics, Govindammal Aditanar College for Women, Tiruchendur 628 215, Tamil Nadu, India

⁎Corresponding author. geeclau@yahoo.com (Gee-Choon Lau),

Received: 2017-2-24, Accepted: 2017-9-22, Published: 2017-04-01

Disclaimer:
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.

Peer review under responsibility of King Saud University.

Abstract

Let $G = (V, E)$ be a simple, finite and undirected $(p, q)$ -graph with p vertices and q edges. A graph G is Skolem odd difference mean if there exists an injection $f : V (G) \to {0, 1, 2, \dots, p + 3 q - 3}$ and an induced bijection $f^{*} : E (G) \to {1, 3, 5, \dots, 2 q - 1}$ such that each edge uv (with $f (u) > f (v)$ ) is labeled with $f^{*} (uv) = ⌈\frac{f (u) - f (v)}{2}⌉$ . We say G is Skolem even difference mean if there exists an injection $f : V (G) \to {0, 1, 2, \dots, p + 3 q - 1}$ and an induced bijection $f^{*} : E (G) \to {2, 4, 6, \dots, 2 q}$ such that each edge uv (with $f (u) > f (v)$ ) is labeled with $f^{*} (uv) = ⌈\frac{f (u) - f (v)}{2}⌉$ . A graph that admits a Skolem odd (or even) difference mean labeling is called a Skolem odd (or even) difference mean graph. In this paper, first, we construct some new Skolem odd difference mean graphs and then investigate the Skolem even difference meanness of some standard graphs.

Keywords

Mean labeling

Odd mean labeling

Skolem difference mean labeling

Skolem odd difference mean labeling

Skolem even difference mean labeling

05C78

1 Background

Let $G = (V, E)$ be a simple, finite and undirected $(p, q)$ -graph of order $| V | = p$ and size $| E | = q$ . A graph labeling is an assignment of integers to the vertices or edges (or both) of a graph subject to certain conditions. Many types of labeling have been introduced over the last few decades. An excellent survey of graph labeling is available in Gallian (2016). Terms and notations not defined here are used in the sense of Harary (1972). The concept of mean graph was introduced in Somasundaram and Ponraj (2003). A graph G is called a mean graph if there is an injection $f : V (G) \to {0, 1, 2, \dots, q}$ such that each edge uv is labeled with $⌈\frac{f (u) + f (v)}{2}⌉$ and the resulting edge labels are distinct. In 2006, Manickam and Marudai studied the odd mean labeling of graphs. A graph G is said to be odd mean if there exists an injection $f : V (G) \to {0, 1, 2, \dots, 2 q - 1}$ and an induced bijection $f^{*} : E (G) \to {1, 3, 5, \dots, 2 q - 1}$ such that edge uv is labeled with $⌈\frac{f (u) + f (v)}{2}⌉$ . The notion of Skolem difference mean graph was due to Murugan and Subramanian (2011) and further studied by Ramya et al. (2013) and Ramya and Selvi (2014). A graph is difference mean if there exists an injection $f : V (G) \to {1, 2, \dots, p + q}$ and an induced bijection $f^{*} : E (G) \to {1, 2, 3, \dots, q}$ such that each edge uv (with $f (u) > f (v)$ ) is labeled with $⌈\frac{f (u) - f (v)}{2}⌉$ . Ramya et al. (2014) defined the concept of Skolem odd difference mean graph and further studied in Jeyanthi et al. (2016). A graph G is Skolem odd difference mean if there exists an injection $f : V (G) \to {0, 1, 2, \dots, p + 3 q - 3}$ and an induced bijection $f^{*} : E (G) \to {1, 3, 5, \dots, 2 q - 1}$ such that each edge uv (with $f (u) > f (v)$ ) is labeled with $⌈\frac{f (u) - f (v)}{2}⌉$ . Moreover, G is a Skolem even vertex odd difference mean graph if for each vertex $v, f (v)$ is even. Motivated by the results in Ramya et al. (2014) and Jeyanthi et al. (2016), in this paper, we introduce the dual version of Skolem odd difference mean labeling. A graph G is Skolem even difference mean if there exists an injection $f : V (G) \to {0, 1, 2, \dots, p + 3 q - 1}$ and an induced bijection $f^{*} : E (G) \to {2, 4, 6, \dots, 2 q}$ such that each edge uv (with $f (u) > f (v)$ ) is labeled with $⌈\frac{f (u) - f (v)}{2}⌉$ . Moreover, G is a Skolem even vertex even difference mean graph if for each vertex $v, f (v)$ is even. In the present study, we also use the following definitions.

Let $K_{m, n}$ be the complete bipartite graph with partite sets of size m and n respectively. A caterpillar $S (n_{1}, n_{2}, \dots, n_{m})$ is obtained from a path $P_{m} : v_{1} v_{2} v_{3} \dots v_{m}$ by adding $n_{i}$ pendant edges to vertex $v_{i}$ $(1 ⩽ i ⩽ m)$ . The coconut tree $T (n, m)$ is obtained by identifying the central vertex of the star $K_{1, n}$ with a pendant vertex of a path $P_{m}$ . The graph $P_{m} @ P_{n}$ is obtained from $P_{m}$ and m copies of $P_{n}$ by identifying one pendant vertex of the i-th copy of $P_{n}$ with the i-th vertex of $P_{m}$ . The graph ${mP}_{n}$ is the disjoint union of m copies of $P_{n}$ . Let $B (m, n)$ be the bistar obtained from a $K_{1, m}$ and a $K_{1, n}$ by joining their central vertex u and v with an edge. The graph $B (m, n$ $: P_{w}), w ⩾ 2$ , is obtained from the bistar $B (m, n)$ by replacing the edge uv with $P_{w}$ . A graph obtained from a path by attaching exactly two pendant edges to each internal vertex of a path $P_{m}, m ⩾ 3$ , is called a twig and is denoted by $Tg (m)$ .

This study is organized into three sections. In Section 2, we show that there exist Skolem odd difference mean graphs with non-cycle and non-tree component(s). In Section 3, we investigate the Skolem even difference meanness of some standard graphs.

2 Construction of Skolem odd difference mean graphs

By definition, it is a fact that if G is a Skolem odd difference mean $(p, q)$ -graph, then $p ⩾ q$ (also see Theorem 2.6 in Selvi et al. (2015) for a proof by contrapositive). If G is connected, then $q = p$ or $q = p - 1$ . Hence, G is a graph with one cycle or a tree.

Lemma 2.1

If G is a connected Skolem odd difference mean $(p, p)$ -graph, then $f (u)$ is odd for some $u \in V (G)$ .

Proof

By definition, $p + 3 q - 3 = 4 p - 3$ which is odd. Hence the largest edge label $2 p - 1$ must be obtained by labeling two adjacent vertices with 0 and $4 p - 3$ giving us an odd vertex label. □

Theorem 2.2

The disjoint union of paths of length at least 2 is a Skolem even vertex odd difference mean graph.

Proof

Suppose the paths are $⋃ P_{n_{i}}, 1 ⩽ i ⩽ t, t \geq 2$ and $n_{i} ⩽ n_{j}$ for $i < j$ . Let the vertices of the i-th path $P_{n_{i}}$ be $u_{i, 1}$ to $u_{i, n_{i}}$ . Now we have $\sum n_{i}$ vertices and $\sum n_{i} - t$ edges. Hence, we need to label the vertices by integers in $[0, 4 \sum n_{i} - 3 t - 3]$ .

Label $u_{1, j}$ by $0, 4, 8, \dots$ for $j = 1, 3, 5, \dots, n_{1}$ (or $n_{1} - 1$ if $n_{1}$ is even).
For $i = 1, 2, \dots, t - 1$ , let $a_{i}$ be the largest used label for $P_{n_{i}}$ . Label $u_{i + 1, j}$ of $P_{n_{i + 1}}$ by $a_{i} + 2, a_{i} + 6, a_{i} + 10, \dots$ for $j = 1, 3, 5, \dots, n_{i + 1}$ (or $n_{i + 1} - 1$ if $n_{i + 1}$ is even).
Label $u_{t, j}$ by $a_{t} + 2, a_{t} + 6, a_{t} + 10, \dots$ for $j = n_{t}, n_{t} - 2, n_{t} - 4, \dots, 2$ (or $n_{t} - 1, n_{t} - 3, n_{t} - 5, \dots, 2$ if $n_{t}$ is odd).
For $i = t, t - 1, \dots, 2$ , let $b_{i}$ be the largest used label for $P_{n_{i}}$ . Label $u_{i - 1, j}$ of $P_{n_{i - 1}}$ by $b_{i} + 2, b_{i} + 6, b_{i} + 10, \dots$ for $j = n_{t}, n_{t} - 2, n_{t} - 4, \dots, 2$ (or $n_{t} - 1, n_{t} - 3, n_{t} - 5, \dots, 2$ if $n_{t}$ is odd).

It is easy to verify that the largest vertex label used is $4 \sum n_{i} - 4 t - 2$ . Moreover, all the vertex labels are even such that the induced edge labels are odd integers from 1 to $2 \sum n_{i} - 2 t - 1$ . □

For example, we can label the vertices of $2 P_{3} \cup P_{4} \cup P_{6} \cup P_{7}$ by $0, 70, 4; 6, 68, 10; 12, 66, 16, 62; 18, 60, 22, 56, 26, 52; 28, 50, 32, 46, 36, 42, 40$ according to the labeling function as defined above.

Theorem 2.3

The graph $C_{m} \cup P_{n}$ is a Skolem odd difference mean graph for $m = 4, 6$ and $n ⩾ 2$ .

Proof

Consider $C_{4} \cup P_{n}$ . Let $C_{4} = u_{1} u_{2} u_{3} u_{4} u_{1}$ . Define a function $f : V \to {0, 1, \dots, 4 n + 10}$ by $f (u_{1}) = 0, f (u_{2}) = 4 n + 10, f (u_{3}) = 8, f (u_{4}) = 4 n + 6, f (v_{2 i - 1}) = 4 n + 2 - 4 (i - 1)$ for $1 ⩽ i ⩽ ⌈\frac{n}{2}⌉$ , and $f (v_{2 i}) = 5 + 4 i$ for $1 ⩽ i ⩽ ⌊ \frac{n}{2} ⌋$ .

The induced edge label function $f^{*}$ is defined as $f^{*} (u_{1} u_{2}) = 2 n + 5, f^{*} (u_{2} u_{3}) = 2 n + 1, f^{*} (u_{3} u_{4}) = 2 n - 1, f^{*} (u_{4} u_{1}) = 2 n + 3$ , and $f^{*} (v_{i} v_{i + 1}) = 2 n - 3 - 2 (i - 1)$ for $1 ⩽ i ⩽ n - 1$ .

Consider $C_{6} \cup P_{n}$ . Let $C_{6} = u_{1} u_{2} u_{3} u_{4} u_{5} u_{6} u_{1}$ . Define a function $f : V \to {0, 1, 2, \dots, 4 n + 18}$ by $f (u_{1}) = 0, f (u_{2}) = 4 n + 14, f (u_{3}) = 4, f (u_{4}) = 4 n + 6, f (u_{5}) = 12, f (u_{6}) = 4 n + 18, f (v_{1}) = 4 n + 2, f (v_{2 i - 1}) = 2 (2 n - 2 i + 1)$ for $2 ⩽ i ⩽ ⌈\frac{n}{2}⌉$ , and $f (v_{2 i}) = 1 + 4 i$ for $1 ⩽ i ⩽ ⌊ \frac{n}{2} ⌋$ .

The induced edge label function $f^{*}$ is defined as $f^{*} (u_{1} u_{2}) = 2 n + 7, f^{*} (u_{2} u_{3}) = 2 n + 5, f^{*} (u_{3} u_{4}) = 2 n + 1, f^{*} (u_{4} u_{5}) = 2 n - 3$ , $f^{*} (u_{5} u_{6}) = 2 n + 3, f^{*} (u_{6} u_{1}) = 2 n + 9, f^{*} (v_{1} v_{2}) = 2 n - 1, f^{*} (v_{i} v_{i + 1}) = 2 n - 2 i - 1$ for $2 ⩽ i ⩽ n - 1$ . Thus, f is a Skolem odd difference mean labeling of $C_{m} \cup P_{n}$ for $m = 4, 6$ and $n ⩾ 2$ . □

Theorem 2.4

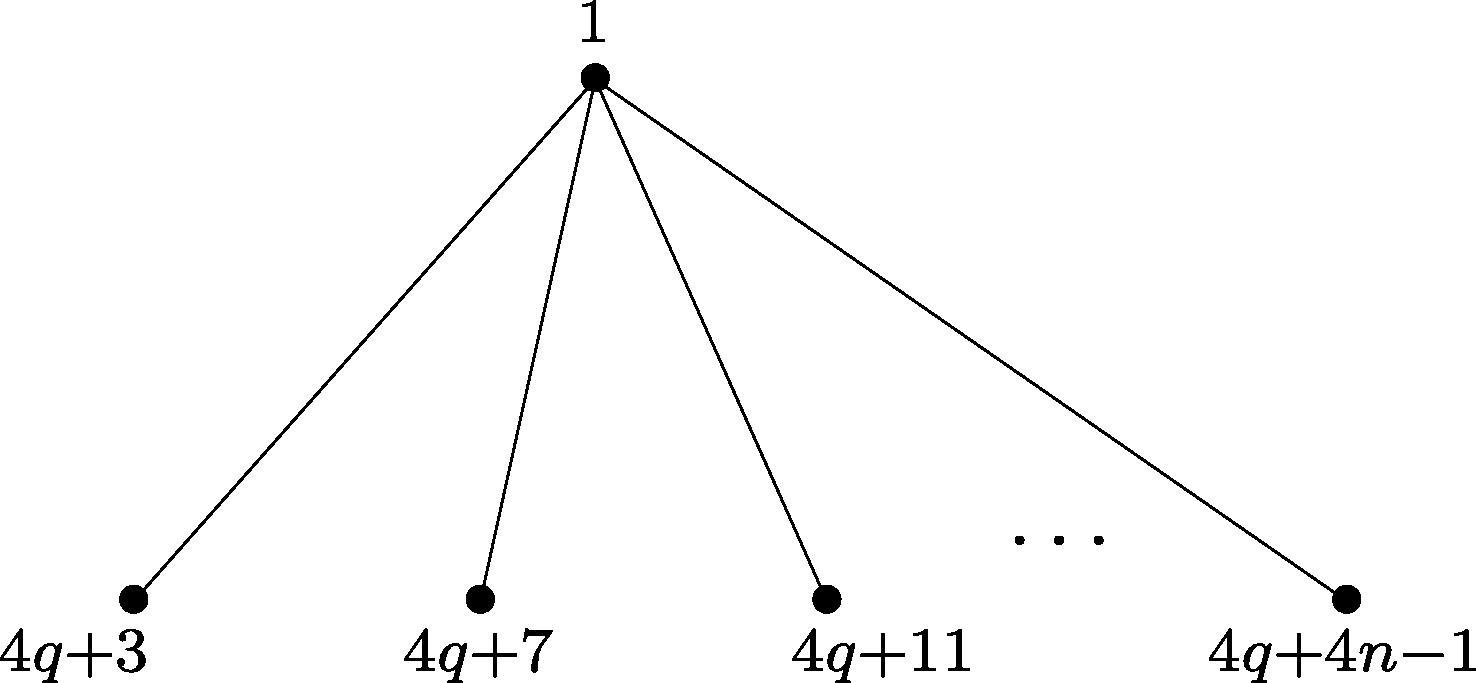
The graph $K_{2, n} \cup (n - 1) K_{2}$ is a Skolem even vertex odd difference mean graph for all $n ⩾ 2$ .

Proof

Let the vertices of $K_{2, n}$ be $u_{1}, u_{2}$ and $v_{i}, 1 ⩽ i ⩽ n$ whereas the vertices of $(n - 1) K_{2}$ be $x_{j}, y_{j}, 1 ⩽ j ⩽ n - 1$ so that the edges are $u_{1} v_{i}, u_{2} v_{i}$ and $x_{j} y_{j}$ . Define a function $f : V \to {0, 1, 2, \dots, 12 n - 6}$ as $f (u_{1}) = 0, f (u_{2}) = 4 n, f (v_{i}) = 12 n - 2 - 4 i, 1 ⩽ i ⩽ n$ and $f (x_{j}) = 2 j, f (y_{j}) = 4 n - 2 - 2 j, 1 ⩽ j ⩽ n - 1$ (see Fig. 1).

The induced edge label function $f^{*}$ is defined as $f^{*} (u_{1} v_{i}) = 6 n - 1 - 2 i, f^{*} (u_{2} v_{i}) = 4 n - 1 - 2 i, 1 ⩽ i ⩽ n$ and $f^{*} (x_{j} y_{j}) = 2 (n - j) - 1$ for $1 ⩽ j ⩽ n - 1$ . Thus f is a Skolem even vertex odd difference mean labeling of $K_{2, n} \cup (n - 1) K_{2}$ . □

Corollary 2.5

The graph ${nK}_{2}$ is Skolem odd difference mean for $n ⩾ 1$ with all vertex labels of same parity.

Theorem 2.6

If G is a Skolem even vertex odd difference mean $(q + 1, q)$ -graph, then $G \cup {nK}_{2}$ is a Skolem odd difference mean graph for all $n ⩾ 1$ .

Proof

Let G be a Skolem even vertex odd difference mean $(q + 1, q)$ -graph with a labeling $f : V (G) \to {0, 1, 2, \dots, 4 q - 2}$ and its induced edge labeling $f^{*}$ . The edge set labels are $1, 3, 5, \dots, 2 q - 1$ . Define $G' = G \cup {nK}_{2}$ with $V ({nK}_{2}) = {u_{i}, v_{i} : 1 ⩽ i ⩽ n}$ and $E ({nK}_{2}) = {u_{i} v_{i} : 1 ⩽ i ⩽ n}$ so that $| V (G') | = q + 1 + 2 n$ and $| E (G') | = q + n$ . Define an injective function $g : V (G') \to {0, 1, 2, \dots, 4 q - 2 + 5 n}$ such that $g (v) = f (v)$ for each $v \in V (G)$ . Similarly to the vertex labeling of $(n - 1) K_{2}$ for Theorem 2.4, also define $g (u_{i}) = 2 i - 1, g (v_{i}) = 4 q + 4 n - 2 i + 1$ for $1 ⩽ i ⩽ n$ . The induced edge label function $g^{*}$ is defined as $g^{*} (e) = f^{*} (e)$ and $g^{*} (u_{i} v_{i}) = (4 q + 4 n - 4 i + 2) / 2 = 2 (q + n - i) + 1$ for $1 ⩽ i ⩽ n$ . Thus, $g (u_{i}), g (v_{i})$ are odd and ${g^{*} (u_{i} v_{i})} = {2 q + 1, 2 q + 3, \dots, 2 (q + n) - 1}$ . Hence g is a Skolem odd difference mean labeling of $G \cup {nK}_{2}$ . □

Corollary 2.7

The graph $G \cup {nK}_{2}$ is a Skolem odd difference mean graph if G is a Skolem even vertex odd difference mean graph as in Theorems 2.2 and 2.3 or in Somasundaram and Ponraj (2003).

Theorem 2.8

If G is a Skolem even vertex odd difference mean $(q + 1, q)$ -graph, then $G \cup P_{n}$ is a Skolem odd difference mean graph for all $n ⩾ 2$ .

Proof

Let G be a Skolem even vertex odd difference mean $(q + 1, q)$ -graph with a labeling $f : V (G) \to {0, 1, 2, \dots, 4 q - 2}$ and its induced edge labeling $f^{*}$ . The edge set labels are $1, 3, 5, \dots, 2 q - 1$ . Define $G' = G \cup P_{n}$ with $V (P_{n}) = {u_{i}, 1 ⩽ i ⩽ n}$ and $E (P_{n}) = {u_{i} u_{i + 1}, 1 ⩽ i ⩽ n - 1}$ so that $| V (G') | = q + n + 1$ and $| E (G') | = q + n - 1$ . Define an injective function $g : V (G') \to {0, 1, 2, \dots, 4 q + 4 n - 5}$ such that $g (v) = f (v)$ for each $v \in V (G), g (u_{2 i - 1}) = 4 i - 3$ for $1 ⩽ i ⩽ ⌈\frac{n}{2}⌉$ and $g (u_{2 i}) = 4 q + 4 (n - i) - 1$ for $1 ⩽ i ⩽ ⌊ \frac{n}{2} ⌋$ . The induced edge label function $g^{*}$ is defined as $g^{*} (e) = f^{*} (e)$ and $g^{*} (u_{i} u_{i + 1}) = 2 (q + n - i) - 1$ for $1 ⩽ i ⩽ n - 1$ . It can be verified that $g (u_{i})$ is odd for $1 ⩽ i ⩽ n$ , and ${g^{*} (u_{i} u_{i + 1})} = {2 q + 1, 2 q + 3, \dots, 2 (q + n) - 1}$ . Hence g is a Skolem odd difference mean labeling of $G \cup P_{n}$ for all $n ⩾ 2$ . □

Corollary 2.9

The graph $G \cup P_{n}$ is a Skolem odd difference mean graph if G is a Skolem even vertex odd difference mean graph as in Theorems 2.2 and 2.3 or in Somasundaram and Ponraj (2003).

Theorem 2.10

If G is a Skolem even vertex odd difference mean $(q + 1, q)$ -graph, then $G \cup K_{1, n}$ is a Skolem odd difference mean graph for all $n ⩾ 1$ .

Proof

The induced edge label function $g^{*}$ is defined as $g^{*} (e) = f^{*} (e)$ and $g^{*} ({uu}_{i}) = 2 (q + i) - 1$ for $1 ⩽ i ⩽ n$ . It can be verified that $g (u_{i})$ is odd for $1 ⩽ i ⩽ n$ , and ${g^{*} (u_{i} u_{i + 1})} = {2 q + 1, 2 q + 3, \dots, 2 (q + n) - 1}$ . Hence g is a Skolem odd difference mean labeling of $G \cup K_{1, n}$ for all $n ⩾ 1$ . □

Corollary 2.11

The graphs $G \cup K_{1, n}$ are Skolem odd difference mean graph if G is a Skolem even vertex odd difference mean graph as in Theorems 2.2 and 2.3 or in Somasundaram and Ponraj (2003).

Vertex labeling of K 2 , n ∪ ( n - 1 ) K 2 .

Vertex labeling of K 1 , n in G ∪ K 1 , n .

3 Skolem even difference mean graphs

As a natural extension, we introduce in this section the Skolem even difference mean labeling of graphs.

Observation 3.1

If G is a Skolem even difference mean $(p, q)$ -graph, then $p ⩾ q$ (similar to Theorem 2.6 in Selvi et al. (2015)).

Observation 3.2

If $p = q + 1$ , then any Skolem even difference mean labeling of G must admit an even vertex labeling.

Theorem 3.1

The caterpillar $S (n_{1}, n_{2}, \dots, n_{m})$ is a Skolem even vertex even difference mean graph.

Proof

Let $V (S (n_{1}, n_{2}, \dots, n_{m})) = {v_{j}, u_{i}^{j} : 1 ⩽ i ⩽ n_{j}, 1 ⩽ j ⩽ m}$ and $E (S (n_{1}, n_{2}, \dots, n_{m})) = {v_{j} v_{j + 1} : 1 ⩽ j ⩽ m - 1} \cup {v_{j} u_{i}^{j} : 1 ⩽ i ⩽ n_{j}, 1 ⩽ j ⩽ m}$ . Define a function $f : V (S (n_{1}, n_{2}, \dots, n_{m})) \to {0, 1, 2, 3, 4, \dots, p + 3 q - 1 = 4 (m + n_{1} + n_{2} + \dots + n_{m} - 1)}$ such that

$f (v_{1}) = 0, f (v_{2 j - 1}) = 4 (n_{2} + n_{4} + \dots + n_{2 j - 2}) + 4 (j - 1)$ for $2 ⩽ j ⩽ ⌈\frac{m}{2}⌉$ ,
$f (v_{2 j}) = 4 (m + n_{1} + n_{2} + \dots + n_{m}) - 4 (n_{1} + n_{3} + \dots + n_{2 j - 1} + j)$ for $1 ⩽ j ⩽ ⌊ \frac{m}{2} ⌋$ ,
$f (u_{i}^{1}) = 4 (m + n_{1} + n_{2} + \dots + n_{m}) - 4 i$ for $1 ⩽ i ⩽ n_{1}$ , and $f (u_{i}^{2 j - 1}) = 4 (m + n_{1} + n_{2} + \dots + n_{m}) - 4 (n_{1} + n_{3} + \dots + n_{2 j - 3} + i + j - 1)$ for $2 ⩽ j ⩽ ⌈\frac{m}{2}⌉, 1 ⩽ i ⩽ n_{2 j - 1}$ ,
$f (u_{i}^{2}) = 4 i$ for $1 ⩽ i ⩽ n_{2}$ , and $f (u_{i}^{2 j}) = 4 (n_{2} + n_{4} + \dots + n_{2 j - 2} + i + j - 1)$ for $2 ⩽ j ⩽ ⌊ \frac{m}{2} ⌋, 1 ⩽ i ⩽ n_{2 j}$ .

Let $e_{j} = v_{j} v_{j + 1}$ for $1 ⩽ j ⩽ m - 1$ and $e_{i}^{j} = v_{j} u_{i}^{j}$ for $1 ⩽ i ⩽ n_{j}, 1 ⩽ j ⩽ m$ . For each vertex label f the induced edge label $f^{*}$ is defined as follows: $f^{*} (e_{i}^{j}) = 2 (m + n_{j} + n_{j + 1} + \dots + n_{m}) - 2 (i + j - 1)$ for $1 ⩽ j ⩽ m, 1 ⩽ i ⩽ n_{j}$ , $f^{*} (e_{j}) = 2 (m + n_{j + 1} + n_{j + 2} + \dots + n_{m}) - 2 j$ for $1 ⩽ j ⩽ m - 1$ .

Thus f is a Skolem even difference mean labeling of $S (n_{1}, n_{2}, \dots, n_{m})$ . Hence $S (n_{1}, n_{2}, \dots, n_{m})$ is a Skolem even difference mean graph. □

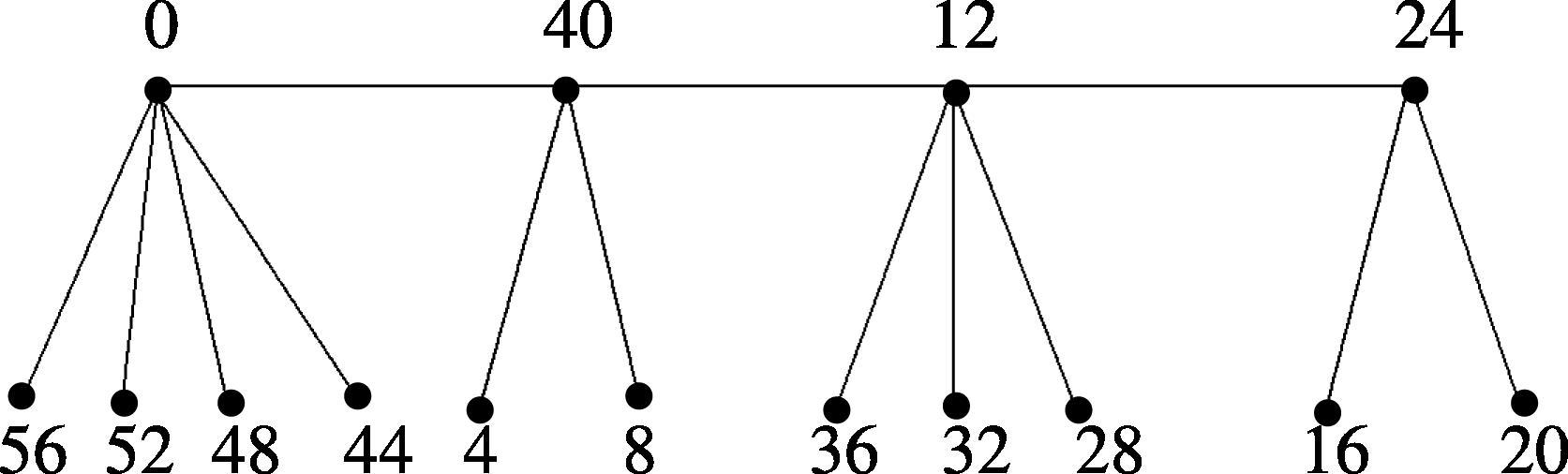
For example, the Skolem even difference mean labeling of $S (4, 2, 3, 2)$ is shown in Fig. 3.

Corollary 3.2

The graphs (i) $T (n, m)$ , (ii) $B (r, s$ $: P_{w})$ and (iii) $Tg (m)$ are Skolem even difference mean.

Proof

It follows from Theorem 3.1 such that for (i), we take $n_{1} = n, n_{2} = n_{3} = \dots = n_{m} = 0$ ; for (ii), we take $n_{1} = r, n_{2} = n_{3} = \dots = n_{w - 1} = 0, n_{w} = s$ ; for (iii), we take $n_{1} = n_{m} = 0$ and $n_{2} = n_{3} = \dots = n_{m - 1} = 2$ . □

S ( 4 , 2 , 3 , 2 ) is a Skolem even difference mean graph.

The following examples illustrate the three cases in the corollary.

Case (i).

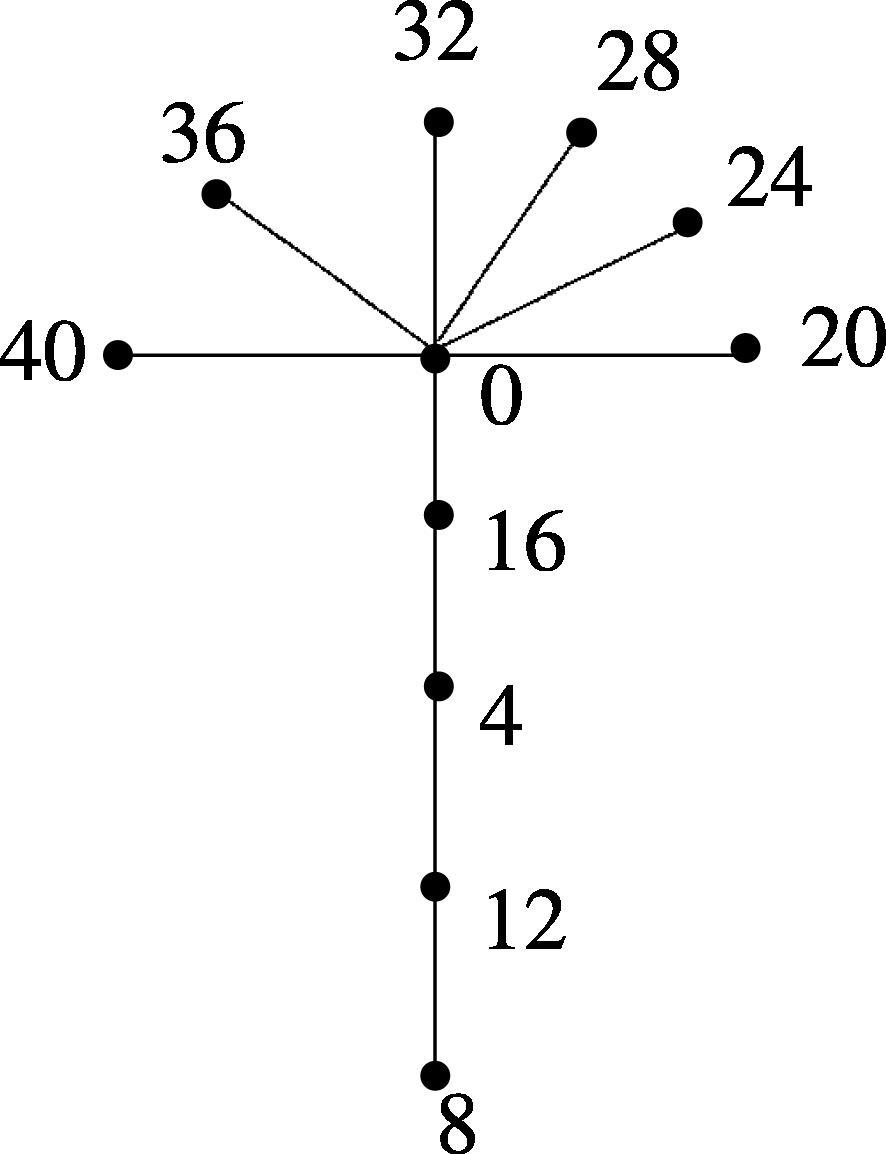
The Skolem even difference mean labeling of $T (5, 6)$ is shown in Fig. 4.
Case (ii).

The Skolem even difference mean labeling of $B (4, 3$ $: P_{5})$ is shown in Fig. 5.
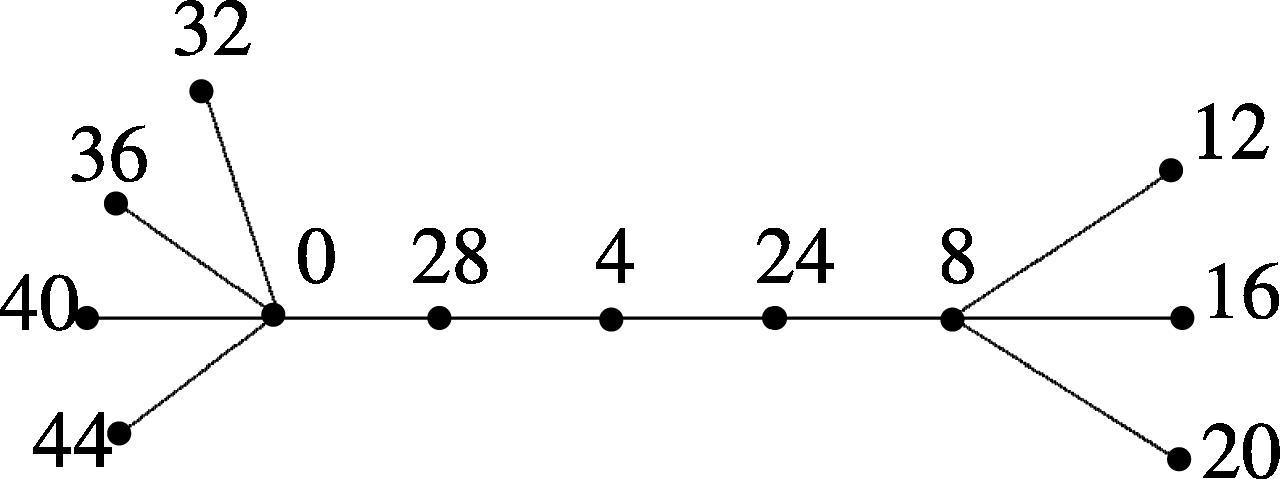
Case (iii).

The Skolem even difference mean labeling of $Tg (4)$ is shown in Fig. 6.

Theorem 3.3

The graph $P_{m} @ P_{n}$ is a Skolem even difference mean graph.

Proof

Let $V (P_{m} @ P_{n}) = {u_{i}^{j} : 1 ⩽ i ⩽ n, 1 ⩽ j ⩽ m}$ and $E (P_{m} @ P_{n}) = {u_{n}^{j} u_{n}^{j + 1} : 1 ⩽ j ⩽ m - 1} \cup {u_{i}^{j} u_{i + 1}^{j} : 1 ⩽ i ⩽ n - 1, 1 ⩽ j ⩽ m}$ . Define a function $f : V (P_{m} @ P_{n}) \to {0, 1, 2, 3, \dots p + 3 q - 1 = 4 (mn - 1)}$ such that $\begin{matrix} f (u_{i}^{j}) = 2 n (j - 1) + 2 (i - 1) & for 1 ⩽ i ⩽ n, 1 ⩽ j ⩽ m and i is odd, j is odd, \\ f (u_{i}^{j}) = 2 n (2 m - j + 1) - 2 i & for 1 ⩽ i ⩽ n, 1 ⩽ j ⩽ m and i is even, j is odd, \\ f (u_{i}^{j}) = 2 n (2 m - j) + 2 (1 - i) & for 1 ⩽ i ⩽ n, 1 ⩽ j ⩽ m and i is odd, j is even, \\ f (u_{i}^{j}) = 2 nj - 2 i & for 1 ⩽ i ⩽ n, 1 ⩽ j ⩽ m and i is even, j is even. \end{matrix}$

Let $e_{j} = u_{n}^{j} u_{n}^{j + 1}$ for $1 ⩽ j ⩽ m - 1$ and $e_{i}^{j} = u_{i}^{j} u_{i + 1}^{j}$ for $1 ⩽ i ⩽ n - 1, 1 ⩽ j ⩽ m$ . For each vertex label of f, the induced edge label function $f^{*}$ is defined as follows: $\begin{matrix} f^{*} (e_{j}) = 2 n (m - j) & for 1 ⩽ j ⩽ m - 1, \\ f^{*} (e_{i}^{j}) = 2 n (m - j + 1) - 2 i & for 1 ⩽ i ⩽ n - 1, 1 ⩽ j ⩽ m and j is odd, \\ f^{*} (e_{i}^{j}) = 2 n (m - j) + 2 i & for 1 ⩽ i ⩽ n - 1, 1 ⩽ j ⩽ m and j is even. \end{matrix}$

Thus f is a Skolem even difference mean labeling of $P_{m} @ P_{n}$ . □

T ( 5 , 6 ) is a Skolem even difference mean graph.

B ( 4 , 3 : P 5 ) is a Skolem even difference mean graph.

Tg ( 4 ) is a Skolem even difference mean graph.

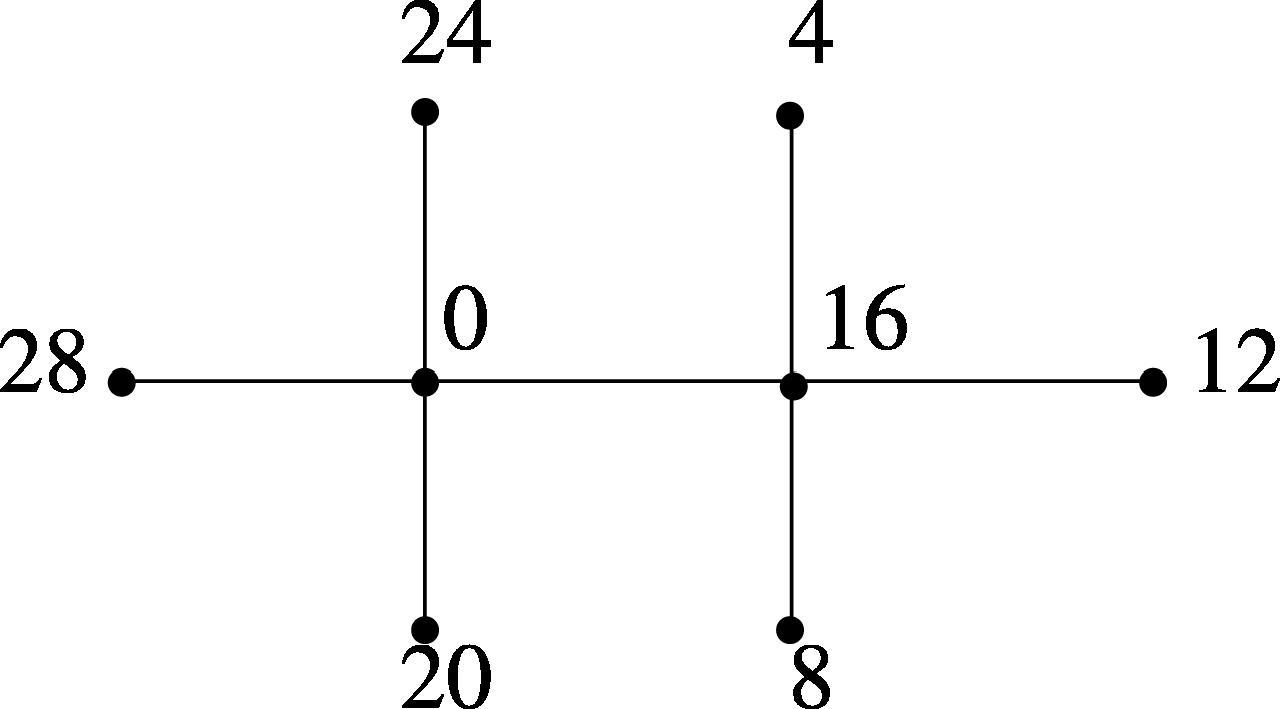
The Skolem even difference mean labeling of $P_{4} @ P_{4}$ is shown in Fig. 7.

Theorem 3.4

The graph ${mP}_{n}$ is a Skolem even difference mean graph.

Proof

Let $V ({mP}_{n}) = {u_{i}^{j} : 1 ⩽ i ⩽ n, 1 ⩽ j ⩽ m}$ and $E ({mP}_{n}) = {u_{i}^{j} u_{i + 1}^{j} : 1 ⩽ i ⩽ n - 1, 1 ⩽ j ⩽ m}$ . Define a function $f : V ({mP}_{n}) \to {0, 1, 2, \dots, p + 3 q - 1 = 4 mn - 3 m - 1}$ as follows:

If n is odd, then $\begin{matrix} f (u_{2 i - 1}^{j}) = 2 n (2 m - j + 1) - 4 (m + i - 1) & for 1 ⩽ i ⩽ ⌈\frac{n}{2}⌉, 1 ⩽ j ⩽ m, \\ f (u_{2 i}^{j}) = 2 (n - 2) (j - 1) + 4 (i - 1) & for 1 ⩽ i ⩽ ⌊ \frac{n}{2} ⌋, 1 ⩽ j ⩽ m . \end{matrix}$

If n is even, then $\begin{matrix} f (u_{2 i - 1}^{j}) = 4 m (n - 1) + 2 n (1 - j) + 2 (1 + j - 2 i) & for 1 ⩽ i ⩽ ⌈\frac{n}{2}⌉, 1 ⩽ j ⩽ m, \\ f (u_{2 i}^{j}) = 2 (n - 1) (j - 1) + 4 (i - 1) & for 1 ⩽ i ⩽ ⌊ \frac{n}{2} ⌋, 1 ⩽ j ⩽ m . \end{matrix}$

For each vertex labeling of f, the induced edge label function $f^{*}$ is defined as $f^{*} (u_{i}^{j} u_{i + 1}^{j}) = 2 (n - 1) (m - j + 1) - 2 (i - 1)$ for $1 ⩽ i ⩽ n - 1, 1 ⩽ j ⩽ m$ . Thus f is a Skolem even difference mean labeling of ${mP}_{n}$ .

P 4 @ P 4 is a Skolem even difference mean graph.

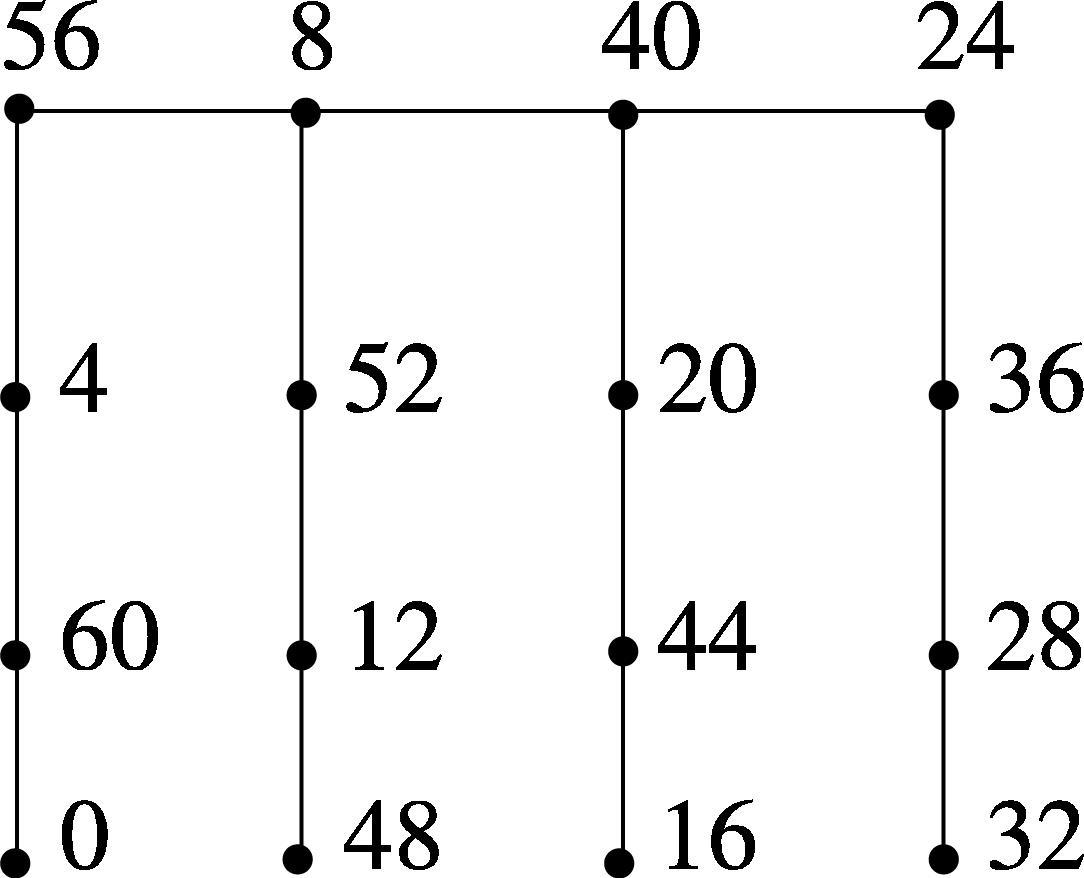
The Skolem even difference mean labeling of $3 P_{4}$ is shown in Fig. 8.

Theorem 3.5

If G is a Skolem even vertex even difference mean $(q + 1, q)$ -graph, then $G \cup {nK}_{2}$ is a Skolem even difference mean graph for all $n ⩾ 1$ .

Proof

Let G be a Skolem even vertex even difference mean $(q + 1, q)$ -graph with labeling $f : V (G) \to {0, 1, 2, \dots, 4 q}$ and its induced edge labeling function $f^{*}$ . Clearly, $f (v)$ is even for each $v \in V (G)$ and ${f^{*} (e)} = {2, 4, 6, \dots, 2 q}$ . Define $G' = G \cup K_{2}$ with $V ({nK}_{2}) = {u_{i}, v_{i}, 1 ⩽ i ⩽ n}$ and $E ({nK}_{2}) = {u_{i} v_{i}, 1 ⩽ i ⩽ n}$ so that $| V (G') | = q + 1 + 2 n$ and $| E (G') | = q + n$ . Define an injective function $g : V (G') \to {0, 1, 2, \dots, 4 q + 5 n}$ such that $g (v) = f (v)$ for each $v \in V (G)$ and $g (u_{i}) = 2 i - 1, g (v_{i}) = 4 q + 4 n - 2 i + 3$ for $1 ⩽ i ⩽ n$ . The induced edge label function $g^{*}$ is defined as $g^{*} (e) = f^{*} (e)$ and $g^{*} (u_{i} v_{i}) = (4 q + 4 n - 4 i + 4) / 2 = 2 (q + n - i + 1)$ for $1 ⩽ i ⩽ n$ . Thus, $g (u_{i}), g (v_{i})$ are even and ${g^{*} (u_{i} v_{i})} = {2 q + 2, 2 q + 4, \dots, 2 (q + n)}$ . Hence, g is a Skolem even difference mean labeling of $G \cup K_{2}$ . □

3 P 4 is a Skolem even difference mean graph.

By an argument similar to that in Theorems 2.8 and 2.10, we have the following corollary.

Corollary 3.6

If G is a Skolem even vertex even difference mean $(q + 1, q)$ -graph, then $G \cup P_{n}$ $(n \geq 2)$ and $G \cup K_{1, n}$ $(n \geq 1)$ are Skolem even difference mean graph.

Theorem 3.7

The graph $K_{m, n} \cup (m - 1) (n - 1) K_{2}$ is a Skolem even difference mean graph for all $m, n ⩾ 2$ .

Proof

Let $V (K_{m, n} \cup (m - 1) (n - 1) K_{2}) = {u_{i}, v_{j} : 1 ⩽ i ⩽ m, 1 ⩽ j ⩽ n} \cup {x_{i}, y_{i} : 1 ⩽ i ⩽ (m - 1) (n - 1)}$ and $E (K_{m, n} \cup (m - 1) (n - 1) K_{2}) = {u_{i} v_{j} : 1 ⩽ i ⩽ m, 1 ⩽ j ⩽ n, x_{i} y_{i} : 1 ⩽ i ⩽ (m - 1) (n - 1)}$ . Define a function $f : V (K_{m, n} \cup (m - 1) (n - 1) K_{2}) \to {0, 1, 2, 3, 4, \dots, p + 3 q - 1 = m + n + 3 mn + 5 (m - 1) (n - 1) - 1}$ such that

$f (u_{i}) = 4 n (i - 1)$ for $1 ⩽ i ⩽ m$ ,
$f (v_{j}) = m + n + 3 mn + 5 (m - 1) (n - 1) - 4 j + 3$ for $1 ⩽ j ⩽ n$ ,
$f (x_{i}) = 1 + 2 (i - 1)$ for $1 ⩽ i ⩽ (m - 1) (n - 1)$ ,
$f (y_{i}) = 4 (m - 1) (n - 1) - 2 (i - 1) + 1$ for $1 ⩽ i ⩽ (m - 1) (n - 1)$ .

The induced edge label function $f^{*}$ is defined as follows: $f^{*} (u_{i} v_{j}) = (m + n + 3 mn + 5 (m - 1) (n - 1) - 1) / 2 - 2 n (i - 1) - 2 (j - 1)$ for $1 ⩽ i ⩽ m, 1 ⩽ j ⩽ n$ , and $f^{*} (x_{i} y_{i}) = 2 (m - 1) (n - 1) - 2 (i - 1)$ for $1 ⩽ i ⩽ (m - 1) (n - 1)$ . Thus, f is a Skolem even difference mean labeling of $K_{m, n} \cup (m - 1) (n - 1) K_{2}$ . □

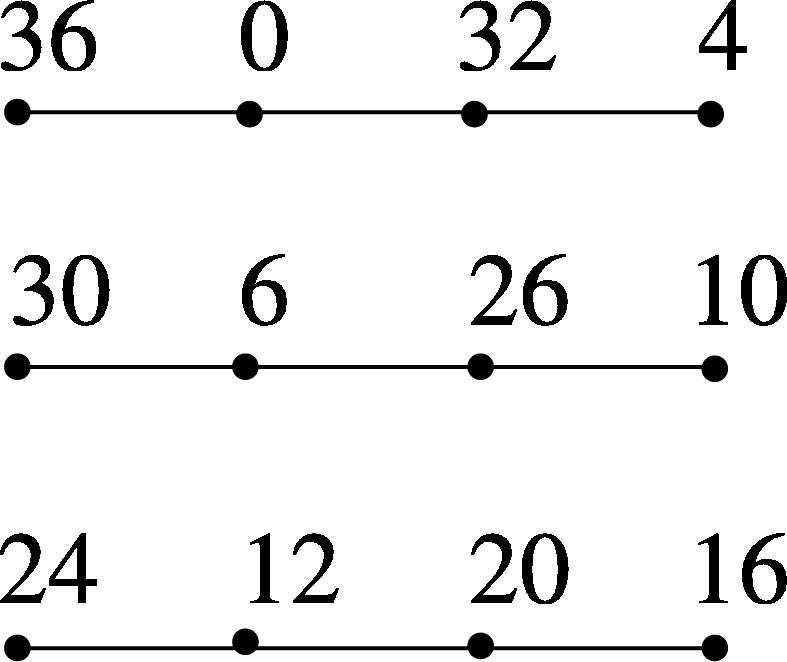
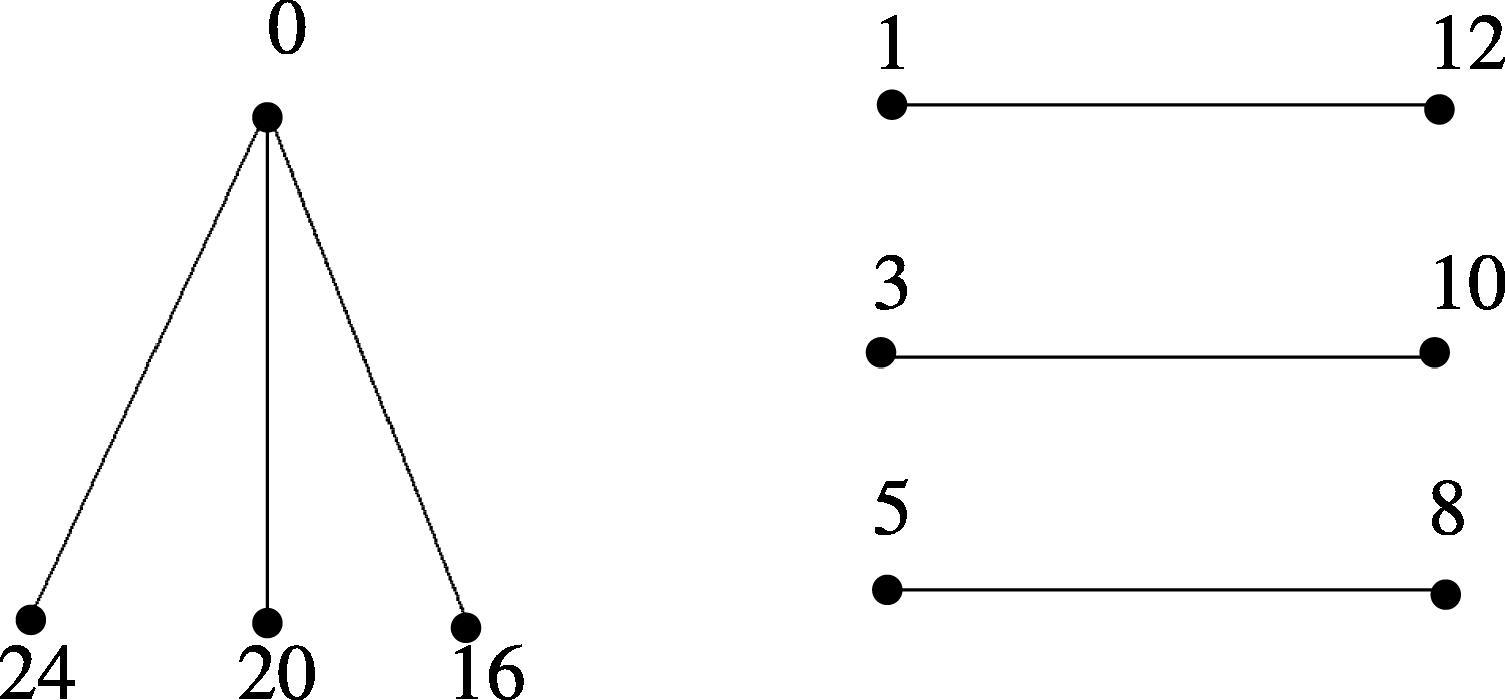
The Skolem even difference mean labeling of $K (2, 3) \cup 2 K_{2}$ is shown in Fig. 9.

Theorem 3.8

The graph $K_{1, n} \cup {nK}_{2}$ is a a Skolem even difference mean graph graph for all $n ⩾ 1$ .

Proof

Let $V (K_{1, n} \cup {nK}_{2}) = {v_{0}, v_{j} : 1 ⩽ j ⩽ n} \cup {x_{i}, y_{i} : 1 ⩽ i ⩽ n}$ and $E (K_{1, n} \cup {nK}_{2}) = {v_{0} v_{i}, x_{i} y_{i} : 1 ⩽ i ⩽ n}$ . Define a function $f : V (K_{1, n} \cup {nK}_{2}) \to {0, 1, 2, 3, \dots, p + 3 q - 1 = 9 n}$ such that $f (v_{0}) = 0, f (v_{i}) = 8 n - 4 (i - 1)$ for $1 ⩽ i ⩽ n, f (x_{i}) = 2 i - 1$ for $1 ⩽ i ⩽ n$ , and $f (y_{i}) = 4 n - 2 (i - 1)$ for $1 ⩽ i ⩽ n$ . The induced edge label function $f^{*}$ is defined as $f^{*} (v_{0} v_{i}) = 4 n - 2 (i - 1)$ for $1 ⩽ i ⩽ n$ , and $f^{*} (x_{i} y_{i}) = 2 n - 2 (i - 1)$ for $1 ⩽ i ⩽ n$ . Thus, f is a Skolem even difference mean labeling of $K_{1, n} \cup {nK}_{2}$ . □

K ( 2 , 3 ) ∪ 2 K 2 is a Skolem even difference mean graph.

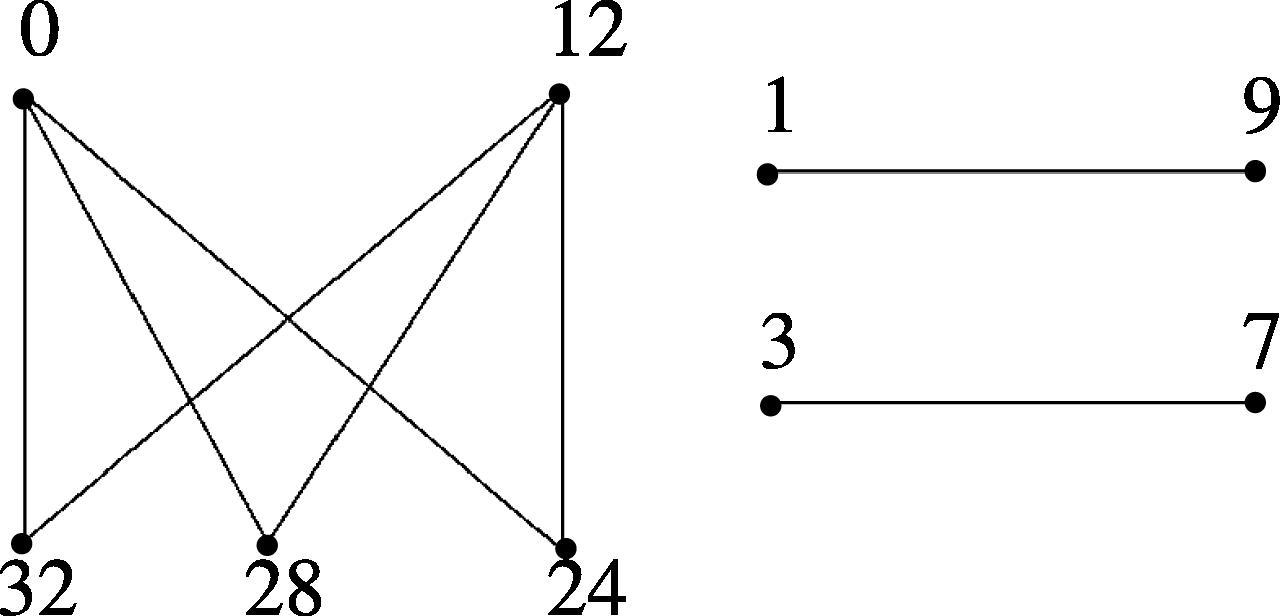
The Skolem even difference mean labeling of $K_{1, 3} \cup 3 K_{2}$ is shown in Fig. 10.

Theorem 3.9

The graph $K_{1, 1, n} \cup {nK}_{2}$ is a Skolem even difference mean graph for all $n ⩾ 1$ .

Proof

Let $V (K_{1, 1, n} \cup {nK}_{2}) = {u, w, u_{i}, x_{i}, y_{i} : 1 ⩽ i ⩽ n}$ and $E (K_{1, 1, n} \cup {nK}_{2}) = {uw, {uu}_{i}, {wu}_{i}, x_{i} y_{i} : 1 ⩽ i ⩽ n}$ . Define a function $f : V (K_{1, 1, n} \cup {nK}_{2}) \to {0, 1, 2, 3, \dots, p + 3 q - 1 = 4 (3 n + 1)}$ such that $f (u) = 0, f (w) = 4 n, f (u_{i}) = 4 (3 n - i + 2)$ for $1 ⩽ i ⩽ n, f (x_{i}) = 2 i - 1$ for $1 ⩽ i ⩽ n, f (y_{1}) = 4 (n + 1), f (y_{i}) = 4 n - 2 i + 3$ for $2 ⩽ i ⩽ n$ . The induced edge label function $f^{*}$ is defined as follows:

$f^{*} (uw) = 2 n$ ,
$f^{*} ({uu}_{i}) = 2 (3 n - i + 2)$ for $1 ⩽ i ⩽ n$ ,
$f^{*} ({wu}_{i}) = 2 (2 n - i + 2)$ for $1 ⩽ i ⩽ n$ ,
$f^{*} (x_{1} y_{1}) = 2 (n + 1)$ ,
$f^{*} (x_{i} y_{i}) = 2 (n - i + 1)$ for $2 ⩽ i ⩽ n$ .

Thus f is a Skolem even difference mean labeling of $K_{1, 1, n} \cup {nK}_{2}$ . □

K 1 , 3 ∪ 3 K 2 is a Skolem even difference mean graph.

The Skolem even difference mean labeling of $K (1, 1, 3) \cup 3 K_{2}$ is shown in Fig. 11.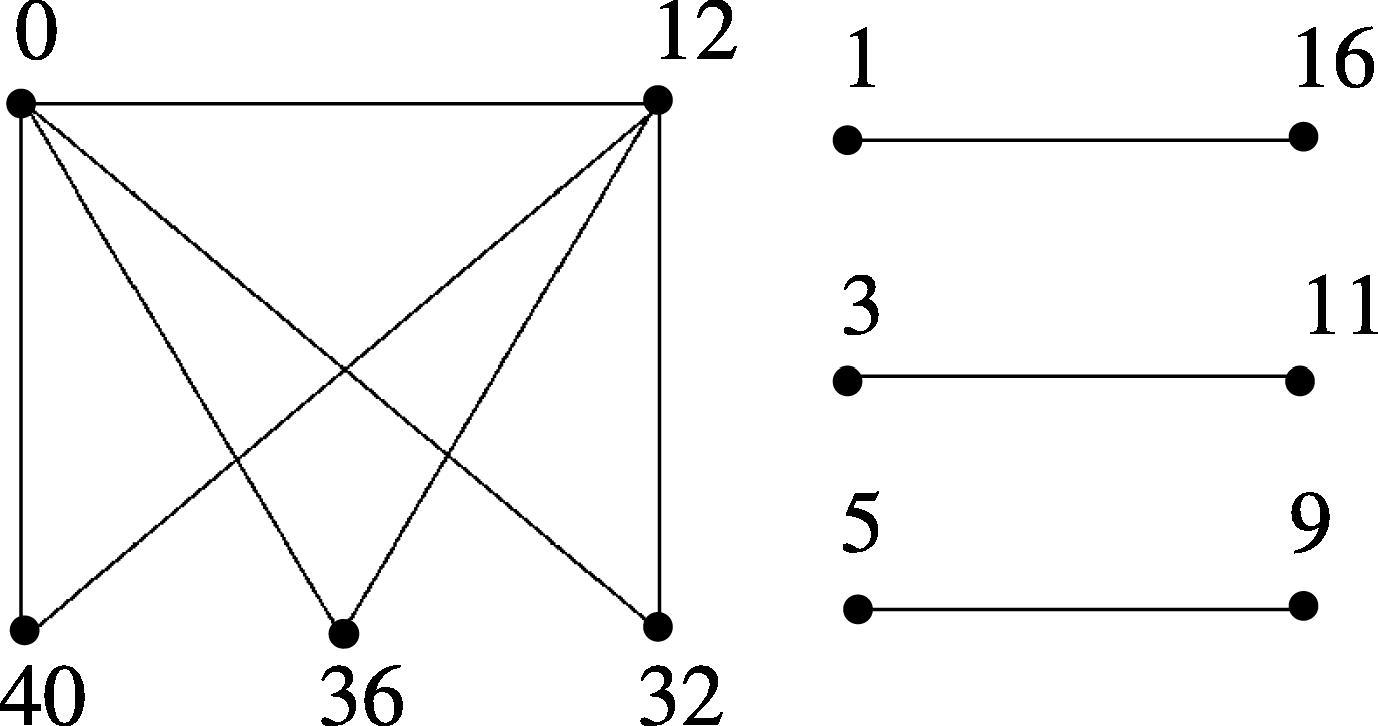

K ( 1 , 1 , 3 ) ∪ 3 K 2 is a Skolem even difference mean graph.

4 Conclusion

In this paper first we show that there exist Skolem odd difference mean labeling for graphs with non-cycle and non-tree components. Further, we introduce the concept of Skolem even difference mean labeling. We conclude the paper with the following open problem.

Problem 4.1

Establish the Skolem even difference mean labeling of $G \cup {nK}_{2}$ where G is a (complete) multipartite graph and $n ⩾ 1$ .

Acknowledgements

The authors sincerely thank the reviewers for their constructive suggestions that help to improve the presentation of this paper to a great extent.

References

Gallian, J., 2016. A Dynamic Survey of Graph Labeling, Electron. J. Combin. # DS 6.
Harary F., . Graph theory. Massachusetts, USA: Addison Wesley; 1972.
Jeyanthi P., Kalaiyarasi R., Ramya D., Saratha Devi T., . Some results on skolem odd difference mean labeling. Proyecciones J. Maths.. 2016;35(4):407-417.
[Google Scholar]
Manickam K., Marudai M., . Odd mean labelings of graphs. Bull. Pure Appl. Sc.. 2006;25E(1):149-153.
[Google Scholar]
Murugan K., Subramanian A., . Skolem difference mean labeling of H-graphs. Int. J. Math. Soft Comput.. 2011;1(1):115-129.
[Google Scholar]
Ramya D., Kalaiyarasi R., Jeyanthi P., . Skolem odd difference mean Graphs. J. Algorithms Comput.. 2014;45:1-12.
[Google Scholar]
Ramya D., Selvi M., Kalaiyarasi R., . On Skolem difference mean labeling of graphs. Int. J. Math. Arch.. 2013;4(12):73-79.
[Google Scholar]
Ramya D., Selvi M., . On Skolem difference mean labeling of some trees. Int. J. Math. Soft Comput.. 2014;4(2):11-15.
[Google Scholar]
Selvi M., Ramya D., Jeyanthi P., . Skolem difference mean graphs. Proyecciones J. Maths.. 2015;34(3):243-254.
[Google Scholar]
Somasundaram S., Ponraj R., . Mean labelings of graphs. Nat. Acad. Sci. Lett.. 2003;26:210-213.
[Google Scholar]

Background

Construction of Skolem odd difference mean graphs

Skolem even difference mean graphs

Conclusion

Fulltext Views
4

PDF downloads
13

View/Download PDF
Download Citations

BibTeX
RIS

Show Sections

[1] Gallian, J., 2016. A Dynamic Survey of Graph Labeling, Electron. J. Combin. # DS 6.

[2] Harary F., . Graph theory. Massachusetts, USA: Addison Wesley; 1972.

[3] Jeyanthi P., Kalaiyarasi R., Ramya D., Saratha Devi T., . Some results on skolem odd difference mean labeling. Proyecciones J. Maths.. 2016;35(4):407-417.
[Google Scholar]

[4] Manickam K., Marudai M., . Odd mean labelings of graphs. Bull. Pure Appl. Sc.. 2006;25E(1):149-153.
[Google Scholar]

[5] Murugan K., Subramanian A., . Skolem difference mean labeling of H-graphs. Int. J. Math. Soft Comput.. 2011;1(1):115-129.
[Google Scholar]

[6] Ramya D., Kalaiyarasi R., Jeyanthi P., . Skolem odd difference mean Graphs. J. Algorithms Comput.. 2014;45:1-12.
[Google Scholar]

[7] Ramya D., Selvi M., Kalaiyarasi R., . On Skolem difference mean labeling of graphs. Int. J. Math. Arch.. 2013;4(12):73-79.
[Google Scholar]

[8] Ramya D., Selvi M., . On Skolem difference mean labeling of some trees. Int. J. Math. Soft Comput.. 2014;4(2):11-15.
[Google Scholar]

[9] Selvi M., Ramya D., Jeyanthi P., . Skolem difference mean graphs. Proyecciones J. Maths.. 2015;34(3):243-254.
[Google Scholar]

[10] Somasundaram S., Ponraj R., . Mean labelings of graphs. Nat. Acad. Sci. Lett.. 2003;26:210-213.
[Google Scholar]