Seismic velocity tomography for CO₂ monitor in subsurface geological structures

1 Introduction

This study deals with seismic velocity tomography; a technology that can be deployed to ensure safe and secure storage of carbon dioxide in underground geological formation as a means to reducing greenhouse gas (GHG) emission. There is an increasingly urgent need to mitigate greenhouse gas emission especially those related to energy production and consumption. Reliable energy supplies are needed for economic growth, but the increase in the associated carbon dioxide (CO₂) emissions is a cause for global concern. About 60% of Greenhouse gas emission is attributed to CO₂ released to the atmosphere (Metz et al., 2006). The threats of destructive climate due to GHG emission include temperature rise, acid rain, flood, food scarcity, etc. The most effective way to reduce CO₂ emission and its negative consequences is to capture CO₂ from it major sources (e.g., large fossil fuel and biomass energy facilities, major CO₂-emitting industries, natural gas production, synthetic fuel plants, and fossil fuel-based hydrogen production plants) and isolate it from the atmosphere through secure storage. The most reliable and cost effective technology for safe CO₂ storage is sequestration in underground geologic formations, for examples, CO₂ storage in depleted hydrocarbon reservoirs, un-mineable coal beds, and saline water aquifers (Hepple and Benson, 2005). Being a low density and low viscosity gas under subsurface condition, CO₂ has a higher risk of leakages than other gases. Leaks of CO₂ can lead to acidification of groundwater, killing of aquatic lives, and contamination of the atmosphere.

One way to mitigate CO₂ leakages at sequestrated sites is to monitor its movement and activity in the storage. Laboratory and field experiments (Harris et al., 1995; Nolen-Hoeksema et al., 1995; Wang et al., 1998) have shown that the effects of CO₂ saturation on seismic properties of rocks are strong and detectable. Wang and Nur (1989) and Daley et al. (2008) applied time-lapse traveltime tomography to cross-well data from the Frio CO₂ injection site and found a velocity decrease in the sandstone aquifer of about 500 m/s due to the presence of CO₂. Wang et al., 1998 have shown that the presence of CO₂ can decrease seismic velocities by over 10%. Xue and Lei (2006) and Xue et al. (2006) show that replacing saline water with CO₂ in sandstone aquifers through injection may cause about 30% decrease in velocity of the aquifer. Studies by Saito et al. (2006), Ajo-Franklin et al. (2013), Böhm et al. (2015) among others also showed that injection of CO₂ into aquifers or reservoirs would reduce the seismic velocity of the reservoirs or aquifers and that seismic tomography can be used to image the velocity reduction in the injected geological structures. Therefore, a technology that measures velocity changes in subsurface formation storing CO₂ can be used to monitor CO₂ movements and to forestall the occurrence of leakages.

Surface seismic data have characteristic long wavelength because of low frequency (Zhu, 2014). This long wavelength causes resolution problem when dealing with layers with limited vertical extent (Raji and Rietbrock, 2013). Subsurface lithologies suitable for storing CO₂ may have limited vertical extent that is below the resolution of surface seismic data but have significant lateral extent (Jibrin and Raji, 2014; Raji, 2016). Crosswell seismic tomography offers a solution to the poor resolution in conventional seismic data. Crosswell data have a resolution that is at least four-times higher than conventional seismic data (Pereira and Jone, 2010). Therefore, crosswell seismic data would be used for this study. Baseline and time lapse tomography offer the opportunity to characterize geologic formation before, during, and after fluid injection. Comparing the velocity structures of the pre-injection and post injection data would reveal the changes in the velocity structure due to the movement of the injected fluid (Bregman et al., 1989; Paulsson et al., 1992; Justice et al., 1989, 1993). The speed of seismic waves in fluid saturated rock depends on the properties of fluid and rock matrix (Biot, 1956). Seismic compressional wave velocity is more responsive to pore fluid change than seismic shear velocity because compressional velocity is strongly dependent on fluid property. The effect of saturation and fluid type(s) on the speed of elastic waves in reservoir and aquifers rocks (patchy-saturated rocks) can be described by mesoscopic loss model. Description of mesoscopic model is given in White (1975), Carcione et al. (2003), among others.

The objective of the study is to show the appropriateness of the inversion procedure for imaging velocity changes in rocks due to CO₂ presence. The overall aim of the study is to show the capability of the method for monitoring CO₂ in geological sequestration sites. Using compressional (P) wave first arrival time and the ray theory, we applied an in-house tomographic inversion method to reconstruct velocity structure of the subsurface rock before and after the injection of CO₂ at supercritical condition. First, we describe the imaging procedure and demonstrate the appropriateness of the method by inverting the velocity structure of a known west Texas oil field using a crosswell survey. The inversion result is compared with the true velocity model. Second, we simulated CO₂ injection in a complex geological structure, inverted the velocity structure for the pre-injection and the two post injection stages. Third, we show the seismic response of CO₂ saturation on reflection data – traveltime and amplitude. Finally, we discussed the results, limitation and the future direction of the study.

2 Tomographic velocity inversion

In this section, we describe the procedure used for inverting velocity structure from traveltime data and test the appropriateness of the method by comparing the inversion results with the true velocity model. Traveltime based seismic tomography uses the time a seismic wave takes to travel from a source to the receiver to invert the velocity structure along the travel path. Using the ray theory, traveltime can be modeled by a line integral that connects the source to the receiver as:

In Eq. (3) $S$ is the slowness vector and $G$ is the ray path in each cell of the matrix. The concept behind this velocity tomography inversion is to obtain the best representative geological model of the subsurface structure that best satisfy the measured data. In general, the mathematical description of velocity tomography is ill-possed, the inversion problem is nonlinear, involves ray tracing, and crosswell geometry has limited aperture. The inverse problem is formulated as an optimization that minimizes the objective function, $\beta$ which consists of two parts as:

The inversion method is tested to invert the velocity structure of a west Texas carbonate oil field, U.S. The survey geometry consisted of 280 piezoelectric sources deployed in a well between depth levels of 4000 and 5500 ft at 5 ft spacing (or 1212–1667 m at 1.6 m interval). The receiver geometry consists of 280 hydrophone receivers deployed in another well within a similar depth range and spacing. The two well heads are separated by a distance of 825 feet (250 m). The source frequency band is 100–1200 Hz and the sample interval is 0.25 ms. A representative seismogram recorded by the hydrophone at depth level 4760 feet is shown in Fig. 1 with traveltime picks shown in red. A plot of the traveltime picked for the full survey with the source and receiver location is shown in Fig. 2. The dataset consists of 78,400 traces of length 200 ms. These traveltimes are the observed data used for the procedure described in equation 5. The tomographic inversion was set up for 10 iterations. The starting model is a 1D (constant) velocity model computed as the average value of the velocity log from the source well (Fig. 3b). Convergence was achieved at the 8th iteration.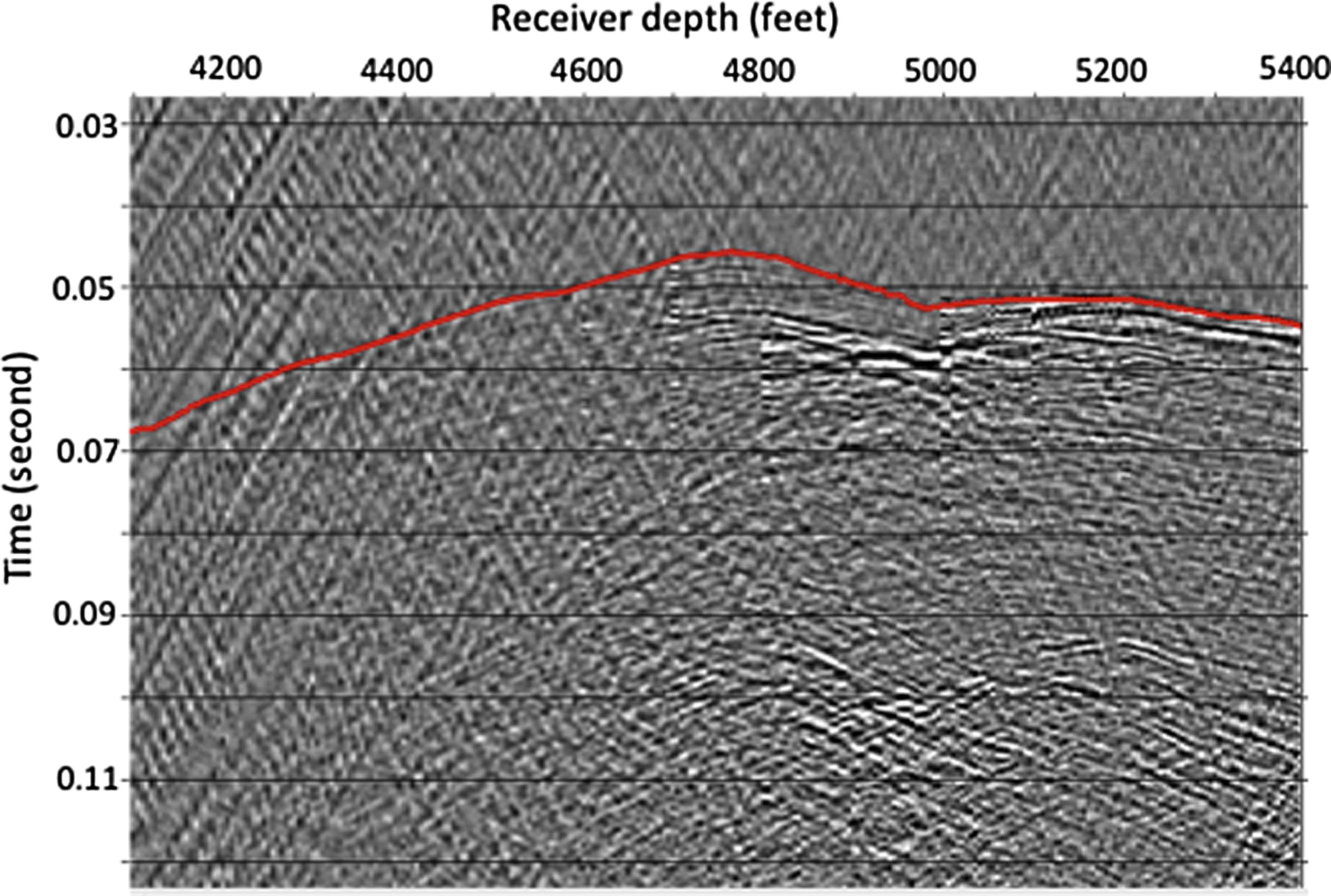

Close

Figure 1

Common Receiver Gather from a receiver at 4760 feet. Traces are truncated at 125 ms.

Export to PPT

Close

Figure 2

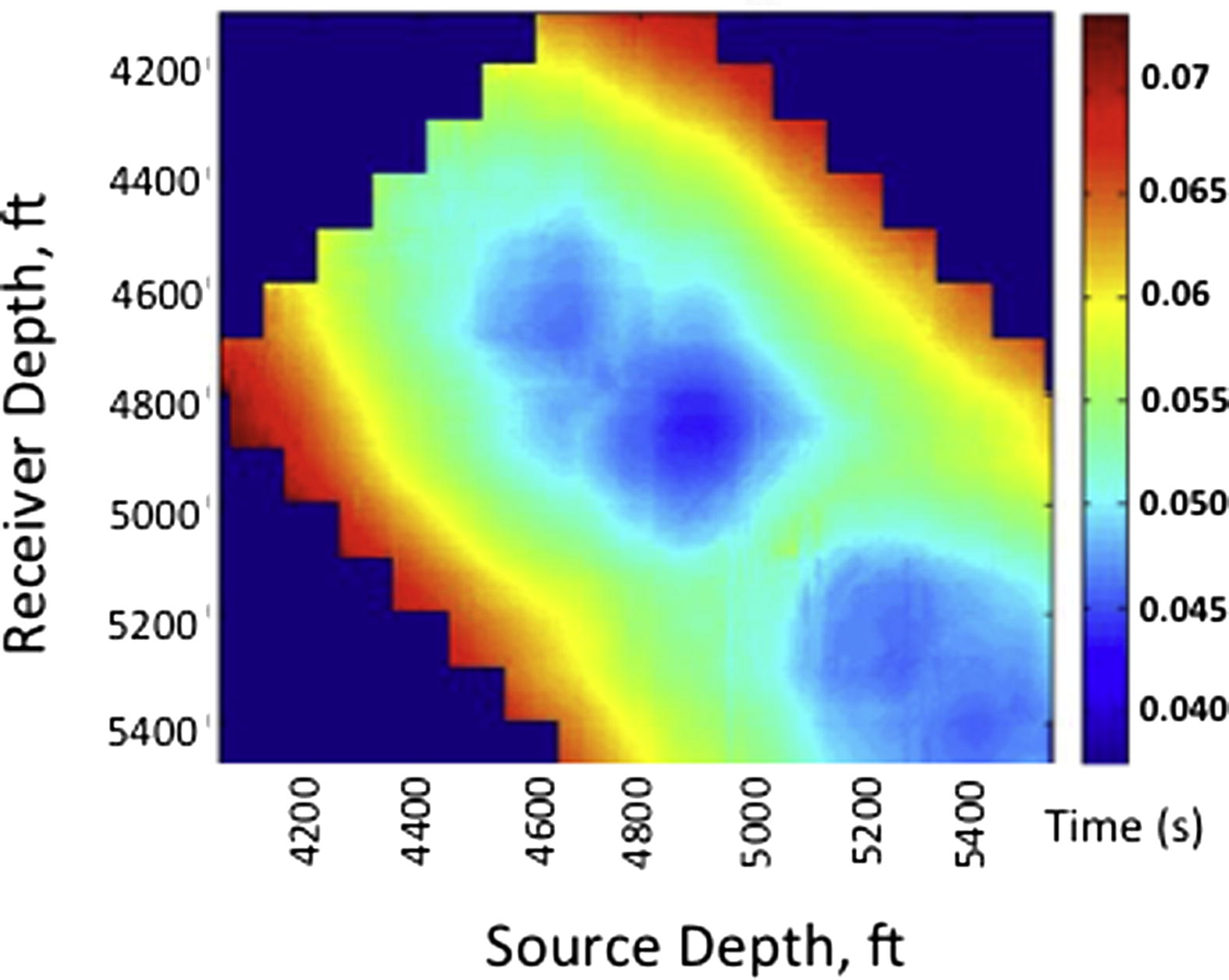
Time Map of the picked traveltime (ms) for the full survey.

Export to PPT

Close

Figure 3

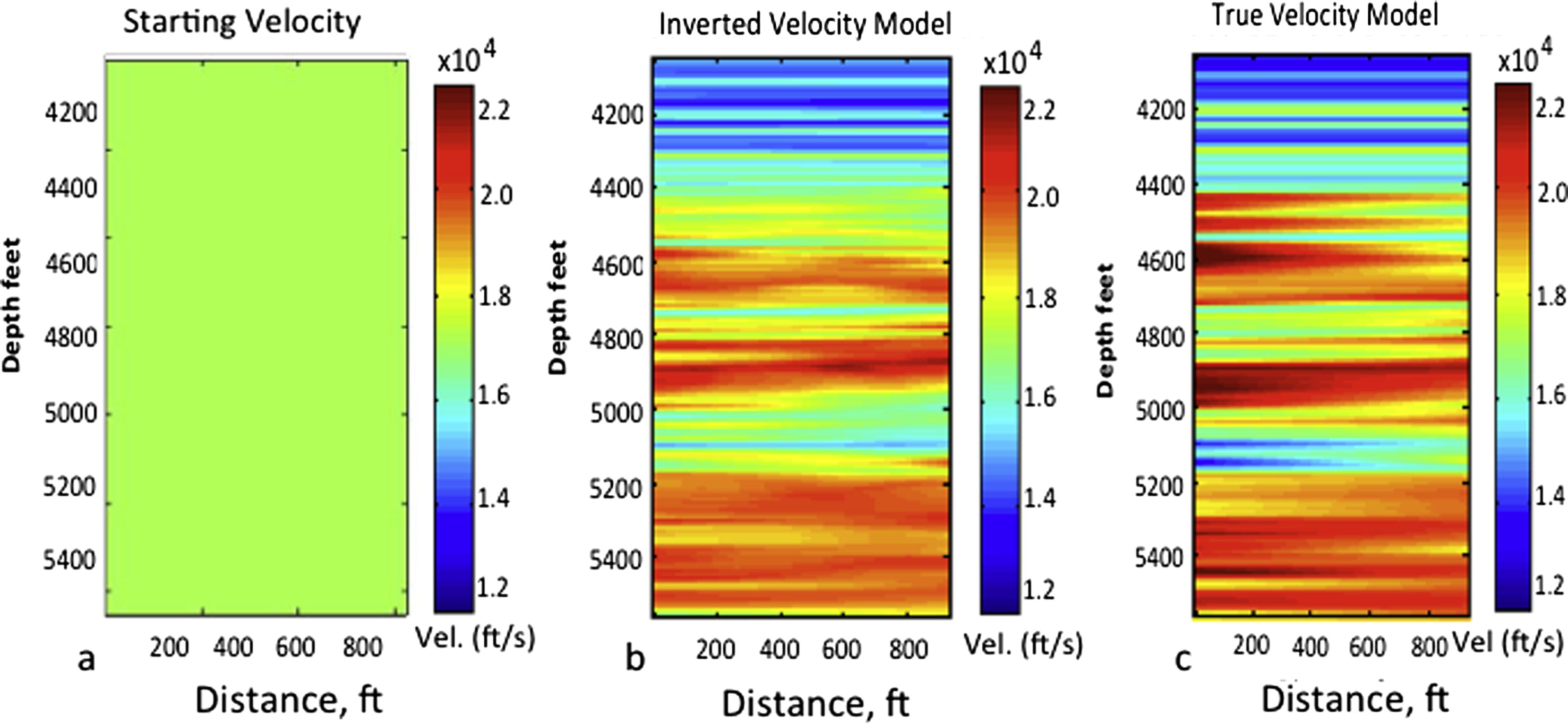
Velocity structures. (a) Initial/starting velocity for the forward modeling, (b) inverted velocity model, and (c) true velocity model.

Export to PPT

The inverted velocity tomogram is compared with the ‘true’ velocity model in Fig. 3b and c. The ‘true’ velocity is a pseudo-synthetic velocity model built from well logs. The source and receiver velocity logs computed from their respective sonic logs, were linearly interpolated. To make the example very simple, we assumed flat layer geometry. The misfit between the observed traveltime and the calculated traveltime is shown in Fig. 4. A comparison of the true model and inverted velocity model confirms the appropriateness of the inversion method. A more realistic and complex geological model is tested in the next section. The misfit between the observed traveltime and the inverted traveltime is very small – ranges from −0.004 ms to 0.003 ms. This value is approximately 4% of the observed data shown in Fig. 2. The RMS error of the misfit is about 0.00015. With this result, we proceed to demonstrate the procedure for using the method to monitor CO₂ storage in subsurface geological structures.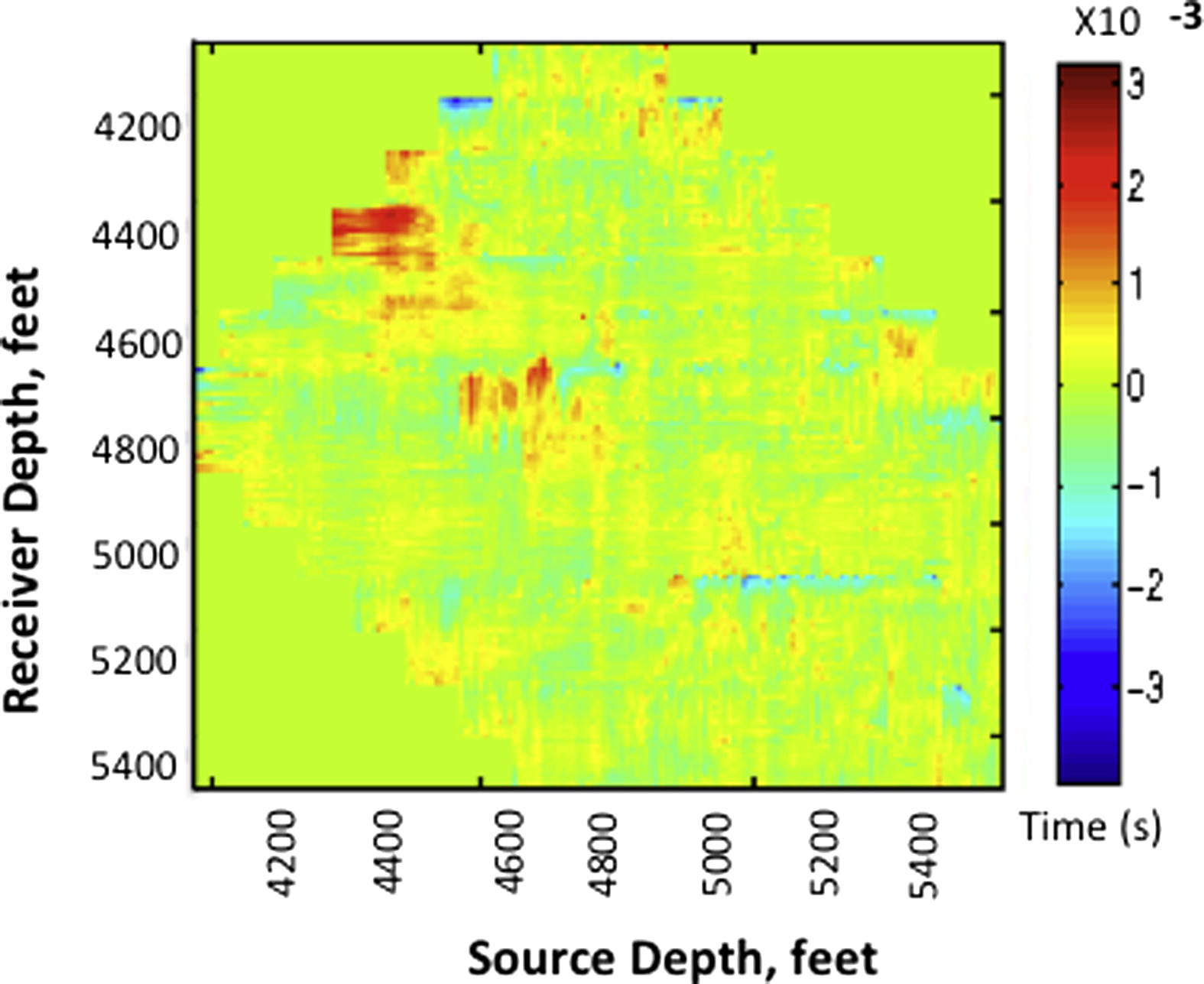

Close

Figure 4

Traveltime residual between the observed and computed traveltime data, $t_{\mathit{Obs}}-t_{\mathit{Cal}}$ . The maximum misfit is about −0.0038 s.

Export to PPT

3 Demonstration of CO₂ monitoring at a sequestration site

After demonstrating the appropriateness of the velocity inversion procedure for imaging the velocity of a west Texas oil field, we proceed to show how traveltime velocity tomography can be used to monitor CO₂ storage in subsurface geological formations at a sequestration site. Our ‘site’ for CO₂ monitor is The Marmousi. Marmousi is one of the most complex known geological structures (Versteeg, 1994; Martins et al., 2006). Marmousi Model is based on the geology of North Quenguela Trough in the Quanza Basin of Angola. The section is primarily composed of shale units with occasional sand layers (Versteeg, 1994). The sand layers host the hydrocarbon. The core of the complex faulted area is an anticline that is composed of marl. An unconformity and a partially evacuated salt layer separate the marls from the deeper anticlinal units. The choice of this model is informed by its structural and stratigraphic complexity: if our inversion scheme is able to image this structure adequately and use it to demonstrate CO₂ monitoring, we would be confident that our approach can produce dependable result at many CO₂ geological sequestration sites.

First, we applied the velocity tomography method to invert the baseline velocity structure prior to CO₂ injection. In this case, the true velocity model of Marmousi was sourced from http://www.agl.uh and is described in Martins et al. (2006). Our initial velocity model for the inversion is a 1D velocity model computed from the average value of the true model (Fig. 5a). The set up for the crosswell survey consists of 130 sources and 130 receivers. The first and the last receiver are located at 980 ft and 2915 ft respectively in one well. Similarly, the first and last sources were located at 1025 ft and 2960 ft in the other well. The source and receiver spacing is 15 ft. The computation space discretization consists of 101 by 201 cells/grids. The cell dimension is 10 ft by 10 ft and the source signature is 200 Hz Ricker wavelet. The inversion was set up for 50 iterations. The true velocity is used to compute the observed traveltime, $t_{\mathit{obs}}$ . At every iteration, the updated velocity model is used to compute traveltime $t_{\mathit{cal}}$ until convergence between the observed and calculated traveltime, or a set limit, is achieved. The inversion process is effected using an in-house finite difference code. The code is written in C++ but executed in MATLAB. First arrival traveltimes, $t_{\mathit{Obs}}$ for the observed data were picked using a MATLAB program specifically designed for first break picking. The inverted velocity obtained after 34th iteration is shown in Fig. 5b. The true velocity model is shown in Fig. 5c.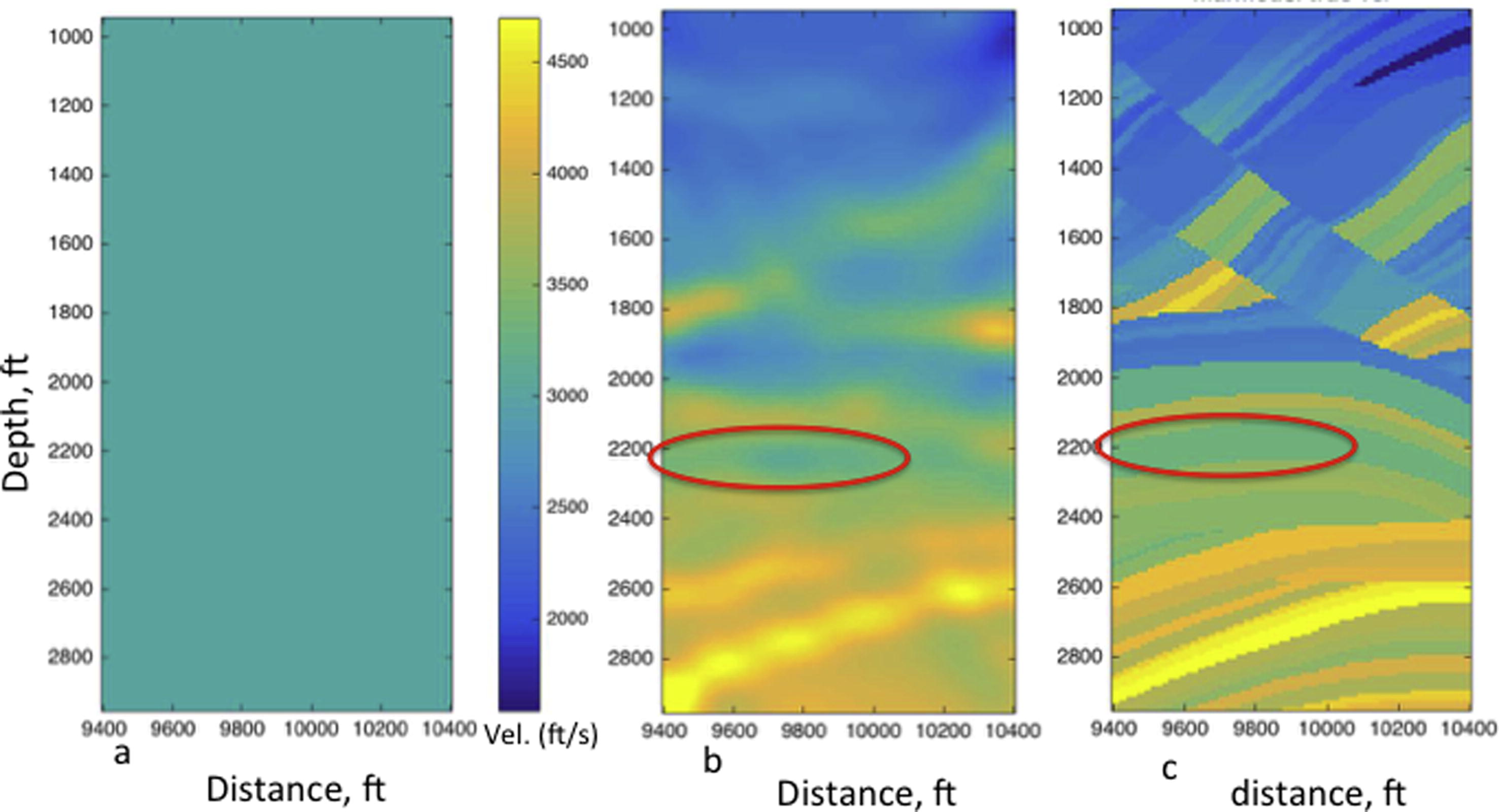

Close

Figure 5

Pre-injection velocity structures for Marmousi. (a) Initial 1D velocity model for the forward modeling, (b) inverted velocity model, and (c) true velocity model. The color code for all velocity models is shown in (a).

Export to PPT

Next, supercritical CO₂ is theoretically injected in the sand layers at depth level 2200–2400 ft (the red ellipse) in two phases. The second phase is a continuation of the first injection phase. The sand layer is capped by low porosity shale that can prevent vertical movement of CO₂ across the sand layer. The velocity perturbation in the injected layer is accomplished by reduction in velocity of the sand layer based on a study by Xue and Lei (2006). Alternatively, velocity decrease due to CO₂ injection can be estimated by fluid substitution method (Gassmann, 1951; Smith et al., 2003). When building the true velocity model for post-injection structure, we retain the velocity model outside the injected sand layer as we have in the pre-injection stage (Fig. 5b), but we reduced the velocity in the sand (or reservoir) layer by 900 ft/s– since we only expect velocity change in the sand layer at about 2200–2400 ft depth where CO₂ injection is taking place. The velocity change (difference) in the sand layer due to CO₂ injection in the true model is shown in Fig. 6a and b. This is here known as the CO₂ structure or CO₂ plume. The velocity reduction in the sand layer was accomplished by assuming a 30% velocity drop when CO₂ partially replaced brine according to a study by Xue and Lei (2006). This approach drastically reduced the number of model parameterization and the computation time (Lee et al., 1995).

The post injection ‘true’ velocity model is used to simulate seismograms and the first arrival times are picked for these seismograms using the MATLAB program described in the previous paragraph. These traveltimes are known as $t_{\mathit{Obs}}$ . The starting velocity model for the post injection velocity modeling is a 1D velocity model similar to the one shown in Fig. 5a. The post-injection velocity structures were inverted using the same process, survey geometry, and grid numbers used for the pre-injection study. The inverted velocity model after CO₂ injection stage I and II are shown in Fig. 6c and d respectively. The difference plot between the inverted velocity model for post injection stage I and inverted pre-injection model (Fig. 6c minus Fig. 5b) is shown in Fig. 6e, while the difference plot between the inverted model for post-injection stage II and pre-injection model (Fig. 6d minus Fig. 5b) is shown in Fig. 6f. Comments on the results of the inversion are given in the next section.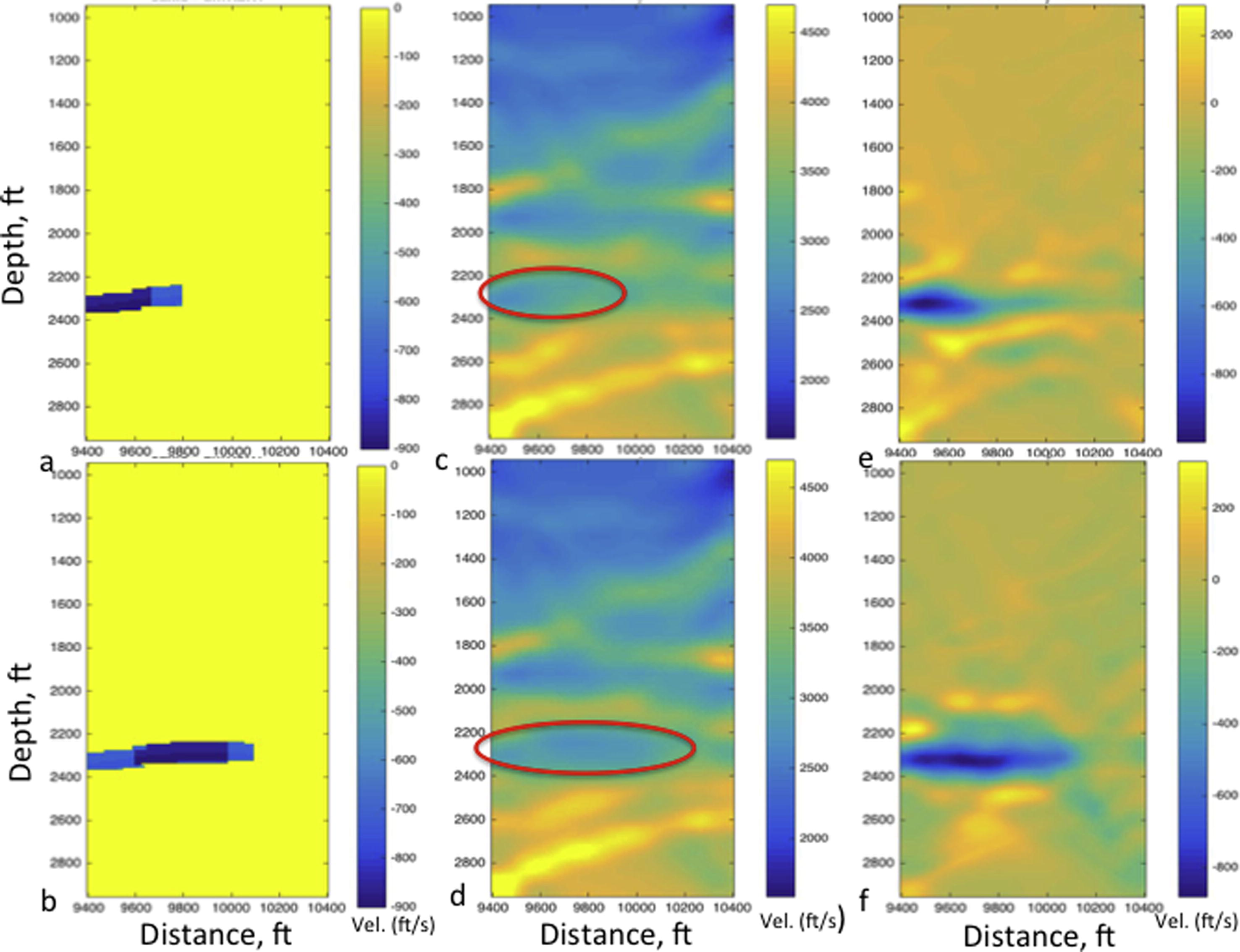

Close

Figure 6

CO₂ velocity structure and the inverted velocity model after CO₂ injection. (a) The difference plot of the true velocity after CO₂ injection stage I and before CO₂ injection. (b) The difference plot of true velocity after CO₂ injection stage II and before CO₂ injection, (c) the inverted velocity model after CO₂ injection stage I, (d) the inverted velocity model after CO₂ injection stage II, (e) the difference plot of inverted velocity model after CO₂ injection stage I and before CO₂ injection. (f) The difference plot of inverted velocity model after CO₂ injection stage II and before CO₂ injection. The negative velocity values in (a, b, e, and f) show the reduction in velocity due to CO₂ presence.

Export to PPT

4 Discussion

In this study, we used direct arrival traveltime tomography with crosswell geometry to demonstrate the detectability of CO₂ movement in underground geologic storages. The results show that seismic velocity tomography can be used to ensure safe and secure storage of CO₂ in geological structures such as depleted hydrocarbon reservoirs and saline water aquifers. Rather than releasing them to the atmosphere to constitute threat of global warming, CO₂ produced at fossil fuel plants and other major CO₂ -emitting industries can be stored in abandoned or depleted oil fields. Our approach to monitor CO₂ in a sequestrated site is built on the concept: CO₂ causes a decrease in P-wave seismic velocity, which in turn delays seismic arrival time; the higher the CO₂ saturation, the higher the velocity decrease. So, time-lapse velocity changes in a CO₂ sequestrated site can be attributed to CO₂ movement and saturation; a significant velocity decrease outside the CO₂ injected layer can be attributed to CO₂ leakages. Kumar et al. (2008) showed that velocity change due injection-induced pressure is not significant compared to the velocity change due to CO₂. Therefore, we ignored the velocity change due to injection pressure in this study. The inversion method produced good results when applied to image the velocity structure of a west Texas carbonate oil field (Fig. 3). The inverted P wave velocity model shows good similarities to the true velocity model. The misfit between the observed and calculated data is less than 5% (Fig. 4).

When applied to image pre-injection and post-injection velocity structures of Marmousi, the results show different velocity structures in the injected layer due to the presence of CO₂. A noticeable velocity decrease is observed in the injected layer as shown in Fig. 6c and d compared to Fig. 5b. The velocity of the sand layer in the inverted velocity model for the pre-injection stage (Fig. 5b) is about 3100ft ft/s, while the velocity in the post-injection stages I and II (Fig. 6c and d) is about 2270 ft/s and 2320 ft/s respectively. The major difference between the results in Fig. 6c and d is the advancement in the CO₂ fronts from the left to the right. This difference shows that seismic velocity tomography can be used to monitor CO₂ movement in rocks in addition to detecting CO₂ presence. The difference in the pre-injection and post injection inverted velocity in the sand layer (shown in Fig. 6e and f is about -800ft/s. This result is similar to the velocity difference of the pre-injection and post injection true models shown in Fig. 6a and b where the maximum value is about -900ft/s. The similarities in Fig. 6a and e on one hand, and Fig. 6b and f on the other hand confirms the appropriateness of the inversion procedure and the uniqueness of the inversion results. Figs. 5b and 6d show a decrease in velocity that characterizes the presence of CO₂ in brine-saturated sand.

Our results are consistent with laboratory observations of Ivanova et al. (2012). A significant velocity decrease would be seen above the injected sand layer if CO₂ leakages were present. Because of the buoyancy of CO₂ compared to brine, CO₂ leakage at the bottom of the injected layer is unlikely. The right lower side of the inverted models (Fig. 6c and d) shows some inversion artifacts that appear to be velocity reduction. This velocity drop cannot be attributed to CO₂ structure because they are present in the inverted pre-injection model (Fig. 5b). The artifact is probably due to ray coverage, complexity of the Marmousi structures, and the insufficiency of the inversion method. Consideration of rays with angles not more 30° (Böhm et al., 2015) for the inversion could reduce the artifacts. Incorporation of boundary preserving strategy (Zhu, 2014; Portniaguine and Zhdanov, 1999) to the inversion scheme would improve the quality of the inverted model at the layers’ boundaries.

In Fig. 7a and b, we show the seismograms computed for the pre-injection and post injection stage II surveys using the inverted velocity models shown in Fig. 5b and 6d respectively. The seismogram shown in Fig. 7a and b are the same shot gather with the source located at depth 2800. Comparing Fig. 7a and b, we observe some similarities and differences. The similarity in the two seismograms (Fig. 7a and b) confirms the consistency in the structures of the inverted tomographic velocities and the geometries of the crosswell survey. The Delay in the first arrival times in Fig. 7b, compared to Fig. 7a shows a major difference. This delay is due to the decrease in velocity caused by the presence of CO₂ in the injected layer. Further study on this subject will investigate the effects of dissolution and precipitation reactions, and the reactive transport of CO₂ on the seismic response especially after long years of CO₂ storage. Future work will also include ways to reduce the inversion artifacts and improve the image resolution at lithological boundary.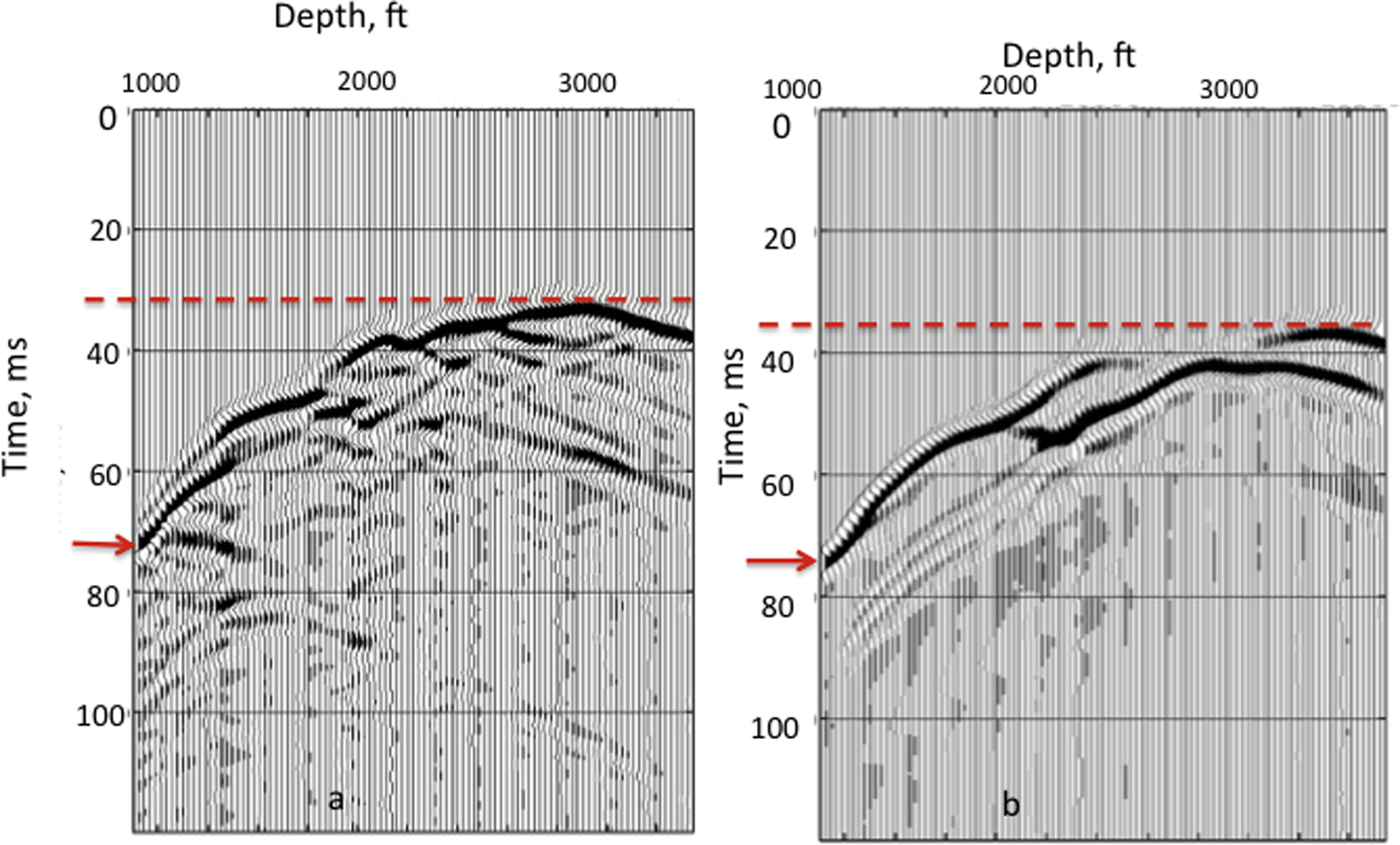

Close

Figure 7

Crosswell seismic records computed for the pre-injection survey (a) and post-injection stage II survey. Red lines compare the shortest traveltime for the two plots, while the red arrows compared the longest traveltime for the two plots. The traveltime delay in (b) compared to (a) is due to the velocity decrease caused by CO₂ presence in the sand layer.

Export to PPT

5 Conclusion

In this study, we demonstrate the utility of traveltime tomography for monitoring CO₂ in underground geological structure to ensure safe and secure CO₂ storage from the atmosphere. The appropriateness of the tomographic inversion method was first tested to estimate the velocity model of a west Texas carbonate oil field, where the inverted and true velocity models shows good similarities. Application of the inversion procedure to estimate the velocity structure of Marmousi before and after CO₂ injection show velocity decrease of about 800 ft/s in the injected sand layer due to CO₂ presence. The inverted post-injection velocity shows the progression in CO₂ movement from left to right as the injection continues in the sand layer. Overall, results of the study show that the method can be used to detect CO₂ presence, movement, and leakages in underground geological formations. The presence of artifact in the results is noted for the improvement of the inversion. It is worthy of note that the capability of the inversion method to give acceptable results for Marmousi models, being one of the most complex known geological models, suggests the appropriateness of the inversion method for monitoring CO₂ storage in many complex geological structures.