Translate this page into:
A numerical method for solving singular fractional Lane–Emden type equations
⁎Corresponding author. a.kazeminasab@usm.edu.my (A. Kazemi Nasab)
-
Received: ,
Accepted: ,
This article was originally published by Elsevier and was migrated to Scientific Scholar after the change of Publisher.
Peer review under responsibility of King Saud University.
Abstract
In this paper, a hybrid numerical method combining Chebyshev wavelets and a finite difference approach is developed to obtain solutions of singular fractional Lane–Emden type equations. The properties of the Chebyshev wavelets and finite difference approaches are used to convert the problem under consideration into a system of algebraic equations which can be conveniently solved by suitable algorithms. A comparison of results obtained using the present strategy and those reported using other techniques seems to indicate the precision and computational effectiveness of the proposed hybrid method.
Keywords
Chebyshev wavelets
Finite difference method
Fractional Lane–Emden
Singular problems
Initial and boundary value problems
1 Introduction
Certain phenomena in physics and engineering sciences can best be mathematically modeled using differential equations. The Lane–Emden equation is an ordinary differential equation which arises in mathematical physics. In astrophysics, the Lane–Emden equation is a dimensionless form of Poisson’s equation for the gravitational potential of simple models of a star (Momoniat and Harley, 2006). Due to the singularity behavior at the origin, it is numerically challenging to solve the Lane–Emden problem, as well as other various linear and nonlinear singular initial value problems in quantum mechanics and astrophysics. This paper deals with the numerical solution for the singular fractional Lane–Emden equation using Chebyshev wavelet finite difference method.
A given function can be represented in terms of a set of basis functions localized both in location and scale using wavelets. Advantages of wavelet analysis include the capacity of carrying out local analysis to uncover signal features such as trend, breaking points, and discontinuities which other analysis methods might fail to detect (Misiti et al., 2000). The multiresolution analysis of wavelet transform makes it a powerful tool to represent correctly a variety of functions and operators. Wavelet analysis results in sparse matrices which in turn enables fast computation. Such advantageous aspects of wavelet analysis make it a powerful analytical technique to deal with differential equations in which the solution might become distorted due to singularities or sharp transitions.
There has been much research on wavelet based method for the integer order Lane–Emden equations in recent years. Solving Lane–Emden equations using Chebyshev wavelet operational matrix was proposed in (Pandey et al., 2012). Kaur et al. (2013) obtained the solutions for the generalized Lane–Emden equations using Haar wavelet approximation. More recently, Youssri et al. (2015) used ultraspherical wavelets for solving such equations. Kazemi Nasab et al. (2015) proposed Chebyshev wavelet finite difference method for solving singular nonlinear Lane–Emden equations arising in astrophysics. Laguerre wavelets was employed in (Zhou and Xu, 2016).
Approximate solution methods for fractional differential equations developed over the last decade include homotopy analysis method (Abdulaziz et al., 2008), variational iteration method (Wu and Lee, 2010; Odibat and Momani, 2006), finite difference method for fractional partial differential equations (Zhang, 2009), Adomian decomposition method (Daftardar-Gejji and Jafari, 2007; Momani and Odibat, 2007), fractional differential transform method (Odibat et al., 2008), and generalized block pulse operational matrix method (Li and Sun, 2011). El-Ajou et al. (2010) employed homotopy analysis method to find symbolic approximate solutions for linear and nonlinear differential equations of fractional order. In particular for fractional Lane–Emden equations, the least square method was used in (Mechee and Senu, 2012). Dávila et al. (2014) classified solutions of finite Morse index of the fractional Lane–Emden equation. Two hybrid methods were proposed to solve two-dimensional linear time-fractional partial differential equations in (Jacobs and Harley, 2014). More recently, Modified differential transform was proposed in Marasi et al. (2015) to obtain numerical solutions of the nonlinear and singular Lane–Emden equations of fractional order. Akgül et al. (2015) suggested the reproducing kernel method to study the fractional order Lane–Emden differential equations. The operational matrices of fractional order integration for the Chebyshev wavelet, Legendre wavelet, and Haar wavelet were introduced in Li (2010), Jafari et al. (2011), Li and Zhao (2010) and Yuanlu (2010) to solve the differential equations of fractional order. Bhrawy et al. (2016) introduced a space–time Legendre spectral tau method for the two-sided space–time Caputo fractional diffusion-wave equation.
Kazemi Nasab et al. (2013) proposed Chebyshev wavelet finite difference method for solving fractional differential equations. It is a hybrid method based on Chebyshev wavelet analysis and a finite difference method which converts a given problem to a system of algebraic equations. Ibrahim (2012) studied the general dual form of fractional order as follows:
The objective of this study is to investigate the effectiveness of Chebyshev wavelet finite difference method when it is applied to a new generalized dual form of the Eq. (1.1).
In this paper we consider the singular fractional Lane–Emden equations formulated as
2 Preliminaries
2.1 Fractional calculus
Fractional calculus is the theory of derivatives and integrals of any arbitrary real or complex order that its high significance in a variety of disciplines, including mathematical, physical and engineering sciences is undeniable. It is indeed a generalized conception of integer-order differentiation and n-fold integration. The main benefit of fractional derivatives in comparison with integer-order one is that they provide us with a superb tool to describe general properties of various materials and process specifically dynamical processes in a fractal medium while standard integer-order cases are fail to do so. The benefits of fractional derivatives is evident in representing physical systems more accurately, in demonstrating mechanical and electrical properties of real materials, and also in the depiction of properties of gasses, fluids and rocks, and in numerous different fields (Hilfer, 2000; Lewandowski and Chorazyczewski, 2010; Mainardi, 2012). These equations incorporate the effects of memory and can account for subdiffusion (due to crowded systems) and superdiffusion (due to active transport processes). Thus, taking into account the memory effects are better described within the fractional derivatives, the fractional Lane–Emden equations extract hidden aspects for the complex phenomena they describe in various field of applied mathematics, mathematical physics, and astrophysics. An advantage of the fractional case is that it converges to the integer case. Therefore, it has the same benefits (Ibrahim, 2012; Akgül et al., 2015). There have been many books and articles in the area of fractional calculus and its application in astrophysics (Miller and Ross, 1993; Samko et al., 1993; Podlubny, 1999; Saxena et al., 2004; Kilbas et al., 2006; Stanislavsky, 2010; Diethelm, 2010; Chaurasia and Pandey, 2010; El-Nabulsi, 2011a,b; El-Nabulsi, 2012; Sharma et al., 2015; El-Nabulsi, 2016a,b).
The calculus of variations is a branch of mathematical analysis dealing with extrema of functionals that is of remarkable significance in a variety of disciplines, including science, engineering, and mathematics (Bliss, 1946; Weinstock, 1974). The problems relating to find minimum of a functional such as, Lagrangian, strain, potential, and total energy, actually occur in engineering and science that give the laws governing the systems behavior (Agrawal, 2002). It has been indicated in many textbooks and monographs that all fundamental equations of modern physics can be obtained from corresponding Lagrangians (Lanczos, 1986; Doughty, 1990; Burgess, 2002; Basdevant, 2007). Some basic equations of mathematical physics such as Bessel, Legendre, Laguerre, Hermite, Chebyshev, Jacobi, hypergeometric and confluent hypergeometric equations, and the Lane–Emden equation admit the Lagrangian description. Musielak (2008) suggested some methods to obtain standard and non-standard Lagrangians and identify classes of equations of motion that admit a Lagrangian description equation. Fractional calculus of variations dates back to year 1996 when Riewe successfully described dissipative systems from potentials represented by fractional derivatives (Riewe, 1996, 1997). The advantage of fractional calculus of variations in comparison with the standard one is its ability to describe dissipative classical and quantum dynamical systems where the standard calculus of variations cannot illustrate them well (El-Nabulsi, 2013). The fractional action-like variational approach is a subclass of the fractional calculus of variations was introduced in Nabulsi (2005a,b) and El-Nabulsi and Torres (2008). El-Nabulsi (2013) generalized the fractional action-like variational approach for the case of non-standard power-law Lagrangians which can be used to derive the generalized Lane–Emden-type equations. The fractional Chandrasekhar or Lane–Emden non-linear differential equation was also obtained in (El-Nabulsi, 2011a,b). The interested reader may refer to a number of references to get more information on fractional calculus of variations (Hartley and Lorenzo, 1998; Baleanu et al., 2010; El-Nabulsi, 2011b; Malinowska and Torres, 2012; Odzijewicz et al., 2012, 2013; Almeida et al., 2015; El-Nabulsi, 2016c).
There are several definitions of fractional integral and derivatives including Riemann–Liouville, Caputo, Weyl, Hadamard, Marchaud, Riesz, Grunwald–Letnikov, and Erdelyi–Kober (Miller and Ross, 1993; Samko et al., 1993; Hilfer, 2000). The most frequently used definition of fractional derivatives is of Riemann-Liouvile and Caputo. None of these definitions has satisfied the whole prerequisite required. There is no need of a function to be continuous at the origin and differentiable to have Riemann–Liouville fractional derivative. nevertheless, the derivative of a constant is not zero. It also has certain weaknesses to model real-world phenomena with fractional differential equations. Moreover, if an arbitrary function such as exponential and Mittag–Leffler functions, is zero at the origin, its fractional derivation has a singularity at the origin. Furthermore, the Riemann–Liouville method cannot incorporate the nonzero initial condition at lower limit. These disadvantages reduce the field of application of the Riemann–Liouville fractional derivative. The Caputo derivative is very useful when dealing with real-world problem because, it allows the utilization of initial and boundary conditions involving integer order derivatives, which have clear physical interpretations. in addition, the derivative of a constant is zero. In contrast to the Riemann Liouville fractional derivative, it is not necessary to define the fractional order initial conditions (Podlubny, 1999) when using Caputo’s definition. however, with the Caputo fractional derivative, the function needs to be differentiable which diminishes the field of utilization of it (Atangana and Secer, 2013). In this study, we use the Caputo fractional derivative .
A real function , is said to be in the space if there exists a real number such that , where , and it is said to be in the space if .
The Riemann–Liouville fractional integration of order
of a function
is defined as (Podlubny, 1999)
The fractional derivative of u(x), in the Caputo sense is defined as (Podlubny, 1999)
2.2 Properties of Chebyshev wavelets
Wavelets are a collection of functions created from dilation and translation of a single function
called the mother wavelet. If we continuously vary the dilation parameter r and the translation parameter s, we then obtain the following family of continuous wavelets (Daubechies, 1992):
For some very special choices of
and
, the family of functions
constitutes an orthonormal basis for the Hilbert space
. Chebyshev wavelets in turn are defined as:
In view of orthonormality of the Chebyshev wavelets, a function
may be expanded as
3 Chebyshev wavelet finite difference method
Clenshaw and Curtis (1960) suggested employing Chebyshev polynomials as a basis to approximate a function u as
Elbarbary and El-Kady (2003) obtained the derivatives of the function u at the points
as
Let us define
, as the corresponding Chebyshev-Gauss–Lobatto collocation points at the nth subinterval
such that,
A function u can be approximated in terms of Chebyshev wavelet basis functions as follows
From Eqs. (3.3)–(3.5), the derivatives of the function u at the points
, can be obtained as
4 Characterization of the proposed method
In this section, the CWFD method is used to solve the fractional Lane–Emden equations introduced in Eqs. (1.2) and (1.3). To do so, the interval
is divided into
subintervals
,
. It is also assumed shifted Chebyshev-Gauss–Lobatto points be the collocation points on the nth subinterval
which are defined as
is approximated using Eq. (3.7) and then collocate Eq. (1.2) at the collocation points
to obtain
Moreover, we rewrite
in the Caputo sense by virtue of Eq. (2.2) as
In view of the Clenshaw-Curtis quadarature formula (Davis and Rabinowitz, 1984), the first integral can be calculated as
Substitute Eqs. (4.4) and (4.6) into Eq. (4.1) to obtain
equations. Furthermore, replacing conditions in Eq. (1.3) with Eqs. (3.7) and/or (3.9) results in obtaining 2 more equations. Moreover, continuity condition on the approximate solution and its first derivative at the interface between subintervals should be imposed to have other
equations.
From the above procedures carried out, we will have a system for a total of algebraic equations, which can be solved for the . As a consequence, we get the solution of Eqs. (1.2) and (1.3) using Eqs. (3.7) and (3.8).
The convergence of the method has been shown in Kazemi Nasab et al. (2015).
5 Illustrative examples
In this section, fractional Lane–Emden problems of different types are solved to verify the applicability and accuracy of the proposed method in solving singular fractional Lane–Emden problems.
As a first example for illustration, consider the following nonlinear Lane–Emden type equation:
Wazwaz (2001) employed Adomian decomposition method to obtain a series solution as follows.
.
We apply the introduced method with M = 10, k = 5 for solving Eq. (5.1). In Table 1, we compare the y(x) values obtained by the present method and those reported in Wazwaz (2001) and Parand et al. (2010). The results are in well agreement with those obtained by Adomian decomposition method and more accurate than those acquired by the introduced method in Parand et al. (2010).
Consider the following nonlinear fractional spherical isothermal Lane–Emden type equation:
We used the technique introduced in Abdel-Salam and Nouh (2015) to obtain the exact solution of this problem when and as
We employ the CWFD method with different values of M and k for solving this problem. In Table 2, we compare the absolute errors of at different points. Fig. 1 shows the absolute errors in solutions obtained by the introduced method in this paper with and .
Consider the following nonlinear fractional Lane–Emden type equation:
Wazwaz (2001) employed Adomian decomposition method to obtain a series solution of (5.4) and (5.5) when and as follows
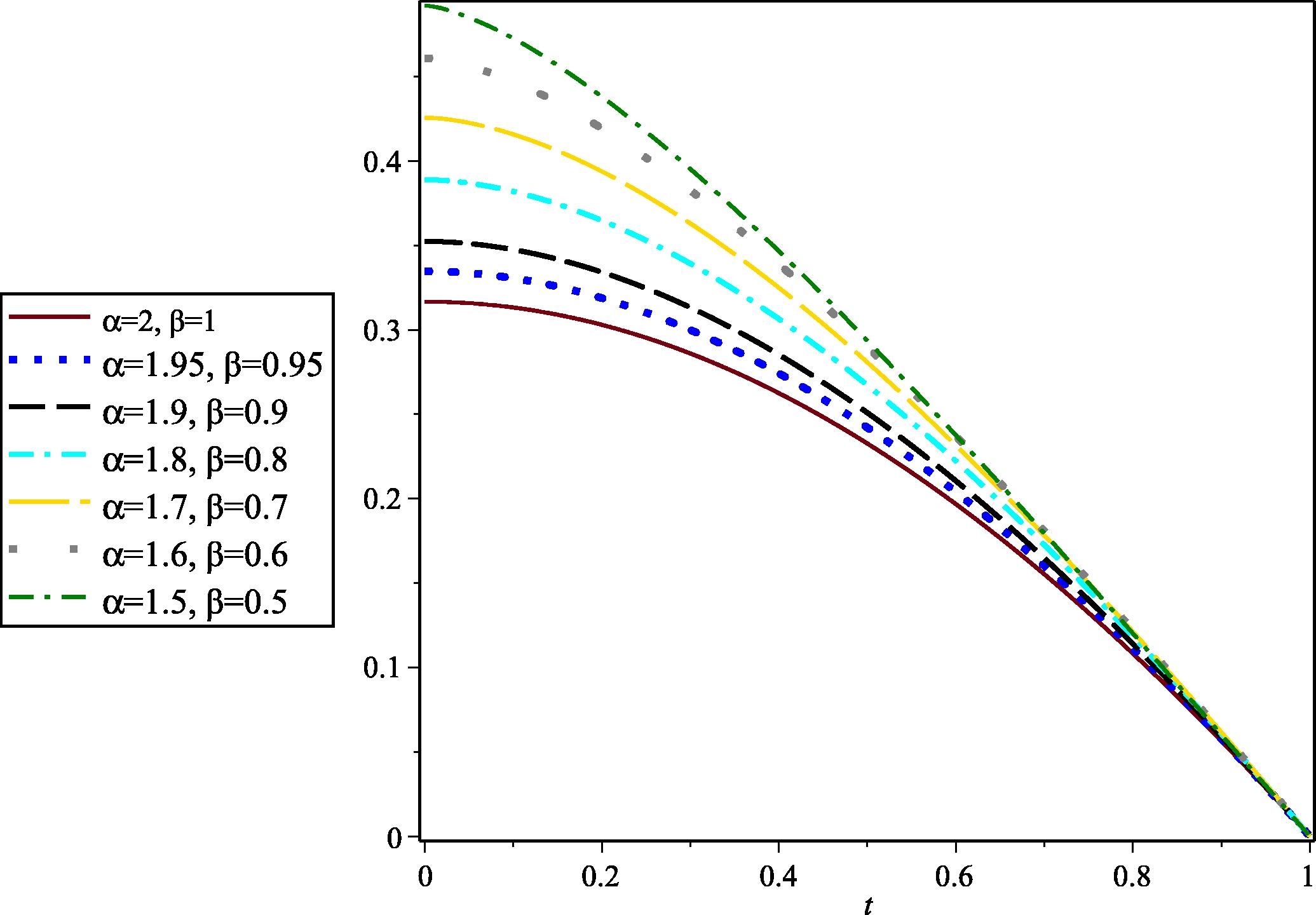
We apply the method introduced in Section 4 with and and solve this problem with different values of and . It can be seen from Fig. 2 that as and approach 2 and 1, respectively, the solution of the fractional differential equation approaches that of the integer-order differential equation.
Consider the following linear singular boundary value problem:
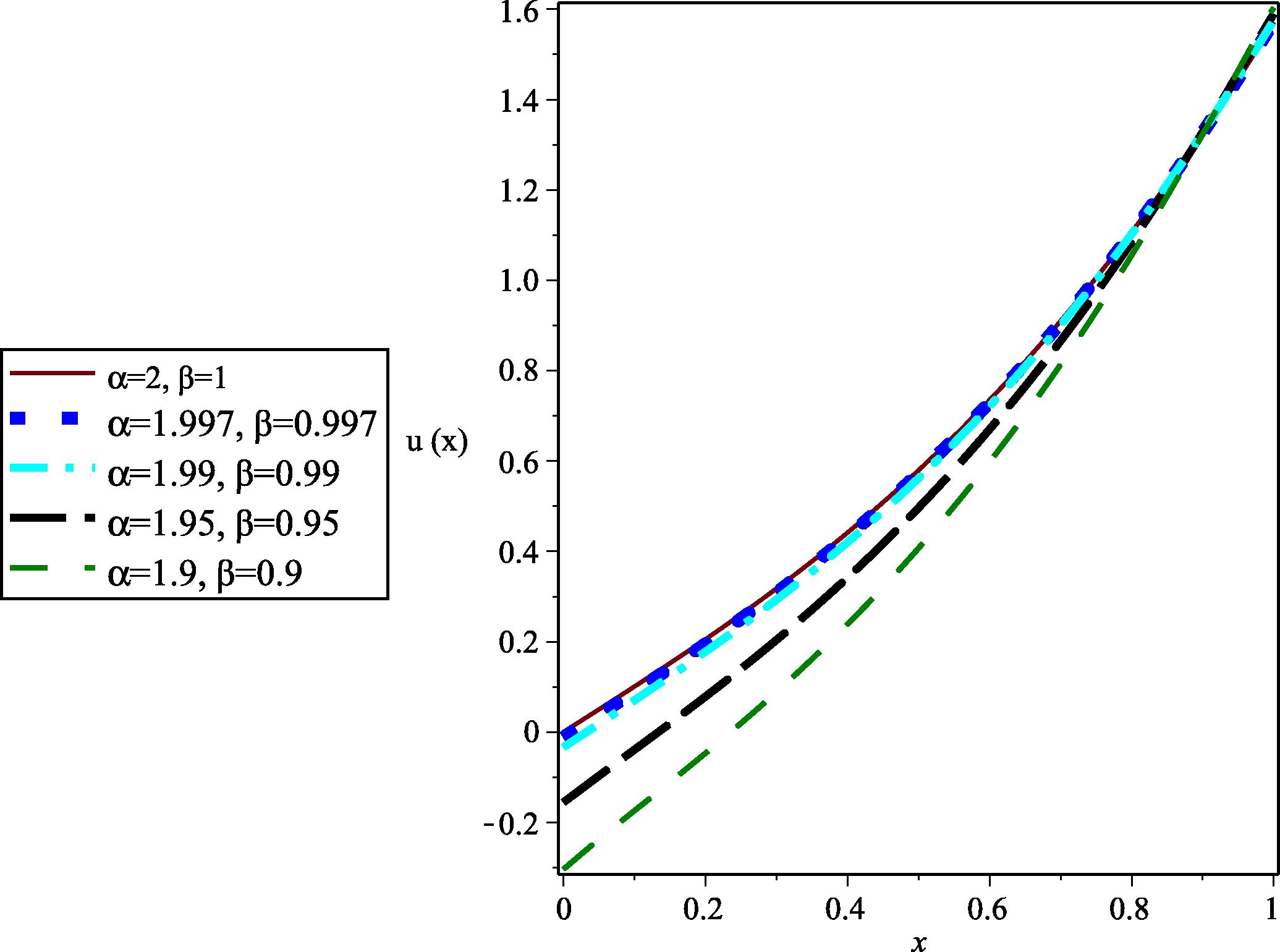
The exact solution of this example is given in (Zhou and Xu, 2016) as when and . We set and for this problem. In Table 3, we report the obtained values of for different values of and . It can be seen from Table 3, the closer the values of and are respectively to 2 and 1, the more accurate are the results. For further investigation, we plot the graph of for different values of and with and in Fig. 3.
Consider the following nonlinear fractional Lane–Emden type equation:
If and , the exact solution of this problem is (Zhou and Xu, 2016). In Fig. 4, the graph of for different values of and is plotted. Furthermore, Fig. 5 shows the absolute error between the approximate and exact solution when and .
Consider the following nonlinear fractional boundary value problem:
The exact solution of this problem as and is given as (Zhou and Xu, 2016) In Fig. 6, we plot the graph of for different values of and with .
Consider the following linear fractional Lane–Emden type equation:
There is no exact solution for this problem even for integer case. We solve this problem using CWFD with . In Table 4, the values of for different fractional values of and at different points are tabulated. We make a comparison between the results obtained by the CWFD method, The Laguerre wavelet (LW) method in Zhou and Xu (2016), and a numerical method based on the operational matrix of orthonormal Bernoulli polynomial (BP) in Mohsenyzadeh et al. (2015) for integer values of and in Table 5. It can be seen from Tables 4 and 5, as and are increasing closer to integer values, the results are increasing closer to the ones of integer values. Table 5 shows that our results are very close to the results reported in other two papers and indicates the applicability and accurateness of the proposed method. It can be clearly observed from Tables 4 and 5, as and approach 2 and 1, the solution of fractional differential equation approaches to that of the integer-order differential equation.
Consider the following nonlinear singular fractional two-point BVP:
The exact solution of this problem if and is given as in (Zhou and Xu, 2016). The graphs of for different values of and are plotted in Fig. 7.
| t | Present method | Error | Hermit function collocation method | Adomian decomposition method |
|---|---|---|---|---|
| 0.0 | ||||
| 0.1 | ||||
| 0.2 | ||||
| 0.5 | ||||
| 1.0 | ||||
| 1.5 | ||||
| 2.0 |
| x | Exact solution | ||
|---|---|---|---|
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 |
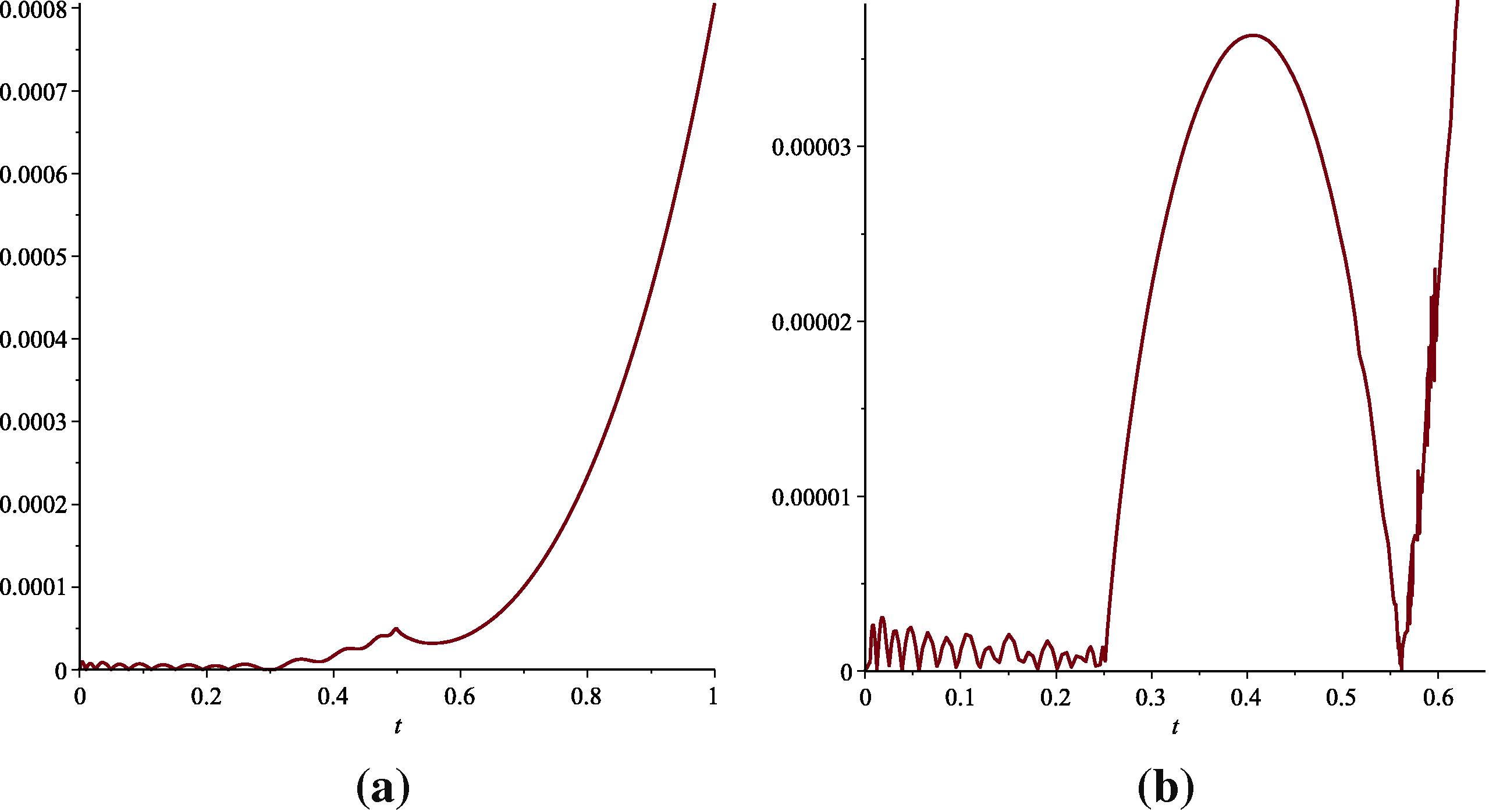
- The graph of absolute errors between approximate and exact solutions with
and
(Right)
and
for Example 5.2.
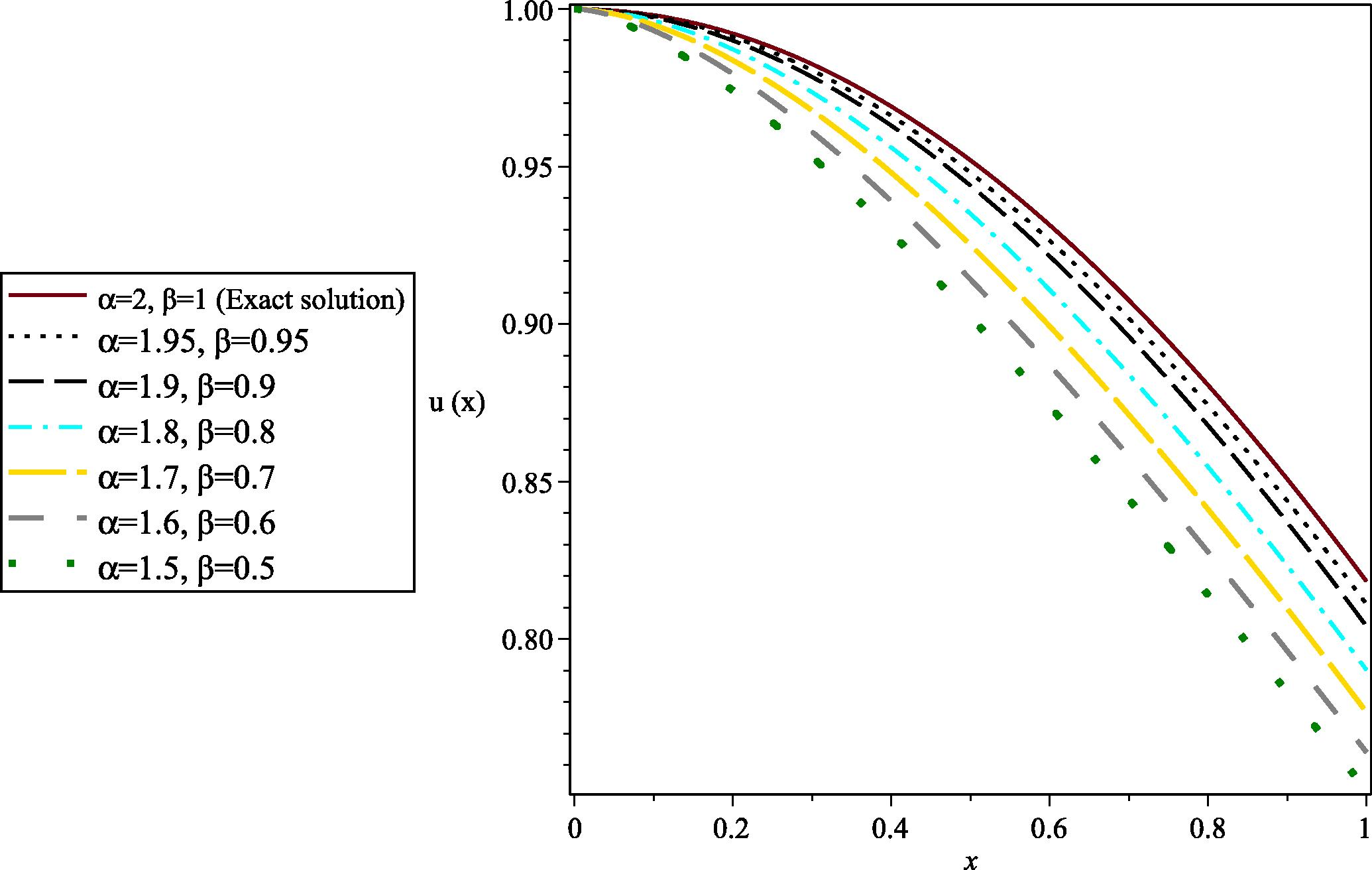
- Comparison of u(x) for
and different values of
and
for Example 5.3
| x | |||||
|---|---|---|---|---|---|
| 0.1 | |||||
| 0.3 | |||||
| 0.5 | |||||
| 0.7 | |||||
| 0.9 |
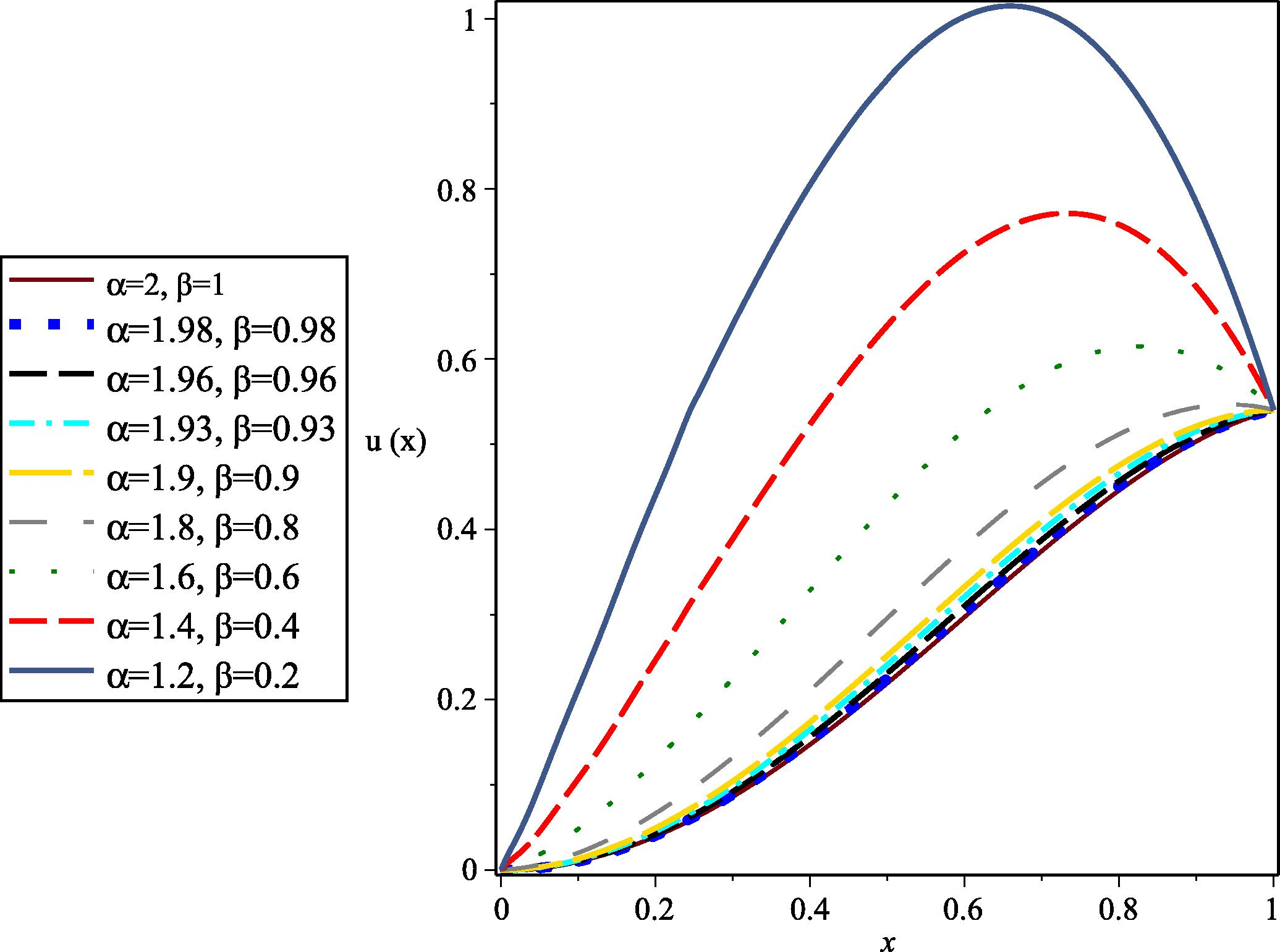
- The graph of u(x) for different values of
and
with
for Example 5.4.
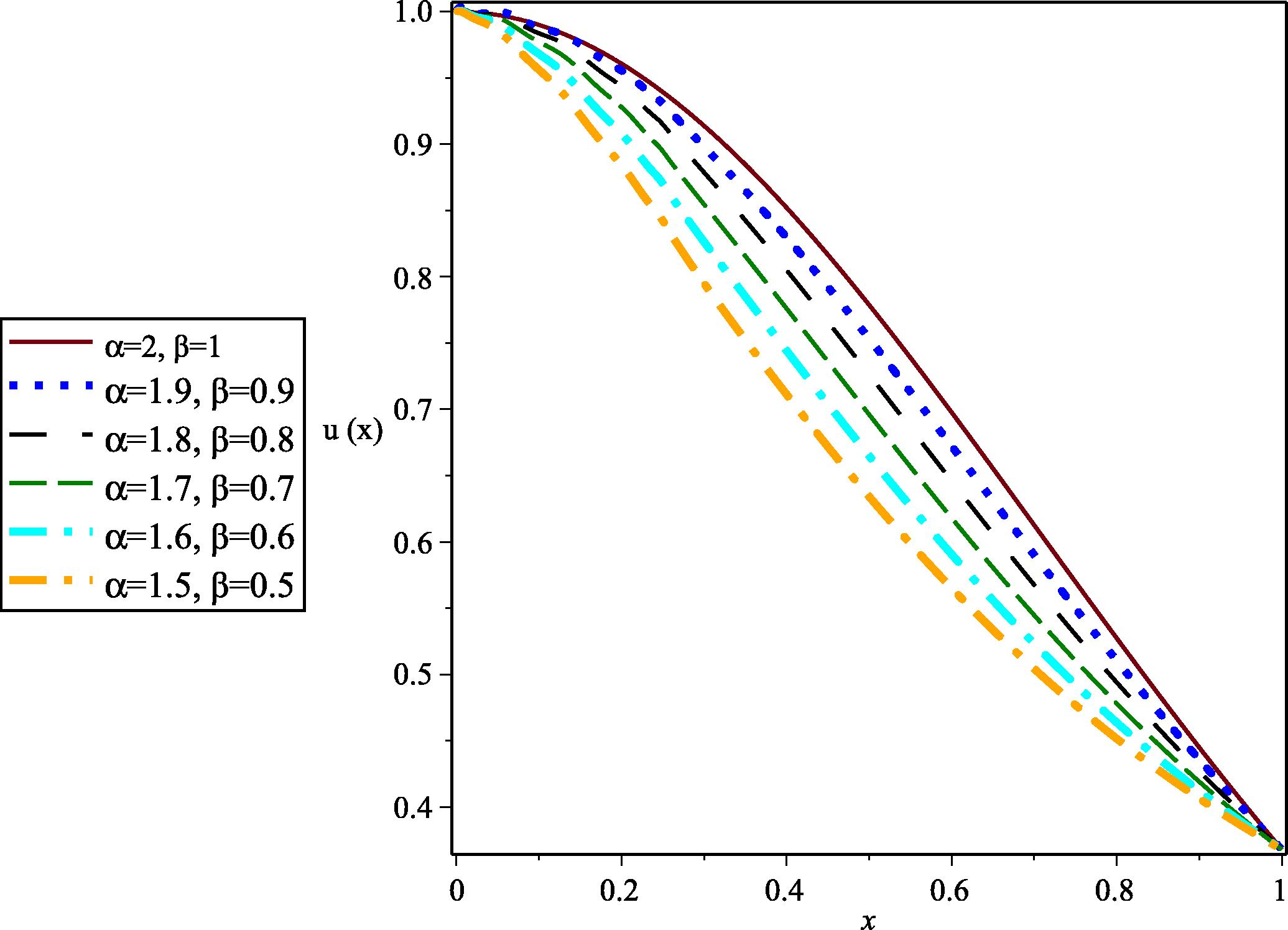
- The graph of u(x) for different values of
and
with
for Example 5.5.
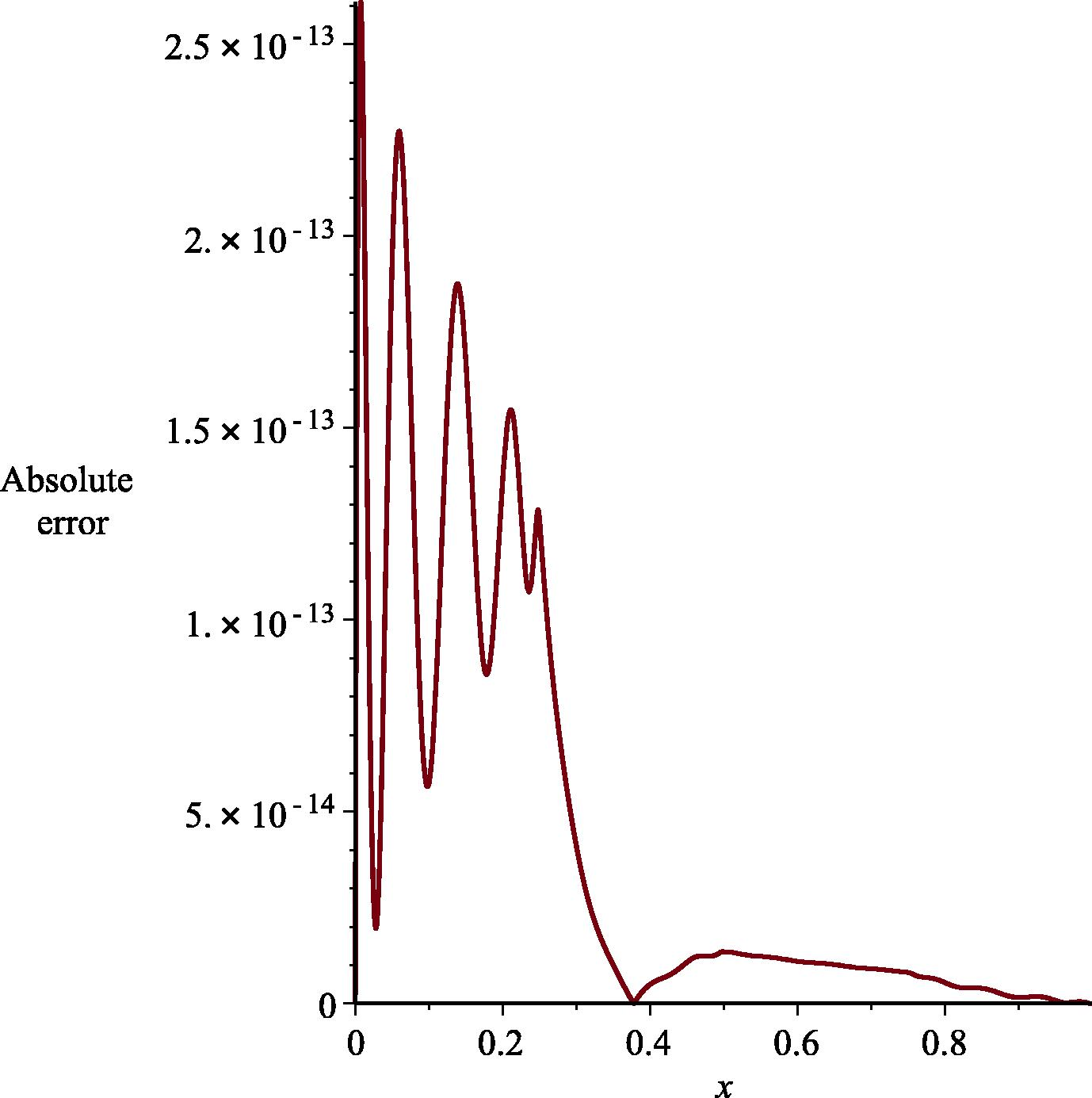
- Absolute error as
and
with
for Example 5.5.
- The graph of u(x) for different values of
and
with
for Example 5.6.
| x | |||||
|---|---|---|---|---|---|
| 0.1 | 0.765457385293227 | 0.777849130711797 | 0.790555364088865 | 0.803503300386760 | 0.816514521141764 |
| 0.2 | 0.776130801423652 | 0.786585663532280 | 0.797659339431068 | 0.809242556063937 | 0.821123173757560 |
| 0.3 | 0.789838168401597 | 0.798441923158554 | 0.807825369576831 | 0.817890936326706 | 0.828429359689670 |
| 0.4 | 0.806115080193247 | 0.812991206693056 | 0.820716305422740 | 0.829224626275748 | 0.838326176512752 |
| 0.5 | 0.824626305619186 | 0.829933285174916 | 0.836100384725762 | 0.843090763744000 | 0.850740215946676 |
| 0.6 | 0.845309532918059 | 0.849128944523233 | 0.853839766598646 | 0.859385533350940 | 0.865614149890049 |
| 0.7 | 0.867713969757805 | 0.870328122893672 | 0.873779197287922 | 0.878013361169784 | 0.882901208768500 |
| 0.8 | 0.891762974684848 | 0.893431592884813 | 0.895829358309583 | 0.898910454952620 | 0.902571377092311 |
| 0.9 | 0.917364124571176 | 0.918348799523956 | 0.919913436181026 | 0.922022206810561 | 0.924598283236026 |
| x | CWFD | LW | BP |
|---|---|---|---|
| 0.1 | 0.82970609243381 | 0.82970609243388 | 0.82970609243390 |
| 0.2 | 0.83337473359101 | 0.83337473359108 | 0.83337473359110 |
| 0.3 | 0.83948991395371 | 0.83948991395376 | 0.83948991395381 |
| 0.4 | 0.84805278499607 | 0.84805278499610 | 0.84805278499617 |
| 0.5 | 0.85906492716924 | 0.85906492716925 | 0.85906492716933 |
| 0.6 | 0.87252831995829 | 0.87252831995828 | 0.87252831995828 |
| 0.7 | 0.88844530562320 | 0.88844530562317 | 0.88844530562329 |
| 0.8 | 0.90681854806681 | 0.90681854806678 | 0.90681854806690 |
| 0.9 | 0.92765098836558 | 0.92765098836555 | 0.92765098836568 |
- The graph of u(x) for different values of
and
for Example 5.8.
6 Conclusion
The singular fractional Lane–Emden type equations as a generalized form of the standard ones subject to the different conditions have been considered. The Chebyshev wavelets finite difference method has been successfully applied to obtain numerical solutions of fractional Lane–Emden type equations with linear and nonlinear terms arising in mathematical physics and astrophysics. It can be clearly seen from figures and tables, as and approach the integer values, the solution of fractional differential equation approaches to that of the integer-order differential equation. From obtained results, it can be observed that the proposed method is effective and accurate for solving such type of singular fractional equations. It has also been shown that the accuracy can be enhanced either by expanding the number of subintervals or by expanding the quantity of collocation points in subintervals.
References
- Approximate Solution to the Fractional Second Type Lane–Emden Eq. 2015 2015arXiv151209116A
- Solving system of fractional differential equations by homotopy perturbation method. Phys. Lett. A. 2008;372(4):451-459.
- [Google Scholar]
- Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl.. 2002;272(1):368-379.
- [Google Scholar]
- Numerical solutions of fractional differential equations of Lane–Emden type by an accurate technique. Adv. Differ. Eq.. 2015;220:1-12.
- [Google Scholar]
- Computational Methods in the Fractional Calculus of Variations. London: Imperial College Press; 2015.
- A note on fractional order derivatives and table of fractional derivatives of some special functions. In: Abstract and Applied Analysis. Vol vol. 2013. Hindawi Publishing Corporation; 2013.
- [Google Scholar]
- Numerical computation method in solving integral equations by using Chebyshev wavelet operational matrix of integration. Appl. Math. Comput.. 2007;188:1016-1022.
- [Google Scholar]
- New Trends in Nanotechnology and Fractional Calculus Applications. New York, NY, USA: Springer; 2010. pp. xii+-531
- Variational Principles in Physics. New York: Springer; 2007.
- A space-time Legendre spectral tau method for the two-sided space-time Caputo fractional diffusion-wave equation. Numer. Algorithms. 2016;71(1):151-180.
- [Google Scholar]
- Bliss, G.A., 1946. Lectures on the Calculus of Variations.
- Classical Covariant Fields. Cambridge: Cambridge University Press; 2002.
- Computable extensions of generalized fractional kinetic equations in astrophysics. Res. Astron. Astrophys.. 2010;10(1):22.
- [Google Scholar]
- A method for numerical integration on an automatic computer. Numerische Mathematik. 1960;2:197-205.
- [Google Scholar]
- Ten Lectures on Wavelets.CBMS-NSF Regional Conference Series in Applied Mathematics. Vol vol. 61. Philadelphia, Pa, USA: SIAM; 1992.
- Dávila, J., Dupaigne, L., Wei, J., 2014. Trans. On the fractional Lane–Emden equation, to appear in Trans. Am. Math.
- Solving a multi-order fractional differential equation using Adomian decomposition. Appl. Math. Comput.. 2007;189:541-548.
- [Google Scholar]
- Methods of numerical integrationComputer Science and Applied Mathematics (2nd ed.). Orlando, Florida: Academic Press; 1984. pp. 1–2
- The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operator of Caputo Type. -Verlag Berlin Heidelberg: Springer; 2010.
- Lagrangian Interaction. New York: Addison-Wesley; 1990.
- Construction of analytical solutions to fractional differential equations using homotopy analysis method. IAENG Int. J. Appl. Math.. 2010;40(2):43-51.
- [Google Scholar]
- Chebyshev finite difference approximation for the boundary value problems. Appl. Math. Comput.. 2003;139:513-523.
- [Google Scholar]
- Applications of Fractional Calculus in Physics. 1–85: World Scientific; 2000.
- EL Nabulsi, R.A., 2005a. A fractional approach to non-conservative Lagrangian dynamical systems.
- EL Nabulsi, R.A., 2005. A fractional action-like variational approach of some classical, quantum and geometrical dynamics.
- The fractional white dwarf hydrodynamical nonlinear differential equation and emergence of quark stars. Appl. Math. Comput.. 2011;218(6):2837-2849.
- [Google Scholar]
- Universal fractional Euler-Lagrange equation from a generalized fractional derivate operator. Cent. Eur. J. Phys.. 2011;9(1):250-256.
- [Google Scholar]
- Gravitons in fractional action cosmology. Int. J. Theor. Phys.. 2012;51(12):3978-3992.
- [Google Scholar]
- A Cosmology governed by a fractional differential equation and the generalized kilbas-saigo-mittag-leffler function. Int. J. Theor. Phys.. 2016;55(2):625-635.
- [Google Scholar]
- Implications of the Ornstein-Uhlenbeck-like fractional differential equation in cosmology. Rev. Mex. Física. 2016;62(3):240-250.
- [Google Scholar]
- Fractional variational approach with non-standard power-law degenerate Lagrangians and a generalized derivative operator. Tbilisi Math. J.. 2016;9(1):279-293.
- [Google Scholar]
- Hartley, T.T., Lorenzo, C.F., 1998. A solution to the fundamental linear fractional order differential equation.
- Ibrahim RW., 2012. Existence of nonlinear Lane–Emden equation of fractional order, Miskolc Mathematical Notes. 13(1), 39–52
- Jacobs, B.A. and Harley, C., 2014, April. Two hybrid methods for solving two-dimensional linear time-fractional partial differential equations. In Abstract and Applied Analysis (Vol. 2014). Hindawi Publishing Corporation.
- Application of Legendre wavelets for solving fractional differential equations. Comput. Math. Appl.. 2011;62(3):1038-1045.
- [Google Scholar]
- Haar wavelet approximate solutions for the generalized Lane–Emden equations arising in astrophysics. Comput. Phys. Commun.. 2013;184:2169-2177.
- [Google Scholar]
- Chebyshev wavelet finite difference method: a new approach for solving initial and boundary value problems of fractional order. Abstr. Appl. Anal. 2013 [Article ID: 916456]
- [Google Scholar]
- A numerical approach for solving singular nonlinear Lane–Emden type equations arising in astrophysics. Astronomy. 2015;34:178-186.
- [Google Scholar]
- Kilbas, A.A., Srivastava, H.M., Trujillo, J.J., 2006. Theory and Applications of Fractional Differential Equations, 1st ed. Math Studies, 204, 2006, Elsevier (North-Holland), Amsterdam.
- The Variational Principles of Mechanics. New York: Dover; 1986.
- Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct.. 2010;88(1):1-17.
- [Google Scholar]
- Solving a nonlinear fractional differential equation using Cheby- shev wavelets. Commun. Nonlinear Sci. Numer. Simul.. 2010;15:2284-2292.
- [Google Scholar]
- Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput. Math. Appl.. 2011;62(3):1046-1054.
- [Google Scholar]
- Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput.. 2010;216(8):2276-2285.
- [Google Scholar]
- Mainardi, F., 2012. Fractional Calculus: Some Basic Problems in Continuum and Statistical Mechanics. arXiv preprint arXiv:1201.0863.
- Introduction to the fractional calculus of variations. London: Imperial College Press; 2012. (pp. xvi+-275)
- Marasi, H.R., Sharifi, N., Piri, H., 2015. Modified differential transform method for singular LaneEmden equations in integer and fractional ordert. TWMS J. App. Eng. Math. 5(1), 124–131.
- Miller, K.S. and Ross, B., 1993. An introduction to the fractional calculus and fractional differential equations.
- Misiti, M., Misiti, Y., Oppenheim, G., Poggi, J.-M., 2000. Wavelet toolbox, the MathWorks, Inc., Natick, MA.
- A numerical approach for the solution of a class of singular boundary value problems arising in physiology. Adv. Differ. Equ.. 2015;1:1-10.
- [Google Scholar]
- Numerical approach to differential equations of fractional order. J. Comput. Appl. Math. 2007:96-110.
- [Google Scholar]
- Approximate implicit solution of a Lane–Emden equation. New Astronomy. 2006;11(7):520-526.
- [Google Scholar]
- Musielak, Z.E., 2008. Standard and non-standard Lagrangians for dissipative dynamical systems with variable coefficients. Journal of Physics A: Mathematical and Theoretical, 41(5), p.055205.
- Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonlinear Sci. Numer. Simul.. 2006;7:271-279.
- [Google Scholar]
- Generalized differential transform method: application to differential equations of fractional order. Appl. Math. Comput.. 2008;197(2):467-477.
- [Google Scholar]
- Generalized fractional calculus with applications to the calculus of variations. Comput. Math. Appl.. 2012;64(10):3351-3366.
- [Google Scholar]
- Fractional calculus of variations of several independent variables. Eur. Phys. J. Spec. Top.. 2013;222(8):1813-1826.
- [Google Scholar]
- Solution of Lane–Emden type equations using Chebyshev wavelet operational matrix of integration. J. Adv. Res. Sci. Comput.. 2012;4(1):1-12.
- [Google Scholar]
- An approximation algorithm for the solution of the nonlinear Lane–Emden type equations arising in astrophysics using Hermite functions collocation method. Comput. Phys. Commun.. 2010;181:1096-1108.
- [Google Scholar]
- An Introduction to Fractional Derivatives. In: Fractional Differential Equations. In: Some Methods of Their Solution and Some of Their Applications. San Diego: Academic Press; 1999.
- [Google Scholar]
- Nonconservative lagrangian and hamiltonian mechanics. Phys. Rev. E. 1996;53(2):1890-1899.
- [Google Scholar]
- Fractional Integrals and De riv a tives; The ory and Ap pli ca tions. London: Gordon and Breach; 1993.
- Advanced generalized fractional kinetic equation in astrophysics. Prog. Fract. Differ. Appl.. 2015;1(1):65-71.
- [Google Scholar]
- Stanislavsky, A.A., 2010. Astrophysical applications of fractional calculus. In: Proceedings of the Third UN/ESA/NASA Workshop on the International Heliophysical Year 2007 and Basic Space Science, Springer, Berlin Heidelberg, pp. 63–78
- A new algorithm for solving differential equations of Lane–Emden type. Appl. Math. Comput.. 2001;118:287-310.
- [Google Scholar]
- Weinstock, R., 1974. Calculus of variations: with applications to physics and engineering. Courier Corporation.
- Fractional variational iteration method and its application. Phys. Lett. A. 2010;374:2506-2509.
- [Google Scholar]
- Ultraspherical wavelets method for solving Lane–Emden type equations. Rom. J. Phys.. 2015;60(9)
- [Google Scholar]
- Solving a nonlinear fractional differential equation using Chebyshev wavelets. Commun. Nonlinear Sci. Numer. Simul.. 2010;15(9):2284-2292.
- [Google Scholar]
- Finite difference method for fractional partial differential equation. Appl. Math. Comput.. 2009;215:524-529.
- [Google Scholar]
- Numerical solutions for the linear and nonlinear singular boundary value problems using Laguerre wavelets. Adv. Differ. Equ.. 2016;17
- [Google Scholar]







